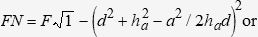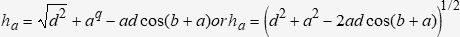In order to determine forces acting upon an articular joint during hand rehabilitation, a dynamic splint was built and connected to a dynamometer (capable of measuring forces in the range 0 – 600 gf). Through trigonometric calculation, the authors measured the flexing force in the proximal interphalangeal joint of the middle finger at 30°, 45°, 60°, and 90° of flexion. Measurements were obtained in a population of 40 voluntary adults, 20 females and 20 males, This flexing force was correlated with age, sex, and anthropometric measures.
RESULTSForce in the flexing tendon is maximal at the start of flexion, and decreases as the angle of joint flexion increases. A relationship was observed between finger length and the magnitude of the force exerted on the tendon: the longer the finger, the greater the force exherted upon the tendon. Force is greater at all the measured angles, (except 30°) in males and in individuals of higher stature, and bigger arm span.
CONCLUSIONSThe flexing force can be effectively measured at all flexing angles, that it correlates with a number of different anthropometric parameters, and that such data are likely to open the way for future studies.
Em virtude do desconhecimento relativo às forças que atuam em uma articulação durante o processo de reabilitação da mão, foi confeccionada uma órtese dinâmica que, acoplada a um dinamòmetro, mediu, através de cálculos trigonométricos, a força (entre 0 a 600gf), flexora na articulação interfalângica proximal do terceiro dedo, a 30°, 45°, 60° e 90° de flexão. Estas medidas foram obtidas, em uma população de 40 adultos voluntários, 20 do sexo feminino e 20 do masculino, e confrontadas com idade, sexo e medidas antropométricas como estatura, envergadura e comprimento do dedo.
RESULTADOSOs resultados do estudo demonstraram que o tendão flexor é submetido à máxima força no início da flexão e que a força no tendão flexor diminui conforme aumenta o grau de amplitude articular. Observou uma relação entre o comprimento do dedo e a magnitude da força exercida no tendão durante a flexão do dedo, sendo que nos dedos mais compridos os tendões são submetidos a forças maiores. Quando comparou a estatura e envergadura com a magnitude da força aplicada no tendão flexor, observou uma relação positiva em todos os graus de flexão estudados, exceto a 30°. O sexo masculino apresentou maior força em todos os graus de amplitude articular.
CONCLUSÕESConclui que é possível medir a força de flexão transmitida pelos tendões flexores através de uma órtese acoplada a um dinamômetro, que esta força é maior nos indivíduos do sexo masculino, com dedos mais longos, de maior altura e envergadura e que tais dados permitirão o desenvolvimento de futuros trabalhos no campo da reabilitação da mão, auxiliando pacientes portadores de lesões de tendões, retração cicatricial, deformidades e rigidez articular.
Connected to one or more parts of the body, splints help to improve function by providing support to joints, bones, and soft tissues. As a result, there is improved limb alignment and a more adequate functional position may be arrived at.
The “dynamic device” used in splints, whether pulled by an elastic band or by a spring, can be made of several materials and presents several physical and mechanical properties, including angle of adjustment, torque, pressure, and friction. It is extremely important that those engaged in the rehabilitation process, such as occupational therapists, know and apply knowledge of these properties1, because improper use of splints may be inefficient, or cause injuries.2 Excessive force, torque, or pressure may lead to inflammation, deformity, and even injury of the adjoining tissues,3 while low intensity forces may fail to foster the patient's expected recovery.4 A thorough understanding of the vascular distribution to the hand is also essential.5
When prescribing the application of an external force—ideally controlled and measurable—caution and accuracy are essential, i.e. the necessary torque and the time of application must be calculated, lest ischemia, pain, or other possible injuries ensue. Several authors have discussed how important it is to define the intensity of the force to be applied when using splints,6,7 a point which still remains to be properly established.
We devised a dynamic splint connected to a dynamometer which allows us to measure the force applied by flexor tendons (flexing force of the finger), intended for use in the rehabilitation of several injuries of the hand. By means of trigonometric calculations, measurements were taken, using as sample a population of voluntary adults.
We also compared data on the magnitude of the flexing force with anthropometric measures such as stature, arm span, and finger length. This dynamic splint, connected to a dynamometer, which allows the application and measurement of known forces, will certainly aid occupational therapists as well as create parameters for future research.
MATERIALS AND METHODSOur sample consisted of 40 volunteers, 20 of each gender, aged 25 to 55, and without any pathology or sequela affecting the upper limb. Collected anthropometric data included middle finger length, stature, and arm span.
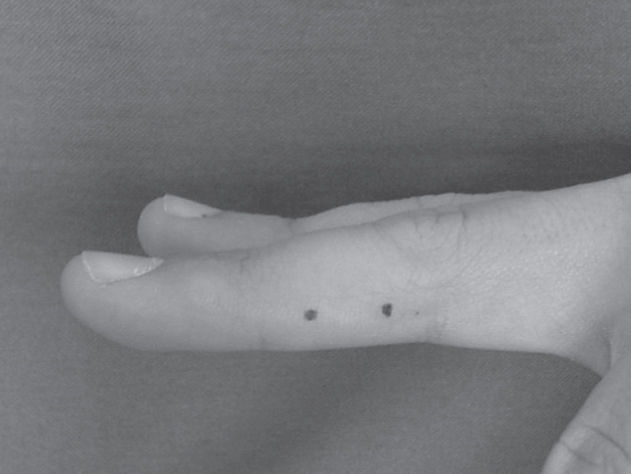
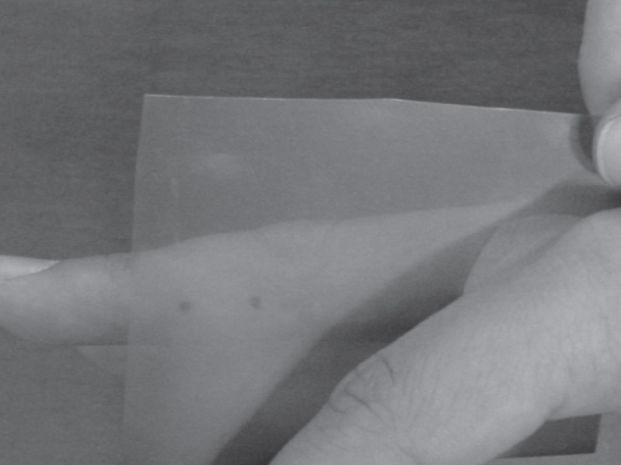
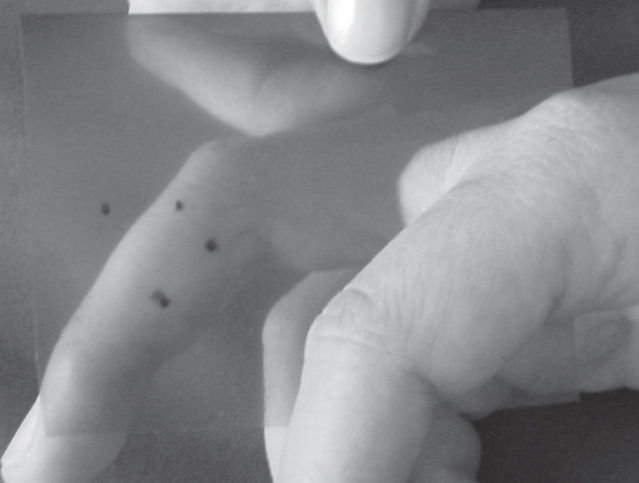
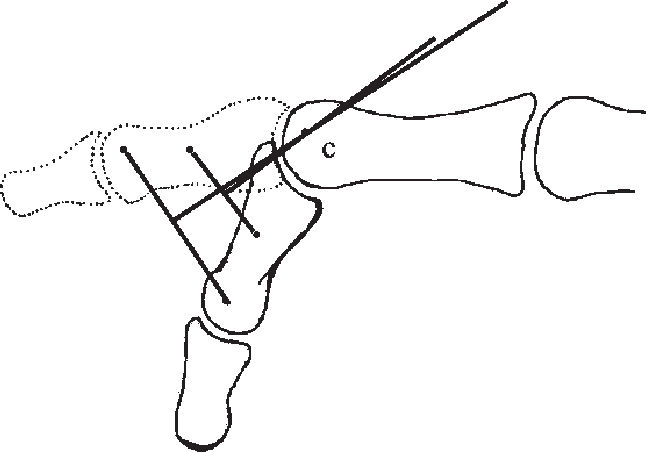
Location of the Axis of Rotation of the Proximal Interphalangeal JointWe followed a method based on Reuleaux8 to determine the axis of rotation of the proximal interphalangeal joint (Figures 1 to 4). It is based on the geometric properties of the mediatrix: two points are marked along the direction of the middle phalanx. By printing these points at 2 different flexion angles of the proximal interphalangeal joint while keeping fixed the proximal phalanx, the chords of the 2 concentric arcs of movement of the middle phalanx were determined; the intersection of the respective mediatrices determines the approximate center of rotation (Fig 4).
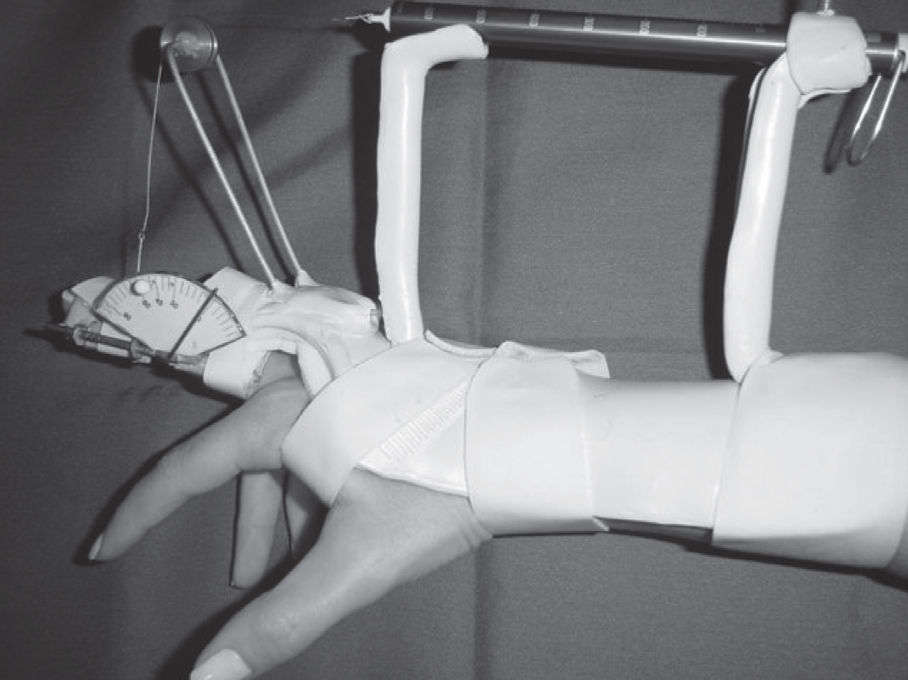
Method of Making the Dynamic Splint Connected to a DynamometerThe material used to make the dynamic splint was a thermoplastic of low melting temperature. Figure 5 shows the complete structure. Only the joint of the wrist and the metacarpophalangeal of the middle finger, both in neutral position, were immobilized. Also made with the same thermoplastic material were 2 pillars whose bases had been embedded in the splint and served to connect a PesolaÒdynamometer. An aluminum bar and a polished metal pulley were made at the same height as the pillars. An inelastic steel wire was used, which was fixed at one end at the mobile portion of the dynamometer; this wire was passed around the pulley and fitted through a hook into the goniometer placed at the proximal interphalangeal joint of the middle finger. The direction of the wire pointed to the middle third of the middle phalanx at a 90o angle with the proximal interphalangeal joint in extension.4
The splint was fastened into place by Velcro® straps on the forearm and on the proximal interphalangeal joint in order to be properly positioned throughout data collection.
Dynamometer.A Pesola® dynamometer with a 0- to 600-gram force scale and a 5-gram resolution was used. A spring is displaced as its inner portion is pulled. When it is blocked/released, the spring immediately returns to 0.
Goniometer. The goniometer used, made of aluminum, was validated. It was connected to the finger by means of Velcro straps. Through the small holes made on the goniometer scale it was possible to block it when the desired range of motion was reached, that is to say, the goniometer prevented the patient from reaching a range of motion greater than was desired.
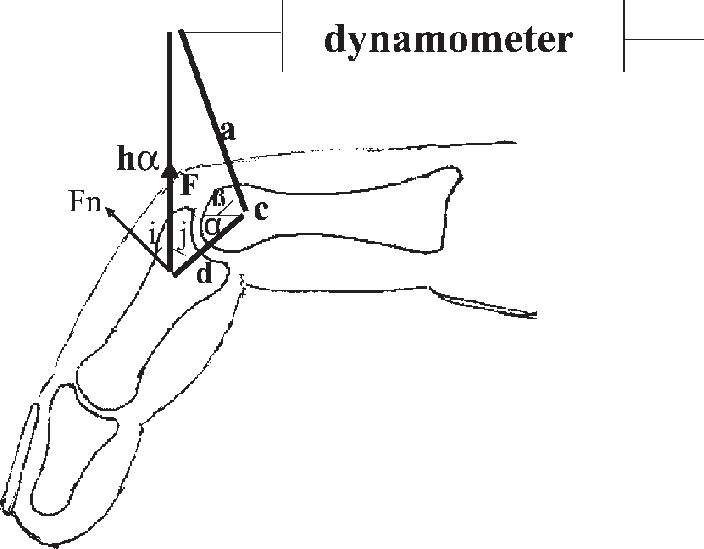
Data CollectionAfter establishing the axis of rotation of the proximal interphalangeal joint and placing the splint in proper position, we requested that the volunteer perform the flexion of the proximal interphalangeal joint with the splint on. This was repeated consecutively 3 times; and the average of the values recorded on the dynamometer scale was calculated. The displacement values registered on the dynamometer spring were collected, the proximal interphalangeal joint being at 30, 45, 60 and 90 degrees of flexion. We measured the distance between the center of the interphalangeal joint and the point where the wire was applied (d), and the distance of the aluminum bar (a). We then calculated the value of the2 angle by applying the formula cos b = d/a, since a right-angle triangle is formed. The distance between the point where the wire is applied and the pulley (h) was calculated at the degrees of the joint flexion studied.
Determination of the Flexing Force MagnitudeIn order to determine the magnitude of the flexing force, the following trigonometric calculation was used. Figure 6 demonstrates the system of forces found when the flexion of the proximal interphalangeal joint occurs. In this particular case, the system of forces is applied on the proximal interphalangeal joint at 45° and establishes the force Fn according to length “h” at the 2 different degrees of joint flexion (a and b) angle. This force F is read on the dynamometer scale and the force Fn (resulting rotational force) is calculated by the formula Fn = Fcos(i), F being the only known variable, since it is read on the dynamometer scale.
To calculate cos(i), we used the formula cos2(i) + sin2(i) = 1 so that cos(i) = √1 – sin2(i) or cos(i) = (1 – sin2i)1/2 (Figure 6).
The value of sin(i) equals cos(j) because j + i = 900; to calculate such values we used the cosine law:
a2 = d2 + ha2 + 2hadcos(j), where, by isolating cos(j) we get:
cos(j) = sin(i)=d2+ha2-a22had
Therefore, if we consider a certain angle of the proximal interphalangeal joint (a) we have:
Fn = Fcos(i) or
Fn = F(1 - (d2 + ha2 - a2)/2had)2)½
The values of F, d, a, are known, but not ha, which is also calculated through the cosine law. We have:
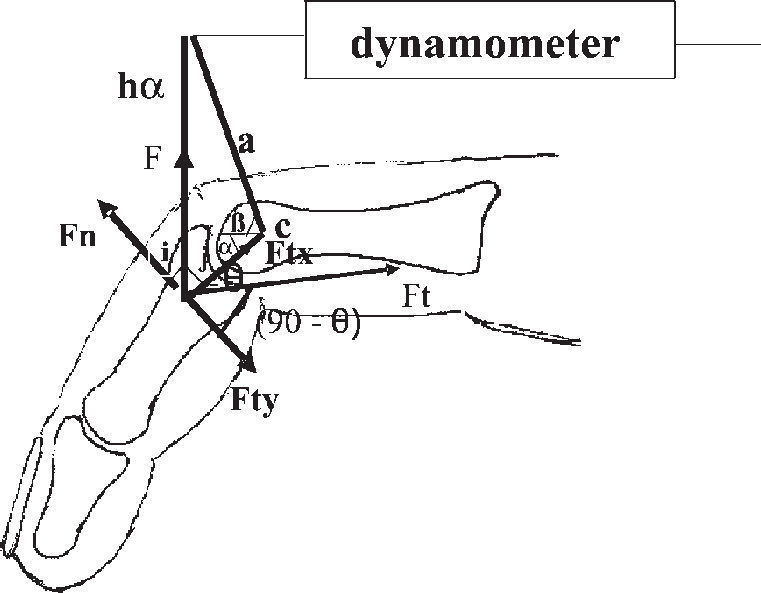
After determining Fn, we can calculate the force exerted in the flexor tendons, or Ft. This force (Ft) has the same direction as that of the flexor tendons. The flexing force (Ft) exerted through the tendon inserted in the middle phalanx can be decomposed into Fty and Ftx (Figure 7), Fty being equal in magnitude but in opposite direction to Fn, thus maintaining the finger static and in balance.
We assumed that the force Fn and the flexor force Fty are applied at the same point, the middle third of the middle phalanx. This is because the point of application of the wire is located in the middle third of the middle phalanx, and the location of the insertion of the superficial flexor tendon is a few millimeters proximal to the neck of the middle phalanx.9 Additionally, we believe that its insertion occurs in a triangular shape10 and thus, not at one point, but over an area.
To calculate the flexing force exerted (Ft), we used the formula Fty = Ft(cos(90 –θ)), θ being the angle of insertion of the superficial flexor tendon in the middle phalanx.
Based on anatomical data and images from a magnetic resonance scanner, we assumed that the angle θ ranged from 25° to 45°, according to the position of the finger.
Statistical AnalysisComparisons among groups of quantitative data were made using the Student t test, and the function of the angle of the joint and the force calculated at the tendon was determined by polynomial regression.
In all the cases, a significance level of 5% (a = 0.01) was adopted. The significant results were marked with an asterisk.
RESULTSThe data relative to arm span, stature, finger length, age, lateral dominance, and gender are presented in Table 1. Predictably, the male volunteers were taller, had longer arm spans and middle fingers in comparison to the female volunteers.
Data distribution among the 40 volunteers included in the study
| Female (n = 20) | |||||
|---|---|---|---|---|---|
| attribute | Age | Stature (m) | Arm span (m) | Finger length(cm) | Dominance |
| mean | 37.0 | 1.63 | 1.63 | 8.58 | Right: 17 |
| std dev | 12.1 | 0.09 | 0.10 | 0.43 | Left: 3 |
| Male (n=20) | |||||
| attribute | Age | Stature (m) | Arm span (m) | Finger length(cm) | Dominance |
| mean | 36.7 | 1.74 | 1.77 | 9.52 | Right: 18 |
| std dev | 8.8 | 0.08 | 0.08 | 0.53 | Left: 2 |
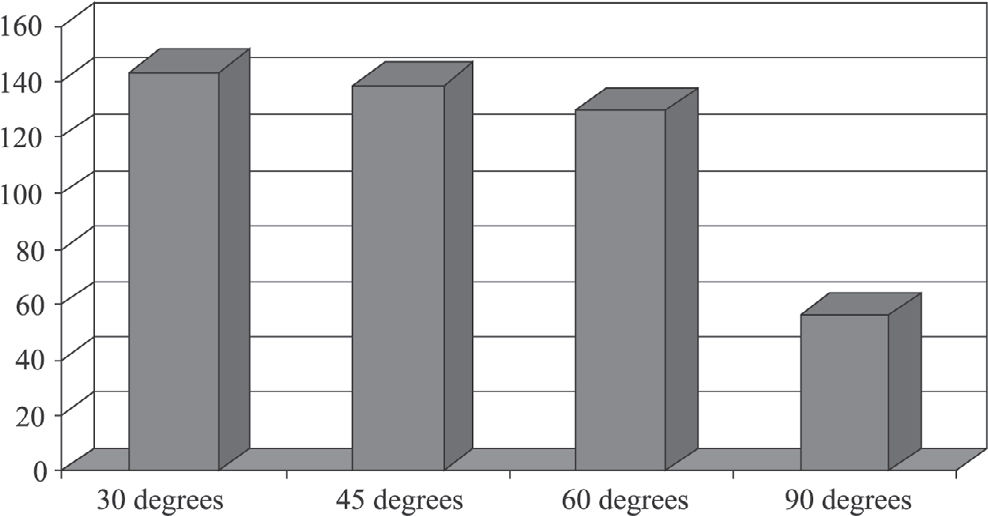
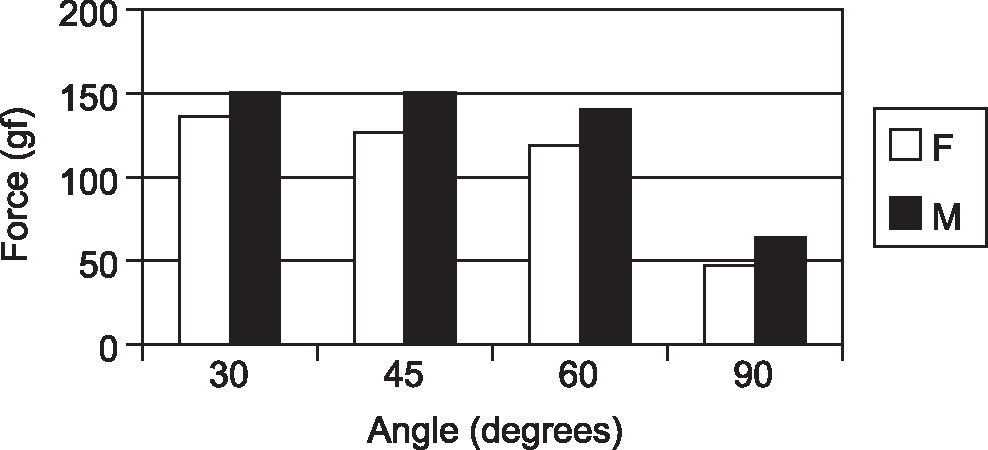
Figure 8 shows that force measured in the flexor tendons of the third finger of the dominant hand decreases progressively as the flexion angle increases. Figure 9 compares these same forces at the various angles of the joint range, between genders, and shows that males consistently generate circa 10% more force than females. Table 2 presents the significance attached to the correlation between the force exerted at 30°, 45°, 60°, and 90° and the various anthropometric parameters of this population. It can be seen that age is not an independent determinant of force at any of the studied angles. Stature and arm span significantly correlated with force at all angles, except 30°, while finger length was found to be a highly significant determinant of exerted force at all angles.
By using dynamic splints, certain joints are immobilized and others are mobilized under the control of elastic traction. However, such traction exerts forces that are often unknown and applied in an inconsistent way. It is difficult to measure the force magnitude applied by an elastic band due to great variability during its deformation.7 The lack of control over the force magnitude exerted may produce bad results related to insufficient or excessive force, the latter of which may even cause iatrogenic tissular injuries as a consequence of exaggerated force.11
It is essential that all the concepts related to the mechanics of movement be well known so as to avoid exerting too much or too little force on joints. Therefore, new devices or splints must be devised, which will allow the measurement of the force applied during rehabilitation.
The development of a splint connected to a dynamometer makes it possible to calculate the magnitude of torque during joint movement. This calculation is obtained by the measurement of the distance between the axis of rotation and the support of traction, and by the force (measured on the dynamometer) necessary to generate movement at the various possible joint angles.
Obtaining these measures can be considered an advance, which may encourage further research, since there are no references concerning the force magnitude needed to correct a deformity or rehabilitate an injury such as that, for instance, of the flexor tendons.11
Strickland and Glocovac13 corroborated the efficiency of early movement in the rehabilitation of tenorrhaphies. The use of a splint connected to a dynamometer, as proposed in this study, allows early movement to be totally monitored and controlled, a new treatment strategy which permits, for instance, the performance of tendinous glide with full knowledge of the force exerted by the tendon and tolerated by the suture. We are aware that the current tendency is towards tendon sutures that are mechanically more resistant and capable of withstanding rehabilitation with early active movement.14 We are also aware that mechanical stress in the suture area promotes intrinsic healing of the tendon15,16 and that more resistant sutures allow active and controlled movement.17,18 However, we believe that the ideal control of this movement is based on the measurement of the force exerted by the affected motor system (flexor or extensor). The splint developed in this study makes it possible to promote active and controlled movement, by applying a force of a known and progressively greater magnitude.
In the occupational therapist's daily practice, dynamic splints and traction are used even though the ideal magnitude of tension is not determined, and there is no consensus as to the magnitude of tension to be applied by elastic traction.19
Some authors2,20 recommend that the value of traction should vary between 100 and 300 grams of force, applied for a maximum of 8 hours. We think this is too large a range of variation, and that the highest value may be related to iatrogenic injuries by pressure as time of use elapses, and the lowest to inefficient traction.11 Others report what they consider to be the ideal application force for each clinical situation, but there is a great variability among them.22,23
In the field of hand therapy, there has been empiricism, which may result in iatrogenic problems, such as when excessive force is applied in patients suffering from rheumatoid arthritis in the postoperative period.24 Reported descriptions of methods used to calculate the magnitude of tension are also scarce.25,26
In this study, we applied the method to 40 volunteers who used splinting only during data collection. In order to calculate the values of the force transmitted by tendons, we used the trigonometric formulae decribed previously in this study. Landsmeer27 also made use of trigonometric analysis to calculate the effect of tendinous dislocation/glide while movement is performed.
This model of splint has allowed us to note a number of relevant facts.
First, the force exerted in the flexor tendons is smaller among female volunteers. This difference begins from the 45 degree of flexion of the proximal interphalangeal joint. This confirms earlier reports.28,29
Second, as the angle of the joint increases, so does the angle of tendon insertion, while the magnitude of the force transmitted by the flexor tendon decreases. This is explained by the increase in the moment arm as the angle formed by the insertion of the tendon increases. Because the force exerted in the tendon decreases as the angle of joint increases; we suppose this to be related to the fact that the smaller the moment arm and the angle of traction of the flexor tendon, the greater the difficulty in starting joint flexion.30 Additionally, there is a direct relationship between the moment arm of the force exerted in the tendon and the mechanical advantage to the movement.31 In theory, there is more risk in starting the flexion, since the tendon transmits a greater force and the chances of rupture are higher.
Third, longer fingers exert greater force at any degree, probably because the distance between the axis of rotation of the joint and the point of application of the force is larger (torque). Others, who also take into consideration an increase in the tendinous excursion of the longer fingers when recording grip strength of the hand with a dynamometer, have found that, percentwise, the middle finger exerts the greatest strength.32–34 However, at the beginning of flexion (up to 30° of flexion of the proximal interphalangeal joint), no increased force was observed among taller volunteers, nor among those with wider arm spans. It is expected that people having wider arm span and higher stature have longer fingers, as shown in this study.
For any clinical situation, the splint we developed allows guiding the patient more safely to exercise at home during muscular strength gain that is controlled and measured by the connected dynamometer.
The analysis of the data obtained may produce information supporting the replacement of dynamic splints that apply elastic traction with splints connected to a dynamometer. This technology paves the way for new research and new approaches to the several pathologies of the upper limb, with ample clinical application in the field of hand rehabilitation and surgery. The practice of accurately measuring will probably lead to improved training and practice of therapists.12
Bearing in mind that muscular strength varies considerably from person to person,35 the method proposed in this study will make it possible not only to personalize treatment but also to complete the methods of result assessment after flexor tendon suturing.36
This study illustrates the force magnitude exerted in flexor tendons in volunteer users of the splint. It has flaws related to the variability of the axis of rotation of the joint (we considered a fixed point) and the angle of insertion of the flexor tendon in the middle phalanx (we considered a constant value). These variations may be considered as a bias in the study. Another bias lies in the simplification of the anatomic model, given that in the finger, the proximal interphalangeal joint is under the action of only one muscular-tendinous unity (the flexor digitorum superficialis tendon). From the anatomic point of view, this bias is not as important, since othes have emphasized the parallelism between the flexor digitorum superficialis tendon and the flexor digitorum profundus tendon.10,37
We believe that the use of this kind of splint may contribute to the revision and alteration of rehabilitation procedures in patients suffering from a number of injuries such as deformities, capsular ligamentous injuries, tendinous injuries, and others.
CONCLUSIONWe conclude that it is possible to measure the force of flexion transmitted by flexor tendons by means of a dynamic splint connected to a dynamometer; also, that the greater the flexion of the proximal interphalangeal joint of the finger, the smaller the force transmitted by the tendon. Finally, we conclude that there is a correlation between gender, stature, arm span, and finger length and the force transmitted by flexor tendons.
Although nothing was proved experimentally regarding whether the methylmethacrylate cement objectively contributed to the low rate of recurrence in this series, we feel confident that after 24 years of experience with 214 cases, this technique is a reliable, safe, and simple method of treatment, not only for giant cell tumors, but also for other aggressive benign lesions.