In this paper we approach financial investors to see how they analyze financial markets, adopt their investment decisions, and buy financial products. Our main goal is to ascertain whether or not the investment guidelines provided by the most accepted normative theories in Finance are carried out in practice by investors. In order to do that, we review the main financial theories, either normative or descriptive, and we then provide empirical evidence of the investors' behaviour. Findings show that investors often disobey the recommendations offered by normative theories in Finance.
En este artículo abordamos cómo los agentes que adquieren productos financieros toman sus decisiones de inversión. El objetivo es averiguar si las pautas de actuación emanadas de las modernas teorías de Finanzas se reproducen o no en la práctica. Para ello ofrecemos una panorámica de las principales teorías financieras de tipo normativo y descriptivo, así como evidencia empírica del comportamiento de los inversores. La conclusión es que el comportamiento de los inversores suele discrepar a menudo de las indicaciones ofrecidas por las teorías financieras de carácter normativo.
1. Introduction
An essential taxonomy in Finance - and, generally speaking, in all social sciences - is the one that divides financial knowledge into normative and descriptive (a.k.a. positive) theories. This way, normative theories attempt to set rules about the optimal behaviour of the individual decision maker ('how should a rational agent behave'). Descriptive theories, instead, do not give recommendations about what an optimal behaviour would be, but they are bound to identify how economic agents actually behave under specific circumstances. Consequently, it would be of great interest to test the empirical validity of normative theories, i.e. finding out whether or not the theoretical models that are most accepted and used in the financial industry are realistic.
We claim a model to be realistic if it has the reasonable potential to explain and predict the behaviour of agents and/or variables under analysis. This is of vital importance in financial economics - as well as many other fields - not only from an academic point of view, but for practical purposes, given its implications in people's lives and society at large. In particular, when we deal with financial models and its empirical validity regarding investors' behaviour, three questions become essential. First, how do investors make their financial decisions? Second, do these decisions reproduce the guidelines and recommendations that modern theories of Finance provide about financial markets, or do they exhibit some kind of bias? Third, and in case they exhibit some bias, could we find similarities across investors? Our main goal in this paper will be to answer these and similar questions in order to clarify whether investors' behaviour has a solid background on the main theories of Finance in the last fifty years.
In order to fulfil this goal, we will focus on two aspects. On one hand, we shall analyze the most relevant normative theories on financial markets and investments, paying special attention to the so¿called Efficient Market Hypothesis (EMH) as the analytical starting point.1 It is indeed rather easy for investors to get lost among the many investment rules and strategies that promise an attractive return at a low risk. However, we must never forget what EMH suggests about how financial markets work: no investor can make above¿market returns systematically - a conclusion that would severely limit the optimal strategies available to investors.
On the other hand, and opposed to those normative theories, we shall ask ourselves how investors make their financial decisions in practice. Are they really convinced that beating the market is 'mission: impossible'? Or do they believe that their financial advisors, who are more prepared and informed than themselves, could make it for them instead? Furthermore, do they really believe that their crucial investment goal must be beating the market? Or are they (more) aware that a more suitable strategy would be to investing their savings according to their financial objectives and constraints, framed by the stage of the 'investor life cycle' they are at? Answering these and other related questions will be determinant in understanding how investors make their financial decisions and whether they agree with what normative models predict.
The bulk of this article sets its background on Kahneman and Tversky (1979), the foundational paper on behaviourist literature - Prospect Theory - in which we base our empirical research to illustrate people's behaviour towards risk; and Hens and Bachmann (2008) who, in their book 'Behavioral finance for private banking', explain how to provide consultancy services taking into account not only how financial markets work according to the most accepted normative theories in finance, but also how private clients make their decisions and evaluate the results of their investments according to Prospect Theory.
The remainder of the article is organized as follows. In section 2, we briefly review some of the most relevant theories about the functioning of financial markets and the investment rules that follow from them. In section 3, we describe how investors make their financial decisions in practice, differentiating between active investors (those that make their own investment decisions) and passive investors (those that hire professional services). We then provide empirical evidence on how people face risk and whether they are aware of the consequences. In section 4, we examine some features that most investors were found to share when we analyzed their portfolios. Finally, in section 5, we highlight the disparity between what normative models in Finance predict and what investors do in practice. Section 6 concludes.
2. A brief review of the most relevant theories about financial markets and investments
An exhaustive description of the many theories about how financial markets work as well as the investment strategies available to investors — according to the academic literature and the financial industry — is beyond the scope of this paper (according to the academic literature and the financial industry). Notwithstanding, in this section we shall provide a brief description of the most relevant theories with the purpose of comparing them with the actual behaviour of investors and determining whether or not the practice is aligned with the theory.
To understand how financial markets work, we need to take into account three basic foundations of traditional Finance: the Efficient Market Hypothesis (EMH), the Modern Portfolio Theory (MPT) and asset pricing models like the Capital Asset Pricing Model (CAPM) and similar ones, and the pricing of financial derivatives. Though the jargon may be confusing, an efficient market is not necessarily perfect nor infallible2; contrarily, EMH actually lays on the concept of informational efficiency of financial markets (Blake, 2000). In detail, we say that a market is efficient when prices fully reflect all information available at any moment (Fama, 1970), regarding events that have already happened, as well as events that, given information available, the market expects to happen in the future and, hence, anticipates (Fama, 1965). Alternatively, Richard Roll tried to make it simpler by saying that the EMH asserts that 'there is no free lunch', particularly in financial markets.3 Following this, Statman (1999) interestingly highlights that the term 'efficiency', (which) when applied to financial markets, has actually two meanings: that investors cannot systematically beat the market; and that security prices are rational, meaning they reflect only fundamental characteristics (risk and expected return), but not subjective characteristics such as emotional or heuristic biases.
A second pillar of traditional Finance lies on MPT and asset pricing models, such as CAPM and similar. While all of them are simplified depictions of financial markets, they have the virtue of providing two essential interpretations about them. On one hand, MPT4 highlights the benefits of diversification, as well as the trade-off relationship that exists between risk and return: investors must be aware that looking for a higher return on their savings imperatively requires exposing themselves to a higher market risk (a.k.a. systematic or un¿diversifiable risk). On the other hand, asset pricing models accordingly take into account either that the required return of an asset depends exclusively on that systematic risk (as in CAPM5), or that under an efficient market in equilibrium arbitrage opportunities6 should not exist (like APT7 predicts).
Finally, the absence of arbitrage opportunities is also key in the third foundation of traditional Finance, i.e. the pricing of financial derivatives. The fundamental theorem of arbitrage links an arbitrage-free market in equilibrium with a risk-neutral valuation by market participants. Applied to option derivatives, a classic result of this theorem is the famous pricing equation for European options by Black and Scholes (1973).8
The three above are the basic foundations of traditional Finance that explain how financial markets work. However, which strategies and investment rules are provided to investors by the academic literature and the financial industry? Firstly, it should be pointed out that, if EMH holds, there would be a strong limit on investors' ability to obtain higher risk-weighted returns than the market average. Furthermore, even theories opposed to EMH (like the Behavioural Finance Theory) assert as well that investors will (also) be unable to systematically beat an inefficient market.9 Indeed, investment recommendations like those suggested by Siegel (1998) are in favour of a 'buy-and-hold strategy' as the one that, in view of the successful track record of equities markets during the last two centuries,10 provides the highest return expectations to investors. Other recommendations, like investing in index funds, most Exchange Traded Funds (ETFs)11 and similar strategies, follow the assumption that markets are efficient and hence not even the best informed highly-skilled fund manager will be able to systematically beat them. On the other hand, (the) investment strategies based on technical and fundamental analysis, among other (financial) theories, attempt to make a profit out of the possible inefficiencies of markets to obtain higher returns.
In any case, no matter whether financial markets are indeed efficient or not, from the investors' point of view it is essential to set investment guidelines that are in accordance with their risk profile, life horizon, (their) objectives and constraints. In fact, the 'investor life cycle' model12 — a classic in the financial industry when advising to customers — prescribes that a suitable analysis of an individual investment framework must take into account the investment goals as well as the financial constraints, both often influenced by the stage of the investor life cycle is at (determined by their age, present and future income, living standards, financial needs...). As a final result, customers should design their investment strategy in three steps: first, which asset classes are to be included and in which proportion (asset allocation); then, which individual assets are to be included in the portfolio (asset choice); and finally, deciding when to buy or sell each of those securities (market timing).13
3. Investors' behaviour in practice
Once the main normative theories of financial markets and investing have been surveyed, we shall ascertain whether investors follow those rules in practice or not. In order to answer this question we distinguish between individual investors, who make their investments motu proprio, and investors that manage their savings through expert intermediation (fund managers, financial advisors, private banking...).
3.1. Amateur investors and financial consultancy
What do individual or amateur investors pay attention to? Perhaps the best answer to this question was provided by Robert Shiller (1984) when he asserted that investing in speculative assets is a 'social activity'. Consequently, most investors that make their own investment decisions "spend a substantial part of their leisure time discussing investments, reading about investments, or gossiping about others' successes or failures in investing" (p. 457).
This way, the role of mass media in provoking attention cascades becomes determinant. The first only¿news TV station (CNN in 1980) was followed by those specialized in financial and business news (CNBC, CNNfn, Bloomberg TV...), ordinary newspapers dedicate more and more pages to the Finance section, business magazines increase their market share... (Shiller, 2000). What is also noticeable is the tendency of most amateur investors to follow the advices and opinions by 'renowned gurus' in business magazines and other specialized media, as well as the interest they demonstrate for technical analysis, despite the fact that this technique has a diminishing level of recognition within the academics. The attractiveness of technical analysis among amateur investors might be due to the fact that it offers investment rules that are largely subjective and require little financial knowledge.
Investing through professional intermediation, on the other hand, represents a large stake of the industry's revenue with a growing volume of assets under management, as it can be inferred from the evolution of the world's high income population.14 This group doubled in just ten years; indeed, its figure increased from 5.2 million investors in 1997 to 10.1 million in 2007 and, despite the current financial crisis, it reached to the record figure of 10.9 million in 2010 (Capgemini & Merrill Lynch, 2008, 2011). The majority of these investors manage their assets through private banking services; services that are usually more profitable to the companies that provide them than the traditionally asset management services, because they require advice and personalized management.15 Indeed, even with the global crisis and the economic uncertainty, reports by Credit Suisse (Credit Suisse, 2007, 2011) or PricewaterhouseCoopers (PriceWaterhouseCoopers, 2011) predict that private banking will maintain a high growth potential and provide a high rate of return in the following years.
Why are high¿net¿worth¿individuals (HNWIs) willing to pay for advising? We should not be naive here to believe that professional managers and financial advisors are free of the biases that pervade most investor's decisions: there is plenty of empirical research showing that financial experts do exhibit the same 'social behaviour' as individual investors.16 However, these experts have far more financial knowledge than the average amateur investor, at least enough to be aware of the enormous difficulty to systematically beat the market. That is why there is a growing feeling in the industry that being successful in financial advising services largely depends on knowing your customers well and maintaining a stable and reliable relationship with them, in order to provide them at any time with the investment guidelines that are in accordance with their risk profile, their life horizon, their goals and restrictions.
Hens and Bachmann17 (2008), for example, make a series of recommendations to private banking professionals in order to help them taking into account that "each customer is unique" when providing consultancy services. This way, a financial advisor's main goal must be to offer investment advice through a close relationship with the customer, in a way that enables them to achieve their financial goals while avoiding, as much as possible, the classic psychological traps we fall into when making decisions under risk or uncertainty. A tailor-made advisory service must always best suit the risk ability, the risk preference, and — this is particularly relevant — the risk awareness of the client. Indeed, Hens and Bachmann (2008) point out that while traditional finance — with its cornerstones of mean¿variance analysis, efficient market hypothesis, and derivative pricing — has provided good models to understand the market, it is not appropriate for understanding clients. (Preface, p. xxi.)
Two reasons are provided by the authors to support their view. Firstly, behavioural biases of clients are not included in the financial models: this makes advisors unable to understand their customers' reactions in face of the investment outcomes. Secondly, traditional finance uses a simplified vision of risk, measured by the variance. This does not fit with the interpretation most investors make about it. At this point a crucial concept appears; namely, the one that determines the investors' ability to fully understand the consequences of their investment decisions and the professional advisors' capacity to provide investment recommendations that are suitable to each customer: risk. Do we really understand the true meaning of the word 'risk'? We all understand the difference between earning 5% or 10% out of our investments, and we understand we all prefer the latter, too; but this is a tricky preference if analyzed when the outcome of our decisions is known. It is ex¿ante when an investor has to choose among several options, and where the outcomes of such alternatives depend on different states of nature with their corresponding probabilities.
Investing in financial assets may be tough and confusing for many amateur investors. We have no 'sure rules' to tell us what the result of our investments will be, only probabilities. Furthermore, those probabilities are not only difficult to understand for neophytes in finance, but they are also sometimes loaded with subjectivity. What is, for example, the probability of the Euro depreciating by 5% against the U.S. dollar in the next few months? And what is the probability for the price of a barrel of crude oil to rise by 20%? And for the average price of the real estate market in Spain to fall by 10%?... Allocating probabilities to events like these might even be tautological: we would use the probabilities of occurrence we think they might be (subjective probabilities).18 In Medicine, Biology, Physics and Natural sciences in general we use (objective) probabilities based on the survival rate of a disease, the ability of a virus to reproduce..., i.e. based on previous experiments made under similar characteristics. However, in Finance we cannot do that; generally we face unique events with no possibility of an experimental test.19 This makes financial knowledge particularly ambiguous and opaque, both to amateur investors and experts. And for financial advisors it entails a puzzle that is hard to solve, because they seem to be doomed to satisfy the classic demand of their clients (obtaining high returns20) without being sure that their customers are indeed aware of the risks assumed.
3.2. Risk awareness
Let us assume the following situation (Situation I). Imagine 1,000 euros on the left hand of a third person, and 1,000 euros on his or her right hand: would you consider them identical? Or would you have any preference for the 1,000 euros on his or her left hand instead of those in his or her right hand (or vice versa)? Probably not: one thousand euros are one thousand euros anyway, right? Well, we will see that sometimes, for many of us, it is not.
Let us now consider the following alternative situation (Situation II). Imagine the day of your birthday is coming and a relative of yours wants to give you a present. What would you prefer: a bike, or that same bike plus 100 euros? All of us would prefer the second option, correct? That means 'more is better' (monotonicity of preferences) in the sense that we all prefer more to less, particularly if we are talking about money. However, we shall also see that, under specific conditions, the vast majority of us would let those 100 euros go.
There is much to say about our behaviour towards risk, and even more about whether people are fully aware of it (a concept known as 'risk awareness') or not. In what follows we present some results about risk perception that come from a test to 96 undergraduate students at the University of A Coruña. The test was performed as part of the subject Financial Management and included a broader list of questions. We have used some of these questions and the tests results to illustrate our conclusions in this paper.
Standard finance's rationality means two things (Barberis and Thaler, 2003). First, agents are bayesian, meaning they update their beliefs when new information comes to the market according to the well-know Bayes' law, a formula for calculating the probability that something (called A) is true or will be true, given that a certain set of circumstances (called B) is true, as follows
Second, agents' choices are consistent with the notion of a subjective expected utility. The expected utility theory (EUT) - the generally accepted normative model of rational choice under risk - is derived from a set of axioms everyone should follow to make rational decisions; namely, that preferences21 should be complete, transitive, continuous, and satisfy the independence axiom. Decision making under risk can be viewed as a choice between prospects or gambles, where the concept of stochastic dominance becomes determinant. We are not going to deal with this concept but (shall) only say that risk aversion plays a key role here: all risk¿averse agents that maximize expected utility prefer a lottery that dominates another in the second order stochastic dominance (SSD) sense.22 Modern Portfolio Theory (MPT), for example, assumes all investors are risk averse so they never choose a portfolio that has larger variance with the same mean return. The prevalence of risk aversion is the best known generalization regarding risky choices, and led theorists to propose that utility is a concave function of money (Kahneman & Tversky, 1979) because risk aversion is equivalent to the concavity of the utility function.
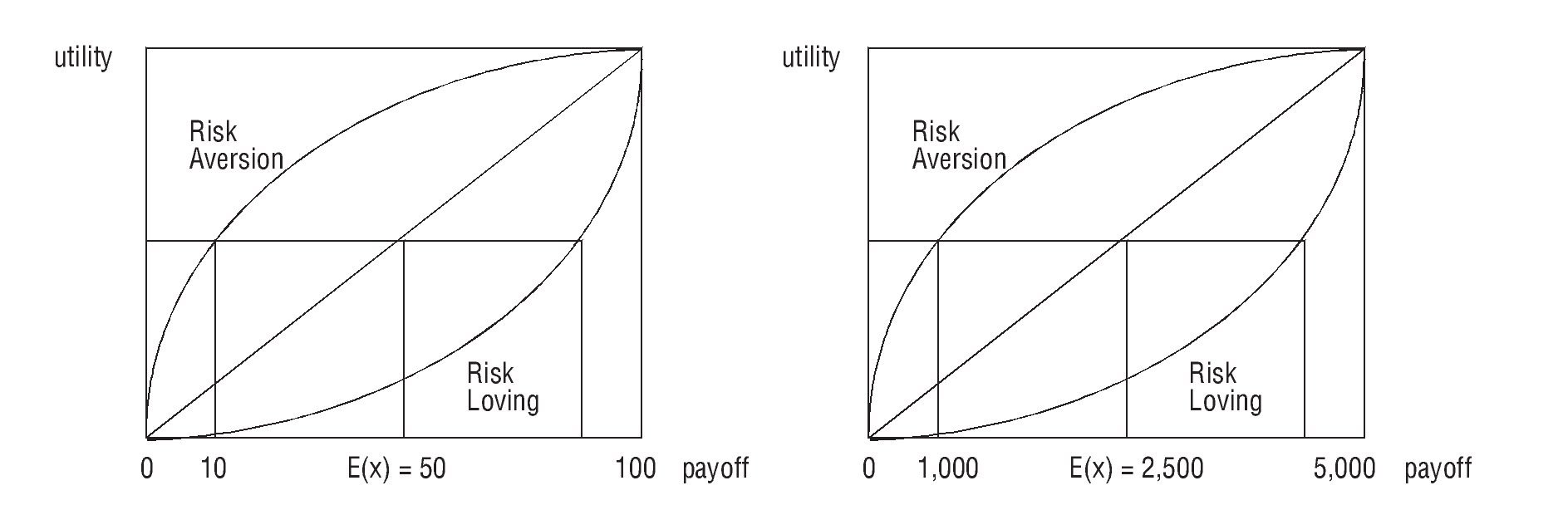
How do we know whether people are risk averse or not? A simple way to infer the risk profile of an individual is to make them choose between a lottery and a certain payoff. The sure quantity that makes an individual indifferent between the lottery and the payoff is known as the certainty equivalent. If such level is below (above) the expected payoff of the gamble, then this individual is said to be risk-averse (risk-loving).23 In our test, students were asked to imagine they were participating in a TV contest where they had to choose one of the two following alternatives:
(a) tossing a coin with 50% chance to win 100 euros and 50% chance to win nothing, or
(b) earning 20 euros for sure.
Well, most of them preferred the gamble defined in (a). Indeed, most people chose the lottery even the certain payoff was above the expected return of the game (50 euros).24 However, we should not draw a hasty conclusion here to believe this implies most people are risk-loving: what it actually means is that we were not talking about 'big money' yet. Indeed, when we asked them "imagine now the possible outcomes of the coin tossed are 5,000 euros (50%) or nothing (50%), and the alternative is a certain payoff of 1,000 euros", some respondents that thought 20 euros were not enough to disesteem playing the lottery now preferred the sure option, with most people requiring a certain quantity below 2,500 euros in order not to gamble. This is illustrated in Figure 1.
Figure 1 Change in risk attitude.
This change in behaviour (being risk-loving for small quantities of prizes and risk¿averse when the bet is significant) is recognized in the two alternative measures of risk-aversion: the Arrow-Pratt measure of absolute risk aversion (ARA) and the relative risk aversion (RRA). As is well known, the ARA is defined as
where w denotes wealth, and u'(w) and u''(w) are, respectively, the first and second derivative of the (expected) utility function u(w).25 In turn, the RRA is obtained by multiplying ARA by wealth,
and is a measure that has the advantage that is still a valid measure of risk aversion even if the utility function changes from risk-averse to risk-loving as wealth changes (as we saw in the test). This way, if an agent has constant absolute risk aversion (CARA), the agent shall not increase a single euro invested in risky assets as his or her wealth increases. On the contrary, an agent having constant relative risk aversion (CRRA) would increase the amount invested in risky assets as his or her wealth increases, so as the share of wealth invested in risky assets remains constant.
Therefore, nothing surprising has happened in our test so far. However, the next few questions in the test offer evidence of what Prospect Theory came to highlight: in practice, individuals do not behave as the EUT suggests,26 violating some of the axioms and hypothesis above. Prospect Theory (Kahneman & Tversky, 1979) is the best known and most accepted descriptive model of decision making under risk. When analyzing how people actually perceive risk and make decisions, Daniel Kahneman and Amos Tversky detected several anomalies with respect to the normative prescriptions of traditional Finance. Two of them are loss aversion and the reflection effect. Loss aversion means that investors assign more significance to losses than to gains of an equivalent value. It represents a challenge to the EUT, because if loss aversion is present, the basic property of EUT that two indifference curves never intersect, i.e. that indifference curves are 'reversible',27 no longer holds (Knetsch, 1989). Reflection effect, on the other hand, is the tendency to exhibit risk aversion when returns are positive, and risk seeking when facing the possibility of suffering losses.28
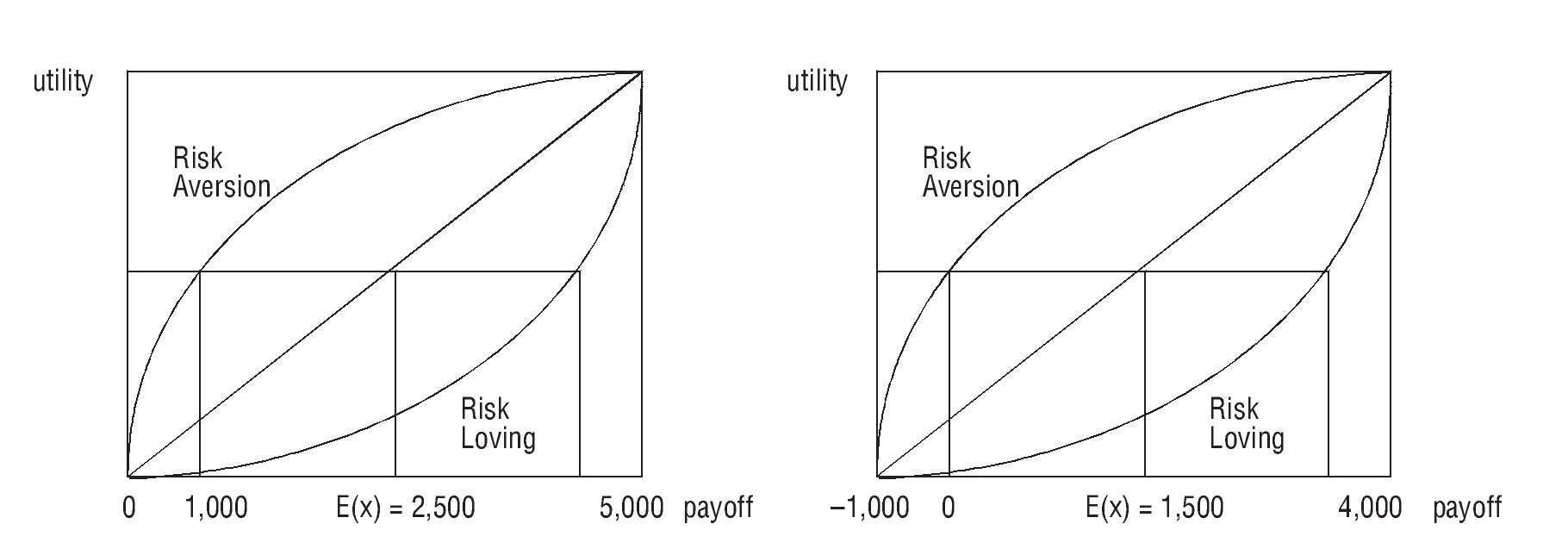
Students in our test where asked to choose between tossing the coin to win 4,000 euros (50%) or to lose 1,000 (50%), i.e. the lottery (-1,000, 0.5; 4,000, 0.5), or doing nothing so the (certain) payoff would be zero. The surprising result was that most students preferred not to gamble, even those that preferred a lottery as (0, 0.5; 5,000, 0.5) to a sure gain of 1,000 euros.29 Why is it so surprising? Because both games are, indeed, financially identical, but they lead to different choices. The Figure 2 illustrates both choices.
Figure 2 Lottery A (left) and lottery B (right).
Please note we are not saying lottery A defined as (0, 0.5; 5,000, 0.5) is identical to lottery B defined as (-1,000, 0.5; 4,000, 0.5), obviously not. But choosing between lottery A or a certain payoff of 1,000 euros, and lottery B or nothing are (financially) identical choices. Then, why did many respondents change their views? Because, for most of us, it is not true that "one thousand euros are one thousand euros anyway" (recall the above mentioned Situation I). People feel the certain payoff of one thousand euros in the first choice as 'pennies from heaven': if they choose gambling and lose them, that won't be painful. On the contrary, if in the second choice they choose gambling and lose one thousand euros, "that's MY money!" they say. Indeed, when asked why they viewed those 1,000 euros differently, one student said "because I earned those thousand euros by the sweat of my brow!", while other said she went to the contest to win some money or nothing if she had no luck, but "if you go to the contest and lose money, your friends will think you are a fool!".
Finally, students were also asked which options they would choose if they had the possibility to choose between
(c) win 2,400 euros for sure, or
(d) playing a lottery with 25% probability to win 10,000 euros and 75% of earning zero,
... and then between...
(e) a sure loss of 7,500 euros, or
(f) playing a lottery with 75% probability to lose 10,000 euros and 25% of losing zero.
92.7% of students (89 respondents out of 96) chose alternatives (c) and (f). This implies a reflection effect as Kahneman and Tversky predicted: students showed risk aversion for positive returns (they preferred a certain payoff of 2,400 euros to the higher expected payoff of the gamble, 2,500 euros), and risk loving in the negative domain.
The above implies two relevant results. On one hand, people exhibit aversion to a sure loss (also known as 'risk seeking' for negative domains): when the alternative is a sure loss, people prefer to gamble even if chances are really low! We made our students notice that, in the previous question, most of them considered it painful the possibility of losing 1,000 euros of 'their own money' with 50% probability, but now they were willing to bet 75% probability of losing 2,500 euros more... and they just did not care! On the other hand, we may see the combination of both choices led 93% of people in our sample to prefer 'the bike' instead of 'the same bike plus 100 euros' (recall Situation II). Indeed, the combination of options (c) and (f) is equivalent to play a lottery with
• 75% probability to lose 7,600 euros, and
• 25% probability to win 2,400 euros,
whereas had they chosen options (d) and (e) that would have been equivalent to play a lottery with:
• 75% probability to lose 7,500 euros, and
• 25% probability to win 2,500 euros.
Clearly (d) and (e) should be preferred to (c) and (f) when it represents the same lottery plus 100 euros, but at least 93% of the respondents30 did not see it.
There are much more anomalies identified by the Behavioural Finance, but just not enough space in this paper. We have summarized some of them: we are not good at probabilities, we avoid ambiguity and dislike doubt, we constantly seek to confirm evidence while ignoring counter facts (often leading us to make overconfident decisions), we exhibit preference reversals in inter-temporal decision making,31 and we fail to account for events that are unfamiliar to us, while we tend to exaggerate the likelihood of rare outcomes when we do consider them! In fact, given that individuals are known to exhibit this tendency to overweight the mere possibility of something to happen — no matter how small the probability of occurrence is32 — it would explain why experts (engineers, economists...) tend to disregard the probability of rare events to occur. Examples are: Japan could not suffer a tsunami like the recent one in 2011, nuclear power plants are designed to be safe against all possible contingencies, the Twin Towers of New York could not collapse, the Titanic was unsinkable...
4. Which features do investors share according to the structure of their portfolios?
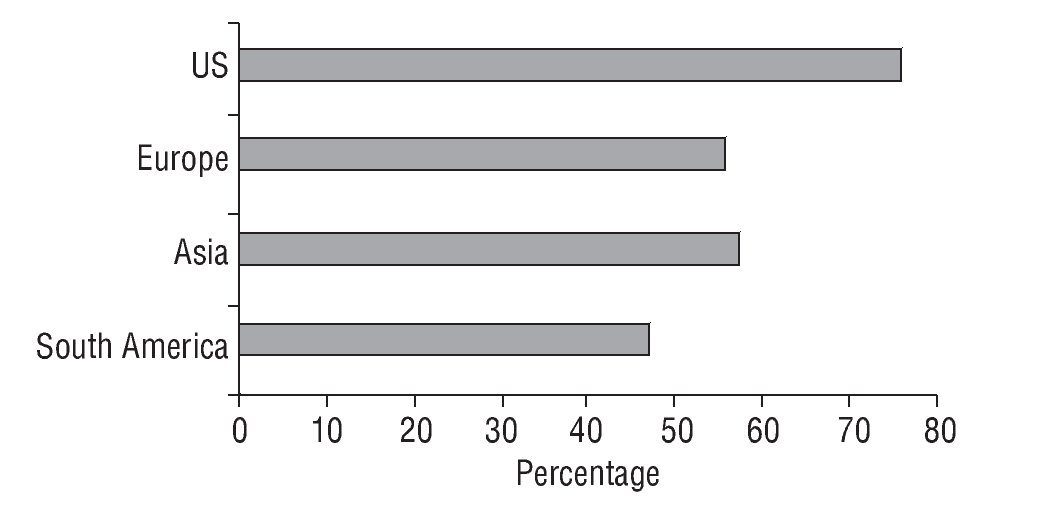
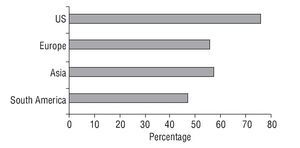
If there is a bias that could be observed among investors of any kind it is clearly the tendency to invest in domestic securities, a phenomenon known as home (or local) bias.33 Capgemini and Merrill Lynch (2011) provide empirical evidence of this bias. If we analyze data from the four global macroeconomic regions (US, Europe, Asia and South America) we can see that, in year 2010, 76% of the wealth of US HNWIs was invested in domestic securities, for European investors it represented 56%, 57% for Asian investors, and 47% for South American investors. (See Figure 3.)
Figure 3 The proportion of wealth of HNWIs invested in domestic securities.
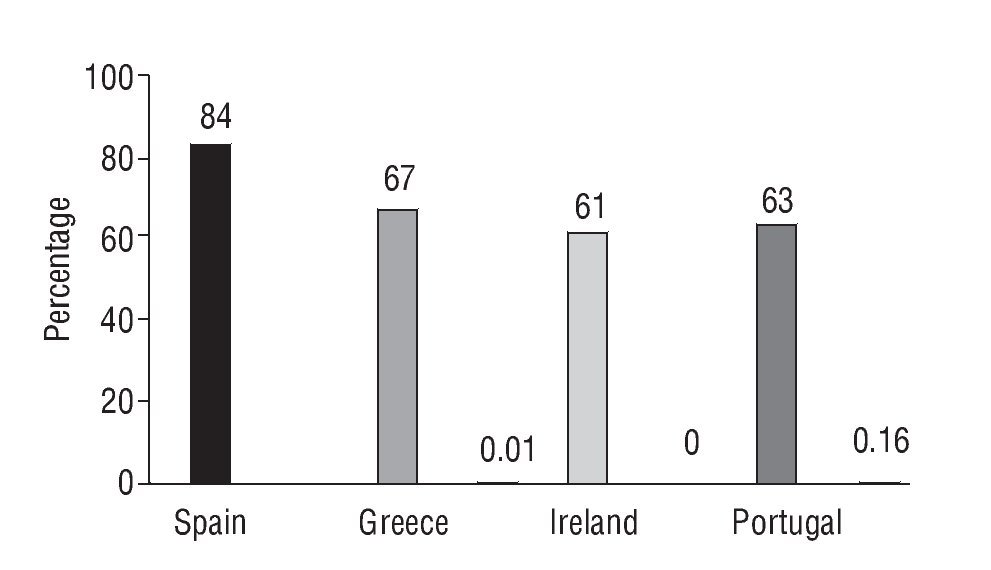
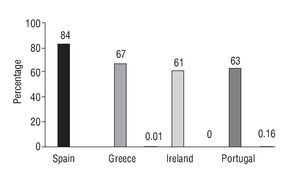
We can see this bias affects not only individual investors, but institutional investors too: the exposure of European banks to sovereign debt securities of the so-called European peripheral countries is a good example. According to the EBA34 stress tests, 84% of Spanish government debt is held by Spanish banks,35 67% of Greek debt was purchased by Greek banks, 61% of Irish debt by Irish banks and 63% of Portuguese government securities by Portuguese financial institutions (European Banking Authority, 2011).
On the contrary, according to Banco de España, Spanish banks had a tiny percentage of their assets invested in other peripheral government securities. To illustrate, 0.01% in Greek debt, negligible in Irish securities, 0.16% in Portuguese debt... (See Figure 4). Is this diversification? Obviously not.
Figure 4 Percentage of public debt held by national banks in some European countries.
A classical rationality for home and local bias is familiarity: people simply prefer to invest in the familiar - see Huberman's (2001) empirical evidence from the geographical distribution of shareholders of seven 'regional bell operating companies' in the U.S. — so familiarity becomes a key determinant of investors' behaviour (see empirical evidence in Ackert et al., 2005). Indeed, this familiarity bias would be related to the evidence that people fear change and the unknown (Cao et al., 2011). However, in our opinion this behaviour could be a valid shortcut for amateur investors but not for institutional investors, who have plenty of resources available and easy access to information. The exposure of European banks to sovereign debt securities, as well as any other evidence of home bias in institutional investing across Europe, might on the contrary be interpreted as a proof of a lack of integration of the European financial system.
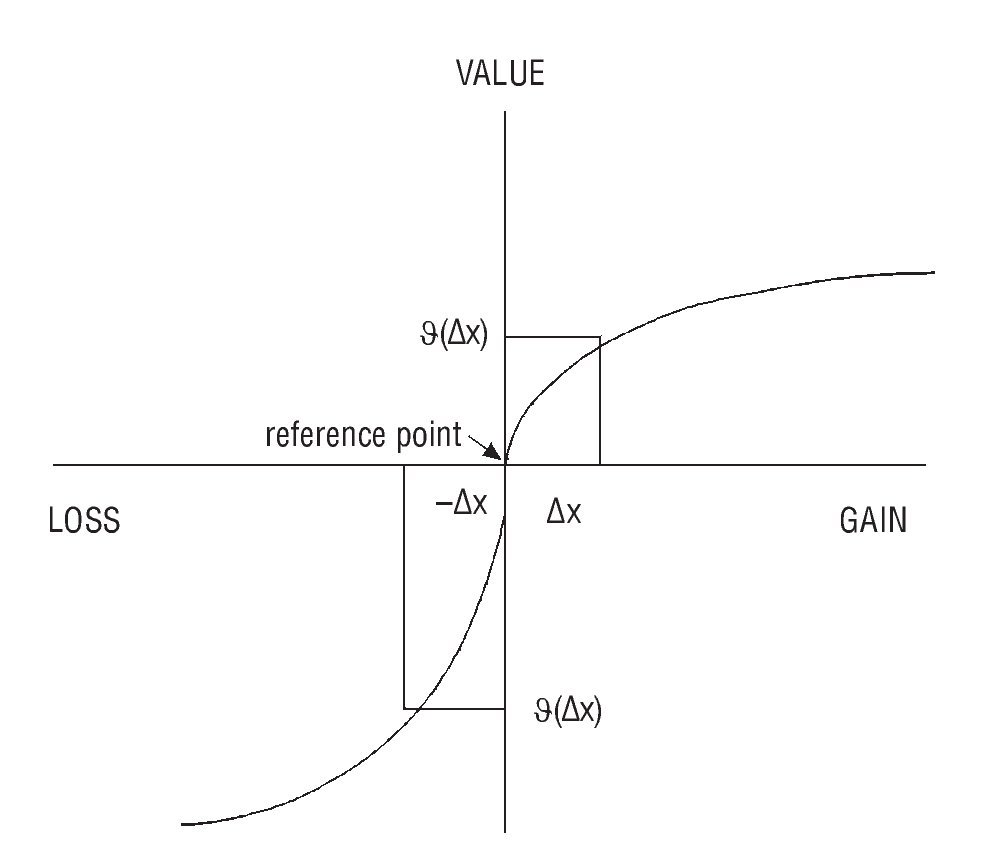
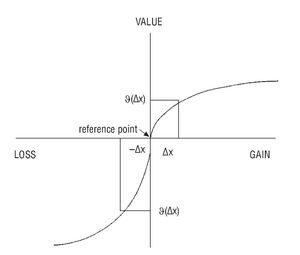
Another feature that investors share, as we saw in section 3, is loss aversion. Prospect Theory replaces the utility function by a value function defined over changes in wealth, v(Δx), and which has three relevant properties: (i) It is defined over gains and losses with respect to a reference point, (ii) it is (strictly) concave for gains but convex for losses, and (iii) it is flatter for gains than for losses. This is illustrated in Figure 5.
Figure 5 The value function.
The third property of the value function determines loss aversion: investors losing 1,000 euros in their portfolios will require gaining more than 1,000 euros as compensation. Indeed, Tversky and Kahneman (1991) provide empirical findings suggesting losses are weighted about twice as much as gains, though the debate is still open.36 Furthermore, since investors exhibit a tendency to over-weight the probability of extreme events, they overestimate the probability of suffering a loss. This psychological effect should be taken into account in risk management (Hens & Bachmann, 2008), and a properly diversified portfolio should be designed to accommodate losses. This is because losses that are anticipated are indeed psychologically easier to cope with (Chancellor, 2012).
Most investors also tend to analyze their investment on a security basis, ignoring the most basic precepts of MPT about diversification. That is why, beyond just selling financial products, a good financial advisor should be concerned about providing his or her clients with financial knowledge on essential topics as the benefits of diversification. Besides, and according to what we described in section 3, amateur investors are usually keen on fads, often generated by the financial industry itself or the media, and probably exacerbated by changes in fiscal rules (like the regulation of pension funds in Spain). Finally, given that not only amateur investors but professionals too - and sometimes with more intensity - exhibit the cognitive and emotional biases the behavioural finance describes, such as fear, greed, herd instinct,37 heuristics and framing biases, it is not surprising finding similar portfolios held by clients of a different kind and risk profile, neglecting the most basic investment rules.
We should not blame it solely on professionals. Individual investors should also look for advice and should improve their financial knowledge, but most of them seem to be interested only in trying to get the highest possible return out of their investments. An interesting observation is the concept of a 'psychological call option', introduced by Hens and Bachmann (2008): many investors hire advising services not (just) to get some advice, but to attribute a favourable outcome to his or her skills when the investment decision turns out well, whereas if it turns badly he or she has someone to blame... True or not, it is easy to observe investors are more concerned with quickly achieving their return expectations, whereas financial institutions are more worried about fulfilling those expectations as soon as possible; a short¿termism that benefits neither investors nor institutions.
5. Summary: What models predict and what investors do
The basics of normative financial models suggest the existence of markets where the information available is fully reflected by the pricing mechanism, so investors cannot systematically beat the market (EMH), where the benefits of diversification are essential to invest (MPT), where systematic risk and expected return are intertwined (CAPM), and where markets in equilibrium can offer no arbitrage opportunities (APT and derivatives pricing).
Traditional investment rules by the financial industry, on the other hand, include both recommendations that agree with the EMH (buy¿and¿hold strategies, index funds, etc.) and those that contradict the EMH to some extent (technical analysis, fundamental analysis). Even some theories opposed to EMH, like the Behavioural Finance, support some of its conclusions when referred to the impossibility for investors to systematically beat the market. A classic in the financial industry is the investor life cycle model: investment recommendations should be in accordance not only with the investor's risk profile, but with his or her life expectancy, goals and financial restrictions. Finally, investments should be implemented in three stages: asset allocation, asset choice and market timing.
Opposed to those rules, empirical evidence suggests amateur investors have a strong tendency to follow fads, rumours, recommendations by financial 'gurus' and magazines, and to base their analysis, at least some individual investors, on technical analysis and chartism (a technique with a low reputation among academics). Those factors would explain why their investment portfolios are often poorly diversified, and exposed to fads, changes in fiscal rules, interests of the financial industry, and to the emotional and cognitive biases of the investor themselves.
Passive investors who hire professional services (private banking in particular) to help them manage their savings have an additional support to mitigate the biases and mistakes described for amateur investors. However, this assertion should be qualified. On one hand, professional investors - and even institutions - exhibit some of the biases observed in amateur investors.38 On the other hand, for the support of financial advisors to be helpful it is essential to develop a relationship of mutual trust between clients and advisors. Such a relationship of trust should rely on three pillars: first, the ability of the financial advisor to instruct customers in concepts like probability, risk-return tradeoff, decision-making under risk (prospect theory), risk awareness...; second, they must know in advance the risk ability, the risk preference, and the risk awareness of their client; and third, the customer must understand (and perceive) the advisor really looks after their interests and not (only) for the interests of their financial institution.
To illustrate decision making under risk by investors we provided some empirical results of a test to undergraduate students designed to highlight how framing (the way the setting for a decision task is framed) influences people's decisions, which is a critical aspect of Kahneman and Tversky's (1979) Prospect Theory. Besides, some insight on the other branches of Behavioural Finance is also provided: how heuristics and biases (e.g., overconfidence, confirmation bias, etc.) could affect investors' behaviour, and henceforth how market anomalies (e.g., home bias) could be identified. Finally, Hens and Bachmann (2008) provided a first insight on how to integrate the foundations of Behavioural Finance in the consultancy services of private banking, a line of thought we tackle in this paper and which we consider interesting for future research. Following this, an open question is how to reconcile normative and positive theories: should normative models account for the empirical behaviour observed of agents, or should our better understanding of the most common biases people exhibit help us introduce some sort of 'debiasing' techniques? For those who would choose the second option... don't you think we could make the same mistakes, even if we are aware of them? How many of us would bet for tails after a coin tossed resulted in seven heads in a row, even though we are aware that the probability of both head and tails is still 50%?
6. Conclusions
Although our knowledge about financial markets is - and always will be - incomplete, and the models we use imperfect, their recommendations should serve as guidelines for us. However, many investors tend to ignore the most basic investment rules. Besides, given uncertainty is inherent to financial markets, most investors have difficulties to understand the risks they are assuming or they are required to assume in order to get their expected returns, particularly those amateur investors not used to work with probabilities.
Hence, one important role of financial professionals should be helping their customers understand the basic precepts in finance: for example, that both their risk appetite and risk awareness should play an essential role when constructing their portfolios. However, this puts customers in an uneven relationship with the financial industry: advisors could behave for their own benefit's sake instead of their customers'. That is one of the reasons why the European Union set MiFID, the harmonized regulation for investment services, in 2004. In this context, working to increase the financial knowledge of the people and to establish long-term and trusty relationships between clients and financial managers should benefit both investors and the financial industry as well.
Acknowledgements
We are indebted to one anonymous referee of this journal for useful comments. Suggestions received from D.J. García-Coto are also appreciated. Manel Antelo gratefully acknowledges financial aid from Galician Autonomous Government (Xunta de Galicia) through Grant INCITE09201042PR. The usual disclaimer applies.
1. This hypothesis was stated by Eugene Fama in his famous article of 1970 (Fama, 1970).
2. A perfect market requires costless information, no transaction costs, no taxes, perfect competition... An infallible market should be able to 'prophesize' the future, knowing in advance what is not known yet by market participants. Obviously, financial markets do not fulfil those definitions, but neither of them is required to be efficient.
3. Roll's foreword to Lo (1997).
4. For which Harry Markowitz (1952) represents the starting point.
5. See the classic paper by William Sharpe (1964).
6. Where arbitrage means buying undervalued securities, financed with the simultaneous sale of overpriced securities, this way earning a riskless profit with no additional capital resources required (Sharpe & Alexander, 1990).
7. Arbitrage Pricing Theory.
8. The paper by Black and Scholes (1973) was later extended by Robert Merton (1973), who named this equation the 'Black-Scholes equation' for the first time.
9. Shefrin (2000), for example, warns that even though agents' behavioural biases generate investment opportunities, they also introduce an additional source of risk beyond fundamental risk. Besides, limits of arbitrage introduced by Shleifer and Vishny (1997) would imply, according to Barberis and Thaler (2003), that the two interpretations of market efficiency, i.e. that prices fully reflect information available and that investors cannot systematically beat the market, are no longer equivalent, because the latter interpretation would also hold in an inefficient market.
10. Mehra and Prescott (1985) highlighted the 'equity premium' obtained by the S&P 500 index from 1889 to 1978. During that period equities obtained a 7% average return, whereas short-term debt only yielded 1%.
11. Most ETFs are indeed index funds.
12. For detailed information about the validity of investor life cycle models and whether they fit with other classic theories like MPT, see Antelo and Peón (2011).
13. Not only is the first stage (asset allocation) the more important of the three because of the risk diversification obtained when combining assets of different nature, but it is also a basic foundation of MPT (Antelo & Peón, 2011).
14. This population is defined as people that are more than a million dollars invested in financial assets.
15. As an example we may analyze Credit Suisse, one of the global leaders of the private banking sector. Its annual reports of 2007 and 2010 show a growing tendency of net revenues from the private banking area (9.58 billion Swiss francs and 11.63 billion, respectively), whereas the institutional asset management division of Credit Suisse generated 2.59 and 2.33 billion Swiss francs, respectively. The higher profitability of the private banking area becomes clear when we see that, in year 2010, assets under management were just more than double than in the asset management division: 932.9 billion Swiss francs (1.25% margin) vs 425.8 billion (0.55% margin).
16. A behaviour exists known as herding, which suggests professional investors tend to imitate each other when making decisions and/or providing investment recommendations. This behaviour would be inefficient on a market basis but, according to Scharfstein and Stein (1990), it would be rational from the point of view of a professional manager worried about their reputation in the labour market.
17. Thorsten Hens and Kremena Bachman are professors at the Swiss Banking Institute of the University of Zürich and experts in Behavioural Finance and Wealth Management.
18. The debate between objective probabilities (frequentist distributions) and subjective probabilities (bayesian distributions) is a classic in Statistics. It is easy to see then why understanding probabilities is hard for a layman, when the debate continues among experts! If we assume objective probabilities, we are suggesting randomness and probabilities do exist in fact in Nature. Nevertheless, many statisticians and philosophers reject this point of view: they instead interpret probabilities as a measure of our lack of knowledge about all the conditions and variables that might affect the outcome of an event or a set of circumstances, and for such reason we call it a 'random event'. Probabilities, interpreted like this, would be subjective: a measure of our beliefs about the possible outcomes of a given event.
19. As Paul Samuelson (1994) interestingly pointed out, "we only have one history of capitalism", and we should never make definitive conclusions out of "a sample of size one". In brief, we should be aware that our knowledge about financial markets is, and always will be, limited.
20. Something that necessarily requires to assume a higher level of risk.
21. A preference is a binary relationship on a choice set X. Given two alternatives, x,yÎ X, a preference x ≥ y means that alternative x is at least as good as alternative y, x > y means x is strictly preferred, and finally x ~ y means both alternatives are equally good. A preference relation is complete if for all alternatives in the choice set X the individual has a well¿defined preference. Besides, it is transitive if for all x,y,zÎ X, such as x ≥ y and y ≥ z, then x ≥ z holds. Finally, preferences are representative of a rational choice, and a utility function exists and describes those preferences, if the preference relation on Χ is continuous, that is, if for all lotteries such as x,y,z, satisfying x > y ≥ z, there exists a number α,αÎ (0,1), and such that αx + (1 - α)z > y. In words, preferences neither exhibit erratic behaviour like sudden jumps caused by minor changes in data, nor there are alternatives infinitely better or worse than others that 'poisons' any compound alternative in which it is included. Completeness, transitivity and continuousness ensure a preference relation can be assigned numerical values (a utility function) to the outcomes of different alternatives in order to compare them. Finally, independence axiom is satisfied if for all lotteries x,y,z (being a lottery a set of consequences and the probabilities of occurrence) and for all numbersαÎ [0,1], we have x ≥ y if and only if αx + (1 - α)z ≥ αy + (1 - α)z, i.e. if one lottery is preferred to another, and we mix both with the same third one, then the preference ordering is independent of the particular third lottery used. Hence, if preferences, besides being complete, transitive and continuous, satisfy the independence axiom, they can be represented by an expected utility function, where the expected utility of a lottery is the sum of utilities derived from each of the consequences the lottery offers, weighted with their probabilities.
22. A lottery dominates another if the former yields a better outcome in any state of nature. SSD is a weaker condition than first order stochastic dominance (FSD): it holds whenever the area under one cumulative distribution is equal to, or larger than, that under the other cumulative distribution (Hadar & Russell, 1969, p. 27).
23. An alternative way to define risk aversion is that it measures the reluctance of a person to accept the lottery with the higher, but uncertain, payoff.
24. Most subjects in the test said they would require 60 to 80 euros to choose not to gamble.
25. As is well known, we can measure the degree of risk aversion by the curvature of the utility function. If the utility function is concave, the higher the curvature, the higher the risk aversion. We could use the second derivative for such purpose, but such measure would not be invariant under positive affine transformations of the utility function. The simplest way to solve that is to use the Arrow¿Pratt measure of ARA (Hens & Bachmann, 2008).
26. "The modern theory of decision making under risk emerged from a logical analysis of games of chance rather than from a psychological analysis of risk and value. The theory was conceived as a normative model of an idealized decision maker, not as a description of the behavior of real people". See Tversky and Kahneman (1986, p. S251).
27. That is, if an individual owns x and is indifferent between keep ing it and trading it for y, then when owning y the individual should be indifferent about trading it for x. See Kahneman et al. (1991).
28. A behaviour already noted by Harry Markowitz (1952).
29. See Figure 1 and the discussion therein.
30. We say 'at least' because of the seven people that did not choose (c) and (f) only two persons did choose (d) and (e).
31. Rational evaluation of future decisions requires time consistency, but often when people say they prefer 110 dollars within 31 days to 100 dollars within 30 days, they then change to 100 dollars today better than 110 dollars tomorrow. That represents a preference reversal, inconsistent with inter-temporal rational expectations.
32. Hens and Bachmann (2008) explain that Prospect Theory emerged indeed to explain why nuclear energy is largely repudiated by the public. Kahneman and Tversky received a grant from the US government to analyze why people protested so much against it, and their results showed the public did not buy the argument that nuclear power was safe, because the mere possibility of a nuclear catastrophe to occur, even though its probability is very small, made them see it as a risky business. Hence, over¿weighting small probabilities became one of the cornerstones of Prospect Theory.
33. Home bias for securities of the same country as the investor, and local bias for local securities.
34. European Banking Authority.
35. To illustrate, BBVA (with 55.7 billion euros) and Banco Santander (with 46.0 billion euros) were the larger holders of Spanish government debt on December 31, 2010 (see European Banking Authority, 2011).
36. See McGraw et al. (2010) for a discussion on this topic.
37. See Shleifer (2000) regarding herding among traders, market analysts, etc.
38 Recall the home bias in sovereign debt portfolios by European banks (see Figure 4).
Received February 9, 2012; accepted May 22, 2012
* Corresponding author.
E-mail address: manel.antelo@usc.es (M. Antelo).
References
Ackert, L.F., Church, B.K., Tompkins, J., Zhang, P., 2005. What's in a name? An experimental examination of investment behavior. Review of Finance 9, 281-304.
Antelo, M., Peón, D., 2011. Productos financieros y perfil del inversor: de la práctica a la teoría. In: García¿Coto, D.J. (Ed.), Ahorro familiar en España. Papeles de la Fundación de Estudios Financieros 39, 193-211.
Antelo, M., Peón, D., 2012. Financial markets: A guided tour. Nova Science Publishers, New York.
Barberis, N., Thaler, R., 2003. A survey of behavioral finance. In: Constantinides, G.M., Harris, M., Stulz, R.M. (Eds.). Handbook of the economics of finance. Elsevier, Amsterdam.
Black, F., Scholes, M., 1973. The pricing of options and corporate liabilities. Journal of Political Economy 81, 637¿654.
Blake, D., 2000. Financial market analysis. John Wiley and Sons, Chichester, UK.
Cao, H.H., Han, B., Hirshleifer, D., Zhang, H.H., 2011. Fear of the unknown: Familiarity and economic decisions. Review of Finance 15 (19), 173¿206.
Capgemini, Merrill Lynch, 2008. World wealth report. Available at: www.ml.com
Capgemini, Merrill Lynch, 2011. World wealth report. Available at: www.ml.com
Chancellor, E., 2012. Humans are naturally bad investors. Financial Times 9, 24.
Credit Suisse, 2007. Credit Suisse annual report. Credit Suisse Group AG. Available at: www.credit-suisse.com
Credit Suisse, 2011. Credit Suisse annual report. Credit Suisse Group AG. Available at: www.credit-suisse.com
European Banking Authority, 2011. 2011 EU-Wide stress test. Available at: www.eba.europa.eu
Fama, E.F., 1965. Random walks in stock market prices. Financial Analysts Journal 21, 55¿59.
Fama, E.F., 1970. Efficient capital markets: a review of theory and empirical work. Journal of Finance 25, 383¿417.
Hadar, J., Russell, W.R., 1969. Rules for ordering uncertain prospects. American Economic Review 59 (1), 25¿34.
Hens, T., Bachmann, K., 2008. Behavioral finance for private banking. John Wiley and Sons, Chichester, UK.
Huberman, G., 2001. Familiarity breeds investment. The Review of Financial Studies 14 (3), 659¿680.
Kahneman, D., Knetsch, J.L., Thaler, R.H., 1991. Anomalies: The endowment effect, loss aversion, and status quo bias. The Journal of Economic Perspectives 5 (1), 193¿206.
Kahneman, D., Tversky, A., 1979. Prospect theory: An analysis of decision under risk. Econometrica 47, 263-291.
Knetsch, J.L., 1989. The endowment effect and evidence of non-reversible indifference curves. American Economic Review 79 (5), 1277¿1284.
Lo, A.W., 1997. Market efficiency: Stock market behaviour in theory and practice. Edward Elgar, Cheltenham, UK.
Markowitz, H.M., 1952. Portfolio selection. Journal of Finance 7, 77-91.
McGraw, A.P., Larsen, J.T., Kahneman, D., Schkade D., 2010. Comparing gains and losses. Psychological Science 21 (10), 1438¿1445.
Mehra, R., Prescott E.C., 1985. The equity premium: A puzzle. Journal of Monetary Economics 15, 145¿161.
Merton, R.C., 1973. Theory of rational option pricing. Bell Journal of Economics and Management Science 4, 141-183.
PriceWaterhouseCoopers, 2011. Global private banking and wealth management survey. Available at: www.pwc.com
Samuelson, P.A., 1994. The long term case for equities and how it can be oversold. Journal of Portfolio Management, Fall, 15¿24.
Scharfstein, D., Stein, J., 1990. Herd behavior and investment. American Economic Review 80, 469¿475.
Sharpe, W.F., 1964. Capital asset prices - A theory of market equilibrium under conditions of risk. Journal of Finance 19, 425¿442.
Sharpe, W., Alexander, G., 1990. Investments. Prentice Hall, Englewood, New Jersey.
Shefrin, H., 2002. Beyond greed and fear. Understanding behavioral finance and the psychology of investing. Oxford University Press, New York.
Shiller, R.J., 1984. Stock prices and social dynamics. Brookings Papers on Economic Activity, Fall, 457¿498.
Shiller, R.J., 2000. Irrational exhuberance. Princeton University Press, Princeton, New Jersey.
Shleifer, A., 2000. Inefficient markets. An introduction to behavioural finance. Oxford University Press, Oxford, UK.
Shleifer, A., Vishny, R.W., 1997. The limits of arbitrage. Journal of Finance 52, 33¿55.
Siegel, J., 1998. Stocks for the long run. McGraw¿Hill, New York.
Statman, M., 1999. Behavioral finance: Past battles, future engagements. Financial Analysts Journal 55, 18¿27.
Tversky, A., Kahneman, D., 1986. Rational choice and the framing of decisions. The Journal of Business 59 (S4), S251¿S278.
Tversky, A., Kahneman, D., 1991. Loss aversion in riskless choice: A reference-dependent model. The Quarterly Journal of Economics 106, 1039-1061.