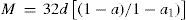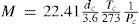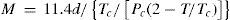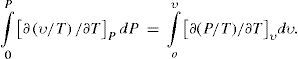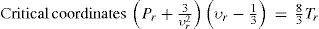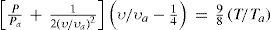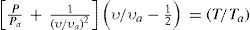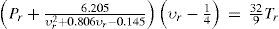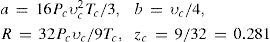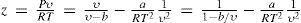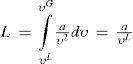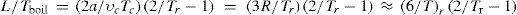Daniel Berthelot (1865-1927) did fundamental research on the conductivity of electrolyte solutions, thermodynamics, pyrometry, and photochemistry. In thermodynamics he proved that the limiting density of gases can be used to determine their atomic and molecular weights; he provided the first proof that the principle of corresponding states requires a third parameter and discovered several thermodynamic loci that could be used for this purpose. He improved the van der Waals equation of state by making the term a/v2 a function of the temperature and developed a new equation of state that may be considered the basis of the Redlich-Kwong equation of state.
Daniel Berthelot (1865-1927) realizó investigación fundamental en las áreas de conductividad de soluciones electrolíticas, termodinámica, pirometría y fotólisis. En termodinámica demostró que la densidad límite de un gas puede emplearse para determinar su peso molecular o atómico, ofreció la primera prueba de que el principio de los estados correspondientes requiere un tercer parámetro y descubrió varios lugares geométricos que pueden ser usados para este propósito. Mejoró la ecuación de estado de van der Waals haciendo el término a/v2 función de la temperatura y desarrolló una ecuación de estado que puede ser considerada como la base de la ecuación de Redlich-Kwong.
The only information about the background of Daniel Berthelot is that given in the eulogies pronounced by Charles Barrois (1851-1939), President of the Académie de Sciences, on the occasion of the death of Berthelot (Barrois, 1927), and by A. Boutaric (Boutaric, 1927).
Daniel Paul Alfred Berthelot was born in Paris, on November 8, 1865, the fourth of the six children of Sophie Caroline Niaudet (1837-1907) and Marcelin Berthelot (1827-1907), one of the most famous French chemists of the second half of the nineteenth century. After finishing his studies he became préparateur at the Sorbonne, at the Musèum, and at the Collège de France. He was then appointed professor at the École de Pharmacie of the Université de Paris, and there and in his own laboratory of physics of the vegetables at Meudon, he accomplished the researches that made him famous in the areas of chemistry of the electrolytes, thermodynamics, pyrometry, and photochemistry.
Berthelot was elected a member of the Physics Section of the Académie on February 24, 1919, replacing Emile Hilaire Amagat (1841-1915). He received 26 votes against 19 votes for Marcel Louis Brillouin (1854-1948), 3 votes for Jean Baptiste Perrin (1870-1942, 1926 Nobel Prize for Physics), and one vote each for Aimé Cotton (1969-1951) and Anatole Leduc (1856-1937).
Daniel Berthelot, who remained single all his life, died March 8, 1927, at the age of 62. Charles Fabry (1867-1945) was elected to replace him at the Académie des Sciences.
Scientific contributionBerthelot's research work followed four clearly defined stages. His first works were related to the study of reactions in solution, which he carried on by the method of electrical conductivity. He studied the general problem of the neutralization of organic and mineral acids, as well as the mechanistic aspects of the same. From this work came out the method named “neutralization curves”, still in practice today. The results led him to receive the 1898 Jecker Prize of the Académie (for a total of ten thousand francs awarded for work destined to the progress of organic chemistry), jointly with Joseph Louis François Bertrand (1822-1900) (for his work on soluble ferments) and Alphonse Buisine (-1917) (for his work on the chemical composition of the lamb grease).
The second stage was on pyrometry. At his time there were serious difficulties in measuring high temperatures accurately; the results of the best scientists showed deviations of up to 40°C on the values of the pyrometric constants needed for working at 1000°C or more (the temperature of fusion of gold). Thermometers gave uncertain results at the red temperature because of the nature of their casings. Berthelot solved the problem by developing a new optical procedure, based on the application of interference phenomena, for the determination of the absolute value of temperature. He also introduced the precision of electrical measurements in the generation of high temperatures and thus was able to determine very accurately the most important fixed points for calibrating thermometers (Berthelot, 1900g, 1902ab, 1904).
The third stage was in the area of properties of fluids in the gas and liquid states, determination of the atomic weight using the method of limiting densities, and reduction of the readings of a gas thermometer to the scale of absolute temperatures. In his work in thermodynamics he proved that the available data on the density of gases were underestimated and developed the method of the limiting densities to improve the quality of the data and allow their use in the determination of atomic weights with a precision similar to the one employing chemical methods. He also evaluated the limiting thermal expansion of gases, which together with the limiting density, allowed a highly precise determination of the constant of the perfect gases, the most important of the physicochemical constants (Berthelot, 1914). His study of the properties of gases and fluids led him to develop an improved equation of state, which eliminated many of the limitations of the van der Waals' equation and which probably was the basis for the development of the Redlich-Kwong equation of state (Redlich and Kwong, 1949).
For his achievements in this subject the Académie des Sciences awarded him the 1906 Hughes Prize.
The last stage of his researches was devoted to the study of the chemical and physical effects of light, particularly ultraviolet radiation (photochemistry). Berthelot used the invisible ultraviolet radiation from the mercury vapor lamp to discover a myriad of unknown phenomena. For example, he found that under exposure a mixture of water vapor and carbon dioxide dissociated, the vapor into oxygen and hydrogen, and the CO2 into oxygen and carbon monoxide, resulting in the formation of formaldehyde, the simplest ternary compound of C, H, and O. The latter could condense and polymerize, signalling the first stage for the synthesis of vegetable sugars, starches, and celluloses. Adding nitrogen and operating under similar conditions at ordinary temperatures, led to the synthesis of formamide, the starting substance for the synthesis of albuminoidal substances that constitute the basis of living matter. As a result, Berthelot succeeded in splitting the carbon dioxide and water vapor present in the air in precisely the same way that the green cells of plants do it. Berthelot used photochemistry to carry on many chemical reactions, such as oxidation, nitrification, and polymerization, and proved that many reactions carried on by electrolysis could also be performed by photolysis.
Berthelot published a summary of his research activities, as was customary for a candidate to the Académie des Sciences (Berthelot, 1917).
In this paper we will describe Berthelot's contributions to the determination of physical properties, thermodynamics in general, and to equations of state in particular. These should be judged against the state of the art in the early years of the 20th century.
Atomic and molecular weightsOne of the first methods used to determine molecular weights of a compound and the atomic weight of the elements was by performing a chemical analysis or the chemical synthesis of the substance. The chemical equivalents represented the ponderable proportions in which bodies combined. A second method, physical in nature, was based on the researches about water of Joseph-Louis Gay-Lussac (1778-1850), where he proved that the volume ratio of combining substances in the gaseous state were simple numbers, a conclusion that afterwards became important for the determination of the density of gases. Knowledge of the volume ratio did not help in selecting between the many possible molecular weights, multiples of one another, to put into evidence association phenomena, or to replace chemical analysis for the determination of atomic or molecular weights of simple or composite substances. This limitation was due to a lack of precision in the methods; the classical researches of Victor Regnault (1810-1878) on the density of the permanent gases had a precision of the order of 1/1000, substantially larger than that of the best chemical methods (Regnault, 1842, 1870; Berthelot, 1917).
Anyhow, there was a strong theoretical reason against the application of Gay-Lussac's law on the combination of volumes of substances: it was not rigorous enough. Regnault's experiences had shown that hydrogen deviated from the law of ideal gases in one direction, while other gases did it in the opposite one. From this resulted that if the combining volumes were in the ratio 2:1 at a certain pressure, they were in a smaller ratio at a lower pressure, and at a higher ratio at a higher pressure. Actually, there was no reason why gases should follow Gay-Lussac's law at one pressure better than at another. In other words, this law was inadequate for making precise measurements. This led Jean Servais Stas (1813-1891) to decry the use of density measurements to determine molecular weights.
This was the situation until Berthelot published his paper on the determination of atomic weights (Berthelot, 1898a). He was intent in proving that molecular volumes could be evaluated exactly from the compressibility (factor) and the density of the gas. Regnault's experiments had proven that gases tended to obey the same law of compressibility and expansion as the pressure was decreased. In other words, the so-called law of the ideal gases was a limiting law, valid only for very low pressures. In the same manner, Amedeo Avogadro's (1776-1856) law (equal volumes of all gases contain the same number of molecules) was also to be considered a limiting law, valid at all temperatures but at extremely low pressures. It could then be said that the molecular weight of a gas is proportional to its limiting density.
According to Berthelot (Berthelot, 1898a), the deviation from ideality (e) could be described by the relation ϵ = (Poυ0/Pυ)−1 = a(P−P0), where P0 and P were the atmospheric pressure and another pressure near it, respectively. In addition, according to Regnault the factor a for the permanent gases had a constant value between 1 and 6 atm. Since two gases at a very low pressure P should have the same molar volume, the above relation led to v0/v′0 = 1−aP0/1−a′P0), which for P0 = 1 atm simplified to v0/v′0 = 1−a/1−a′. In other words, molar volumes ' 0 0 should be proportional to (1 – a) and their molecular weights equal to the product (1 – a)d, where d is the density. The result was a system of proportional numbers for the molecular weights and to fix the series it was enough to assign an arbitrary value to one of them, for example H2 = 2, O2 = 32, etc.
Berthelot adopted the second convention and proceeded to calculate molecular weights knowing only the density of the gas at atmospheric pressure and its compressibility at the same pressure and another pressure close to the atmospheric. Under these conditions his equation became
In his first publication (Berthelot, 1898a) he reported the values of the variables a, vm, d, and M for hydrogen (2.01472), nitrogen (28.0132), carbon monoxide (28.0068), and oxygen (32, by convention, as assumed by Stas), and in a series of following memoirs (a-eg, 1899a-cf, 1907abcd), he compared his results to the ones obtained by chemical analysis and showed that the difference between the two amounted to less than 1/5000. His values for hydrogen and nitrogen were 1.0077 and 14.007, respectively, giving 15.88 for the ratio oxygen/hydrogen, which was significantly smaller than the value 15.96, which had been accepted for more than 30 years after the measurements of Jean-Baptiste André Dumas (1800-1884).
According to Berthelot, modern ideas regarding the continuity between the liquid and gaseous states suggested that the general formula relating the molecular weight of a fluid to its density should be equally applicable to liquids and gases. He examined this supposition using Johannes Diderik van der Waals' (1837-1923; 1910 Nobel Prize for Physics) theory (van der Waals, 1873) and drawing the curves showing the factor by which it was necessary to multiply the density of gas or a liquid, to obtain its molecular weight under different pressures (the memoir includes the graph). Berthelot then discussed the curve for a pressure equal to 1/66.67 of the critical pressure, which corresponded, for a large number of gases to pressure levels between 0.5 and 1.2 atm, that is, within the range of measurement of the density of gases and liquids. The factor by which it was necessary to multiply the density of hydrogen was larger than 1 (1.00014), while for other gases it was less than 1. All the results indicated clearly not only that the same formula should be applicable to gases and liquids, but also it would allow recognizing if the body in the liquid state was polymerized or dissociated.
Berthelot went on to develop a better relation, particularly applicable to liquids, and based on laws that Sidney Young (1857-1937) and Émile Mathias (1861-1942) had developed previously (Cailletet and Mathias, 1886; Young, 1892; Berthelot, 1899c). First of all, the ratio of the critical volume and the ideal gas volume at the same conditions was constant and independent of the nature of the substance, a value which Berthelot assumed to be 1/3.6 based on the experimental data of Amagat for CO. Taking the fact that at standard conditions one mole of a substance occupies 22.41 liters then the molecular weight is given by
where dc is the critical density in relation to that of water at 4°C. As a consequence of his law of rectilinear diameter, Cailletet and Mathias established that if the temperature was not too close to the critical one, then the critical density was given bywhere d is the density of the liquid at temperature T (Cailletet and Mathias, 1886). Combining eqs 1 and 2 we getwhere Tc and Pc are the critical temperature and pressure respectively.Berthelot applied his formula to 47 different liquids, compared the results with the density calculated from the chemical formula and found an excellent agreement for 42 of them, which indicated that they have the same molecular weight in the liquid and gas state. The remaining five, acetic acid, methanol, ethanol, propanol, and water, were known to associate in the liquid state. In addition, his results indicated that if the alcohols are associated, then their degree of association varied very little in the ranges 0° to 40°C and 1 to 100 atm (Berthelot, 1900c).
In a following publication (Berthelot, 1898c) Berthelot addressed the question of gases which could be easily liquefied and for which the value of parameter a (which he now designed as A21) was unknown. In this situation, the formula representing this coefficient was not linear but parabolic; it was always necessary to make a very small correction which increased as the critical temperature increased and which could be calculated using van der Waals' equation of state, yielding 2 the relation A12 = a1−b−b/1−a1−b, which Berthelot used to calculate the molecular weights of CO2, N2O, HCl, C2H2, PH3, and SO2, and to show that these values could be used to determine the atomic weights of carbon, nitrogen, chlorine, phosphorus, and sulphur, with a precision better that the best chemical methods (Berthelot, 1898dg).
The next subject was related to the description of gaseous mixtures (Berthelot, 1899def). The best equation available was that of van der Waals, which when applied to a mixture of gases used the relations a = ∑∑aijxi and b = ∑bixi for determining the parameters of a mixture (for a binary mixture a = a11x12 + 2a12x1x2 + a22x22 and b =b1x1 +b2x2). According to Berthelot these relations did not allow the calculation of the properties of the mixture from those of the pure components because of the introduction of the new parameter a12. He believed that it was possible to apply the law of mass action and write a12 = a11a22, as done in the case of the universal attraction of masses. His assumption allowed the calculation of all the properties of the mixture from knowledge of those of the pure components alone. Van der Waals objected to this hypothesis (van der Waals, 1898) because he did not believe in the generality of the geometric mean of the constants of the pure components; his studies of the critical behaviour of binary mixtures had shown that there were cases for which a was larger or smaller than a11a22. Berthelot did not agree with this argument because the term a/v2 present in van der Waals' equation of state was applicable only to large gas volumes, and should be replaced by a more complex form, such as 1/v2 + nbv +mb2, for small volumes, where m and n were constants.
Berthelot and Paul Élias Sacerdote (Berthelot and Sacerdote, 1899) measured the compressibility and changes in pressure that took place in the vicinity of atmospheric pressure, for the mixtures CO2 + SO2, N2 + O2, and H2 + O2, and found that the experimental results justified the geometrical mean rule. Eventually, Johannes Jacobus van Laar (1860-1938) published a paper (van Laar, 1916) in which he stated that Berthelot relation was correct and where divergences were to be found, these were due to phenomena such as association, molecular combination etc.
In another paper (Berthelot, 1900f) discussed the importance of the principle of corresponding states. The experimental verification of the law had showed that when using the values of P, v, and T, reduced by the pertinent critical values, the principle described the general behaviour of gases in a better manner, but still approximate. One of the explanations for this limitation was that it was not enough to replace the properties by the relative ones, but it was also necessary to calculate them from a minimum value (Tm, vm), characteristic for each substance, that is, the correct reduced variables were (T – Tm) / (Tc – Tm) and (v – vm) / (vc – vm) and not T/Tc and v/vc. There was no need to correct the pressure because real gases behaved as ideal ones at sufficiently low pressures. Berthelot found that at the critical point there seemed to exist a constant ratio between the critical volume and the volume of the perfect gas under the same conditions, and that this ratio could be used as the reference point m indicated above. Hence it could be stated that “there is a constant ratio between the theoretical volume occupied by a fluid at [Pc, (Tc –Tm)] and the excess volume (vc – vm),” the value of the ratio being about 4.68. The value of Tm could be easily calculated from the knowledge of the critical properties, vm, and the molecular weight of the gas.
Berthelot concluded his paper by stating that it was not enough to know the critical properties of a substance to define rigorously the function F (P,v,T), that is to say, to define the equation of state. It was necessary to add two new constants, Tm and vm, corresponding to the displacement of the zero points of the temperature and the volume.
The reader familiar with the modern versions of the theorem of corresponding states will realize that Berthelot was already advancing the concept that “all gases having the same values of the reduced properties and the same value of the third parameter, behave similarly.”
In his analysis of the principle of corresponding states Berthelot commented that the principle made no assumption regarding the equation of state. For each substance it contains as many parameters as variables (hence three), which can be found in the domain of the fluid or on three points defined by analytical relations. The coordinates of any of these points can serve as specific units. In a general form, the notion of the corresponding states is presented as a mathematical concept, which may well have no physical application. In the same way as the laws of thermodynamics, it is independent of the nature of the substance and the mechanism of the phenomena. It says nothing a priori if the properties of real fluids allow determining a large number of singular points apt for furnishing the specific units for P, V, and T or, on the contrary, none exists. Van der Waals showed in his thesis that the critical point can be used to play this role (van der Waals, 1873). In his studies, Berthelot discovered the existence of three additional points of this gender, none of them related to the critical point, which appeared naturally when studying the energy of fluids. Particularly simple results were obtained when tracing a net of isotherms in the plane Pv /P (work against pressure). For similar reasons, it was advisable to use the variable (Pv /T) in problems where the entropy changes are important. Berthelot showed that defining by ΔPv the external work of a fluid and by ΔU the change in internal energy of a perfect gas, then the van der Waals' equation of state indicated the existence of the following four geometrical loci in the Pv /P domain, each having the shape of a parabola:
(1) The geometrical locus of the states where the cooling due to the external work is maximum, defined by the analytical condition (∂Pυ /∂P)T = 0. This locus can also be described as the locus where the fluid follows the ideal gas law, and can also be used to define the temperature of Boyle as lim(∂Pυ /∂P)T when P → 0.
(2) The geometrical locus where the cooling due to the external work is nil. Cooling in the Joule-Thomson effect is due to the internal work only and the locus can be defined by the equation ∫0PcP∂T∂PHdP = ∫0υcυ∂T∂υPdυ where cP and cv are the specific heats, (∂T /∂υ)H the Joule-Thomson effect, and (∂T /∂υ)P the Gay-Lussac-Joule effect. The inversion curve for the effect is defined by (∂T /∂υ)P = T/v (Berthelot, 1900e). The condition may be replaced by the purely analytical condition
(3) The geometrical locus of the points where the cooling effect is maximum, defined by ∂υ/T/∂TP=0=1/T∂υ/∂TP−υ/T2. It can be said that it corresponds P to the geometrical locus of the points were the fluid follows the Gay-Lussac law, that is, where the true expansion coefficient is equal to the inverse of the absolute temperature, 1/υ∂υ/∂TP=1/T.
(4) The geometrical locus of the points were the total cooling is nil and is defined by ∫0P∂υ/T/∂TPdP = 0.
In his paper Berthelot developed the equations of these loci for gases that followed the van der Waals equation of state, and also for the case where it was modified by assuming that the molecular attraction varied in inverse ratio to the absolute temperature (Berthelot's equation of state, see below). He then compared the resulting curves with the experimental results reported by Amagat (Amagat, 1872, 1873, 1881, 1883, 1893). Since the vertexes of parabolas 1, 2, and 3 are points defined analytically, they can be calculated as precisely as the critical coordinates, and their coordinates used as reference points for the reduced states.
Berthelot called (Pc, Tc, vc) the coordinates of the critical point, (Pa, Ta, va) those of the vertex of parabola 1; (Pf, Tf, vf) those of the vertex of parabola 2, and (Pb, Tb, vb) those of the vertex of parabola 3. Then he used the three sets of singular points to reduce the actual coordinates and to develop the following corresponding expressions for the van der Waals equation of state:
Vertex of parabola 1
Vertex of parabola 2
Vertex of parabola 3PPa + 13(υ/υa)2υ/υa−13 = 89T/Ta
From a thermodynamic viewpoint, the most important of these points is the summit of parabola 2, which has the property of being also located on parabola 3. At this point the internal pressure of a gas is equal to the external one and its volume is equal to the ideal one, that is, we have a perfect gas. The van der Waals equation of state indicates that on the isotherm of this point the variation of internal energy between this point and that of the perfect gas (evaluated at the reduced coordinates) is equal to 1, the same as the total change in energy. It results then, that if the coordinates of the critical point provide the natural units to which relate the problems connected with liquefaction, vapor pressure, etc., the coordinates of the summit of parabola 2 provide the natural units to introduce in problems related to the energy of fluids, evaluation of molecular forces, etc.
According to Berthelot, in the same manner that the coordinates of the critical point provide the natural units for problems related to liquefaction, the singular points and loci he had discovered should find immediate application in machines that produce cooling by a throttling process. Notably, parabola 3 because it gives the locus of the points of maximum yield of the Linde engine, widely used for the liquefaction of gases, and for which the theory was only known approximately.
Berthelot did not discuss the possibility of using the summit of parabola 4 for providing the reference coordinates because two of its coordinates take extreme values at the absolute zero and the volume becomes equal to the covolume. Only the pressure assumes a definite value, 27 times the critical pressure.
It is worth mentioning that in his studies about thermometry, Berthelot pointed to other possibilities of singular points (Berthelot, 1917).
Equations of stateAnother important contribution of Berthelot is in the area of equations of state. The corresponding relations, although predicted by the van der Waals equation of state, had the important property of being independent of the form of the characteristic equation of a fluid. Nevertheless, for many applications it was important to know as exactly as possible, the explicit form of the function F(P,v,T) = 0. Up to 1850, most scientists accepted the strictness of the equation Pv = RT, based on the idea that nature behaved in a simple manner. Eventually, Regnault's experiences forced the giving up of this idea. Regnault himself concluded that it was necessary to develop the means of expressing the behaviour of a gas based on molecular forces.
Van der Waals had shown that his cubic equation of state accounted for the essential properties of fluids, and in particular, it predicted the existence of a critical point (van der Waals, 1873). Although his equation represented the phenomena in its broad aspect, it left much to be desired from a quantitative point of view. Berthelot asked if in order to explain the deviations between the equation and the experimental results, it was necessary to modify the evaluation of the internal pressure or that of the covolume (Berthelot, 1900ab). Although the theories of Hendrik Antoon Lorentz (1853-1928; 1902 Nobel Prize in Physics), Rudolf Julius Emmanuel Clausius (1822-1888), van der Waals, Ludwig Boltzmann (1844-1906), and others, seemed to suggest that the covolume should be variable, the calculations of Berthelot (Berthelot, 1900b) indicated that several formulas assuming a variable covolume led to the critical isotherm deviating more from the experimental results than the assumption of a constant covolume. To him, the covolume was the limit of the liquid volume (when the temperature decreased to the absolute zero) to the tangent of the curve in the plane Pv /P when the temperature increased, and the limit of the liquid or gaseous state when the pressure was increased indefinitely.
In a following publication (Berthelot, 1900b) analyzed the expression b = b∞1−β1b∞/υ + β2b∞2/υ2−… that van der Waals had proposed for the covolume, where b∞ is the value of the covolume corresponding to the perfect gas, β1 = 3/8 and β2 = 0.958, and showed that it led to results against the experience; for example, at the critical temperature and in the pressure range between the atmospheric and the critical one, the compressibility of real gases was less than the one predicted by the law of ideal gases. Berthelot believed that this result was a consequence that van der Waals had considered only two terms in the expansion of b and that a better fit could be obtained by using simpler expressions for the covolume, which included the temperature as a factor. Using again Amagat's data (Amagat, 1872, 1873, 1881, 1883, 1893) he was able to get a good fit of them by assuming that b=bc1+0.3T/Tc−1 where b and bc are the values of the covolume at the temperatures T and Tc, respectively.
Once again, the reader familiar with equations of state will notice immediately the similarity of Berthelot's equation with the expressions of Edward Armand Guggenheim (1901-1970) (Guggenheim, 1945) and Pitzer and Curl for the second virial coefficient (B) of non-polar gases (Pitzer and Curl, 1957), particularly when considering that at low pressures B is equal to the difference between the real and the ideal volumes of a gas.
Berthelot showed (Berthelot, 1900d) that the liquid volumes tended to the same fraction of the critical volume when the temperature was reduced to 0 K, the same result predicted by the van der Waals equation of state, except that this fraction was 1/4 instead of 1/3. He also proved that the slopes of the isotherms tended towards the same value as the temperature was increased, namely, 1/4 of the critical volume. Although Amagat's data rendered extrapolation to high temperatures too sensitive, it was clear that the value of slope of the curves was less than the 1/3 predicted by van der Waals. From this Berthelot concluded that all the evidence pointed out that it was highly probable that the covolume was constant and equal to 1/4 of the critical volume. Berthelot then proposed the following equation of state, based on replacing denominator of the term for the internal pressure in de van der Waals equation of state, from a square, to a second degree trinomial (Berthelot, 1900h):
The above equation gives a better fit the van der Waals' equation of state, but still presents significant deviations in the liquid region.
Berthelot succeeded in developing another equation of state applicable to low and medium pressures (several tens of atmospheres), representing the experimental data with high exactitude, in all the temperature range (Berthelot, 1900h). To do so he first analyzed the plot of Prvr against Pr for different temperatures. If the gas were ideal, the slope of the curve would be zero at every temperature. Using Regnault's data the slope was found to be positive for hydrogen and negative for the other gases, as had been reported by Regnault. Now, plotting the reciprocal of the reduced slope ∂Prυr/∂PrTr against the reciprocal of the reduced temperature (1/Tr), the points for all gases should fall on one curve if the law of corresponding states was correct. The experimental values justified this assumption. A plot of the van der Waals equation of state in this plane was a straight line instead of a curve and gave a very poor fit of the experimental data (Berthelot, 1900h). If now it was assumed that the molecular attraction was not constant, as assumed by van der Waals, but instead varied inversely with temperature, as assumed by Clausius, the straight line was replaced by a parabola, which again deviated significantly from the experimental plot. Berthelot found that the following equation gave an excellent fit of the experimental data:
and predicted very well the experimental data at all temperatures, for low and medium pressures.Application of the condition for the critical point, ∂P/∂υTc=0 and ∂2P/∂υ2Tc = 0 to eq 10 yields:
The last equation predicts that all real gases should have the same critical compressibility, a result that contradicts the experimental evidence. Nevertheless, it should be remembered that all modern cubic equations of state (Redlich-Kwong, Soave, and Peng-Robinson) also predict that the critical compressibility of a gas should be constant (zc = 1/3). The actual values of zc fall in the short range of about 0.15 to 0.30, with more than 60% of them gases having zc ≈ 0.27. Berthelot's equation of state predicts a value of zc very close to the latter.
The Berthelot equation can be expressed in virial form as follows. First the variable P is separated and then multiplied by v/RT to yield:
Since the ratio b/v is very small compared to 1, the first term may be expanded as a geometric series of ratio b/v, to give
Comparison of eq 12 with the virial expansion z =1 +B / v +C /v2+... indicates that the Berthelot equation of state predicts that the second virial coefficient is B = b−aRT2, a function of the temperature as required but 2 RT the following virial coefficients turn out to be independent of the temperature, C = b2, D = b3,…, a wrong conclusion. The Boyle temperature corresponds to B(TB) = 0, that is, TB = a/bR and its reduced value TB/Tc = 6 = 2.45, constant for all gases, which is against the experimental evidence, but not too far from the actual range (2.50 to 2.70).
Berthelot applied his equation to the numerical calculation of different thermodynamics properties and relations, among them, Trouton's law, which indicates that the molar heat of vaporization ΔHvap, divided by the absolute normal boiling temperature (Tboil) is approximately equal to 21 cal/mol for all pure substances (Berthelot took the value to be 20). Now, if instead the normal heat of vaporization we consider only the internal heat of vaporization L, it is necessary to subtract 2 cal/mol from 20 cal/mol to account for the external work. In other words, Trouton's rule becomes L /Tboil ≈ 18 cal/mol. Inspection of this equation indicates that dimension-wise it corresponds to the ratio Pv/T, hence the ratio should be the same for all the substances at their corresponding states. In addition, since experience indicated that for a given substance, its normal boiling temperature was about 2/3 of the critical one, it was possible to deduce Trouton's rule using the law of the corresponding states and an equation of state (Berthelot, 1915a). The internal heat of vaporization of 2 cal/mol represents the work realized against the forces of molecular attraction. For the case of van der Waals' equation of state, this force is expressed by the term a/v2 so that
neglecting the density of the vapor in comparison to that of the liquid. Berthelot used now Cailletet and Mathias' law of rectilinear diameters (Cailletet and Mathias, 1886) to express the density of the liquid, 1/vL, as a function of the L reduced coordinates 1/υL = 2/υc2−Tr, so that Trouton's rule become L/Tboil = 2a/υcTc2Tr−1.Assuming that the gas behaves according to the van der Waals equation of state then R = 8Pcυc/3Tc and a = 3Pcυc2 = 9RTcυc/8. Replacing in the expression for Trouton's rule, remembering that R is approximately equal to 2 cal/mol.K, we get L/Tboil = 9R/42/Tr−1 ≈ 9/22/Tr−1 cal/mol × K. Since Tboil ≈ 2Tc/3c,Tr = 2/3 and L / Tboil ≈ 9, that is, only one-half the experimental one. The disagreement is due to the fact that the factor a/v2 is a poor approximation to the internal force of molecular attraction. Berthelot now repeated the calculations using his expression for the internal force of attraction, a /Tv2 , and the relations for the constants a and b to the critical point (see eqs 12) to get
which yields L/Tboil = 18 cal/mol·K, in perfect agreement with Trouton's rule.The reader interested in the general development of Trouton's law can consult a previous publication (Wisniak, 2001).
In a paper published in 1882, Jacques Rose Ferdinand Sarrau (1837-1904) showed that that for different explosive gases, the value of the covolume, which plays an important role in the theory of explosives, varied between 0.0008 and 0.0012 (Sarrau, 1882). François Ernest Mallard (1833-1894) and Henri Louis Le Châtelier (1850-1930) suggested adopting the value b = 0.001 when calculating the power of an explosive (Mallard and Le Châtelier, 1885). Berthelot found that the theorem of the corresponding states did not agree with this supposition, which was applicable only to a special group of substances characterized by having a constant ratio between the critical temperature and the critical pressure. According to the van der Waals equation of state, in order to have b = 0.001 it was necessary for the ratio Tc /Pc to be about 2.2, a value quite different from the one for the gases studied. Berthelot calculated from his equation of state that for b to vary between 0.0008 and 0.0012, the ratio Tc /Pc had to vary between 3 and 4.3, which fitted very well the experimental value for the explosive gases released during chemical reactions. For complex organic substances the ratio is not observed, being 12 for benzene, 13 for ether, 19 for naphthalene, etc. (Berthelot, 1915b).