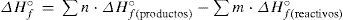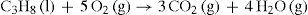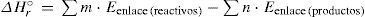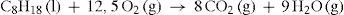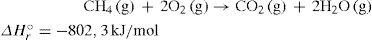This paper presents a description about the potentiality and versatility of the spreadsheets in science teaching, and it shows some examples in chemistry teaching.
Uno de los números del vigésimo aniversario de Educación Química estuvo dedicado a la educación y las TICs y al desafío que implican para los profesores. En él, Talanquer (2009) discute los principales factores que dificultan la integración de las TICs en las aulas, Daza y otros (2009) describen las distintas posibilidades de las TICs y algunos proyectos internacionales, Jiménez y Núñez (2009) desarrollan el tema del aprendizaje cooperativo asistido por computadora especialmente en el entorno de Internet, Rosas y otros (2009) definen el aula inteligente y muestran ejemplos para cambiar las clases tradicionales y Giordan y Gois (2009) hacen una revisión de los entornos virtuales de aprendizaje de la química en función de la visualización que ofrecen y de su accesibilidad.
A continuación se presenta una descripción de la potencialidad y versatilidad de las hojas de cálculo en la enseñanza de las ciencias y algunos ejemplos de actividades para la enseñanza de la química. Como se muestra en este trabajo existen pocas revisiones y experiencias publicadas en español sobre el empleo de la hoja de cálculo en la enseñanza de la química.
La hoja de cálculoLas hojas de cálculo están generalmente instaladas en cualquier computadora y una de las más difundidas en la actualidad es la aplicación Microsoft Excel®. La hoja de cálculo es un programa que al abrirlo muestra un formato de tabla, una matriz de celdas identificadas por una letra para cada columna (vertical) y por un número para cada fila (horizontal). Las dimensiones de las celdas son variables y pueden contener: números, letras, o almacenar fórmulas matemáticas y mostrar su resultado numérico. Este formato en celdas es fácilmente comprensible y con pocas instrucciones el usuario puede comenzar a utilizarlo. En ellas se pueden realizar secuencias de operaciones donde los datos pueden ser cambiados o estar enlazados a otros. También permiten visualizar y tratar la información en variadas formas gráficas. La bibliografía destaca que el empleo de las hojas de cálculo favorece el desarrollo de las siguientes habilidades de:
- •
Organización y presentación de la información, que puede ser visualizada en una variedad de formas: tablas de números, diagramas, gráficos y animaciones.
- •
Interpretación cuali y cuantitativas. Análisis de datos, extraer regularidades y generalizaciones, sacar conclusiones.
- •
Comunicación. Secuenciación lógica de planteos.
- •
Resolución de problemas. Búsqueda de estrategias.
- •
Toma de decisiones. A partir de modelos.
- •
Elaboración de informes. Organización del texto.
- •
Control. Revisión y depuración de lo realizado.
Una de las principales ventajas de operar con una hoja de cálculo es que un usuario puede realizar tareas de programación (o de resultados similares) sin necesidad de dominar un lenguaje específico. Además de que su funcionamiento básico es estable en el tiempo, dado que las actualizaciones mantienen las principales características de su funcionamiento. En cambio, los lenguajes de programación suelen ser reemplazados totalmente por otros.
Una clasificación de las utilidades de la computadora en educación (Reparaz y Tourón, 1991) distingue dos categorías fundamentales: (1) como fin del aprendizaje curricular y (2) como medio del aprendizaje curricular. En la primera categoría incluyen la alfabetización y la programación; en la segunda diferencian: (2a) como medio directo, por ejemplo, ejercitación y práctica, tutorial, simulación y juego, programación y resolución de problemas, tutorial inteligente, y (2b) como medio indirecto, por ejemplo procesadores de textos, bases de datos, y otras aplicaciones. En esta última categoría, de herramientas sin relación directa al contenido escolar, engloban a las hojas de cálculo. Sin embargo, como se planteará más adelante, y dada la versatilidad de las mismas, con las hojas de cálculo se pueden realizar actividades de aprendizaje que se ubican en otras categorías, como crear simulaciones o reemplazar tareas de un lenguaje de programación. Incluso pueden constituirse en un fin de aprendizaje, si consideramos a la alfabetización informática como una necesidad de las personas para desenvolverse en la sociedad actual.
Otros autores clasifican a la computadora como una “herramienta de productividad personal” (ej. procesador de textos), o como un “objeto con el que pensar”. De nuevo, la versatilidad de usos de la hoja de cálculo y los distintos enfoques para su utilización, permitirían ubicarla en ambas categorías, o en posiciones intermedias entre ellas.
Con respecto al aprendizaje de las hojas de cálculo, algunos autores (como Drier, 2001) destacan la ventaja de aprender su uso con contenidos específicos en lugar de hacerlo en cursos básicos de computación que no garantizan, necesariamente, una transferencia real de ese conocimiento a las asignaturas.
Utilización de las hojas de cálculo en la enseñanza de las cienciasLas hojas de cálculo alcanzaron difusión en la década de los 80 con el desarrollo de las computadoras personales, principalmente en temas de economía, y rápidamente comenzaron a ser usadas en ambientes científicos. Por ejemplo se emplearon los programas VisiCalc o Lotus 1-2-3 en la realización de cálculos o en la ejecución de modelos matemáticos.
En la enseñanza de las ciencias, aproximadamente en 1985, aparecen los primeros artículos sobre aplicaciones educativas de las “spreadsheets” en revistas norteamericanas, por ejemplo en The Science Teacher, Journal of Chemical Education, etc. En 1987, Osborn advierte que este recurso ha sido poco considerado y realiza una invitación desde la revista inglesa School Science Review a la presentación de contribuciones, que se sucedieron en los años siguientes hasta la actualidad. A modo de ejemplo: (a) artículos generales: Goodfellow (1990); Carson (1997); (b) en Biología: Carson (1996); (c) en Química: Brosnan (1990); Finnemore (1990), y (d) en Física: Penman (1990), Diament y Cleminson (1996).
En el Journal of Chemical Education, se presentan las primeras experiencias con VisiCalc en 1985. Por ejemplo, Rosenberg (1985) comenta las generalidades de una hoja de cálculo y la utiliza para calcular el potencial de electrodo; Sparrow (1985) la usa para el seguimiento de las notas de sus alumnos, e Ibrahim (1986) la emplea para el tratamiento de datos experimentales de laboratorio. Las propuestas están dirigidas a estudiantes de distintos niveles educativos, incluso se han publicado algunos libros que incluyen actividades para los últimos años de la primaria y para el nivel medio, como por ejemplo: Whitmer (1993) y Tebbutt y Flavell (1995).
En Educación Química se encuentra la presentación de un programa, basado en la hoja de cálculo, sobre el equilibrio químico (Quílez y Castelló, 1996) y más recientemente (Rojas et al., 2010) se ha empleado para el cálculo de pH de la gráfica de Flood.
En la enseñanza de las ciencias, la utilidad de las hojas de cálculo radica en que permiten realizar:
- •
Registro de resultados: tablas de resultados obtenidos en experimentos.
- •
Análisis de datos: tratamiento de errores, cálculos de promedios y otras funciones estadísticas.
- •
Búsqueda de relaciones: uso de distintas fórmulas para valorar las relaciones existentes entre las variables de un fenómeno.
- •
Cálculos: simplificar o evitar cálculos complejos.
- •
Uso de gráficos: uso de distintos tipos de gráficos para representar los datos.
- •
Ajuste de curvas: ajustar las relaciones de los datos a curvas (lineal, potencial, exponencial). El análisis de algunas curvas permite obtener nueva información, como por ejemplo parámetros que se obtienen de la pendiente de una recta.
- •
Modelización: responder preguntas del tipo “¿Qué pasa si?”. Introducción de datos a un modelo (por ej. a una ecuación o conjunto de ecuaciones relacionadas) y obtención de resultados.
Sin embargo, la utilización de las hojas de cálculo ha tenido poco impacto en las aulas de países latinoamericanos, posiblemente porque los docentes, por más que hayan contado con el equipamiento necesario, no han podido acceder a la información publicada disponible, ni intercambiar experiencias (Raviolo, 2002).
Actividades con la hoja de cálculo en la enseñanza de la químicaNuestra experiencia con las hojas de cálculo se ha centrado en dos líneas de trabajo. La primera, sobre la búsqueda y diseño de actividades tipo, que constituyan un puente entre el contenido científico abordado y el conocimiento operativo de informática (Raviolo, 1999 y 2003). La segunda consiste en la evaluación de experiencias didácticas implementadas sobre la aplicación de ese tipo de actividades con alumnos; por ejemplo, la realización de la totalidad de las prácticas de problemas de química, de un curso universitario, en la sala de informática utilizando la hoja de cálculo (Raviolo, 2002 y 2005).
En esos artículos se definieron y ejemplificaron seis tipos de actividades para enseñar y aprender química con una hoja de cálculo. Estas actividades mostraron procedimientos para enfrentar problemas de química en un sentido amplio, que constituyen un nexo para transferir actividades de aprendizaje de la química a la hoja de cálculo.
En este trabajo se ejemplificarán dos tipos de actividades, renovadas con respecto a las formuladas en los artículos iniciales:
- a.
Construcción de una “tabla-programa”.
- b.
Construcción de una “planilla de cálculo” (secuencia de operaciones encadenadas).
- c.
Y en un posterior artículo se presentará un nuevo tipo de actividad: Verificación y re-creación de simulaciones.
La construcción de una “tabla-programa” consiste en utilizar en forma directa y sistemática los datos presentados en una tabla. Para ello se transforma la tabla con datos en una hoja que calcule automáticamente el resultado buscado de la aplicación de una fórmula. Esta fórmula requiere los datos presentados en la tabla. A continuación se ejemplifica la construcción de estas “tablas-programas” con dos cuestiones de termoquímica: cálculo de la energía de reacción a partir de las entalpías estándar de formación y cálculo de la energía de reacción a partir de las energías de enlace. Esta idea está inspirada en una actividad presentada por Brosnan (1990).
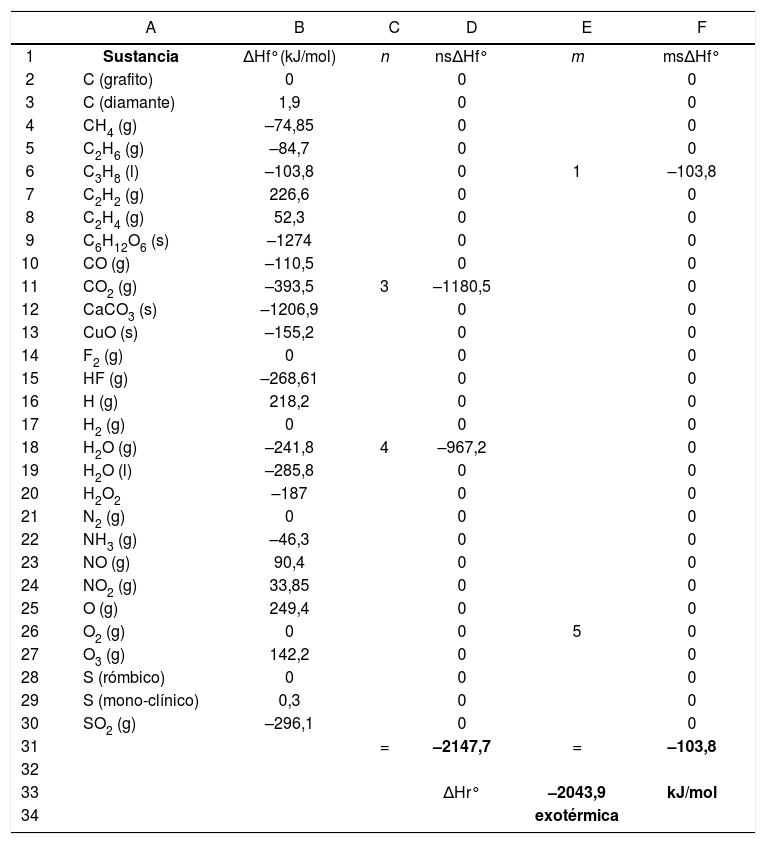
Tabla-programa 1Una forma de hallar la entalpía de reacción, tal como lo plantean los textos de química general, es a partir de las entalpías estándar de formación (ΔHf°), que se encuentran tabuladas a 25°C y 1 atm, mediante la ecuación:
siendo n y m los coeficientes estequiométricos de productos y reactivos respectivamente. En la tabla 1 se muestra cómo se transformó una tabla de energías estándar de formación en una “tabla-programa” que calcula automáticamente la variación de entalpía estándar de una reacción, en este caso la reacción de combustión del propano; se utiliza la función “SI” para indicar si la reacción es exotérmica o endotérmica. La ecuación química ajustada es:Tabla-programa para ilustar la variación de entalpía estándar de una reacción
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 1 | Sustancia | ΔHf°(kJ/mol) | n | nsΔHf° | m | msΔHf° |
| 2 | C (grafito) | 0 | 0 | 0 | ||
| 3 | C (diamante) | 1,9 | 0 | 0 | ||
| 4 | CH4 (g) | –74,85 | 0 | 0 | ||
| 5 | C2H6 (g) | –84,7 | 0 | 0 | ||
| 6 | C3H8 (l) | –103,8 | 0 | 1 | –103,8 | |
| 7 | C2H2 (g) | 226,6 | 0 | 0 | ||
| 8 | C2H4 (g) | 52,3 | 0 | 0 | ||
| 9 | C6H12O6 (s) | –1274 | 0 | 0 | ||
| 10 | CO (g) | –110,5 | 0 | 0 | ||
| 11 | CO2 (g) | –393,5 | 3 | –1180,5 | 0 | |
| 12 | CaCO3 (s) | –1206,9 | 0 | 0 | ||
| 13 | CuO (s) | –155,2 | 0 | 0 | ||
| 14 | F2 (g) | 0 | 0 | 0 | ||
| 15 | HF (g) | –268,61 | 0 | 0 | ||
| 16 | H (g) | 218,2 | 0 | 0 | ||
| 17 | H2 (g) | 0 | 0 | 0 | ||
| 18 | H2O (g) | –241,8 | 4 | –967,2 | 0 | |
| 19 | H2O (l) | –285,8 | 0 | 0 | ||
| 20 | H2O2 | –187 | 0 | 0 | ||
| 21 | N2 (g) | 0 | 0 | 0 | ||
| 22 | NH3 (g) | –46,3 | 0 | 0 | ||
| 23 | NO (g) | 90,4 | 0 | 0 | ||
| 24 | NO2 (g) | 33,85 | 0 | 0 | ||
| 25 | O (g) | 249,4 | 0 | 0 | ||
| 26 | O2 (g) | 0 | 0 | 5 | 0 | |
| 27 | O3 (g) | 142,2 | 0 | 0 | ||
| 28 | S (rómbico) | 0 | 0 | 0 | ||
| 29 | S (mono-clínico) | 0,3 | 0 | 0 | ||
| 30 | SO2 (g) | –296,1 | 0 | 0 | ||
| 31 | = | –2147,7 | = | –103,8 | ||
| 32 | ||||||
| 33 | ΔHr° | –2043,9 | kJ/mol | |||
| 34 | exotérmica |
Operaciones:
Celda D2: =C2*B2 y replicar hacia abajo hasta el final de la tabla
Celda F2: =E2*B2 y replicar hacia abajo hasta el final de la tabla
Celda D31: =SUMA(D2:D30)
Celda F31: =SUMA(F2:F30)
Celda E33: =D31-F31
Celda E34: =SI(E33<0;“exotérmica”; “endotérmica”)
Las columnas A y B constituyen un fragmento de la tabla original. Introduciendo los coeficientes estequiométricos en las columnas C y E, la tabla-programa calcula automáticamente la energía de reacción.
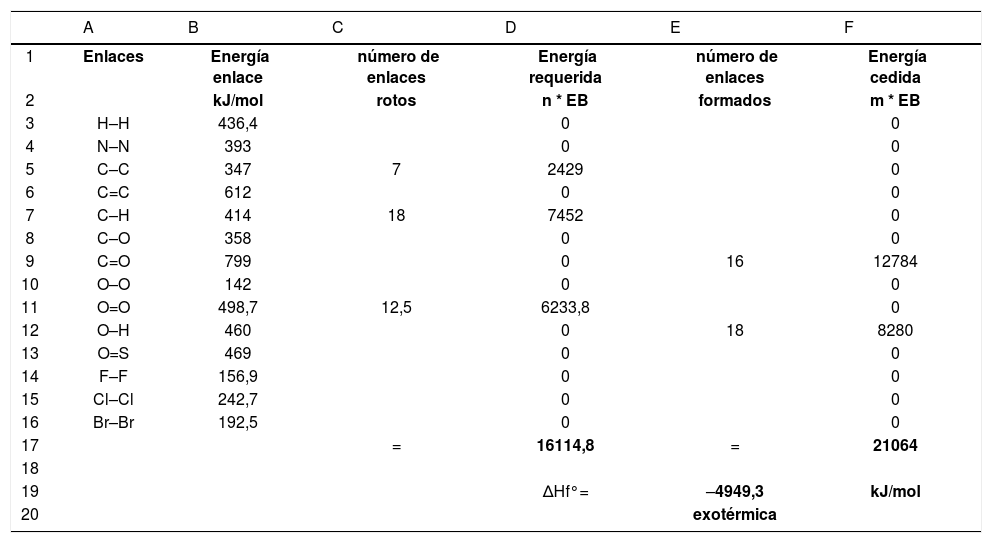
Tabla-programa 2Se puede calcular la entapía de reacción a partir de las energías de enlace con la siguiente fórmula:
siendo m y n el número de enlaces de reactivos y productos respectivamente. Se utilizan tablas de energías de enlace promedio como las que aparecen en textos de química general (tabla 2).Tabla-programa para ilustar la variación de entalpía estándar de una reacción
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 1 | Enlaces | Energía enlace | número de enlaces | Energía requerida | número de enlaces | Energía cedida |
| 2 | kJ/mol | rotos | n * EB | formados | m * EB | |
| 3 | H–H | 436,4 | 0 | 0 | ||
| 4 | N–N | 393 | 0 | 0 | ||
| 5 | C–C | 347 | 7 | 2429 | 0 | |
| 6 | C=C | 612 | 0 | 0 | ||
| 7 | C–H | 414 | 18 | 7452 | 0 | |
| 8 | C–O | 358 | 0 | 0 | ||
| 9 | C=O | 799 | 0 | 16 | 12784 | |
| 10 | O–O | 142 | 0 | 0 | ||
| 11 | O=O | 498,7 | 12,5 | 6233,8 | 0 | |
| 12 | O–H | 460 | 0 | 18 | 8280 | |
| 13 | O=S | 469 | 0 | 0 | ||
| 14 | F–F | 156,9 | 0 | 0 | ||
| 15 | Cl–Cl | 242,7 | 0 | 0 | ||
| 16 | Br–Br | 192,5 | 0 | 0 | ||
| 17 | = | 16114,8 | = | 21064 | ||
| 18 | ||||||
| 19 | ΔHf°= | –4949,3 | kJ/mol | |||
| 20 | exotérmica |
Operaciones:
Celda D3: =C3*B3 y replicar hacia abajo hasta el final de la tabla
Celda F3: =E3*B3 y replicar hacia abajo hasta el final de la tabla
Celda D17: =SUMA(D3:D16)
Celda F17: =SUMA(F3:F16)
Celda E19: =D17-F17
Celda E20: =SI(E19<0;“exotérmica”; “endotérmica”)
Para el caso de la combustión completa del octano, la ecuación química ajustada es:
Las columnas A y B constituyen un fragmento de la tabla original. Introduciendo los números de enlaces que se rompen y se forman en las columnas C y E, la tabla-programa calcula automáticamente la energía de reacción.
b. Construcción de una “planilla de cálculo”Este tipo de actividad consiste en la construcción de una secuencia de operaciones encadenadas, es decir la construcción de “pequeños programas” que al introducir datos de entrada realicen automáticamente una serie de operaciones y den resultados de salida.
Los estudiantes tienen que organizar la secuencia de pasos, de datos y cálculos, de forma tal que las operaciones estén encadenadas y que sea claro de leer por otra persona. Además seguir el formato: “magnitud-valor-unidad”, que permite que se pueda hacer referencia a ese valor en operaciones posteriores. Este formato ayuda a que los estudiantes identifiquen las magnitudes y tengan en cuenta las unidades, y no cometan errores relacionados con ellas. Estas cuestiones promueven el desarrollo de habilidades de comunicación.
El siguiente problema trata sobre la distancia que debería recorrer un auto para amortizar el costo de conversión de nafta (gasolina) a gas. Fue formulado inicialmente por Jansen (2000) sin la utilización de la hoja de cálculo, para la conversión de gasolina a propano en los Estados Unidos.
Este problema puede presentarse con un enunciado abierto en donde los alumnos tengan que buscar cuáles son los datos y variables relevantes y diseñar una estrategia de resolución. Por ejemplo: ¿Cuántos kilómetros debe hacer un auto para cubrir los gastos de conversión de gasolina a gas?
En la resolución siguiente, para el caso de los Estados Unidos, se toman los datos originales de Jansen para un auto que consume 13 litros de nafta cada 100 km, y además se asume que:
- •
El propano es un gas que se vende bajo presión como un líquido.
- •
La nafta es sólo octano puro: C8H18.
- •
Que ambos combustibles se queman completamente.
- •
El auto viaja una distancia fija por kilojoule de energía independientemente de la fuente de energía.
- •
Con el propano o el octano se logra la misma eficiencia en la combustión.
Como datos se requieren los calores de combustión del propano y del octano líquidos, para ello pueden utilizarse las “tablas-programas” como se hizo anteriormente; para calcular el ΔHf° del propano se usan las tablas de entalpías de formación estándar; y, dado que seguramente no esté disponible el ΔHf° del octano, para calcular su calor de combustión se emplea las tablas de energías de enlace promedio.
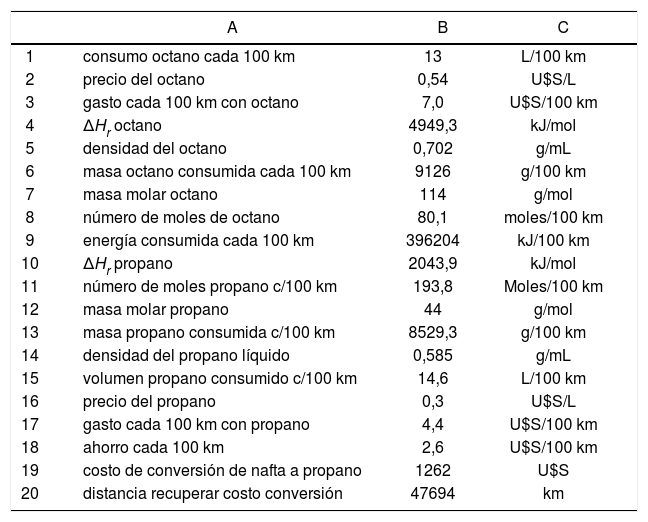
Luego, se realiza una “planilla de cálculo” que permite introducir los datos de entrada y que, a través de una serie de operaciones encadenadas, calcula automáticamente el resultado final, es decir la cantidad de kilómetros que deberá recorrer el automóvil para amortizar el costo de la reconversión a gas. Recordando que se asume el mismo consumo de energía para recorrer 100 km con octano que con propano. Los resultados obtenidos para los calores de combustión (en valor absoluto al ser considerados como energía), así como los demás datos necesarios, deben ser incluidos en la planilla (tabla 3).
Planilla para calcular la cantidad de kilómetros que deberá recorrer el automóvil para amortizar el costo de la reconversión a gas
| A | B | C | |
|---|---|---|---|
| 1 | consumo octano cada 100 km | 13 | L/100 km |
| 2 | precio del octano | 0,54 | U$S/L |
| 3 | gasto cada 100 km con octano | 7,0 | U$S/100 km |
| 4 | ΔHr octano | 4949,3 | kJ/mol |
| 5 | densidad del octano | 0,702 | g/mL |
| 6 | masa octano consumida cada 100 km | 9126 | g/100 km |
| 7 | masa molar octano | 114 | g/mol |
| 8 | número de moles de octano | 80,1 | moles/100 km |
| 9 | energía consumida cada 100 km | 396204 | kJ/100 km |
| 10 | ΔHr propano | 2043,9 | kJ/mol |
| 11 | número de moles propano c/100 km | 193,8 | Moles/100 km |
| 12 | masa molar propano | 44 | g/mol |
| 13 | masa propano consumida c/100 km | 8529,3 | g/100 km |
| 14 | densidad del propano líquido | 0,585 | g/mL |
| 15 | volumen propano consumido c/100 km | 14,6 | L/100 km |
| 16 | precio del propano | 0,3 | U$S/L |
| 17 | gasto cada 100 km con propano | 4,4 | U$S/100 km |
| 18 | ahorro cada 100 km | 2,6 | U$S/100 km |
| 19 | costo de conversión de nafta a propano | 1262 | U$S |
| 20 | distancia recuperar costo conversión | 47694 | km |
Operaciones:
Celda B3: =B1*B2
Celda B6: =B4/B5
Celda B10: =B6*B8*B9/B7
Celda B11: =B10/1000
Celda B13: =B11*B12
Celda B14: =B3-B13
Celda B16: =B15/B14*100
Ese automóvil deberá andar cerca de 48.000 km para amortizar el costo de la instalación del equipo de gas. Cambiando cualquier dato de entrada, como por ejemplo el consumo cada 100 kilómetros, el programa recalcula automáticamente el resultado final, con lo que se puede determinar que a mayor consumo, menor será la distancia necesaria a recorrer para amortizar el gasto de reconversión. Lo mismo ocurre si aumenta el precio de la gasolina. Puede solicitarse a los estudiantes que utilicen gráficos para ilustrar esas tendencias.
Estos planteos se pueden adecuar a la situación de cada país, por ejemplo en Argentina se utiliza gnc (gas natural comprimido), que es fundamentalmente metano y se vende por metro cúbico en condiciones estándar de presión y temperatura. Esto permitiría, luego de la resolución de la situación anterior, presentar a los alumnos un problema con enunciado abierto como el siguiente: ¿Cuántos kilómetros debe hacer un auto para cubrir los gastos de conversión a gas de acuerdo a los costos actuales de nuestra localidad?
La ecuación química ajustada de la combustión completa del metano es:
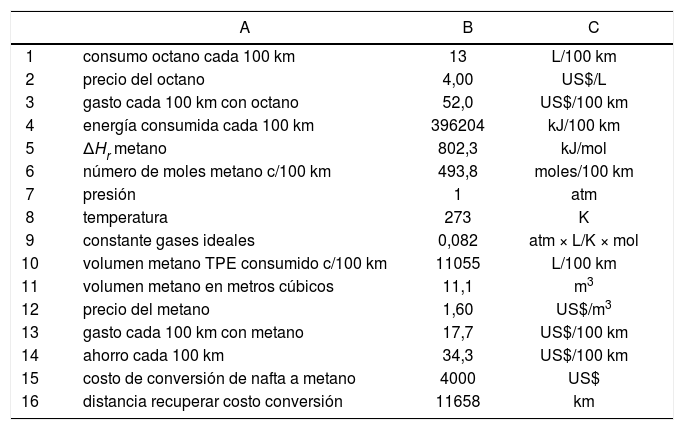
Con sólo 12.000 km (tabla 4) se amortiza el costo de la conversión de nafta a GNC, lo que explica el auge de este combustible en Argentina, aunque también se reconoce que existe una pérdida de potencia del automóvil cercana al 10%.
Tabla-programa para calcular la amortización de la conversión de nafta a GNC en Argentina
| A | B | C | |
|---|---|---|---|
| 1 | consumo octano cada 100 km | 13 | L/100 km |
| 2 | precio del octano | 4,00 | US$/L |
| 3 | gasto cada 100 km con octano | 52,0 | US$/100 km |
| 4 | energía consumida cada 100 km | 396204 | kJ/100 km |
| 5 | ΔHr metano | 802,3 | kJ/mol |
| 6 | número de moles metano c/100 km | 493,8 | moles/100 km |
| 7 | presión | 1 | atm |
| 8 | temperatura | 273 | K |
| 9 | constante gases ideales | 0,082 | atm × L/K × mol |
| 10 | volumen metano TPE consumido c/100 km | 11055 | L/100 km |
| 11 | volumen metano en metros cúbicos | 11,1 | m3 |
| 12 | precio del metano | 1,60 | US$/m3 |
| 13 | gasto cada 100 km con metano | 17,7 | US$/100 km |
| 14 | ahorro cada 100 km | 34,3 | US$/100 km |
| 15 | costo de conversión de nafta a metano | 4000 | US$ |
| 16 | distancia recuperar costo conversión | 11658 | km |
Operaciones:
Celda B3: =B1*B2
Celda B6: =B1*B5*1000
Celda B8: =B6/B7
Celda B9: =B4*B8
Celda B11: =B9/B10
Celda B13: =B11*B12
Celda B15: =B13/B14/1000
Celda B17: = B15*B16
Celda B18: =B3-B17
Celda B20: =B19/B18*100
Se dice que las TICs para la educación cuestionan los papeles de la escuela y del profesor. Este cuestionamiento no significa hacer prescindibles a los establecimientos educativos y a los docentes; por el contrario, son los profesores los que darán el marco adecuado y formal para el aprendizaje. Las TICs cuestionan la institución educativa actual cuando ésta mantiene una actitud cerrada, impermeable y reticente a los cambios. Su inclusión debe cambiar los estilos de enseñanza más allá de un cambio cosmético, de un barniz bajo el cual se esconde la vieja enseñanza tradicional. No se trata de una actualización y modernización de herramientas tecnológicas, se trata de superar lo que tan a menudo se afirma: ciencia y alumnos en el siglo xxi y escuelas y profesores del siglo xix.
Las hojas de cálculo constituyen un recurso accesible para favorecer que los profesores se inicien con experiencias de TICs en el aula y puedan sentirse creativos. En este sentido, Carson (1997) sostiene que la utilidad de una hoja de cálculo para la enseñanza de las ciencias está limitada más por nuestra imaginación que por el potencial del software.
El trabajo del alumno frente a la computadora facilita lograr el objetivo de respetar los ritmos individuales de aprendizaje. Aunque el docente debe planificar la articulación de los momentos individuales y grupales, que favorezcan la colaboración y el enriquecimiento conceptual. Para que generen aprendizajes significativos los estudiantes deben estar intelectualmente activos: los alumnos realmente interactuando, pensando y poniendo en juego los conceptos científicos, y de esta forma, superar el uso anecdótico y meramente activista de la computadora.
Una vez que los estudiantes adquieran cierto dominio y confianza en actividades sencillas como las aquí presentadas pueden encarar en forma autónoma la solución de otros problemas de enunciado cerrado o abierto. Al emplear estas actividades como tareas extra aula aumentan el tiempo que los alumnos están operando con los contenidos de química. Una experiencia exitosa consistente en la realización de los trabajos prácticos con la hoja de cálculo en un curso de química general puede documentarse en Raviolo (2002 y 2005).
En definitiva, las principales ventajas de las hojas de cálculo son:
- a)
están realmente disponibles,
- b)
constituyen una herramienta poderosa y con una amplia variedad de usos,
- c)
los alumnos y profesores están cada vez más familiarizados con ellas,
- d)
son de rápido aprendizaje y uso inmediato,
- e)
en muchos casos pueden remplazar a un lenguaje de programación de difícil aprendizaje,
- f)
motivan a los estudiantes,
- g)
respetan el ritmo individual de aprendizaje y posibilitan el trabajo en grupo cooperativo, y
- h)
mejoran la confianza de los profesores en las tecnologías informáticas.