In the present work a study of the buffer capacity behavior for poly-donor systems is presented. The buffer capacity is analyzed when the pKa values of polyprotic acids are near and far between them. Furthermore, the effect of size of the system over the buffer capacity is also analyzed, as well as the effect of dilution on the poly-donor system.
En el presente trabajo se hace un estudio del comportamiento de la capacidad buffer de sistemas polidonadores. Se analiza la capacidad buffer cuando los valores de pKa de los ácidos polipróticos están cercanos y alejados unos de otros. Además, se analiza el efecto del tamaño del sistema sobre la capacidad buffer así como el efecto de dilución del sistema polidonador.
En los libros de textos contemporáneos de Química Analítica el tema de capacidad buffer se presenta con mayor frecuencia que hace 25 años; sin embargo, prácticamente en todos ellos se presenta el material en unos cuantos párrafos y con poca profundidad cuantitativa, a pesar de que en la literatura científica se encuentran varios trabajos sobre capacidad buffer de sistemas monodonadores y polidonadores de protones. Entre estos trabajos se pueden citar los de De Levie (1996), Rojas-Hernández y col. (2012), King y Kester (1990), Efstathiou, Tarapčík & Beinrohr, Rilbe (1992), Asuero (2007), Asuero y Michałowski (2011), Skoog y col. (2005), Urbansky y Schock (2000) y Segurado (2003).
De Levie ha mostrado expresiones generales para titulaciones ácido base de mezclas arbitrarias que describen todo el proceso de titulación (1996). Rojas-Hernández y col., en un trabajo reciente (2012), también muestran expresiones analíticas de volumen agregado (de base fuerte o ácido fuerte) a mezclas de un mismo sistema polidonador, como función del pH. Es por ello que también en ese trabajo se presentan expresiones analíticas de la primera derivada de pH con respecto al volumen, así como de su capacidad buffer con efecto de dilución.
En el presente trabajo se retoman las ecuaciones que presentan Rojas-Hernández y col. (2012) para construir curvas de valoración, de la primera derivada y de la capacidad buffer para algunos sistemas triprótricos, con el fin de discutir cuantitativamente características de la capacidad buffer que normalmente se establecen en los libros de texto en forma cualitativa. Con ello se espera contribuir al desarrollo de conceptos mejor establecidos y justificados en este tema.
TeoríaExpresiones para curvas de valoración de mezclas de especies en un mismo sistema polidonadorUn sistema polidonador es el conjunto de las especies que forman el sistema y puede ser representado como HnLn−a/Hn−1Ln−a−1+/…/HLa−1−/La−/H+, donde HnLn−a es el ácido poliprótico (o polidonador), La– es la base poliprótica (o componente del ácido polidonador), y la especie neutra es HaL; H+ es la partícula que se intercambia en la reacción, n es el número de protones del ácido poliprótico, a es la carga de la base poliprótica en valor absoluto. Las especies que van desde H(n–1)L(n–a–1)+ hasta HL(a–1)– son los anfolitos del sistema, la especie HjL(j–a) puede representar todas las especies que contienen a L si j ∈ {0,1,…,a,…,n} (Rojas-Hernández y col., 2012).
Los equilibrios de formación global del sistema polidonador tienen la siguiente forma
donde βj son las constantes de formación global, considerar que β0 = 1 y j ∈ {0, 1, …, n}.
La especie HnL(n–a) es el polidonador de protones, y la especie La– es el polirreceptor de protones. Las expresiones para determinar el volumen de base fuerte o ácido fuerte agregado (Vb y Va respectivamente) a un sistema formado por una mezcla de especies del mismo sistema polidonador de protones son (Rojas-Hernández y col., 2012):
Los términos f j representan las fracciones molares de las especies que contienen al componente L, tales que:
donde j ∈ {0, 1, …, n}. Con estas fracciones se construyen los diagramas de distribución de los sistemas polidonadores de dos componentes, en este caso L y H. Cabe mencionar que en este trabajo se usa la simbología fj de acuerdo con Rojas-Hernández y col. (2012) y (Moya-Hernández y col., 2002), porque, aunque en muchos libros de texto estas fracciones molares también se pueden representar como αi=α(n–j) (Christian, 2009; Skoog y col., 2005), o αHjL (Harris, 2012); se consideró que el contador i aumenta en sentido inverso al contador j, o la nomenclatura queda muy recargada, lo que complica las expresiones de las sumas mostradas en las diferentes ecuaciones.
Expresiones de dpH/dV: puntos de equivalenciaLas ecuaciones (2) y (3) son funciones de una variable, el pH, por lo que sus expresiones analíticas para sus primeras derivadas también pueden obtenerse en forma analítica (dVb /dpH y -dVa /dpH respectivamente). El recíproco de estas derivadas permite obtener las derivadas de dpH/dVb y -dpH/dVa, (Rojas-Hernández y col., 2012); estas expresiones son:
Cabe mencionar que la derivada -d pH /dVa lleva un signo negativo debido a que al agregar ácido fuerte a un sistema dado, el pH disminuye.
Expresiones de capacidad buffer con efecto de dilución: βdilDe igual manera, Rojas-Hernández y col. (2012) muestran las expresiones (7) y (8) para calcular la capacidad buffer de sistemas polidonadores, las cuales se obtienen haciendo uso de las funciones recíprocas de las ecuaciones (5) y (6), es decir, dVb/dpH y –dVa /dpH.
Aplicación del modelo variando la naturaleza del sistema polidonadorEn este trabajo se estudia la capacidad buffer de disoluciones que contienen diferente sistema polidonador de protones, clasificándolos a su vez, con respecto a la distancia que existe entre los valores de pKa vecinos de los pares ácido-base.
En esta sección se muestra el estudio del sistema de fosfatos PO4'=H3PO4/H2PO4−/HPO42−/PO43−/H+ y del sistema de citratos Cit'=H3Cit/H2Cit−/HCit2−/HCit3−/H+, mostrando que la teoría presentada anteriormente es aplicable a cualquier sistema polidonador de n protones. Los gráficos que se muestran en este trabajo de pH = f(V), dpH/dV y de βdil = f (pH) se han construido con un simulador de curvas elaborado en Microsoft Office Excel.
Sistemas polipróticos con valores de pKa separadosEl sistema de fosfatos (PO4’) es un sistema tridonador de protones, los valores de pKa son pKa1 = 2.1 (Turner y col., 1992), pKa2 = 6.75 (Saha y col., 1996) y pKa3 = 11.71 (Martínez-Calatayud y col., 1987). Si 10 mL de una solución que contiene a las especies H3PO4 y H2PO4- con [PO4’]T = 0.5 M, se valora con NaOH de concentración Cb = 0.5 M, es posible construir gráficos como: la curva de valoración, la primera derivada y la capacidad buffer con dilución.
El uso de la numeración en el subíndice de pKa indica el orden de disociación de los equilibrios de acidez sucesivos, a partir del poliácido (iupac, 2012). A veces se omite el subíndice «a» (Harris, 2007). Para el caso del sistema de PO4’, el conjunto de equilibrios de disociación ácida está dado en las ecs. 9 a 11:
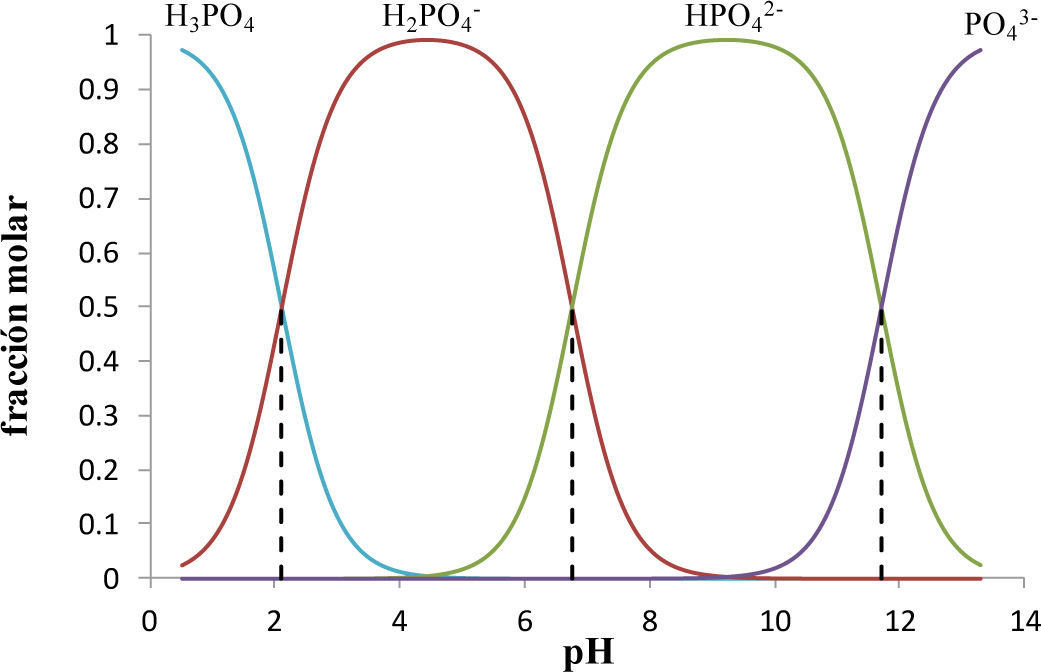
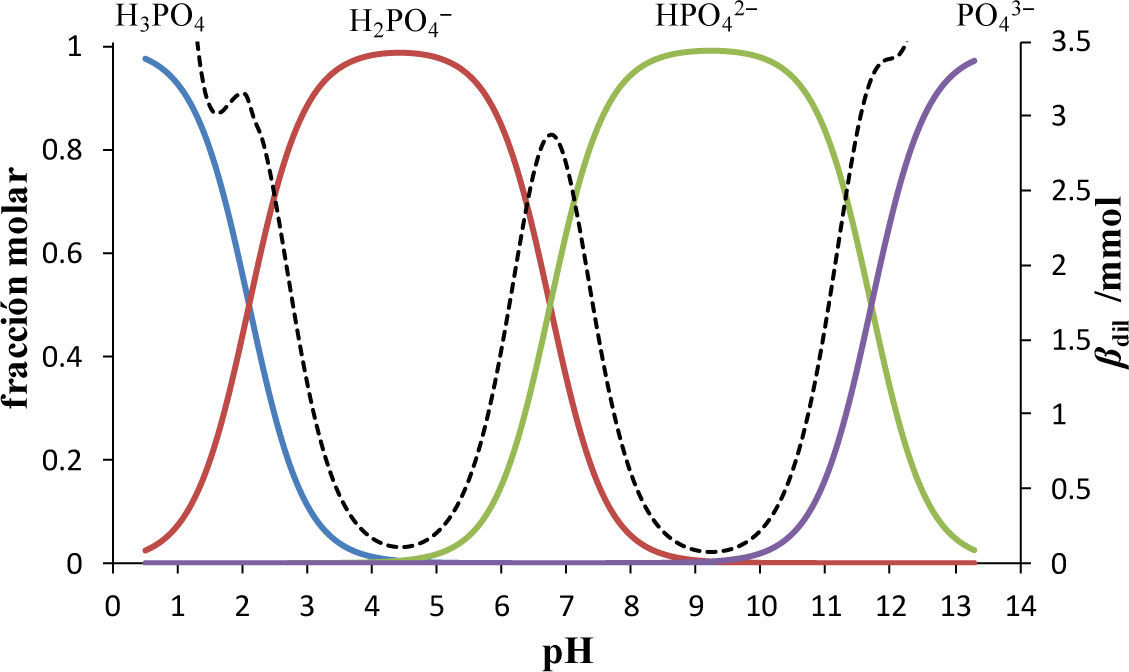
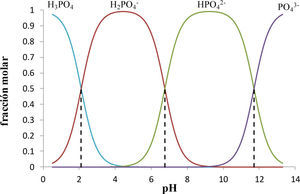
En la figura 1 se muestra el diagrama de distribución correspondiente al sistema de fosfatos. Los puntos de intersección de las fracciones entre dos especies conjugadas que contienen a PO43-, está dado por el valor de
Diagrama de distribución de especies químicas del sistema de PO4’.
pK a1 = 2.1 (Turner y col., 1992), pK a2 = 6.75 (Saha y col., 1996) y pK a3 = 11.71 (Martínez-Calatayud y col., 1987).
—fH3PO4,—fH2PO4−,—fH2PO42−,—fH2PO43−,, --- Intersección con valores de pH igual a pK a1, pK a2 y pK a3.
En estas intersecciones, las fracciones molares de las especies predominantes son iguales. Si la fracción de la especie HjL(j–a) es más grande que todas las demás especies que contienen a L, se dice que esa especie predomina en el sistema. Basta observar el intervalo de pH donde la fracción de una especie es más grande que cualquier otra para construir el diagrama de zonas de predominio (DZP) de especies que contienen L en el sistema (Rojas-Hernández y col., 1995).
En la figura 1 también se observa que cuando las fracciones molares de las especies predominantes se igualan, las concentraciones de las especies de cada par, H3PO4/H2PO4−,H2PO4−/HPO42− y HPO42−/PO43−, son iguales. Se observa también que todas las especies de PO43− predominan en un cierto intervalo de pH.
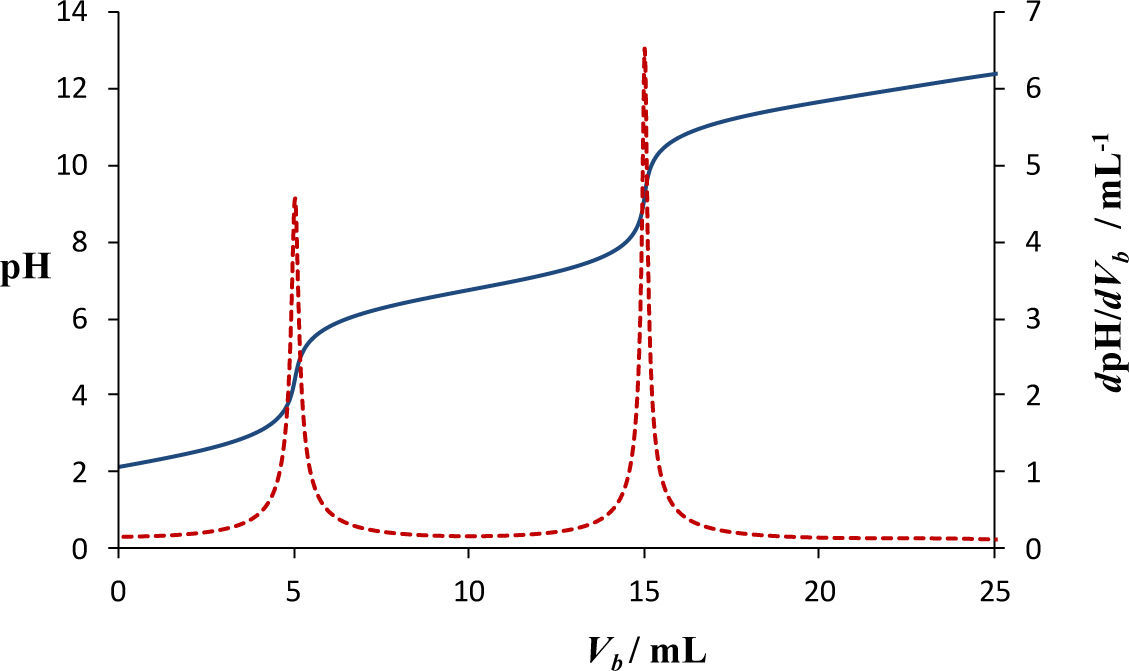
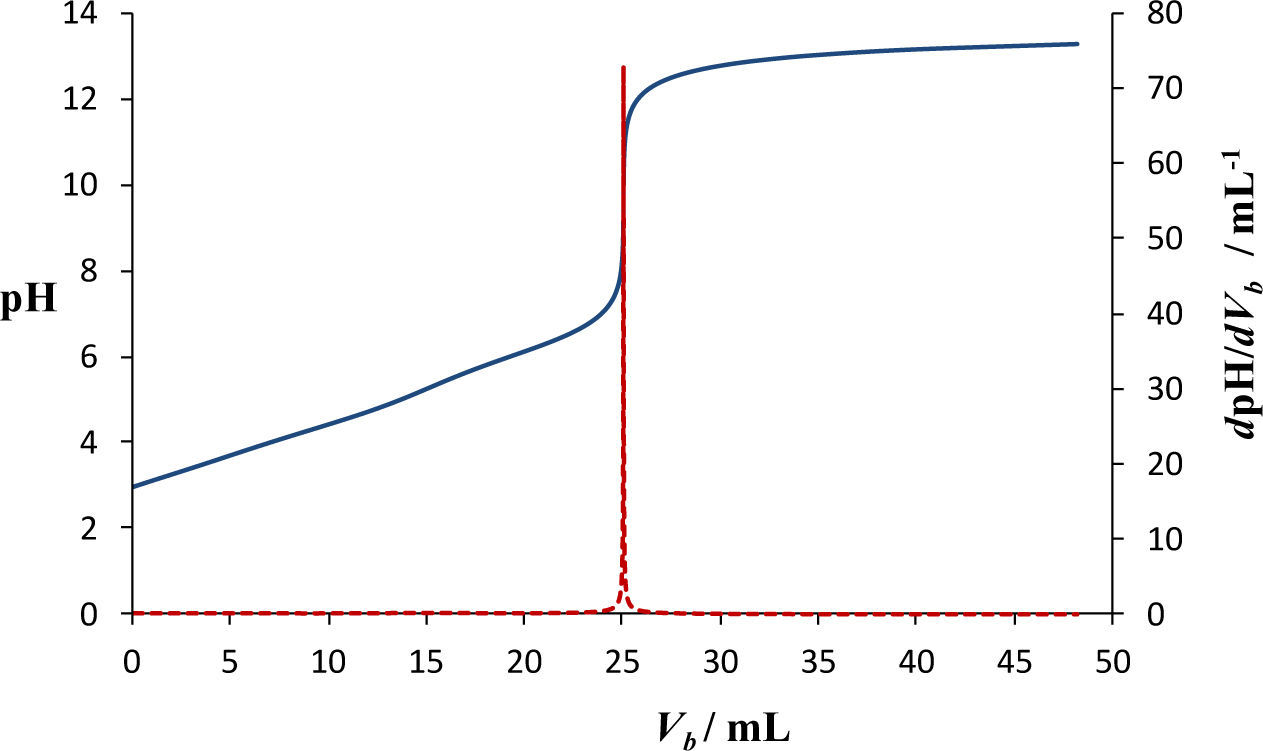
Las curvas de pH = f (Vb) y de dpH/dVb calculadas empleando las ecuaciones (2) y (4), respectivamente, se muestran en la figura 2. Las ecuaciones mostradas hasta el momento, aunque constituyen un modelo robusto, no proporcionan una interpretación sobre las reacciones que ocurren durante el proceso de valoración. Sin embargo, el modelo es una gran herramienta debido a que predice, de manera rápida y sin aproximaciones, la forma de la curva de valoración que se espera obtener experimentalmente.
Debido a que el sistema de PO4’ es un sistema tridonador de protones, en la curva de valoración de pH = f (Vb) se esperaría observar tres puntos de equivalencia; sin embargo, esto no es así ya que la tercera reacción de valoración, RV3, (ec. 15) no es cuantitativa y solo se observan los puntos de equivalencia de la primera y la segunda reacciones de valoración, RV1 y RV2 respectivamente, (ecs. 13 y 14). Esto se explica empleando el método de Charlot basado en la teoría ácido-base de Brønsted.
Los textos mencionan que β tiene un valor máximo cuando se cumple que pH = pKa de un par conjugado ácido-base, y que este par debe usarse para imponer el pH en un intervalo pKa –1 < pH < pKa + 1. Finalmente, este comportamiento es generalizado para sistemas polipróticos, pero los textos no explican la razón para justificar dichas afirmaciones.
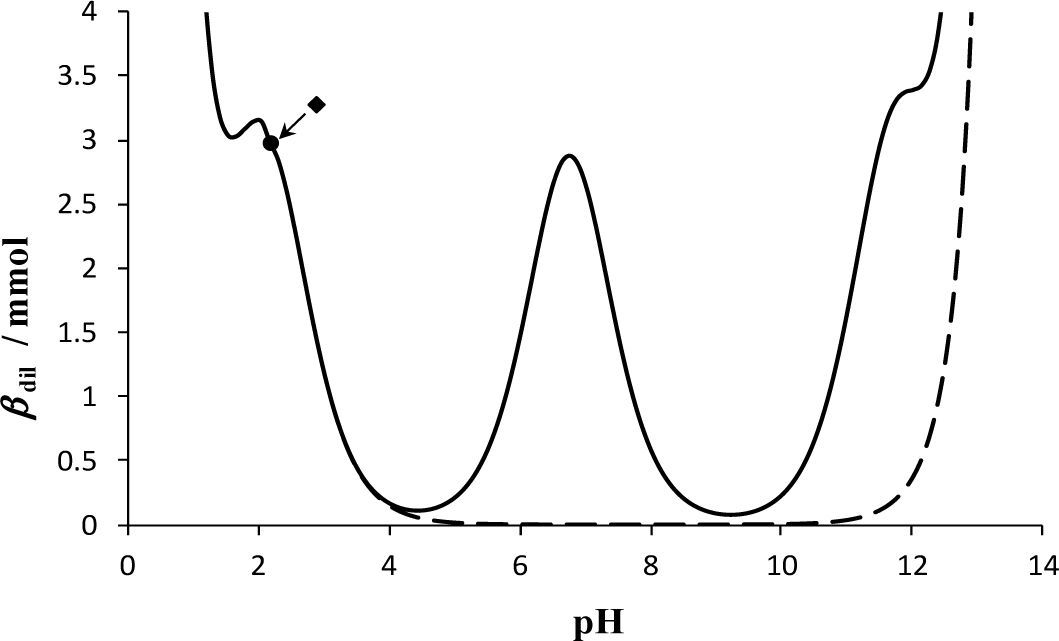
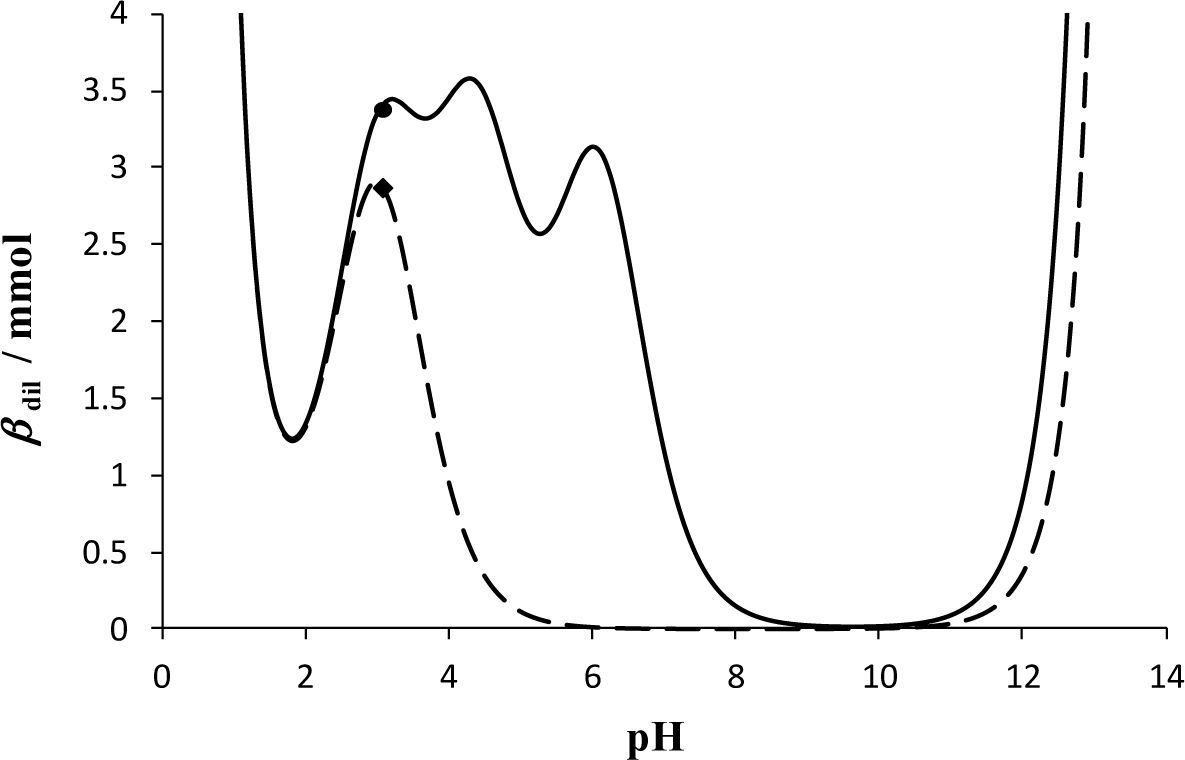
La figura 3 muestra las curvas de βdil = f (pH) de un sistema monodonador con pKa = 2.1 (línea punteada) y concentración total 0.5 M, así como la del sistema de fosfatos a la misma concentración y con valores de pKa1 = 2.1, pKa2 = 6.75 y pKa3 = 11.71 (línea continua). De acuerdo con los libros de texto, se esperaría observar tres picos (máximos) en la curva de βdil para el sistema de fosfatos. Esto no es así porque el máximo colocado en el valor de pH = pKa3 = 11.71 está enmascarado por una alta concentración de OH- (de la base fuerte agregada) y porque hay mucha dilución para llegar a este punto (Rojas-Hernández y col., 2012).
Curva de βdil = f (pH) con Cb = Ca = 0.5 M. La línea continua corresponde a una solución que contiene H3PO4 y H2PO4− con [PO4’]T = 0.5 M, Vo =10mL. La línea segmentada corresponde a una solución conteniendo un par HL/L- con [L’]T = 0.5 M, Vo = 10mL, pKa = 2.1. • Sistema inicial de PO4’, ♦ Sistema inicial de L’.
También se observa en la figura 3 que el máximo correspondiente a pKa1 = 2.1 del sistema de fosfatos presenta el mismo comportamiento que el máximo del sistema HL/La–. Esto es cierto porque el valor de pKa2 es mucho más grande que pKa1. Además, en las zonas donde βdil es pequeña (o nula), pequeñísimas adiciones de base fuerte o ácido fuerte generan un cambio muy grande en el pH de la disolución.
Finalmente, la figura 3 muestra que a la derecha o izquierda del máximo de βdil (βdil máx = 2.9 mmol) dado por el par H2PO4−/HPO42− con pKa2 = 6.75, βdil disminuye una tercera parte de su valor máximo; βdil = βdil máx / 3 = 0.97 mmol, para valores de pH = 5.75 y 7.75. Estos valores de pH definen prácticamente el mismo intervalo establecido en los libros de texto, pero esto solo es cierto cuando los picos en βdil no están cerca de los extremos de la escala de pH como se observa en el pico dados por el par H3PO4/H2PO4− con pKa1 = 2.1.
La relación que existe entre los diagramas de distribución y la capacidad buffer, puede observarse en la figura 4. Se observa que βdil es máxima en los puntos de intersección entre dos especies químicas predominantes, en estos puntos las fracciones molares (o concentraciones) son iguales; por lo tanto, la capacidad buffer se encuentra en un valor de pH igual al valor del pKa, es decir donde se tiene presente el ácido y la base conjugada.
Diagrama de distribución y curva de βdil del sistema de PO4’, partiendo de una solución que contiene H3PO4 y H2PO4− con [PO4’]T = 0.5 M, Vo =10mL, empleando concentraciones de ácido fuerte y base fuerte Cb = Ca = 0.5 M. pKa1 = 2.1 (Turner y col., 1992), pKa2 = 6.75 (Saha y col., 1996) y pKa3 = 11.71 (Martínez-Calatayud y col., 1987).
—fH3PO4,—fH2PO4−,—fH2PO42−,—fH2PO43−,, --- βdil.
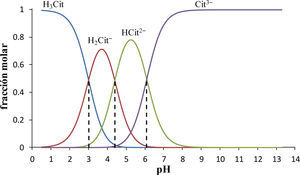
En este apartado se estudia el sistema de citratos (Cit’) por tener valores de pKa cercanos uno del otro. Estos valores de pKa son: pKa1 = 3.0, pKa2 = 4.4 y pKa3 = 6.1 (Ringbom, 1979). Si se considera la valoración de 10 mL de una solución que contiene a las especie H3Cit y H2Cit- con [Cit’]T = 0.5 M, con base fuerte de concentración Cb = 0.5 M.
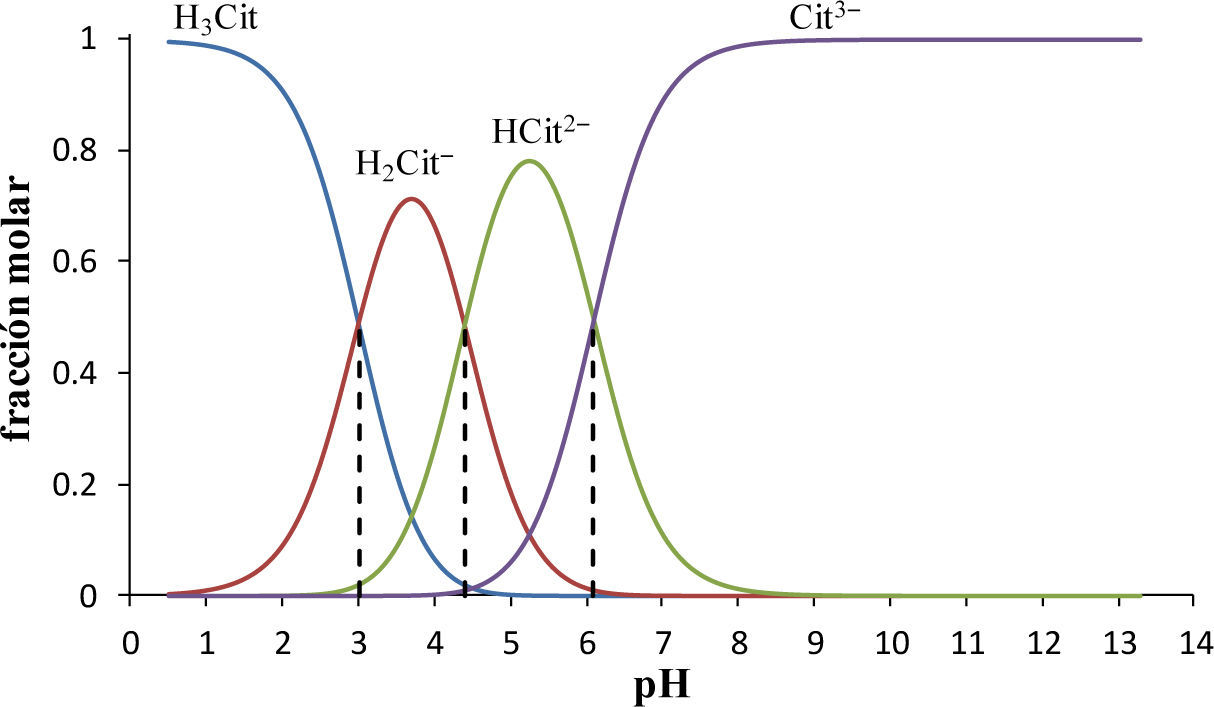
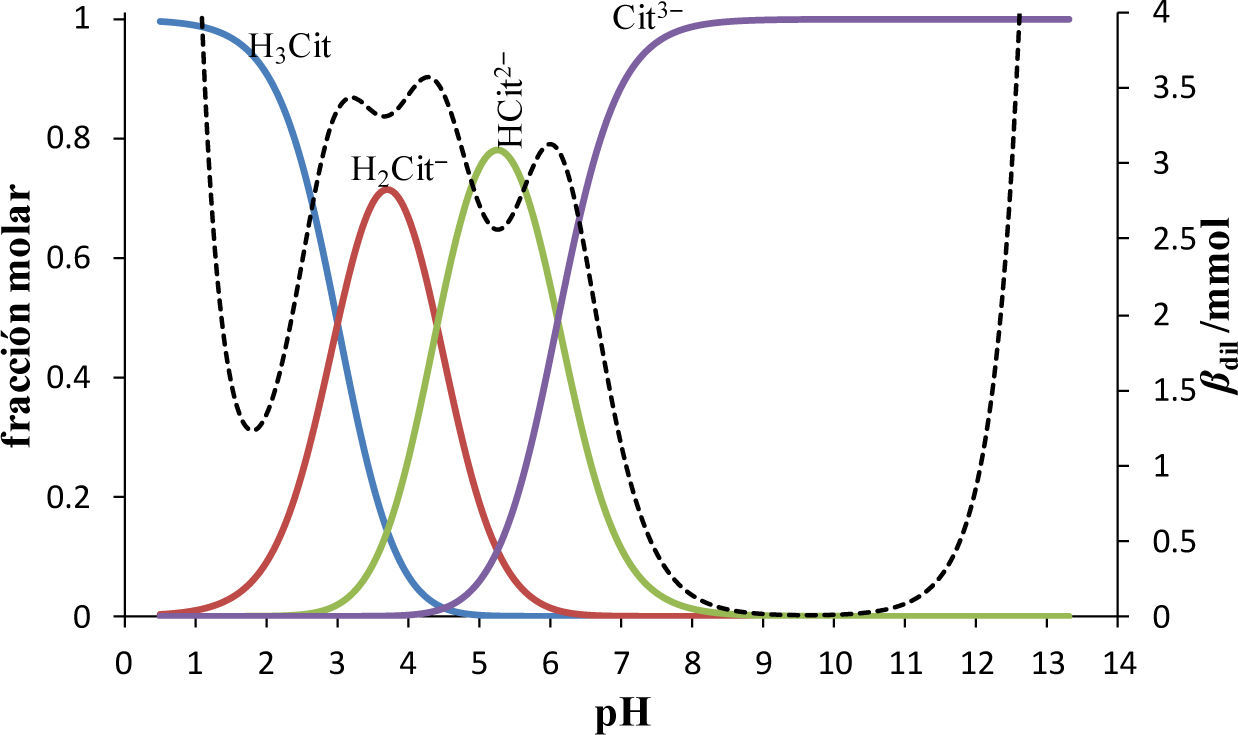
En la figura 5 se muestra el diagrama de distribución de las especies que contienen Cit3-; la interpretación de estos gráficos es similar a la que se hace en la figura 1, correspondiente al sistema de PO43–. Asimismo, se observa que todas las especies de Cit3- predominan en cierto intervalo de pH.
Diagrama de distribución de especies químicas del sistema de Cit’. pKa1 = 3.0, pKa2 = 4.4 y pKa3 = 6.1 (Ringbom, 1979).—fH3Cit,—fH2Cit−,—fH2PO2−,—fCit3−,, ---- Intersección con valores de pH igual a pKa1, pKa2 y pKa3.
Las curvas pH = f(Vb) y de dpH/dVb para la valoración mencionada anteriormente se muestra en la figura 6. En teoría, la curva de valoración debería presentar tres puntos de equivalencia debido a que el sistema de Cit’ es un sistema tridonador de protones, pero solo se ve el tercer punto de equivalencia, porque la primera y segunda reacciones de valoración, RV1 y RV2 respectivamente (ecs.16 y 17), son poco cuantitativas.
Los libros de texto no mencionan cuál sería el comportamiento esperado de un buffer que contiene un sistema de poliprótico con valores de pKa cercanos entre sí. La figura 7 muestra la comparación de la curva de βdil = f (pH) de un sistema de monoprótico HL/L- (línea punteada) con la curva del sistema de Cit’ (línea continua) considerando que pKa = pKa1 = 3.0 (Ringbom, 1979) y la misma concentración total.
Curvas de βdil = f(pH) con Cb = Ca=0.5 M. La línea continua corresponde a una solución que contiene H3Cit y H2Cit– [Cit’]T = 0.5M, Vo = 10mL, pKa1 = 3.0, pKa2 = 4.4 y pKa3 = 6.1 (Ringbom, 1979). La línea segmentada corresponde a una solución conteniendo un par HL/L- con [L’]T = 0.5M, Vo = 10mL, pKa = 3.0. • Sistema inicial de Cit’, ♦ Sistema inicial de L’.
La figura 7 muestra tres picos asimétricos traslapados en la curva de βdil del sistema citratos, sus valores máximos no corresponden con los valores de pKa en la escala de pH, debido a que, al menos dos pares conjugados ácido-base contribuyen a βdil para cada pico; provocando además, que βdil del sistema de citratos sea mayor que el de un pico determinado solamente por un par ácido-base.
La figura 7 también muestra que para el sistema de citratos, con pKa1 ≈ pKa2 y pKa2 ≈ pKa3, el intervalo útil de imponer pH va de 2.0 a 7.1 aproximadamente, porque βdil es grande en este intervalo. Esto sugiere que para los sistemas de polipróticos con valores de pKa cercanos, que van desde pKai a pKaj, se puede encontrar una capacidad buffer adecuada en un intervalo de pH útil que va desde pKai–1 a pKaj +1.
La relación que existe entre los diagramas de distribución y la capacidad buffer (línea punteada) del sistema de Cit’ se observa en la figura 8. Se muestra que los máximos de βdil no corresponden con los valores de pH = pKa debido a que los pares ácido-base están interferidos entre sí por sus valores de pKa cercanos.
Diagrama de distribución y curva de βdil del sistema de Cit’, partiendo de una solución que contiene H3Cit y H2Cit– con [Cit’]T = 0.5M, Vo = 10mL, empleando concentraciones de ácido fuerte y base fuerte Cb = Ca = 0.5 M. pKa1 = 3.0, pKa2 = 4.4 y pKa3 = 6.1 (Ringbom, 1979). —fH3Cit,—fH2Cit−,—fH2PO2−,—fCit3−, --- βdil.
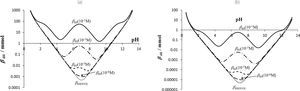
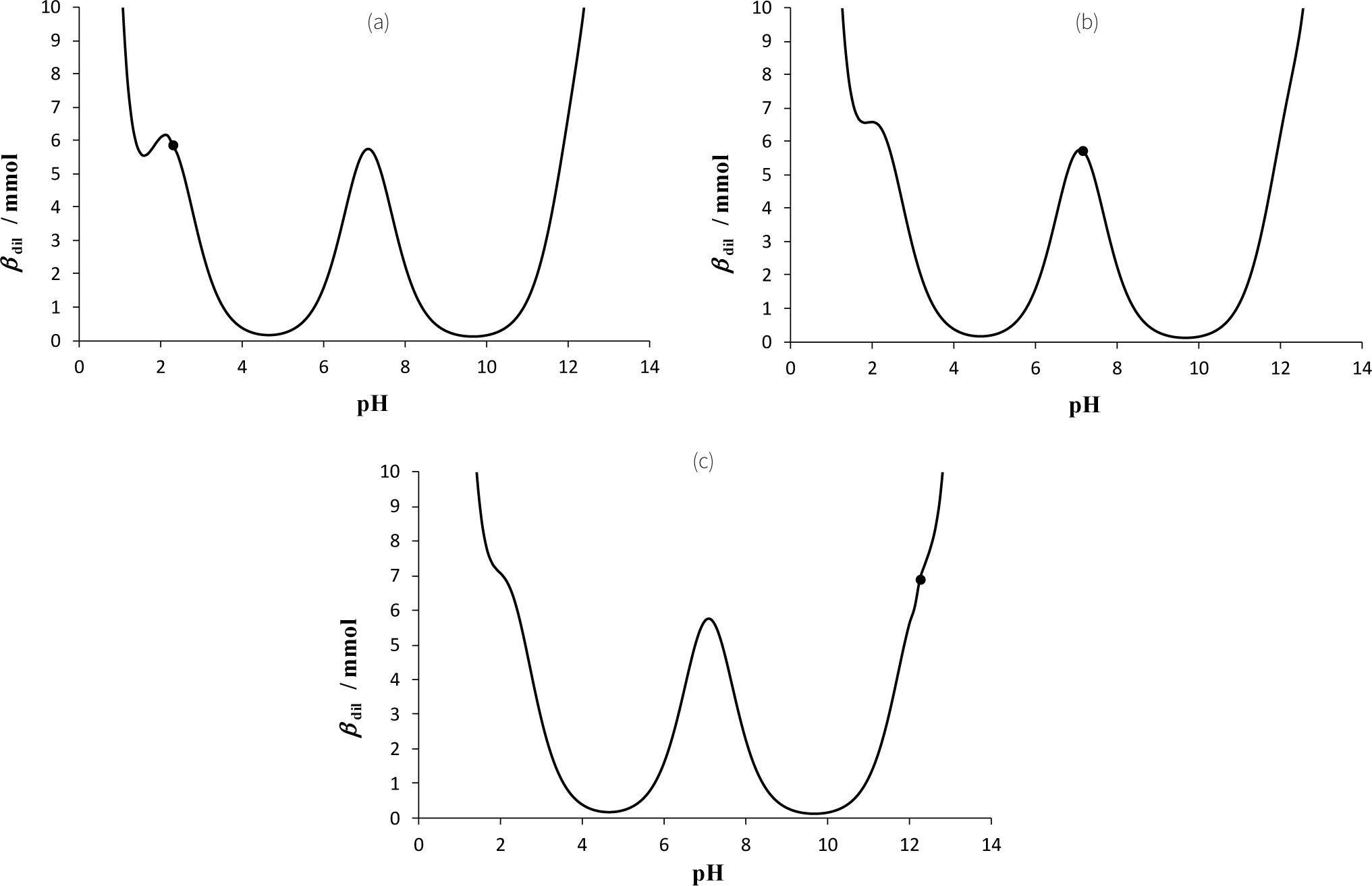
En la figura 9 se muestran curvas de βdil = f (pH) de tres soluciones que contienen diferentes especies del sistema de fosfatos a una concentración total de [PO4’] = 0.5 M, el volumen de estas soluciones son 20 mL los cuales se valoran con NaOH y con HCl de concentración Cb=Ca=0.5 M. Los valores de pKa que se emplean en este apartado son pKa1 = 2.2, pKa2 = 7.1 y pKa3 = 12.3 (Ringbom, 1979). En la figura 9a, la solución está formada porH3PO4=0.25 M y H3PO42−=0.25 M en la mezcla; la figura 9b hace referencia a una solución formada por H2PO4−=0.25 M y HPO42−=0.25 M y, finalmente, la figura 9c se construyó a partir de una solución de HPO42−=0.25 M y PO43−=0.25 M.
Curvas de βdil = f(pH) para el sistema de PO4’con Cb = Ca=0.5 M. • Sistema inicial de PO4’. pKa1 = 2.2, pKa2 = 7.1 y pKa3 = 12.3 (Ringbom, 1979). a) Vo = 20 mL, H3PO4– con [PO4’]T = 0.5 M; b) Vo =20mL, H2PO4– y HPO42– con [PO4’]T = 0.5 M, y c) Vo = 20mL, HPO42– y PO43– con [PO4’]T = 0.5 M.
En la figura 9 se observa que mientras se mantenga la misma concentración total y el mismo volumen inicial del sistema polidonador, la capacidad buffer es prácticamente la misma salvo por el efecto de dilución; por ejemplo, viendo el punto inicial del sistema de PO4’ en la figura 9a, se observa que en esta zona sí existe un máximo en la curva de βdil, mientras que en la 9c esto no es así debido a que el sistema inicial presenta un pH muy básico, y para llegar a este punto (pH ≈ 2.3), se ha agregado mucho ácido HX. Por lo tanto, es posible cambiar de par ácido-base (o zona para fijar el pH) con tan solo agregar la suficiente cantidad de base fuerte o ácido fuerte.
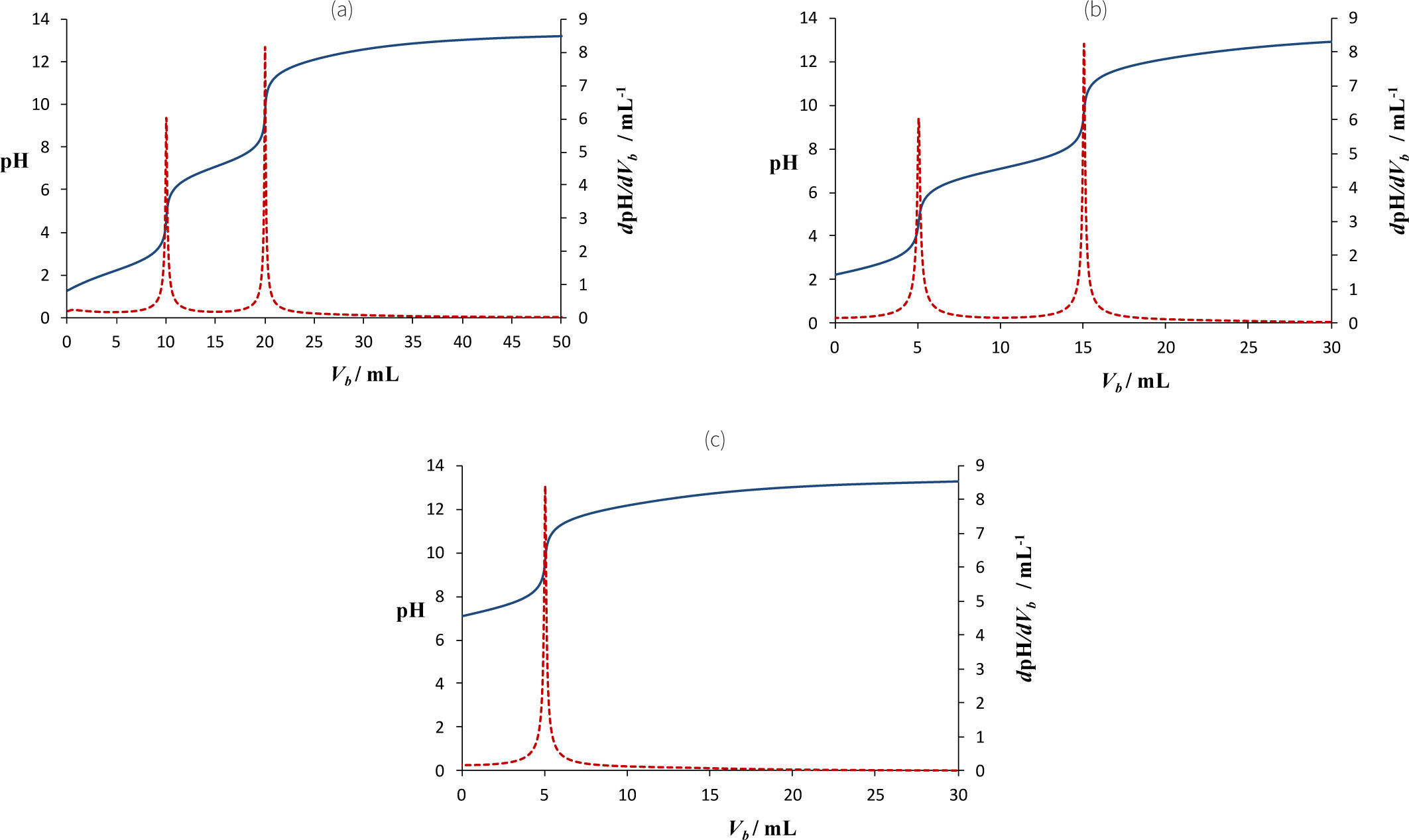
En la figura 10 se analiza el comportamiento de las curvas pH = f(Vb) y de dpH/dVb variando el número de especies de un sistema de PO4′. Se tienen tres soluciones de 10 mL: la primera contiene únicamente [H3PO4] = 0.5 M; la segunda está formada por H3PO4=0.25 M y H2PO4−=0.25 M en la mezcla, y la tercera está formada por las especies: H3PO4=0.125 M, H2PO4−=0.125 M, HPO42−=0.125 M y PO43−=0.125 M. Las tres soluciones tienen una concentración total de fosfatos de [PO4′]T = 0.5 M, las cuales se valoran con base fuerte (NaOH) de concentración Cb = 0.5 M.
Curvas de pH = f (Vb) con Cb = 0.5 M. Sistema inicial de PO4’. pKa1 = 2.2, pKa2 = 7.1 y pKa3 = 12.3 (Ringbom, 1979). a) Vo = mL, H3PO4 con [PO4’]T = 0.5 M; b) Vo = 10mL, H3PO4 y H2PO4– con[PO4’]T = 0.5 M; c) Vo = 10mL, H3PO4, H2PO4–, HPO42– y PO43– con [PO4’]T = 0.5M.
En la figura 10 también se observa que el volumen de los puntos de equivalencia y el número de puntos de equivalencia es diferente para cada solución, lo cual depende de la(s) especie(s) que esté(n) presente(s) cuando la solución llega al equilibrio termodinámico; es decir, cuando todos los equilibrios químicos (de acuerdo con la escala de predicción de reacciones del método de Charlot) tienen valores de los logaritmos de las constantes de equilibrio negativos (log K < 0) (Rojas-Hernández y col., 1995). En la solución 3 existen reacciones previas entre las especies que se mezclan antes de reaccionar con el valorante (OH-).
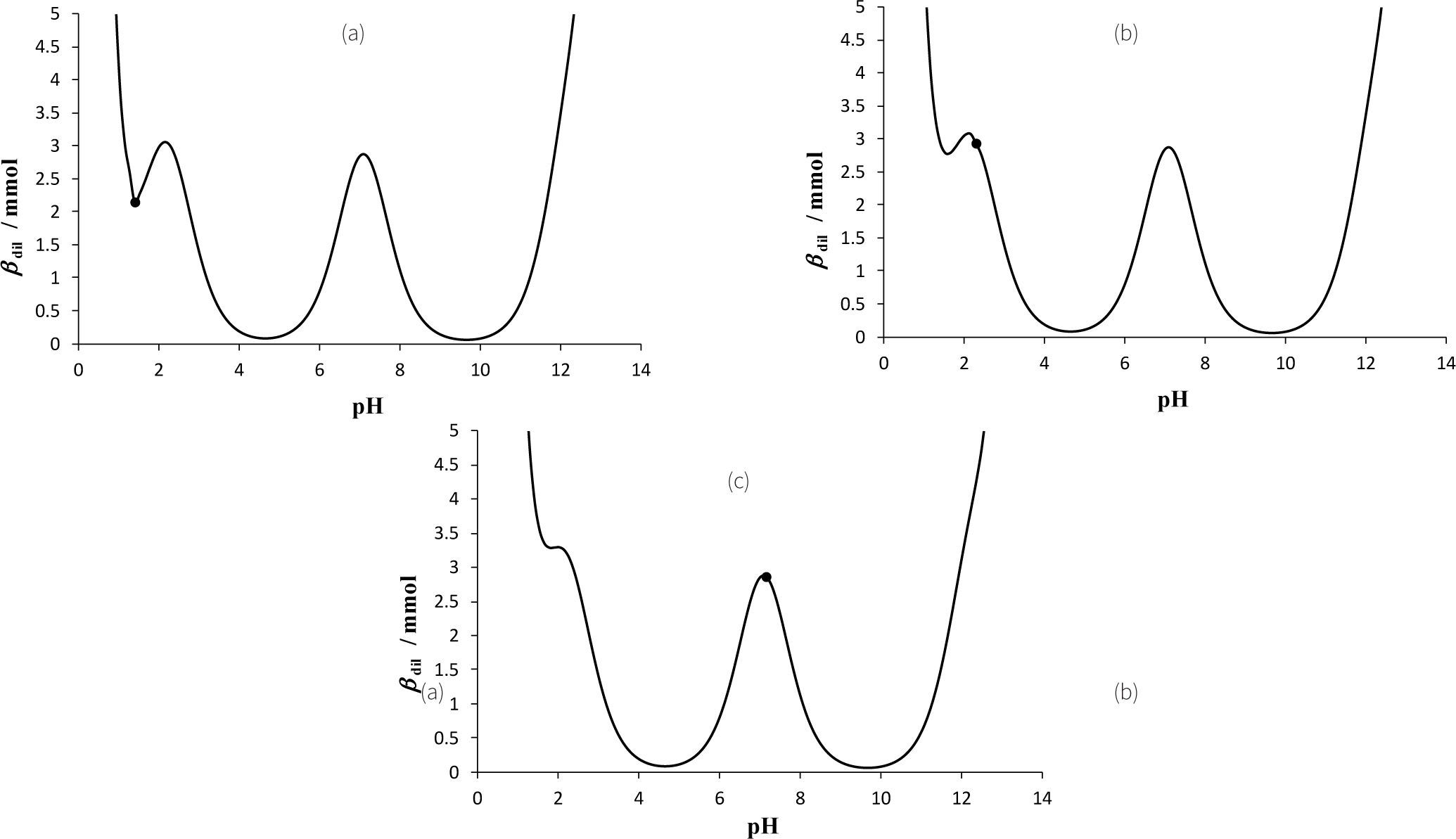
Si ahora se construyen las curvas de βdil para las tres soluciones mencionadas anteriormente, se obtiene la figura 11 empleando ambas valoraciones (Vb y Va).
Curvas de βdil = f(pH) con Cb = 0.5 M. • Sistema inicial de PO4’. pKa1 = 2.2, pKa2 = 7.1 y pKa3 = 12.3 (Ringbom, 1979). a) Vo = 10mL, H3PO4 con [PO4’]T = 0.5 M; b) Vo = 10mL, H3PO4 y H2PO4– con [PO4’]T = 0.5 M, y c) Vo = 10mL, H3PO4 y H2PO4– HPO42– y PO43– con [PO4’]T = 0.5M.
Al analizar la figura 11 se concluye que no importa la especie ni el número de especies de un sistema polidonador que estén presentes en una solución mientras se mantenga la concentración total del sistema, [L′]T, y el mismo V0 ; la βdil es la misma salvo por el efecto de dilución.
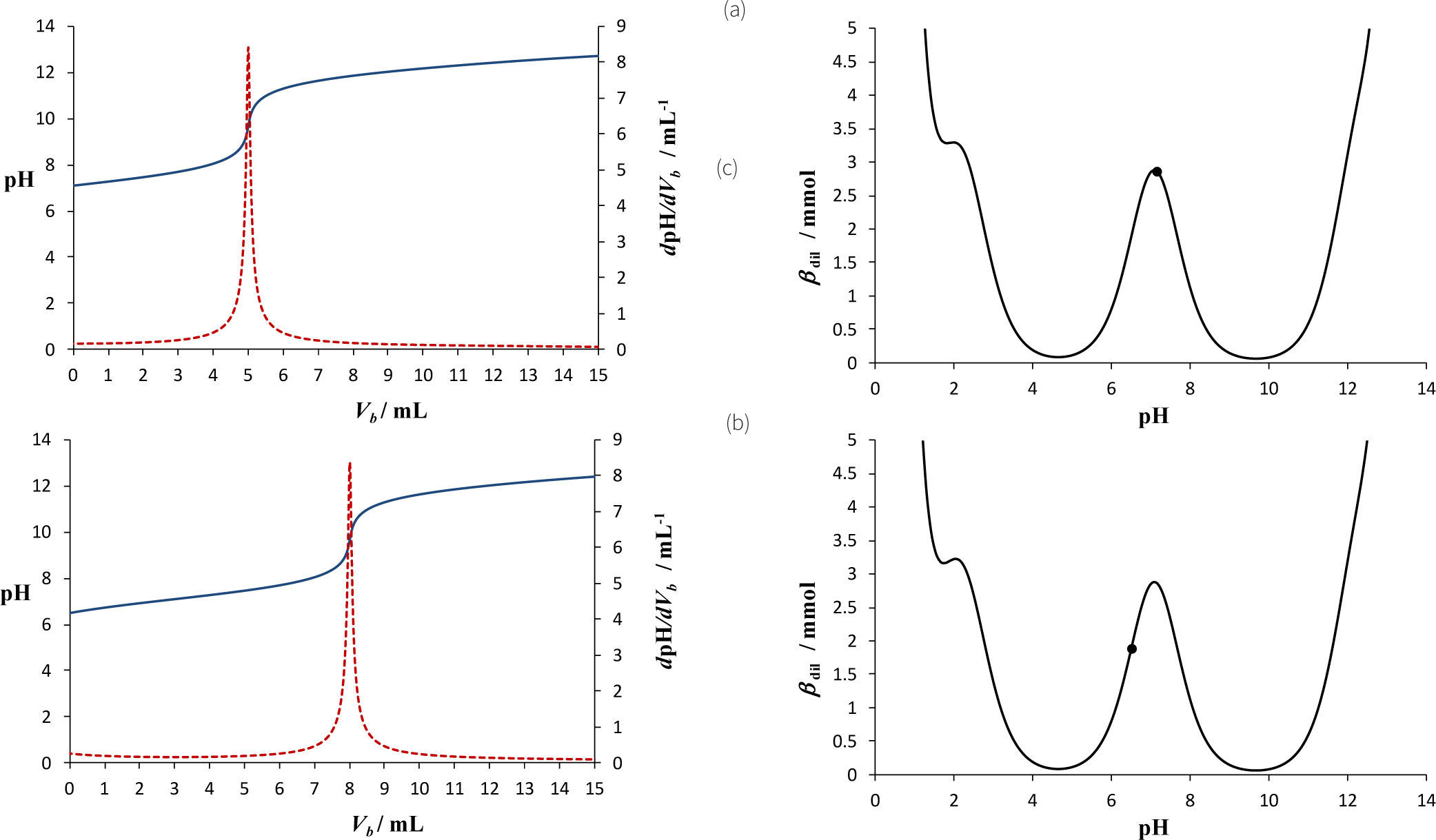
Si se analiza el comportamiento de las curvas pH = fV) y de βdil = f (pH) cuando se mantienen las mismas especies en solución pero a diferentes concentraciones de cada una de ellas, manteniendo igual concentración total del sistema, [L′]T, se concluye que las curvas de valoración también serán diferentes mientras que la βdil será la misma como se muestra en la figura 12. En la figura 12a se aborda el estudio de pH = f (Vb) y de βdil = f(pH) de una solución formada al mezclar 2.5 mL de H3PO4=0.5, 2.5 mL de H2PO4−=0.5, 2.5 mL de H2PO42−=0.5 y 2.5 mL de H2PO43−=0.5, con [PO4′]T = 0.5 M; la figura 12b muestra curvas de pH = f(Vb) y de βdil = f(pH) de una mezcla formada al combinar 2.5 mL de [H3PO4] = 0.6, 2.5 mL de H2PO4−=0.8, 2.5 mL de [HPO42-] = 0.2 y 2.5 mL de [PO43-] = 0.4, con [PO4′]T = 0.5 M.
Curvas de pH = f(Vb), dpH/dVb y βdil = f(pH) teóricas. Cb= Ca = 0.5 M. • Sistema inicial de PO4’. pKa1 = 2.2, pKa2 = 7.1 y pKa3 = 12.3 (Ringbom, 1979). Vo = 10mL, 25mL de [H3PO4] = 0.5, 2.5mL de [H2PO4– = 0.5, 2.5mL de [HPO42–] = 0.5 y 2.5mL de [PO43–] = 0.5 con [PO4’]T = 0.5 M.
Hoy en día, no hay índices de desempeño para evaluar condiciones en las que un buffer es útil para fijar un pH. Muchos de los trabajos que existen en la literatura científica que hablan sobre β no consideran el tamaño del sistema; sin embargo, la capacidad de imponer un valor de pH debería ser mayor para 1 L de solución que para 1 mL de esa misma solución. Como se verá en esta sección, βdil toma en cuenta el tamaño del sistema.
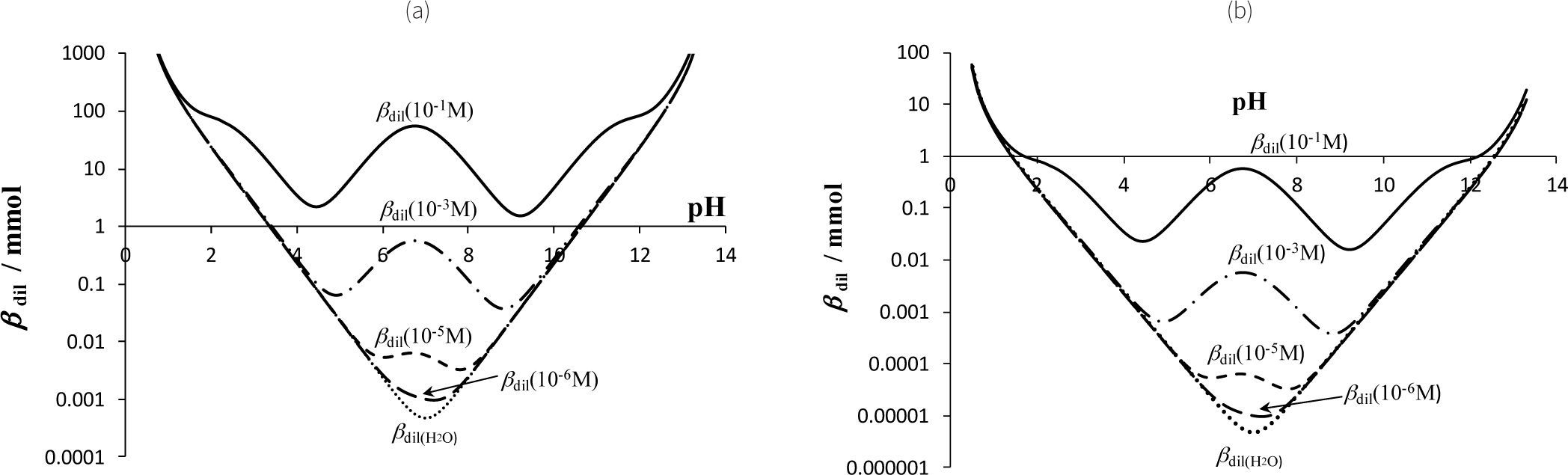
La figura 13 muestra una serie de curvas βdil = f (pH) para soluciones de igual volumen inicial, y que contiene las especies H3PO4 y H2PO4- a diferentes concentraciones del sistema de PO4′. En la figura 13a se considera un V0 = 1000 mL y para la figura 13b, un V0 = 10 mL. Es necesario remarcar que el eje βdil tiene una escala logarítmica a fn de comparar βdil en una amplia gama de concentraciones de PO4′, según lo sugerido por Urbansky y Schok (2000).
Curvas calculadas de βdil = f (pH) de sistemas valorados conteniendo las especies H3PO4 y H2PO4– a concentraciones totales de PO4’ de 10–1 M, 10–3 M, 10–5 M y 10–6 M. La línea punteada representa la curva de βdil = f(pH) del agua y sus partículas básica y ácida. Cb = Ca = 0.5 M. pKa1 = 2.1 (Turner y col., 1992), pKa2 = 6.75 (Saha y col., 1996) y pKa3 = 11.71 (Martínez-Calatayud y col., 1987). a) Vo = 1000 mL, y b) Vo = 10 mL.
Por otra parte, la figura 13 muestra la curva del agua, βdilH2O=fpH, valorada con base fuerte y ácido fuerte, la cual permite ver un límite inferior dado por este disolvente y de sus partículas ácida y básica (línea punteada). Por lo tanto, se establece que cualquier solución, incluso el mismo disolvente, tiene una cierta βdil. Se observa que la disminución de la concentración del sistema de PO4′ provoca que βdil disminuya y que también disminuya la anchura del intervalo de pH donde el sistema de PO4′ contribuye más a βdil que el disolvente.
La figura 13 muestra también que hay una concentración mínima del sistema buffer (CSBmin), pequeña, donde el sistema de PO4′ ya no contribuye a βdil, y solo las especies ácida y básica del disolvente la determinan independientemente del tamaño de la solución buffer; en este caso, la CSBmin ≈ 10 –6 M para que la curva de βdil del sistema de PO4′ se distinga de la curva de βdil(H2O), y porque pKa2 = 6.75 ≈ 7.0; pero en otros casos (cuando pKa < 7.0 o pKa > 7.0) se debe esperar que la CSBmin sea mayor; es decir, para pKa 5 o 9, la CSBmin =10 –5 M y para pKa 3 u 11, la CSBmin = 10 –3 M.
Por otro lado, la figura 13a representa un sistema buffer más grande que el representado en la figura 13b, debido a que los volúmenes iniciales son 1000 y 10 mL, respectivamente. Como se observa en estas figuras, βdil crece cuando aumenta el tamaño del sistema. Así, βdil indica bien el comportamiento esperado para un sistema buffer: que debería imponer mejor el pH de un sistema de interés cuando el buffer es más grande.
ConclusionesSe diseñó un modelo general para estudiar la curva de valoración y la capacidad buffer de mezclas de especies de un solo sistema polidonador.
Al estudiar la capacidad buffer de soluciones que contienen un sistema polidonador a diferentes concentraciones, se concluye que la capacidad buffer de un sistema disminuye cuando la concentración total del sistema polidonador disminuye. Asimismo, se concluye que la contribución del sistema polidonador a la capacidad buffer con dilución depende del volumen inicial de la solución y del pH.
Cuando se tienen valores de pKa separados entre sí y en el intervalo de 3 < pH < 11, un máximo en la capacidad buffer se logra cuando son iguales las concentraciones de un ácido y de su base conjugada; es decir, en un valor de pH igual a su pKa. Fuera de este intervalo, es decir en los extremos de la escala de pH, contribuyen más las partículas ácida y básica del disolvente. En los libros se menciona que el pH que se pretende imponer con la solución buffer debe estar en un intervalo de 2 unidades de pH centrado en el valor de pKa de un par ácido-base. En este trabajo, se determinó que esta afirmación se cumple porque la capacidad amortiguadora de la solución buffer disminuye aproximadamente a una tercera parte de la capacidad buffer máxima en ese intervalo de pH. En estos casos, cada máximo en la curva de capacidad buffer se comporta como el máximo de un monodonador de mismo valor de pKa correspondiente al par ácido-base involucrado e igual concentración total del sistema polidonador (concentración total de L).
Para valores de pKa cercanos entre sí y en un intervalo de 3 buffer no se da en valores de pH exactamente iguales a los valores pKa de los pares ácido-base del sistema polidonador, debido a que éstos se ven interferidos entre sí. Un sistema polidonador con valores de pKa muy cercanos que van desde pKai hasta pKaj, tendrá capacidad amortiguadora útil en un intervalo de pH que va desde pKai–1 hasta pKaj +1.
Se afirma que toda solución e incluso el mismo disolvente anfiprótico (solvente o medio que pueda donar o aceptar un protón), ya tiene una cierta capacidad buffer. Cuando un sistema polidonador llega a una concentración muy pequeña, prácticamente ya no contribuye a la capacidad buffer y solo el disolvente y sus especies ácida y básica la determinan. Esta concentración define una concentración mínima del sistema buffer (CSBmin) para que se manifieste en el sistema.
Finalmente, se establece que βdil crece cuando el tamaño del sistema aumenta. Por lo tanto, cuando se tiene un sistema más grande que otro, el sistema de mayor tamaño impondrá mejor el pH que el de menor tamaño.




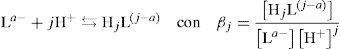
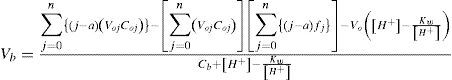
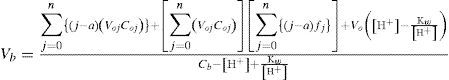
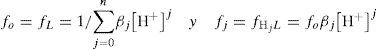
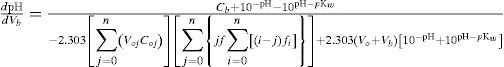
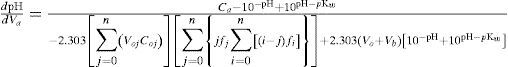
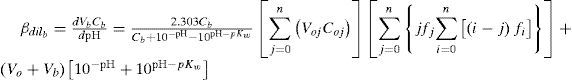
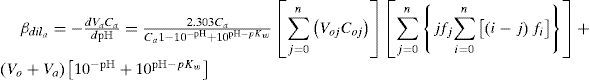
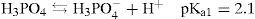
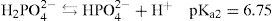
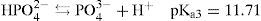
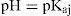
![Valoración de 10mL de una solución que contiene a las especiesH3PO4 y H2PO4− con [PO4’]T = 0.5 M, valorados con NaOH de concentración Cb = 0.5 M.— Curva de valoración teórica de pH = f (Vb). --- Curva de dpH/dVb teórica. Valoración de 10mL de una solución que contiene a las especiesH3PO4 y H2PO4− con [PO4’]T = 0.5 M, valorados con NaOH de concentración Cb = 0.5 M.— Curva de valoración teórica de pH = f (Vb). --- Curva de dpH/dVb teórica.](https://static.elsevier.es/multimedia/0187893X/00000025000000S1/v1_201412221110/S0187893X14705609/v1_201412221110/es/main.assets/thumbnail/gr2.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
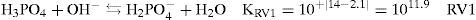
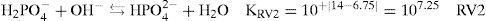
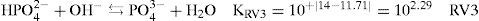
![Curva de βdil = f (pH) con Cb = Ca = 0.5 M. La línea continua corresponde a una solución que contiene H3PO4 y H2PO4− con [PO4’]T = 0.5 M, Vo =10mL. La línea segmentada corresponde a una solución conteniendo un par HL/L- con [L’]T = 0.5 M, Vo = 10mL, pKa = 2.1. • Sistema inicial de PO4’, ♦ Sistema inicial de L’. Curva de βdil = f (pH) con Cb = Ca = 0.5 M. La línea continua corresponde a una solución que contiene H3PO4 y H2PO4− con [PO4’]T = 0.5 M, Vo =10mL. La línea segmentada corresponde a una solución conteniendo un par HL/L- con [L’]T = 0.5 M, Vo = 10mL, pKa = 2.1. • Sistema inicial de PO4’, ♦ Sistema inicial de L’.](https://static.elsevier.es/multimedia/0187893X/00000025000000S1/v1_201412221110/S0187893X14705609/v1_201412221110/es/main.assets/thumbnail/gr3.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Diagrama de distribución y curva de βdil del sistema de PO4’, partiendo de una solución que contiene H3PO4 y H2PO4− con [PO4’]T = 0.5 M, Vo =10mL, empleando concentraciones de ácido fuerte y base fuerte Cb = Ca = 0.5 M. pKa1 = 2.1 (Turner y col., 1992), pKa2 = 6.75 (Saha y col., 1996) y pKa3 = 11.71 (Martínez-Calatayud y col., 1987). —fH3PO4,—fH2PO4−,—fH2PO42−,—fH2PO43−,, --- βdil. Diagrama de distribución y curva de βdil del sistema de PO4’, partiendo de una solución que contiene H3PO4 y H2PO4− con [PO4’]T = 0.5 M, Vo =10mL, empleando concentraciones de ácido fuerte y base fuerte Cb = Ca = 0.5 M. pKa1 = 2.1 (Turner y col., 1992), pKa2 = 6.75 (Saha y col., 1996) y pKa3 = 11.71 (Martínez-Calatayud y col., 1987). —fH3PO4,—fH2PO4−,—fH2PO42−,—fH2PO43−,, --- βdil.](https://static.elsevier.es/multimedia/0187893X/00000025000000S1/v1_201412221110/S0187893X14705609/v1_201412221110/es/main.assets/thumbnail/gr4.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
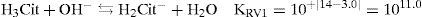
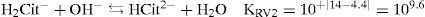
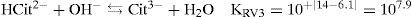
![Valoración de 10mL de una solución que contiene a las especies H3Cit y H2Cit– con [Cit’]T = 0.5M, valorados con NaOH de concentración Cb = 0.5M. — Curva de valoración teórica de pH=f(Vb). ---- Curva de dpH/dVb teórica. Valoración de 10mL de una solución que contiene a las especies H3Cit y H2Cit– con [Cit’]T = 0.5M, valorados con NaOH de concentración Cb = 0.5M. — Curva de valoración teórica de pH=f(Vb). ---- Curva de dpH/dVb teórica.](https://static.elsevier.es/multimedia/0187893X/00000025000000S1/v1_201412221110/S0187893X14705609/v1_201412221110/es/main.assets/thumbnail/gr6.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Curvas de βdil = f(pH) con Cb = Ca=0.5 M. La línea continua corresponde a una solución que contiene H3Cit y H2Cit– [Cit’]T = 0.5M, Vo = 10mL, pKa1 = 3.0, pKa2 = 4.4 y pKa3 = 6.1 (Ringbom, 1979). La línea segmentada corresponde a una solución conteniendo un par HL/L- con [L’]T = 0.5M, Vo = 10mL, pKa = 3.0. • Sistema inicial de Cit’, ♦ Sistema inicial de L’. Curvas de βdil = f(pH) con Cb = Ca=0.5 M. La línea continua corresponde a una solución que contiene H3Cit y H2Cit– [Cit’]T = 0.5M, Vo = 10mL, pKa1 = 3.0, pKa2 = 4.4 y pKa3 = 6.1 (Ringbom, 1979). La línea segmentada corresponde a una solución conteniendo un par HL/L- con [L’]T = 0.5M, Vo = 10mL, pKa = 3.0. • Sistema inicial de Cit’, ♦ Sistema inicial de L’.](https://static.elsevier.es/multimedia/0187893X/00000025000000S1/v1_201412221110/S0187893X14705609/v1_201412221110/es/main.assets/thumbnail/gr7.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Diagrama de distribución y curva de βdil del sistema de Cit’, partiendo de una solución que contiene H3Cit y H2Cit– con [Cit’]T = 0.5M, Vo = 10mL, empleando concentraciones de ácido fuerte y base fuerte Cb = Ca = 0.5 M. pKa1 = 3.0, pKa2 = 4.4 y pKa3 = 6.1 (Ringbom, 1979). —fH3Cit,—fH2Cit−,—fH2PO2−,—fCit3−, --- βdil. Diagrama de distribución y curva de βdil del sistema de Cit’, partiendo de una solución que contiene H3Cit y H2Cit– con [Cit’]T = 0.5M, Vo = 10mL, empleando concentraciones de ácido fuerte y base fuerte Cb = Ca = 0.5 M. pKa1 = 3.0, pKa2 = 4.4 y pKa3 = 6.1 (Ringbom, 1979). —fH3Cit,—fH2Cit−,—fH2PO2−,—fCit3−, --- βdil.](https://static.elsevier.es/multimedia/0187893X/00000025000000S1/v1_201412221110/S0187893X14705609/v1_201412221110/es/main.assets/thumbnail/gr8.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Curvas de βdil = f(pH) para el sistema de PO4’con Cb = Ca=0.5 M. • Sistema inicial de PO4’. pKa1 = 2.2, pKa2 = 7.1 y pKa3 = 12.3 (Ringbom, 1979). a) Vo = 20 mL, H3PO4– con [PO4’]T = 0.5 M; b) Vo =20mL, H2PO4– y HPO42– con [PO4’]T = 0.5 M, y c) Vo = 20mL, HPO42– y PO43– con [PO4’]T = 0.5 M. Curvas de βdil = f(pH) para el sistema de PO4’con Cb = Ca=0.5 M. • Sistema inicial de PO4’. pKa1 = 2.2, pKa2 = 7.1 y pKa3 = 12.3 (Ringbom, 1979). a) Vo = 20 mL, H3PO4– con [PO4’]T = 0.5 M; b) Vo =20mL, H2PO4– y HPO42– con [PO4’]T = 0.5 M, y c) Vo = 20mL, HPO42– y PO43– con [PO4’]T = 0.5 M.](https://static.elsevier.es/multimedia/0187893X/00000025000000S1/v1_201412221110/S0187893X14705609/v1_201412221110/es/main.assets/thumbnail/gr9.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Curvas de pH = f (Vb) con Cb = 0.5 M. Sistema inicial de PO4’. pKa1 = 2.2, pKa2 = 7.1 y pKa3 = 12.3 (Ringbom, 1979). a) Vo = mL, H3PO4 con [PO4’]T = 0.5 M; b) Vo = 10mL, H3PO4 y H2PO4– con[PO4’]T = 0.5 M; c) Vo = 10mL, H3PO4, H2PO4–, HPO42– y PO43– con [PO4’]T = 0.5M. Curvas de pH = f (Vb) con Cb = 0.5 M. Sistema inicial de PO4’. pKa1 = 2.2, pKa2 = 7.1 y pKa3 = 12.3 (Ringbom, 1979). a) Vo = mL, H3PO4 con [PO4’]T = 0.5 M; b) Vo = 10mL, H3PO4 y H2PO4– con[PO4’]T = 0.5 M; c) Vo = 10mL, H3PO4, H2PO4–, HPO42– y PO43– con [PO4’]T = 0.5M.](https://static.elsevier.es/multimedia/0187893X/00000025000000S1/v1_201412221110/S0187893X14705609/v1_201412221110/es/main.assets/thumbnail/gr10.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Curvas de βdil = f(pH) con Cb = 0.5 M. • Sistema inicial de PO4’. pKa1 = 2.2, pKa2 = 7.1 y pKa3 = 12.3 (Ringbom, 1979). a) Vo = 10mL, H3PO4 con [PO4’]T = 0.5 M; b) Vo = 10mL, H3PO4 y H2PO4– con [PO4’]T = 0.5 M, y c) Vo = 10mL, H3PO4 y H2PO4– HPO42– y PO43– con [PO4’]T = 0.5M. Curvas de βdil = f(pH) con Cb = 0.5 M. • Sistema inicial de PO4’. pKa1 = 2.2, pKa2 = 7.1 y pKa3 = 12.3 (Ringbom, 1979). a) Vo = 10mL, H3PO4 con [PO4’]T = 0.5 M; b) Vo = 10mL, H3PO4 y H2PO4– con [PO4’]T = 0.5 M, y c) Vo = 10mL, H3PO4 y H2PO4– HPO42– y PO43– con [PO4’]T = 0.5M.](https://static.elsevier.es/multimedia/0187893X/00000025000000S1/v1_201412221110/S0187893X14705609/v1_201412221110/es/main.assets/thumbnail/gr11.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Curvas de pH = f(Vb), dpH/dVb y βdil = f(pH) teóricas. Cb= Ca = 0.5 M. • Sistema inicial de PO4’. pKa1 = 2.2, pKa2 = 7.1 y pKa3 = 12.3 (Ringbom, 1979). Vo = 10mL, 25mL de [H3PO4] = 0.5, 2.5mL de [H2PO4– = 0.5, 2.5mL de [HPO42–] = 0.5 y 2.5mL de [PO43–] = 0.5 con [PO4’]T = 0.5 M. Curvas de pH = f(Vb), dpH/dVb y βdil = f(pH) teóricas. Cb= Ca = 0.5 M. • Sistema inicial de PO4’. pKa1 = 2.2, pKa2 = 7.1 y pKa3 = 12.3 (Ringbom, 1979). Vo = 10mL, 25mL de [H3PO4] = 0.5, 2.5mL de [H2PO4– = 0.5, 2.5mL de [HPO42–] = 0.5 y 2.5mL de [PO43–] = 0.5 con [PO4’]T = 0.5 M.](https://static.elsevier.es/multimedia/0187893X/00000025000000S1/v1_201412221110/S0187893X14705609/v1_201412221110/es/main.assets/thumbnail/gr12.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)