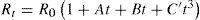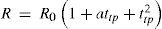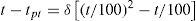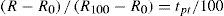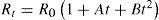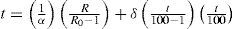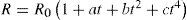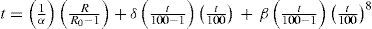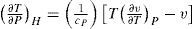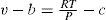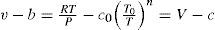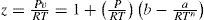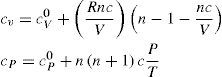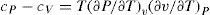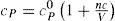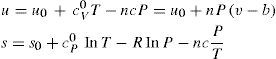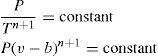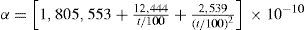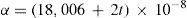Hugh Longbourne Callendar

Abstract

Hugh Longbourne Callendar (1863-1930) studied and developed the platinum resistance thermometer as we know today and used it to determine the mechanical equivalent of heat, the precise fusion temperature of sulfur, and the thermal properties of liquid water and steam. He developed a new equation of state for gases and applied it to steam to generate the first detailed steam tables, which included the thermal properties.

Resumen

Hugh Longbourne Callendar (1863-1930) estudió y desarrollo el termómetro de resistencia platino como lo conocemos hoy en día y lo usó para determinar el equivalente mecánico del calor, el punto preciso de fusión del azufre, y las propiedades térmicas del agua líquida y el vapor. Desarrolló una ecuación de estado general para gases y la aplicó al vapor de agua para generar las primeras tablas detalladas de vapor que incluían las propiedades térmicas.

Life and career

Hugh Longbourne Callendar was born at Hatherop, Gloucestershire, England, on April 18, 1863, the eldest son of Reverend Hugh Callendar, a local Anglican rector, and Anne Cecilia Longbourne. He received his early education at Marlborough College at a time when little encouragement was given to a gifted student to take up any form of experimental science. After Marlborough College, where he ranked top in classics and mathematics, he entered Trinity College, Cambridge, in 1882, obtaining a first class in the Classical Tripos at the end of his second year of residence (1884) and graduating a wrangler in the Mathematical Tripos of 1885 (Tripos are the different types of honors bachelor's degrees awarded by the University of Cambridge). Towards the end of 1885 he took a position with Joseph John Thomson (1856-1940), director of the Cavendish Laboratory, who assigned him to do experimental research and accurate measurement of electrical resistance. This project led to the development of the platinum resistance thermometer, with which he obtained an accuracy of 0.1°C in 1,000°C, about 100 times better than previous results. Callendar's thesis on platinum thermometry and continuous electric calorimetry was accepted and led to his election of fellow of Trinity in 1886 (Callendar, 1898a; Callendar, 1902a; Callendar, L. H., 1961; S.W.J.S., 1932; Snelders, 1934).

After graduating from Cambridge, Callendar served as Professor of Physics at the Royal Holloway College, Egham, during the period 1888 and 1893; in 1893 he accepted an appointment as professor of physics at McGill University, Montreal, where he remained for five years. In 1898 he returned to England as Quain professor of physics at University College, London. Ernest Rutherford (1871-1937; Nobel Prize in Chemistry, 1908) replaced him at McGill. In 1902 Callendar succeeded Sir Arthur Rücker (1848-1915) at the Chair of physics at the Royal College of Science (which in 1907 became part of the Imperial College of Science and Technology), a post he held until his death. Frederick Trouton (1863-1922) replaced Callendar as Quain professor of physics (S.W.J.S., 1932).

Callendar did research on the gas thermometer (Callendar, 1892a, 1901b), the radio balance (Callendar, 1910a, 1921), on a more precise determination of the specific heat of water (Callendar, 1913), a quantitative study of the behavior of steam to pressures well above the critical state, and on engineering problems connected flow of steam through nozzles, with steam turbines and internal combustion engines. In his paper on the properties of gases and vapors, deduced from a modified form of the Joule-Thomson equation (Joule and Thomson, 1852), he put forward his equation of state for a real gas and derived all the thermodynamic properties of steam (Callendar, 1901a). This paper led to compilation of reliable steam tables, The Callendar Steam Tables (Callendar, 1915, 1921, 1927c, 1928b; Callendar and Moss, 1925) and the book The Properties of Steam and Thermodynamic Theory of Turbines that enabled engineers to design advanced steam machinery (Callendar, 1902b). Callendar and John Thomas Nicolson determined the temperature of steam expansion behind a piston and the heat transmission and leakage losses from steam engine cylinders (Callendar and Nicholson, 1897, 1898). Among his many projects in the area of thermodynamics, Callendar, alone or with his collaborators, studied the specific heat of gases, the osmotic pressure of solutions (Callendar, 1908, 1909bc), the absolute expansion of mercury (Callendar and Moss, 1912), and the boiling point of sulfur (Callendar and Griffiths, 1892; Callendar, 1909a; Callendar and Moss, 1910). His determination of the boiling point of sulfur was four degrees lower than the value previously accepted and was only 0.07°C different from the value of the sulfur point adopted on the International Temperature Scale, established in 1927. The correction was based on a very precise determination of the absolute expansion of mercury above 100°C. Later Callendar developed the electrical continuous-flow calorimeter for measuring the heat-carrying properties of liquids; with Howard Turner Barnes (1873-1950) he applied it to the study of the calorimetric properties of water (Callendar and Barnes, 1900). For the Air Ministry he investigated anti-knock additives (dopes) and detonation (Callendar, 1927ab), and in 1926 he published on the cause of knock in petrol engines and the effects of anti-knock additives to gasoline (Callendar et al., 1926). Callendar and John Cox (1851-?) carried on the first X-Ray experiments in Canada, which produced satisfactory images used in hospitals (Cox and Callendar, 1896).

In a completely different field Callendar was the inventor a system of shorthand, A Manual of Cursive Shorthand, which came into fairly general use in some of the British colonies, were older systems had not become firmly established prior to its advent, and A System of Phonetic Spelling Adapted to English (Callendar, 1889ab; Snelders, 1934)

In his autobiography, Thomson says that Callendar was the most brilliant of all his research students during 40 years of teaching a Cambridge… “he did everything well. In less than eight months he obtained results of absolutely first class importance. He gave physics a new tool to determine temperature with am easy an accuracy never before obtainable and he was the first to suggest, from his experiments, the existence of superconductivity of metal at or about absolute zero” (Thomson, 1936).

Honors and awards

Callendar received many awards and honors for his contributions to science and technology. In 1894 he was elected a fellow of the Royal Society. He received the Watt Medal of the Institution of Civil Engineers for his work with Nicolson on the laws of condensation of steam (1898); the Rumford Medal of the Royal Society (1906) for an “outstandingly important recent discovery in the field of thermal or optical properties of matter made by a scientist working in Europe”; and the Hawksley Gold Medal of the Institution of Mechanical Engineers, for his research of the flow of steam through nozzles and throttles (1915). He was for some years treasurer of the Physical Society of London in 1910, its president during 1910 to 1912, and their first Duddell memorial medalist for his contributions to the advancement of knowledge by the invention or design of scientific instruments (1924). He was president of Section A (Mathematical and Physical Science) of the British Association in 1912, and was made a C.B.E. (Commander of the Order of the British Empire) in 1920 for his work for the Air Ministry and the Anti Submarine Department of the Admiralty. During World War I Callendar was a consultant to the Board of Inventions, which received more than 100,000 ‘war-winning’ ideas. McGill University conferred on him an honorary LL.D. (doctor of laws degree) (Snelders, 1934).

His tables of properties of steam were officially adopted by the turbine manufacturers of Great Britain through the British and Electrical Allied Manufacturers’ Association, and used for turbine tests and contracts, and his later work on high pressure steam was supported and financed by the manufacturers’ research association. Callendar took part in the first International Steam Tables Conference, held in London in 1929, to coordinate research work in various countries.

Callendar died at Ealing, London, on 21 January 1930. His wife, Victoria Mary Stewart, and his three sons, Leslie Hugh (1896-?), Guy Stewart (1898-1964), Max Victor, and one daughter survived him. The Callendar effect, the name given to the effect of combustion-produced carbon dioxide on the global climate, is named after Guy Stewart Callendar, who proposed the effect in 1938 based on earlier work by John Tyndall (1820-1893) and Svante Arrhenius (1859-1927; 1903 Nobel Prize for Chemistry).

Scientific contribution

Resistance thermometry

In 1821 Humphry Davy (1778-1819) discovered the dependence of the electrical resistance of metals on temperature (Davy, 1821) and in 1861 Ernst Werner von Siemens (1816-1892) used this phenomenon in the construction of a platinum resistance thermometer (Siemens, 1861). Day reported, “The most remarkable result that I obtained…was that the conducting power of metallic bodies varied with temperature, and was lower, in some inverse ratio, as the temperature was higher. Thus a wire of platinum of 1/220 and 3 inches in length, when kept cool by oil, discharged the electricity of two batteries, or of twenty double plates, but when suffered to be heated by exposure to air, it barely discharged one battery”. Siemens wrote “As it would be impossible to introduce mercury thermometers into the interior of the mass, I thought of having recourse to an instrument based on the well-ascertained fact that the conductivity of a copper wire increases in a simple ratio inversely with its temperature”. Siemens instrument was built of a rod wound with silk-covered wire in several layers, covered with rubber and connected to a battery and a galvanometer. He then added “…the ratio of increase of resistance of copper wire with increase in temperature may be regarded as perfectly constant within the ordinary limits of temperature…by substituting an open coil of platinum for the insulated copper coil this instrument would be useful also as a pyrometer”.

Based on his findings, Siemens developed the platinum resistance temperature detector (RTD) and presented a threeterm interpolation formula. In 1871 the British Association for the Advancement of Science appointed a committee (two of its members were Lord Kelvin and James Clerk Maxwell) to test Siemens’ apparatus and issued an adverse report after finding that the RTD temperature readings were unstable. The instrument gave almost identical results if the measurements were made within a few days of each other, but when carried after an interval of several months they were usually very different from the early results. In addition, Siemens’ resistor changed its resistance after heating to a high temperature, followed by cooling.

When Callendar joined the Cavendish Laboratory in Cambridge, the standard tool for measuring temperatures was Victor Regnault's (1810-1878) normal air thermometer. Thomson suggested Callendar to study the possibility of using the variation of resistance of platinum as an alternative means of measuring temperature. Stating from where Siemens had stopped Callendar made an extensive experimental comparison between the readings of the platinum resistance thermometer and Regnault's instrument. In 1886 he presented his results to the Royal Society in 1887 and in the same year registered the first of his many patents (Callendar, 1887).

In general, the resistance of metal is a complex function of temperature. For most metals, however, the dependence or resistance on temperatures near and above the Debye temperature can be written as a power series

where A, B, and C’ are constants of the material. Callendar found that at temperatures above the ice point the third term was unnecessary, so that the resistance of platinum could be well represented by the following power series of the temperature

and the readings of the platinum thermometer, t_pt, and of the air thermometer, t, were well-related by the following parabolic expression:

where δ is a constant of which the value depends upon the purity of the platinum employed, and the platinum temperature was related to the corresponding resistance R of the metal by the equation

Developed at a time when computers were not available, the Callendar equation was solved in two parts. The first term gave a nominal platinum temperature t_pt, which was then substituted in the second term yielding a small correction which was added algebraically to t_pt, giving a estimate of the temperature. Callendar prepared tables of the correction term, which allowed him to solver for the temperature quickly. Substituting the corrected temperature into the correction term allowed him to calculate a better second approximation. A third approximation was seldom necessary.

Callendar showed that his formula for the resistance was accurate within 1% over a range of 600°C (S.W.J.S., 1932). In addition, he discovered that the insulator Siemens had used to build his RTD embrittled the platinum causing internal stresses that induced temperature instability. Callendar solved the problem by changing the insulator material and annealing the RTD at temperatures above the highest desired measurement temperature.

In following publications (Callendar, 1891, 1892b, 1899ab), Callendar gave practical suggestions for the construction of stable platinum thermometers. A resistance wire, 0.1 or 0.2 mm diameter, was wound on a mica cross, serrated at the edges in a bifilar fashion. Platinum leads of about 0.6 mm diameter were used inside the thermometer stem with a compensating loop of similar wire alongside them. This loop was connected in series with the measuring coils of an equalratio bridge so as to compensate for changes in the resistance of the leads. To avoid errors due to the resistance of the leads to the coil itself, Callendar introduced a pair of dummy leads that followed the actual leads as closely as possible and were short-circuited at one end. The leads were threaded through mica spacing washers, which fitted closely in the porcelain sheath. The washers insulated the wires and prevented convection along the sheath.

Callendar results indicated that the sensing element reliability required high-purity platinum, annealing the wire at a temperature at least as high as the intended use temperature, freedom from mechanical strains in winding, and support in use so that thermal or mechanical dimensional changes would not stress the wire. He discovered that iron was a serious contaminant at high temperatures. To this discoveries we can add that heating platinum in contact with phosphorus, arsenic, antimony, selenium, and tellurium causes embrittlement; that platinum is attacked by molten metals and their vapors; and that heating in a strongly reducing atmosphere in a system containing silica, silicates, or sulfur will lead to failure.

According to Barber and Hall (Barber and Hall, 1962) the construction of modern platinum thermometers is based on Callendar's original design, with the following improvements: (a) the wire is made of highly purified platinum, leading to greater stability of resistance, (b) the compensating lead has been substituted by four terminal resistors, which make possible a more precise elimination of changes in lead resistance, (c) the thermometers are smaller and lighter; the lighter construction gives better precision since heat transfer is better and the lag constant less, (d) the thermometer is usually hermetically sealed, (e) the external terminals have been eliminated. Callendar found that the best approximation to a constant heating effect was given by a constant current rather than by a constant wattage in the bulb, and that for an accuracy to ±0.001°C it is sufficient to operate at a current of 1 mA at all temperatures and to take to account of the heating effect.

Callendar's work on the platinum resistance thermometer also led to the invention of a rolling-chart thermometer that allowed long-duration collection of climatic temperature data, as well as registering temperature profile in industrial uses such as metallurgy. It was the first electrical instrument using the servo principle (Callendar, 1898b; Callendar, H. L., 1961).

In 1899 the Committee on Electrical Standards, headed by Lord Rayleigh (John William Strutt, 1842-1919), accepted Callendar's proposals for a standard scale of temperature based on the platinum thermometer and this led to recognition of this instrument as the international means of interpolation between the boiling point of liquid oxygen (–182.97°C.) and the melting point of antimony (630.5°C).

At the General Conference of Weights and Measures, held in Paris in 1927, it was agreed to take the temperature of equilibrium between liquid sulfur and its vapor at a pressure of one standard atmosphere to be 444.60°C and that the temperature t in the range 0° to 660°C is to be deduced from the resistance R_t of a standard platinum thermometer by the formula

the constants R_o, A and B being determined by calibration at the air, steam and sulfur points respectively. This formula corresponds exactly with to the one proposed by Callendar in 1887 (eq. (2).

According to Milton S. Van Dusen (Van Dusen, 1925), in platinum-resistance thermometry temperatures above 0°C are calculated according to the Callendar equation, written as

where R and R₀ are the resistance at t°C and 0°C, respectively, and α and δ are constants the value of which depend on the purity and treatment of the platinum. The fundamental coefficient α is determined from observations at the boiling point of water, while the constant δ is determined at some other fixed point, preferably at moderately high temperature. When δ is determined from observations at the boiling point of sulfur, the temperature scale defined by the Callendar equation is indistinguishable from the thermodynamics scale in the temperature range –40° to 600°C, to the accuracy with which the latter has been determined.

Below the region of –40°C, however, temperatures defined by the Callendar equation depart from the thermodynamic scale by amounts, which increase very rapidly below –100°C, the calculated temperatures being about 2°C too low at liquid air temperatures. Furthermore, it has been noted that such deviations are not the same for all thermometers. In other words, the Callendar equation does not define an accurate reproducible scale at low temperatures.

Experimental work on resistance thermometers done after Callendar's work has shown that the resistance of platinum between 0°C and –190°C can be better represented by an equation of the form

where the constants a, b, and c, are determined from three fixed points, namely, the freezing point of mercury, the normal sublimation point of carbon dioxide (–78.51°C), and the normal boiling point of oxygen (–183.00°C). Using this information, Van Dusen modified the Callendar equation, in which the departures are expressed by a term containing a single characteristic constant determined from a single calibration below zero, as follows:

For temperatures above zero the last term is omitted and the equation is then identical with the Callendar formula, with identical constants determined from the usual calibration in ice, steam, and sulfur. The constant β is determined from a calibration at or near the normal boiling point of oxygen. For the range between –200°C to 0°C eq. (6) reduces to eq. (2).

In 1968 the International Electrotechnical Commission recognizing the shortcomings of the Callendar-Van Dusen equation defined a 20 term polynomial equation for the resistance versus temperature curve for 100 Ohm platinum RTDs.

Callendar used the platinum thermometer in a number of investigations. One of them, done with Ernest Howard Griffiths (1851-1932), was the re-determination of the boiling point of sulfur. Previously, following Regnault, this temperature had been taken to be 448.34°. As a result of their work, Callendar and Griffiths obtained the value 444.53°, of which they said: “We believe this to be within 0.1° of the true temperature of the vapour of sulphur boiling freely under a pressure of 760 mmHg” (Callendar and Griffiths, 1892). In a joint study with Barnes Callendar determined the variations, with temperature and with strength of solution, of the electromotive force of different forms of the Clark standard cell¹ (Callendar and Barnes, 1898).

Thermodynamics

During his stay at McGill University, Callendar developed his method of continuous electrical calorimetry (Callendar, 1902a), which his assistant Barnes applied for the first time to the measurement of the specific heat of water between its freezing and boiling points, and to determine of the mechanical equivalent of heat (Callendar and Barnes, 1897, 1899, 1900). The Callendar and Barnes's apparatus consisted of two concentric tube cylinders; the space between the two cylinders was evacuated to provide good thermal insulation. A constant stream of water flowed through the internal narrow tube and was heated a few degrees by a resistance wire placed along the axis. The inlet and outlet temperatures of the water were measured with platinum resistance thermometers. The heat lost by the water to the evacuated space was calculated by performing two separate experiments, each with a different flow of water and a different electric current, but with the same change in temperature. In both experiments the heat loss was the same and could be eliminated from the heat balance equations. The amount of energy added to the water was given by the product εI of the potential difference ε in volts and the electric current I in amperes. For m grams of water flowing through the calorimeter in τ seconds, the energy supplied per gram of water was εIτ/m J/g. This quantity was determined for various temperature intervals starting at a number of different initial temperatures. The mechanical equivalent of heat was then calculated by subtracting the heat losses from εIτ/m and using the definition of one calorie as the energy required to heat one gram of water from 14.5 to 15.5°C. The value found was 4.182 J/cal, which compares very well with the accepted value today of 4.184. The method developed by Callendar's method had the advantages that once the steady state was reached, no change in temperature occurred in any part of the apparatus and therefore no correction had to be made for the energy supplied to the glass tube, to the resistance wire, etc. In addition, it was not necessary to correct for the heat capacity of the apparatus and lags in the reading of the thermometers.

Another application of continuous calorimetry led to the determination of the enthalpy and specific heat of steam at different conditions of pressure and temperature (Callendar, 1924). Callendar's method was based on the Joule-Thomson effect (Joule and Thomson, 1852) and consisted in throttling steam through a porous plug and measuring (with a continuous calorimeter) the heat removed to maintain constant enthalpy. These experiments led also to the development of an equation of state (EOS) for steam and other gases. The Joule-Thomson effect is expressed by the following equation

This effect has been found experimentally to be inversely proportional to the square of the absolute temperature, that is, T∂v∂TP−v=cpαT2 where α is a constant. Dividing the latter relation by T² gives ∂vT/∂TP=−cpαT4 which integrates to vT=−cpαT3 + constant. The constant may be determined by assuming that at very high temperatures the gas behaves ideally, that is,v/T=R/P. Hence v=RT/P−βT2 where β is constant. The latter equation may also be written Pv = RT −a /Tv, which is Rankine's EOS (Rankine, 1849).

Callendar then proposed that the Rankine EOS be modified as follows:

To justify the changes Callendar argued that because the molecules are not simply mathematical points but have some size, the volume of the gas is increased by the quantity b, which Callendar treats as a constant and calls the “co-volume”. Against this, there is a reduction in volume c caused by a temporary linking of the molecules during their encounters. This aggregation is not constant but depends on the temperature, becoming less as the temperature rises. Callendar called it the “co-aggregation volume” and expressed it in the form c = C/Tⁿ, where C is a constant; he interpreted the superscript n as the number of degrees of freedom lost by a molecule in co-aggregation (Callendar, 1901b).² For steam the index n is taken as 10/3. Increase in the number of such aggregates of greater mass makes RT/P to become increasingly greater than the ideal volume. A curious point is that the co-aggregation volume does not lead to the existence of a critical point [defined by ∂P/∂vTc and ∂2P/∂v2Tc=0], which Callendar tried to prove does not exist for water (see below). Thus, the Callendar EOS becomes

where V = RT / P is the theoretical (ideal gas) volume, T₀= 273 K, n is a constant, and c=c0T0/Tn is “co-aggregation” volume, which is a function of temperature and, except at moderate pressures, also of pressure. From theoretical considerations Callendar concluded that n = cv0/R where cv0 is the limiting value of c_V for P = 0 (ideal gas). Thus for argon and monatomic gases n = 1.5, for diatomic gases 2.5, and for triatomic gases (i.e. steam) 3.5; but for carbon dioxide n = 2. An interesting point is Callendar's conclusion that the absolute zero of temperature is probably within one or two hundredths of a degree of 273.10 K.

Callendar's equation may be written in the form of the pressure virial EOS

which indicates that the second virial coefficient is B = b −a/RTⁿ where a=Rc0T0n, and that the higher virial coefficients are nil. The expression for the second virial coefficient compares very well with that of the second virial coefficient for modern EOSs like those of Redlich-Kwong and Soave. It predicts that the temperature of Boyle is given by n TBoyle=a/bRn. The fact that the higher coefficients are Boyle nil indicates that the Callendar EOS is nor adequate for high pressures (> 15 atm).

Using thermodynamic relations the Callendar EOS yields:

where cV0 and cP0 are the values of the specific heat at constant volume and constant pressure, respectively, of the ideal gas. From the TdS equations we have

and since cP0−cV0=R we get

Additional relations that can be derived are

For a reversible process the latter equation yields

The paper on the thermodynamic properties of gases and vapors (Callendar, 1901ab) formed the basis of Callendar's subsequent work on steam, which led him to the formulation of his steam equation and the publication of the Callendar Steam Tables (Callendar, 1915, 1921, 1927c), which provide the thermodynamic properties of steam up to and beyond the critical pressure. In these tables the volumes is expressed in ft³/lb and the pressure in lb/ft². The values of the properties are calculated using cV0=0.36707,  cP0=047719,  R=0.11012 (all three in cal/g·°C), and n = 10/3. The energy properties u, h, s, and g, are calculated using as reference state h(100°C) = 100 cal/g.

Callendar results indicated that the latent heat of vaporization of water at the critical temperature is not zero but 72.4 cal/gm and that it become zero at 380.5°C is reached. Although Callendar took extreme care in degassing the water his results indicate that he did not eliminate air completely (S.W.J.S, 1932).

We will now describe how Callendar reached the (wrong) conclusion that water does not have a critical state. The standard method for determining the critical temperature of a substance is to heat a small amount of the liquid in a sealed glass tube and note the temperature at which the interface (meniscus) disappears. This method presents no difficulties with substances like carbon dioxide and sulfur dioxide; but until fused-quartz tubes became available, it was impracticable to apply to water owing to the corrosive effect of the latter upon ordinary glass. Callendar used quartz tubes and, in agreement with other observers, he found the critical temperature of water to be 374°C. He made many experiments using different quantities of water in tubes of similar volume to measure the densities of the liquid and the saturated vapor at temperatures below the critical one. Using his EOS he calculated the values of the enthalpy of the saturated liquid and vapor, and plotted them at various temperatures against the saturation pressure. His results indicated that both curves met at a sharp angle at 380.5°C. At 374°C where the curves for water containeing a trace of air coalesced in a rounded maximum, there was still a latent heat (Callendar, 1928ab, 1929). Work by others (for example, Eck, 1939) did not confirm Callendar curious results.

Another important research project was the determination of the absolute density of mercury by the hydrostatic method of balancing two vertical columns maintained at different temperatures (Callendar and Moss, 1912). Accurate determination of this property was critical for measuring temperatures with high accuracy. Callendar and Barnes concluded that in the range of temperature 0°C to t°C the coefficient of expansion α could be represented by the following empirical equation:

Although it was impossible to represent the results satisfactorily over the whole range by a linear formula, for approximate work eq. (17) could be substituted by

Callendar also studied engineering problems connected with steam turbines and internal combustion engines. With John Thomas Nicolson he made many valuable experiments on the heat of transmission and leakage losses from steamengine cylinders. In the discussion of steam engine trials it had generally been assumed that the rate of condensation of steam on a surface was practically infinite, so that any surface in contact with the steam was immediately heated to the saturation temperature corresponding to the pressure of the steam. It had also been supposed that the amount of condensation under any given conditions was limited by the resistance of the film of condensed water to the passage of heat, or by the capacity of the metal or of the circulating water to carry off the heat. In many cases condensation was diminished by films of oil or grease, or by accumulations of air, or by other incrustations or deposits (Callendar and Nicolson, 1898).

Callendar and Nicolson found, on the contrary, that a practically clean and dry metal surface was not immediately heated to the temperature of the saturated steam in contact with it, that the rate of condensation of steam was not infinite but finite and measurable, and that the rate of condensation in any given case was limited chiefly by this finite rate of condensation, and could be calculated in terms of it. It was also found that the temperature of the steam in different parts of the cylinder differed in a systematic way from the saturation temperature. The rate of condensation at any moment was found to be proportional to the temperature difference between the temperature of the steam and the of the metal surface. Assuming this law the total amount of condensation at any point of the stroke of the piston could be inferred by measuring the condensation areas on the temperature cycle diagram (Callendar and Nicolson, 1898).

These results were extended in another work done with William Ernest Dalby (1864-1936) (Callendar and Dalby, 1908) on the temperature profile in a gas engine.

The experience acquired by Callendar led to his work on fuels and additives for the Air Ministry (Callendar et al., 1926, Callendar, 1927ab). In his first publication, Callendar reviewed the general theory of detonation of liquid fuels and outlined the nuclear theory of self-ignition. In the latter, the nuclei of liquid heavy paraffins present in the compressed airfuel mixture on ignition were thought to be the most usual cause of detonation with ordinary gasoline. It was assumed that a certain amount of adsorption might take place on the carbon present in the cylinder. The organo-metallic anti-knock additives (called dopes) appeared to coat the nuclei with a film of metal and so check the tendency to detonate. Detonation would take place by one of three possible modes: (a) the pressure-wave type, in which the mixture was fired by a compression wave of sufficient intensity, (b) the nuclear type, which depended on the presence of particles of relatively low ignition temperature, and (c) the molecular type in which the temperature of a completely gaseous mixture was raised sufficiently to induce direct molecular combination. The nuclear type was thought to be the most common in gasoline engines. The anti-knock effect of carbon disulfide and the knock-inducing effect of ether were explained using the nuclear hypothesis. Some known organo-metallic additives were tested to study their behavior at high temperatures and pressures. Lead tetraethyl began to boil at 210° and exploded at 215°. The explosion of a very small amount of this compound in gasoline was enough to cover the surface of the nuclei with metallic lead, but not strong enough to pre-ignite the mixture. A mixture of lead tetraethyl and ether decomposed at 243° forming a yellow cloud of probably lead oxide, which seemed to neutralize the anti-knock effect of lead tetraethyl by ether. The behavior of other systems, such as lead tetraethyl and ethyl dibromide, lead tetraethyl and water, and nickel carbonyl, were also studied. Callendar and his assistants also tested many organic compounds as possible candidates to raise the ignition temperature of the gasoline nuclei. According to Callendar, addition of 0.2% of lead tetraethyl to the fuel led to a 33% increase in the highest useful compression ratio; with addition of 0.4% the increase was 50%. A large number of organic substances were tested as possible candidates for raising the ignition temperature of gasoline and for anti-knock properties in 5% solution in gasoline. The results indicated that methylaniline possessed half the anti-knock efficiency of aniline, while dimethylaniline showed no anti-knock properties; the efficiency of toluidines and xylidines decreased in the meta, ortho, and para (Callendar et al., 1926).

Additional work included determination of the temperature of initial combustion (identified by formation of carbon dioxide, aldehydes, etc.) of several compounds. This parameter was obtained by passing a mixture of the compound with air through a heated glass tube. Some results were pentane, 295°C; hexane, 265°C; benzene, 670°C; toluene, 550°C; acetaldehyde, 205°C; ethanol 445°C; and aniline, 502°C (Callendar, 1927a).

Callendar concluded that detonation of paraffin fuels and ethers was due to the accumulation of organic peroxides in the liquid drops during high compression. The peroxides acted as a primer in causing the simultaneous ignition of the drops (Callendar, 1927b).