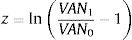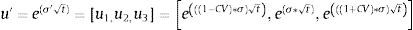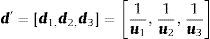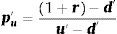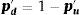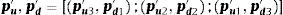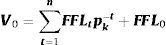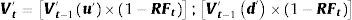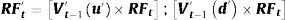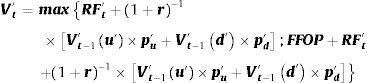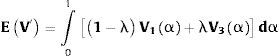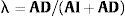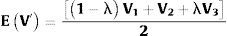Valoración probabilística versus borrosa, opciones reales y el modelo binomial. Aplicación para proyectos de inversión en condiciones de ambigüedad

Resumen

El trabajo tiene por objeto exponer la metodología, las ventajas y las debilidades del modelo binomial borroso de valoración de opciones reales como complemento del modelo binomial probabilístico. Para lograr lo anterior primero se presentan los modelos de opciones reales clasificados en probabilístico y borroso; luego se desarrolla el modelo binomial borroso incorporando: el método Marketed Asset Disclaimer (MAD), rejillas binomiales borrosas y el índice pesimismo-optimismo, para estimar el valor esperado de las opciones del proyecto (VEOP). Se ilustra con un caso comparando los resultados obtenidos con el modelo borroso y el probabilístico. Finalmente se concluye que, en situaciones de falta de información (ambigüedad), la lógica borrosa es un complemento del modelo probabilístico para determinar el valor de la flexibilidad estratégica.

Abstract

The aim of this paper is to present the methodology, advantages and weakness of the fuzzy binomial real option model as a complement to the probabilistic binomial model. The structure is as follow: first, it shows the real option models classified into probabilistic and fuzzy. Second, it develops the binomial fuzzy model, incorporating: the MAD method (Marketed Asset Disclaimer); fuzzy binomial lattice, and the pessimistic-optimistic index for estimates of the real option expected value of the project (ROEV). It illustrates, using a case comparing, the results obtained with the fuzzy and probabilistic model. It concludes that in lack of information situations (ambiguity), the fuzzy logic is a complement of the probabilistic model for estimates of the strategic flexibility value.

Resumo

O trabalho tem como objectivo expor a metodologia, vantagens e pontos fracos do modelo binomial impreciso de avaliação de opções reais como complemento ao modelo binomial probabilístico. Para alcançar o anterior, primeiro apresenta-se os modelos de opções reais classificados em probabilístico e impreciso; depois desenvolve-se o modelo binomial impreciso juntado: o método MAD (Marketed Asset Disclaimer), redes binomiais imprecisas e o índice pessimismo-optimismo, para estimar o valor esperado das opções do projecto (VEOP). Ilustra-se com um caso comparando os resultados obtidos com o modelo impreciso e o probabilístico. Por fim, conclui-se que em situações de falta de informação (ambiguidade); a lógica imprecisa é um complemento do modelo probabilístico para determinar o valor da flexibilidade estratégica.

1

Introducción

La valoración de decisiones de inversión mediante métodos tradicionales, como el descuento de flujos de fondos, no captura la flexibilidad estratégica total del activo objeto de la valoración. Principalmente esto se debe a que el método supone irreversibilidad de la inversión (Dixit y Pindyck, 1994), puesto que asume una conducta pasiva de gerencia frente a potenciales oportunidades estratégicas (por ejemplo: proyecciones suponiendo el comienzo inmediato del proyecto, su funcionamiento ininterrumpido con base en una capacidad de planta fija, sin ningún tipo de alteración hasta la finalización del horizonte de proyección especificado) (Mun, 2004). El actual ambiente de negocios se caracteriza por su importante dinamismo, incertidumbre y fuerte interacción de los agentes de mercado. Esto conduce a concluir que una importante fuente del valor correspondiente a los proyectos de inversión está formada por la capacidad adaptativa, oportunidades y flexibilidad estratégica, y contextos turbulentos. Por lo expuesto, es necesario valorar inversiones con métodos que permitan capturar beneficios de las nuevas oportunidades o reaccionar para mitigar potenciales pérdidas (por ejemplo: diferir, expandir, contraer, abandonar o alterar el proyecto en diferentes etapas de su vida). La teoría financiera, a través de la teoría de opciones, provee de los modelos de valoración de opciones reales cuantificando el valor adicional de las oportunidades de potenciar ganancias y limitar pérdidas que eventualmente presente el proyecto. Los modelos de opciones reales tienen como fin calcular el valor expandido o estratégico (Trigeorgis, 1995; Calle Fernández y Tamayo Bustamante, 2011), entendido como la suma del valor actual neto estático (descuento de flujo de fondos) y el valor de las «opciones reales» operativas y estratégicas de la inversión¹. El activo subyacente se encuentra representado por el valor actual de los flujos de fondos libres del activo real.

Para su aplicación es importante que se verifique la condición de mercados completos, eficientes y perfectos que permitan trabajar con activos financieros gemelos, carteras réplicas y argumentos de arbitraje, con el fin de replicar los flujos de fondos riesgosos del proyecto (Smith y Nau, 1995; Wang y Halal, 2010).

Una alternativa consiste en utilizar la teoría de los conjuntos borrosos en los modelos de opciones reales de forma complementaria a los métodos tradicionales, donde existe una amplia y difundida literatura en la cual los tradicionales modelos de valoración y en particular los modelos de opciones reales son originalmente planteados en términos probabilísticos (probabilidad). En los últimos años ha surgido una corriente de modelos de valoración de opciones que hace uso de la matemática borrosa (fuzzy sets). A diferencia de los modelos probabilísticos que definen grados de incertidumbre (Landro, 2010), los modelos borrosos se caracterizan por emplear escalas semánticas disponiendo niveles de ambigüedad-vaguedad en términos de posibilidades (Fornero, 2012). Son adecuados en situaciones donde la insuficiente información transforma un panorama totalmente incierto en una situación ambigüa, como pueden ser los casos de contextos cambiantes y mercados turbulentos. Algunas ventajas de los modelos de valoración de opciones borrosas residen en que: a) definen escalas semánticas de posibilidad donde se sostienen la facilidad de comprensión e interpretación en la toma de decisiones empresariales (Kinnunen, 2010); b) permiten capturar el sesgo positivo correspondiente al potencial valor de la flexibilidad estratégica (Carlsson y Fullér, 2003), y c) son alternativos en situaciones de valoración donde no existe información de mercado que permita trabajar con activos financieros gemelos o carteras réplicas (proyectos de inversión de base tecnológica, nuevos productos o estrategias innovadoras, empresas de capital cerrado o firmas que operan en mercados emergentes).

Cabe destacar que por el tradicional desarrollo de la teoría de la probabilidad, en las evaluaciones económicas la forma más difundida es la expresión de estimaciones de probabilidad. No obstante, probabilidad y posibilidad son marcos de descripción bastante próximos, debido a la noción de probabilidad subjetiva como marco de creencia. Ambas son un lenguaje adecuado para muchas estimaciones técnicas y económicas, ya que se relaciona con la medida que se hace a partir de un conocimiento incompleto. En ese sentido son base para valorar proyectos, específicamente en el marco de la teoria de opciones, sin perjuicio de que la lógica borrosa carece de la difusión académica y profesional que tiene el enfoque probabilístico.

El objetivo del trabajo es científico-didáctico, centrándose en desarrollar, comparar y diferenciar los resultados obtenidos de aplicar el tradicional modelo binomial de valoración de opciones (Trigeorgis, 1995) con el modelo binomial borroso (fuzzy binomial valuation approach) (Liao y Ho, 2010). También se expone la metodología de cálculo del valor esperado de las opciones del proyecto (VEOP) o valor puntual medio (crisp mean value) (Yoshida, Yasuda, Nakagami y Kurano, 2006).

La estructura es la siguiente: en la sección 2 se presenta una resumida clasificación de los principales modelos de valoración de opciones reales agrupados en función al uso de probabilidades o lógica borrosa. En la sección 3 se desarrolla la propuesta metodológica para el tratamiento y valoración de proyectos de inversión en condiciones de ambigüedad: el modelo binomial borroso. En esta se integra el enfoque Marketed Asset Disclaimer (MAD) con el uso de rejillas binomiales (Smith, 2005), su adecuación a los conjuntos borrosos y la metodología de cálculo para obtener el VEOP. La sección 4 ilustra el funcionamiento del modelo propuesto y las diferencias con el modelo binomial tradicional, utilizando y adaptando para el presente trabajo el caso de aplicación desarrollado por Smith (2005). Finalmente, se exponen las principales conclusiones.

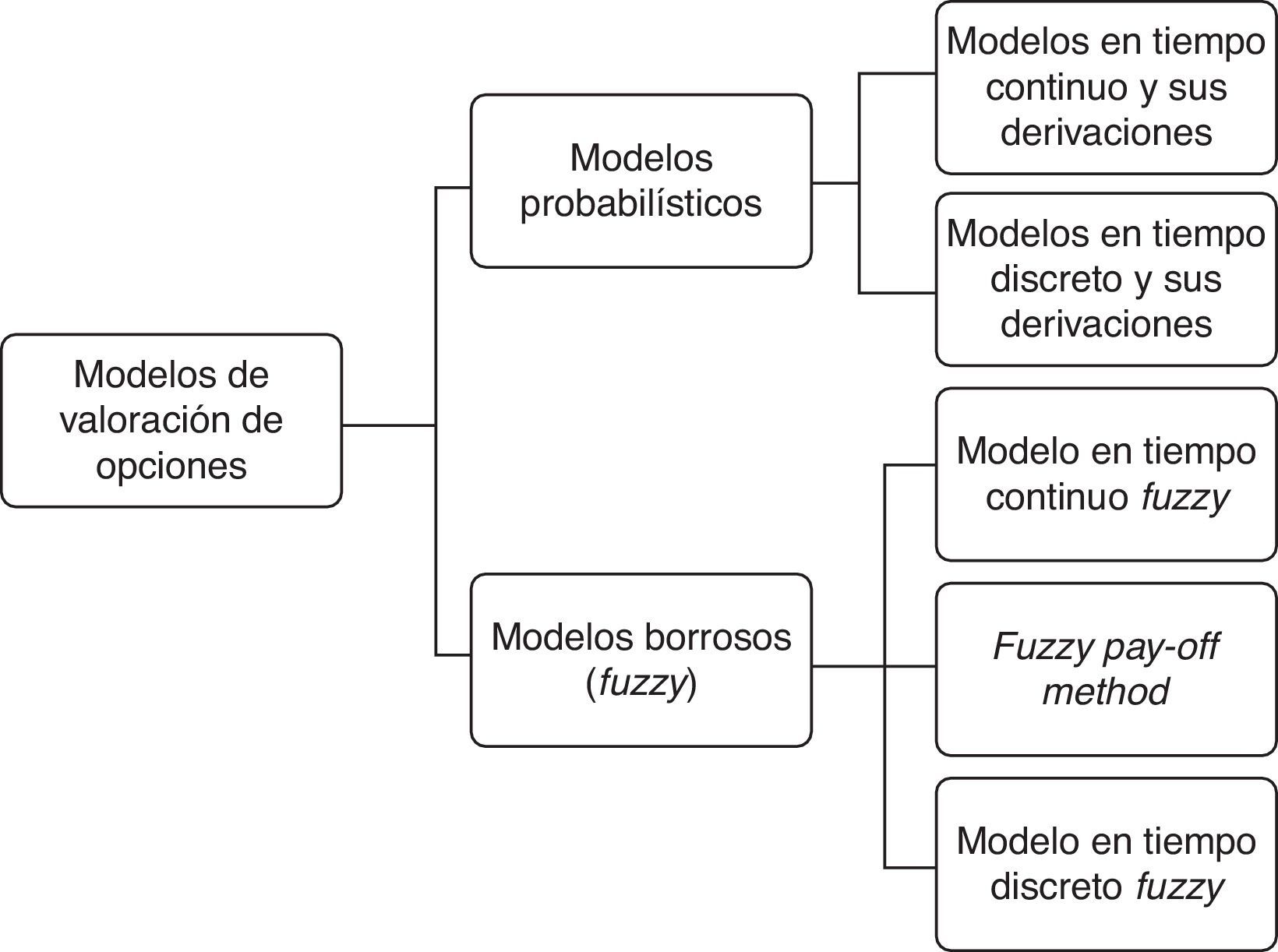
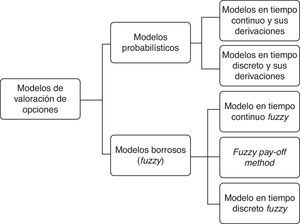
2

Marco conceptual

A continuación se referencian los principales modelos y derivaciones de estos para valorar opciones reales, y con el objeto de trazar una línea divisoria según sea el enfoque, estos son clasificados en probabilísticos y borrosos. A su vez, los primeros se dividen en: a) tiempo continuo y sus derivaciones, donde se encuentran los desarrollos seminales de la teoría de opciones; b) discretos y sus derivaciones, donde surgen la mayoría de las propuestas en el campo de las opciones reales. El segundo grupo se cimienta en las nociones de conjunto borroso y se clasifican en 3 grupos: a) modelos continuos borrosos; b) método de flujos de fondos borrosos, y c) modelos binomiales borrosos. En la figura 1 se exponen las ideas precedentes.

Figura 1.

Modelos de valoración de opciones probabilístico y borrosos.

Fuente: elaboración propia.

2.1

Modelos probabilísticos

En la presente clasificación se exponen los principales modelos tradicionales de valoración de opciones reales y sus derivaciones concebidas en un entorno probabilístico. Estos son agrupados en función del proceso estocástico, continuo o discreto, empleado en el modelo.

• a)

  Modelos en tiempo continuo y sus derivaciones: la teoría de opciones reales nace con el modelo de valoración para opciones europeas conocido como Black-Scholes y el posterior aporte de Merton (BMS) (Black y Scholes, 1973; Merton, 1973). Varias han sido las transformaciones y adecuaciones desde su formulación original, y estas han avanzado introduciendo modificaciones al proceso estocástico sobre el subyacente, incorporando cantidad de momentos estocásticos de orden superior, definiendo complejidad, características y estructura de la opción (exóticas-simples), introduciendo imperfecciones y efectos del mercado (apalancamientos del subyacente), entre otras (Dixit y Pindyck, 1994; Luherman, 1998; Copeland y Tufano, 2004; Baliero Filho y Rosenfeld, 2004; Hull, 2006; León, Mencia y Sentaria, 2007; Haug Gaarder, 2007; Wilmott, 2009). Los modelos en tiempo continuo mayoritariamente reconocen su campo de aplicación en la valoración de opciones financieras. No obstante, existen métodos que derivan en sencillos algoritmos utilizando modelos en tiempo continuo para valorar opciones reales. Estos respetan los supuestos de cartera réplica del modelo BMS empleando las técnicas de escenarios y simulaciones con el objeto de inferir la distribución de probabilidad de los posibles valores del subyacente. El valor de la flexibilidad estratégica surge del promedio de valores positivos asignando valor cero a los negativos (Datar y Mathews, 2004; Datar, Matews y Johnson, 2007).

• b)

  Modelos en tiempo discretos y sus derivaciones: la valoración de la flexibilidad estratégica en proyectos de inversión, empresas en marcha y activos reales ha quedado reservada preferentemente para los modelos formulados en tiempo discreto. Estos son utilizados preferentemente en el planteamiento de modelos de decisión y en la mayoría de las aplicaciones de opciones reales (Trigeorgis, 1995, 1997; Luherman, 1998; Amram y Kulatilaka, 1998, Mun, 2004), reconociendo sus raíces en el clásico modelo binomial (Cox, Ross y Rubinstein, 1979). Producto de su versatilidad se adapta a distintas modalidades y adecuaciones según: a) se trabaje modelando el proceso estocástico con rejillas recombinantes de nodos intermedios o árboles de decisión (Brandao, Dyer y Hahn, 2005; Smith, 2005); b) el proceso estocástico sea binomial (2 sucesos posibles) o trinomial (3 sucesos posibles) (Rendleman y Bartter, 1979; Jarrow y Rudd, 1982; Boyle, 1988, Rubinstein, 2000; Jabbour, Kramin y Young, 2001); c) se usen los equivalentes ciertos correspondientes al tradicional modelo binomial o las probabilidades implícitas calculadas a partir del precio de mercado observado de la opción utilizando algoritmos de optimización (Rubinstein, 1994; Derman, Kani y Chriss, 1996; Arnold, Crack y Schwartz, 2004; Arnold y Crack, 2004); d) se presenten momentos estocásticos de orden superior transformando la distribución binomial para incorporar asimetrías y curtosis en la proyección del recorrido aleatorio del subyacente (Rubinstein, 1998; Haahtela, 2010; Milanesi, 2012; e) se presenten enfoques para la estimación de la volatilidad correspondiente al activo real ante la carencia de activos financieros gemelos en mercados incompletos (MAD-riesgos de mercados y privados-volatilidades cambiantes) (Smith y Nau, 1995; Copeland y Antikarov, 2001; Haahtela, 2011), y f) se cuente con aplicaciones a la teoría de juegos (Smith y Trigeorgis, 2004).

2.2

Modelos borrosos

En esta categoría se agrupan los modelos que trabajan en un esquema de posibilidad aplicando matemáticas borrosas (fuzzy) (Zadeh, 1965; Dubois y Prade, 1980; Carlsson y Fullér, 2001). Los algoritmos de valoración y el análisis del riesgo se circunscriben al concepto de posibilidad y al empleo de la matemática borrosa (Fullér y Majlender, 2003; Kahraman, Ruan y Tolga, 2002). El presente grupo es el resultado de adecuar los modelos tradicionales de valoración de opciones reseñados en la subsección 2.1, a la lógica de los conjuntos borrosos, clasificándose en:

• a)

  Modelo en tiempo continuo fuzzy (MCF): en el clásico modelo de Black-Merton-Scholes se utilizan las nociones de conjuntos borrosos para valorar opciones financieras o reales. Se supone comportamiento borroso mediante el uso de números trapezoidales con el objeto de describir los posibles valores del subyacente (activo financiero o real) y precios de ejercicio, respectivamente (Carlsson y Fullér, 2003; Carlsson, Fullér, Heikkila y Majlender, 2007).

• b)

  Fuzzy pay-off method (FPOM): desarrollado por Collan, Fullér y Mezei (2009), quienes emplean la técnica de escenarios, trabajando con distribuciones triangulares y valiéndose de las matemáticas borrosas (fuzzy). El valor de la opción surge del producto entre el cociente representativo del área de valores positivos sobre el área total de posibles valores del triángulo y el valor posible medio del escenario borroso. Los resultados obtenidos con el presente método son consistentes con el método desarrollados por Datar y Mathews (2004) y Datar et al., 2007.

• c)

  Modelos en tiempo discreto fuzzy (MDF): consiste en adaptar el tradicional modelo binomial a la lógica borrosa. Estos permiten operar y definir la ambigüedad propia del subyacente mediante números borrosos triangulares o trapezoidales, en particular para estimar los movimientos ascendentes y descendentes (Muzzioli y Torricelli, 2004; Yoshida et al., 2006; Zdnek, 2010; Liao y Ho, 2010).

3

El modelo binomial borroso y la valoración de activos reales

La ventaja de la teoría fuzzy aplicada a los modelos de opciones reales consiste en la posibilidad de capturar el sesgo positivo en la distribucion de probabilidad de posibles valores del proyecto, rasgo característico de las opciones reales del proyecto (incorporando en el valor el potencial beneficio de la inversión, limitando el riesgo de las posibles pérdidas). Las principales variables que afectan el valor de la opción en el modelo binomial son los factores u (coeficiente de ascenso) y d (coeficiente de descenso), siendo u=eσt y d = 1/u. La base para su estimación se encuentra en la volatilidad (σ) derivada de la cartera de activos financieros gemelos. En aquellos proyectos donde no existen activos financieros gemelos negociados en el mercado de capitales surge como alternativa para estimar la volatilidad el enfoque MAD. El mencionado enfoque parte del supuesto de que el mercado financiero es completo y el valor del activo réplica del proyecto surge de su valor actual neto. Este valor intrínseco es calculado actualizando los flujos de fondos del proyecto sin flexibilidad estratégica, utilizando una tasa de mercado que refleje el riesgo de inversiones en activos equivalentes al objetivo de valoración. El proceso estocástico se supone del tipo geometric brownian motion (GBM) y, consecuentemente, la distribución de los rendimientos del activo es normal. La volatilidad del proyecto se obtiene calculando la desviación estándar de los rendimientos con simulación Monte Carlo de los flujos de fondos del proyecto y, consecuentemente, de su valor actual neto. Estos son simulados desde el periodo 1 hasta n, obteniéndose los flujos de fondos futuros (FF_i, i = 1…n) por iteración, y se calcula el valor actual del proyecto al final del primer periodo VAN1=∑i=1nFFi(1+k)i−1. Luego se estima el rendimiento del proyecto (z) correspondiente a cada iteración con la siguiente expresión:

Del conjunto de valores z se obtiene el rendimiento medio (z¯=E(z)) y su desviación estándar (s) entre el momento 0 y 1. La volatilidad del proyecto (σ) se define como la desviación anualizada del rendimiento y se calcula con la relación sΔt, donde Δt representa la amplitud del intervalo de tiempo de los flujos de fondos. Si la distancia entre V₁ y V₀ es un año, entonces σ = s.

Alternativamente es posible adaptar el modelo binomial a la lógica borrosa (Dubois y Prade, 1980) empleando números borrosos triangulares. El modelo requiere estimar los factores borrosos u¿ = [u₁, u₂, u₃] y d¿ = [d₁, d₂, d₃], en donde u_1;d₁ corresponden al peor escenario, u_3;d₃ es el mejor escenario y u_2;d₂ es el caso base. El modelo caracteriza la incertidumbre a través de la posibilidad, y para ello se propone el uso de un número borroso triangular para estimar la volatilidad. Esta se calcula a través del coeficiente de variación (CV−+), que representa los juicios y opiniones de expertos sobre las máximas variaciones positivas y negativas respecto del valor de máxima posibilidad (Liao y Ho, 2010). Esta queda determinada como σ′=1−CV*σ;σ;1+CV*σ. En este caso σ puede ser, eventualmente, la medida de riesgo inferida con el enfoque MAD. El modelo binomial borroso es una adaptación del modelo binomial de valoración de opciones a la lógica borrosa. Para estimar los coeficientes de ascenso y descenso borrosos se emplea la volatilidad borrosa siguiendo la misma lógica que en el modelo binomial,

Debido al sesgo que existe en la distribución de posibilidad triangular, el factor de ascenso crea mayor valor y el factor de descenso los revierte a cero. El caso base es similar al resultado obtenido en el modelo binomial tradicional. La combinación de los 3 resultados crea la distribución de posibilidad y, consecuentemente un número borroso en cada nodo de la rejilla binomial. Los coeficientes equivalentes ciertos son obtenidos de los factores de ascenso y descenso (ecuaciones 2 y 3):

El modelo binomial borroso crea una distribución de posibilidad en cada nodo que maximiza y minimiza los posibles valores del subyacente. Esto se logra combinando el mínimo coeficiente equivalente cierto borroso de ascenso y descenso para el peor escenario. De igual manera, el mejor escenario debe ser actualizado con los máximos coeficientes equivalentes ciertos de ascenso y descenso. El caso base se resuelve de similar manera al tradicional modelo binomial. Suponiendo un número borroso triangular (1 = peor, 2 = base, 3 = mejor), las parejas de coeficientes equivalentes ciertos quedan planteadas de la siguiente manera:

Las posibilidades neutrales al riesgo son creadas para expresar los valores extremos de la distribución (Liao y Ho, 2010). Para la construcción de la rejilla binomial borrosa se parte del valor actual neto del proyecto (V₀) estimado con la siguiente expresión:

La ecuación precedente indica que el valor actual neto del proyecto en t = 0 surge de actualizar, por el factor p_k, la corriente de flujos de fondos proyectados (FFL_t) desde el periodo t = 1 hasta t = n, adicionando el valor del flujo de fondos del periodo actual (FFL₀). Para los siguientes periodos el valor del proyecto se integra por los flujos esperados (primer término de la expresión) más el valor del flujo en el momento actual (segundo término). Los pasos necesarios para aplicar el modelo binomial borroso requieren la estimación de 3 rejillas, las cuales son:

• a)

  Rejilla binomial borrosa correspondiente a la evolución del subyacente descontando los flujos de fondos del periodo actual.

• b)

  Rejilla binomial borrosa correspondiente a la evolución de los flujos de fondos para cada periodo en función de la evolución del valor del subyacente.

• c)

  Rejilla binomial borrosa con las opciones donde el valor del subyacente surge de la suma de las rejillas precedentes.

Para la estimación de la primera rejilla previamente se debe estimar la razón flujo de fondos libres a valor actual del proyecto para cada periodo RFt=FFLt/Vt. Esta representa la magnitud a ser descontada del valor borroso proyectado Vt′, siendo la expresión utilizada:

La segunda rejilla, estimación del flujo de fondos borrosos (RF¿_t), requiere aplicar la razón flujo de fondos-valor actual al valor proyectado borroso estimado precedentemente:

Finalmente, agregando las rejillas precedentes, se determina el valor borroso para cada nodo del subyacente y se estima el valor de las opciones reales.

En la ecuación precedente FFOP representa el valor de las opciones y r la tasa de interés libre de riesgo, tomando en cada nodo borroso el mayor valor entre el proyecto sin opciones (primer término) y con opciones (segundo término). La rejilla binomial borrosa se resuelve recursivamente para cada nodo borroso.

El supuesto de que la distribución de posibilidades de flujos de fondos se encuentra sesgada a la derecha altera la manera de computar el valor medio del número borroso, es decir, el valor de la opción real. Suponiendo que V′=V1α;V3α es un número borroso y λ ∈ [0, 1], el valor puntual medio (crisp mean value) de V^¿ es:

El factor de ponderación λ es conocido por Yoshida et al. (2006) como índice optimismo-pesimismo, quienes establecen que su valor es definido por una decisión subjetiva del agente. Liao y Ho (2010) establecen que el valor del índice se puede determinar objetivamente. Para capturar el sesgo hacia la derecha (positivo) del número borroso triangular que representa el valor de las opciones estratégicas del proyecto E(V)¿, se propone calcular el índice λ con la siguiente expresión:

donde AD representa el área derecha del área del número borroso triangular y AI el área izquierda del número borroso triangular². Calculando la integral definida de la expresión 10 se obtiene la ecuación 12 correspondiente al valor medio borroso. Los valores V₁ (0)-V₂ (1)-V₃ (0), representan los valores de mínima y el de máxima posibilidad de la función de pertenencia.

4

Un caso de aplicación. Valoración de un proyecto de inversión de explotación de un yacimiento de petróleo

A continuación se desarrolla el caso planteado en Smith (2005). Se pretende determinar el valor para el inversor privado, relativo a la concesión y explotación de un yacimiento de petróleo bajo la forma jurídica de consorcio con el sector público. La participación privada representa el 75% de la inversión, el saldo restante representa la propiedad estatal. Las reservas totales se estiman en 99 millones de barriles, previéndose una extracción inicial de 9 millones de barriles. La duración nominal del contrato de concesión es de 10 años. Adicionalmente se espera: a) decrecimiento de la producción a razón de una tasa anual del 15%; b) crecimiento del precio del crudo a razón de un 3% anual; c) crecimiento de costos de explotación a razón del 2% anual, y d) costos fijos estables (no hay cambio de estructura).

Los valores utilizados como base de proyección son: a) precio del crudo por barril 87,28 dólares americanos; los costos de producción representan el 77% del precio de venta (67,21 dólares americanos); b) costos fijos 7 millones de dólares anuales (U$ 7 millones); c) amortización de la inversión fija a 10 años (300 millones de dólares americanos/10 años), y d) no se toma deuda y la tasa ajustada por riesgo asciende al 10%.

El contrato dispone las siguientes opciones que pueden ejercitarse en el quinto año de vida. Contractualmente se permite continuar, abandonar o expandir, bajo las siguientes condiciones: a) continuar la explotación hasta el décimo año sin variación alguna (estrategia continuar); b) vender la explotación con valor fijado en 100 millones de dólares americanos (estrategia abandono), y c) comprar participación estatal con un costo de 50 millones de dólares americanos (U$ 50 millones) y un incremento del 33% (o 4/3) sobre los ingresos originales proyectados a percibir por los titulares del capital privado (estrategia expandir). En la tabla 1 se expone la proyección de las variables que integran el flujo de fondos libres del proyecto y el valor actual inicial (V₀) de 592,84 millones de dólares americanos (ecuación 6). En las 2 últimas filas se calcula el valor actual neto en cada periodo y la razón flujos de fondos libres-valor actual neto del proyecto. El valor estimado no incorpora la flexibilidad estratégica que el contrato depara en el quinto año.

Tabla 1.

Flujos de fondos proyectados y valor actual neto del proyecto

Conceptos (millones)	0	1	2	3	4	5	6	7	8	9	10
Reservas de petróleo	99,00	90,00	81,00	73,35	66,85	61,32	56,62	52,63	49,23	46,35	43,90
Nivel de producción	9,00	9,00	7,65	6,50	5,53	4,70	3,99	3,39	2,89	2,45	2,08
Costo variable operativo	67,21	68,55	69,92	71,32	72,75	74,20	75,68	77,20	78,74	80,32	81,92
Precio de crudo (por barril)	87,28	89,90	92,60	95,37	98,23	101,18	104,22	107,34	110,56	113,88	117,30
Ingresos por ventas		809,09	708,35	620,16	542,95	475,36	416,17	364,36	319,00	279,28	244,51
Costos de producción		–616,95	–534,89	–463,75	–402,07	–348,60	–302,23	–262,04	–227,19	–196,97	–170,77
Costo fijo		–7,00	–7,00	–7,00	–7,00	–7,00	–7,00	–7,00	–7,00	–7,00	–7,00
FF después de impuestos		185,14	166,46	149,41	133,88	119,76	106,94	95,32	84,81	75,31	66,74
Participación minoritaria		–46,28	–41,62	–37,35	–33,47	–29,94	–26,74	–23,83	–21,20	–18,83	–16,68
Flujo de fondos libres (FFL)	0,00	138,85	124,85	112,06	100,41	89,82	80,21	71,49	63,61	56,48	50,05
Vt valor actual	592,84	652,12	564,60	483,73	408,83	339,27	274,39	213,61	156,32	101,99	50,05
RFt = FFL/Vt	0,00%	21,29%	22,11%	23,17%	24,56%	26,47%	29,23%	33,47%	40,69%	55,38%	100,00%

Fuente: elaboración propia.

Para valorar las opciones del proyecto es necesario calcular los parámetros del modelo binomial para la construcción de la rejilla. En la tabla 2 se presentan los valores correspondientes a volatilidad, coeficientes de ascenso, descenso, tasa libre de riesgo y coeficiente equivalente cierto.

Tabla 2.

Parámetros modelo binomial

σ	u	d	r	p	1-p
35,00%	1,41907	0,70469	5%	0,48515	0,51485

Fuente: elaboración propia.

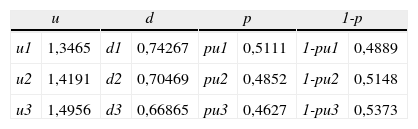
La volatilidad (35%) se obtiene empleando el enfoque MAD, y para ello, mediante simulación³, se iteran los flujos de fondos como entrada para calcular las variables de la ecuación 1. De la muestra de rendimientos (z) obtenidos en cada iteración se obtiene el rendimiento medio (z¯=E(z)) y su desviación estándar (s) entre el momento 0 y 1 y, consecuentemente, la volatilidad del proyecto (σ)=s/Δt. El rango de variación (CV) se supone con base en el juicio de expertos en un 15%, siendo la volatilidad borrosa del 29,75, del 35 y del 40,25%. Con estos datos se está en condiciones de calcular los factores de ascenso, descenso (ecuaciones 2 y 3) y coeficientes borrosos equivalente ciertos (ecuación 4). Estos se exponen en la tabla 3.

Tabla 3.

Parámetros modelo binomial fuzzy

u		d		p		1-p
u1	1,3465	d1	0,74267	pu1	0,5111	1-pu1	0,4889
u2	1,4191	d2	0,70469	pu2	0,4852	1-pu2	0,5148
u3	1,4956	d3	0,66865	pu3	0,4627	1-pu3	0,5373

Fuente: elaboración propia.

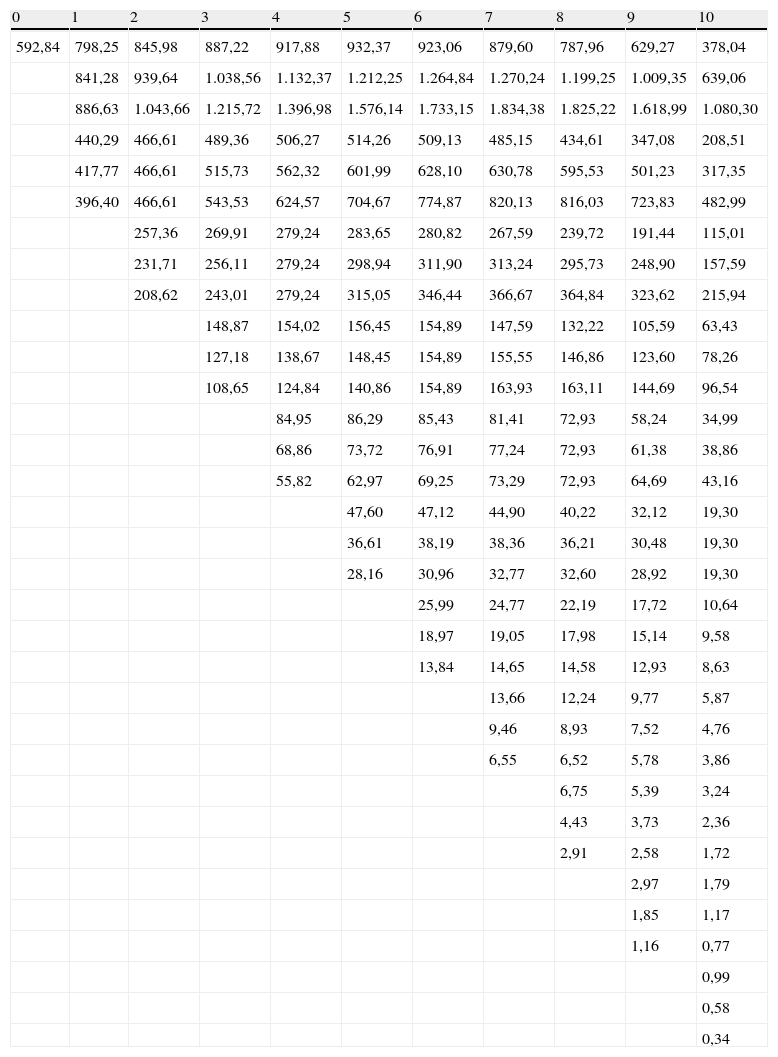
Las parejas de coeficientes equivalentes ciertos borrosos (ecuación 5) queda planteada como p¿_u = [0,4627; 0,4852; 0,5111] y p¿_d = [0,4889; 0,5148; 0,5373]. Este es el orden empleado para identificar los escenarios del número borroso triangular (peor escenario, base, mejor escenario) a ser aplicados en el procedimiento recursivo sobre los nodos borrosos, sobre el peor escenario. La primera rejilla a construir proyecta el valor borroso del activo (V¿_(i,j)t) descontada la razón de flujos de fondos del periodo (1-RF_t) (ecuación 7); los valores proyectados en cada nodo se ordenan de menor a mayor, donde el valor intermedio corresponde al modelo binomial clásico (tabla 4).

Tabla 4.

Rejilla binomial borrosa proyección valor del proyecto neto flujo de fondos del periodo

0	1	2	3	4	5	6	7	8	9	10
592,84	798,25	845,98	887,22	917,88	932,37	923,06	879,60	787,96	629,27	378,04
	841,28	939,64	1.038,56	1.132,37	1.212,25	1.264,84	1.270,24	1.199,25	1.009,35	639,06
	886,63	1.043,66	1.215,72	1.396,98	1.576,14	1.733,15	1.834,38	1.825,22	1.618,99	1.080,30
	440,29	466,61	489,36	506,27	514,26	509,13	485,15	434,61	347,08	208,51
	417,77	466,61	515,73	562,32	601,99	628,10	630,78	595,53	501,23	317,35
	396,40	466,61	543,53	624,57	704,67	774,87	820,13	816,03	723,83	482,99
		257,36	269,91	279,24	283,65	280,82	267,59	239,72	191,44	115,01
		231,71	256,11	279,24	298,94	311,90	313,24	295,73	248,90	157,59
		208,62	243,01	279,24	315,05	346,44	366,67	364,84	323,62	215,94
			148,87	154,02	156,45	154,89	147,59	132,22	105,59	63,43
			127,18	138,67	148,45	154,89	155,55	146,86	123,60	78,26
			108,65	124,84	140,86	154,89	163,93	163,11	144,69	96,54
				84,95	86,29	85,43	81,41	72,93	58,24	34,99
				68,86	73,72	76,91	77,24	72,93	61,38	38,86
				55,82	62,97	69,25	73,29	72,93	64,69	43,16
					47,60	47,12	44,90	40,22	32,12	19,30
					36,61	38,19	38,36	36,21	30,48	19,30
					28,16	30,96	32,77	32,60	28,92	19,30
						25,99	24,77	22,19	17,72	10,64
						18,97	19,05	17,98	15,14	9,58
						13,84	14,65	14,58	12,93	8,63
							13,66	12,24	9,77	5,87
							9,46	8,93	7,52	4,76
							6,55	6,52	5,78	3,86
								6,75	5,39	3,24
								4,43	3,73	2,36
								2,91	2,58	1,72
									2,97	1,79
									1,85	1,17
									1,16	0,77
										0,99
										0,58
										0,34

Fuente: elaboración propia.

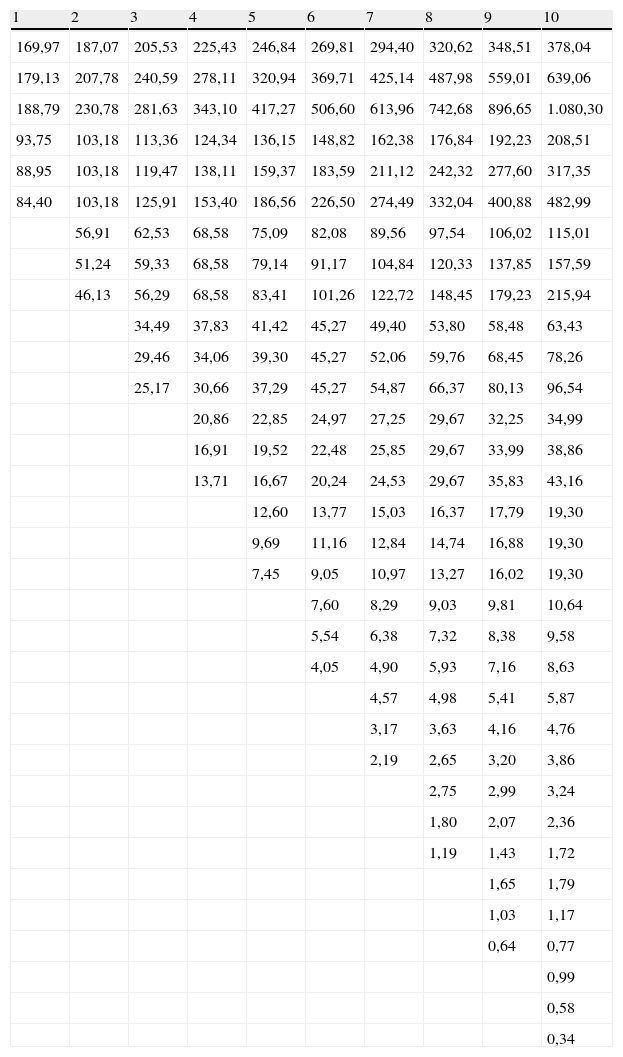
La segunda rejilla sirve para estimar los flujos de fondos borrosos por periodo, empleando la ecuación 8 (tabla 5).

Tabla 5.

Rejilla binomial borrosa proyección flujos de fondos

1	2	3	4	5	6	7	8	9	10
169,97	187,07	205,53	225,43	246,84	269,81	294,40	320,62	348,51	378,04
179,13	207,78	240,59	278,11	320,94	369,71	425,14	487,98	559,01	639,06
188,79	230,78	281,63	343,10	417,27	506,60	613,96	742,68	896,65	1.080,30
93,75	103,18	113,36	124,34	136,15	148,82	162,38	176,84	192,23	208,51
88,95	103,18	119,47	138,11	159,37	183,59	211,12	242,32	277,60	317,35
84,40	103,18	125,91	153,40	186,56	226,50	274,49	332,04	400,88	482,99
	56,91	62,53	68,58	75,09	82,08	89,56	97,54	106,02	115,01
	51,24	59,33	68,58	79,14	91,17	104,84	120,33	137,85	157,59
	46,13	56,29	68,58	83,41	101,26	122,72	148,45	179,23	215,94
		34,49	37,83	41,42	45,27	49,40	53,80	58,48	63,43
		29,46	34,06	39,30	45,27	52,06	59,76	68,45	78,26
		25,17	30,66	37,29	45,27	54,87	66,37	80,13	96,54
			20,86	22,85	24,97	27,25	29,67	32,25	34,99
			16,91	19,52	22,48	25,85	29,67	33,99	38,86
			13,71	16,67	20,24	24,53	29,67	35,83	43,16
				12,60	13,77	15,03	16,37	17,79	19,30
				9,69	11,16	12,84	14,74	16,88	19,30
				7,45	9,05	10,97	13,27	16,02	19,30
					7,60	8,29	9,03	9,81	10,64
					5,54	6,38	7,32	8,38	9,58
					4,05	4,90	5,93	7,16	8,63
						4,57	4,98	5,41	5,87
						3,17	3,63	4,16	4,76
						2,19	2,65	3,20	3,86
							2,75	2,99	3,24
							1,80	2,07	2,36
							1,19	1,43	1,72
								1,65	1,79
								1,03	1,17
								0,64	0,77
									0,99
									0,58
									0,34

Fuente: elaboración propia.

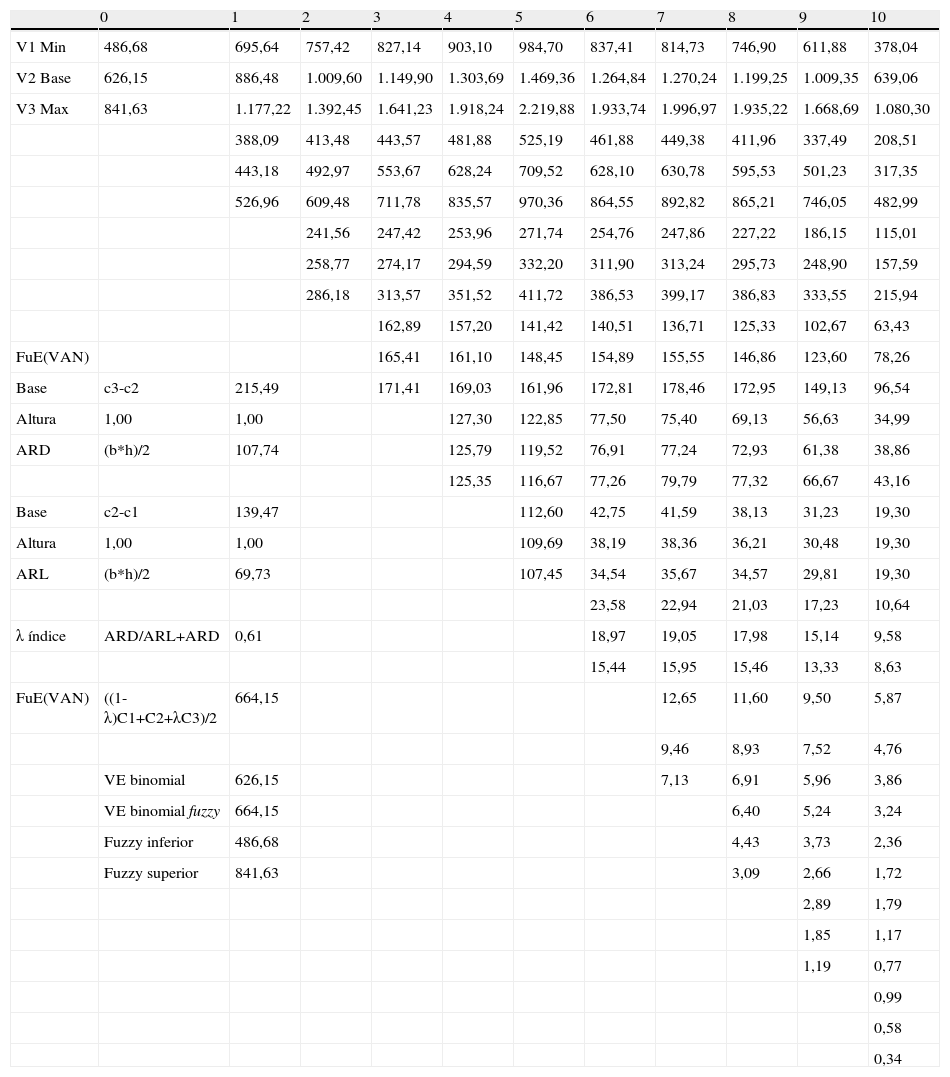
Finalmente, la tabla 6 expone la tercera rejilla empleando la ecuación 9. Los insumos son las rejillas precedentes (tablas 4 y 5) y los parámetros del modelo binomial borroso (tabla 3). A modo de ejemplo, en t = 10 el nodo superior para el escenario pesimista asciende a US$378,04=max378,04+1+0,05−1×0×0,4627+0×0,4889;0+378,04+1+0,05−1×0×0,4627+0×0,4889. El valor esperado del proyecto en t = 10 + 1 es igual a cero, ya que el contrato de concesión dura 10 años sin opción a renovación. Siguiendo con el mismo escenario y nodo, recursivamente en t = 9 el valor es de US$611,18=max348,51+1+0,05−1×378,04×0,4627+258,51×0,4889;0+348,51+1+0,05−1×378,04×0,4627+258,51×0,4889. El número borroso binomial y sus 3 escenarios (optimista, neutro y pesimista) en t = 10 correspondiente al nodo superior es [1.080,30; 639,06; 378,04]. Cabe destacar que el valor intermedio correspondiente al escenario neutro de la rejilla binomial borrosa es el mismo que se obtendría de aplicar el tradicional modelo binomial.

Tabla 6.

Rejilla binomial borrosa valor de las opciones reales

	0	1	2	3	4	5	6	7	8	9	10
V1 Min	486,68	695,64	757,42	827,14	903,10	984,70	837,41	814,73	746,90	611,88	378,04
V2 Base	626,15	886,48	1.009,60	1.149,90	1.303,69	1.469,36	1.264,84	1.270,24	1.199,25	1.009,35	639,06
V3 Max	841,63	1.177,22	1.392,45	1.641,23	1.918,24	2.219,88	1.933,74	1.996,97	1.935,22	1.668,69	1.080,30
		388,09	413,48	443,57	481,88	525,19	461,88	449,38	411,96	337,49	208,51
		443,18	492,97	553,67	628,24	709,52	628,10	630,78	595,53	501,23	317,35
		526,96	609,48	711,78	835,57	970,36	864,55	892,82	865,21	746,05	482,99
			241,56	247,42	253,96	271,74	254,76	247,86	227,22	186,15	115,01
			258,77	274,17	294,59	332,20	311,90	313,24	295,73	248,90	157,59
			286,18	313,57	351,52	411,72	386,53	399,17	386,83	333,55	215,94
				162,89	157,20	141,42	140,51	136,71	125,33	102,67	63,43
FuE(VAN)				165,41	161,10	148,45	154,89	155,55	146,86	123,60	78,26
Base	c3-c2	215,49		171,41	169,03	161,96	172,81	178,46	172,95	149,13	96,54
Altura	1,00	1,00			127,30	122,85	77,50	75,40	69,13	56,63	34,99
ARD	(b*h)/2	107,74			125,79	119,52	76,91	77,24	72,93	61,38	38,86
					125,35	116,67	77,26	79,79	77,32	66,67	43,16
Base	c2-c1	139,47				112,60	42,75	41,59	38,13	31,23	19,30
Altura	1,00	1,00				109,69	38,19	38,36	36,21	30,48	19,30
ARL	(b*h)/2	69,73				107,45	34,54	35,67	34,57	29,81	19,30
							23,58	22,94	21,03	17,23	10,64
λ índice	ARD/ARL+ARD	0,61					18,97	19,05	17,98	15,14	9,58
							15,44	15,95	15,46	13,33	8,63
FuE(VAN)	((1-λ)C1+C2+λC3)/2	664,15						12,65	11,60	9,50	5,87
								9,46	8,93	7,52	4,76
	VE binomial	626,15						7,13	6,91	5,96	3,86
	VE binomial fuzzy	664,15							6,40	5,24	3,24
	Fuzzy inferior	486,68							4,43	3,73	2,36
	Fuzzy superior	841,63							3,09	2,66	1,72
										2,89	1,79
										1,85	1,17
										1,19	0,77
											0,99
											0,58
											0,34

Fuente: elaboración propia.

En la tabla 6, en el quinto periodo son ejercidas las opciones (E: expansión; C: continuar; A: abandono/venta) dependiendo del escenario acontecido. Por ejemplo, en el caso correspondiente al escenario optimista con 5 ascensos (5u), la ecuación 9 se aplica de la siguiente manera: US$2.219,88=max417,27+1+0,05−1×1933,74×0,5110+864,65×0,5373;(417,27−50)+1+0,05−1×1/3×378,04×0,4627+258,51×0,4889;(417,27+100), siendo la estrategia que mayor valor agrega es la de expandir (E). En la tabla 7 se presenta la opción ejecutada en cada nodo borroso en t = 5.

Tabla 7.

Valor de la opción real t = 5 para el nodo borroso y decisión a ser adoptada

Nodos	Decisión: V1		Decisión: V2		Decisión: V3
5*u	984,70	E	1.469,36	E	2.219,88	E
	830,23		1.212,25		1.799,23
	346,84		420,94		517,27
4*u+1*d	525,19	E	709,52	E	970,36	E
	457,93		601,99		804,41
1*d+4*u	236,15		259,37		286,56
3*u+2*d	271,74	E	332,20	E	411,72	E
	252,58		298,94		359,64
2*d+*3u	175,09		179,14		183,41
3*d+2*u	131,94		144,83		161,96	E
	139,31		148,45	C	160,79
2*u+3*d	141,42	A	139,30		137,29
1*d+4*u	54,84		51,78		50,29
	76,84		73,72		71,89
4*u+1*d	122,85	A	119,52	A	116,67	A
	12,31		5,58		0,37
5*d	42,38		36,61		32,14
	112,60	A	109,69	A	107,45	A

En cursiva se indican los mayores valores correspondientes a la opción real seleccionada.

Fuente: elaboración propia.

El sesgo positivo del número borroso triangular se puede observar analizando los resultados obtenidos y presentados en la tabla 7. En efecto, los nodos correspondientes al escenario pesimista indican seleccionar 3 alternativas de expansión y 3 de abandono; para el escenario base las estrategias a seleccionar en sus nodos son 2 de expansión, 2 de abandono y una de continuar; finalmente, el escenario optimista indica seleccionar en 4 nodos la estrategia de expansión y en 2 la estrategia de abandono. Cabe destacar que el escenario base representa los resultados correspondiente al modelo binomial, por lo tanto la anatomía del conjunto de posibles decisiones se ve expandida en el caso borroso frente al modelo binomial tradicional. Como consecuencia de ello, el valor actual neto expandido (estratégico) t = 0 es un número triangular borroso [V_1(min) = $468,68 (millones de dólares americanos); V_2(base) = $626,15 (millones de dólares americanos); V_3(max) = $841,63 (millones de dólares americanos)] (tabla 6). El cálculo del índice λ se detalla en el recuadro de la tabla 6, siendo de 0,61 (ecuación 11). El valor expandido del proyecto (crisp mean value) (ecuación 12) asciende a $664,15 (millones de dólares americanos), levemente superior al valor de $626,15 (millones de dólares americanos) del modelo binomial tradicional. La diferencia a favor del modelo borroso surge del sesgo asimétrico positivo (a-α = US$468,68; a = US$626,15; β + a = US$841,63) del índice λ, potenciando los valores positivos y limitando los negativos, producto de las opciones contenidas en el contrato en el periodo t = 5.

5

Conclusiones

El trabajo expuso los pasos que requiere la aplicación del enfoque binomial borroso en la valoración de opciones reales. Este complementa el enfoque MAD, ya que la volatilidad es obtenida mediante simulación (caso base), con los posibles valores extremos propios de la medida de variación (CV) empleada para la volatilidad borrosa, siendo esta el insumo utilizado para calcular coeficientes equivalentes que reflejan los valores extremos del número borroso triangular.

Las rejillas binomiales borrosas representan el mapa de posibles valores del modelo. Los posibles escenarios (peor, base y mejor) pueden ser analizados y determinar el conjunto de decisiones posibles involucradas, las cuales son: para el peor escenario las combinaciones son 2 expansiones y 3 abandonos; el mejor escenario presenta 3 expansiones y 2 abandonos; finalmente, el caso base pronostica 2 expansiones y abandonos, respectivamente, y una continuación en condiciones normales. El grado de aversión a la ambigüedad del agente se estima con el coeficiente pesimista-optimista con el cual se obtiene el valor borroso esperado del proyecto. Este número es superior al valor de las opciones reales del método binomial, ya que se ponderan los valores positivos sobre todo el conjunto de posibilidades.

La lógica borrosa aplicada a modelos de decisión financiera transforma a estos en una herramienta útil en contextos caracterizados por la ambigüedad en la información disponible, siendo el caso de los nuevos proyectos de inversión, empresas de base tecnológica y nuevas empresas en marcha. Adicionalmente se complementan con el uso de herramientas para el análisis del riesgo, como son los escenarios y la simulación estimando el área de posibilidades, cuya forma es un número borroso triangular. Desde el punto de vista de la toma de decisiones gerenciales, hablar en términos de posibilidades puede ser pensado como un vehículo complementario de las probabilidades.

Conflicto de intereses

El autor declara no tener ningún conflicto de intereses.