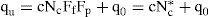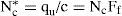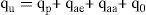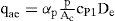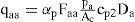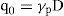Capacidad de carga tridimensional de celdas estructuradas apoyadas en suelo cohesivo: método de análisis simplificado

Resumen

En este artículo se propone un método de análisis simplificado para calcular la capacidad de carga de cimentaciones a base de celdas estructuradas, sometidas a carga vertical sostenida y apoyadas en suelo cohesivo blando. Una celda estructurada está constituida por una losa tapa y muros perimetrales e intermedios de concreto reforzado, sin losa de fondo. El método simplificado propuesto considera la geometría tridimensional de la celda, la resistencia al corte no-drenada del suelo cohesivo y la existencia de continuidad estructural entre losa y muros. El método propuesto se desarrolló a partir de los resultados de un análisis paramétrico-numérico. Además, se define el mecanismo de falla por penetración de este tipo de cimentación.

Abstract

In this paper a simplified analysis method to compute the bearing capacity of structured cell foundations subjected to vertical loading and supported in soft cohesive soil is proposed. A structured cell is comprised by a top concrete slab structurally connected to concrete external walls that enclose the natural soil. Contrary to a box foundation it does not include a bottom slab and hence, the soil within the walls becomes an important component of the structured cell. This simplified method considers the three-dimensional geometry of the cell, the undrained shear strength of cohesive soils and the existence of structural continuity between the top concrete slab and the surrounding walls, along the walls themselves and the walls structural joints. The method was developed from results of numerical-parametric analyses, from which it was found that structured cells fail according to a punching-type mechanism.

Introducción

Las celdas estructuradas, similares a los conocidos “caissons”, son una alternativa para cimentar en suelos difíciles (Romo et al., 2002), con un procedimiento constructivo simple. Una celda estructurada de cimentación está compuesta por muros perimetrales e intermedios, estos últimos se requieren cuando las dimensiones en planta de la cimentación son grandes (> 6 m), estructuralmente ligados a una losa tapa; y la losa de fondo no existe (figura 1). Esta cimentación presenta, a priori, algunas ventajas desde el punto de vista constructivo: los muros perimetrales e intermedios pueden construirse en el sitio con la técnica conocida como muro Milán o pueden colocarse tableros pre-fabricados (Rioboó, 2004; Rioboó y Romo, 2004), en donde la relación peso del tablero pre-fabricado vs potencia de la grúa condiciona su geometría. Después se procede a la construcción monolítica de la losa tapa. Este procedimiento constructivo tiene dos ventajas:

Figura 1.

Esquema de una celda estructurada de cimentación

• 1)

  No se requiere excavación profunda, como en el caso de un cajón de cimentación y

• 2)

  la rapidez de construcción.

Además, la losa tapa funciona horizontalmente como un elemento que da rigidez y liga estructural al grupo de muros, en la corona de la celda.

El uso de cajones de cimentación implica excavaciones profundas que generan costos, tiempo de construcción y control de calidad del propio proceso de excavación. Además, el cálculo de este tipo de cimentaciones es más complejo debido a que los pilotes responden de manera muy diferente que el cajón, lo cual implica que en el análisis debe cumplirse la compatibilidad de deformaciones (desplazamientos) en el conjunto pilote-cajón. Como se verá en el cuerpo de este artículo, este problema no se presenta en el caso de celdas estructuradas.

Objetivos y alcances

En este artículo se presenta un método de análisis simplificado para calcular la capacidad de carga vertical de celdas estructuradas apoyadas en suelo cohesivo (arcilla blanda). Este método es el resultado de un extenso y riguroso análisis numérico, donde se definen relaciones para los factores de forma y de profundidad que son utilizados, de manera simple, en el cálculo de la capacidad de carga última de celdas estructuradas apoyadas en arcilla blanda. Las relaciones de los factores de forma y de profundidad se determinaron de manera sistemática a partir del cálculo numérico de la capacidad de carga última de celdas con varias geometrías y profundidades de desplante (incluida la superficial). En los cálculos se consideran interfaces suelo-concreto lisa y rugosa, donde se permiten o no desplazamientos relativos de traslación. Los factores Nc*, y F_f, que se calculan en esta investigación, se comparan con los más representativos publicados en la literatura técnica de cimentaciones desplantadas superficialmente, para las mismas condiciones del suelo, con el objeto de comparar el procedimiento de análisis.

La solución que se propone corresponde a una del límite superior de la teoría de la plasticidad y es aplicable a celdas estructuradas circulares, cuadradas, rectangulares y de longitud “infinita” (en deformación plana) sujetas sólo a la carga vertical sin excentricidad.

Antecedentes

El objetivo principal del análisis de esfuerzos y deformaciones en una estructura geotécnica es asegurar que tenga un factor de seguridad adecuado contra colapso, además de que cumpla con los requerimientos de servicio para la cual fue diseñada. En general, estos problemas se dividen en dos grupos: los de estabilidad y los de deformabilidad, que abarcan compresibilidad y distorsión. Los problemas de estabilidad y deformabilidad requieren conocer los esfuerzos en la masa de suelo bajo las cargas de trabajo que no inducen falla plástica ni entorpecen el servicio de la estructura.

La característica más importante de los problemas de estabilidad es determinar la carga en la cual la masa de suelo falla plásticamente. En suelos con comportamiento elasto-plástico, se requiere ubicar las zonas donde los esfuerzos han alcanzado la resistencia del suelo para determinar la superficie de falla plástica; existen varios métodos, tres de ellos son:

• 1)

  El método de equilibrio límite ha proveído a la mecánica de suelos varios métodos de análisis simples que consideran la aplicación de la estática para una superficie de falla plana, circular o espiral logarítmica y una ley de resistencia del suelo.

• 2)

  El método de análisis límite de la teoría de la plasticidad con sus conceptos de límites superior e inferior también ha generado soluciones para determinar la estabilidad de estructuras geotécnicas, tal como la solución de Prandtl (1921) para el cálculo de capacidad de carga en cimentaciones superficiales.

• 3)

  Recientemente, la combinación de los métodos numérico y de análisis límite ha generado soluciones o métodos de análisis para problemas de estabilidad de estructuras geotécnicas, por ejemplo, Gouvernec et al. (2006), Salgado et al. (2004), Martin (2001), Reséndiz y Romo (1981) y Romo (1972).

El método de análisis que se propone en este artículo es el resultado de la combinación de los métodos de análisis numérico y de análisis límite, para determinar la capacidad de carga de las celdas estructuradas. La ecuación de capacidad última (q_u) ante una carga vertical de compresión de cimentaciones rígidas desplantadas en una masa de suelo puramente cohesivo es:

donde

• c = cohesión determinada de pruebas no drenadas,

• N_c = factor cohesivo de capacidad de carga, igual a 5.14,

• F_f = factor de forma,

• F_p= factor de profundidad,

• q₀ = esfuerzo vertical total a la profundidad de desplante (D) de la cimentación y

El factor de forma se define como la relación de la capacidad límite de una cimentación de cualquier forma respecto a la de una zapata larga de cimentación, ambas desplantadas sobre la superficie del suelo. El factor de profundidad es la relación de la capacidad límite de una zapata larga de cimentación desplantada a la profundidad D, respecto a la de una zapata idéntica desplantada en la superficie del suelo.

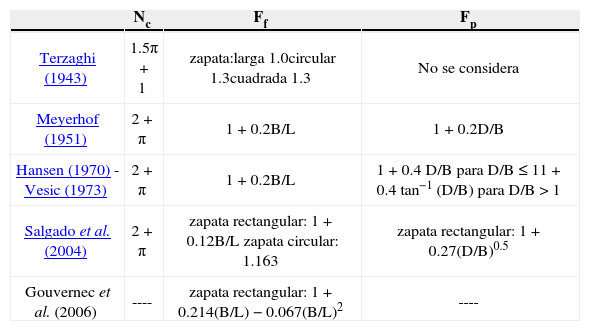
La ecuación 1 se fundamenta en la relación propuesta por Terzaghi (1943). Modificaciones a esta ecuación, realizadas por Meyerhof (1951), Hansen (1970), Vesic (1973), Salgado et al. (2004) y Gouvernec et al. (2006), consideran una magnitud de N_c (solución de Prandtl) diferente a la propuesta por Terzaghi y proponen diferentes relaciones para F_f y F_p (tabla 1).

Tabla 1.

Factores N_c, F_f y F_p para calcular la capacidad última ante carga vertical de compresión de cimentaciones superficiales

	Nc	Ff	Fp
Terzaghi (1943)	1.5π + 1	zapata:larga 1.0circular 1.3cuadrada 1.3	No se considera
Meyerhof (1951)	2 + π	1 + 0.2B/L	1 + 0.2D/B
Hansen (1970) - Vesic (1973)	2 + π	1 + 0.2B/L	1 + 0.4 D/B para D/B ≤ 11 + 0.4 tan^−1 (D/B) para D/B > 1
Salgado et al. (2004)	2 + π	zapata rectangular: 1 + 0.12B/L zapata circular: 1.163	zapata rectangular: 1 + 0.27(D/B)^0.5
Gouvernec et al. (2006)	----	zapata rectangular: 1 + 0.214(B/L) − 0.067(B/L)^2	----

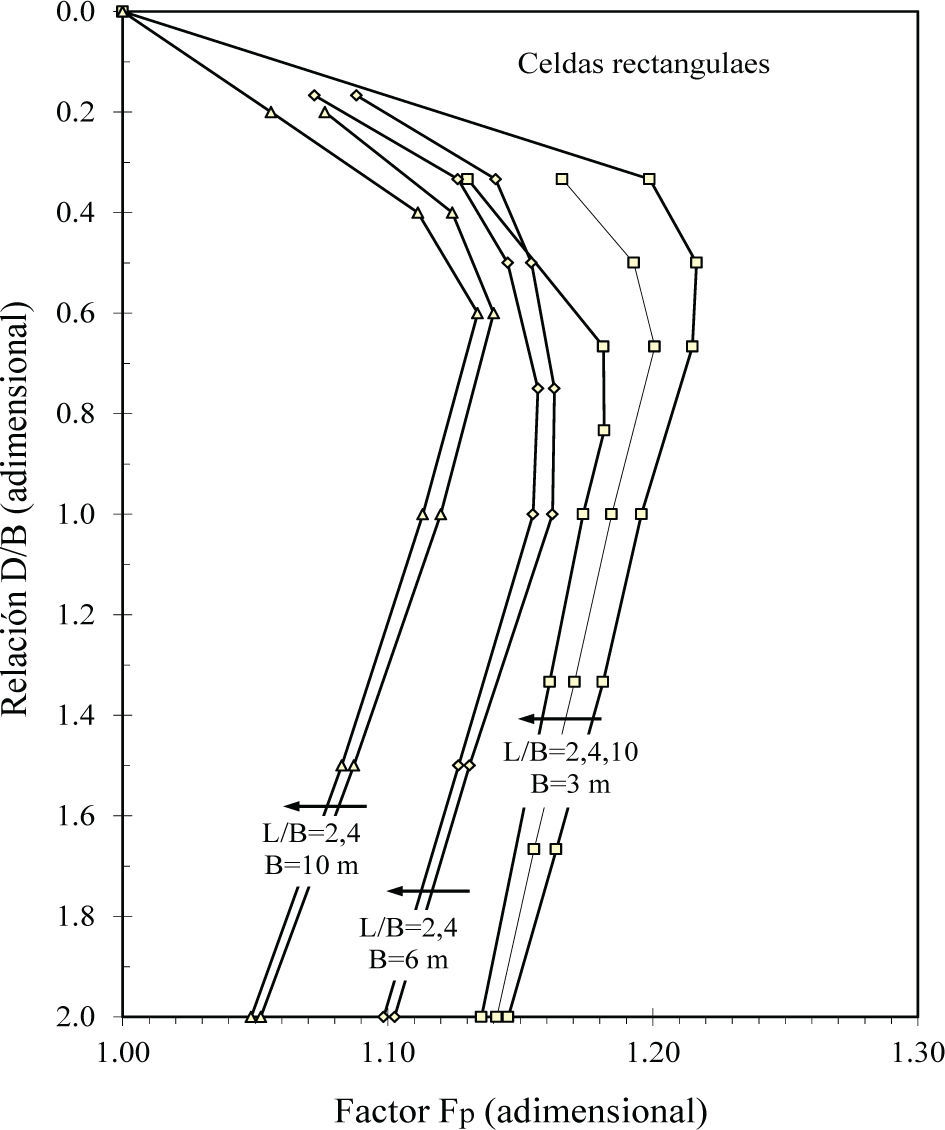
La variación de los factores de forma y de profundidad (incluidos en la tabla 1) se muestran en las figuras 2 y 3 en función de la geometría de la zapata, donde B es su ancho, L su largo y D la profundidad de su desplante. En la figura 2 se observa que para una zapata larga (B/L = 0) el factor F_f = 1 y cuando la zapata es cuadrada (B/L = 1), el factor F_f varía entre 1.12 y 1.20 dependiendo del autor. Por otro lado, la figura 3 muestra que el factor F_p siempre aumenta con la profundidad de desplante.

Figura 2.

Factor de forma, F_f, datos publicados

Figura 3.

Factor de profundidad, F_p, datos publicados

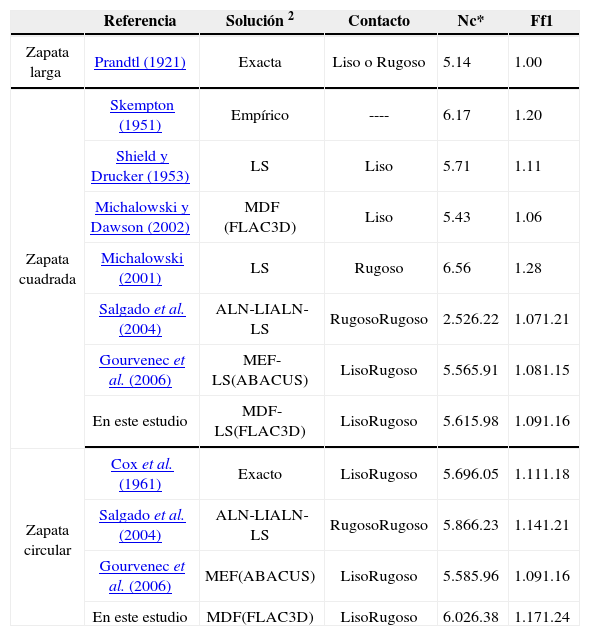
La tabla 2 muestra las soluciones de carga de colapso de zapatas desplantadas superficialmente en suelo cohesivo calculadas con análisis numérico, análisis límite y algunas son propuestas empíricas, también se incluyen los resultados del presente estudio obtenidos con análisis numérico de diferencias finitas con el programa FLAC-3D (Itasca, Consulting Group, Inc., 1997). Para desplante superficial q₀ = 0 y F_p = 1, de acuerdo con la ecuación 1 la solución se reduce a:

Tabla 2.

Factores Nc* y F_f para cimentaciones superficiales, calculados con análisis límite, con la combinación de análisis numérico y análisis límite, así como propuestas empíricas

	Referencia	Solución ^2	Contacto	Nc*	Ff1
Zapata larga	Prandtl (1921)	Exacta	Liso o Rugoso	5.14	1.00
Zapata cuadrada	Skempton (1951)	Empírico	----	6.17	1.20
	Shield y Drucker (1953)	LS	Liso	5.71	1.11
	Michalowski y Dawson (2002)	MDF (FLAC3D)	Liso	5.43	1.06
	Michalowski (2001)	LS	Rugoso	6.56	1.28
	Salgado et al. (2004)	ALN-LIALN-LS	RugosoRugoso	2.526.22	1.071.21
	Gourvenec et al. (2006)	MEF-LS(ABACUS)	LisoRugoso	5.565.91	1.081.15
	En este estudio	MDF-LS(FLAC3D)	LisoRugoso	5.615.98	1.091.16
Zapata circular	Cox et al. (1961)	Exacto	LisoRugoso	5.696.05	1.111.18
	Salgado et al. (2004)	ALN-LIALN-LS	RugosoRugoso	5.866.23	1.141.21
	Gourvenec et al. (2006)	MEF(ABACUS)	LisoRugoso	5.585.96	1.091.16
	En este estudio	MDF(FLAC3D)	LisoRugoso	6.026.38	1.171.24

1 Factor calculado a partir de la solución exacta de deformación plana, N_c = 5.14.

2 Indica: calculado con alguno de los métodos:

LS = Límite superior, LI = Límite inferior,

ALN = Análisis límite numérico,

MEF = Método de los elementos finitos

y MDF = Método de diferencias finitas.

Adicionalmente, ABACUS (HKS, 2002) y FLAC3D son programas comerciales de elemento finito y de diferencias finitas, respectivamente.

La tabla 2 muestra los valores de los factores Nc* y F_f, y éstos se dividen en los casos bidimensional (zapata larga) y tridimensional (zapatas cuadrada y circular). La solución bidimensional es exacta (claro, circunscrita en las hipótesis de la teoría de la plasticidad) en la cual coinciden las soluciones de los límites inferior y superior de la teoría de la plasticidad, la magnitud del factor Nc* = N_c = 2 + π = 5.14; además, esta solución bidimensional se aplica a superficies de contacto liso o rugoso, Gouvernec et al. (2006).

Procedimiento de análisis

El método de análisis que se propone para calcular la capacidad última a la compresión vertical de celdas estructuradas considera que:

donde

• q_p = resistencia a la penetración de la celda,

• q_ae = resistencia por adherencia lateral de las caras ex ternas de los muros perimetrales y

• q_aa = resistencia por adherencia lateral de las caras internas de los muros perimetrales.

El efecto potencial de los muros intermedios es evidente cuando la losa tapa de la celda de cimentación es flexible; es decir, los muros intermedios aumentan la rigidez de la losa de la celda, con lo cual se reduce la distorsión de la losa y el volumen de concreto de la celda; consecuentemente pueden reducir la magnitud del asentamiento máximo si el peso propio de la celda es factor determinante, más detalles en Martínez (2012). En el método propuesto (ecuación 3) sólo se consideran muros perimetrales.

Definición de la carga de colapso

El procedimiento para determinar la carga de colapso considera, mediante análisis numérico de diferencias finitas, incrementar por etapas el desplazamiento vertical de compresión aplicado uniformemente en el área en planta de la cimentación, hasta que la masa de suelo llega a la falla plástica. Los desplazamientos uniformes modelan una rigidez vertical infinita de la cimentación, losa o celda. En cada incremento de desplazamiento se calcula la carga vertical de compresión en el suelo. Los análisis se realizan en términos de esfuerzos totales.

El criterio de falla plástica considera que en la curva presión externa (q) vs asentamiento máximo entre semiancho de la losa (2δ_max/B) se dé la condición de falla plástica (colapso) de acuerdo con lo indicado en la figura 4. Para el estado de esfuerzos que corresponde al punto de colapso, se revisa que la velocidad de desplazamiento forme una superficie de falla plástica cinemáticamente admisible, criterio del límite superior de la teoría de la plasticidad, como es el caso de la superficie de falla mostrada en la figura 5.

Figura 4.

Criterio de falla plástica

Figura 5.

Mecanismo de falla de Prandtl en suelo cohesivo

Factor de forma (F_f)

Para evaluar el método de análisis con el cual se calculó la carga de colapso de las celdas de cimentación, se analizaron losas de cimentación circulares, cuadradas y rectangulares desplantadas en la superficie de una masa de suelo cohesivo con ángulo de fricción interna nulo, donde la solución es conocida (tabla 2).

El ancho y el diámetro de las losas varían entre 0.5 y 10.0 m. La relación ancho/largo (B/L) de las losas rectangulares varía de 1.0 a 0.1. La masa de suelo es homogénea y la resistencia al corte no-drenada del suelo se consideró c = 30 kPa, el módulo de elasticidad E = 100c y la relación de Poisson se mantuvo constate, υ = 0.49, congruente con suelos arcillosos saturados. Se analizaron superficies de contacto lisa y rugosa. Es importante señalar que, para las mismas condiciones geométricas de las cimentaciones, se evaluó el efecto de la variación de la resistencia al corte en el intervalo de 30 a 60 kPa, los resultados mostraron que el factor Nc* (o el factor de forma F_f) permanece prácticamente inalterado (Martínez, 2012); esto implica que la normalización que se realiza en el cálculo de estos factores minimiza la influencia de la resistencia al corte, por lo que los factores definidos en esta investigación tienen aplicación al menos en el intervalo de resistencia al corte citado.

Como ejemplos, la figura 6 muestra las superficies de colapso, definidas por los contornos de velocidad de desplazamiento de losas circular, cuadrada y rectangular con contacto rugoso. Se observa que los mecanismos de falla son superficiales y similares entre sí y, además, al propuesto por Prandtl (figura 5). La diferencia entre ellos es el volumen relativo de suelo movilizado: mientras todo el suelo alrededor de la losa circular opone resistencia al desplazamiento, las losas cuadrada y rectangular el suelo cercano a la esquina tienen menos desplazamiento con respecto al suelo ubicado a los lados. Note que mientras los mecanismos de falla en los dos sentidos de la cimentación cuadrada son idénticos, en la cimentación rectangular la superficie de falla en el sentido transversal presenta más desarrollo que en el longitudinal.

Figura 6.

Contornos de velocidad de desplazamiento que definen la superficie de falla plástica de losas circular, cuadrada y rectangular, vista de la cuarta parte de cada modelo

Con el criterio de falla descrito (figura 4) para cada una de las losas analizadas se calculó la carga última (q_u) y conocida la resistencia al corte, con la ecuación 2 se calcularon los correspondientes factores Nc*. Asimismo, al considerar el factor N_c = 5.14 (deformación plana), los valores calculados de Nc*, y con base en la misma ecuación 2, se determinaron los factores de forma (F_f). Los factores Nc* y F_f de las losas circulares y cuadradas resultantes se grafican en función de su diámetro o ancho en la figura 7. En las gráficas se observa que a menor diámetro o ancho, mayor es la magnitud de ambos factores, una posible causa de este efecto se debe a que la presión en el contacto cimentación-suelo, para igual carga sobre la losa, es inversamente proporcional al área en planta de la cimentación.

Figura 7.

Factores Nc* y F_f de losas de cimentación circulares y cuadradas desplantadas superficialmente en suelo puramente cohesivo

Cox et al. (1961) encontraron soluciones exactas para losas circulares con contactos rugoso (Nc*) y liso (Nc*). Los resultados del presente estudio (figura 7), muestran que cuando la curva para losa circular tiende a ser asintótica (B = 10 m) la magnitud de Nc* = 6.38, contacto rugoso. Además, resultados no incluidos aquí, muestran que para B = 10 m y contacto liso, Nc* (Martínez, 2012). Al comparar estos resultados con las soluciones exactas, se calculan diferencias de 5.45 y 5.80%, respectivamente, para contacto rugoso y liso. Además, en la tabla 2 se observa que para zapatas cuadradas la solución no está bien definida y sólo existen aproximaciones, la magnitud del factor Nc* varía de 5.43 a 6.56.

Por otro lado, Levin (1955) argumenta que el factor Nc* de una zapata cuadrada debe encontrarse en el intervalo de los factores de cimentaciones larga (B/L → 0) y circular, entre 5.14 y 6.05 para superficie rugosa y entre 5.14 y 5.69 para superficie lisa. En el caso de losas cuadradas, en este trabajo se calcularon magnitudes del factor que caen en el intervalo que sugiere Levin (figura 7). Asimismo, como se observa en esta figura, para diámetro y ancho equivalentes de losas circular y cuadrada, el factor Nc* de la losa circular es mayor. Esto es comprensible por el mayor volumen de suelo involucrado en el mecanismo de falla para cimentaciones circulares, comparado con el movilizado por la cimentación cuadrada, como se muestra en las figuras 6a y 6b.

En la tabla 1, varios autores proponen que el factor N_c y por ende el Nc* de zapatas rectangulares depende de la relación B/L, pero no consideran su variación en función de B para relaciones B/L iguales. Este efecto (denominado efecto geométrico de escala) se observa en la figura 8, donde se aprecia que los factores Nc* y F_f dependen tanto de la relación B/L como de B. Los resultados mostrados en esta figura indican que el efecto geométrico de escala decrece al aumentar el ancho B y para valores de B superiores a 6.0 m, tal efecto es despreciable. La mayor influencia, para los casos estudiados, corresponde a B = 0.5 m. Además, se observa que para losas cuadradas (B/L = 1) los factores Nc* y F_f alcanzan su magnitud máxima, la cual decrece a medida que se alarga la zapata (B/L → 0). Los resultados de este estudio indican que la curva correspondiente a B = 10.0 m proporciona valores de Nc* y F_f semejantes a los propuestos por Meyerhof (1951), Hansen (1970), Vesic (1973), Salgado et al. (2004) y Gouvernec et al. (2006). Además, esta curva parece representar, conforme a los casos estudiados en esta investigación, la frontera inferior a partir de la cual el ancho B de la cimentación no influye en los factores Nc* y F_f.

Figura 8.

Factores Nc* y F_f de losas de cimentación rectangulares desplantadas superficialmente en suelo puramente cohesivo

Cabe resaltar que la capacidad última ante una carga vertical de compresión (q_u) de una losa de cimentación con desplante superficial depende únicamente de la resistencia a la penetración (q_p), q_u = q_p, y particularmente del factor de forma, F_f, ecuación 2. La comparación de los factores aquí calculados (Nc* y F_f) con los de la tabla 2, muestra que el método de análisis para definir la carga de colapso proporciona resultados congruentes con los publicados en la literatura técnica. Consecuentemente, el método de análisis descrito se usa en esta investigación para calcular los factores de forma, F_f, y de profundidad, F_p.

Mecanismo de falla por penetración de la celda

La resistencia a la penetración (q_p) de las celdas estructuradas se calculó con la misma metodología utilizada en la determinación del factor de forma. Asimismo, se consideró que las celdas están desplantadas a diferentes profundidades y para eliminar el efecto de los esfuerzos cortantes que se desarrollan en el contacto muro-suelo, los modelos numéricos incluyeron elementos de interfaz para permitir libremente el movimiento relativo en el contacto. Además, se consideró que el mecanismo de falla se desarrolla libremente (sin ser afectado por la sobrecarga), con q₀ = 0. En los análisis numéricos se considera que existe deformabilidad del suelo ubicado entre los muros de la celda; es decir, el suelo confinado por los muros no se mueve como cuerpo rígido. La deformabilidad del suelo depende del módulo de elasticidad y la relación de Poisson utilizados. Las propiedades del suelo son las mismas a las utilizadas en el caso de losas superficiales. Adicionalmente, el espesor de los muros es de 0.50 m y se modelan como sólidos con propiedades de concreto, con f′c = 350 kg/cm² y relación de Poisson de υ = 0.20.

De acuerdo con la profundidad de desplante (D) de los muros perimetrales de las celdas de cimentación, se desarrollan tres tipos de falla: general, transición y punzonamiento (Vesic, 1973). Como ejemplo, la figura 9 muestra las superficies de falla de cuatro celdas circulares con diferente profundidad de desplante, se observa que para pequeñas profundidades de desplante (relación D/B < 0.5) la superficie de falla plástica es del tipo general o de transición y para profundidades mayores, es de punzonamiento. En este último caso, se observa que la superficie de falla no emerge hasta la superficie del terreno, como ocurre para los otros dos mecanismos.

Figura 9.

Contornos de velocidad de desplazamiento que definen la superficie de falla plástica de celdas circulares de diámetro B = 6.0 m, vista de la cuarta parte de cada modelo

En general, el mecanismo de falla de la celda circular forma un sólido de revolución axisimétrico. Las superficies de falla de las celdas cuadradas y rectangulares, en función de la profundidad de desplante, presentan esquemas similares a los mostrados en la figura 9 (Martínez, 2012).

Factor de profundidad, F_p, de las celdas estructuradas

Con el procedimiento descrito para calcular del factor de forma y con base en las consideraciones adoptadas para definir en el mecanismo de falla por penetración de la celda, se calculó la carga de colapso (q_u) de cada una de las celdas consideradas en este estudio, al utilizar la ecuación 2 se definieron los correspondientes factores Nc*. Además, con base en la ecuación 1, el factor N_c = 5.14 y los factores de forma F_f definidos en las figuras 7 y 8 (para losas con desplante superficial), se calcularon los factores de profundidad F_p para cada celda analizada.

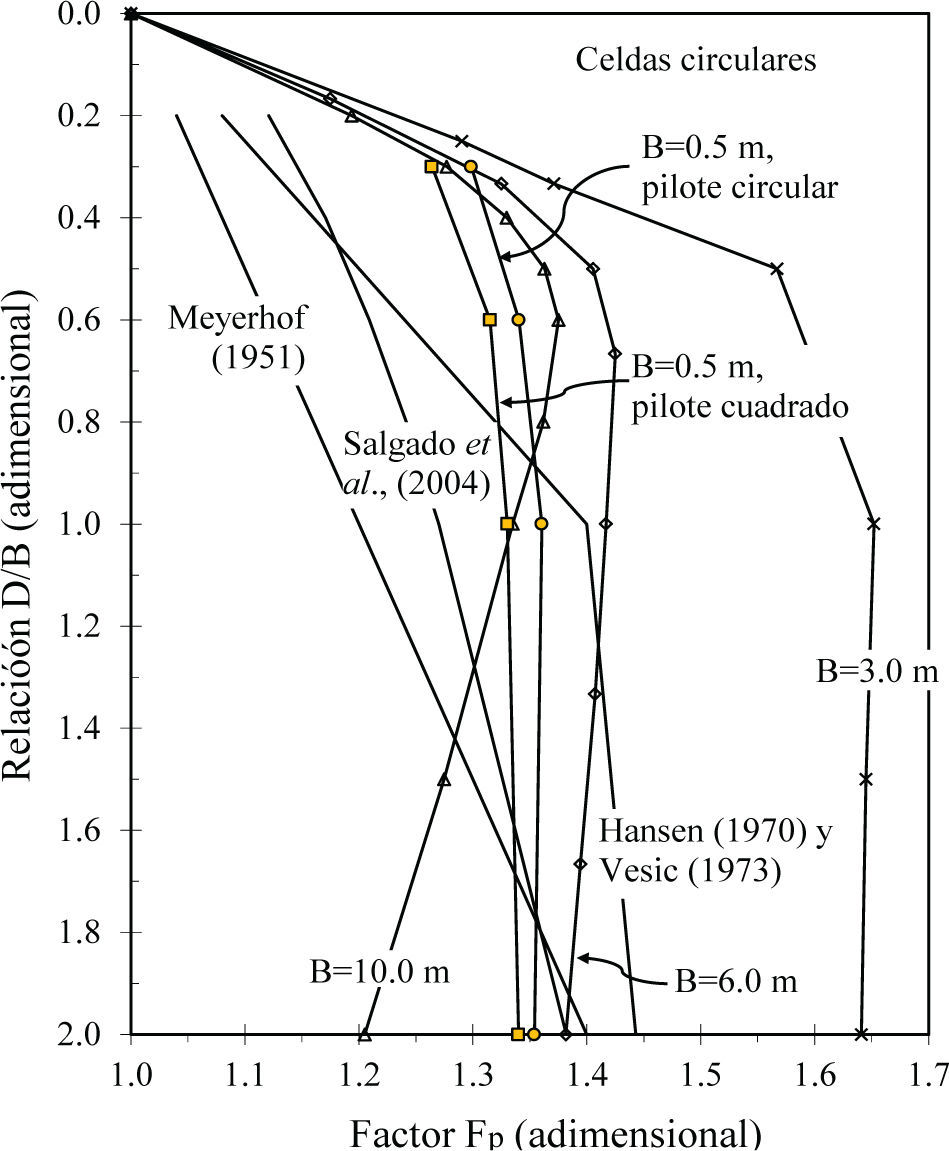
Celdas circulares

La figura 10 muestra la variación del factor de profundidad (F_p) de las celdas circulares, en función de la relación D/B y del diámetro de la celda, se observa que:

• •

  Como las celdas no tienen losa de fondo, al desplante su sección trasversal es un anillo, por lo que la separación de los muros influye en la magnitud del factor de profundidad F_p. Los resultados indican que el factor de profundidad F_p se incrementa casi linealmente para profundidades D/B menores que 0.4 hasta un valor de F_p = 1.35, aproximadamente, donde F_p no depende del diámetro de la celda. A relaciones D/B mayores que 0.5:

  • 1)

    Para diámetros pequeños (B = 3 m) el factor F_p tiende a ser constante con la profundidad.

  • 2)

    Para B = 6 m el factor F_p decrece con la profundidad y su tendencia es semejante a la propuesta por Vesic (1973) y Hansen (1970), a partir de D/B = 1.0.

  • 3)

    Para B = 10 m el factor F_p también disminuye con la profundidad.

Figura 10.

Factores de profundidad (F_p) de celdas circulares de cimentación apoyadas en suelo puramente cohesivo

Con base en estos resultados se puede argüir que a mayor separación de los muros, la resistencia a la penetración disminuye.

• •

  Para secciones pequeñas (B = 0.5 m, equivalentes a pilotes con sección trasversal sólida, cuadrada o circular), la variación del factor F_p sigue una tendencia parecida a la de las celdas con diferentes separaciones entre los muros perimetrales hasta alcanzar la profundidad D/B ≈ 0.5, para luego mantenerse constante a mayores profundidades con F_p = 1.35.

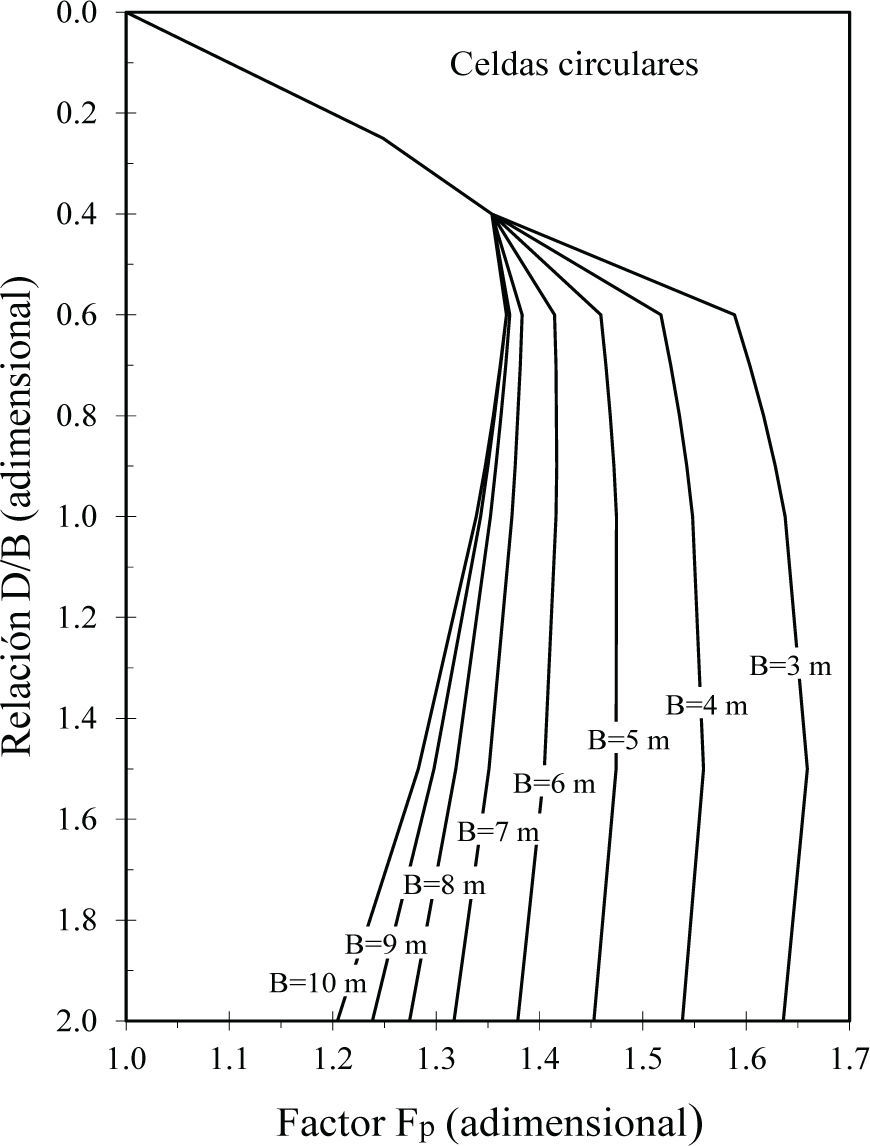
A partir de los valores del factor F_p calculados en el presente estudio para diámetros B = 3, 6 y 10 m, y mediante interpolación, se calcularon las curvas intermedias para los diámetros que se muestran en la figura 11.

Figura 11.

Interpolación de los factores de profundidad (F_p) de celdas circulares de cimentación apoyadas en suelo puramente cohesivo

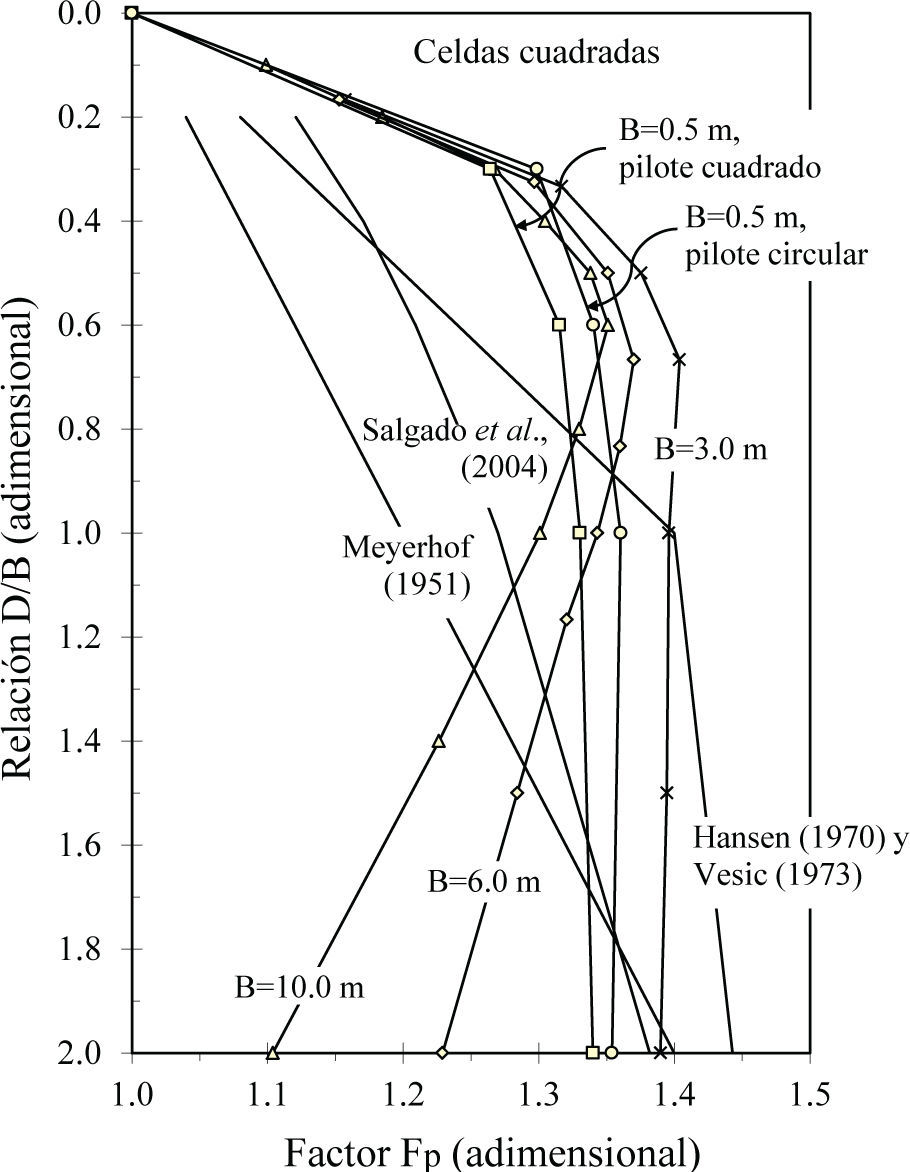
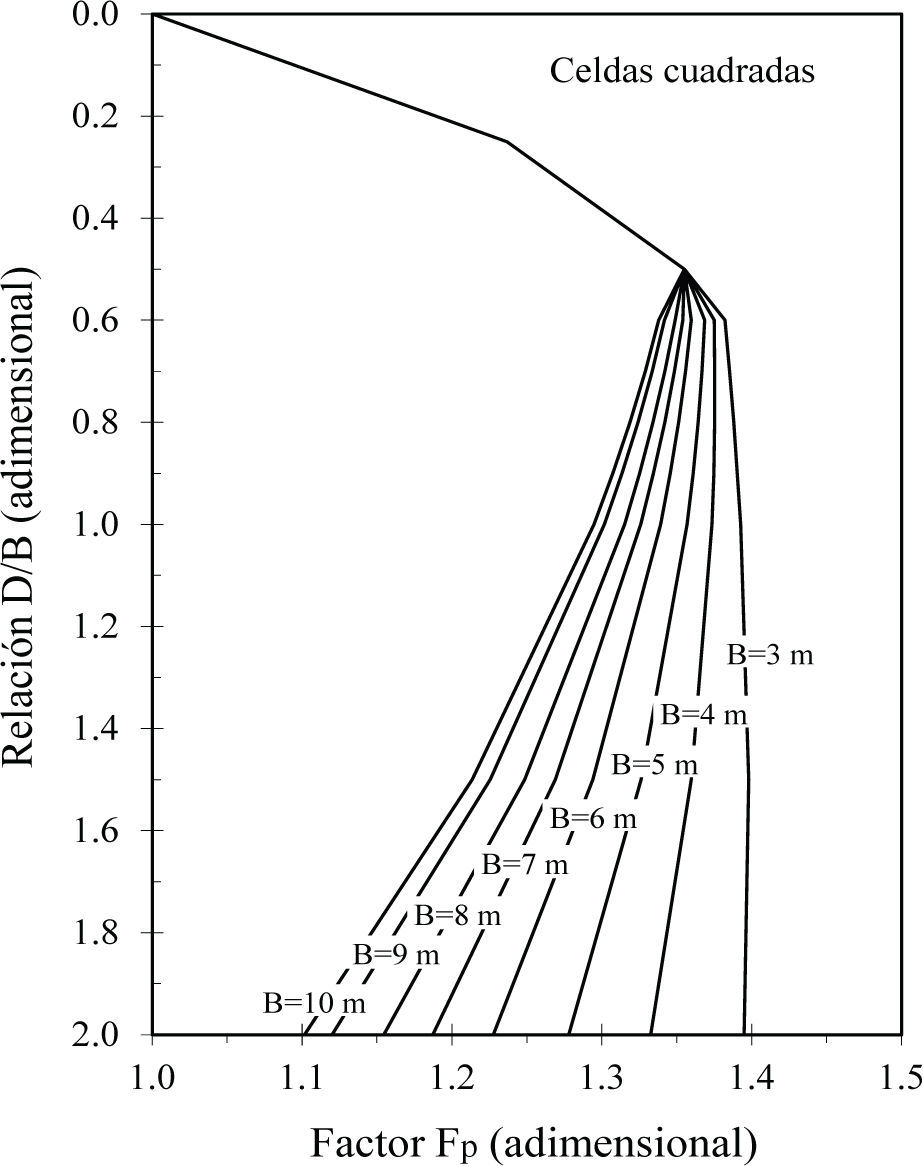
Celdas cuadradas

La tendencia del factor F_p de las celdas cuadradas (figura 12), es similar al de las celdas circulares, los valores de F_p se incrementan hasta la profundidad de D/B ≈ 0.5. Para relaciones D/B mayores que 0.5: cuando B = 3 m el valor de F_p se mantiene constante y para B ≥ 6 m los valores de F_p disminuyen. Asimismo, con base en los valores del factor F_p calculados en el presente estudio para los anchos B = 3, 6 y 10 m, y mediante interpolación, se calcularon las curvas intermedias para los anchos que se muestran en la figura 13.

Figura 12.

Factores de profundidad (F_p) de celdas cuadradas de cimentación apoyadas en suelo puramente cohesivo

Figura 13.

Interpolación de los factores de profundidad (F_p) de celdas cuadradas de cimentación apoyadas en suelo puramente cohesivo

Celdas rectangulares

La figura 14 muestra la variación del factor de profundidad (F_p) para celdas rectangulares en función de la relación D/B, este factor se incrementa a valores máximos que oscilan entre 1.1 y 1.2 para la relación D/B ≈ 0.4, luego a partir de ahí, F_p disminuye con la profundidad con una tasa que depende del ancho B de la celda. En esta figura se observa que las tendencias de variación de los valores de F_p son semejantes, pero sus magnitudes difieren entre sí. Asimismo, se observa que, al igual que para las secciones cuadrada y circular, la relación L/B no influye en el factor de profundidad, para un mismo ancho B.

Figura 14.

Factores de profundidad (F_p) de celdas rectangulares de cimentación apoyadas en suelo puramente cohesivo

Método de análisis simplificado

El método de análisis que se propone considera que la resistencia última a la compresión vertical (q_u) se calcula con la ecuación 3 y que la sección en planta de la celda se mantiene constante en profundidad. A continuación se describen cada uno de los sumandos de la ecuación 3.

La resistencia a la penetración de la celda (q_p) considera el efecto combinado de la penetración de los muros perimetrales, la rigidez infinita de la losa y la deformación del suelo confinado por los muros de la celda, se calcula con:

donde los factores de forma (F_f) y de profundidad (F_p) se pueden calcular con base en las figuras 7 y 8, y 10 a 14, respectivamente, en función de la geometría de la celda a analizar.

La resistencia por adherencia lateral de las caras externas de los muros perimetrales (q_ae) se calcula con:

donde

• α_p = factor que considera el comportamiento de la interfaz muro-suelo, depende del procedimiento y calidad de la instalación del muro y del tipo de suelo, para contacto concreto-suelo, varía de 0.6 a 1.0 y para arcilla del Valle de México es común utilizar 0.7,

• p = perímetro externo de la sección de la celda,

• A_c = área en planta de la celda,

• c_p1 = resistencia al corte no-drenada promedio ponderada por el espesor de los estratos de arcilla a lo largo en profundidad de la cara externa de los muros perimetrales y

• D_e = longitud en profundidad de la cara externa de los muros de la celda.

La resistencia por adherencia lateral de las caras internas de los muros perimetrales (q_aa) se calcula con:

donde

• p_a = perímetro interno de la sección celda,

• c_p2 = resistencia al corte no-drenada promedio ponderada por el espesor de los estratos de arcilla a lo largo en profundidad de la cara interna de los muros perimetrales,

• D_a = longitud en profundidad de la cara interna de los muros de la celda y

• F_aa = factor por adherencia interna que depende de la separación de los muros y de la profundidad de desplante, considera la deformación del suelo confinado por los muros de la celda.

El factor F_aa de las celdas de cimentación se calculó con base en los análisis numéricos con los cuales se definieron los factores de profundidad (Martínez, 2012). En resumen, este factor considera la deformación que se produce en el suelo confinado por los muros perimetra- les de la celda. La deformación del suelo enclaustrado es muy pequeña en comparación con la deformación del suelo que circunda la celda, por lo tanto, este factor es menor que la unidad. En condiciones de suelo homogéneo y para celdas circulares y cuadradas con diámetro o ancho entre 3 y 10 m, este factor varía entre 0.25 y 0.36 en función de B y D; se recomienda usar el límite bajo, 0.25, con lo cual se está del lado de la seguridad en el diseño geotécnico de la celda de cimentación.

Como es conocido, en el diseño geotécnico de cimentaciones desplantadas en suelos cohesivos, la presión vertical total (q₀) debida al peso del suelo a la profundidad de desplante (D) de la celda, se calcula con:

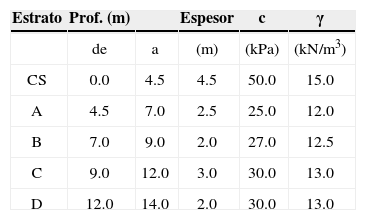
donde γ_p = peso volumétrico promedio, ponderado por los espesores de los estratos de suelo que confinan a la celda.

Aplicación

A manera de ejemplo se presenta la aplicación del método propuesto a un caso hipotético. La tabla 3 muestra la estratigrafía y las propiedades para el diseño geotéc- nico de la celda estructurada. El depósito de suelo presenta una capa superficial desecada (CS) constituida por suelo limo-arenoso cohesivo-friccionante; en este ejemplo sólo se considera la resistencia al corte no-dreanada. Los estratos de A a D están constituidos por arcilla blanda. La celda es de sección cuadrada de 6 × 6 m y profundidad de desplante D = 12 m. Los espesores de los muros perimetrales y de la losa son de 0.60 m y 1.50 m, respectivamente.

Tabla 3.

Estratigrafía y propiedades para el diseño geotécnico del caso hipotético

Estrato	Prof. (m)		Espesor	c	γ
	de	a	(m)	(kPa)	(kN/m^3)
CS	0.0	4.5	4.5	50.0	15.0
A	4.5	7.0	2.5	25.0	12.0
B	7.0	9.0	2.0	27.0	12.5
C	9.0	12.0	3.0	30.0	13.0
D	12.0	14.0	2.0	30.0	13.0

Note que al aplicar el método propuesto en casos prácticos donde el suelo presenta sub-estratos (recuerde que el método propuesto se desarrolló a partir de análisis en suelo homogéneo) se desprenden, entre otros, los siguientes casos: si los sub-estratos son de arcilla compresible con diferente valor de resistencia al corte no-dreanada, se debe obtener un promedio de la resistencia al corte ponderado por los espesores de cada sub-estrato para calcular los sumandos de la ecuación 3. En el caso de suelos limo-arenosos (cohesivo-friccio- nante, como el estrato CS de este ejemplo hipotético), el ángulo de fricción interna se puede despreciar, lo cual está del lado de la seguridad; asimismo, la adherencia de este contacto se desarrolla durante el colado de los muros perimetrales de la celda de cimentación.

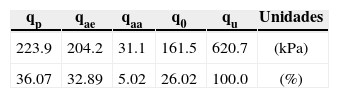
La tabla 4 muestra el aporte de cada uno de los sumandos (ecuaciones 4, 5, 6 y 7) que integran la ecuación 3. En este caso, el mayor aporte a la capacidad de carga lo genera la resistencia a la penetración (q_p) con el 36.1% y la menor, como era de esperarse, la adherencia interna de los muros con 5.0 %. La capacidad de carga última de la celda es q_u = 620.7 kPa.

Tabla 4.

Aporte de cada uno de los sumandos de la ecuación de capacidad última (q_u) ante carga vertical de compresión, ecuación 4

qp	qae	qaa	q0	qu	Unidades
223.9	204.2	31.1	161.5	620.7	(kPa)
36.07	32.89	5.02	26.02	100.0	(%)

Para calcular la resistencia a la penetración se consideró la resistencia al corte no-drenada del estrato en que se apoyan los muros de la celda (a 12 m de profundidad), c = 30 kPa. En otros casos donde la resistencia al corte no-drenada varíe con la profundidad, la resistencia al corte no-drenada se puede calcular como el promedio ponderado por los espesores de los estratos de suelo ubicados entre el desplante de los muros y 0.7B abajo del desplante de los muros. De acuerdo con las figuras 7 y 12, los factores F_f y F_p son 1.18 y 1.23, respectivamente.

Para calcular la adherencia externa se tiene que p = 24 m y A_c = 36 m², y se considera el factor α_p = 0.7. Además, la resistencia al corte no-drenada (c_p1 = 36.46 kPa) y la longitud en profundidad de la cara externa de los muros de la celda es D_e = 12.0 m que comprende los estratos CS, A, B y C.

La adherencia interna se calcula con F_aa = 0.25 y p_a = 19.2 m. A diferencia del cálculo de la adherencia externa, el espesor del estrato CS se reduce debido al espesor de la losa, por lo tanto, D_a = 10.5 m. Debido a la magnitud pequeña de capacidad de carga que aporta la adherencia interna, ésta se puede omitir, esta consideración cae del lado de la seguridad en el cálculo de la capacidad de carga.

El cálculo de q₀ considera la estratigrafía del sitio (tabla 3) y que las características piezométricas del sitio están dadas por nivel freático en superficie y variación hidrostática. En otros casos particulares se deben determinar las condiciones piezométricas.

Conclusiones

En este artículo se propone un método de análisis simplificado para determinar la capacidad de carga última (q_u) de celdas estructuradas de cimentación. El método propuesto está formado por las ecuaciones 3, 4, 5, 6 y 7. Los factores de forma y de profundidad para el cálculo de la capacidad por penetración de celdas estructuradas, ecuación 4, se definen con base en los resultados de análisis numérico de diferencias finitas en combinación con los conceptos del límite superior de la teoría de la plasticidad.

El procedimiento de análisis que se utilizó para definir el método simplificado se verificó con soluciones publicadas que son el resultado del análisis límite, de la combinación de métodos numéricos con análisis límite y algunas propuestas empíricas.

Se encontró que el factor es función del ancho o diámetro de la cimentación debido al efecto geométrico de escala, lo cual se muestra en las figuras 7 y 8. Hasta donde los autores tienen conocimiento, es la primera vez que el efecto de escala geométrico se considera explícitamente en el cálculo de capacidad de carga.

El ejemplo de aplicación muestra que la aportación más importante a la q_u la otorga la resistencia a la penetración de la celda (q_p), seguida por la resistencia por adherencia lateral de las caras externas de los muros perimetrales (q_ae) y por la presión vertical total (q₀) debida al peso del suelo a la profundidad de desplante (D) de la celda. La resistencia por adherencia lateral de las caras internas de los muros perimetrales (q_aa) contribuye con un porcentaje pequeño por lo que, para fines prácticos, se puede despreciar.