Simulación multi-física del secado de madera en COMSOL Multiphysics 3.4.

Resumen

En este trabajo se simulan las cinéticas de secado utilizando un modelo matemático de tipo fenomenológico que describe el secado por convección de aire caliente de madera Pinus pseudostrobus. El desarrollo del modelo parte del balance de masa y calor en el elemento de volumen representativo (EVR), que contiene las fases sólida, líquida, y gaseosa. Se obtiene un sistema de ecuaciones diferenciales parciales que es resuelto por factorización numérica utilizando COMSOL Multiphysics 3.4. Se resuelven tres variables primarias: contenido de humedad; temperatura y densidad del aire seco. Los resultados del modelo fueron comparados con los datos experimentales y contra un modelo semi-empírico. Los resultados son satisfactorios; se describen las cinéticas de secado simuladas, los perfiles espaciales de contenido de humedad al interior del material, la evolución de la masa del aire seco y los perfiles de temperatura.

Abstract

In this work, the numerical simulation of drying of Pinus pesudostrobus wood is presented by using a phenomenological model. The model is developed by considering the heat and mass balance in the representative elementary volume (REV), which involves the solid, liquid and gas phases. We obtained a system of partial differential equations which was solved by numerical factorization by using COMSOL multiphysics 3.4. Three primary variables were solved: the moisture content, the temperature, and the dry-air mass. The numerical results were compared against experimental data and the semi-empirical model. Our results are satisfactory; we describe the drying kinetics, the moisture distribution within the wood, the dry-air mass evolution and the temperature profiles.

Introducción

La eliminación de agua en materiales higroscópicos como la madera es un fenómeno muy complejo, el cual involucra una serie de mecanismos acoplados que ocurren simultáneamente en el proceso de secado. En el proceso de transferencia de masa, el agua libre se elimina primero de la matriz sólida por mecanismos de capilaridad, hasta llegar al punto de saturación de la fibra PSF (aproximadamente en el contenido de humedad de 0.30 kg de agua/kg de sólido seco para coníferas). Al mismo tiempo que el agua es eliminada de los capilares en la madera es reemplazada por el aire que se introduce al material debido a un gradiente de concentraciones además de la diferencia de presiones en el sistema. Finalmente el agua ligada es removida de la matriz sólida por vaporización, y posteriormente por los mecanismos de difusión y presión de vapor de agua hasta llegar al contenido de humedad de equilibrio.

Existen diferentes tipos de modelos de secado de madera; sin embargo, los modelos que involucran en sus ecuaciones los fenómenos de transporte descritos aquí, son los modelos de tipo fenomenológico que parten de las ecuaciones de Whitaker (1977), y que son modificadas por Perré y Turner (1999). Estas ecuaciones involucran balances acoplados de masa, calor y momentum, utilizando propiedades en un volumen promedio EVR (elemento de volumen representativo).

Por lo tanto, un modelo de tipo fenomenológico para el secado de madera se compone de un conjunto de ecuaciones diferenciales parciales EDP, que sólo puede ser resuelto por métodos numéricos. Comsol Multiphysics 3.4 ofrece una forma de incluir la geometría a modelar y el sistema de EDP, evitando la necesidad de programación; además de que el programa incluye los códigos más avanzados para la solución numérica, lo que disminuye tiempos de cómputo, y asegura la convergencia de las ecuaciones.

Se han realizado diferentes estudios similares para especies de pino y encino europeo (Fernandez y Howell, 1997; Raji et al., 2009; Turner et al., 1998), sin embargo, para especies de pinos mexicanos existen pocos estudios con el enfoque de este trabajo, por lo que al modelar el proceso de secado se obtendrá información que podría utilizarse en la elaboración de modelos de secado más complejos que se apliquen en la optimización del diseño y control automático de secadores para especies endémicas, además de contribuir con el aprovechamiento forestal mexicano.

El objetivo de este trabajo es desarrollar un modelo matemático unidimensional que describa los mecanismos de transporte de calor y masa durante el secado por convección de aire caliente de madera Pinus pseudostrobus y resolverlo numéricamente utilizando COMSOL Multiphysics 3.4

Desarrollo

Con el objetivo de comparar las simulaciones del modelo con resultados experimentales se realizaron experimentos de secado basados en un diseño uni-factorial con la temperatura como factor y cuatro niveles: 50, 60, 70 y 80° C, manteniendo la velocidad del aire constante (2.5 m/s), y sin controlar la humedad relativa del aire. Se utilizó un túnel de secado que está diseñado para hacer pasar por la muestra un flujo de aire con velocidad y temperatura uniforme y controlada. El aire se calienta mediante dos resistencias eléctricas de 20Ω, (2.4 kW), controlada por medio de un control PID. La medición de la temperatura se da a través de termopares tipo J, conectados simultáneamente y aislados eléctricamente para reducir el error del sistema. El peso de la muestra durante el proceso es registrado por el sistema de adquisición de datos conectado a una celda de carga (rango de 0–11.34 kg, precisión de 0.1%) que mide la tensión que se produce por el peso de la muestra.

El túnel cuenta con un controlador automático programable National Instruments de la serie FP-1000, que realiza el control del proceso y la adquisición de datos en tiempo real, conectado a un programa de computadora que registra las cantidades por medio del software LabVIEW.

Las muestras de madera fresca se obtuvieron al azar del almacén del aserradero ubicado en la comunidad de Macuilxóchitl de Artigas Carranza, Oaxaca. Las dimensiones de las muestras fueron de 25 cm de largo, 15 cm de ancho con un espesor de 2.54 cm. Las tablas frescas de madera fueron rociadas con ayuda de un dispersor y cubiertas con plástico impermeable para su traslado al laboratorio, en donde fueron almacenadas a 0° C en el refrigerador, para evitar su degradación.

Por cada experimento se utilizaron dos tablas de madera fresca. Los bordes fueron sellados con silicón con el objetivo de que el transporte de humedad ocurra sólo en la dirección del espesor de la madera. Una tabla fue perforada en los extremos del espesor para la introducción de termopares en el centro y a un milímetro de la superficie, como se muestra en la figura 1. Los experimentos tuvieron una duración promedio de 70 horas, cada uno con su réplica.

Figura 1.

Arreglo experimental en el tunel de secado y geometría a modelar

Formulación matemática

Se desarrolló una formulación matemática, la cual representa el proceso de secado por convección de aire caliente basado en el modelo de (Whitaker, 1977), y posteriormente de (Perré y Turner, 2001). Debido a los arreglos experimentales, configuración de los poros y punteaduras en la madera, además de la temperatura del aire del túnel debajo del punto de ebullición del agua, se puede suponer que el transporte de humedad se da principalmente en la dirección del espesor del material (Turner 1996). La geometría a modelar será el espesor de la madera, una línea recta (figura 1).

Los balances de materia y calor son incorporados en COMSOL Multiphysics 3.4, en el navegador de modelos, en la forma EDP general (ecuación diferencial parcial) para los balances de humedad y aire seco, y en la forma de EDP de coeficientes para el balance de calor, donde se declaran las variables primarias a resolver: contenido de humedad (W); densidad intrínseca del aire (ρ_a); y temperatura (T). Como se muestran en la tabla 1.

Tabla 1.

Ecuaciones de conservación

Subdominio	Ecuación	Variable a resolver	Núm. de ecuación
Conservación total de humedad	∂W∂t=−∇⋅1ρsρ¯lV¯ll+ρ¯υV¯υg+Jb	W	(1)
Conservación total de aire seco	∂∂tρ¯a+∇⋅ρ¯agv¯a=0	ρa	(2)
Ecuación de conservación de energía	ρCp∂T∂t+Δhυapm¯lυ+Δhsorpm¯bυ+CplρlVl+CpbρbVb+CpυρυVυ+CpaρaVa⋅∇T=∇⋅λ⋅∇T	T	(3)

La ecuación de conservación del aire seco (2) permite una correcta descripción de los gradientes de presión, los cuales se hacen presentes durante el secado. La ecuación de transferencia de humedad (1) es una versión más elaborada del modelo difusivo. Sin embargo, la principal diferencia entre las dos aproximaciones es la separación de fases, así como las relaciones constitutivas que comprenden la contribución de cada una de las fases (Krabbenhøft, 2003). La ecuación de conservación de energía (3) involucra la conducción de calor, y la transferencia de calor convectivo, además de los cambios de entalpia debidos a los cambios de fase (m_bvy m_lv).

Los flujos de humedad, calor y aire seco, son descritos en COMSOL en ajustes del subdominio; el flujo de agua libre se supone que sigue un comportamiento generalizado que se puede describir con la ley de Darcy, para la cual la velocidad promedio de masa está dada por la ecuación 4. Además se ha demostrado que las fuerzas que ejerce el cuerpo debido a la gravedad son muy pequeñas y por lo tanto despreciables (Plumb y Prat, 1992; Turner et al.,2010).

La transferencia de vapor de agua y aire seco puede ser descrita por la combinación de la ley de Fick y la ley de Darcy. A través de esto podemos representar el transporte de vapor de agua con la siguiente formulación matemática de la ecuación 6. El flujo de aire seco (ecuación 7) tiene un comportamiento parecido al del vapor, pero en sentido opuesto (tabla 2).

Tabla 2.

Ecuaciones de subdomi

	Ecuación y número	Ecuación
Flujo de agua	ρlvl=ρlKkrlμl∇⋅Pc−ρlKkrlμl∇⋅Pgg	4
Flujo de agua ligada	Jb=−ρsDb⋅∇Wb−ρsD∇Tbt	5
Flujo de vapor	ρ¯υgv¯υ=−ρ¯υgKkrgμg⋅∇P¯gg−ρ¯ggDeff∇ρ¯υgρ¯gg	6
Flujo de aire seco	ρ¯gv¯a−ρ¯υgKkrgμg⋅∇ρ¯gg−ρ¯ggDeff∇ρ¯υgρ¯gg	7

Por último, el mecanismo de transporte de agua ligada en el dominio higroscópico se describe en la ecuación 5, donde el flujo de difusión-desorción del agua ligada toma en cuenta dos mecanismos, el primero es difusión debido a los gradientes de contenido de humedad, y la segunda parte a los gradientes de temperatura (efecto Soret).

En la figura 1 se puede observar al lado derecho la geometría a modelar. Existen dos condiciones de frontera CF1 y CF2, las cuales están a la misma temperatura y por las que pasa el mismo flujo de masa (mezcla airevapor), a la misma velocidad de flujo de aire. Por lo tanto, los ajustes de contorno de la geometría propuesta para las superficies expuestas al secado son las mostradas en la tabla 3.

Tabla 3.

Ecuaciones de contorno

Condición de frontera	CF1 y CF2	Ecuación	Condiciones iniciales
Conservación total de humedad	Jw⋅nˆ=kmcMυIn1−xυ∞1−xυ	8	Winicial
Conservación total de aire seco	Pgg=Patm   c=PatmRT∞	9	ρa inicial
Ecuación de conservación de calor	Je⋅nˆ=h(T−T∞)+ΔhυkmcMυIn1−xυ∞1−xυ	10	Tinicial = 25° C

La ecuación 8 representa el flujo de agua que se está perdiendo en la superficie de la madera por evaporación; debido a las presiones atmosféricas la cantidad de aire en los alrededores no cambiará, por lo tanto, la condición de frontera para la ecuación de conservación total de aire seco (9) se mantendrá constante en todo el proceso de secado (condición de contorno tipo Dirichíet). El calor en la superficie se remueve por convección forzada que se representa con la ley del enfriamiento de Newton en la ecuación 10. Asimismo, es necesario considerar el calor que se pierde en la superficie, debido a la cantidad de agua que se está evaporando. h y k_m son los coeficientes de transferencia de calor y masa, respectivamente, cuyos valores son determinados experimentalmente a las condiciones de secado.

Para la simulación de las cinéticas de secado es necesario contar con las propiedades termo-físicas de la madera de la especie Pinus pseudostrobus, la cual ha sido poco estudiada. Por lo tanto, existen parámetros que aún se desconocen, sin embargo, se han utilizado propiedades de maderas similares en densidad. Algunas de las propiedades utilizadas se muestran en la tabla 4.

Tabla 4.

Propiedades de transporte

	Valor	Fuente
Porosidad	ε = 0.66	Hernández y Puiggali (1994)
Punto de saturación de la fibra	Wpsf = 0.30	Fuentes (2000)
Permeabilidad absoluta	K = 1 x 10^−17	Raji et al. (2009)
Calor especifico del sólido	Cps = 1400	Hernández y Puiggali (1994)
Permeabilidad relativa del gas	Krg = 1 + (2S - 3) S^2	Perré y Turner (2006)
Permeabilidad relativa del líquido	Krl = S^3	Perrí y Turner (2006)
Presión capilar	Pc = 1.4 x 106 S^−0.63	Kang y Chung (2009)
Coeficiente de Difusión del agua ligada	Db = 2 x 10^−13exp [5.46W + 2.54 x 10^−2T]	Colakoglium (2009)
Coeficiente de Difusión del aire-vapor	Dav=2.2×10−5101325pggT273.151.81	Baronasa et al. (2001)
Coeficiente de Difusión efectiva	Deff = k rgDav (1 x 10^−3)	Wook et al. (2008)
	Weq(T,Hr)=Xm⋅C⋅K⋅Hr(1−K⋅Hr)(1+C⋅K⋅Hr−K⋅Hr)
Isotermas de desorción	C = 0.0064 T^2 − 0.5807 T + 21.962 Xm = − 0.0006 T + 0.0883 K = 0.0022 T + 0.695	Sandoval et al. (2001)
Conductividad tírmica de la madera	λ = 0.137 + 0.386 W	Hernández y Puiggali (1994)

El sistema de ecuaciones fue resuelto utilizando una computadora con procesador AMD Athlon(tm)X2 DualCore, 2100 Mhz, con un tiempo de cómputo de 20 s.

Discusión y análisis de resultados

A continuación se presentan los resultados de la simulación, en la que se considera una temperatura del aire en el túnel de 60° C, con temperatura inicial de 25° C y contenido de humedad inicial de la madera de 96%.

Las cinéticas de contenido de humedad promedio son simuladas con el modelo fenomenológico y comparadas con datos experimentales, así como con el modelo de la curva característica de secado previamente publicados en Hernández et al. (2010). La figura 2 muestra los ajustes de los modelos comparados con datos experimentales, además se incluye un eje del lado derecho para mostrar los perfiles de temperatura y su evolución durante el proceso de secado simulados y experimentales en el centro de la madera y en la superficie.

Figura 2.

Cinéticas de contenido de humedad promedio y perfiles de temperatura, simulados y experimentales a temperatura de 60° C

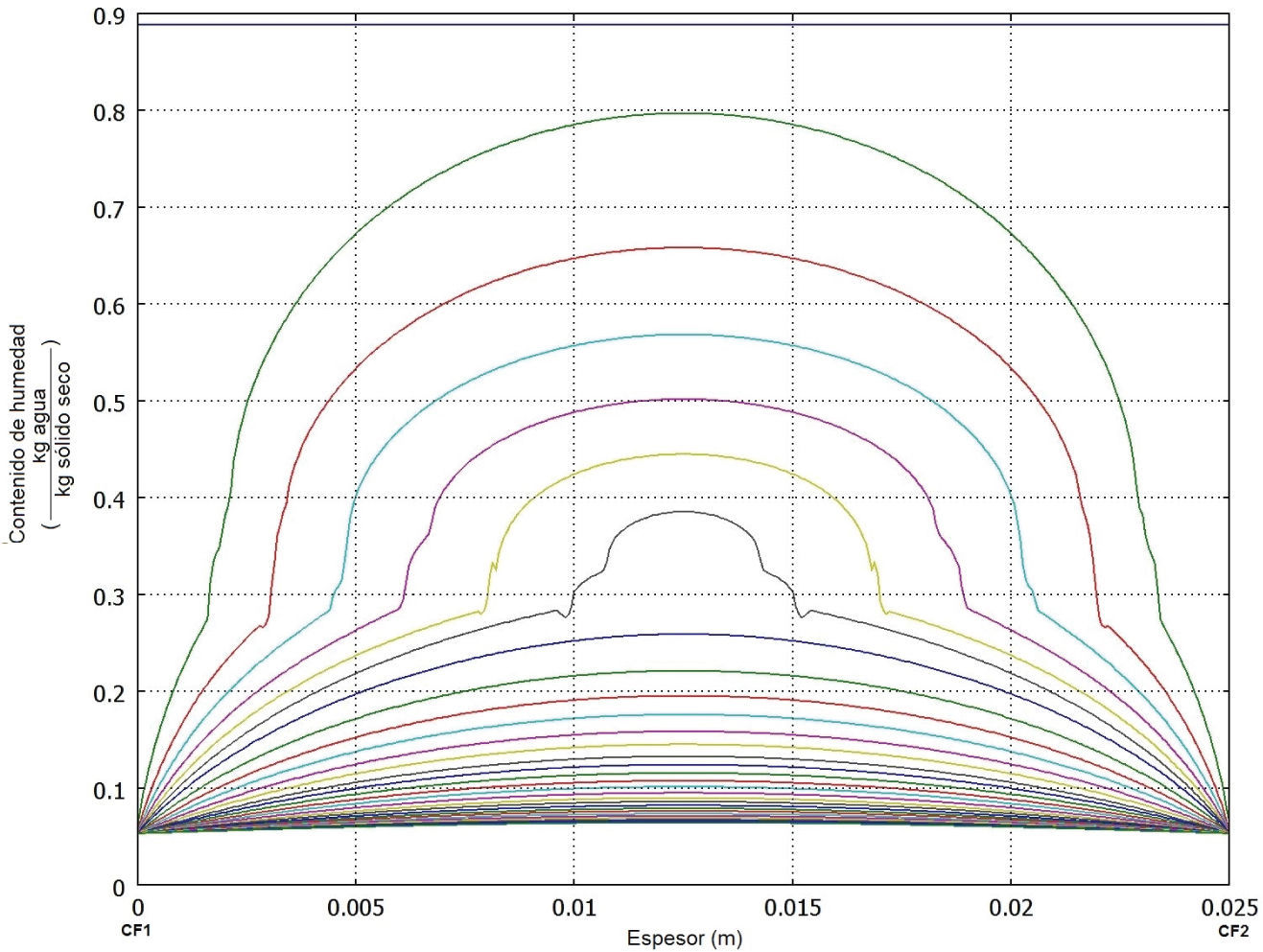
La figura 3 muestra el contenido de humedad en el espesor de la madera y su evolución durante el tiempo en intervalos de dos horas. Durante el secado, a medida que se elimina el agua, es reemplazada con aire. En las superficies la densidad del aire se incrementará primero (figura 4). Estos perfiles tienen un comportamiento contrario a la densidad del vapor, ya que el desplazamiento de vapor de agua es reemplazado por aire seco. Recordemos que la mezcla gaseosa es una combinación de vapor de agua y aire seco, la cual es descrita por la ley de Dalton, que dice que la presión de una mezcla de gases, que no reaccionan químicamente, es igual a la suma de las presiones parciales de cada una de ellas.

Figura 3.

Perfiles de contenido de humedad en el espesor de la madera, simulados cada dos horas

Figura 4.

Perfiles de densidad de aire seco en el espesor de la madera, simulados cada dos horas

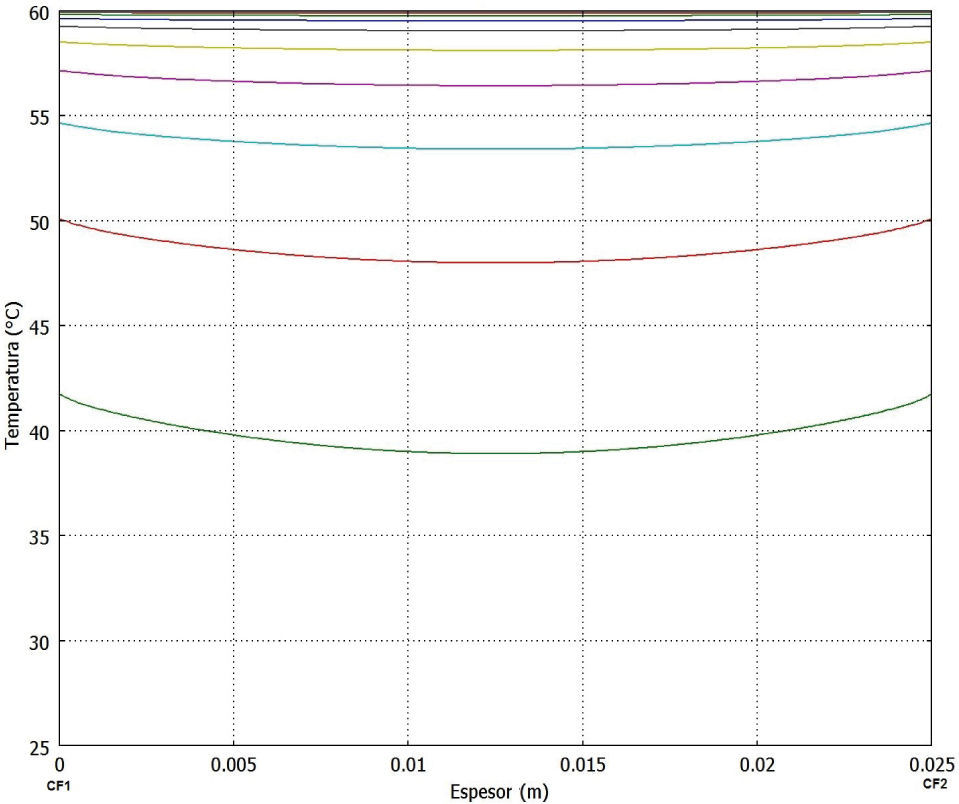
La temperatura del material es la tercera variable que fue resuelta con el modelo. La figura 5 muestra los perfiles de temperatura en el espesor de una tabla de madera cada media hora durante el proceso.

Figura 5.

Perfiles de temperatura en el espesor de la madera, simulados cada treinta minutos

Discusiones

El modelo matemático del tipo fenomenológico implementado muestra una asertiva simulación de las curvas de secado, lo cual es expuesto en la figura 2. Se puede observar un mejor ajuste utilizando el modelo de la curva característica (CCS); esto es de esperarse debido a que el modelo fenomenológico no parte de datos experimentales, ni es un ajuste de datos. Muchas de las propiedades de transporte requeridas por el modelo corresponden a especies de pino similares en densidad, por lo cual las variaciones en las cinéticas simuladas pueden disminuir si se tiene acceso a esta información (Perré y Turner, 2001).

En la figura 2, se muestra una parte del calentamiento al principio de la cinética de secado, que es mucho más notable a altas temperaturas debido a la solución numérica, incluso mostrada en otros modelos, por ejemplo en Perré (1999). Al principio se muestra siempre el fenómeno de incremento en el contenido de humedad en los primeros segundos. Por otra parte, el contenido de humedad de equilibrio se simula adecuadamente en la mayoría de las cinéticas, dado que los datos utilizados sobre las isotermas de desorción son específicos para esta especie de madera (Pinus pseudostrobus). Por lo tanto, para contenidos de humedad debajo del PSF se simula adecuadamente en comparación con la fase capilar.

En cuanto a los perfiles de temperatura que se muestran en la figura 2, éstos exponen una diferencia notable entre la temperatura superficial del material, la temperatura del centro y las simuladas por el modelo. Estas discrepancias pueden ser atribuidas al desconocimiento de las funciones exactas de la conductividad térmica del material, de la permeabilidad y de la presión capilar, entre otras propiedades utilizadas en el modelo; en este trabajo se tomaron las funciones de otros estudios de pino previamente realizados en Hernández y Puiggali (1994).

La cantidad de calor que se suministra a la madera también depende de la velocidad y de la humedad relativa del aire; estos parámetros son considerados en el coeficiente de transferencia de calor y de masa, pues entre más grande sea este coeficiente mayor será la cantidad de calor transferida en la interfase. Si el coeficiente es muy grande, la temperatura superficial aumenta rápidamente.

En la figura 3 se muestra la variación espacial del contenido de humedad en el espesor de una muestra de madera y su evolución durante el tiempo en intervalos de dos horas. A tiempo cero se tiene un contenido de humedad homogéneo (0.9 kg de agua/kg de sólido seco) en todo el espesor, el cual comienza a decrecer rápidamente en las orillas, producto del transporte de masa en la interfase. En dos horas de secado los extremos casi llegan al contenido de humedad de equilibrio. Por otra parte, se observa que al contenido de humedad cercano al PSF, existe una fluctuación en la parábola que forma el perfil de contenido de humedad en cada determinado tiempo. Esto se debe a la transición de la fase capilar a la fase higroscópica. Esta fluctuación depende principalmente de la permeabilidad relativa del líquido que decrece durante el secado. Krabbenhøft (2003) describe la influencia de la permeabilidad relativa en la simulación del secado y explica cómo la ecuación en función de la saturación suaviza las parábolas con funciones de saturación al cuadrado. Los perfiles presentados en este trabajo son similares a los presentados por Krabbenhøft (2003).

Al incrementar la densidad del aire en el interior de la madera también incrementa la presión en el gas. En el secado por convección de aire caliente a bajas temperaturas, la ecuación del aire seco describe con precisión el desarrollo de los gradientes de presión de gas en el material. El lugar en donde primero se elimina el agua libre es en la superficie (figura 3). Es ahí donde la densidad del aire incrementa primero, al tener también un perfil de densidad del aire dentro del material, que varia con el tiempo de secado (figura 4). Nótese cómo la masa de aire en el medio poroso es también alterada por la transición de la zona capilar a la zona higroscópica, producto de una fuerte interacción entre las fases.

La figura 5 muestra los perfiles de temperatura en el espesor de una tabla de madera cada media hora, es importante ver cómo la temperatura del material aumenta rápidamente. Aproximadamente en 4 horas se alcanza una temperatura homogénea de 60° C en el material, desde el centro hasta la superficie, contrariamente a lo que pasa en la realidad. La estabilización de temperaturas ocurre en 10 horas y el gradiente de temperatura entre la superficie y el centro es aproximadamente de 5° C. La diferencia entre la temperatura del centro y la superficie disminuye con el tiempo de secado (figura 2). En la simulación la diferencia es aproximadamente de un grado centígrado o menor entre el centro y la superficie de la madera. Como se explicó anteriormente esto se debe al flujo de calor en la madera, expresado en la conductividad térmica. En este caso, dicha conductividad térmica varía con el contenido de humedad solamente (tabla 4), y ésta va disminuyendo a lo largo del secado linealmente, ya que el agua tiene un coeficiente de conductividad térmico más grande que el del aire o el vapor, por lo que la conductividad térmica de la madera es alterada por la presencia de las fases líquida y gaseosa. Al final del secado, sólo se tiene la matriz sólida y aire seco, los cuales son menos conductivos. Es necesario mencionar que en la realidad el coeficiente de conductividad térmica no sólo varía con respecto al contenido de humedad: también lo hace con la temperatura, pero dicho parámetro no siempre está disponible para todos los materiales.

Conclusiones

Se desarrolló un modelo matemático unidimensional que describe los mecanismos de transporte de calor y masa durante el secado convencional de madera de Pinus pseudostrobus. El modelo fue comparado con el modelo de la curva característica de secado y con datos experimentales, describiendo correctamente las cinéticas de secado.

En las simulaciones realizadas se encontraron fluctuaciones en los perfiles espaciales de masa, en la transición de la fase capilar a la higroscópica, y diferencias en los perfiles térmicos; por lo tanto, es necesario un análisis más detallado de esta transición, y el cálculo de las propiedades termofísicas de esta madera.

Sin embargo el modelo fenomenológico desarrollado toma en cuenta automáticamente las modificaciones en las condiciones del proceso y los fenómenos de transporte de calor y masa que existen dentro del espesor de la madera, describiendo con mayor detalle el transporte de humedad y de energía al interior del material.

Se espera que la información generada por las simulaciones pueda ofrecer un preámbulo para propósitos de análisis de procesos de secado o diseño de nuevos modelos que se aproximen mejor a la realidad. Estos resultados pueden ser utilizados para la optimización y diseño de procesos de secado.

Nomenclatura

C

Constante de la ecuación de Gab

c

Concentración (mol/m³)

C_p

Calor específico (J/ (kg K))

C_pa

Calor específico del aire (J/ (kg K))

C_pb

Calor específico del agua ligada (J/ (kg K))

C_pl

Calor específico del agua líquida (J/ (kg K))

C_pv

Calor específico del vapor (J/ (kg K))

D_av

Coeficiente de difusión del aire en vapor (m²/s)

D_b

Coeficiente de difusión del agua ligada (m²/s)

D_bt

Coeficiente de termo-difusión (m²/s)

D_eff

Coeficiente de difusión efectivo (m²/s)

H_r

Humedad relativa

h

Coeficiente de transferencia de calor (W/(m² K))

J_b

Flujo de agua ligada (kg/(m² s))

J_w

Flujo de agua (kg/(m² s))

J_e

Flujo de energía (J/(m² s))

K

Permeabilidad absoluta de la madera (m²)

K_m

Coeficiente de transferencia de masa (m/s)

k_rg

Permeabilidad relativa del gas

k_rl

Permeabilidad relativa del líquido

Mv

Peso molecular del vapor (mol/kg mol)

n

Vector normal unitario (m)

m_bv

Tasa de transferencia masa del agua líquida-agua ligada (kg/ m³s)

m_lv

Tasa de transferencia masa del agua líquida-agua vapor (kg/ m³s)

P_atm

Presión atmosférica (Pa)

P_c

Presión capilar (Pa)

P_g^g

Presión del gas (Pa)

R

Constante universal de los gases (J/(mol K))

t

Tiempo (s)

T

Temperatura (K)

T_∞

Temperatura ambiente (K)

v_a

Velocidad promedio del aire (m/s)

v_l

Velocidad promedio del líquido (m/s)

v_v

Velocidad promedio del vapor (m/s)

W Contenido de humedad (kg agua/kg madera seca) W_b

Contenido de humedad del agua ligada (kg agua/ kg madera seca)

W_eq

Contenido de humedad de equilibrio (kg agua/kg madera seca)

W_inicial

Contenido de humedad inicial (kg agua/kg madera seca)

W_psf

Contenido de humedad en el punto de saturación de la fibra (kg agua/kg madera seca)

X_m

Constante de la ecuación de Gab

x_v

Fracción molar del vapor en la superficie (mol/mol)

x_v∞

Fracción molar de vapor en el túnel de secado (mol/mol)

Δh_sorp

Calor de desorción (J/kg)

Δh_vap

Calor de vaporización (J/kg)

ε

Porosidad del material (m³/m³)

λ

Coeficiente de conductividad térmica de la madera (W/(m K))

μ_g

Viscosidad del vapor (Pa s)

μ_l

Viscosidad del agua líquida (Pa s)

ρ_a

Densidad del aire (kg/m³)

ρ_b

Densidad del agua ligada (kg/m³)

ρ_l

Densidad del líquido (kg/m³)

ρ_s

Densidad del sólido (kg/m³)

ρ_v

Densidad del vapor (kg/m³)

Agradecimientos

Al Instituto Politécnico Nacional.