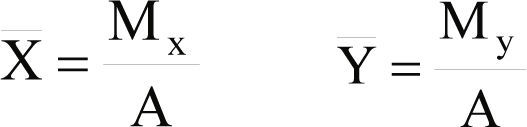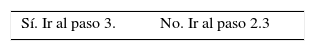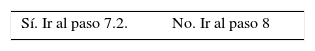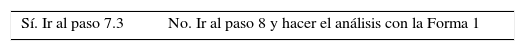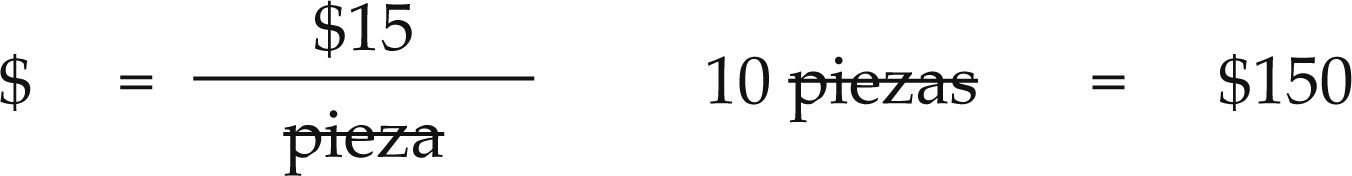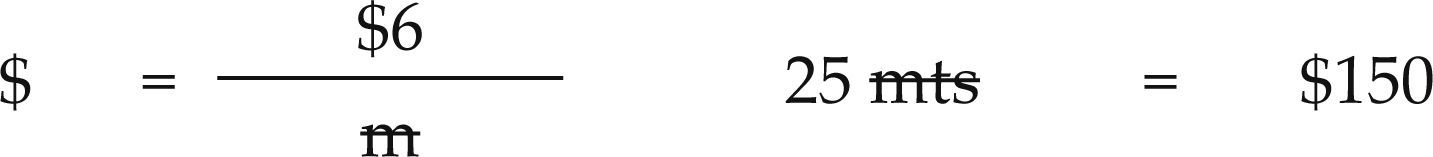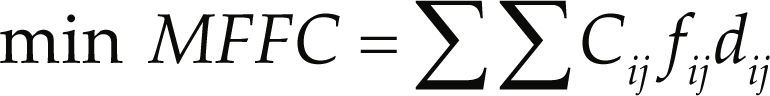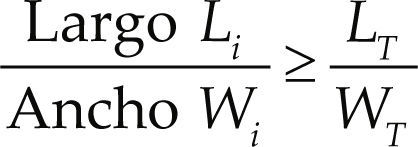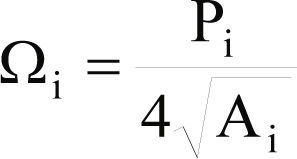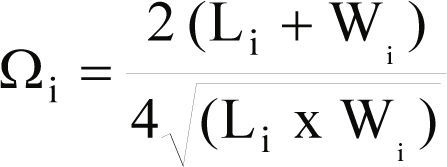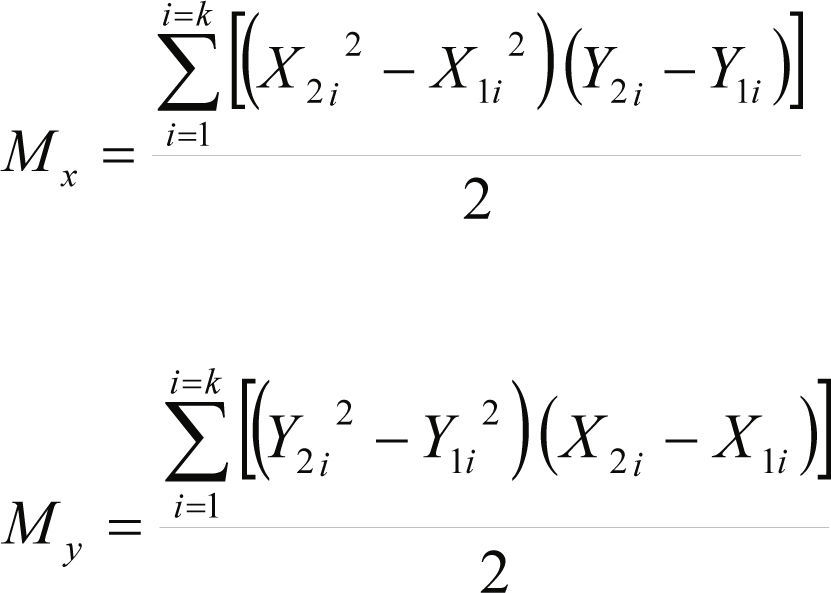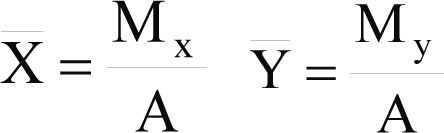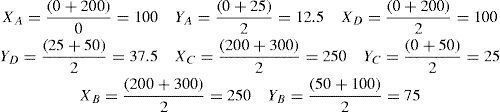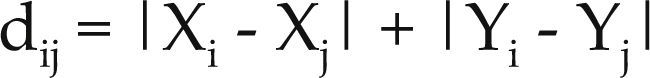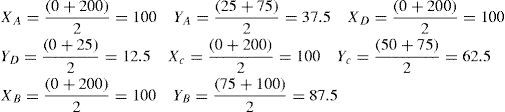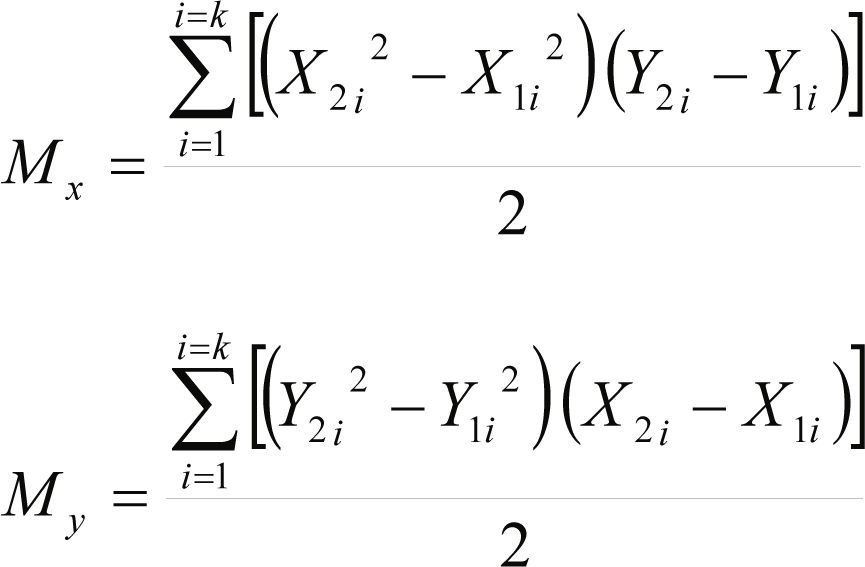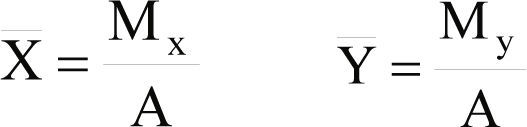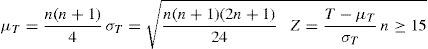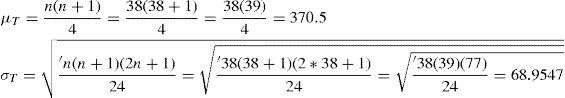En este trabajo se presenta una heurística eficiente e innovadora para determinar el diseño óptimo de la distribución de planta (layout) que minimiza el costo total de flujo de materiales dentro de una empresa, incluyendo reglas para realizar la distribución inicial y el proceso lógico para reducir el trabajo de detectar el arreglo que ofrece las mejores oportunidades para reducir el costo total de la distribución. Esta nueva heurística se basa en el uso modificado del problema de transporte clásico (PTC), que es una herramienta propia de la programación lineal y que forma parte de la investigación de operaciones. La heurística LDMTP de creación propia ha demostrado que es eficiente para resolver el diseño óptimo de la distribución de planta, debido a que este es un método selectivo capaz de distinguir el mejor orden de asignación de todos los departamentos que conforman el layout, incluyendo criterios de forma (largo y ancho) para cada departamento asignado. El proceso de establecer la asignación inicial de la heurística LDMTP no es un asunto subjetivo, debido a que la elección del mejor orden de asignación de los departamentos que conforman la distribución inicial sigue una serie de pasos y tiene hasta 4 diferentes criterios de desempate, lo cual favorece que se elija el arreglo de departamentos que puede aportar la mayor contribución a la reducción del costo total de la distribución.
This paper presents an efficient heuristics to determine the optimal design of plant layout, that minimizes the total cost of material flow within a company, including rules for the initial distribution and logical process to reduce the work to detect the arrangement that offers the best opportunities to reduce total cost process distribution. This new heuristic apply the modified use of Classic Transportation Problem (CTP), which is a proprietary tool of Linear Programming and part of the Operations Research. The LDMTP heuristic of own creation has proven to be efficient for solving the optimal design of plant layout due to is a selective method that is capable of distinguishing the best assignment order of all departments that make up the layout including criteria form (long and width) for each assigned department. Establishing the initial allocation of LDMTP heuristics is not a subjective matter because choosing the best assignment order of departments that make up the initial distribution follows a series of steps and has up to 4 different tiebreakers, so which favors the settlement of departments can make the greatest contribution is chosen to reducing the total cost of distribution.
El diseño óptimo de la distribución de planta Optimal Design of Plant Layout (ODPL) es un problema ampliamente estudiado que repercute en el incremento de la productividad y disminución de los costos de fabricación de una empresa. En este artículo se muestra una heurística de creación propia, que es eficiente e innovadora, ya que está basada en el uso del problema de transporte modificado (PTM) de la programación lineal, la cual se denomina: Diseño de la distribución de planta basada en el problema de transporte modificado, Layout Design based on the Modified Transportation Problem (LDMTP).
Las aplicaciones usuales de la programación lineal (PL) son el método simplex (MS), el problema de transporte (PT) y el método de asignación (MA). Mejía (2012) sugiere el uso de algoritmos genéticos para el problema de OPDL, lo cual involucra el uso de lenguajes de programación. No existe ninguna aplicación encontrada hasta ahora del diseño óptimo de la distribución de planta (ODPL) basada en el problema de transporte que se encuentre referenciada en la literatura. Esta es la razón de la innovación que aporta esta heurística.
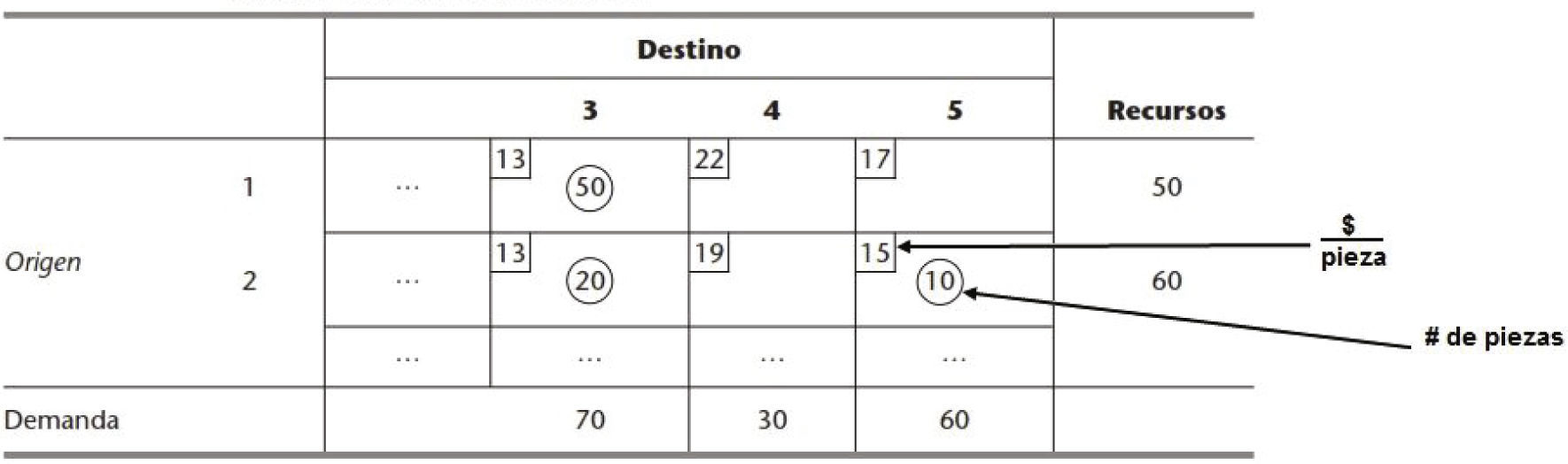
Para entender cómo se construye una tabla del problema de transporte se anexa como ejemplo un extracto de la tabla 8 .22 de Hillier & Lieberman en la figura 1.
Extracto de tabla 8 .22 H&L del problema de transporte
Fuente: Hillier & Lieberman (2001)
La formulación de LDMTP como un problema de transporte se muestra en la figura 2, que guarda una analogía con la figura 1.
La heurística LDMTP se usa para el diseño de layout, emplea criterios de asignación como las rutinas de construcción (CORELAP, ALDEP). La optimización de la heurís- tica se basa en minimizar el costo de manejo de materiales como las rutinas de mejoramiento (CRAFT, COFAD, PLANET, MCRAFT, etcétera). Como combina las características de los dos tipos de rutinas: de construcción y de mejoramiento, esta heurística se puede considerar híbrida, la cual no se ha detectado en la literatura.
DesarrolloLa formulación matemática del diseño óptimo de la distribución de planta que es el objetivo de esta heurística, se describe por Wang et al. (2005) y John et al. (2013) como:
donde
MFFC = Costo del factor de flujo de material
Cij = Costo de transporte de material unitario entre los departamentos i y j
fij = Flujo de material entre los departamentos i y j
dij = Distancia rectilínea entre los departamentos i y j
Fij =Cijfij = Producto costo-flujo de transporte de mate- rial unitario entre los departamentos i y j
La aplicación de la ecuación 1 a condiciones especiales se muestra en las ecuaciones 2, 3 y 4.
Si i = j, entonces Cij = 0, fij = 0, dij = 0, y min MFFC = 0 (2)
Si i ≠ j y fij = 0, entonces min MFFC = 0 (3)
Si i ≠ j y fij > 0, entonces Cij > 0, dij > 0, y min MFFC > 0 (4)
Criterio de forma de departamento (ancho y largo)En este método la relación de forma (Largo Li /Ancho Wi) usualmente se ajusta para cumplir con la condición siguiente
donde
Li = Largo del departamento i y Wi = Ancho del departamento i
LT = Largo total del layout y WT = Ancho total del layout
Se usan los valores de Li y Wi obtenidos para calcular un factor de forma sugerido por Bozer et al. (2005) con la fórmula siguiente
donde se sugiere Ωi ≤ 1.5
Pi = perímetro del departamento i
Ai = Área del departamento i
Para una figura rectangular o cuadrada, la ecuación 6 se puede expresar de la siguiente forma
En caso de que exista un conflicto con la condición de forma y se cumpla la condición de la ecuación 5, pero se rebase el valor de Ωi de la ecuación 6, predomina la condición de la ecuación 5.
Pasos de la aplicación de la heurísticaLos pasos y criterios de asignación y ubicación para los departamentos que integran el layout son los siguientes:
Paso 1. Determinar Fij+
Paso 2. Determinar D1 = Departamento con mayor área de Fij+. ¿Se puede definir D1?
Paso 2.1. En caso de no poder determinar claramente D1 debido a que los dos departamentos que integran Fij+ tengan la misma área, usar los criterios siguientes para tratar de desempatar.
ΣFD1+ = Max (ΣFD1,i, ΣFD1,j) ΣFD2+ = Max (ΣFD2,i, ΣFD2,j) F+ = Max (ΣFD1+, ΣFD2+). ¿Se puede definir D1?
Paso 2.2. En caso de no poder determinar claramente D1 debido a que los dos departamentos que integran Fij+ tengan la misma área, usar los criterios siguientes para tratar de desempatar.
ΣFD1− = Min (ΣFD1,i, ΣFD1,j) FD2− = Min (ΣFD2,i, ΣFD2,j) F− = Max (ΣFD1-, ΣFD2−). ¿Se puede definir D1?
Paso 2.3. Asignación: Libre elección (romper empates arbitariamente). Ubicación: dij− (distancia mínima entre departamentos).
Paso 3. El departamento D1 asignado debe cumplir con los lineamientos de forma sugeridos por las ecuaciones 5, 6 y 7. La longitud del departamento D1 debe estar alineada a la longitud del área disponible, ya que esta alineación asegura que la distancia entre departamentos dij sea mínima.
Paso 4. Ya asignado D1, se asigna D2 (Departamento no asignado en primer lugar de Fij+) usando los mismos lineamientos de forma para alinear D1.
Paso 5. Los criterios para asignación a partir del tercer departamento son: (k ≥ 3)
Fk+ = Max (Fik, Fjk) Dk debe estar relacionado con D1 o D2 o hasta Dk-1.
Paso 6. Repetir el procedimiento a partir del paso 5 hasta realizar todas las asignaciones de departamentos tomando en cuenta los lineamientos de forma sugeridos por Bozer et al. (2005).
Paso 7. Realizar la distribución inicial de la Forma 1 (D1, D2, D3). Determinar el costo total de la primera distribución de planta.
Paso 7.1. Si para el tercer departamento a asignar, se cumple que: D3 debe estar junto a D1 y AD3 = AD2 = AD1, se debe verificar la posibilidad de usar criterios alternativos para asignar el tercer departamento.
Paso 7.2. Reorganizar el layout de la forma siguiente:
D1modificado = D2original D2modificado = D1original D3modificado = D3original
Realizar la distribución inicial de la Forma 2 (D2, D1, D3). Determinar el costo de la distribución inicial de la Forma 2 y comparar con la Forma 1. ¿$Forma2 < $Forma1?
Paso 7.3. Hacer todo el análisis posterior con la Forma 2.
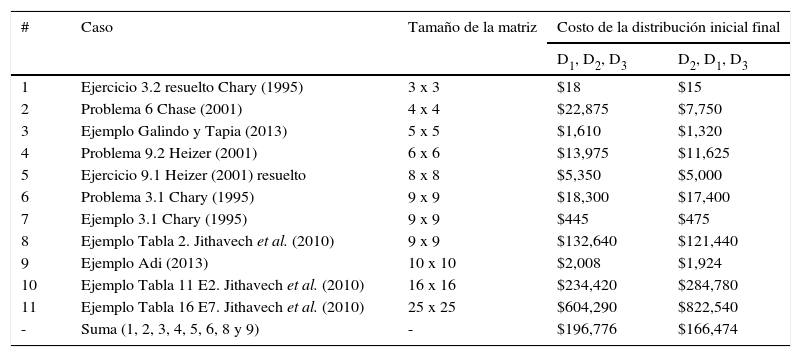
Se presenta un compendio de los casos que cumplen con la condición del paso 7.1. (Tabla 1).
Casos con reorganización del orden de asignación de los tres primeros departamentos. Fuente: elaboración propia (2016)
| # | Caso | Tamaño de la matriz | Costo de la distribución inicial final | |
|---|---|---|---|---|
| D1, D2, D3 | D2, D1, D3 | |||
| 1 | Ejercicio 3.2 resuelto Chary (1995) | 3 x 3 | $18 | $15 |
| 2 | Problema 6 Chase (2001) | 4 x 4 | $22,875 | $7,750 |
| 3 | Ejemplo Galindo y Tapia (2013) | 5 x 5 | $1,610 | $1,320 |
| 4 | Problema 9.2 Heizer (2001) | 6 x 6 | $13,975 | $11,625 |
| 5 | Ejercicio 9.1 Heizer (2001) resuelto | 8 x 8 | $5,350 | $5,000 |
| 6 | Problema 3.1 Chary (1995) | 9 x 9 | $18,300 | $17,400 |
| 7 | Ejemplo 3.1 Chary (1995) | 9 x 9 | $445 | $475 |
| 8 | Ejemplo Tabla 2. Jithavech et al. (2010) | 9 x 9 | $132,640 | $121,440 |
| 9 | Ejemplo Adi (2013) | 10 x 10 | $2,008 | $1,924 |
| 10 | Ejemplo Tabla 11 E2. Jithavech et al. (2010) | 16 x 16 | $234,420 | $284,780 |
| 11 | Ejemplo Tabla 16 E7. Jithavech et al. (2010) | 25 x 25 | $604,290 | $822,540 |
| - | Suma (1, 2, 3, 4, 5, 6, 8 y 9) | - | $196,776 | $166,474 |
73% de los casos (8 de 11) ofreció mejores resultados intercambiando los departamentos, usando D2, D1, D3 en vez de D1, D2, D3 lo cual generó una reducción de 15% ($166,474 – $196,776 / $196,776 × 100) del valor inicial de la primera distribución.
Paso 8. Establecer todos los intercambios válidos entre dos departamentos (Nahmias, 1999) que pueden ser:
- a)
Que los dos departamentos a intercambiar tengan una frontera en común.
- b)
Que los dos departamentos a intercambiar tengan la misma área, aunque no sean contiguos.
Nota: El intercambio que se realizó para generar un nuevo layout, no es un intercambio válido para esa nueva distribución, pero sí para distribuciones siguientes. Por ejemplo, si el intercambio A-B es el origen del 2° layout (no es un intercambio válido para este layout), pero sí puede considerarse un intercambio válido a partir del 3er layout (siempre y cuando se cumpla alguna de las condiciones mencionadas en el paso 8).
Paso 9. Realizar todos los intercambios válidos entre dos departamentos (intercambio de coordenadas: criterio sugerido por CRAFT). Determinar si existe un intercambio que pudiera reducir el costo total de la distribución de planta. ¿Existe un intercambio para el cual el costo del intercambio < costo del origen?
Paso 10. Modificar el layout, recalcular los centroides y determinar el costo del origen del nuevo layout.
Nota: Si un departamento no tiene una forma rectangular o cuadrada, es necesario aplicar las fórmulas para el cálculo de centroides (Nahmias, 1999) mostradas en las ecuaciones 8 y 9.
Mx = Momento en “X” My = Momento en “Y”
X¯= Centroide en “X” Y¯= Centroide en “Y”
Paso 11. Repetir los pasos 8 al 10 (de ser necesario).
Ejemplo de aplicación de la HeurísticaP1. Conflicto de criterios e intercambio de orden D2, D1, D3 (Problema 6-Chase et al., 2001)
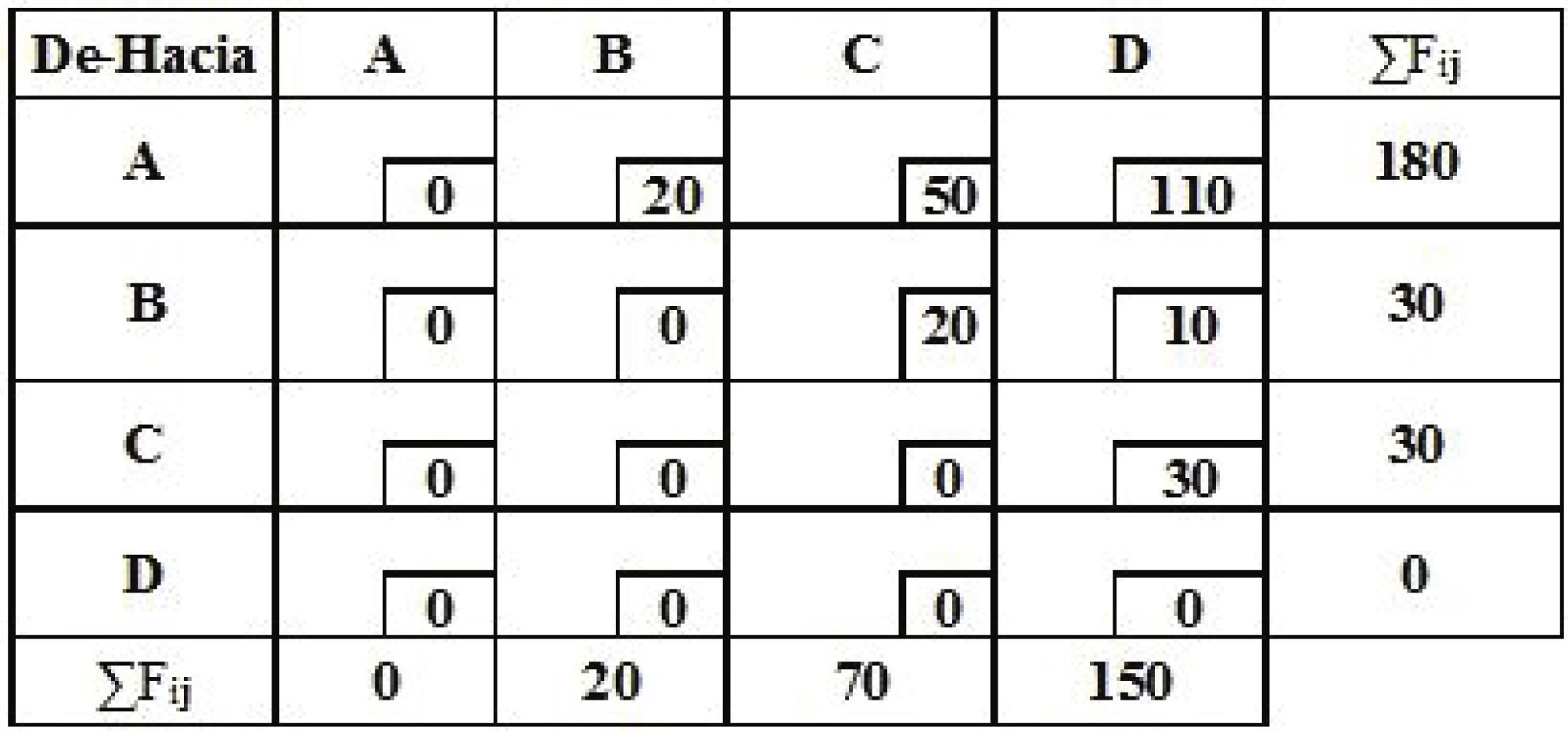
Los datos de P1Forma 1 de la distribución inicial del método LDMTP se muestran en la tabla 2.
Datos de la distribución inicial del método LDMTP Forma 1 (Problema 6-Chase et al., 2001). Fuente: elaboración propia (2016)
Fij = Producto costo-flujo de transporte de material unitario entre los departamentos i y j (valores en cuadro)
ΣFij = Sumatoria de Fij por fila o columna
Pasos de la aplicación de la heurísticaLos pasos y criterios de asignación y ubicación para los departamentos que integran el layout son los siguientes:
Paso 1. Determinar Fij+
En nuestro caso, P1 Forma 1, Fij+ = 110 (intercambio A-D).
Paso 2. Determinar D1 = Departamento con mayor área de Fij+. ¿Se puede definir D1?
En nuestro caso, P1 Forma 1, determinar D1 = Departamento con mayor área de Fij+ (A y D 5000). En nuestro caso no se puede definir D1.
Paso 2.1. En caso de no poder determinar claramente D1 debido a que los dos departamentos que integran Fij+ tengan la misma área, usar los criterios siguientes para tratar de desempatar.
ΣFD1+ = Max (ΣFD1,i, ΣFD1,j) ΣFD2+ = Max (ΣFD2,i, ΣFD2,j) F+ = Max (ΣFD1+, ΣFD2+). ¿Se puede definir D1?
ΣFD1,i= Suma de datos de Fij (Producto costo-flujo) del departamento D1 por fila
ΣFD1,j= Suma de datos de Fij (Producto costo flujo) del departamento D1 por columna
ΣFD2,i= Suma de datos de Fij (Producto costo-flujo) del departamento D2 por fila
ΣFD2,j= Suma de datos de Fij (Producto costo-flujo) del departamento D2 por columna
ΣFD1+ = Valor máximo de (ΣFD1,i, ΣFD1,j)
ΣFD2+ = Valor máximo de (ΣFD2,i, ΣFD2,j)
En nuestro caso P1 Forma 1, ΣFA+ = Max (ΣFA,i, ΣFA,j) = Max (180, 0), ΣFD+ = Max (ΣFD,i, ΣFD,j) = Max (150, 150), F+ = Max (180, 150) = 180. Se define D1 = departamento A.
Nota: ΣF (fila A) = 0 + 20 + 50 + 110 = 180 (suma de los valores dentro de los cuadros).
ΣF (columna A) = 0 + 0 + 0 + 0 = 0 Sí. Ir al paso 3.
Paso 2.2. En caso de no poder determinar claramente D1 debido a que los dos departamentos que integran Fij+ tengan la misma área, usar los criterios siguientes para tratar de desempatar.
ΣFD1− = Min (ΣFD1,i, ΣFD1,j) FD2− = Min (ΣFD2,i, ΣFD2,j) F− = Max (ΣFD1-, ΣFD2−). ¿Se puede definir D1?
En nuestro caso P1 Forma 1, no aplica.
Paso 2.3. Asignación: Libre elección (romper empates arbitariamente). Ubicación: dij− (distancia mínima entre departamentos). En nuestro caso P1 Forma 1, no aplica.
Paso 3. El departamento D1 asignado debe cumplir con los lineamientos de forma sugeridos por las ecuaciones 5, 6 y 7. La longitud del departamento D1 debe estar alineada a la longitud del área disponible, ya que esta alineación asegura que la distancia entre departamentos dij sea mínima.
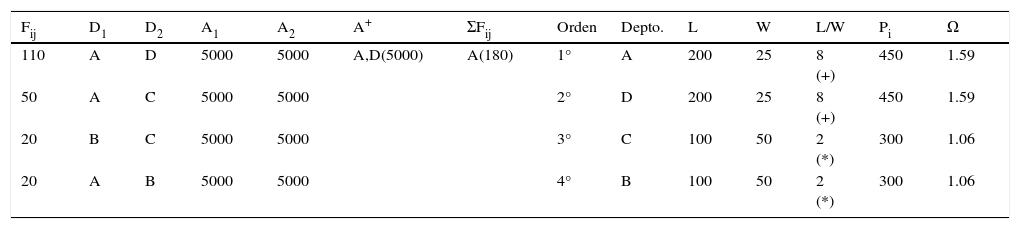
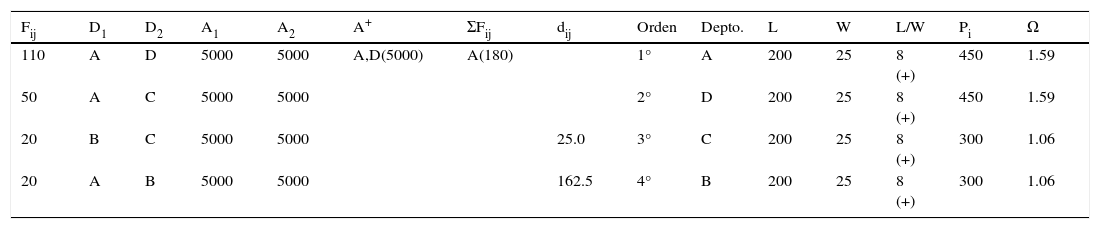
En nuestro caso P1 Forma 1, el departamento D1 asignado debe cumplir con los lineamientos de forma sugeridos por las ecuaciones 5,6 y 7 (tabla 3 y figura 3). La longitud del departamento D1 = A debe estar alineada con la longitud del área disponible, ya que esta alineación asegura que la distancia entre departamentos dij sea mínima.
Criterios de forma de asignación de departamentos de P1usando la metodología LDMTP. Fuente: elaboración propia (2016)
| Fij | D1 | D2 | A1 | A2 | A+ | ΣFij | Orden | Depto. | L | W | L/W | Pi | Ω |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 110 | A | D | 5000 | 5000 | A,D(5000) | A(180) | 1° | A | 200 | 25 | 8 (+) | 450 | 1.59 |
| 50 | A | C | 5000 | 5000 | 2° | D | 200 | 25 | 8 (+) | 450 | 1.59 | ||
| 20 | B | C | 5000 | 5000 | 3° | C | 100 | 50 | 2 (*) | 300 | 1.06 | ||
| 20 | A | B | 5000 | 5000 | 4° | B | 100 | 50 | 2 (*) | 300 | 1.06 |
Paso 4. Ya asignado D1, se asigna D2 (Departamento no asignado en primer lugar de Fij+) usando los mismos lineamientos de forma usados para alinear D1.
En nuestro caso P1 Forma 1, D1 = Departamento A, se asigna D2 = D usando los mismos lineamientos de forma usados para alinear D1.
Paso 5. Los criterios para asignación a partir del tercer departamento son: (k ≥ 3).
Fk+ = Max (Fik, Fjk) Dk debe estar relacionado con D1 o D2 o hasta Dk-1.
Fi,k= Producto costo-flujo del departamento Dk por fila
Fj,k= Producto costo-flujo del departamento Dk por columna
En nuestro caso P1 Forma 1, los criterios para asignación a partir del tercer departamento son que el producto costo-flujo FD3+ =Max (FAC, FCA, FDC, FCD, FAB, FBA, FDB, FBD) = Max (50, 0, 0, 30, 20, 0, 0, 10) = 50 que corresponde a FAC. D3 debe estar relacionado con D1(A) o D2(D). En este caso D3 = C se debe alinear con A.
Nota: Estos valores se toman de la tabla 2.
Paso 6. Repetir el procedimiento a partir del paso 5 hasta realizar todas las asignaciones de departamentos tomando en cuenta los lineamientos de forma sugeridos por Bozer et al. (2005).
En nuestro caso P1 Forma 1, FD4+ = Max (FDB, FBD, FCB, FBC) = Max (0, 10, 0, 20) = 20, que corresponde a FBC. D4 está relacionado con D3(C). En este caso, el cuarto departamento a asignar es D4 = B.
Nota: D4 no puede relacionarse con D1, ya que está bloqueado por D2.
Los datos del problema indican que se cuenta con un área de LT = 300ft x WT = 100ft =30,000ft2
Fij = Producto costo-flujo de transporte de material unitario entre los departamentos i y j
ΣFij = Sumatoria de Fij por fila o columna
A1 = Área del departamento 1, A2 = Área del departa mento 2, A+ = Amayor = 5000 y A− = Amenor = 5000, Amayor/Amenor = 1.00.
Se calcula la relación LT / WT y de acuerdo con la ecuación 5, Largo Li / Ancho Wi ≥ LT / WT se obtiene lo siguiente:
(+): Los departamentos A y D cumplen con la ecuación 5
(*): Los departamentos C y B se ajustan a la ecuación 6
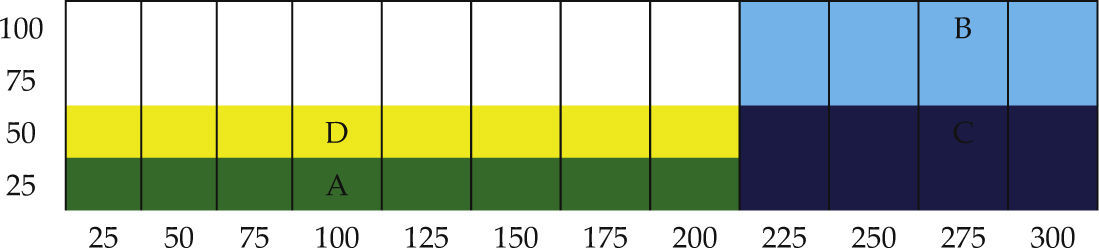
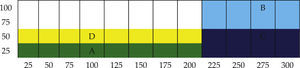
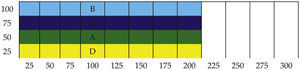
El layout inicial se muestra en la figura 3.
Los datos de los centroides (puntos medios) de los departamentos son: A (XA = 100 y YA = 12.5), B (XB =250, YB = 75), C (XC = 250, YC = 25) y D (XD = 100, YD = 37.5)
La construcción del layout inicial Forma 1 se crea de la siguiente manera:
- 1.
Se asigna el departamento A, ya que da el valor más alto de Fij (110) corresponde al intercambio A-D (tabla 4) y también se obtiene el valor más alto de ΣFij = 180 para el departamento A (tabla 4). El departamento A cumple el criterio de la ecuación 5, LA/WA = 8 > 3 (tabla 3).
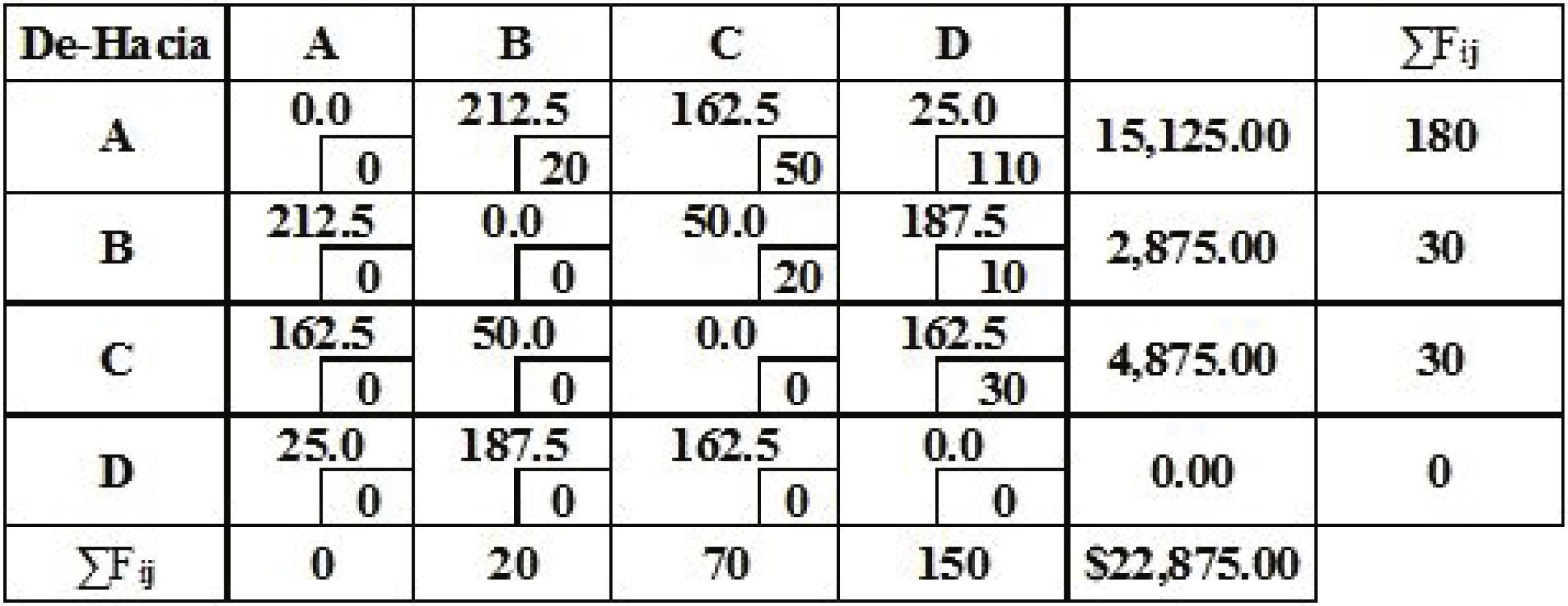
Tabla 4.Distribución inicial del método LDMTP Forma 1 (Problema 6-Chase et al., 2001). Fuente: elaboración propia (2016)
- 2.
Se asigna el departamento D, ya que es el segundo valor del intercambio A-D (tabla 4). El departamento D cumple el criterio de la ecuación 5, LD/WD = 8 > 3 (tabla 3).
- 3.
Se asigna el departamento C, ya que es el valor remanente más alto de Fij (50) y corresponde al intercambio A-C (tabla 4). C debe estar alineado con el departamento A. El departamento C cumple el criterio de la ecuación 6, (tabla 3).
- 4.
Se asigna el departamento B, ya que es el valor remanente más alto de Fij (20) y corresponde al intercambio B-C o A-B (tabla 4). B puede estar asignado junto al departamento A o departamento C, pero como ya no es posible asignar el departamento B junto al departamento A (porque el departamento A está encerrado, ver figura 3), el departamento B debe estar alineado con C. El departamento B departamento C cumple el criterio de la ecuación 6, (tabla 3).
Los centroides de los departamentos A (XA = 100 y YA = 12.5), B (XB =250, YB = 75), C (XC = 250, YC = 25) y D (XD = 100, YD = 37.5), se usan para calcular las distancias entre departamentos de la forma siguiente
La aplicación de la ecuación 10 a los departamentos A, B, C y D es la siguiente:
dA-B = |XA – XB| + |YA – YB| = |100 – 250| + |12.5 - 75| = |– 150| + |- 62.5| = 212.5, de forma semejante se aplica para conocer las distancias A-C (dA-C = |100 - 250| + |12.5 - 25| = 162.5)
A-D (dA-D = |100 – 100| + |12.5 – 37.5| = 25.0), B-C (dB-C = |250 – 250| + |75 – 25| = 50.0)
B-D (dB-D = |250 - 100| + |75 – 37.5| = 187.5) y C-D (dC-D = |250 - 100| + |25 – 37.5| = 162.5).
El costo de la distribución inicial Forma 1 se muestra en la tabla 4.
El costo de la distribución inicial se obtiene de la forma siguiente: 212.5 * $20 + 162.5 * $50 + 25.0 * $110 + 50 * $20 + 187.5 * $10 + 162.5 * $30 = $22,875.00.
Paso 7. Realizar la distribución inicial de la Forma 1 (D1, D2, D3). Determinar el costo total de la primera distribución de planta.
En nuestro caso P1 Forma 1, corresponde a la figura 3 y el costo total de la primera distribución de planta se muestra en la tabla 4 ($22,875).
Paso 7.1. Si para el tercer departamento a asignar, se cumple que: D3 debe estar junto a D1 y AD3 = AD2 = AD1, se verifica la posibilidad de usar criterios alternativos para asignar el tercer departamento.
En nuestro caso P1 Forma 1, el tercer departamento a asignar cumple que: D3(C) debe estar junto a D1(A) y AD3 = AD2 = AD1 = 5,000, y se debe verificar la posibilidad de usar criterios alternativos para asignar el tercer departamento. Como se cumple, se realiza el intercambio D2, D1, D3. Ir al paso 7.2
A partir de este momento, nuestro caso P1 Forma 1 se transforma en P1 Forma 2.
Paso 7.2. Reorganizar el layout de la forma siguiente:
D1modificado =D2original D2modificado = D1original D3modificado = D3original
Realizar la distribución inicial de la Forma 2 (D2, D1, D3).
Determinar el costo de la distribución inicial de la Forma 2 y comparar con la Forma 1. ¿$Forma2 < $Forma1?
En nuestro caso P1 Forma 2, D1modificado = D2original = D , D2modificado = D1original = A y D3modificado = D3original = C.
Realizar la distribución inicial de la Forma 2 (D2, D1, D3), ver tabla 5 y figura 4.
Criterios de forma de asignación de departamentos de P1Forma 2 usando la metodología LDMTP. Fuente: elaboración propia (2016)
| Fij | D1 | D2 | A1 | A2 | A+ | ΣFij | dij | Orden | Depto. | L | W | L/W | Pi | Ω |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 110 | A | D | 5000 | 5000 | A,D(5000) | A(180) | 1° | A | 200 | 25 | 8 (+) | 450 | 1.59 | |
| 50 | A | C | 5000 | 5000 | 2° | D | 200 | 25 | 8 (+) | 450 | 1.59 | |||
| 20 | B | C | 5000 | 5000 | 25.0 | 3° | C | 200 | 25 | 8 (+) | 300 | 1.06 | ||
| 20 | A | B | 5000 | 5000 | 162.5 | 4° | B | 200 | 25 | 8 (+) | 300 | 1.06 |
Fij = Producto costo-flujo de transporte de material unitario entre los departamentos i y j
ΣFij = Sumatoria de Fij por fila o columna
A1 = Área del departamento 1, A2 = Área del departa- mento 2, A+ = Amayor = 5000 y A− = Amenor = 5000, Amayor/Amenor = 1.00.
Se calcula la relación y de acuerdo con LTWT=300100=3 y de acuerdo con la ecuación 5, Largo LiAncho Wi≥LTWT se obtiene lo siguiente:
(+): Los departamentos A, B, C y D cumplen con la ecuación 5.
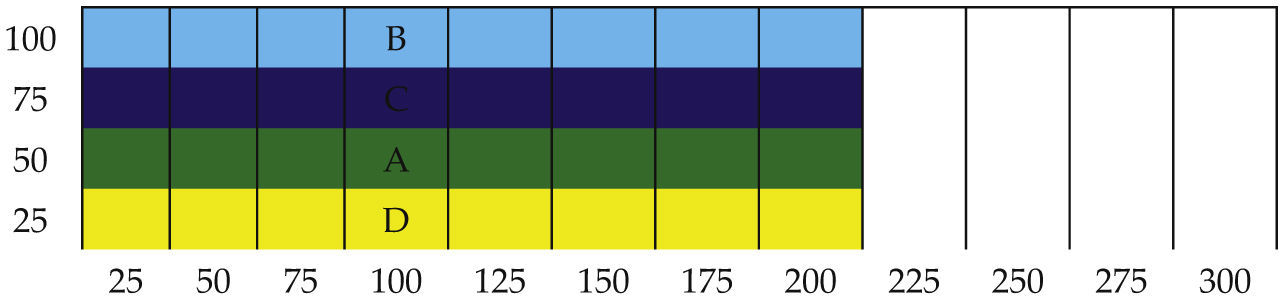
El layout inicial de la Forma 2 se muestra en la figura 4.
Los datos de los centroides (puntos medios) de los departamentos son: A (XA = 100 y YA = 37.5), B (XB =100, YB = 87.5), C (XC = 100, YC = 62.5) y D (XD = 100, YD = 12.5)
La construcción del layout inicial Forma 2 se muestra de la siguiente manera:
- 1.
Se reasigna el departamento D, ya que es el segundo valor del intercambio A-D (tabla 4). El departamento D cumple el criterio de la ecuación 5, LD/WD = 8 > 3 (tabla 5).
- 2.
Se asigna el departamento A como el segundo departamento. El departamento D cumple el criterio de la ecuación 5, LD/WD = 8 > 3 (tabla 5).
- 3.
Se asigna el departamento C, ya que es el valor remanente más alto de Fij (50) y corresponde al intercambio A-C (tabla 5). C debe estar alineado con el departamento A. El departamento C cumple el criterio de la ecuación 5, LC/WC = 8 > 3 (tabla 5).
- 4.
Se asigna el departamento B, ya que es el valor remanente más alto de Fij (20) y corresponde al intercambio B-C o A-B (tabla 5). B puede asignarse junto al departamento A o departamento C, pero como ya no es posible asignar el departamento B junto al departamento A (porque el departamento A está encerrado, ver figura 3), el departamento B debe estar alineado con C. El departamento B cumple el criterio de la ecuación 5, LB/WB = 8 > 3 (tabla 5).
Con los datos de los centroides de los departamentos A (XA = 100 y YA = 37.5), B (XB =250, YB = 87.5), C (XC = 100, YC = 62.5) y D (XD = 100, YD = 12.5), se calculan las distancias entre departamentos con la ecuación 10.
La aplicación de la ecuación 10 a los departamentos A, B, C y D es la siguiente:
dA-B = |XA – XB| + |YA – YB| = |100 – 100| + |37.5 – 87.5| = | 0 | + |– 50| = 50.0, de forma semejante se aplica para conocer las distancias A-C (dA-C = |100 – 100| + |37.5 – 62.5| = 25.0)
A–D (dA-D = |100 – 100| + |37.5 – 12.5| = 25.0), B-C (dB-C = 100 – 100| + |87.5 – 62.5| = 25.0)
B-D (dB-D = |100 – 100| + |87.5 – 12.5| = 75.0) y C-D (dC-D = |100 – 100| + |62.5 – 12.5| = 50.0).
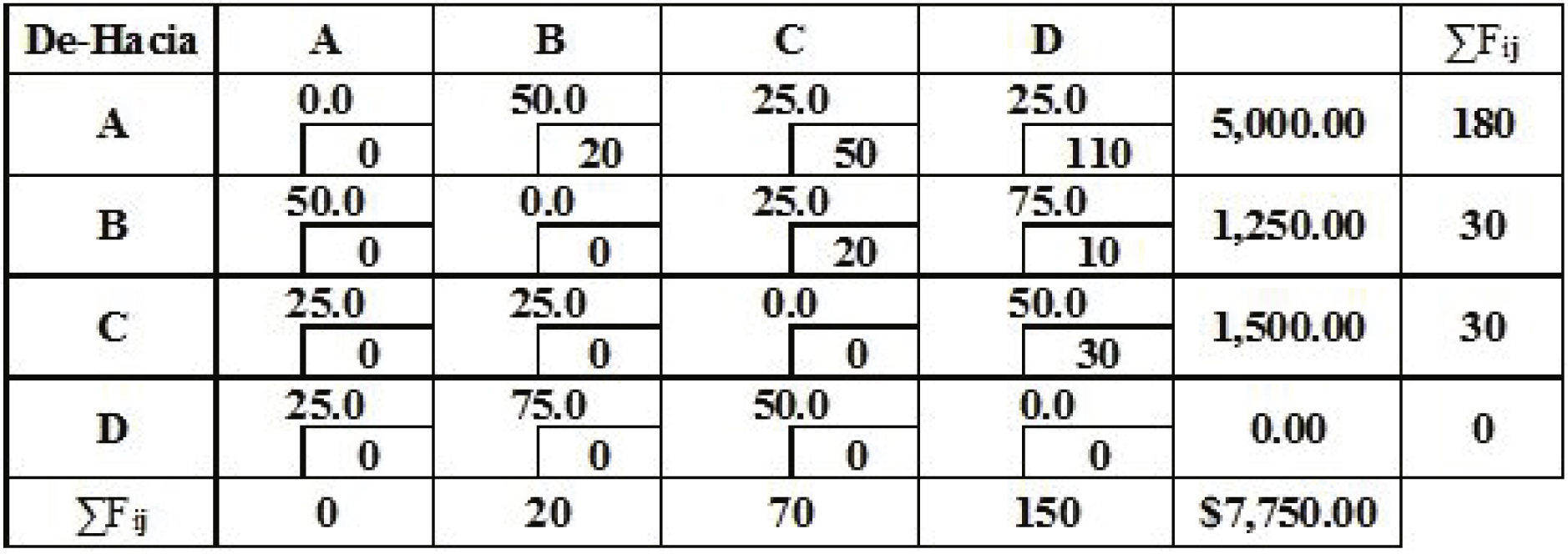
La distribución inicial con intercambio de departamentos (D2, D1, D3) se muestra en la tabla 6.
Distribución inicial del método LDMTP Forma 2 P1 (Problema 6-Chase et al., 2001)
Fuente: elaboración propia (2016)
El costo de la distribución inicial se obtiene de la forma siguiente: 50 * $20 + 25.0 * $50 + 25.0 * $110 + 25 * $20 + 75 * $10 + 50 * $30 = $7,750.00
En nuestro caso P1 Forma 2, se determina el costo de la distribución inicial de la Forma 2 ($7,750) y se compara con la Forma 1. ¿$Forma2 < $Forma1? ($7,750 < $22,875). La respuesta es sí. Ir al paso 7.3.
Paso 7.3 Hacer todo el análisis posterior con la Forma 2.
Paso 8. Establecer todos los intercambios válidos entre dos departamentos (Nahmias, 1999) que pueden ser:
- a)
Que los dos departamentos a intercambiar tengan una frontera en común.
- b)
Que los dos departamentos a intercambiar tengan la misma área, aunque no sean contiguos.
Nota: El intercambio que se realizó para generar un nuevo layout, no es un intercambio válido para esa nueva distribución, pero sí para distribuciones siguientes. Por ejemplo, si el intercambio A-B es el origen del 2° layout (no es un intercambio válido para este layout), pero sí puede considerarse un intercambio válido a partir del 3er layout (siempre y cuando se cumpla alguna de las condiciones mencionadas en el paso 8).
En nuestro caso P1 Forma 2, establece todos los intercambios válidos entre dos departamentos, de acuerdo con la figura 4, que son A-B, A-D y B-C (inciso a, tienen una frontera en común); A-B, B-D y C-D (inciso b, tienen la misma área, aunque no sean contiguos).
Paso 9. Realizar todos los intercambios válidos entre dos departamentos (intercambio de coordenadas: criterio sugerido por CRAFT). Determinar si existe un intercambio que pudiera reducir el costo total de la distribución de planta. ¿Existe un intercambio para el cual el costo del intercambio < costo del origen?
En nuestro caso P1 Forma 2, se realizan los intercambios válidos: A-B, A-C, A-D, B-C, B-D y C-D. Las diferencias se calculan de la forma siguiente: (A-B) = $12,750.00 - $7,750.00 (Origen) = $5,000.00, de forma semejante se obtienen las diferencias A-C ($9,750 - $7,750 = $2,000), A-D ($8,500 - $7,750 = $750), B-C ($9,000 - $7,750 = $ 1,250), B-D ($9,750 - $7,750 = $2,000.00) y C-D ($8,250 - $7,750 = $500). Los resultados de los costos obtenidos de los intercambios válidos se muestran en la tabla 7.
Intercambios válidos de P1 Forma 2 (Problema 6-Chase et al., 2001). Fuente: elaboración propia (2016)
Nota: Como todos los intercambios son mayores que el origen (> $7,750), esto significa que este es el layout óptimo y, por lo tanto, no se aplican los pasos 10 y 11.
Paso 10. Modificar el layout, recalcular los centroides y determinar el costo del origen del nuevo layout.
Nota: Si un departamento no tiene una forma rectangular o cuadrada, es necesario aplicar las fórmulas para el cálculo de centroides (Nahmias, 1999) mostradas en la ecuaciones 8 y 9.
En nuestro caso P1 Forma 2, no aplica.
Paso 11. Repetir los pasos 8 al 10 (de ser necesario).
En nuestro caso P1 Forma 2, no aplica.
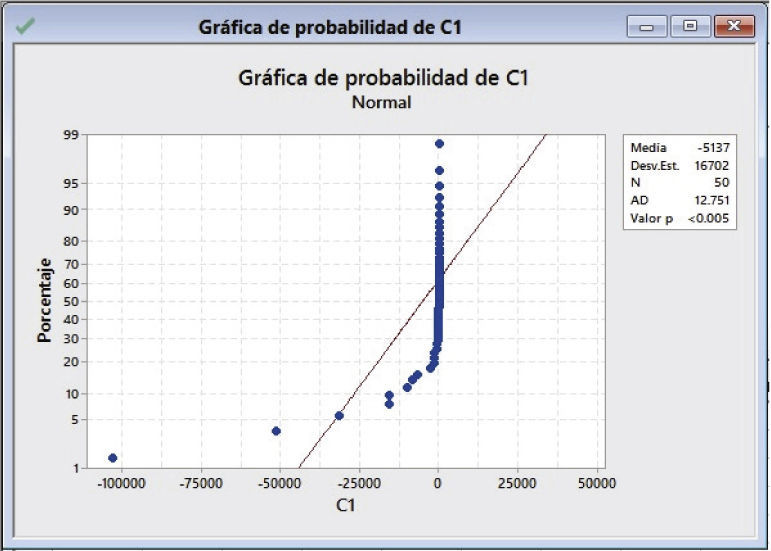
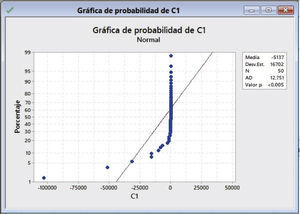
Prueba de normalidad y test de prueba estadísticoEl test de prueba estadístico empleado para validar los resultados obtenidos, depende de la aplicación de la prueba de la normalidad llamada prueba de Anderson Darling (Kvam y Vidakovic, 2007), para los cálculos se empleó el “Menú Estadísticas básicas Prueba de normalidad Anderson-Darling” de MINITAB 17. Las hipótesis son:
H0: Los datos se ajustan a una distribución normal.
Ha: Los datos no se ajustan a una distribución normal.
Criterio de decisiónLa hipótesis nula (H0) se rechaza con un nivel de significancia α si A2* > 0.752 (α=0.05) y si P < 0.05 (Anholeto 2007). Si se acepta H0 se aplica el test “t de muestras dependientes”, si se rechaza H0, se usa la “Prueba Z de los rangos con signo” (Weimer, 1996), figura 5.
Prueba de los rangos con signoμT = Promedio de los n casos
σT = Desviación es tan dar de los n casos
ZT = Estadística de prueba
S = Suma de rangos = T+ + T
H0: LDMTP da peores resultados o ambos métodos dan igual resultado (μLDMTP – μCRAFT ≥ 0).
Ha: LDMTP da mejores resultados (μLDMTP – μCRAFT < 0).
Criterio de decisión: Si Z ≥ Zα se rechaza HO y como α = 0.05, se convierte en Z ≥ Z0.05 (Z ≥ 1.645 valor obtenido de tabla de distribución normal).
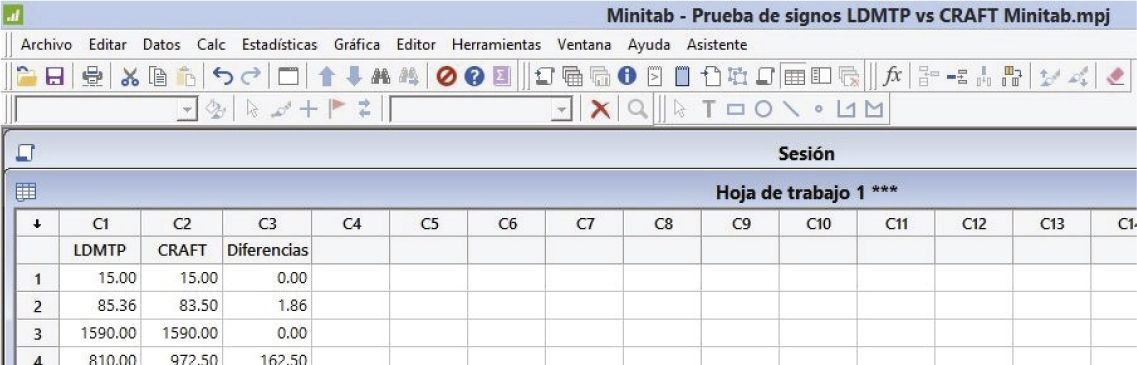
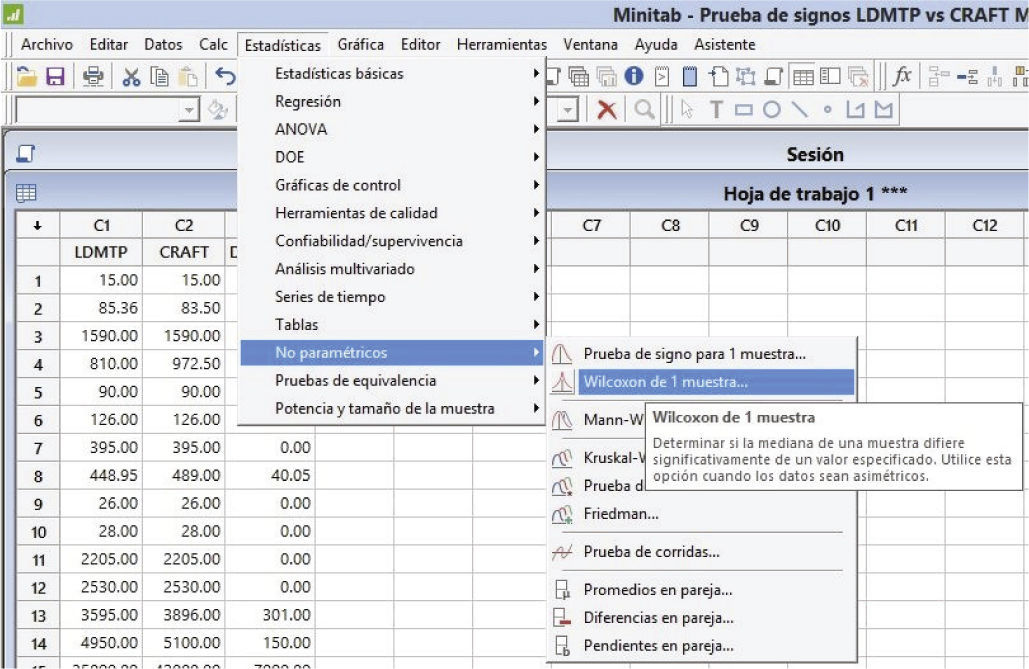
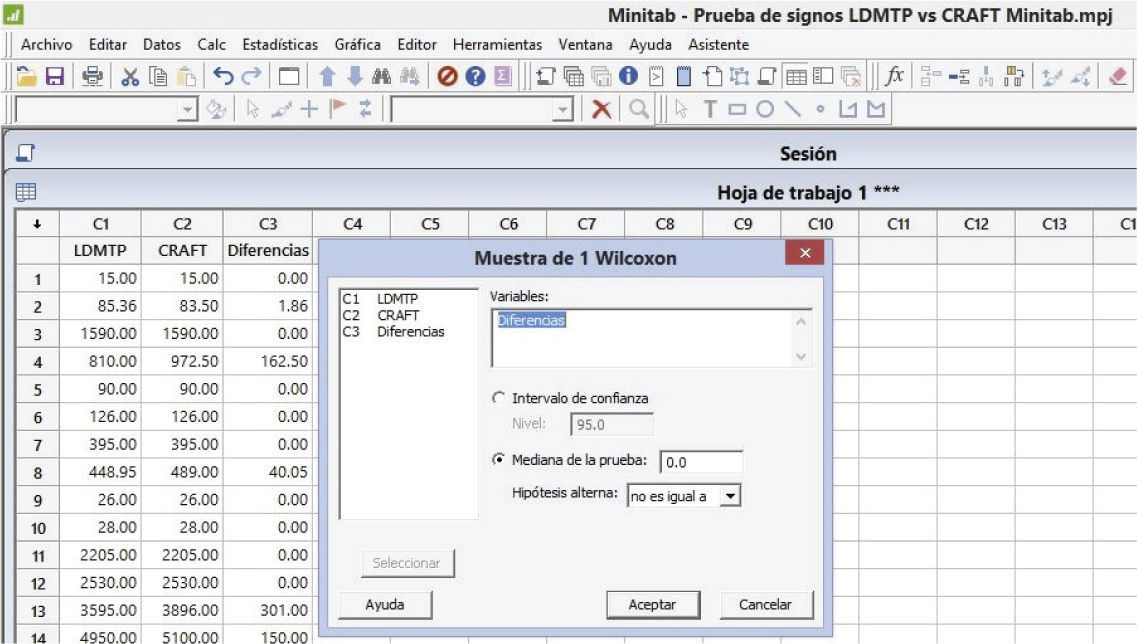
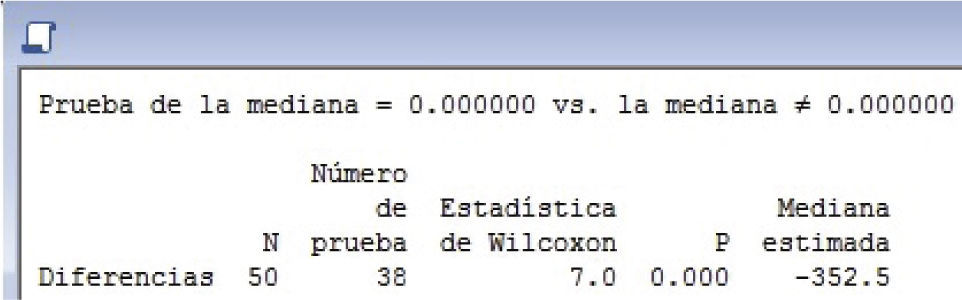
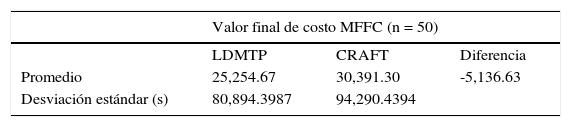
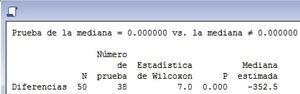
La prueba de los rangos con signo de Wilcoxon para el valor final de costo (MFFC) se realizó calculando las diferencias de MFFC (LDMTP-CRAFT) y usando el software estadístico MINTAB 17 con la prueba Estadísticas No paramétricos de “Wilcoxon de 1 muestra” y se observa el procedimiento de cálculo en las figuras 6 a 10.
El análisis de las figuras 6 a 10 muestra los resultados siguientes:
Nota: Para asignar la posición relativa se excluyen los ceros (0's), n = 50 - 12 = 38.
Las fórmulas y resultados de la Prueba de los Rangos con signo se muestran a continuación:
S = Suma de rangos = T+ + T- = 741.0
T + = 7.0 T − = S – T + = 741.0 – 7.0 T− = T− = 734.0
Como Z > Z0.05 (5.2716 > 1.6450) se rechaza Ho y se acepta Ha, es decir, que LDMTP produce menores valores finales de costo (MFFC) que CRAFT.
ConclusionesLa novedad que aporta esta heurística es que hasta ahora no se ha encontrado en la literatura ninguna aplicación del diseño óptimo de la distribución de planta (ODPL) basada en el problema de transporte. El proceso de establecer la asignación inicial de la heurística LDMTP no es un asunto subjetivo, debido a que la elección del mejor orden de asignación de los departamentos que conforman la distribución inicial sigue una serie de pasos y tiene hasta 4 diferentes criterios de desempate, lo cual favorece que se elija el arreglo de departamentos que puede aportar la mayor contribución a la reducción del costo total de la distribución
La heurística LDMTP ha demostrado que es eficiente para resolver OPDL, debido a que este es un método selectivo capaz de distinguir el mejor orden de asignación de todos los departamentos que conforman el layout, incluyendo criterios de forma (largo y ancho) para cada departamento asignado. Esta información se ve claramente reflejada con los resultados obtenidos para el análisis de 50 casos referenciados en la literatura, para el valor final que se expresa mediante las sumas de las características donde LDMTP obtuvo un valor final de 16.90% menor que con CRAFT.
Estadísticamente se demuestra mediante el uso de la “Prueba Z de los rangos con signo” que el método LDMTP es mejor que CRAFT, que arrojó el resultado siguiente, Valor final Z > Z0.05 (5.2716 > 1.6450), lo que significa que LDMTP es más eficiente y produce menores valores de costo (MFFC) que CRAFT.
El autor desea agradecer al personal de la UTSC, al rector Dr. José Cárdenas Cavazos y la Directora Académica Mtra. Ana Bertha Tamez Salas por las facilidades otorgadas para realizar este trabajo y a los MES. Manuel Cantú Sosa y Anselmo Carpio Hernández, del cuerpo académico de procesos industriales por sus sugerencias de mejora del método.
Héctor Manuel González-Longoria. Ingeniero químico por la Universidad Autónoma de Nuevo León. Maestro en educación superior por el Centro de Estudios Universitarios. Es subdirector de la carrera de procesos industriales área manufactura y responsable del cuerpo académico en la Universidad Tecnológica Santa Catarina, donde imparte las asignaturas de distribución de planta y cadena de suministros. Sus principales áreas de interés son las heurísticas aplicadas a temas de investigación de operaciones.