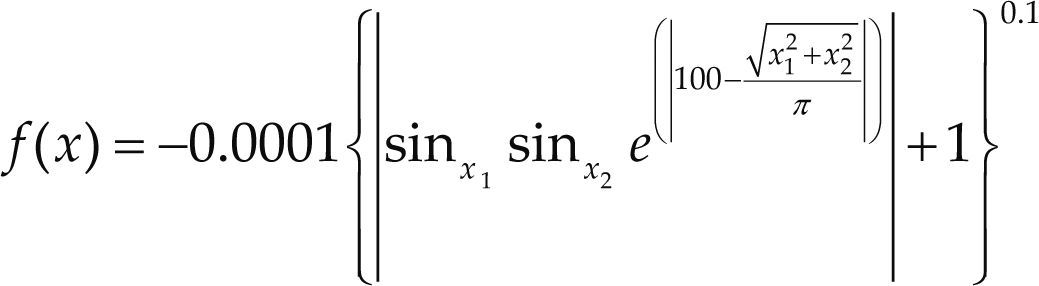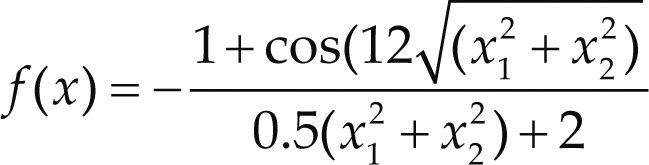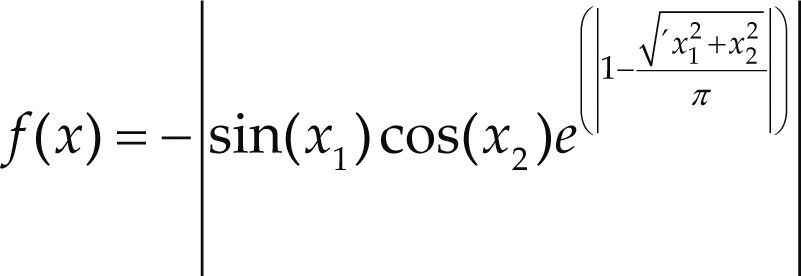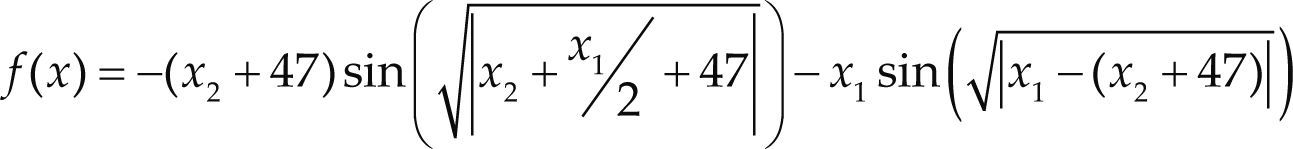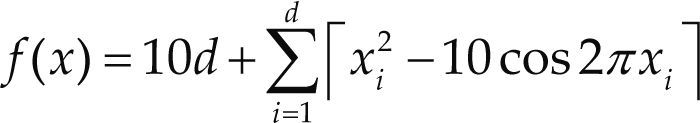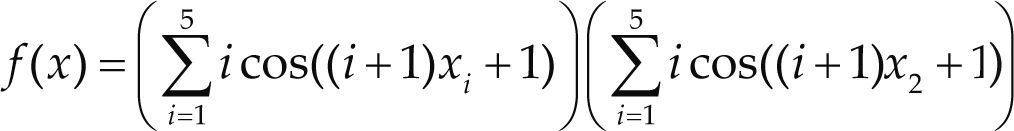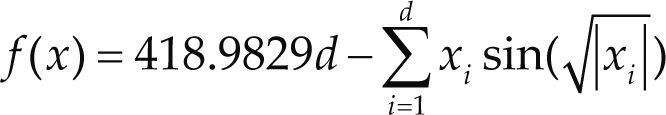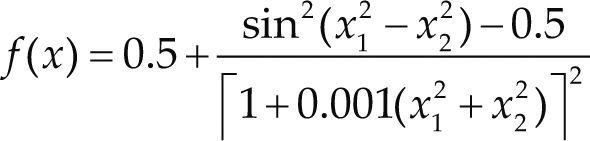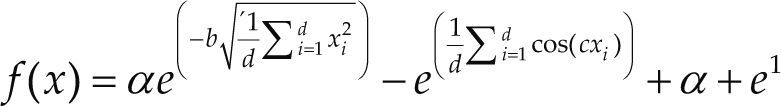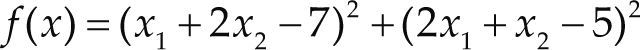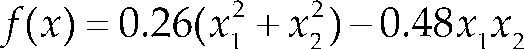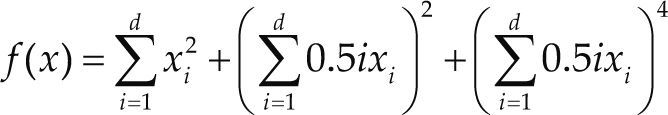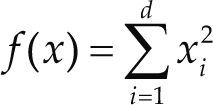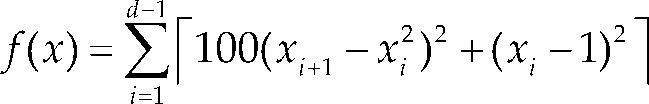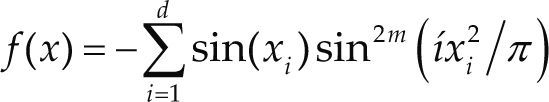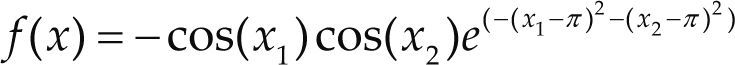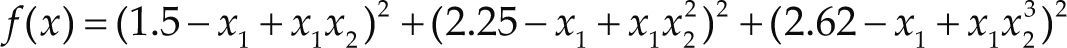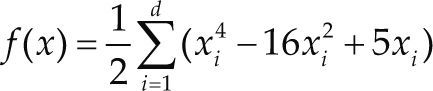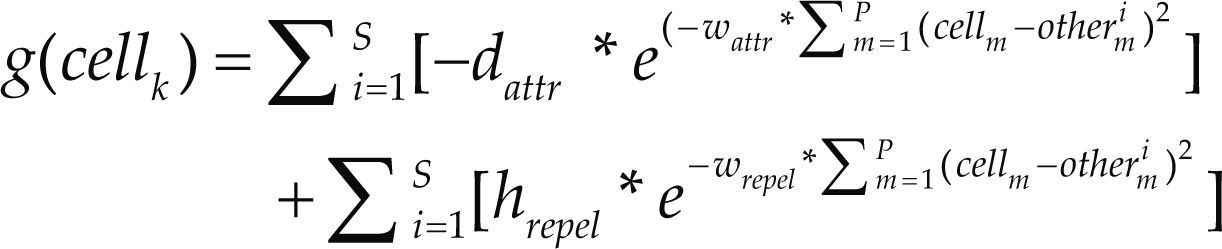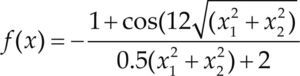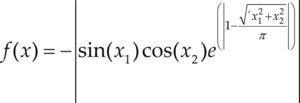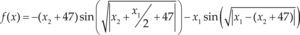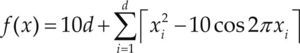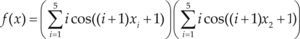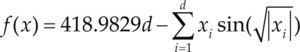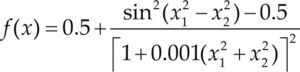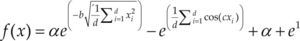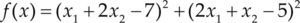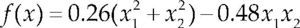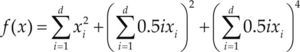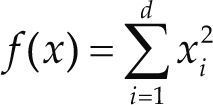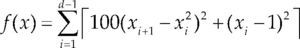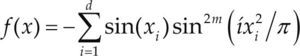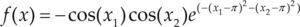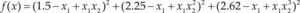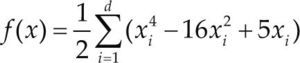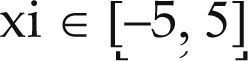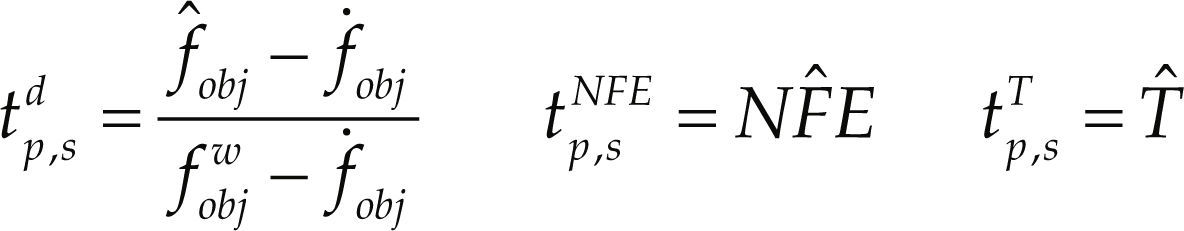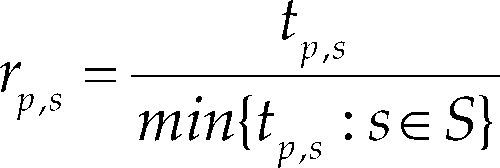En este trabajo se reporta la aplicación del concepto de perfiles de comportamiento numérico en la comparación del desempeño numérico de los métodos Immune Network Algorithm y Bacterial Foraging Optimization en 18 funciones benchmark de optimización. Específicamente la robustez, eficiencia y el tiempo de ejecución de estos métodos se compararon en espacios de búsqueda con múltiples mínimos locales, bowl-shaped, plate-shaped, valley-shaped, steep ridges y otras conocidas funciones de optimización como styblinski-tang y beale function. Los resultados muestran que el método AiNet (Castro et al., 2002) es más robusto que el método BFOA (Passino, 2010) para los casos de estudio considerados en este trabajo. Sin embargo, existen diferencias en la eficiencia (número de funciones evaluadas y tiempo de convergencia) entre ambos métodos. Donde BFOA es el algoritmo con mejor desempeño en cuanto al número de funciones evaluadas.
This paper reports the application of the performance profiles model comparing the numerical methods Immune Network (AiNet) and Bacterial Foraging Optimization Algorithm (BFOA) in 18 benchmark optimization functions. Specifically robustness, efficiency and execution time of these methods were compared in search spaces with local minima multiple, bowl-shaped, plate-shaped, valley-shaped, steep ridges and other known optimization functions as styblinski-tang and beale function. The results show that the method AiNet (Castro et al., 2002) is more robust than the BFOA method (Passino, 2010) for the case studies considered in this work. However there are differences in the efficiency (number of evaluated functions and convergence time) between both methods. BFOA is the algorithm with best perform in terms of the number of evaluated functions.
Los métodos de búsqueda inspirados en procesos naturales se consideran confiables y adecuados para resolver diversos problemas de optimización que se caracterizan por tener funciones objetivo altamente no lineales y no convexas. De forma particular, en el área de ingenierías existen diversas funciones conocidas como benchmark con las que se pretende representar la complejidad de problemas reales. Estas funciones se emplean para el estudio y comparación del desempeño de métodos de optimización (Kämpf et al., 2010). En este contexto, varios estudios han demostrado que los métodos inspirados en procesos naturales, son robustos, fáciles de implementar y de aplicación general para la resolución de problemas en diversos contextos de la aplicación de meta heurísticas (Yang, 2010). Específicamente los métodos basados en optimización según la actividad celular emplean la estrategia de reproducción o clonación de aquellas que ofrecen mejores resultados en la búsqueda. Esta es una característica en común con el conocido algoritmo genético de Holland (1975).
En cuanto a las funciones benchmark, estas tienen diferentes complejidades y suelen ser multimodales, multidimensionales, y con un número n de diferentes mínimos locales. Cada uno de los espacios de búsqueda representa un problema particular para el algoritmo de optimización (Molga et al., 2005). Hasta ahora se han desarrollado diferentes algoritmos inspirados en la actividad celular, como por ejemplo los basados en el sistema inmune de los organismos, que se encargan de la detección y eliminación de potenciales amenazas externas, así como aquellos algoritmos inspirados en la actividad bacterial en búsqueda de nutrientes. También las conocidas redes neuronales son sistemas artificiales inspirados en las células del sistema nervioso, conocidas como neuronas, pero es principalmente explotado en el área de reconocimiento de patrones y aprendizaje (Brownlee, 2011). Con base en lo anterior, en este trabajo se reporta un comparativo de comportamiento numérico entre dos algoritmos inspirados en procesos naturales, particularmente la actividad celular. Estos algoritmos son:
- a)
Bacterial Foraging Optimization Algorithm (Passino, 2010) e
- b)
Immune Network Algorithm (Castro et al., 2002).
La comparación de estos métodos se realizó empleando el concepto de perfiles numéricos propuesto por (Dolan et al., 2002) y recientemente empleado por (Bonilla et al., 2011) con el objeto de establecer las diferencias relativas entre los algoritmos en términos de robustez (capacidad de alcanzar el óptimo global), eficiencia (esfuerzo numérico requerido durante la secuencia de optimización).
Trabajos previos y justificaciónEl algoritmo Bacterial Foraging Optimization Algorithm (BFOA) se emplea en múltiples problemas del área de ingenierías y optimización en general, por ejemplo los siguientes: en (Kou, 2010) una aplicación de BFOA en el diseño de turbinas, o la que presenta Vaisakh (2009) donde se propone una aplicación al problema de ruteo de vehículos. En (Dehghan, 2011) se aplica BFOA como estrategia para el diseño de filtros activos en ingeniería eléctrica y en Ali (2013) para el problema de transferencia de potencia. Mientras que en Regis (2011) y Wu (2013) se emplea para el diseño de un PID un convertidor DC-DC electrónico. Asimismo en Jati (2012) se propone una aplicación al problema de la planificación de movimientos robóticos. Por otro lado, en Minshed (2012) hay una aplicación como estrategia de localización en un radar lasser. En Wu (2013) se usa BFOA en el problema de Hydro Power Dispatch. En Bejinariu (2013) la aplicación de BFOA consiste en la optimización del registro de imágenes en procesadores hardware multinúcleo. En Dasgupta (2008) existe una aplicación al problema de reconocimiento de patrones. Las implantaciones de este algoritmo en diferentes contextos han generado una serie de propuestas y adaptaciones a partir del algoritmo original de Passino. A continuación se clasifican y describen brevemente.
Adaptaciones y mejoras: Por ejemplo, en Dasgupta (2009a) se diseña una versión de BFOA adaptativo con una estrategia para acelerar la convergencia al óptimo. Señalan que este algoritmo puede quedar oscilante cuando está muy cerca del objetivo. Proponen un operador que cambia dinámicamente los pasos de quimiotaxis según los valores de fitness obtenidos. En Abraham (2008) se analiza la etapa de reproducción de BFOA como determinante en la convergencia a través de dos ecuaciones diferenciales y en un escenario de dos bacterias en un plano. En Dasgupta (2009b) se propone una versión BFOA donde la mejor bacteria se mantiene intacta (elitismo) mientras las otras, que son unas cuantas, se reinician. En Borovska (2011) se hace una paralelización de BFOA aplicado al problema de planeación de tareas.
Modelos matemáticos: en Das S.D. (2009); Das S.B. (2009) y Thomas (2013) se hace una descripción detallada del algoritmo desde el punto de vista matemático.
Comparativas de desempeño: en Jati (2012); Rout (2013); Mezura (2009); Baijal (2011) y Mezura (2008) se hace una comparativa del desempeño de BFOA con otros algoritmos de optimización y en el contexto de diferentes problemas.
Hibridaciones: en Praveena (2010) existe una descripción de la hibridación entre PSO, BFOA y Diferential Evolution (DE). En Minshed (2012) se propone un híbrido entre BFOA y Firefly Optimization aplicado al problema de ruteo vehículos. En Narendhar (2012) se describe un híbrido entre ant colony y BFOA aplicado al problema de programación de labores. El trabajo en Moncayo (2014) es un híbrido entre algoritmo genético y BFOA aplicado al problema de distribución de plantas de celdas de manufactura. En Shen (2009) se aplica un híbrido de BFOA y PSO al problema de optimización numérica global.
En cuanto al algoritmo Immune Network Algorithm (AiNet), los trabajos previos también se encuentran en el contexto de ingeniería y optimización. Por ejemplo los siguientes: en Andrews (2006) se explora la eficiencia de un operador que asegura la diversidad en la población de soluciones. El trabajo de Li (2010) se refiere al uso de AiNet en la predicción de desastres naturales a partir de bases de datos históricas del clima. En Ju (2012) se hace una comparativa de desempeño de AiNet en el problema de programación de tareas. Comparan resultados con el algoritmo genético, recocido simulado y colonia de hormigas. En Wei (2011) Aplican AiNet como estrategia de búsqueda en el modelo de aprendizaje cualitativo (QLM), mientras que en Rautenberg (2008) para la construcción de redes neuronales. El trabajo en De Franca (2010) y Agiza (2011) se refiere al desarrollo de dos versiones de AiNet para comparar su desempeño en funciones benchmark. En el contexto de la medicina, el trabajo de Tsankova (2007) se refiere al uso de AiNet en la predicción del desarrollo de Cáncer a partir de bases de datos genéticas y casos fatales versus casos de cura. En el contexto de la ingeniería, en Campelo (2006) existe una Aplicación de AiNet en el diseño de dispositivos electromagnéticos.
En el área optimización es frecuente hacer comparativas de desempeño entre algoritmos en problemas de interés, una de las prácticas comunes es trabajar con promedios de repeticiones de forma que faciliten la comparativa, y en algunos casos se realizan pruebas estadísticas como la conocida prueba t para contrastar promedios. Sin embargo, este procedimiento no permite observar en términos globales el desempeño de un conjunto de algoritmos a la luz de un conjunto de problemas. Ante esto existen herramientas como el perfil de comportamiento numérico. Este trabajo introduce la aplicación de esta herramienta como comparativa para estos algoritmos y se realiza para tres diferentes métricas. Se trata de un aporte para documentar y contrastar la eficiencia y eficacia de los algoritmos presentados.
Métodos inspirados en la naturalezaDesde el comienzo de la humanidad, el hombre fue capaz de obtener recursos de la naturaleza, como alimentos y refugio que encontraba a su paso. Con el tiempo, fue posible comprender mejor las bases de diferentes procesos naturales hasta lograr cultivar alimentos, domesticar animales y construir refugios según las necesidades. Gradualmente, el conocimiento del hombre sobre los procesos naturales se ha incrementado, hasta los días modernos en que es posible “manejar la vida” en diferentes niveles, por ejemplo, crear alimentos transgénicos, combatir enfermedades y cultivar cepas de organismos unicelulares (Castro et al., 2004).
Actualmente con los recursos de cómputo es posible observar la naturaleza como fuente de inspiración para el desarrollo de técnicas de optimización y solución de problemas complejos en ingeniería y otros contextos. En el área de la computación inspirada en procesos naturales, existe la rama de computación inspirada en procesos biológicos que se refiere particularmente a procesos naturales de los organismos vivos. Entre los procesos naturales no biológicos existe por ejemplo el recocido de materiales que inspira el algoritmo de recocido simulado Kirkpatrick (1984).
En el área optimización existen modelos inspirados en procesos biológicos:
- a)
Bacterial Foraging (forrajeo de bacterias). Este modelo se inspira en la forma en que las colonias de bacterias son capaces de trasladarse hacia un punto en el que perciben mayor cantidad de nutrientes. Así mismo, son capaces de apartarse de toxinas y factores desfavorables para la colonia. Este es un modelo relacionado con el algoritmo de quimiotaxis bacterial de Muller (2002) así como otros basados en el modelo de enjambres. Las bacterias como E.Coli segregan sustancias que atraen y repelen a otras bacterias de la misma especie. La movilidad bacterial está determinada por el uso de flagelos que se mueven en dirección o contra-dirección de las manecillas del reloj. El movimiento de una bacteria se puede dar en forma de tumbos (tumble) o nado (swim), y esto se determina por su percepción del entorno, es decir, el gradiente de nutrientes/toxinas en conjunto con la interacción de otras bacterias (Brownlee, 2011). Este trabajo se centra en el algoritmo BFOA.
- b)
Immune System (sistema inmune). El área de sistemas inmunes artificiales (SIA) está relacionada con los métodos computacionales inspirados en el sistema inmuno-biológico de los organismos, principalmente el de los mamíferos, que permite la detección y eliminación de patógenos que significan un riesgo para el organismo en cuestión. Los patógenos pueden ser bacterias, virus, parásitos y polen. La identificación de patógenos se logra por diferenciación. El sistema inmune adquirido, también llamado adaptativo, es responsable de especializar la defensa para amenazas específicas. Este tipo de sistema de defensa está presente en organismos vertebrados, a diferencia del sistema inmune innato. Una característica del sistema inmune es la capacidad de retener información de los patógenos que atacan al sistema, como estrategia para futuras apariciones del mismo patógeno. Las células conocidas como glóbulos blancos, son los principales actores en el sistema inmune, ya que están involucrados tanto en la identificación como en la eliminación de los patógenos (Brownlee, 2011). Los trabajos por incorporar a este modelo biológico en modelos algorítmicos enfocados a la optimización tienen orígenes en trabajos previos (Hoffmann, 1986 y Hofmeyr, 1999). Los SIA modernos están inspirados en alguna de las tres sub-áreas de estudio: clonal selection, negative selection o immune network. Estos modelos se emplean en problemas de optimización, clasificación y reconocimiento de patrones. Destaca el trabajo de Castro (2002) que es una introducción a inmunología con el grado de detalle para diseño de algoritmos. Este trabajo se centra en el algoritmo AiNet.
La optimización por enjambre de bacterias o bacterial foraging optimization algorithm (BFOA) representa una aproximación diferente a la búsqueda de valores óptimos en funciones no lineales, desarrollado por Passino (2010), se basa en el comportamiento quimiotáctico de la bacteria Escherichia Coli (E. Coli). Si bien, utilizar la quimiotaxis como modelo para optimización se propuso por primera vez en Bremermann (1974) y se ha utilizado en trabajos de Leiviskä (2006), el trabajo de Passino incluye algunas modificaciones como la reproducción y la dispersión de los agentes. La E.Coli es quizá el microorganismo más comprendido, ya que su comportamiento y estructura genética están bien estudiados.
Esta consta de una cápsula que incluye sus órganos y flagelos, que utiliza para su locomoción; posee capacidad de reproducirse por división y también es capaz de intercambiar información genética con sus congéneres. Además, es capaz de detectar nutrientes y evitar sustancias nocivas, efectuando un tipo de búsqueda aleatoria, basado en dos estados de locomoción: el desplazamiento o nado (swim) y el giro o tumbo (tumble). La decisión de permanecer en alguno de estos dos estados se basa en la concentración de nutrientes o sustancias nocivas en el medio. Este comportamiento se denomina quimiotaxis. A continuación se describen los pasos de la optimización con el algoritmo BFOA (Regis et al., 2011).
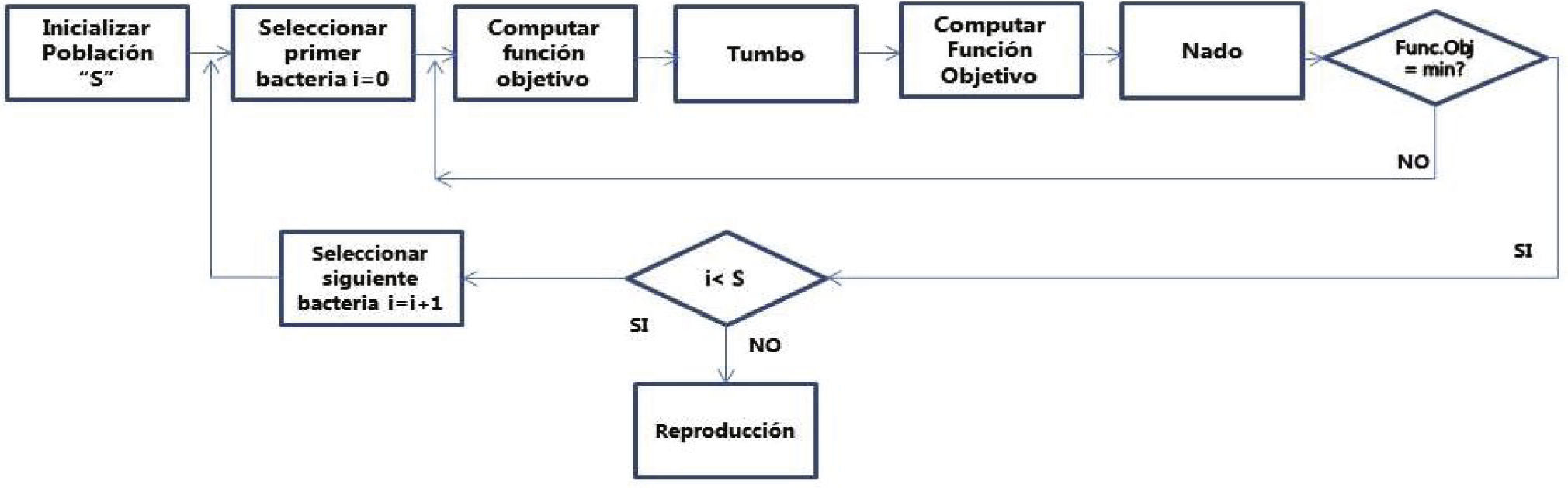
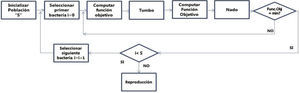
Paso 1: El ciclo de la quimiotaxis se describe en la figura 1. En este proceso el movimiento de E.Coli se simula. El movimiento se efectúa de dos formas: dando tumbos o a nado, una operación a la vez. Se calcula el valor de la función objetivo. La bacteria cambia su posición si el valor de la función objetivo modificada es peor que la anterior. Al completar la quimiotaxis la bacteria estará rondando un punto en el espacio de búsqueda.
Paso 2: El proceso de reproducción. El valor de la función objetivo se calcula para cada una de las bacterias en la población ordenada. La peor mitad de la población se descarta y la mejor mitad se duplica. Para esta nueva generación de bacterias el ciclo de quimiotaxis se inicia y el proceso continúa por el número de pasos de reproducción.
Paso 3: En el ciclo de eliminación-dispersión, algunas bacterias se eliminan con baja probabilidad y se dispersan en un punto aleatorio del espacio de búsqueda. Este proceso mantiene constante el número de bacterias.
Los parámetros de entrada son el número de bacterias Sb, límite de pasos de quimiotaxis Nc, límite de pasos de nado Ns, límite de ciclos de reproducción Nre, número de bacterias a producir Sr, límite del ciclo de eliminación-dispersión Ned, tamaño de paso Ci, y probabilidad de eliminación-dispersión Ped. El costo de cada bacteria se optimiza por su interacción con otras bacterias. La función de interacción se calcula de acuerdo con la expresión g().
dondecellk = bacteria en cuestión
dattr y wattr = coeficientes de atracción
hrepel y wrepel = coeficientes de repulsión
S = número de bacterias en la población
P = número de dimensiones o variables a optimizar en cada bacteria
La representación “other” es “otra célula” interactuando con cellk.
Algoritmo AiNetRecientemente el algoritmo de optimización basado en el sistema inmune (Castro y Timmis 2002) ha llamado la atención de los investigadores por su potente capacidad de manejo de información. El sistema inmune natural es complejo y con diferentes mecanismos de defensa contra organismos invasores, tiene características como: especificidad, reconocimiento de patrones, diversidad, tolerancia a fallas, memoria y aprendizaje, auto-organización, cooperación entre capas, entre otros.
El objetivo de una red inmune es el de preparar o construir un repertorio de detectores para un problema dado, donde las células con mejor desempeño suprimen a aquellas con baja afinidad en la red. Este objetivo se alcanza exponiendo a la población a información externa, a partir de la cual se generan respuestas en forma de clonaciones y dinámica iter-celular.
Las dos teorías que principalmente motivaron el desarrollo de este modelo de optimización son (Aragón et al., 2010): Immune Netrwork Theory (IN) y Clonal Selection Theory (CS). El principio de CS es la teoría que se emplea para describir la respuesta adaptativa del sistema inmune hacia estímulos antigénicos. La premisa de este modelo establece que el sistema inmune reacciona únicamente cuando se invade por estímulos externos. Así que la respuesta del sistema es la producción de anticuerpos por las células B una vez que el antígeno ha entrado al sistema. Entonces en la presencia del antígeno, aquellos anticuerpos con mayor afinidad o capacidad de reconocer el antígeno son los privilegiados para proliferar, produciendo enormes cantidades de anticuerpos clones con diversidad basada en mutación. Por otro lado, la teoría IN establece que los anticuerpos (receptores de las células B) tienen partes llamadas idiotopes que pueden reconocerse por otros anticuerpos en otras células B. Esta característica de reconocer y ser reconocido le da al sistema una dinámica intrínseca. A continuación se describe el pseudo código y la estrategia de optimización del algoritmo AiNet (Brownlee, 2011).
La cantidad de mutación de los clones es proporcional a la afinidad de la célula original (padre) con la función objetivo en términos de que a una mejor aptitud (afinidad) le corresponde menor mutación. También se adicionan células aleatorias. Para limitar la redundancia se efectúa la eliminación de células según su similitud con otras. El tamaño de la población es dinámico y si continúa creciendo, puede significar que el espacio de búsqueda tenga múltiples mínimos locales o que el umbral de afinidad necesite un ajuste. La mutación proporcional a la afinidad se hace con c′ = c + a x N (1, 0) donde a = 1/β x exp (–f ), N es un número gaussiano aleatorio y f es el grado de aptitud o fitness de la célula original (padre), c′ es la mutación de la célula c, β controla el decremento de la función y puede establecerse en 100. El umbral de afinidad es específico del problema y su representación. Por ejemplo, dicho umbral de afinidad se puede establecer en 0.1 como valor arbitrario o se puede calcular como porcentaje del tamaño del espacio de búsqueda. El número de células aleatorias insertadas puede ser 40% de la población. El número de clones a partir de una célula dada suele ser pequeño, por ejemplo 10.
Funciones BenchmarkPara asegurar una diversidad de pruebas se emplea un conjunto de 18 funciones de problemas conocidos en el área de optimización (Chase et al., 2010; Molga, 2005) ver tabla 1. Estos se clasifican según la similitud y forma del espacio de búsqueda (Surjanovic, 2013), algunas funciones tienen múltiples mínimos locales, otras tienen forma plana, forma de valle o profundidad como tazón, otras son escalonadas y de varias formas. Para esta comparativa todas las funciones son bidimensionales (d=2).
Conjunto de funciones Benchmark
| Benchmark | Función | var | Espacio de Búsqueda | Mínimo Global |
|---|---|---|---|---|
| Cross in Tray | xi ∈ [-10, 10] | –2.06261 | ||
| Drop Wave | xi ∈ [-5.12, 5.12] | –1 | ||
| Holder Table | xi ∈ [-10, 10] | –19.2085 | ||
| EggHolder | xi ∈ [-512, 512] | –959.6407 | ||
| Rastrigin | xi ∈ [-5.12, 5.12] | 0 | ||
| Shubert | xi ∈ [-10, 10] | –186.7309 | ||
| Schwefel | xi ∈ [-500, 500] | 0 | ||
| Schaffer 2 | xi ∈ [-100, 100] | 0 | ||
| Ackley | a = 20 b = 0.2 c = 2π | xi ∈ [-32.768, 32.768] | 0 | |
| Booth | xi ∈ [-10, 10] | 0 | ||
| Matyas | xi ∈ [-10, 10] | 0 | ||
| Zakharov | xi ∈ [-5, 10] | 0 | ||
| Sphere | xi ∈ [-5.12, 5.12] | 0 | ||
| Rosenbrok | xi ∈ [-5, 10] | 0 | ||
| Michaelwicz | m = 10 | xi ∈ [0 π] | –1.8013 | |
| Easom | xi ∈ [-100, 100] | –1 | ||
| Beale | xi ∈ [-4.5, 4.5] | 0 | ||
| Styblinski-Tang | –39.16599d |
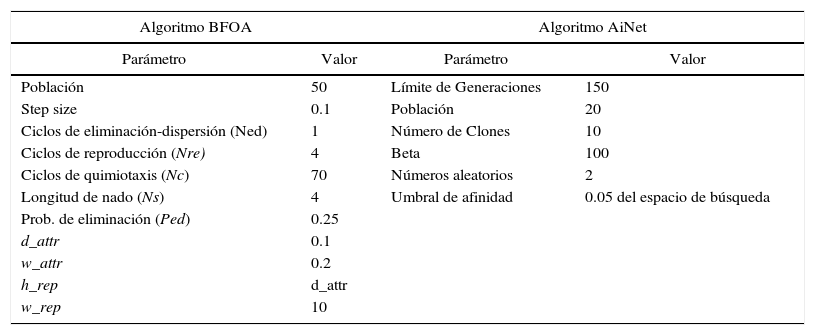
Parámetros de los algoritmos BFOA y AiNet
| Algoritmo BFOA | Algoritmo AiNet | ||
|---|---|---|---|
| Parámetro | Valor | Parámetro | Valor |
| Población | 50 | Límite de Generaciones | 150 |
| Step size | 0.1 | Población | 20 |
| Ciclos de eliminación-dispersión (Ned) | 1 | Número de Clones | 10 |
| Ciclos de reproducción (Nre) | 4 | Beta | 100 |
| Ciclos de quimiotaxis (Nc) | 70 | Números aleatorios | 2 |
| Longitud de nado (Ns) | 4 | Umbral de afinidad | 0.05 del espacio de búsqueda |
| Prob. de eliminación (Ped) | 0.25 | ||
| d_attr | 0.1 | ||
| w_attr | 0.2 | ||
| h_rep | d_attr | ||
| w_rep | 10 | ||
Los algoritmos BFOA y AiNet se desarrollaron en lenguaje Ruby, en equipo de cómputo con procesador Intel core i7, 10Gb en memoria RAM y sistema operativo Windows 7. Las gráficas se generaron en el software Excel de Microsoft. En cuanto a los parámetros de los algoritmos, se adoptaron los considerados default, reportados por Brownlee (2011).
Determinación de los perfiles numéricosLa comparación del comportamiento numérico (robustez, eficiencia) de los métodos BFOA y AiNet se realizó al emplear el concepto de perfil de comportamiento numérico. El perfil de comportamiento para un método de optimización se define como la función de distribución acumulativa para una métrica de comportamiento o desempeño numérico (Dolan, 2002). Dicha métrica puede corresponder a algún factor de interés en la comparativa de desempeño, como el tiempo necesario para alcanzar la convergencia del método de optimización, la cantidad de funciones evaluadas durante la secuencia de cálculo o la capacidad del método para localizar al óptimo global de la función objetivo. En este trabajo, las siguientes métricas se consideran para la comparación de los dos métodos: la distancia relativa entre el óptimo localizado por el método de optimización y el óptimo global conocido: d. La cantidad de funciones evaluadas durante la secuencia de optimización (NFE) y el tiempo de ejecución (T) para la convergencia. La primera métrica se asoció con la robustez del método (es decir, la capacidad de la estrategia numérica para localizar al óptimo global de la función objetivo) mientras que la segunda y tercera corresponden a una medida de la eficiencia de los métodos estocásticos (Ali et al., 2005).
Para la evaluación de estas métricas, se asume que existen ns = 2 métodos de optimización y np = 18 problemas o casos de estudio. Cada uno de los casos de estudio se resolvió en 30 ocasiones con estimaciones iniciales aleatorias y diferentes secuencias de números aleatorios, considerando una tolerancia de 1.0E-06 en el valor de la función objetivo como criterio de convergencia para ambos métodos. Para cada problema y método de optimización, las métricas tp,s se calcularon empleando los resultados de 30 cálculos y las siguientes expresiones.
dondefˆobj = valor promedio de la función objetivo calculado por el método de optimización
f˙obj = óptimo global de la función objetivo
fobjw = valor máximo para la función objetivo encontrado dentro la secuencia de cálculo
NFˆE y Tˆ= valor promedio del número de funciones evaluadas y el tiempo para alcanzar la convergencia del método de optimización
Es importante señalar que los valores de fˆobj, NFˆE y Tˆ se determinaron empleando los 30 experimentos num éricos realizados para el caso de estudio. Conforme a lo establecido por Ali et al. (2005) y Bonilla et al. (2011), en la literatura se suelen usar valores promedio para las métricas de comportamiento con el objeto de describir el desempeño de los métodos. Con base en lo anterior, este estudio también emplea dicho enfoque. Por otro lado, para las tres métricas, la tasa de comportamiento numérico rp,s se define como
Donde S corresponde al conjunto de métodos de optimización analizados. Se puede observar que el valor de dicha tasa es igual a 1 para el método que presenta el mejor comportamiento en un problema específico, ya que para ambas métricas es deseable obtener el valor mínimo posible (Dolan, 2002y Ali et al., 2005). Finalmente, la tasa de probabilidad acumulativa ρs(τ) para el método de optimización s y la métrica en cuestión se define como
Donde τ es un factor que se define en (1,∞). La gráfica del perfil de comportamiento, es decir, el gráfico de ρsversus τ, compara el desempeño relativo entre los métodos de optimización para el grupo de problemas considerados (Dolan, 2002). Hasta el momento los perfiles de comportamiento se han utilizado por Montaz et al. (2005) empleando funciones objetivo clásicas del área de optimización, y por Bonilla et al. (2011) empleando funciones del área de la ingeniería química. No obstante, dicho concepto no se ha empleado en la comparativa de los métodos descritos en este estudio.
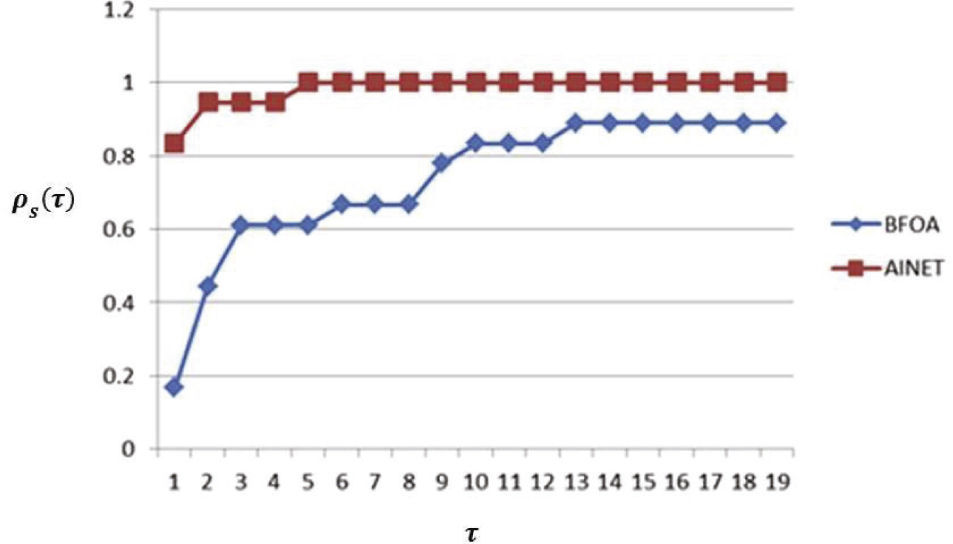
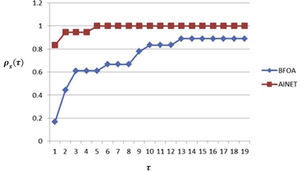
Resultados y discusiónEl perfil de comportamiento para la métrica tp,sd, q ue se asocia a la capacidad del método de optimización para acercarse al óptimo global en los problemas considerados, se muestra en la figura 2. Como se puede observar, el método AiNet presenta un mejor comportamiento para esta métrica, en contraste con el método BFOA dentro del rango analizado para τ. También estos resultados indican que en 81% de los casos de estudio el método AiNet proporciona mejor solución (τ = 1), mientras que BFOA solamente lo consigue en 19% de los casos.
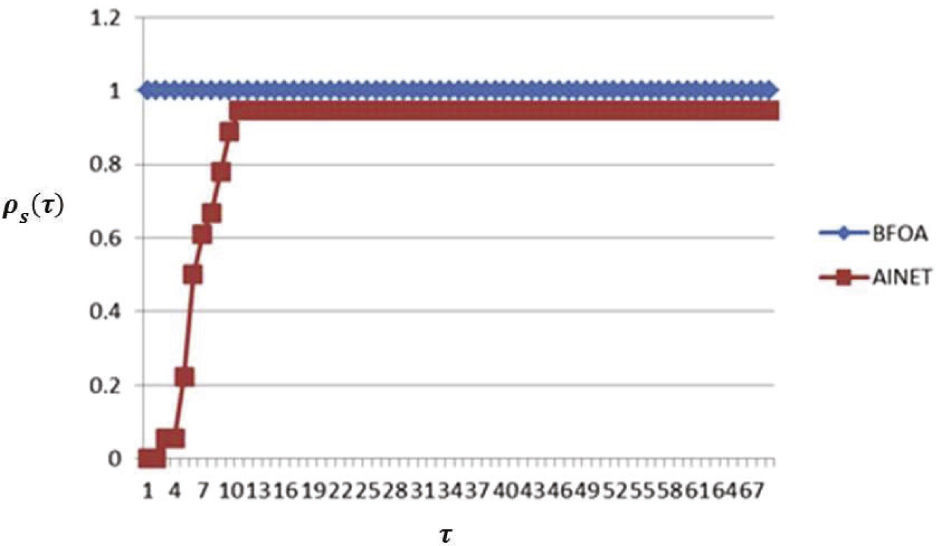
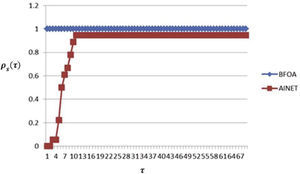
Para el caso de la eficiencia, en la métrica NFˆE es indudable que el método BFOA supera al método AiNet (figura 3) para todos los casos de estudio.
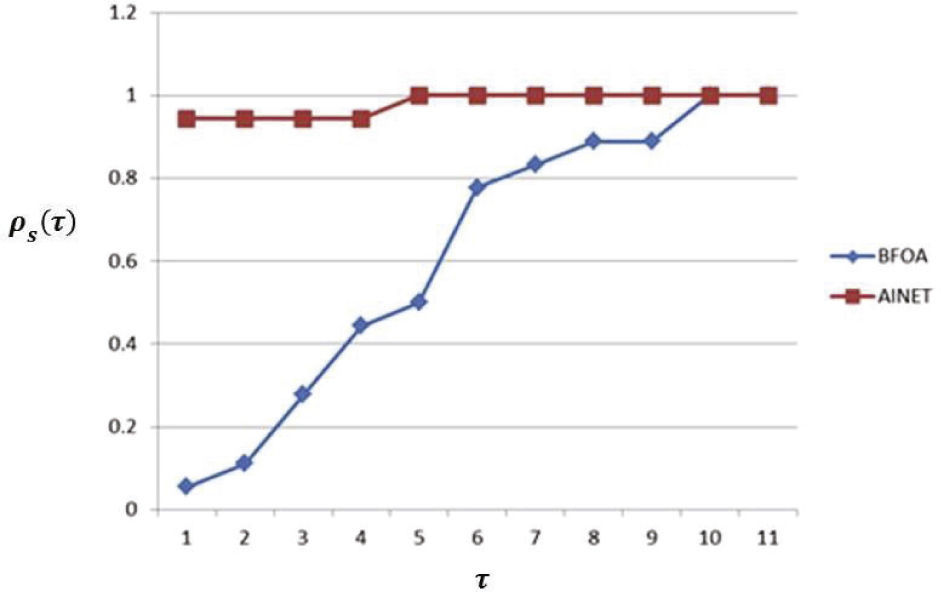
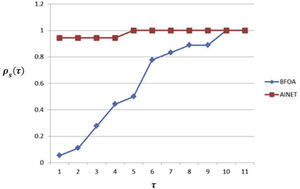
Para el caso de la eficiencia, en la métrica del tiempo empleado por el método de optimización Tˆ, se puede observar en la figura 4 que el método AiNet tuvo un mejor desempeño en contraste con BFOA.
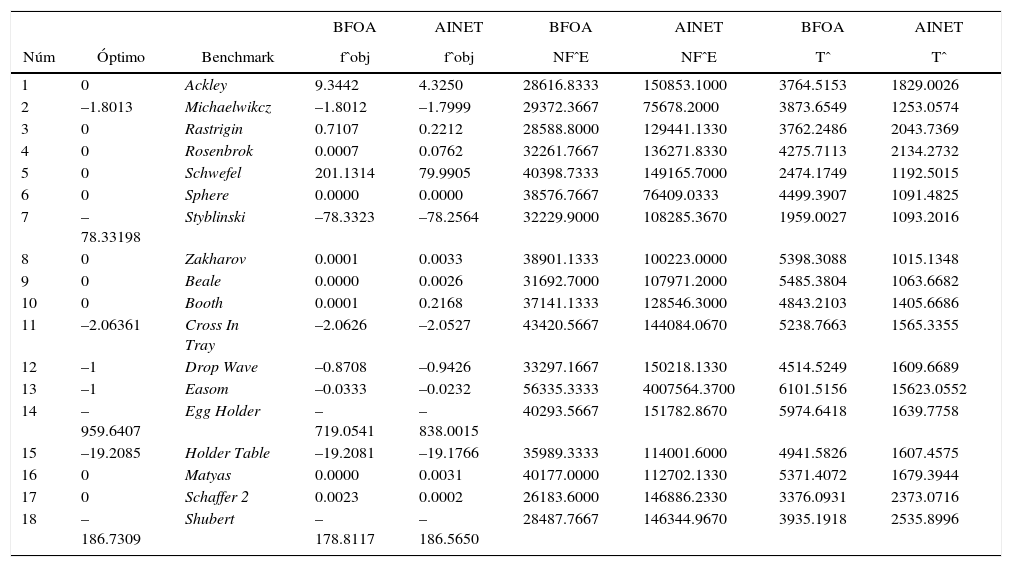
Con el objeto de proporcionar más elementos para el comparativo de estos métodos de optimización, en la tabla 3 se muestran los valores de fˆobj, NFˆE y Tˆ para las dos estrategias de optimización en todos los casos de estudio considerados.
Promedios de las métricas a comparar para los algoritmos BFOA y AiNet
| BFOA | AINET | BFOA | AINET | BFOA | AINET | |||
|---|---|---|---|---|---|---|---|---|
| Núm | Óptimo | Benchmark | fˆobj | fˆobj | NFˆE | NFˆE | Tˆ | Tˆ |
| 1 | 0 | Ackley | 9.3442 | 4.3250 | 28616.8333 | 150853.1000 | 3764.5153 | 1829.0026 |
| 2 | –1.8013 | Michaelwikcz | –1.8012 | –1.7999 | 29372.3667 | 75678.2000 | 3873.6549 | 1253.0574 |
| 3 | 0 | Rastrigin | 0.7107 | 0.2212 | 28588.8000 | 129441.1330 | 3762.2486 | 2043.7369 |
| 4 | 0 | Rosenbrok | 0.0007 | 0.0762 | 32261.7667 | 136271.8330 | 4275.7113 | 2134.2732 |
| 5 | 0 | Schwefel | 201.1314 | 79.9905 | 40398.7333 | 149165.7000 | 2474.1749 | 1192.5015 |
| 6 | 0 | Sphere | 0.0000 | 0.0000 | 38576.7667 | 76409.0333 | 4499.3907 | 1091.4825 |
| 7 | –78.33198 | Styblinski | –78.3323 | –78.2564 | 32229.9000 | 108285.3670 | 1959.0027 | 1093.2016 |
| 8 | 0 | Zakharov | 0.0001 | 0.0033 | 38901.1333 | 100223.0000 | 5398.3088 | 1015.1348 |
| 9 | 0 | Beale | 0.0000 | 0.0026 | 31692.7000 | 107971.2000 | 5485.3804 | 1063.6682 |
| 10 | 0 | Booth | 0.0001 | 0.2168 | 37141.1333 | 128546.3000 | 4843.2103 | 1405.6686 |
| 11 | –2.06361 | Cross In Tray | –2.0626 | –2.0527 | 43420.5667 | 144084.0670 | 5238.7663 | 1565.3355 |
| 12 | –1 | Drop Wave | –0.8708 | –0.9426 | 33297.1667 | 150218.1330 | 4514.5249 | 1609.6689 |
| 13 | –1 | Easom | –0.0333 | –0.0232 | 56335.3333 | 4007564.3700 | 6101.5156 | 15623.0552 |
| 14 | –959.6407 | Egg Holder | –719.0541 | –838.0015 | 40293.5667 | 151782.8670 | 5974.6418 | 1639.7758 |
| 15 | –19.2085 | Holder Table | –19.2081 | –19.1766 | 35989.3333 | 114001.6000 | 4941.5826 | 1607.4575 |
| 16 | 0 | Matyas | 0.0000 | 0.0031 | 40177.0000 | 112702.1330 | 5371.4072 | 1679.3944 |
| 17 | 0 | Schaffer 2 | 0.0023 | 0.0002 | 26183.6000 | 146886.2330 | 3376.0931 | 2373.0716 |
| 18 | –186.7309 | Shubert | –178.8117 | –186.5650 | 28487.7667 | 146344.9670 | 3935.1918 | 2535.8996 |
Es de notar el valor de la métrica fˆobj para el caso de las funciones de optimización Schewfel y EggHolder para los algoritmos de optimización, donde se observa una diferencia que contrasta con el resto de los experimentos. Los parámetros de atracción y repulsión en el caso del algoritmo BFOA son determinantes y para este estudio todos los experimentos se realizaron con valores propuestos en la literatura, pero pueden ajustarse con base en el juicio (Dasgupta et al., 2009). En este sentido, para el caso de la métrica que corresponde al número de funciones evaluadas NFˆE, destaca el resultado del algoritmo AiNet para la función de optimización Easom, donde considerablemente el algoritmo realiza un esfuerzo computacional mayor que BFOA. De acuerdo con la literatura, el parámetro de umbral de similitud puede ajustarse para problemas específicos (Brownlee, 2011). En cuanto al tiempo empleado por el método de optimización, la métrica Tˆ describe dicha característica para los casos de estudio. Destaca el algoritmo AiNet haciendo uso de menos tiempo en todos los experimentos excepto el correspondiente al de la función Easom, que como es de esperarse y en congruencia con la métrica NFˆE presenta mayor tiempo de ejecución.
ConclusionesEste trabajo describe la aplicación del método BFOA y AiNet en comparativa, empleando el modelo de perfil de comportamiento numérico (Dolan, 2002) para un conjunto de conocidas funciones benchmark. Los resultados obtenidos indican que el método AiNet (Castro, 2002) es más robusto que el método BFOA (Passino, 2010) para los casos de estudio considerados en este trabajo. Sin embargo, existen diferencias en la eficiencia (número de funciones evaluadas y tiempo de convergencia) entre ambos métodos. Donde BFOA es el algoritmo con mejor desempeño en cuanto al número de funciones evaluadas.
Con base en los resultados obtenidos, para futuras aplicaciones de los algoritmos aquí descritos se hacen los siguientes contrastes:
El algortimo AiNet tuvo mejor desempeño en términos globales en comparación con BFOA, pero debe señalarse el caso de la función benchmark Easom, en la que AiNet tuvo particularmente dificultades. Esto aparentemente se debe a que la naturaleza de su estrategia basada en clonación puede ser ineficiente en la región plana del espacio de búsqueda, donde el algoritmo “parece perderse”, se recomienda observar la gráfica del espacio de búsqueda Easom. Esto debe tomarse en cuenta para futuras aplicaciones.
En el caso de la función benchmark Schwefel, los dos algoritmos tuvieron resultados alejados del óptimo esperado, donde BFOA fue el peor. Al observar la gráfica del espacio de búsqueda destacan los múltiples mínimos locales. Tal parece que ambos algoritmos tienen dificultades en un escenario de tal complejidad. Se recomienda hacer una sintonización no basada en los default para el parámetro de umbral de afinidad respecto a AiNet y los parámetros de atracción/repulsión (d_attr, w_attr, h_rep, w_rep) respecto a BFOA.
Ernesto Ríos-Willars. Es participante del programa de doctorado en Biotecnología de la Universidad Autónoma de Coahuila. Su trabajo se refiere al área de optimización y metaheurísticas en bioinformática.
Ernesto Liñán-García. Doctorado en ciencias computacionales, maestro en sistemas computacionales e ingeniero en sistemas electrónicos. Su línea de investigación es sobre la aplicación de metaheurísticas aplicadas a problemas NP-Hard, especialmente plegamiento de proteínas, alineamiento de secuencias ADN y ruteo de vehículos.
Rafael Batres. Profesor investigador en la Escuela de Ingeniería y Ciencias del Tecnológico de Monterrey. Las áreas de investigación incluyen: métodos computacionales para el diseño de productos, síntesis de procesos, cadenas de suministro, ingeniería de ontologías, razonamiento basado en casos, optimización meta-heurística, reutilización de modelos matemáticos, minería de datos, modelado basado en agentes y simulación dinámica.