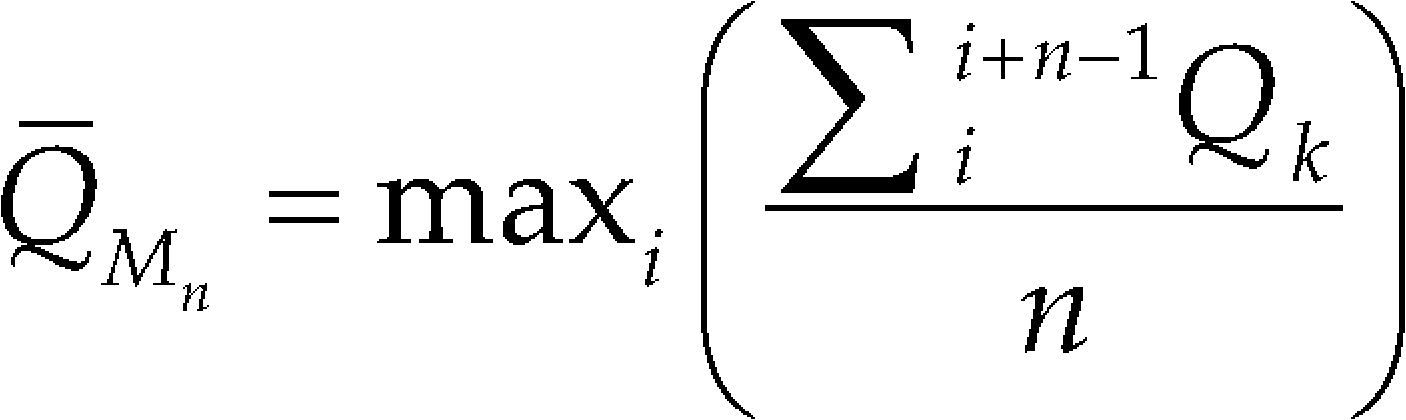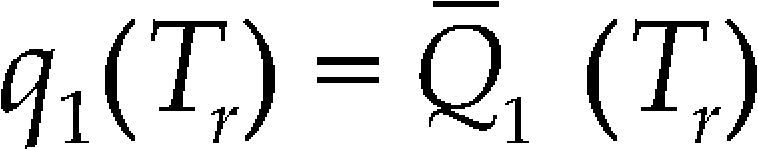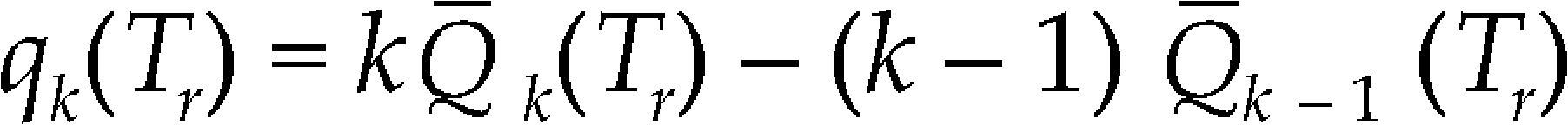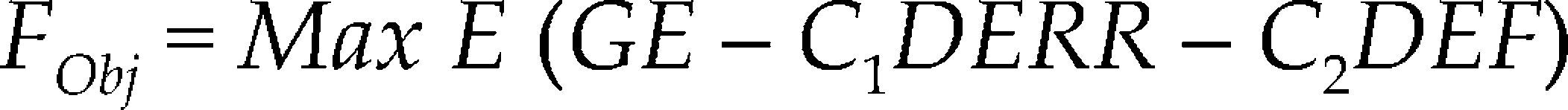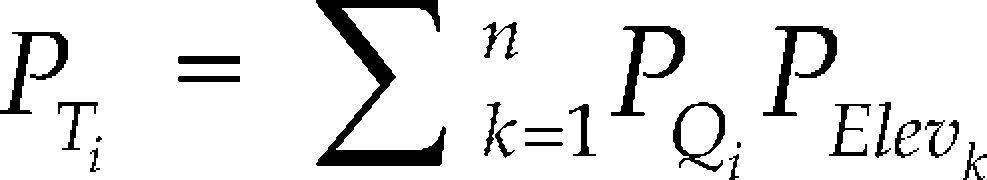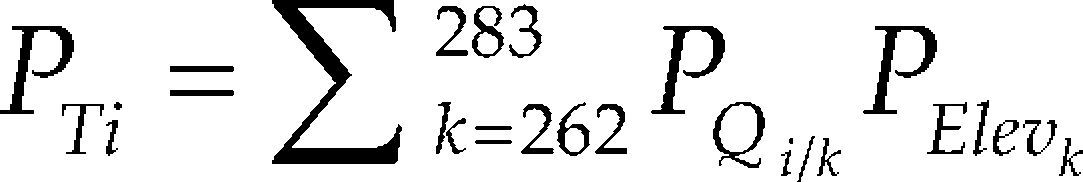La práctica común para evaluar el riesgo de inundaciones aguas abajo de una presa consiste en obtener las avenidas de diseño para diversos periodos de retorno y simular su tránsito por el vaso de acuerdo con las reglas de operación de la obra de excedencias, suponiendo que dichas avenidas se presentan cuando el nivel en el vaso se encuentra en el nivel máximo de operación (NAMO). En este trabajo se presenta una metodología para evaluar el riesgo de inundaciones aguas abajo de una presa tomando en cuenta que, cuando se presentan las avenidas de diseño, el nivel en el vaso es una variable aleatoria que depende de la política de operación a largo plazo de la presa. Para la aplicación de la metodología propuesta se utiliza el caso de la presa Cerro Prieto, situada en el estado de Nuevo León en México; se presentan primero los métodos usados para la estimación de las avenidas asociadas a distintos periodos de retorno, así como para la definición de la política de operación a largo plazo de la presa, de manera que al simular con esta última el funcionamiento de la presa se deducen las probabilidades asociadas al nivel en el embalse durante la época de avenidas. Al simular el tránsito de las avenidas asociadas a cada periodo de retorno se obtienen las probabilidades condicionales asociadas a los gastos máximos de descarga, para finalmente estimar el riesgo de inundaciones aguas abajo de la presa. La metodología propuesta permite obtener resultados precisos del riesgo de inundación sin sobrestimar costos.
The common practice to assess the flooding risk downstream of a dam is to obtain design floods for different return periods and simulate their transit through the reservoir according to the operation rules of the spillway, assuming that those floods occur when the level in the reservoir is in the normal water level (NWL). This paper presents a methodology for assessing the flooding risk downstream of a dam considering that the level in the reservoir when the design flood is presented, is a random variable that depends on the long-term operation policy of the dam. For the application of the proposed methodology Cerro Prieto Dam is used, located in Nuevo Leon state in Mexico, the methods used for estimating floods associated to different return periods and for defining the long-term operation policy of the dam are presented first; therefore, simulating the dam operation based in that policy, the probabilities associated with the reservoir level during flood period are deducted. When simulating flood routing associated to each return period, conditional probabilities associated with the maximum discharge flow are obtained, and finally the flooding risk downstream of the dam can be estimated. The proposed methodology allows estimate accurate flood risk results without overestimating costs.
El problema para determinar la política de operación óptima a largo plazo en un sistema de presas ha sido el tema de numerosas investigaciones y publicaciones en los últimos años.
Rebolledo (1990) analiza la “Operación óptima de un sistema hidráulico formado por dos presas en paralelo”; Avilés (1994) la “Optimación en línea de presas hidroeléctricas”; Contreras (1999) la “Operación óptima de sistema de presas en cascada”; Arganis (2004) estudió la “Operación óptima de un sistema de presas en cascada para generación hidroeléctrica tomando en cuenta condiciones reales de operación y el uso de muestras sintéticas para el pronóstico”.
Sánchez y Wagner (2003) presentan la “Determinación de reglas de operación óptima para dos embalses, utilizando un algoritmo genético” y en 2004 el “Modelo numérico para la operación óptima de un hidrosistema de aguas superficiales”.
En particular, la operación óptima del sistema de presas del río Grijalva ha sido objeto de estudio. Al respecto, Domínguez et al. (1993) plantean el problema de determinar políticas de operación mensual que maximizan una función objetivo que toma en cuenta la generación de energía a largo plazo y que procura evitar derrames y déficit; Domínguez et al. (1998) complementan el estudio de 1993, definen políticas de extracción trabajando el sistema de presas La Angostura y Malpaso, en función del almacenamiento final del mes previo en ambas presas; Domínguez y Mendoza (2000) hacen una revisión del funcionamiento y operación de las presas del río Grijalva; Domínguez et al. (2001) adaptaron el modelo de optimación de políticas de extracciones del sistema de presas, considerando el valor relativo de la energía “de pico” respecto a la “de base”, incorporando restricciones de energía mínima propuesta por la Comisión Federal de Electricidad (CFE); Domínguez et al. (2006) generó nuevas políticas de operación, que toman en cuenta los eventos hidrológicos ocurridos en 2005.
Por otra parte, Dittmann et al. (2008), proponen un funcionamiento dinámico a largo plazo mediante el uso de algoritmos evolutivos, demostrando que el estado de funcionamiento dinámico es superior a la regla de operación estática.
Vigyan (1997) realizó el planteamiento de tres curvas guía de operación para la presa de Tawa en India, las cuales se ajustan a las diversas demandas y propósitos del embalse.
Pradhan y Tripathy (2013) optimizan la operación del embalse multipropósito de Hirakud (India), empleando un algoritmo genético reflejando la eficiencia de los resultados.
Sin embargo, en estos trabajos no se considera explícitamente el efecto que producen las políticas obtenidas en el riesgo de inundaciones aguas abajo de las presas, por lo que este trabajo se enfoca al análisis de las políticas de operación en los embalses considerando el riesgo asociado a las afectaciones aguas abajo de las presas.
MetodologíaExisten diversos criterios para determinar las avenidas que se emplean en el diseño de una obra de excedencias, sin embargo, cualquier metodología que se use para tal fin debe cumplir tres aspectos:
- 1.
Que considere la correlación pico-volumen.
- 2.
Que permita reproducir avenidas similares a las observadas en el periodo de registro.
- 3.
Que conduzca a la definición de distintos tipos de avenidas que, en cada caso, podrán modificar los resultados según las características del vaso en donde se transiten.
La metodología propuesta consiste de los siguientes pasos:
a) Análisis de los registrosA fin de garantizar la confiabilidad de los registros (ya sean horarios, diarios o mensuales) se analiza la congruencia de los mismos, revisando que no se presenten errores de captura, que puedan afectar significativamente el desarrollo del análisis.
b) Avenidas de diseñoEl procedimiento utilizado permite estimar la forma de la avenida de diseño a partir del análisis de los gastos medios diarios históricamente registrados. Para ello se determinan los gastos medios máximos anuales para distintas duraciones. El gasto medio máximo para una duración de 1 día corresponde al gasto medio diario máximo anual. Para obtener los gastos medios máximos para las otras duraciones se procede a encontrar para cada año de registro el promedio máximo para n días consecutivos según la duración que se analice:
donde
Q¯Mn =gasto medio máximo para n días de duración
Qk = gasto medio diario el día k
n = duración en días
i = contador del día en que inicia el lapso de duración n
De esta forma, para cada valor de duración (1, 2, ..., n) se cuenta con una muestra de m valores de gastos máximos anuales, a los que se puede ajustar una función de distribución. Las funciones de distribución ajustadas (una para cada duración) permiten estimar la avenida (sintética) de diseño para cualquier periodo de retorno (Tr).
La construcción de curvas del tipo Gasto-Duración-Periodo de retorno de los eventos extrapolados permite observar su comportamiento, tomando en cuenta que la tendencia que se obtiene para periodos de retorno menores o iguales que el número de años de registro debe conservarse para periodos de retorno mayores, de manera que si esto no ocurre, deben revisarse las extrapolaciones.
Corroborando lo anterior, es necesario pasar de las avenidas sintéticas a avenidas reales. Para ello, con cada periodo de retorno que se seleccione, primero se convierten los gastos medios asociados a distintas duraciones en gastos medios diarios mediante las ecuaciones recursivas
donde
Q¯k(Tr) = gasto medio estimado para una duración de k días y un periodo de retorno Tr
qk(Tr) = gasto medio diario, m3/s
Finalmente, los gastos medios diarios qk(Tr), cuya secuencia tiene una tendencia decreciente, deben reordenarse para tomar la forma de un hidrograma histórico representativo, una forma sencilla de hacer el ordenamiento es el uso del método de bloques alternos, en el que al centro de la avenida se coloca el gasto individual de un día; hacia adelante se coloca el gasto de dos días, hacia atrás del gasto del centro se coloca el de tres días y así, se van colocando el de cuatro días hacia adelante, el de cinco días hacia atrás, hasta construir la forma de la avenida.
c) Operación óptimaCon la finalidad de mejorar la operación de la presa en estudio, se optimiza la misma, asignando diversos tipos de restricciones y penalizaciones, ya sea por derrame o déficit de agua; para ello, se integran los registros en intervalos quincenales con la finalidad de realizar su análisis en políticas a largo plazo. Lo anterior, a manera de repartir el volumen en intervalos semejantes durante todo el año considerando la época de avenidas y de estiaje. Partiendo del volumen útil de la presa, se define el número de estados que contendrá cada uno de los grupos conformados.
Con dichos grupos, mediante el empleo de la programación dinámica estocástica se determinan los máximos beneficios esperados en un horizonte de planeación de N etapas que lleven a la definición de políticas de operación óptima, para todos los posibles estados iniciales y extracciones de una presa.
Para llevar a cabo la optimización se emplea como función objetivo la maximización del valor esperado del beneficio total por generación, imponiendo penalizaciones por déficit o derrames en la presa.
donde
E () =operador valor esperado
GE =energía generada, GWh
DERR =derrame, hm3
DEF =déficit, hm3
C1 =coeficiente de penalización por derrame
C2 =coeficiente de penalización por déficit
Partiendo de dicha optimización, se efectúa la simulación analítica del vaso, comparando los niveles obtenidos respecto a los históricos.
d) Tránsito de avenidasComo resultado del funcionamiento de vaso optimizado, se obtienen los niveles más frecuentes en el embalse (histograma de elevaciones medias), los cuales serán las condiciones de inicio en el tránsito de las avenidas de diseño, generando un escenario de análisis que parte de niveles asociados a su probabilidad de ocurrencia (PElev).
Se efectúa el tránsito de las avenidas estimadas para 2, 5, 10, 20, 50, 100, 200, 500, 1 000, 2 000, 5 000 y 10 000 años de periodo de retorno y para cada elevación inicial obtenida de la operación optima, así mismo se analiza otro escenario considerando como elevación inicial la del NAMO del embalse.
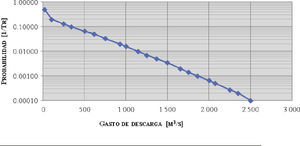
Del resultado de la simulación se obtienen los gastos máximos de descarga, los cuales se asocian a su probabilidad de excedencia (PQ). Con la finalidad de de- terminar gastos máximos de descarga en cifras cerradas (1 000, 2 000, etcétera) se grafican los resultados obtenidos determinando la tendencia a la cual se ajustan, para asociarles su probabilidad de excedencia y periodo de retorno correspondientes.
e) Análisis de la probabilidad de excedencia conjuntaPara determinar la probabilidad de excedencia conjunta asociada al gasto máximo de descarga se realiza la suma total de los productos de cada probabilidad de ocurrencia asociada a la elevación inicial (PElev) por la probabilidad de excedencia (PQ), empleando la formula
donde
PTi = probabilidad de excedencia conjunta para un gasto Qi
PQi = probabilidad de excedencia del gasto Qi dada una elevación inicial k
PElevk = probabilidad de ocurrencia asociada a la elevación inicial k
Como resultado se obtienen tantas probabilidades de excedencia conjunta (PT) como gastos se han analizado, los cuales deberán compararse con los resultados obtenidos, considerando como elevación inicial el NAMO.
f) Tránsito hidráulico por el cauce y costos por afectaciónEmpleando los gastos máximos de descarga seleccionados, se realiza el transito hidráulico por el cauce, aguas abajo del embalse, determinando las áreas afectadas por la inundación.
Dicha área se multiplica por un costo unitario de afectación, determinando los costos asociados a diversas probabilidades de excedencia.
Finalmente, al generar la curva Costos vs Probabilidades de excedencia conjunta, se determina el riesgo esperado, definido por el área bajo la curva, el cual puede compararse con el que se obtuvo, considerando el NAMO como elevación inicial.
AplicaciónAnálisis de los gastos medios mensualesCon la finalidad de validar las avenidas de diseño de la presa Cerro Prieto, se llevó a cabo su actualización partiendo de los registros diarios proporcionados por la Comisión Nacional del Agua (CONAGUA). Para tal efecto, se calcularon las aportaciones al vaso de almacenamiento considerando los ingresos por cuenca propia como la suma del incremento (o decremento) en el almacenamiento (DELTA V)+las salidas medidas (SALIDAS) para el periodo de registro de 1984 a 2009, sin considerar los años de 1995 a 1999 debido a que sus datos son incompletos.
Actualización de las avenidasSe efectuó un análisis probabilístico para el ajuste de los valores medios diarios máximos anuales, mediante el empleo de funciones de distribución de probabilidad, lo cual permitió la obtención de valores extrapolados a diferentes periodos de retorno.
Para realizar los cálculos correspondientes a los ajustes para las diferentes funciones de distribución de probabilidad, se utilizó el programa AX© (1996).
Los registros medios diarios máximos para duraciones de 1 a 15 días (Domínguez y Carlóz, 1981) se analizaron estadísticamente con distintas funciones de dis- tribución, seleccionando la función Doble Gumbel (Gumbel, 1958; Domínguez et al., 2004) como la de mejor ajuste. Para cada duración se determinaron los gastos medios máximos asociados a distintos periodos de retorno (2, 5, 10, 20, 50, 100, 200, 500, 1 000, 2 000, 5 000 y 10 000 años) y se revisó su tendencia mediante la construcción de las curvas gastos-duración-periodo de retorno.
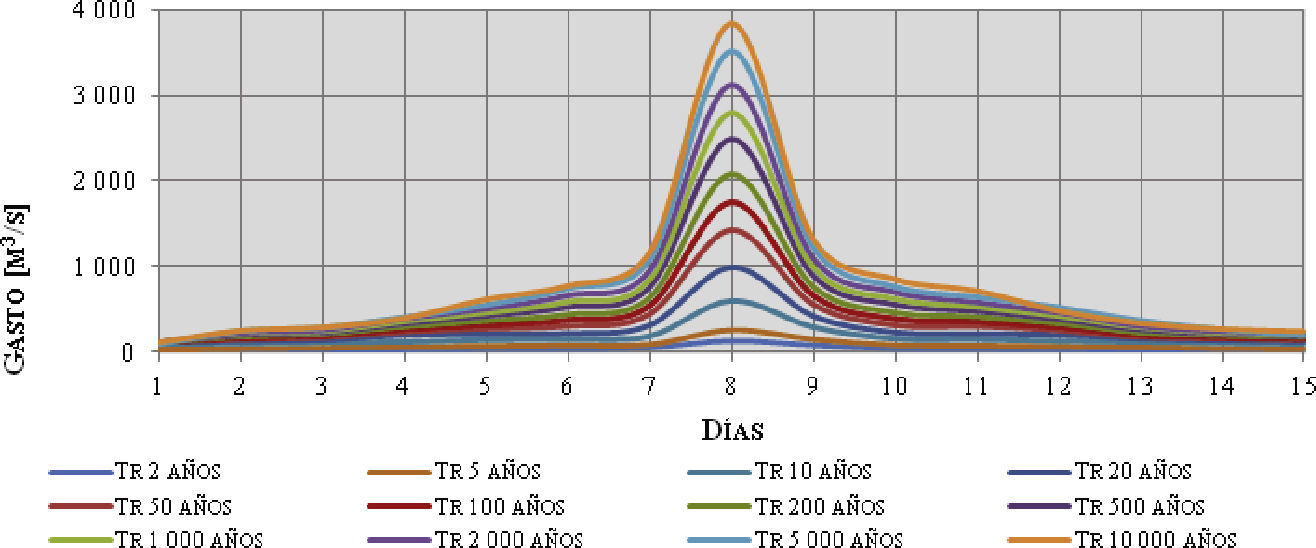
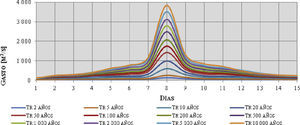
A partir de esos resultados se convirtieron las avenidas sintéticas en reales, determinando la forma de la avenida mediante el método de alternar bloques (Domínguez et al., 1980), en el que a la mitad de la duración total se coloca el valor máximo (Q1), hacia delante se coloca el gasto (Q2), hacia atrás el gasto (Q3), y así sucesivamente. Los resultados obtenidos para las avenidas asociadas a diversos periodos de retorno se aprecian de manera gráfica en la figura 1.
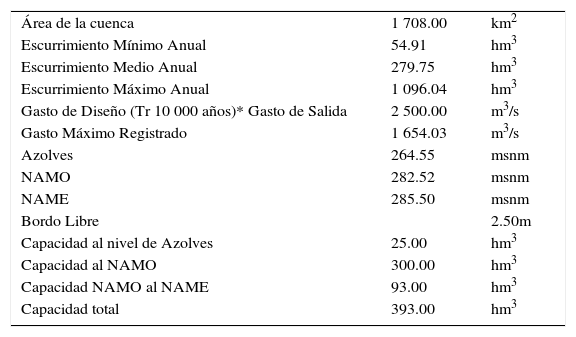
Operación óptimaConsiderando los gastos medios diarios, así como las características del embalse presentadas en la tabla 1, se efectuó la optimización de la operación a largo plazo (Chang y Chang, 2009; Mathur y Nikam, 2009; Kuo et al., 2003). La matriz de escurrimientos para la simulación analítica del vaso se construyó para intervalos quincenales.
Características generales
| Área de la cuenca | 1 708.00 | km2 |
| Escurrimiento Mínimo Anual | 54.91 | hm3 |
| Escurrimiento Medio Anual | 279.75 | hm3 |
| Escurrimiento Máximo Anual | 1 096.04 | hm3 |
| Gasto de Diseño (Tr 10 000 años)* Gasto de Salida | 2 500.00 | m3/s |
| Gasto Máximo Registrado | 1 654.03 | m3/s |
| Azolves | 264.55 | msnm |
| NAMO | 282.52 | msnm |
| NAME | 285.50 | msnm |
| Bordo Libre | 2.50m | |
| Capacidad al nivel de Azolves | 25.00 | hm3 |
| Capacidad al NAMO | 300.00 | hm3 |
| Capacidad NAMO al NAME | 93.00 | hm3 |
| Capacidad total | 393.00 | hm3 |
Por otra parte, para repartir el volumen medio anual en intervalos semejantes durante todo el año (considerando la época de avenidas y de estiaje), se definieron seis grupos de meses, los cuales se conforman en la tabla 2.
Tomando en cuenta el volumen útil de la presa (275,00 hm3) se determinó repartirlo en 50 estados compuestos por 5.5 hm3 cada uno. Se definieron las frecuencias absolutas de los volúmenes de escurrimiento correspondientes a cada estado y cada grupo de meses definidos en la tabla 2; las frecuencias relativas se obtuvieron dividiendo las frecuencias absolutas entre el total de años de la muestra, y se consideraron como una primera aproximación a las probabilidades asociadas a los ingresos.
Al hacer la gráfica de las frecuencias relativas contra el intervalo de volúmenes se observaron discontinuidades, por lo que se suavizaron repartiendo el volumen y cuidando mantener la forma general, obligando a que la suma sea igual a 1.
Con los resultados obtenidos de las frecuencias relativas suavizadas, se desarrolló la simulación de la operación óptima del embalse, obtenida mediante la programación dinámica estocástica (Mendoza, 2010).
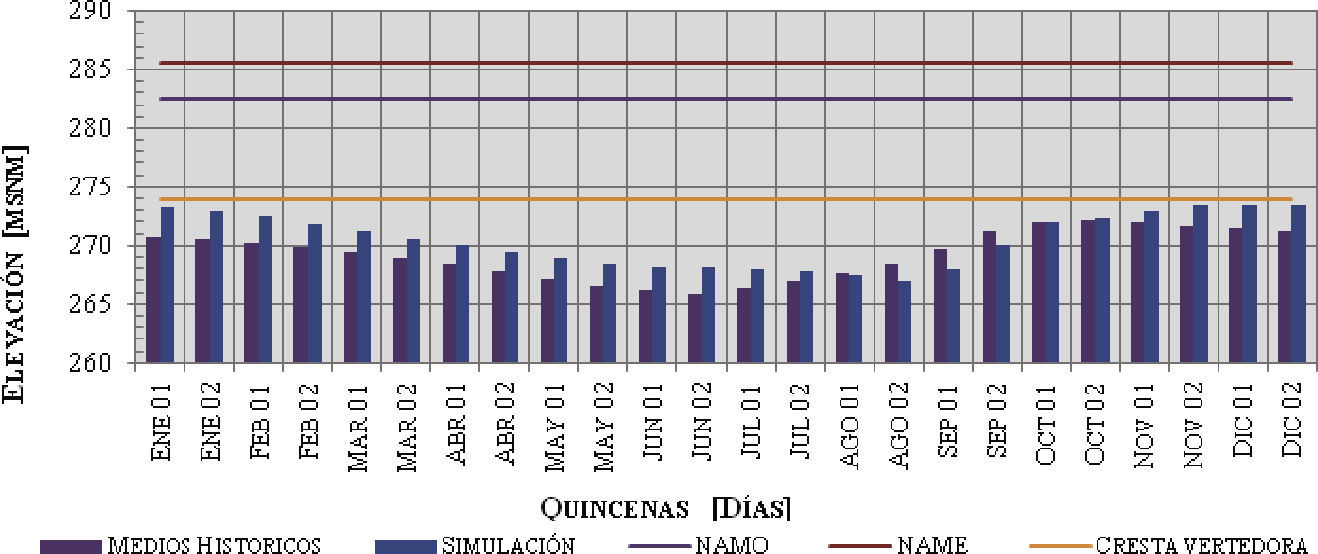
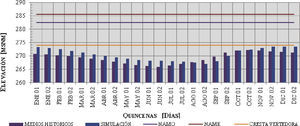
El resumen anual de los niveles obtenidos de la simulación de la política de operación óptima se presentan en la figura 2, en particular, los niveles medios quincenales en el embalse se comparan con los históricos. Como se puede apreciar en la figura 2, la política de operación obtenida de la simulación, conserva los niveles por arriba del régimen medio histórico (con lo que se incrementa la generación), sin llegar al nivel máximo de operación (NAMO).
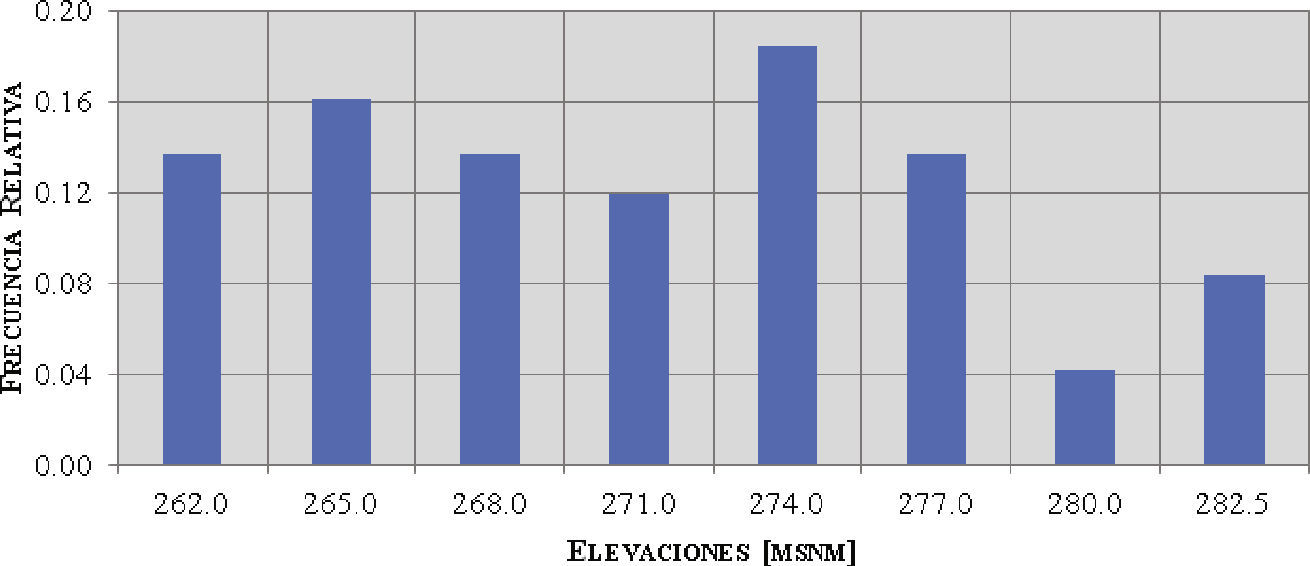
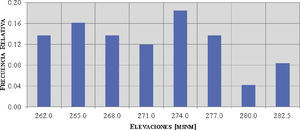
Partiendo de los niveles en el embalse obtenidos en la simulación, se elaboró el histograma de frecuencias relativas de las elevaciones para los meses de agosto a noviembre (considerándolos como el periodo de avenidas). Como resultado, se conformó la figura 3, que presenta dichas frecuencias relativas para intervalos de clase de 3 m (para el último intercalo se consideró la cota del NAMO, es decir, la elevación 282.52 msnm).
Tránsito de avenidasSe llevó a cabo la simulación del tránsito de avenidas considerando diferentes niveles iniciales en el embalse, con la finalidad de obtener la magnitud del gasto máximo de descarga correspondiente.
Para la simulación del tránsito de las avenidas, se empleó la curva Elevaciones-Capacidades del embalse, así como la curva Elevaciones-Gastos del vertedor.
Para el análisis de los tránsitos de avenidas se realizó la simulación mediante el programa: “Tránsito de una avenida por un vaso” (Marengo et al., 2005). Para tal efecto se consideraron dos escenarios posibles:
- 1.
Partiendo como elevación inicial de la cota del NAMO (282.52 msnm).
- 2.
Tomando como elevaciones iniciales las correspondientes a los ocho niveles más frecuentes obtenidos de la simulación analítica del embalse (figura 3).
Las avenidas de entrada al vaso son las que se presentan en la figura 1, las cuales corresponden a los periodos de retorno de 2, 5, 10, 20, 50, 100, 200, 500, 1 000, 2 000, 5 000 y 10 000 años.
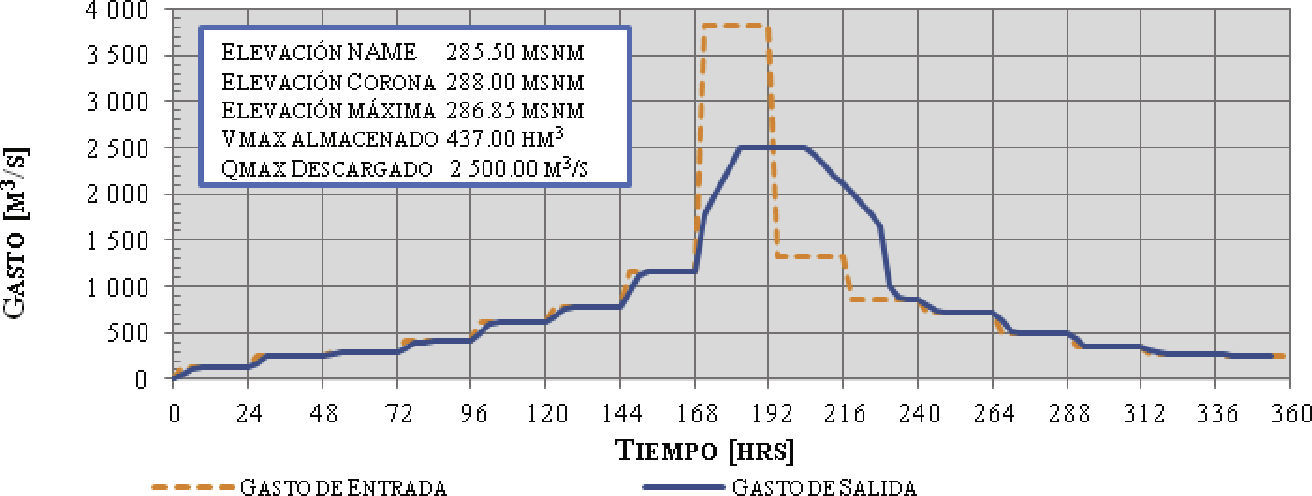
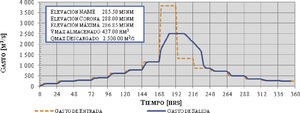
Escenario 1 – Nivel Inicial 282,52 msnm (NAMO)Se realizaron las simulaciones correspondientes al tránsito de avenidas; a continuación se presentan los resultados de la simulación realizada para el caso de la avenida 10 000 años de periodo de retorno (figura 4).
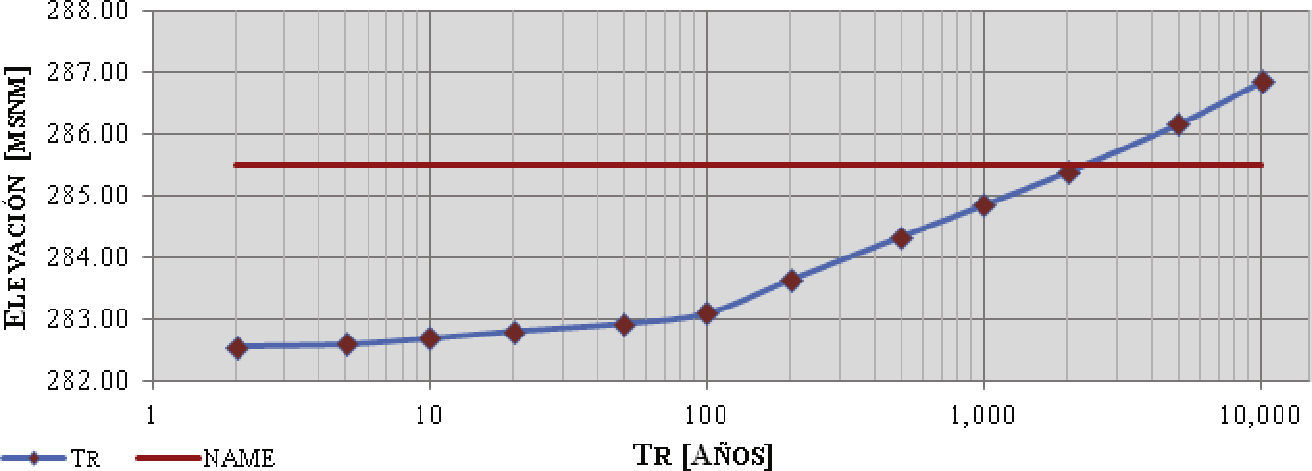
De la figura 4 se aprecia que para avenidas con periodos de retorno de 10 000 años, la máxima elevación lograda es de 286.85 msnm por lo que el nivel alcanzado quedaría 1.35 m sobre el NAME (285.50 msnm).
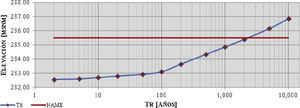
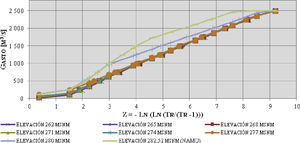
El análisis descrito se realizó del mismo modo para cada una de las avenidas asociadas a diversos periodos de retorno, en la figura 5 se grafican los periodos de retorno (años) respecto a las elevaciones máximas alcanzadas en el embalse, para mostrar la tendencia de los resultados.
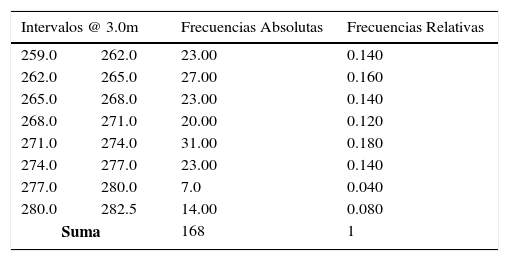
Escenario 2 – Niveles medios más frecuentes en el embalseSe elaboró el análisis de las avenidas simulando su tránsito partiendo de diversos niveles iniciales en el embalse, para ello se empleó el histograma de niveles (figura 3) obtenido de la optimización de la política de operación del embalse. De dicho histograma se obtuvieron como resultado siete niveles más frecuentes en el embalse (tabla 3), cuyas frecuencias relativas corresponderán a las probabilidades de ocurrencia a ser analizadas.
Frecuencias de niveles en el embalse
| Intervalos @ 3.0m | Frecuencias Absolutas | Frecuencias Relativas | |
|---|---|---|---|
| 259.0 | 262.0 | 23.00 | 0.140 |
| 262.0 | 265.0 | 27.00 | 0.160 |
| 265.0 | 268.0 | 23.00 | 0.140 |
| 268.0 | 271.0 | 20.00 | 0.120 |
| 271.0 | 274.0 | 31.00 | 0.180 |
| 274.0 | 277.0 | 23.00 | 0.140 |
| 277.0 | 280.0 | 7.0 | 0.040 |
| 280.0 | 282.5 | 14.00 | 0.080 |
| Suma | 168 | 1 | |
Empleando los niveles iniciales de la tabla 3 y las avenidas de diseño de la figura 3, se realizaron los tránsitos de estas por el embalse, como se describe a continuación:
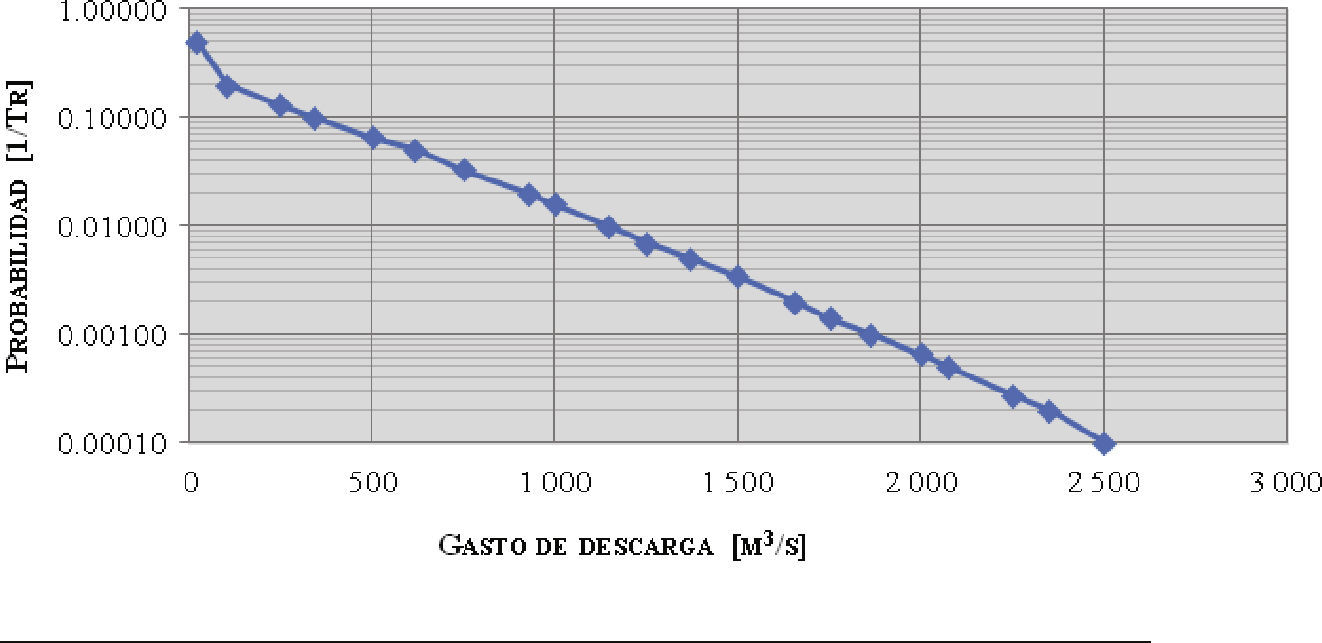
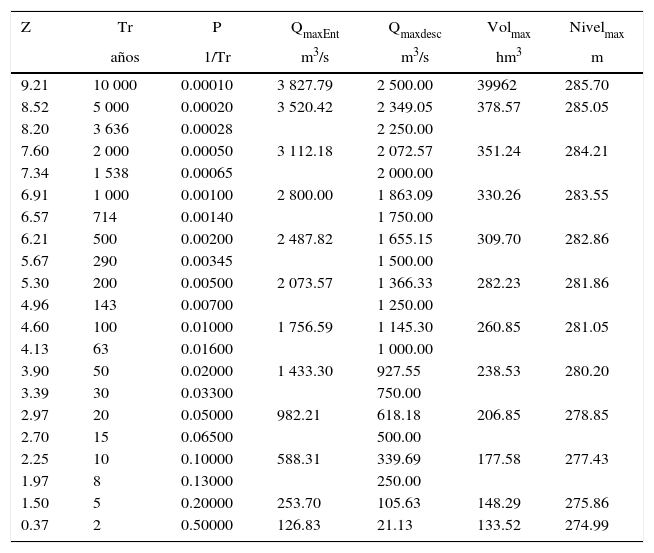
Nivel inicial 262 msnmPartiendo de la elevación inicial a la cota 262.00 msnm, se realizaron las simulaciones del tránsito de las avenidas para los periodos de retorno desde 2 hasta 10 000 años, determinando su gasto máximo de descarga, volumen máximo en el embalse, así como la elevación máxima alcanzada (tabla 4). Para definir la probabilidad de excedencia de los gastos máximos de descarga considerando valores de 250 a 2 500 m3/s, se realizó una interpolación entre los resultados obtenidos, asignándoles su correspondiente periodo de retorno, como se muestra en la tabla 4 y la figura 6.
Resultados de los tránsitos de avenida-Nivel inicial 262 msnm
| Z | Tr | P | QmaxEnt | Qmaxdesc | Volmax | Nivelmax |
|---|---|---|---|---|---|---|
| años | 1/Tr | m3/s | m3/s | hm3 | m | |
| 9.21 | 10 000 | 0.00010 | 3 827.79 | 2 500.00 | 39962 | 285.70 |
| 8.52 | 5 000 | 0.00020 | 3 520.42 | 2 349.05 | 378.57 | 285.05 |
| 8.20 | 3 636 | 0.00028 | 2 250.00 | |||
| 7.60 | 2 000 | 0.00050 | 3 112.18 | 2 072.57 | 351.24 | 284.21 |
| 7.34 | 1 538 | 0.00065 | 2 000.00 | |||
| 6.91 | 1 000 | 0.00100 | 2 800.00 | 1 863.09 | 330.26 | 283.55 |
| 6.57 | 714 | 0.00140 | 1 750.00 | |||
| 6.21 | 500 | 0.00200 | 2 487.82 | 1 655.15 | 309.70 | 282.86 |
| 5.67 | 290 | 0.00345 | 1 500.00 | |||
| 5.30 | 200 | 0.00500 | 2 073.57 | 1 366.33 | 282.23 | 281.86 |
| 4.96 | 143 | 0.00700 | 1 250.00 | |||
| 4.60 | 100 | 0.01000 | 1 756.59 | 1 145.30 | 260.85 | 281.05 |
| 4.13 | 63 | 0.01600 | 1 000.00 | |||
| 3.90 | 50 | 0.02000 | 1 433.30 | 927.55 | 238.53 | 280.20 |
| 3.39 | 30 | 0.03300 | 750.00 | |||
| 2.97 | 20 | 0.05000 | 982.21 | 618.18 | 206.85 | 278.85 |
| 2.70 | 15 | 0.06500 | 500.00 | |||
| 2.25 | 10 | 0.10000 | 588.31 | 339.69 | 177.58 | 277.43 |
| 1.97 | 8 | 0.13000 | 250.00 | |||
| 1.50 | 5 | 0.20000 | 253.70 | 105.63 | 148.29 | 275.86 |
| 0.37 | 2 | 0.50000 | 126.83 | 21.13 | 133.52 | 274.99 |
El procedimiento descrito se aplicó considerando los niveles iniciales a las cotas 265, 268, 271, 274, 277, 280 y 282,52 (NAMO).
Resumen general de los resultados obtenidos para diversos niveles iniciales
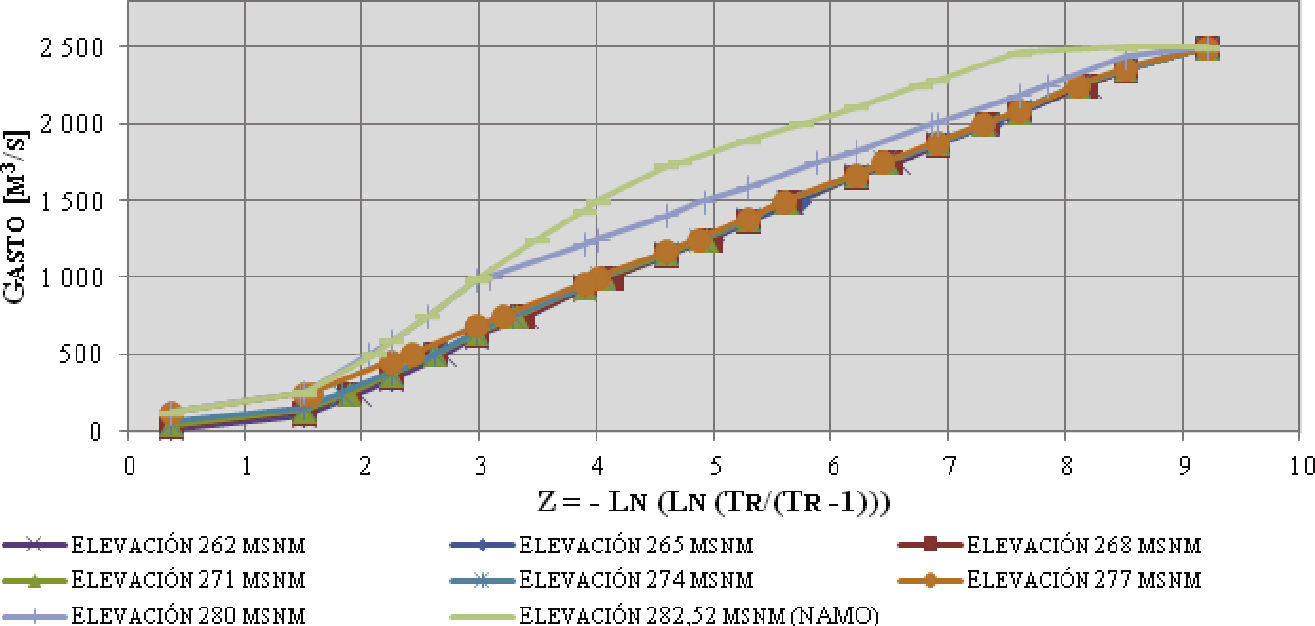
A continuación, en la figura 7, se presenta el análisis gráfico de las distribuciones de probabilidad de los gastos máximos de descarga para los diversos niveles iniciales estudiados.
Análisis de la probabilidad de excedencia conjuntaEn el escenario número dos se describieron los resultados obtenidos del tránsito de las avenidas ante diversos niveles iniciales. Al considerar las probabilidades de excedencias obtenidas para cada gasto de descarga con la probabilidad de ocurrencia correspondiente a cada elevación inicial (PElev), se determinó la probabilidad de excedencia conjunta (PT).
Para ello, se llevó acabo en cada gasto, entre 250 y 2 500 m3/s la suma del producto de la probabilidad asociada a cada nivel inicial (PElev) por la probabilidad de excedencia del gasto correspondiente (PQ/Elev), es decir:
Donde PTi es la probabilidad conjunta de excedencia asociada al gasto máximo de descarga Qi; PElev es la probabilidad de que el tránsito se inicie en la elevación k, y PQi/k la probabilidad de que el gasto máximo de descarga sea mayor o igual que Qi dada la elevación inicial k.
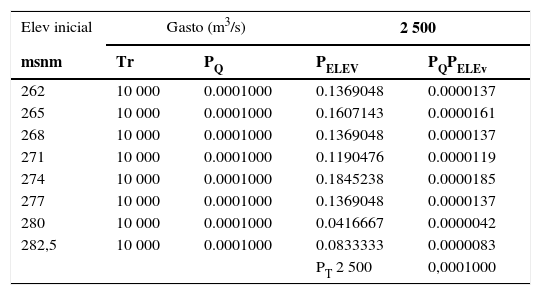
A continuación, en la tabla 5 se presentan las probabilidades conjuntas obtenidas para cada una de las elevaciones analizadas considerando un gasto de 2 500 m3/s, proceso realizado para cada uno de los gastos presentados en la tabla 6.
Probabilidad de excedencia conjunta para un gasto máximo de descarga de 2 500 m3/s
| Elev inicial | Gasto (m3/s) | 2 500 | ||
|---|---|---|---|---|
| msnm | Tr | PQ | PELEV | PQPELEv |
| 262 | 10 000 | 0.0001000 | 0.1369048 | 0.0000137 |
| 265 | 10 000 | 0.0001000 | 0.1607143 | 0.0000161 |
| 268 | 10 000 | 0.0001000 | 0.1369048 | 0.0000137 |
| 271 | 10 000 | 0.0001000 | 0.1190476 | 0.0000119 |
| 274 | 10 000 | 0.0001000 | 0.1845238 | 0.0000185 |
| 277 | 10 000 | 0.0001000 | 0.1369048 | 0.0000137 |
| 280 | 10 000 | 0.0001000 | 0.0416667 | 0.0000042 |
| 282,5 | 10 000 | 0.0001000 | 0.0833333 | 0.0000083 |
| PT 2 500 | 0,0001000 | |||
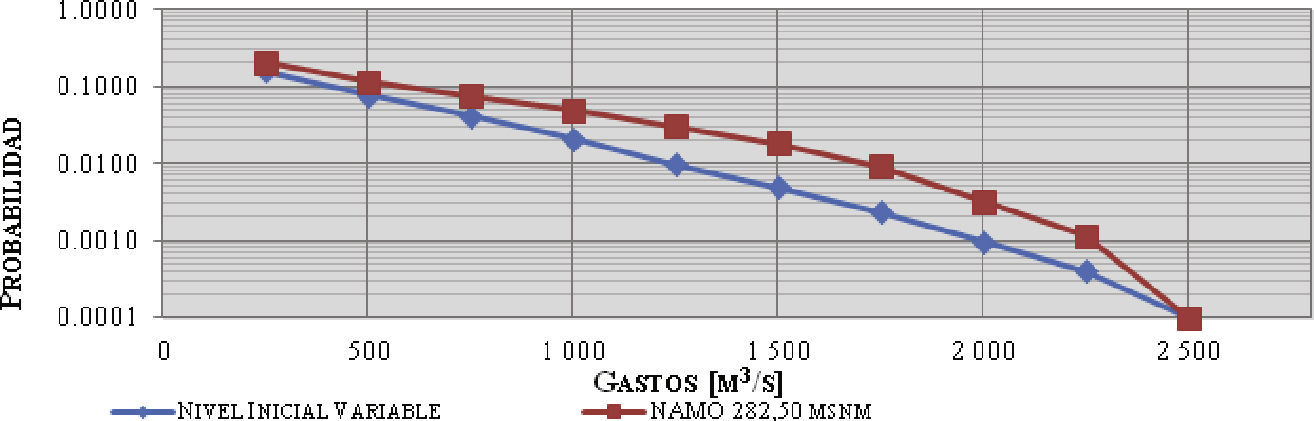
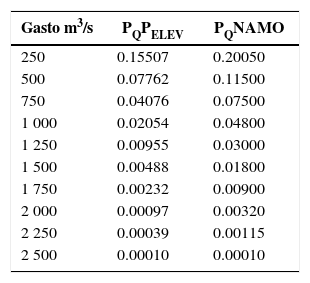
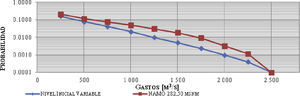
De este análisis se elaboró la tabla 6 y la figura 8, donde se muestra la tendencia de la probabilidad de excedencia conjunta asociada a cada gasto máximo de descarga, comparada con la obtenida considerando el nivel inicial a la elevación del NAMO.
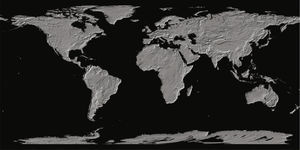
Tránsito hidráulico por el cauceConsiderando los gastos de salida utilizados en el análisis, se procedió a simular su tránsito por el cauce. Para ello, se empleó el modelo digital de elevaciones de la página de ASTER GDEM (2014) (ASTER Global Digital Elevation Model) con una resolución de 20 metros en el plano vertical y de 30 metros en plano horizontal (figura 9), con el cual se efectuó el análisis en el área comprendida entre el vertedor de la presa Cerro Prieto hasta 90km aguas abajo cerca del poblado Cándido Aguilar. Dicha área se delimitó empleando la plataforma Global Mapper ® (2014).
Para llevar a cabo la simulación del tránsito de la avenida por el cauce, el modelo digital de elevaciones se exportó al programa HEC-RAS ® (2014), considerando los distintos gastos analizados, así como las características fisiográficas del cauce.
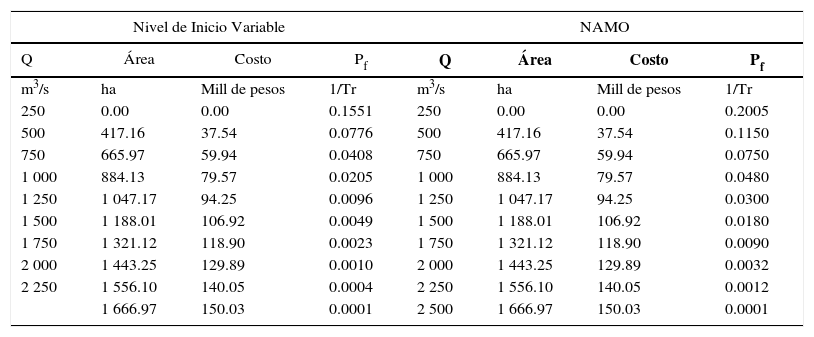
Los resultados obtenidos de la simulación de HEC-RAS, se incorporaron al programa LAMINA ® (2014), que a partir de los niveles del agua logrados por cada sección del cauce determina el área o superficie inundada. En la tabla 7 se presentan las áreas de afectación asociadas a su correspondiente probabilidad de excedencia, para los dos escenarios considerados.
Costo por área de afectación
| Nivel de Inicio Variable | NAMO | ||||||
|---|---|---|---|---|---|---|---|
| Q | Área | Costo | Pf | Q | Área | Costo | Pf |
| m3/s | ha | Mill de pesos | 1/Tr | m3/s | ha | Mill de pesos | 1/Tr |
| 250 | 0.00 | 0.00 | 0.1551 | 250 | 0.00 | 0.00 | 0.2005 |
| 500 | 417.16 | 37.54 | 0.0776 | 500 | 417.16 | 37.54 | 0.1150 |
| 750 | 665.97 | 59.94 | 0.0408 | 750 | 665.97 | 59.94 | 0.0750 |
| 1 000 | 884.13 | 79.57 | 0.0205 | 1 000 | 884.13 | 79.57 | 0.0480 |
| 1 250 | 1 047.17 | 94.25 | 0.0096 | 1 250 | 1 047.17 | 94.25 | 0.0300 |
| 1 500 | 1 188.01 | 106.92 | 0.0049 | 1 500 | 1 188.01 | 106.92 | 0.0180 |
| 1 750 | 1 321.12 | 118.90 | 0.0023 | 1 750 | 1 321.12 | 118.90 | 0.0090 |
| 2 000 | 1 443.25 | 129.89 | 0.0010 | 2 000 | 1 443.25 | 129.89 | 0.0032 |
| 2 250 | 1 556.10 | 140.05 | 0.0004 | 2 250 | 1 556.10 | 140.05 | 0.0012 |
| 1 666.97 | 150.03 | 0.0001 | 2 500 | 1 666.97 | 150.03 | 0.0001 | |
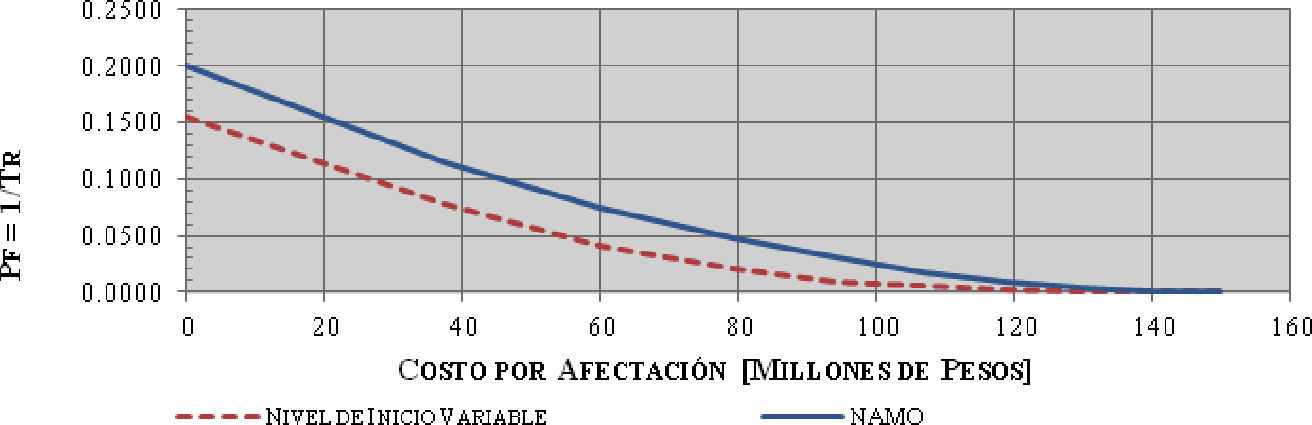
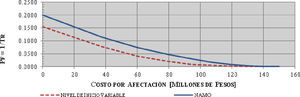
Partiendo de costos por hectárea de afectación obtenidos en el Proyecto Hidroeléctrico Chicoasén II (90 000 pesos en el año 2014), se consideró prudente emplear como ejercicio, un ligero incremento de índice de inflación media de 1% al 2015, correspondiendo a un costo por hectárea de afectación de alrededor de 90 900 pesos; dicho costo se multiplicó por las áreas de afectación (tabla 7), determinando los costos asociados a diversas probabilidades de excedencia (figura 10).
De la figura 10, el costo esperado se determinó como el área bajo las curvas graficadas, cuyo valor se presenta en la tabla 8, en la que se comparan los dos escenarios estudiados.
Análisis y discusión de resultadosLa estimación del riesgo por inundación aguas abajo de una presa se hace tradicionalmente suponiendo que las avenidas de diseño ingresan cuando el nivel en el vaso es el del NAMO, lo que implica una sobrestimación de dicho riesgo. En este trabajo se propone un método que permite obtener una estimación más completa del riesgo de inundaciones aguas abajo de una presa, el cual se aplica a la zona situada aguas abajo de la presa Cerro Prieto.
El desarrollo del método incluye el cálculo de las avenidas de diseño para diferentes periodos de retorno, la definición de la política de operación a largo plazo que hace óptima una función objetivo, el tránsito de las avenidas de diseño - primero por el vaso de la presa y suponiendo distintas elevaciones iniciales y luego por el río -, y la estimación de los daños.
Para el caso de la presa en estudio, se tiene que la avenida de diseño original del embalse (Tr 10 000 años) corresponde a un gasto máximo de salida de 2 500 m3/s. Por otra parte, de la actualización hidrométrica realizada, se obtuvo un gasto máximo de entrada de 3 828 m3/s, sobrepasando por 1 328 m3/s a la capacidad máxima de descarga del diseño original del vertedor. Al realizar la simulación del tránsito de la avenida por el embalse considerando como condición inicial la elevación del NAMO (282.52 msnm), se tiene que la elevación máxima en el embalse es la correspondiente a la cota 286.85 msnm, sobrepasando por 1.35 m al NAME (285.50 msnm), sin embargo no se presenta riesgo por desbordamiento, ya que el nivel máximo queda 1.15 m por debajo de la cota de la corona (288.00 msnm).
Como se puede apreciar en la figura 9 y en la tabla 8, el procedimiento propuesto, que considera los diversos niveles iniciales en el embalse, permite una estimación más precisa del riesgo de inundación aguas abajo de la presa, mientras que el procedimiento tradicional (considerando un nivel inicial a la cota del NAMO) sobrestima los costos del daño por inundación.
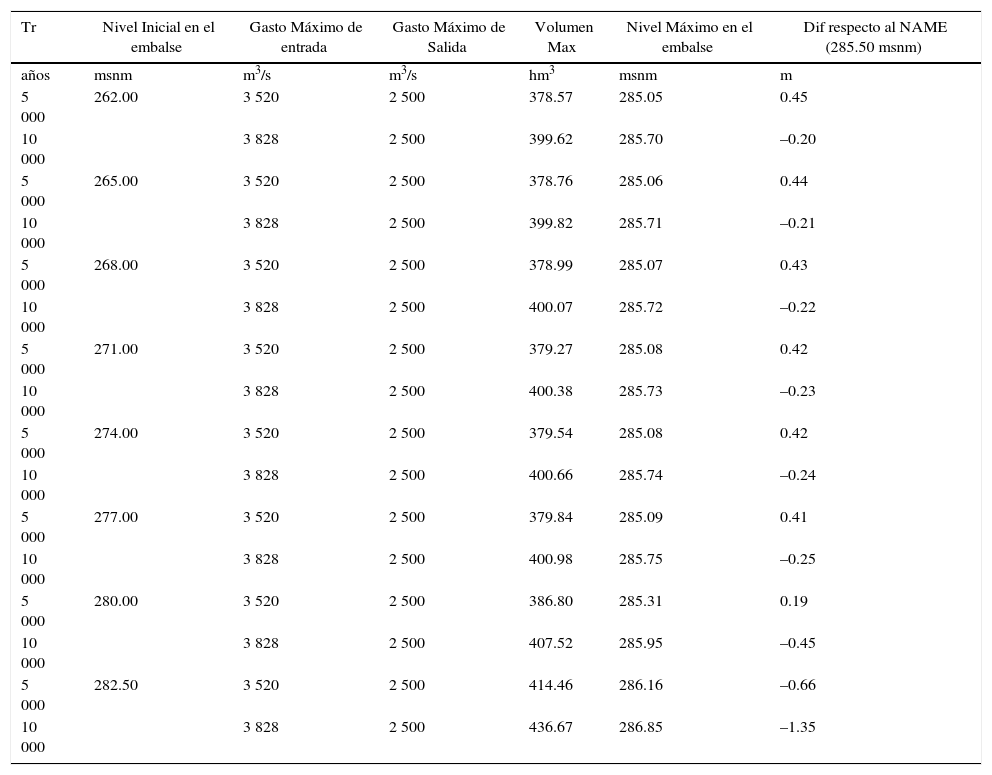
Por otra parte, en la tabla 9 se presenta un resumen de las elevaciones máximas obtenidas del tránsito de avenidas para cada una de las elevaciones más frecuentes empleando las avenidas de 5 000 y 10 000 años de periodo de retorno. De dicha tabla se puede concluir que la obra de excedencias no cuenta con la capacidad de descarga necesaria para desalojar avenidas de más 3 520 m3/s de gasto de entrada (Tr 5 000 años en adelante), comenzando su tránsito a partir de la elevación del NAMO (282.50 msnm) y para avenidas de 3 828 m3/s de gasto de entrada (Tr 10 000 años), comenzado su tránsito bajo cualquier elevación inicial. Por consiguiente, se recomienda considerar la inclusión de una obra de excedencias auxiliar para descargar de manera conjunta las avenidas de 5 000 y 10 000 años de periodo de retorno, con la finalidad de no sobrepasar la cota del NAME.
Tránsitos de avenida-revisión capacidad descarga del vertedor
| Tr | Nivel Inicial en el embalse | Gasto Máximo de entrada | Gasto Máximo de Salida | Volumen Max | Nivel Máximo en el embalse | Dif respecto al NAME (285.50 msnm) |
|---|---|---|---|---|---|---|
| años | msnm | m3/s | m3/s | hm3 | msnm | m |
| 5 000 | 262.00 | 3 520 | 2 500 | 378.57 | 285.05 | 0.45 |
| 10 000 | 3 828 | 2 500 | 399.62 | 285.70 | –0.20 | |
| 5 000 | 265.00 | 3 520 | 2 500 | 378.76 | 285.06 | 0.44 |
| 10 000 | 3 828 | 2 500 | 399.82 | 285.71 | –0.21 | |
| 5 000 | 268.00 | 3 520 | 2 500 | 378.99 | 285.07 | 0.43 |
| 10 000 | 3 828 | 2 500 | 400.07 | 285.72 | –0.22 | |
| 5 000 | 271.00 | 3 520 | 2 500 | 379.27 | 285.08 | 0.42 |
| 10 000 | 3 828 | 2 500 | 400.38 | 285.73 | –0.23 | |
| 5 000 | 274.00 | 3 520 | 2 500 | 379.54 | 285.08 | 0.42 |
| 10 000 | 3 828 | 2 500 | 400.66 | 285.74 | –0.24 | |
| 5 000 | 277.00 | 3 520 | 2 500 | 379.84 | 285.09 | 0.41 |
| 10 000 | 3 828 | 2 500 | 400.98 | 285.75 | –0.25 | |
| 5 000 | 280.00 | 3 520 | 2 500 | 386.80 | 285.31 | 0.19 |
| 10 000 | 3 828 | 2 500 | 407.52 | 285.95 | –0.45 | |
| 5 000 | 282.50 | 3 520 | 2 500 | 414.46 | 286.16 | –0.66 |
| 10 000 | 3 828 | 2 500 | 436.67 | 286.85 | –1.35 |
La metodología propuesta optimiza y mejora la operación de los embalses en diversos puntos, por ejemplo, permite garantizar la confiabilidad de los registros (ya sean horarios, diarios o mensuales).
La optimización de la política de operación en el embalse, preserva los niveles en la presa por encima del régimen medio histórico, incrementando el volumen útil en el embalse para ser empleado según las demandas comprometidas (riego, abastecimiento de agua potable y generación de energía eléctrica), sin superar la cota del NAMO. Al simular el funcionamiento de la presa con los ingresos históricos se estimaron las frecuencias de las elevaciones en el embalse para la época de crecientes.
Como parte del resultado del funcionamiento analítico de vaso optimizado, se obtienen los niveles más frecuentes en el embalse (histograma de elevaciones medias), los cuales serán las condiciones de inicio en el tránsito de las avenidas de diseño generando un escenario de análisis que parte de niveles asociados a su probabilidad de ocurrencia (PElev).
Por otra parte, del tránsito de las avenidas de diseño partiendo de diferentes elevaciones iniciales, se obtuvieron las probabilidades de excedencia (PQ), detallando si la obra de excedencias cuenta con la capacidad de descarga necesaria ante la presencia de ave- nidas máximas sin que el NAME se sobrepase. Lo anterior, permite garantizar la seguridad integral de las obras, guiando al operador a mantener el embalse por debajo un determinado nivel (curva guía), o en su caso, determinando la inclusión de una obra de excedencias auxiliar para preservar que el NAME no se sobrepase.
La parte medular de la presente metodología, consiste en determinar la probabilidad de excedencia conjunta asociada al gasto máximo de descarga, donde se realiza la suma total de los productos de cada probabilidad de ocurrencia asociada a la elevación inicial por la probabilidad de excedencia
Es decir, se define la probabilidad de que una gama de eventos se presente, considerando como otra variable la elevación inicial en el embalse. Lo anterior involucra una condición realista en la presa, ya que convencionalmente se supone que ante cualquier evento la elevación en el embalse es el NAMO.
Para traducir los gastos máximos de descarga de la probabilidad de excedencia conjunta en afectaciones, se realiza el tránsito hidráulico por el cauce aguas abajo del embalse, determinando las llanuras de inundación, cuya área es multiplicada por el costo unitario de afectación, determinando los costos asociados a diversas probabilidades de excedencia.
Con los resultados obtenidos se genera la curva Costos vs Probabilidades de excedencia conjunta, donde el área bajo la curva determina el riesgo esperado, que representa el costo total esperado.
Se puede concluir, que al emplear la metodología propuesta, se refleja un ahorro sustancial en los daños esperados, al comparar los costos obtenidos bajo un nivel inicial variable respecto a un análisis convencional realizado bajo el NAMO, en donde el último sobrestima los costos.
Citación estilo Chicago
Citación estilo ISO 690
Sadoth Fabián Huerta-Loera. Es maestro en ingeniería civil con especialización en hidráulica por la Universidad Nacional Autónoma de México (UNAM), asimismo ingeniero civil especializado en estructuras. Actualmente estudia el doctorado en ingeniería civil con especialización en obras hidráulicas en la UNAM.
Ramón Domínguez-Mora Es egresado de la Facultad de Ingeniería de la UNAM, donde obtuvo también su maestría y doctorado. Se desempeña como investigador titular en el Instituto de Ingeniería, así como profesor en posgrado con las materias de hidrología y aprovechamientos hidráulicos. Ha realizado numerosos trabajos en los campos de la hidrología, la hidrología urbana y los aprovechamientos hidráulicos.