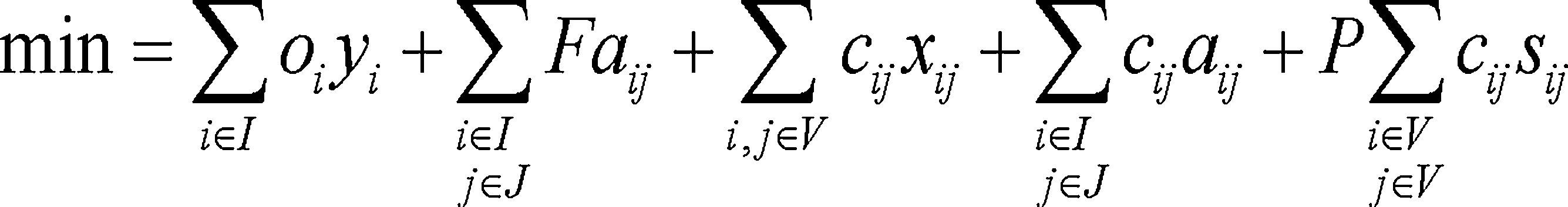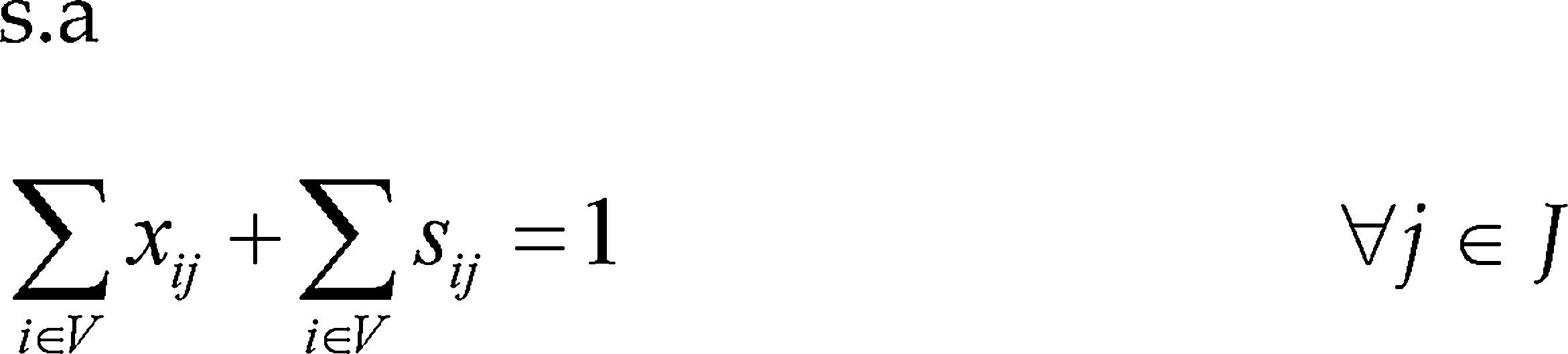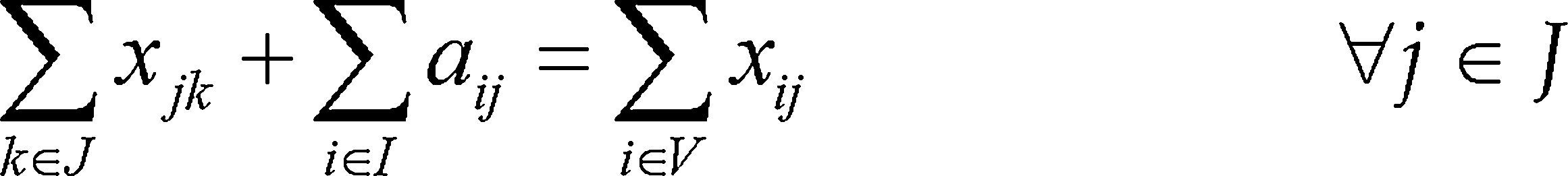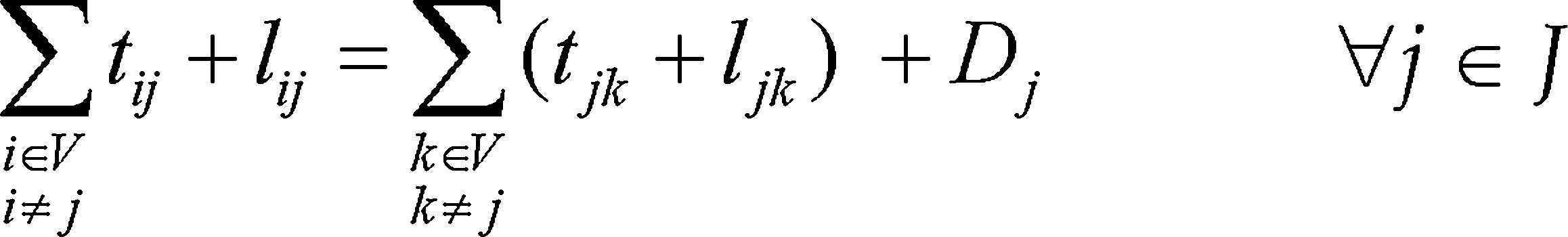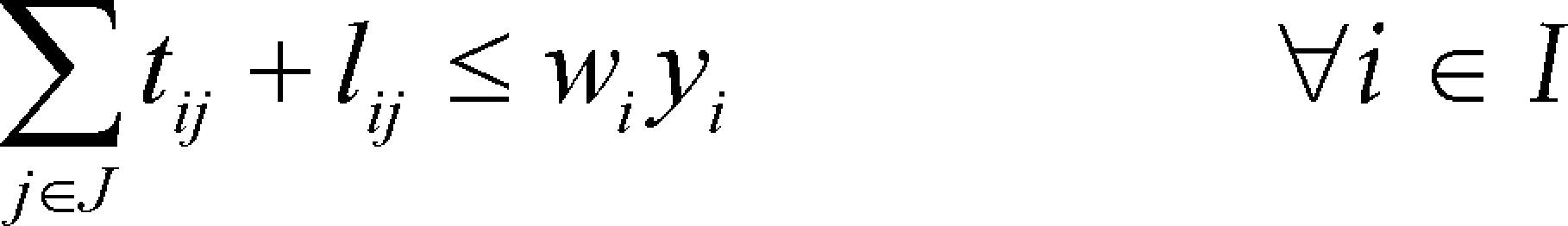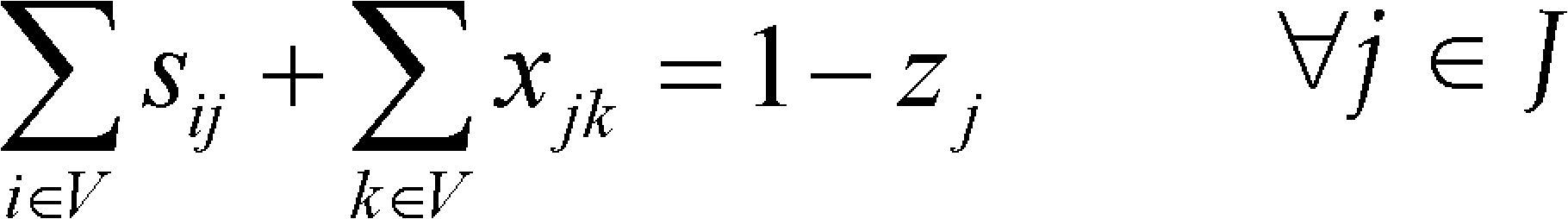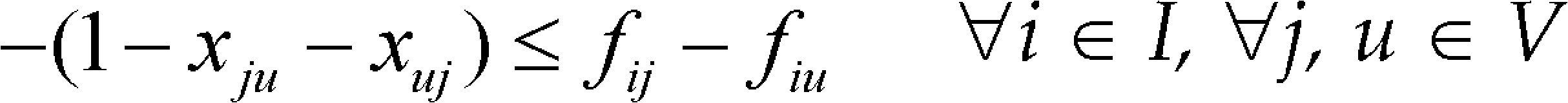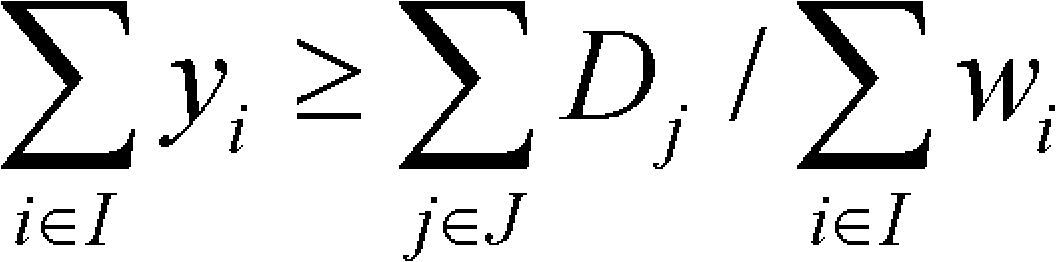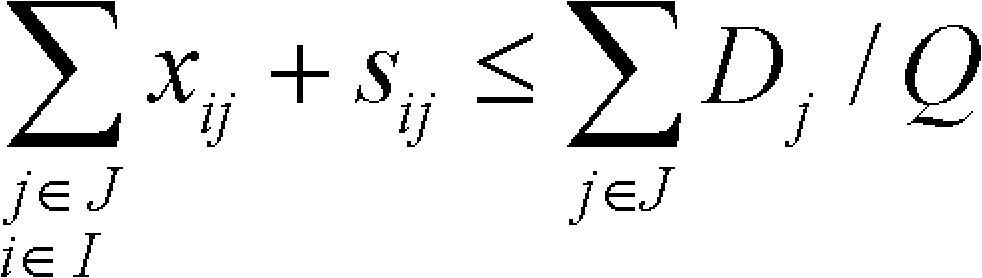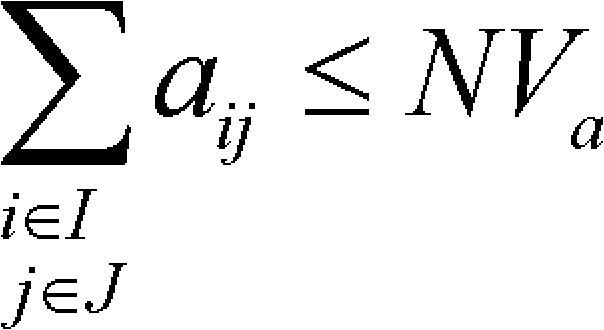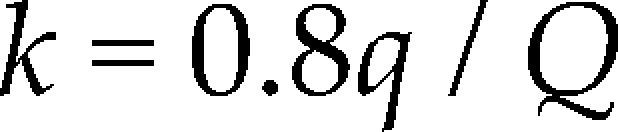El problema de localización y ruteo con restricciones de capacidad (CLRP) consiste en la selección de depósitos y rutas para atender un conjunto de clientes para obtener el mínimo costo. Una variante de este problema, en la que se considera existe la posibilidad de subcontratar la operación de algunas (o todas) las rutas, es el problema de localización y ruteo con flota propia y flota subcontratada (CLRPPC). Este problema aparece cuando la flota propia es insuficiente para atender la totalidad de la demanda, o una parte de los vehículos de la flota propia debe atender actividades de mantenimiento y reparación. El objetivo del CLRPPC es minimizar los costos de apertura de los centros de distribución (CD), el costo de uso de los vehículos propios y los costos variables asociados a la utilización de las rutas recorridas por la flota propia o por la flota subcontratada. En este artículo se presenta un nuevo modelo matemático para el CLRPPC, en el que las restricciones clásicas para evitar los sub-tours se reemplazan por un conjunto de restricciones que establecen conexiones radiales entre los clientes y los depósitos, permi- tiendo resolver de forma exacta instancias de la literatura especializada usando solvers comerciales. El modelo además puede adaptarse para resolver el problema de ruteo atendido con flota propia y subcontratada (VRPPC) y con múltiples depósitos (MDVRPPC). Los modelos se validan con instancias de la literatura especializada, donde los resultados demuestran que la formulación propuesta permite obtener resultados satisfactorios para estos tres tipos de problemas a pesar de su alta complejidad matemática.
The Capacitated Location Routing Problem (CLRP) consists in the selection of depots and routes to serve all the clients such that the minimum cost is obtained. A variant of this problem, where it is considered that there is the possibility of outsourcing the operation of some (or all) routes, is the location routing problem with private fleet and common carrier (CLRPPC). This problem is presented when the own fleet is insufficient to serve the whole demand or part of its own fleet must have maintenance and repairing activities. The CLRPPC objective is to minimize the costs of opening distribution centers (DC), the cost for using their own vehicles and the variable costs associated with the use of the routes traveled by their own fleet or an outsourced fleet. This paper presents a new mathematical model for CLRPPC, where the classical restrictions to prevent sub-tours are replaced by a set of constraints that establish the radio links between customers and depots, solving accurately instances used in the literature using commercial solvers. Moreover, the model can be adapted to solve the Vehicle Routing Problem with Private Fleet and Common Carrier (VRPPC) and Multi-Depot Vehicle Routing Problem with Private Fleet and Common Carrier (MDVRPPC). The models are validated with instances of the literature, where the results show that the proposed formulation gives satisfactory results for these three types of problems despite its high mathematical complexity.
Conjunto de los centros de distribución.
Conjunto de los clientes.
Conjunto de nodos.
Capacidad del centro de distribución i.
Máxima carga que el vehículo puede transportar.
Demanda en unidades del cliente ubicado en el nodo j.
Costo de viajar entre el nodo i y el nodo j.
Número de vehículos disponibles.
Factor de penalización aplicado a cada arco que es transitado usando un Vehículo subcontratado.
Costo fijo asociado a cada vehículo propio utilizado en la operación.
Costo de apertura del centro de distribución i.
Variable binaria que se activa cuando el arco entre los nodos i y j se recorre por un vehículo de la flota propia.
Variable binaria que se activa cuando el arco entre los nodos i y j se recorre usando un vehículo subcontratado.
Variable binaria que indica la construcción del centro de distribución ubicado en el nodo i.
Variable binaria que define si el cliente ubicado en el nodo j se atiende por una ruta que inicia en el centro de distribución i.
Variable binaria que determina si el cliente ubicado en el nodo j es el último atendido en la ruta.
Variable binaria que indica si un vehículo utiliza trayectoria j- para volver desde el final de su recorrido (en el nodo j) a un centro de distribución (en el nodo i).
Variable continua que indica la cantidad de carga transportada por un vehículo de la flota propia entre los nodos i y j.
Variable continua que indica la cantidad de carga transportada por un vehículo de la flota subcontratada entre los nodos i y j.
La subcontratación es una práctica comercial por la que muchas empresas apuestan debido a la necesidad de eficiencia en sus procesos operacionales, medidos a través de la calidad y oportunidad en la entrega de sus productos o servicios. Esta práctica se produce porque no se cuenta con una flota propia de vehículos o porque la flota disponible es inadecuada para satisfacer la demanda de sus clientes. Por lo tanto, la empresa se obliga a contratar parte o la totalidad de la distribución de sus productos con empresas especializadas en la entrega de mercancías.
Cuando se atiende completamente la demanda de los clientes con una flota subcontratada aparece el problema de ruteo abierto, Open Vehicle Routing Problem (OVRP). En este problema una flota de vehículos subcontratados ubicados en el centro de distribución (CD) se asigna a las rutas y los vehículos no se obligan a retornar al CD. Las aplicaciones de esta variante del problema de ruteo “Vehicle routing problem” (VRP) aparecen en la distribución de periódicos y paquetes, rutas escolares, rutas aéreas que no retornan a sus puntos de partida tal como se documenta en Li et al., 2007.
El VRPPC inicialmente propuesto, consideró múltiples vehículos (Chu, 2005), aquí se considera una flota propia de vehículos con capacidad limitada y costos fijos de uso por vehículo. Un conjunto de clientes con demanda conocida se pueden atender por la flota propia, donde se incurre en costos de utilización de los arcos, tal como se contempla en el problema de ruteo con restricciones de capacidad, Capacitated Vehicle Routing problem (CVRP) y los clientes restantes se atienden por una flota subcontratada. Muchas otras aplicaciones de logística y cadenas de suministro utilizan una gran flota de vehículos y operan desde diferentes CDs. Stenger et al. (2013) extienden el problema a considerar con múltiples CDs y proponen el MDVRPPC, donde para cada cliente se decide con qué tipo de flota debe atenderse y a qué depósito debe asignarse.
En este trabajo se presenta una variante de la que no se tiene reporte en la literatura hasta la fecha, la cual se ha denominado problema de localización y ruteo con flota propia y flota subcontratada, Capacitated Location Routing Problem with Private Fleet and Common Carrier (CLRPPC). Este problema consiste en atender a todos los clientes de tal manera que se determinen los siguientes aspectos de forma simultánea: ¿Qué centros de distribución se deben abrir de un conjunto de CDs candidatos?, ¿Cómo asignar los clientes a los CDs abiertos?, identificar a los clientes que se atenderán con los vehículos propios y subcontratados, determinando la secuencia de visita de las rutas, tanto las que se atienden con la flota propia como con la flota subcontratada y todo a un costo mínimo.
Al tener en cuenta que las rutas servidas por la flota propia comienzan y terminan en un CD que se abre, y las rutas atendidas por la flota subcontratada comienzan en un CD de la empresa y terminan el recorrido con el último cliente se tiene que CLRPPC considera la soluciones de varios sub-problemas de forma simultánea:
- 1.
El problema de localización de centros de distribución, Facility Location Problem (FLP).
- 2.
Asignación de clientes a los depósitos.
- 3.
El problema de ruteo capacitado (CVRP).
- 4.
El problema de ruteo abierto aplicado a los clientes que no se atendieron con la flota de vehículos propia (OVRP).
Lo anterior hace que el problema sea de muy alta complejidad computacional debido a que los problemas CVRP, OVRP, FLP y asignación se consideran NP-duros de forma separada, además, la red del problema se duplica al considerarse la opción de recorrer un arco por una ruta propia o por una ruta subcontratada.
En este artículo se presentan tres contribuciones. En primer lugar se propone el CLRPPC como un problema interesante para aplicaciones reales formulado como un problema de programación lineal entera mixta. En segundo lugar las restricciones de eliminación de sub-tours se sustituyen por un conjunto de restricciones que garantizan conexión entre los clientes y depósitos a través de trayectorias radiales, permitiendo que se puedan usar solvers comerciales para resolver de forma exacta problemas de hasta 50 clientes con un gap inferior a 5%. En tercer lugar, el modelo propuesto se puede adaptar a otras variantes del problema de ruteo de vehículos considerando flota propia y subcontratada tales como VRPPC, y MDVRPPC. Finalmente, el modelo se verifica con sistemas de prueba tomados de la literatura especializada, obteniéndose resultados de buena calidad.
Estado del arteLa entrega de mercancías y servicios desde los centros de distribución a los clientes, es un problema importante y práctico dentro de la gestión logística. Cuando se presentan fluctuaciones de la demanda relacionada con aumentos inesperados de la misma que hacen que la flota propia de vehículos sea incapaz de atenderla, se considera el uso de flota subcontratada. Con base en ello, aparecen en la literatura del VRP variantes como VRPPC y MDVRPPC.
VRPPCLos problemas de ruteo considerando flota propia y subcontratada no son comunes en la literatura. Ball et al. (1983), realiza una de las primeras aproximaciones y considera el problema de planeación de la flota de vehículos, la cual debe hacer recorridos largos para realizar las entregas de mercancías a un conjunto de clientes. El estudio se motivó por la observación de una empresa comercial que debía hacer entregas a una gran cantidad de clientes, por tanto, fue necesario considerar el recorrido de las rutas usando la flota propia o subcontratando el servicio de transporte con una empresa externa. La solución del problema consiste en determinar el tamaño óptimo de la flota de forma que se atiendan las rutas sin exceder las restricciones de tiempo de las mismas y asignado las rutas a los vehículos. Se formula el problema, se describen algunas soluciones aproximadas y se discuten aspectos de la implementación.
Klincewicz et al. (1990), plantean la decisión del tamaño y composición de la flota de vehículos que debe atender a los clientes como una decisión estratégica que debe tomarse de forma periódica, donde se determina si se mantiene la flota propia o se emplea una empresa externa de entrega de mercancías. También se considera el uso de una combinación de ambas opciones para determinar el tamaño de la flota propia y la asignación específica a cada sector. El modelo considera una área geográfica dividida por sectores con demandas diarias aleatorias y atendidas por un único CD. Los costos considerados incluyen costos fijos y variables (por milla) de los envíos a través de los vehículos propios o subcontratados. La pieza central de la metodología de solución consiste en la formulación de un FLP con un único depósito, en la cual cada cliente (sector) se atiende por un CD.
Chu (2005), denomina el problema como de camión propio y camión subcontratado (truckload and a less-than truck load carrier) donde propone un modelo matemático lineal entero binario, el cual resuelve casos hasta de 25 clientes y una heurística que modifica el algoritmo de ahorros propuesto por Clarke and Wright (1964), adicionándole una fase de mejoramiento.
En Bolduc et al. (2007) efectúan una propuesta de dos soluciones iniciales diferentes, las cuales se mejoran con sofisticadas estrategias de intercambio de clientes. Bolduc et al. (2008), presentan una metaheurística con procedimientos de perturbación más robustos que combina aleatoriedad, mejoramiento y perturbación. Esta metaheurística realiza una búsqueda local descendente basada en diferentes estructuras de vecindad con dos estrategias de diversificación: un procedimiento aleatorio constructivo y un mecanismo de perturbación basado en estrategias de intercambio de clientes. La metodología se valida sobre instancias donde se considera flota homogénea y heterogénea.
Côté y Potvin (2009), desarrollaron una heurística basada en Búsqueda Tabú y encadenamiento de trayectorias. La integración de estos mecanismos permite encontrar mejores respuestas, particularmente para las instancias heterogéneas propuestas por Bolduc et al. (2008). El vecindario del encadenamiento de trayectorias tiene la propiedad de modificar la asignación de clientes entre la flota propia y la flota subcontratada.
Potvin y Naud (2011), proponen una heurística basada en Búsqueda Tabú con encadenamiento de trayectorias. Para su análisis, se emplearon instancias homogéneas y heterogéneas, obteniendo mejoramiento en las soluciones, sin embargo, los tiempos computacionales son significativamente más altos que los reportados en Bolduc et al. (2008).
Liu y Zhibin (2012), denominan el VRPPC como: close-open vehicle routing problem (COMVRP), considerando en la solución del problema rutas abiertas y rutas cerradas. El objetivo del problema es minimizar los costos fijos y variables de los dos tipos de rutas. Plantean un modelo matemático lineal entero mixto y un algoritmo memético para resolver el problema. Reportan resultados computacionales sobre las instancias de Augerat et al. (1998), adaptadas a las condiciones del problema. El modelo matemático se implementó en CPLEX 12.2 con un límite de tiempo de 48 horas para las instancias entre 32 y 50 clientes, reportan GAPs de 20% en promedio. El algoritmo memético propuesto se compara con los valores encontrados con CPLEX para instancias desde 32 clientes hasta 361 clientes, reportando GAPs de 0.3 a 13.88%.
Kratica et al. (2012), denominan el problema como de selección de ruteo y tercerización (routing and carrier selection problem). En este problema el objetivo es minimizar todos los costos, los cuales constan de tres partes: costos fijos debido al uso de los vehículos de la flota propia, costos variables de cada vehículo y costo de los trayectos realizados por la flota subcontratada. Presentan una heurística basada en un marco de búsqueda genética, donde se ordenan los clientes que no se atendieron por la flota propia, de acuerdo con sus distancias, ya que a través de ellas se orienta la búsqueda en el espacio de soluciones, al aplicar operadores genéticos de selección, recombinación y mutación. Validan la metodología con instancias homogéneas y heterogéneas tomadas de Bolduc et al. (2008).
MDVRPPCChu et al. (2007), consideran una variante multi-centro de distribución del VRPPC, donde se realizan entregas y recepciones simultáneamente a los clientes, pero no presentan de forma especifica cuáles se atienden por la flota subcontratada, aquí se propone un modelo matemático y una heurística simple, que se validan con instancias hasta de 10 clientes y 2 centros de distribución documentadas en el artículo.
Stenger et al. (2013), presentan un problema de ruteo que sucede en las entregas finales, donde los trayectos son inferiores a 1 milla y las cargas son pequeños paquetes, el cual se denomina: problema de ruteo multi-centro de distribución con flota propia y subcontratada, Multi-Depot Vehicle Routing Problem with Private Fleet and Common Carrier (MDVRPPC), se presenta como una extensión del problema de ruteo con múltiples centros de distribución, donde los clientes se pueden atender por la flota propia situada en los centros de distribución de la empresa o por vehículos subcontratados. En este trabajo se desarrolla un algoritmo basado en intercambios de vecindario cíclico que incorporan un mecanismo adaptativo, considerando una etapa aleatoria de perturbación. Los estudios computacionales se realizan sobre dos conjuntos de instancias desarrolladas por los autores. El primer conjunto de instancias se conforma por 55 casos entre 5 y 20 clientes con tres centros de distribución propios y cuatro centros de distribución subcontratados. El segundo conjunto de instancias es una adaptación de 33 instancias tomadas de Cordeau et al. (1998).
CLRPPCEl problema de localización y ruteo considerando restricciones de capacidad atendida con flota propia y flota subcontratada, es una área de interés que se con- sidera como nueva línea de investigación (Prodhon, 2014). Este caso se puede observar cuando el nivel de actividades aumenta, como en la industria de servicios, donde aparecen de forma reiterada actividades como el mantenimiento y reparación de la flota de vehículos, que hacen que la flota no sea suficiente para atender la demanda de los clientes. Esta situación también se presenta en la logística de desastres, donde la demanda desborda la capacidad de atención con los recursos disponibles. De acuerdo con la revisión de la literatura, es un problema que inicia su estudio.
Modelo matemático propuesto para el clrppcPara el CLRPPC se tienen las siguientes consideraciones: Se cuenta con un conjunto I de CDs candidatos a abrirse, un conjunto de clientes J con demanda conocida que se deben servir; una flota propia de vehículos homogénea de tamaño k, insuficiente para atender la demanda de los clientes. La red asociada al problema consta de dos grafos completos, el primero asociado a los arcos recorridos por las rutas propias y el segundo a las subcontratadas, bajo las siguientes consideraciones:
- a)
Un vehículo de la flota propia sirve una sola ruta que comienza y termina en el CD.
- b)
Cada cliente se visita una sola vez, ya sea por un vehículo de la flota propia o por un vehículo subcontratado.
- c)
La demanda total en cada ruta servida por el vehículo k no debe exceder su capacidad Q.
- d)
Cada vehículo de la flota subcontratada realiza solo una ruta r.
- e)
Los despachos desde el depósito i no deben exceder su capacidad Wi.
- f)
Para el CLRPPC, la suma de los costos incluye, costos fijos de apertura de los centros de distribución, costos fijos de los vehículos propios y costos asociados a los arcos recorridos bien sea por la flota propia o por la flota subcontratada.
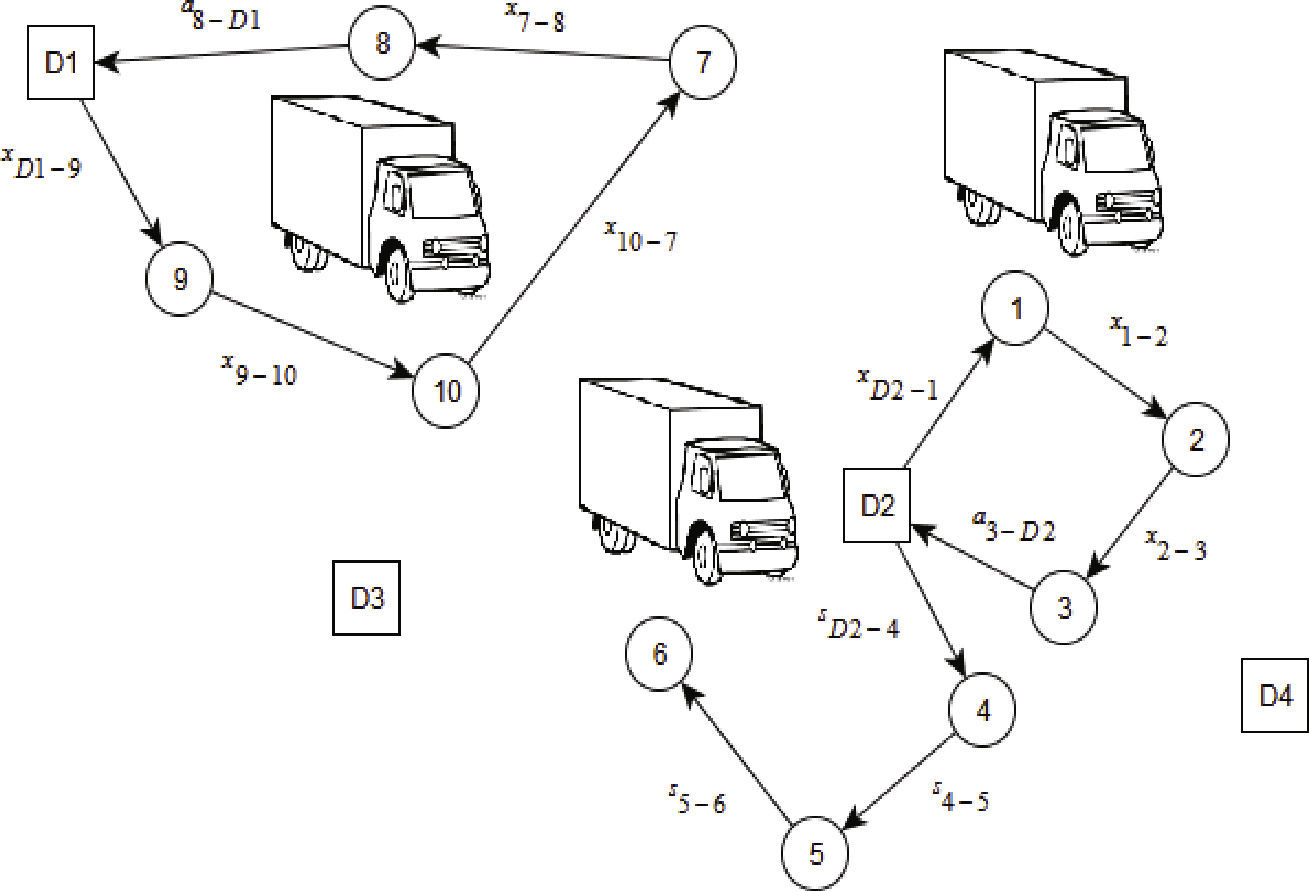
En la figura 1 se representa la solución de un CLRPPC. Los CDs se representan por los nodos cuadrados y notados con la variable Di,se seleccionaron D1 y D2 para abrirse. Los clientes están representados por los nodos circulares en la definición de las rutas, los clientes 4, 5 y 6 que no se atendieron por la flota propia, se asignan a una ruta subcontratada que parte del D2 y termina con el cliente 6. Las variables xij corresponden a los arcos recorridos por la flota propia, las variables aij identifican los arcos de retorno al depósito de inicio de la ruta, este arco solo se activa cuando la ruta se asigna a un vehículo propio, las variables Sij se activan cuando la ruta se asigna a un vehículo de la flota subcontratada, en este caso el vehículo no debe retornar al depósito.
El problema de localización y ruteo con flota propia y flota alquilada (CLRPPC) se formula como un problema lineal entero mixto, el cual se define por las ecuaciones (1)-(28).
El conjunto de restricciones (2)- (9) generan trayectorias radiales en el CLRPPC, tanto en rutas propias como en las subcontratadas, las cuales inician en los depósitos y conectan todos los clientes, de esta forma no se presentan sub-tours en las trayectorias generadas. El conjunto de restricciones (13)-(17) se aplican para las rutas propias e identifican nodos terminales y conectan estos a los depósitos de salida, generando trayectorias cerradas. El conjunto de restricciones (10)-(12) y (18)-(20), establece límites operativos. Las restricciones (21) a (28) se refieren a la naturaleza de las variables.
La función objetivo (1) minimiza los costos de operación, los cuales corresponden a la suma de los costos de apertura de los centros de distribución, costos de apertura de la ruta, costos variables por utilización de los arcos por la flota propia, o bien, por la flota subcontratada.
Un nodo de demanda j debe tener un arco de llegada que lo conecta a la ruta, bien sea un arco recorrido por la flota propia o por la flota subcontratada, esto se representa en (2); (3) indica que la suma de los arcos de salida de un nodo de demanda es igual a la suma de los arcos de entrada: pudiendo ser un arco normal ‘x’ o un arco de retorno al centro de distribución ‘a’, es decir, si se llega a un nodo con una ruta propia, entonces sale de igual forma; (4) garantiza que para un depósito ‘i’ el número de arcos de salida ‘x’ debe ser igual al número de arcos de llegada ‘a’; (5) asegura que si se sale de un nodo con una ruta subcontratada es necesario llegar con una ruta subcontratada, donde es posible que se llegue al nodo, pero no salga (sería un nodo terminal de la ruta subcontratada); (6) evita la duplicación de los arcos, define la orientación de un arco, es decir, si el sentido es de i para j o de j para i.
La restricción (7) representa el balance de flujos para las rutas propias y para las rutas subcontratadas; (8) identifica los arcos activos que generan topologías radiales; (9) garantiza que la demanda de una ruta se debe conectar a un centro de distribución; (10) limita el flujo por una ruta propia de acuerdo con la capacidad de los vehículos y a la variable que determina el uso de este tipo de ruta.
La restricción (11) limita el flujo por una ruta subcontratada de acuerdo con la capacidad de los vehículos y a la variable que determina el uso de este tipo de ruta; (12) limita los flujos que salen de un centro de distribución, de acuerdo con su capacidad y a la decisión de construir ese centro de distribución; (13) define un nodo terminal para rutas propias (identificadas con z=1) cuando no existen arcos de salida para ese nodo de demanda, desde que no se llegue con un arco de ruta subcontratada. Si ‘j’ es un nodo terminal, entonces la restricción (14) obliga a que exista un arco de retorno.
Las restricciones (15) y (16) para los arcos activos propios, identifican a través de la red el nodo de inicio de la ruta propia para activar el arco de retorno al centro de distribución. Si el arco entre el centro de distribución ‘i’ y la demanda ‘j’ está activo, entonces se garantiza que el nodo ‘j’ está conectado con el centro de distribución ‘i’ (fij=1), esto se expresa en (17).
La restricción (18) determina un límite inferior para el número de centros de distribución que deben construirse de acuerdo con la suma de las demandas y con la capacidad de los centros de distribución; (19) garantiza que el número de rutas es suficiente para atender la demanda; (20) establece el máximo número de rutas atendidas por la flota propia; (21)-(26) definen la naturaleza binaria de las variables, xij, sij, yi, fij, zj y aij. Finalmente (27) y (28) precisan las variables tij y lij como continuas y representan la cantidad de flujos de mercancías que se desplazan entre el nodo i y j por las rutas propias o subcontratadas, respectivamente.
Adaptación del modelo CLRPPC a CVRPPC y MDVRPPCEl modelo que se define por las ecuaciones (1)-(28) se puede adaptar al CVRPPC, detallando I como un conjunto de un único elemento, además, para esta variante los parámetros Oi y F se fijan en cero tal como se considera para el CVRP en la literatura especializada. Para resolver casos de prueba donde se considere el MDVRPPC, se debe agregar una restricción donde se indique los depósitos ya están abiertos como se muestra en la ecuación (29). Para este tipo de problema las instancias de la literatura no consideran el costo de apertura Oi, ni el costo asociado al uso de los vehículos de la flota propia F, por lo tanto, tal como en el caso anterior ambos se fijan en cero.
Resultados computacionalesUn gran número de casos se estudian con el fin de analizar el desempeño del modelo propuesto en la solución de CLRPPC, VRPPC y MDVRPPC. El objetivo de los casos estudiados es presentar un nuevo modelo matemático y su potencial en la solución de dichos problemas. Tres conjuntos de sistemas de prueba se usan para validar la propuesta, uno para cada variante considerada. Las instancias van de 20 a 50 clientes y de 1 a 5 depósitos. En las instancias estudiadas se describen las principales características, que dependen del problema estudiado y en general son las siguientes: nombre del caso, número de depósitos, costo e identificación de las rutas propias y subcontratadas, costo por uso de vehículos y depósitos, tiempo requerido en segundos en cada caso estudiado, función objetivo total y GAP en porcentaje.
En todos los casos, los arcos recorridos por vehículos subcontratados se penalizaron con un valor P=2, respecto a los recorridos por vehículos propios.
Tanto para el MDVRPPC como para el VRPPC en la función objetivo solo se consideran los costos de utilización de arcos por la flota propia o por la subcontratada; en estos problemas no se consideran costos por apertura de depósitos, ni costos por utilización de vehículos.
Las instancias usadas para el CLRPPC se tomaron de Prins et al. (2006) y se adaptaron al problema, para ello fue necesario definir el número de vehículos disponibles k, calculado mediante (30), con base en la propuesta presentada en Potvin y Naud (2011a,b), donde q corresponde a la demanda total de los clientes y Q corresponde a la capacidad máxima que el vehículo puede transportar.
El modelo matemático se resolvió bajo CPLEX 12.5 (CPLEX, 2008) en un computador Intel i5-3470 3.2 GHZ, 8 GB y escrito en el lenguaje AMPL, “A Modeling Language for Mathematical Programming” (Fourer et al., 2002).
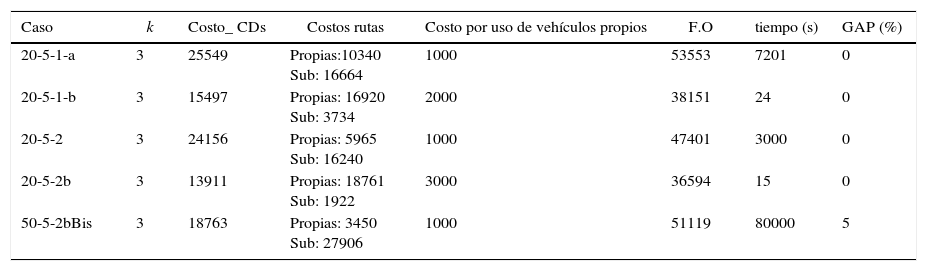
En la tabla 1 se presentan los resultados obtenidos para el CLRPPC, donde k representa el número de vehículos disponibles de la flota propia. F.O corresponde a la función objetivo donde se consideran los costos de apertura de los CDs, costos asociados a la utilización de los arcos por la flota propia o subcontratada y los costos fijos asociados a la utilización de los vehículos propios, tomados de Prins et al. (2006). El tiempo requerido por el software para resolver los casos de prueba se dan en segundos, finalmente el GAP corresponde a la diferencia entre los límites superiores e inferiores.
Resultados CLRPPC
| Caso | k | Costo_ CDs | Costos rutas | Costo por uso de vehículos propios | F.O | tiempo (s) | GAP (%) |
|---|---|---|---|---|---|---|---|
| 20-5-1-a | 3 | 25549 | Propias:10340 Sub: 16664 | 1000 | 53553 | 7201 | 0 |
| 20-5-1-b | 3 | 15497 | Propias: 16920 Sub: 3734 | 2000 | 38151 | 24 | 0 |
| 20-5-2 | 3 | 24156 | Propias: 5965 Sub: 16240 | 1000 | 47401 | 3000 | 0 |
| 20-5-2b | 3 | 13911 | Propias: 18761 Sub: 1922 | 3000 | 36594 | 15 | 0 |
| 50-5-2bBis | 3 | 18763 | Propias: 3450 Sub: 27906 | 1000 | 51119 | 80000 | 5 |
Los resultados muestran un buen desempeño del modelo matemático propuesto, ya que se estudiaron instancias entre 20 y 50 clientes. En estos casos, los valores de GAP son iguales a cero en las instancias de 20 clientes y de 5% para la instancia de 50 clientes, los tiempos computacionales son aceptables.
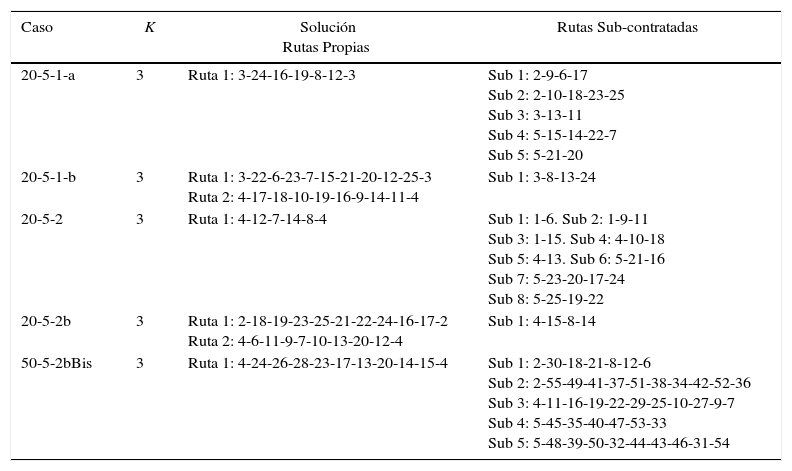
En la tabla 2 se presentan las topologías de las rutas recorridas por la flota propia y subcontratada para los casos estudiados.
Rutas de los vehículos del CLRPPC
| Caso | K | Solución Rutas Propias | Rutas Sub-contratadas |
|---|---|---|---|
| 20-5-1-a | 3 | Ruta 1: 3-24-16-19-8-12-3 | Sub 1: 2-9-6-17 Sub 2: 2-10-18-23-25 Sub 3: 3-13-11 Sub 4: 5-15-14-22-7 Sub 5: 5-21-20 |
| 20-5-1-b | 3 | Ruta 1: 3-22-6-23-7-15-21-20-12-25-3 Ruta 2: 4-17-18-10-19-16-9-14-11-4 | Sub 1: 3-8-13-24 |
| 20-5-2 | 3 | Ruta 1: 4-12-7-14-8-4 | Sub 1: 1-6. Sub 2: 1-9-11 Sub 3: 1-15. Sub 4: 4-10-18 Sub 5: 4-13. Sub 6: 5-21-16 Sub 7: 5-23-20-17-24 Sub 8: 5-25-19-22 |
| 20-5-2b | 3 | Ruta 1: 2-18-19-23-25-21-22-24-16-17-2 Ruta 2: 4-6-11-9-7-10-13-20-12-4 | Sub 1: 4-15-8-14 |
| 50-5-2bBis | 3 | Ruta 1: 4-24-26-28-23-17-13-20-14-15-4 | Sub 1: 2-30-18-21-8-12-6 Sub 2: 2-55-49-41-37-51-38-34-42-52-36 Sub 3: 4-11-16-19-22-29-25-10-27-9-7 Sub 4: 5-45-35-40-47-53-33 Sub 5: 5-48-39-50-32-44-43-46-31-54 |
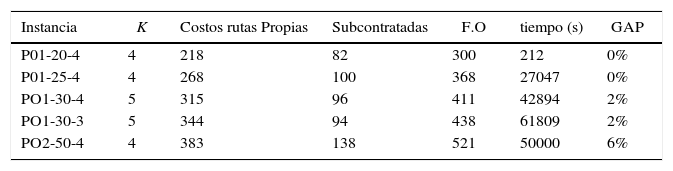
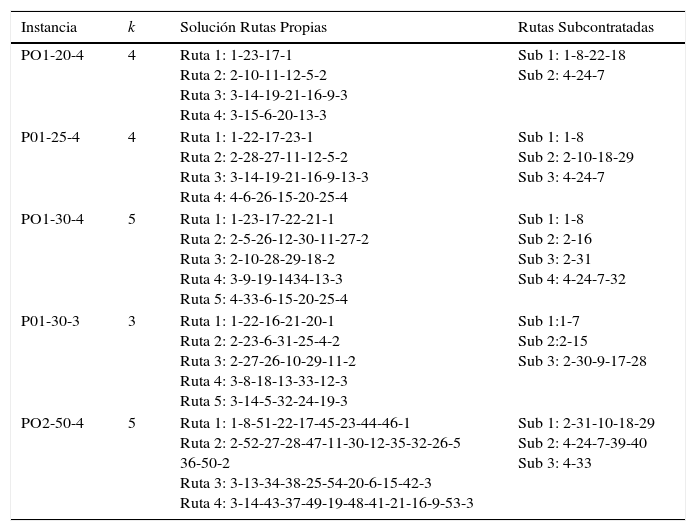
En la tabla 3, se relacionan los resultados obtenidos para el MDVRPPC. Las instancias estudiadas PO1 y PO2 se tomaron de Cordeau et al. (1998). PO1 y PO2 se modificaron para generar a partir de estas, otras instancias que permitieran estudiar el problema. Así el caso P01-20-4 considera los cuatro depósitos y los 20 primeros clientes. La función objetivo (F.O) corresponde a la sumatoria de los costos asociados a los arcos recorridos, bien sea por la flota propia o subcontratada. La ruta subcontratada considera una penalidad de 2. Para instancias de 20 y 30 clientes, los valores de GAP se encuentran entre [0-2]% y en el caso de 50 clientes se obtiene con un GAP de 6%. Los tiempos computacionales son aceptables. En la tabla 4 se identifican las topologías de las rutas propias y subcontratadas.
Rutas de los vehículos del MDVRPPC
| Instancia | k | Solución Rutas Propias | Rutas Subcontratadas |
|---|---|---|---|
| PO1-20-4 | 4 | Ruta 1: 1-23-17-1 Ruta 2: 2-10-11-12-5-2 Ruta 3: 3-14-19-21-16-9-3 Ruta 4: 3-15-6-20-13-3 | Sub 1: 1-8-22-18 Sub 2: 4-24-7 |
| P01-25-4 | 4 | Ruta 1: 1-22-17-23-1 Ruta 2: 2-28-27-11-12-5-2 Ruta 3: 3-14-19-21-16-9-13-3 Ruta 4: 4-6-26-15-20-25-4 | Sub 1: 1-8 Sub 2: 2-10-18-29 Sub 3: 4-24-7 |
| PO1-30-4 | 5 | Ruta 1: 1-23-17-22-21-1 Ruta 2: 2-5-26-12-30-11-27-2 Ruta 3: 2-10-28-29-18-2 Ruta 4: 3-9-19-1434-13-3 Ruta 5: 4-33-6-15-20-25-4 | Sub 1: 1-8 Sub 2: 2-16 Sub 3: 2-31 Sub 4: 4-24-7-32 |
| P01-30-3 | 3 | Ruta 1: 1-22-16-21-20-1 Ruta 2: 2-23-6-31-25-4-2 Ruta 3: 2-27-26-10-29-11-2 Ruta 4: 3-8-18-13-33-12-3 Ruta 5: 3-14-5-32-24-19-3 | Sub 1:1-7 Sub 2:2-15 Sub 3: 2-30-9-17-28 |
| PO2-50-4 | 5 | Ruta 1: 1-8-51-22-17-45-23-44-46-1 Ruta 2: 2-52-27-28-47-11-30-12-35-32-26-5 36-50-2 Ruta 3: 3-13-34-38-25-54-20-6-15-42-3 Ruta 4: 3-14-43-37-49-19-48-41-21-16-9-53-3 | Sub 1: 2-31-10-18-29 Sub 2: 4-24-7-39-40 Sub 3: 4-33 |
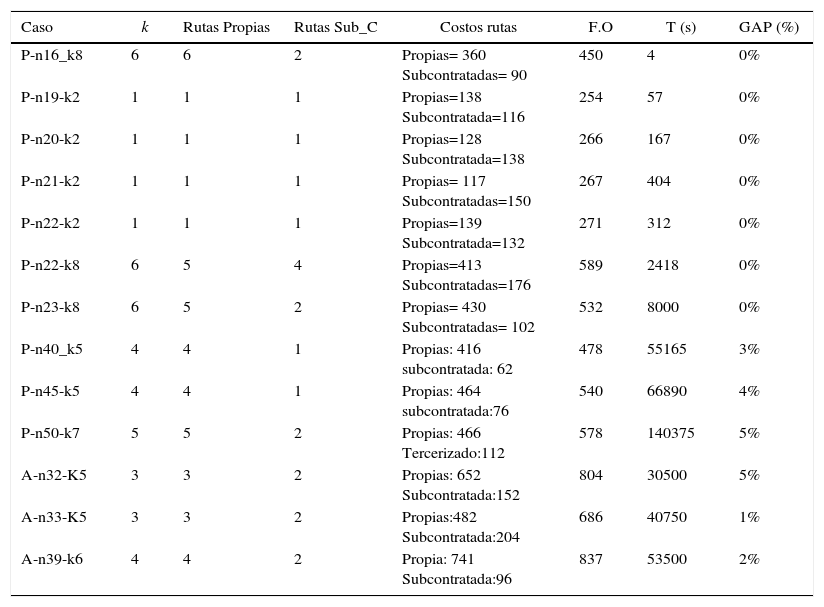
En la tabla 5 se presentan los resultados obtenidos para el VRPPC. Para este tipo de variante se usaron instancias de CVRP de 16 a 50 clientes, que se tomaron de Augerat et al. (1998) y adaptadas con base en la ecuación (30). La F.O incluye los costos de recorrer los arcos por la flota propia o subcontratada. Igual que para el CLRPPC y MDVRPPC se usa una penalidad de 2 para los arcos que se recorren por la flota subcontratada. Los valores de GAP son de 0% para instancias de hasta 23 clientes y el resto de instancias presenta un GAP entre [1-5]%, los tiempos computacionales son aceptables. En la tabla 6 se presentan las topologías de las rutas propias y subcontratadas de cada instancia. Los resultados permiten inferir un buen desempeño del modelo propuesto.
Resultados VRPPC
| Caso | k | Rutas Propias | Rutas Sub_C | Costos rutas | F.O | T (s) | GAP (%) |
|---|---|---|---|---|---|---|---|
| P-n16_k8 | 6 | 6 | 2 | Propias= 360 Subcontratadas= 90 | 450 | 4 | 0% |
| P-n19-k2 | 1 | 1 | 1 | Propias=138 Subcontratada=116 | 254 | 57 | 0% |
| P-n20-k2 | 1 | 1 | 1 | Propias=128 Subcontratada=138 | 266 | 167 | 0% |
| P-n21-k2 | 1 | 1 | 1 | Propias= 117 Subcontratadas=150 | 267 | 404 | 0% |
| P-n22-k2 | 1 | 1 | 1 | Propias=139 Subcontratada=132 | 271 | 312 | 0% |
| P-n22-k8 | 6 | 5 | 4 | Propias=413 Subcontratadas=176 | 589 | 2418 | 0% |
| P-n23-k8 | 6 | 5 | 2 | Propias= 430 Subcontratadas= 102 | 532 | 8000 | 0% |
| P-n40_k5 | 4 | 4 | 1 | Propias: 416 subcontratada: 62 | 478 | 55165 | 3% |
| P-n45-k5 | 4 | 4 | 1 | Propias: 464 subcontratada:76 | 540 | 66890 | 4% |
| P-n50-k7 | 5 | 5 | 2 | Propias: 466 Tercerizado:112 | 578 | 140375 | 5% |
| A-n32-K5 | 3 | 3 | 2 | Propias: 652 Subcontratada:152 | 804 | 30500 | 5% |
| A-n33-K5 | 3 | 3 | 2 | Propias:482 Subcontratada:204 | 686 | 40750 | 1% |
| A-n39-k6 | 4 | 4 | 2 | Propia: 741 Subcontratada:96 | 837 | 53500 | 2% |
Rutas de los vehículos del VRPPC
| Instancia | K | Solución Rutas propias | Rutas Subcontratadas |
|---|---|---|---|
| P-n16_k8 | 6 | Ruta 1: 1-5-12-1 Ruta 2: 1-9-1 Ruta 3: 1-14-10-8-1 Ruta 4: 1-16-13-11-1 Ruta 5: 1-15-6-1 Ruta 6: 1-3-1 | Sub 1: 1-2-4 Sub 2: 1-7 |
| P-n19-k2 | 1 | Ruta1: 1-2-11-5-12-15-13-4-18-17-9-6-1 | Sub 1: 1-7-19-3-8-10-16-14 |
| P-n20-k2 | 1 | Ruta 1: 1-2-11-14-9-18-19-4-13-16-12-5-1 | Sub 1: 1-7-20-6-15-17-10-8-3 |
| P-n21-k2 | 1 | Ruta1:1-5-12-16-13-4-20-19-9-11-2-17-1 | Sub1:1-7-21-6-15-18-10-14-8-3 |
| P-n22-k2 | 1 | Ruta 1: 1-2-11-5-12-16-13-4-20-19-9-14-10-1 | Sub 1: 1-17-7-21-6-15-18-22-8-3 |
| P-n22-k8 | 5 | Ruta 1: 1-10-3-2-7-1 Ruta 2: 1-11-9-4-5-1 Ruta 3: 1-14-12-1 Ruta 4: 1-15-21-22-1 Ruta 5: 1-16-19-18-1 | Sub 1: 1-8-6 Sub 2: 1-13 Sub 3:1-17 Sub 4:1-20 |
| P-n23-k8 | 6 | Ruta 1: 1-2-3-1 Ruta 2: 1-4-20-19-1 Ruta 3: 1-8-5-1 Ruta 4: 1-11-13-16-12-1 Ruta 5: 1-18-10-14-1 Ruta 6: 1-23-15-6-1 | Sub 1: 1-22-7-21 Sub 2: 1-17-9 |
| P-n40_k5 | 4 | Ruta 1: 1-7-25-24-8-27-9-32-29-2-28-1 Ruta 2: 1-15-26-14-20-5-19-1 Ruta 3: 1-18-38-16-34-40-11-31-35-22-30-17-1 Ruta 4: 1-33-23-4-37-36-21-3-12-1 | Sub 1: 1-13-6-39-10 |
| P-n45-k5 | 4 | Ruta1: 1-5-14-42-20-41-43-45-38-6-1 Ruta2: 1-7-24-25-44-8-27-32-29-9-28-1 Ruta 3: 1-12-3-30-21-36-37-4-23-2-33-1 Ruta 4: 1-18-16-34-40-11-31-35-22-17-10-39-1 | Sub 1: 1-13-19-15-26 |
| P-n50-k7 | 5 | Ruta 1: 1-8-36-20-15-12-39-27-1 Ruta 2: 1-13-11-32-26-19-25-45-4-1 Ruta 3: 1-17-50-24-44-42-43-23-2-34-7-1 Ruta 4: 1-28-14-16-21-38-37-6-30-46-1 Ruta 5: 1-31-49-48-22-29-3-1 | Sub 1: 1-5-35-47-9 Sub 2: 1-18-41-33-10-40 |
| A-n32-K5 | 3 | Ruta 1: 1-7-4-3-24-5-12-29-15-1 Ruta 2: 1-27-8-14-18-20-32-22-1 Ruta 3: 1-30-19-9-10-23-16-11-26-6-21-1 | Sub 1: 1-25-28 Sub 2: 1-31-17-13-2 |
| A-n33-K5 | 3 | Ruta 1: 1-21-6-27-8-9-14-33-3-1 Ruta 2: 1-25-7-20-15-22-2-32-12-1 Ruta 3: 1-30-17-4-10-18-16-1 | Sub 1: 1-5-13-11-31-26-28 Sub 2: 1-23 Sub 3: 1-24-29-19 |
| A-n39-k6 | 4 | Ruta 1: 1-19-28-11-17-5-9-8-1 Ruta 2: 1-21-33-35-23-22-24-18-37-2-7-1 Ruta 3: 1-25-4-39-13-10-29-30-6-1 Ruta 4: 1-38-32-15-36-26-34-20-3-1 | Sub 1: 1-16-14-31 Sub 2: 1-27-12 |
Al analizar los resultados obtenidos se observa un buen desempeño en los tres tipos de problemas estudiados, con valores de GAP entre [0-6]% y tiempos de cómputo aceptables. Para instancias entre 50 y 70 clientes el modelo matemático encuentra soluciones con valores de GAP entre 6 y 14%. También se podrían usar conceptos de granularidad para acotar el espacio de soluciones, de manera que el óptimo global no se trunque. Esta estrategia permite resolver estas instancias usando menos tiempo de cómputo y con valores de GAP dentro de rangos aceptables.
ConclusionesEste artículo propone un modelo lineal entero mixto que resuelve el problema de localización y ruteo con restricciones de capacidad, donde se considera el uso de la flota propia y subcontratada (CLRPPC), obteniendo resultados que respaldan la validez del modelo propuesto. El CLRPPC se estudia poco y no se cuenta con un modelo definitivo, por lo tanto, este modelo resulta de interés para la comunidad académica del área de transporte.
El modelo propuesto puede adaptarse para resolver el problema de ruteo atendido con flota propia y subcontratada (VRPPC) y con múltiples depósitos (MDVRPPC). Los modelos se validan con instancias de la literatura especializada, donde los resultados demuestran la capacidad del modelo para resolver estos tres tipos de problemas, a pesar de la alta complejidad matemática, debido a que se resuelven dos grafos completos de manera simultánea, el primero representa las rutas propias y el segundo las rutas subcontratadas.
El modelo matemático planteado puede servir de referencia para la solución de instancias de gran tamaño, cuando se usan otras estrategias de solución, tales como técnicas híbridas que incluyan partición de conjuntos (set partitioning), heurísticas y meta heurísticas. Los resultados presentados en este trabajo pueden servir como punto de referencia para futuros trabajos, ya que actualmente no se cuenta con resultados del CLRPPC en la literatura.
En trabajos futuros se busca explorar el modelo para el caso de ruteo abierto. También se estudiarán otros métodos de solución con éxito en la solución de algunos problemas de transporte, como es el caso del algoritmo ILS y métodos híbridos basados en algoritmos genéticos.
Eliana Mirledy Toro O., expresa su agradecimiento a la Facultad de Ingeniería Industrial de la Universidad Tecnológica de Pereira, por el apoyo a la realización de este proyecto de investigación.
Citación estilo Chicago
Citación estilo ISO 690
Eliana Mirledy Toro-Ocampo. Recibió los títulos de ingeniera industrial, magister en ingeniería eléctrica y magister en investigación de operaciones y estadística por la Universidad Tecnológica de Pereira, Colombia en 1994, 2006 y 2008, respectivamente. Actualmente estudia el doctorado en ingeniería en la misma universidad. Es docente del programa de ingeniería industrial de la Universidad Tecnológica de Pereira, Colombia, desde 2005.
John Fredy Franco-Baquero. Recibió los títulos de ingeniero electricista y magíster en ingeniería eléctrica por la Universidad Tecnológica de Pereira, Colombia en 2004 y 2006, respectivamente, asimismo el título de doctor en ingeniería eléctrica de la Universidade Estadual Paulista, Ilha Solteira, Brazil en 2012. Sus áreas de investigación son el desarrollo de métodos de optimización para el planeamiento y control de sistemas eléctricos de potencia. Actualmente desarrolla el proyecto de póst-doctorado: Planejamento da expansão do sistema de distribuição de energia elétrica usando programação linear inteira mista, en la Universidade Estadual Paulista, IlhaSolteira, Brazil.
Ramón Alfonso Gallego-Rendón. Es ingeniero electricista por la Universidad Tecnológica de Pereira, Colombia en 1981 y magister en ingeniería eléctrica por la Universidad Nacional, Bogotá, Colombia en 1985. Es especialista en planeación energética en la Universidad de los Andes, Bogotá, Colombia en 1987. En 1997 recibió el título de PhD en ingeniería eléctrica por la Universidade Estadual de Campinas, Sao Pablo, Brasil. Sus áreas de investigación incluyen los sistemas eléctricos de transmisión, planeamiento de la distribución, aplicaciones de optimización en sistemas eléctricos y sistemas de producción. Actualmente es profesor de tiempo completo del programa de ingeniería eléctrica en la Universidad Tecnológica de Pereira, Colombia.