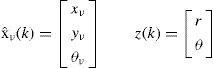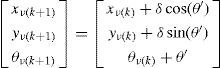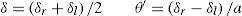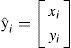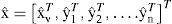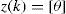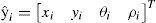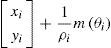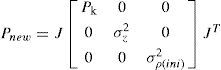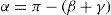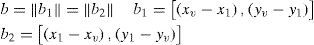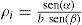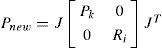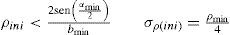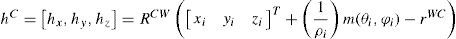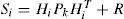SLAM con mediciones angulares: método por triangulación estocástica

Resumen

El SLAM (simultaneous localization and mapping) es una técnica en la cual un robot o vehículo autónomo opera en un entorno a priori desconocido, utilizando únicamente sus sensores de abordo, mientras construye un mapa de su entorno, el cual utiliza al mismo tiempo para localizarse. Los sensores tienen un gran impacto en los algoritmos usados en SLAM. Enfoques recientes se están centrando en el uso de cámaras como sensor principal, ya que generan mucha información y están bien adaptadas para su aplicación en sistemas embebidos: son ligeras, baratas y ahorran energía. Sin embargo, a diferencia de los sensores de rango, los cuales proveen información angular y de rango, una cámara es un sensor proyectivo que mide el ángulo (bearing) respecto a los elementos de la imagen, por lo que la profundidad o rango no puede ser obtenida mediante una sola medición. Lo anterior ha motivado la aparición de una nueva familia de métodos en SLAM: los métodos de SLAM basados en sensores angulares, los cuales están principalmente basados en técnicas especiales para la inicialización de características en el sistema, permitiendo el uso de sensores angulares (como cámaras) en SLAM. Este artículo presenta un método práctico para la inicialización de nuevas características en sistemas de SLAM basados en sensores angulares. El método propuesto implementa mediante un retardo una técnica de triangulación estocástica para definir una hipótesis para la profundidad inicial de las características. Para mostrar el desempeño del método propuesto se presentan resultados experimentales con simulaciones y también se presentan dos casos de aplicación para escenarios con datos reales procedentes de distintos sensores angulares.

Abstract

The SLAM or Simultaneous Localization and Mapping, is a technique in which a robot or autonomous vehicle operate in an a priori unknown environment, using only its onboard sensors to simultaneously build a map of its surroundings and use it to track its position. The sensors have a large impact on the algorithm used for SLAM. Recent approaches are focusing on the use of cameras as the main sensor, because they yield a lot of information and are well adapted for embedded systems: they are light, cheap and power saving. However, unlike range sensors which provide range and angular information, a camera is a projective sensor which measures the bearing of images features. Therefore depth information (range) cannot be obtained in a single step. This fact has propitiated the emergence of a new family of SLAM algorithms: the Bearing-Only SLAM methods, which mainly rely in especial techniques for features system-initialization in order to enable the use of bearing sensors (as cameras) in SLAM systems. In this work a practical method is presented, for initializing new features in bearing-only SLAM systems. The proposed method, defines a single hypothesis for the initial depth of features, by the use of an stochastic technique of triangulation. Several simulations as well two scenarios of applications with real data are presented, in order to show the performance of the proposed method.

Introducción

La localización y mapeo simultáneos, SLAM por sus siglas (simultaneous localization and mapping), es sin duda uno de los problemas más importantes a resolver en robótica, en el camino de construir robots móviles verdaderamente autónomos. Las técnicas de SLAM se refieren a cómo un robot móvil opera en un entorno a priori desconocido utilizando únicamente sus sensores de abordo, mientras construye un mapa de dicho entorno, el cual a su vez utiliza para localizarse.

Los sensores del robot tienen un gran impacto en los algoritmos usados en SLAM. Los primeros enfoques se centraron en el uso de sensores de rango como sónares o láseres (Auat et al., 2011), (Vázquez et al., 2009). Sin embargo, hay algunas dificultades con el uso de este tipo de sensores en SLAM: la asociación de datos es difícil, son costosos y a menudo están limitados a mapas 2D. Puede consultarse (Durrant y Bailey, 2006), para una revisión del problema general del SLAM.

Las cuestiones anteriores han motivado que mucho del trabajo reciente se esté centrando en el uso de cámaras como sensor principal. Las cámaras se han vuelto muy interesantes para la comunidad investigadora en robótica porque proveen cuantiosa información, son ligeras, baratas y de bajo consumo de energía. Usando visión artificial, un robot puede localizarse a sí mismo utilizando objetos comunes del entorno como puntos de referencia (landmarks).

Por otro lado, mientras que los sensores de rango proveen información angular y de rango (profundidad), una cámara es un sensor proyectivo, el cual mide el ángulo (bearing) respecto a características en la imagen. Por tanto, la información de profundidad (rango) no puede ser obtenida en una sola toma. Este hecho ha propiciado la aparición de una nueva familia de métodos de SLAM, que está basada en técnicas especiales para la inicialización de características con la finalidad de permitir el uso de sensores angulares (como cámaras) en los sistemas de SLAM.

En años recientes varias mejoras y variantes a este tipo de métodos han aparecido en la literatura (Williams et al., 2007), (Chekhlov et al., 2006), así como diferentes esquemas para incrementar el número de características soportadas en el mapa (Munguía y Grau, 2009). Sin embargo, el proceso de la inicialización de nuevas características continúa siendo quizás el aspecto más importante a tener en cuenta en los sistemas de SLAM basados en mediciones angulares para incrementar la robustez.

En este artículo, se presentan diferentes resultados de la investigación de los autores de acuerdo con la problemática del SLAM basado en sensores angulares. Particularmente, se presenta un algoritmo llamado método por triangulación estocástica, el cual aborda el problema de la inicialización de nuevas características en el mapa.

Descripción del problema

El SLAM con mediciones angulares es un problema de SLAM parcialmente observable, en el cual el sensor utilizado para percibir el entorno del robot provee únicamente información angular en cuanto a puntos de referencia (landmark) del entorno. Dicha información no es suficiente para calcular el estado completo de la característica (la cual modela el punto de referencia) mediante una sola medición.

Para inferir la profundidad de una característica el sensor debe observarla repetidamente mientras el robot se mueve libremente a través de su entorno, estimando el ángulo entre la característica y el centro del robot. La diferencia entre las mediciones angulares es el paralaje (parallax).

De hecho, el paralaje es la clave que permite la estimación de la profundidad de las características. En el caso de trayectorias en entornos de interiores, un movimiento de centímetros es suficiente para producir paralaje, por otro lado, cuanto mayor sea la distancia donde se encuentre la característica, más tendrá que viajar el sensor para producir paralaje.

a)

Modelo de movimiento del robot

Para un entorno 2D, se considera un robot y/o vehículo de configuración diferencial, cuya posición y orientación están definidas por xˆυ, y el cual está equipado con un sensor capaz de realizar mediciones z(k) angulares y de distancia, θ y r, respectivamente.

Con el modelo predictivo discreto, para el movimiento del robot

siendo δ la distancia recorrida por el centro del robot y θ’ el giro realizado por el robot a cada instante k

donde δ_r y δ_l representan la distancia recorrida por cada rueda del robot y a la separación entre las mismas. Habitualmente δ_r y δ_l se obtienen mediante los codificadores de posición (encoders) de las ruedas del robot.

Mediante el uso de un Filtro de Kalman Extendido se propagan las estimaciones de la posición del robot, así como también las estimaciones de las características.

b)

Medición e inicialización de las características

Para el contexto mencionado, se considera el tipo de característica más simple: un punto tal que para una característica dada ŷ_i

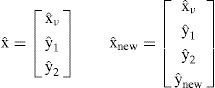
El estado completo xˆ, el cual incluye todas las características ŷ_i, está conformado por

En este caso la ecuación de medición hixˆυ,yˆi viene dada por

Donde atan2 es una función que toma dos argumentos (x e y), para calcular el arco tangente de y/x, dentro de un rango [–π, π].

Para inicializar una nueva característica ŷ_i en el mapa, es necesario invertir hixˆυ,yˆi a yˆiz(k),xˆυ. En este caso invirtiendo (6) tenemos que

c)

Caso de SLAM con mediciones angulares

En el caso particular de SLAM con mediciones angulares, el sensor principal proveería únicamente lecturas z(k) tal que

En este caso, considerando la ecuación de medición hixˆυ,yˆi

Por inspección se observa que no sería posible invertir la ecuación (9) para obtener una función yˆizk,xˆυ con la cual inicializar el estado completo de la característica ŷ_i = [x_i, y_i]. En este caso, una posibilidad podría ser el definir una característica parcialmente inicializada con una forma geométrica diferente (por ejemplo, una línea sobre la cual se asuma que el punto debería encontrarse).

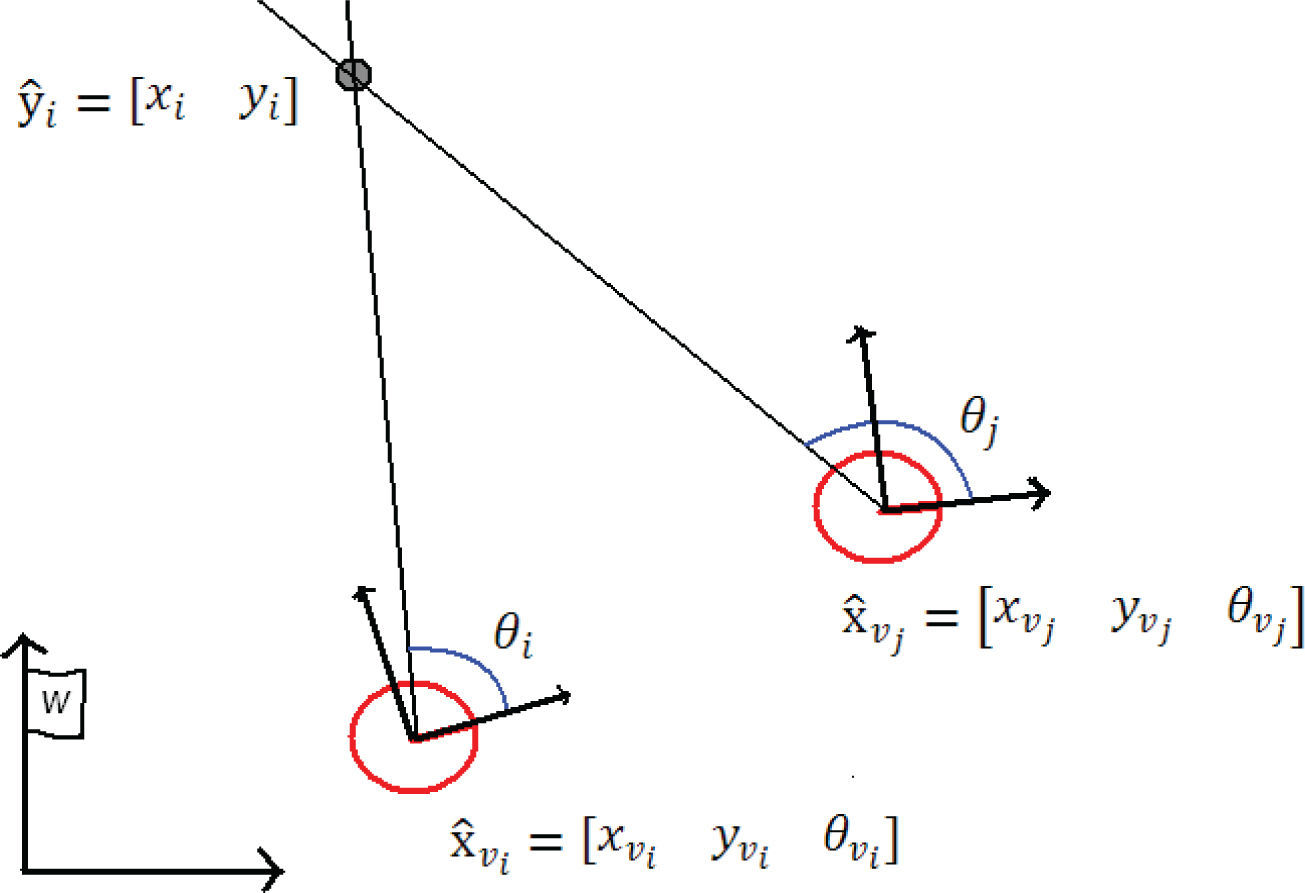
Tenemos entonces que en el proceso de inicialización de características, en el SLAM con mediciones angulares, una sola medición es insuficiente para determinar la posición completa de la característica. Por tanto, se requieren al menos dos mediciones angulares θ_i y θ_j, realizadas en dos posiciones diferentes del vehículo xˆυi y xˆυj (figura 1).

donde:

Figura 1.

Inicialización de una característica mediante la intersección de dos mediciones angulares

Si las mediciones angulares y la posición del vehículo fueran perfectamente conocidas, el cálculo de la posición de la característica seria trivial mediante la función g(xˆυi,xˆυj,θi,θj)(10). Sin embargo, la estimación de la posición de la característica puede estar mal condicionada dependiendo de diferentes factores: i) la incertidumbre en la estimación de las posiciones del vehículo, ii) la incertidumbre en las mediciones angulares, y iii) las particularidades del desplazamiento entre ambas posiciones del vehículo, las cuales producen el paralaje.

Trabajo relacionado

El SLAM basado en mediciones angulares (Bearing-Only SLAM) ha recibido mucha atención por parte de la comunidad investigadora en robótica en la década presente y en la pasada, y particularmente el SLAM monocular, el cual constituye un caso particular del SLAM en el que una cámara de video representa la única entrada sensorial del sistema.

En Deans y Martial (2000), se propone una combinación entre optimización global (ajustamiento de burbuja) para la inicialización de características y un filtro de Kalman para la estimación del estado. En este método, debido a la limitación impuesta por la línea-base, en la cual las características pueden ser inicializadas, y dependiendo del movimiento de la cámara y la locación de los objetos en el entorno, algunas características no pueden ser inicializadas. En Strelow y Sanjiv (2003) se propone un método similar, pero combinando una cámara con sensores inerciales mediante un Filtro de Kalman Iterado (IEKF). En el trabajo de Bailey (2003) se presenta una variante de inicialización restringida (constrained initialization), donde estimaciones pasadas de la posición del vehículo son retenidas en el estado del SLAM conjuntamente con las mediciones respectivas, de manera que la inicialización de las características puede llevarse a cabo hasta que el paralaje sea suficiente para permitir una inicialización Gaussiana de la característica. El criterio utilizado para determinar si la estimación está bien condicionada es la denominada distancia de Kullback. La complejidad del método de muestreo propuesto para evaluar esta distancia es considerablemente alta.

Aparte del Filtro del Kalman, se utilizan habitualmente otras técnicas de estimación como los filtros de partículas (PF) en el SLAM basado en mediciones angulares. En Kwok y Dissanayake (2004) se propone una variación al PF estándar para remediar el problema del empobrecimiento del muestreo en este tipo de sistemas. El estado inicial de las características se aproxima utilizando una suma de funciones de distribución Gaussianas, la cual define un conjunto de hipótesis para la posición de los objetos, incluyendo, desde un principio, a las características dentro del mapa. En observaciones subsiguientes, se pasa un test estadístico para eliminar hipótesis débiles. En Kwok y Dissanayake (2005) se extiende el algoritmo anterior mediante un filtro de suma de Gaussianas. Este método es quizás el primer método de inicialización de características sin retardo propuesto en la literatura. El principal inconveniente de este método reside en que el número de filtros requeridos crece exponencialmente con el número de características, aumentando exponencialmente la carga computacional.

Algunos de los avances más notables en SLAM basado en mediciones angulares fueron presentados en Davison (2003), quien mostró la factibilidad del SLAM en tiempo real utilizando una única cámara (SLAM Monocular) como fuente sensorial del sistema. Su propuesta está basada en el Filtro de Kalman Extendido como técnica de estimación del estado y un filtro de partículas para incorporar nuevas características al mapa mediante un esquema de inicialización parcial. En este caso, el PF no está correlacionado con el resto del mapa, manteniendo un conjunto de hipótesis de profundidad uniformemente distribuidas a lo largo de la línea de vista de cada nueva característica. Después cada nueva observación se utiliza para actualizar la distribución de las posibles profundidades, hasta que la variancia sea suficientemente pequeña para considerarse una estimación Gaussiana. En este punto la característica se agrega al mapa como una entidad tridimensional. Una desventaja de este enfoque reside en que la distribución inicial de partículas tiene que cubrir todos los posibles valores de profundidad, haciéndolo difícil de aplicar cuando se detecta un gran número de partículas, o bien, cuando se consideran características distantes en el entorno.

Jensfelt et al. (2006) presentan un método donde la idea consiste en retrasar N pasos la estimación del SLAM, utilizando dichos N pasos para determinar buenos candidatos a ser considerados como características del mapa, así como también estimar su posición 3D. El principal objetivo de este trabajo se centra en el manejo del mapa para lograr un desempeño en tiempo real. Sola et al. (2005) presentan un método basado en el Filtro de Kalman Iterado. Para la inicialización de características utiliza una aproximación al método de Filtro de Suma de Gaussianas, el cual permite inicializar sin retraso las características en el mapa.

En Eade y Drummond (2006) se propone un método basado en el FastSLAM (Montemerlo et al., 2002). En este tipo de enfoque, la posición del robot es representada por partículas, mientras que un conjunto de filtros de Kalman refina la estimación de las características.

En Montiel et al. (2006) se presenta un método en donde, no existe una transición explícita de un estado “parcial” a uno “totalmente” inicializado para cada característica.

En este sentido, las características son inicializadas en el primer instante en el cual son observadas mediante una profundidad inversa e incertidumbres predeterminadas heurísticamente a cubrir un amplio rango de profundidad. Por lo que características lejanas pueden ser representadas e incluidas en el mapa.

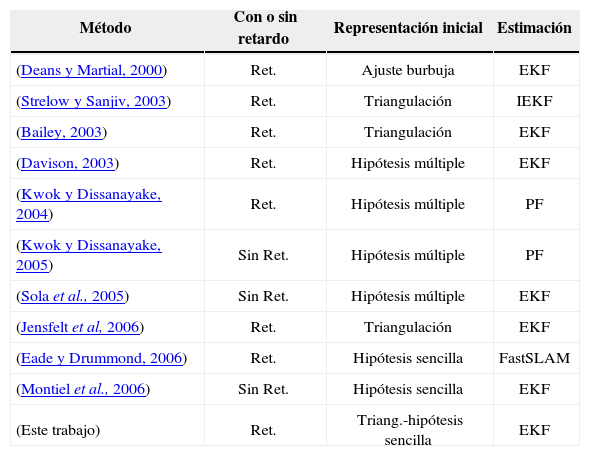
La tabla 1 presenta un resumen de los métodos anteriormente mencionados. En los métodos con retardo, una característica observada en el instante t se agrega al mapa en un tiempo subsiguiente t + k. Por lo general este retardo es utilizado en los diferentes métodos para recabar información que permita inicializar robustamente las características en el mapa. Por otro lado, los métodos sin retardo se aprovechan de la observación de la característica desde el instante t para localizar el vehículo, pero la actualización del mapa estocástico debe calcularse cuidadosamente.

Tabla 1.

Resumen de métodos

Método	Con o sin retardo	Representación inicial	Estimación
(Deans y Martial, 2000)	Ret.	Ajuste burbuja	EKF
(Strelow y Sanjiv, 2003)	Ret.	Triangulación	IEKF
(Bailey, 2003)	Ret.	Triangulación	EKF
(Davison, 2003)	Ret.	Hipótesis múltiple	EKF
(Kwok y Dissanayake, 2004)	Ret.	Hipótesis múltiple	PF
(Kwok y Dissanayake, 2005)	Sin Ret.	Hipótesis múltiple	PF
(Sola et al., 2005)	Sin Ret.	Hipótesis múltiple	EKF
(Jensfelt et al, 2006)	Ret.	Triangulación	EKF
(Eade y Drummond, 2006)	Ret.	Hipótesis sencilla	FastSLAM
(Montiel et al., 2006)	Sin Ret.	Hipótesis sencilla	EKF
(Este trabajo)	Ret.	Triang.-hipótesis sencilla	EKF

Respecto a la representación inicial, en la tabla 1, el ajuste de burbuja se refiere a métodos que están basados en procesamiento por lotes, y buscan una solución óptima utilizando todas las mediciones disponibles. Los métodos de triangulación calculan explícitamente la intersección de las líneas definidas por las observaciones, éstos requieren definir una condición para considerar la estimación bien condicionada. Los métodos de hipótesis sencilla definen la representación inicial de las características con la única función de distribución de probabilidad. A menudo estos métodos son fáciles de calcular, pero requieren atención con respecto a la linealidad en la ecuación de medición. Los métodos de hipótesis múltiple definen la representación inicial de las características con una función de probabilidad múltiple. Usualmente son métodos robustos en relación con la linealidad de la ecuación de medición, pero su complejidad es alta. La columna estimación se refiere a la técnica empleada para el proceso de estimación principal del SLAM. La mayoría de los algoritmos están basados en el Filtro de Kalman Extendido, pero otros emplean filtros de partículas u otras variaciones, como FastSLAM.

Parametrización de la profundidad inversa

Como se mencionó en la sección anterior, los métodos basados en hipótesis múltiples son robustos para su aplicación con problemas altamente no lineales, a costa de una complejidad de implementación usualmente alta. En contraste, los métodos basados en una sola hipótesis (de implementación menos compleja), como el EKF, el cual recurre a la linealización de primer orden, sufren cuando la incertidumbre no puede ser representada de manera Gaussiana.

a)

Mejora de la linealidad

En Eade y Drummond (2006) y Montiel et al. (2006) se ha mostrado que el uso de una parametrización inversa para la profundidad de las características mejora notablemente la linealidad de la ecuación de medición, incluso para pequeños cambios en la posición del sensor, los cuales producen pequeños cambios en el ángulo de paralaje.

Este hecho permite representar la incertidumbre en la profundidad de un rango (desde lo cercano hasta lo infinito) de manera Gaussiana, permitiendo a su vez, utilizar un esquema estándar EKF para la implementación robusta del SLAM con mediciones angulares.

Tomando como referencia la parametrización propuesta en Montiel et al. (2006), una característica en un entorno 2D estaría definida por el vector de 4 dimensiones

el cual modela un punto localizado en

Siendo x_i e y_i las coordenadas del centro del vehículo cuando la característica es observada por primera vez, y θ_i representa el acimut (respecto al marco de referencia global W) para el vector direccional unitario m(θ_i). La profundidad del punto d_i se codifica por su inversa ρ_i = 1/d_i (figura 2).

Figura 2.

Parametrización de una característica 2D mediante la profundidad inversa

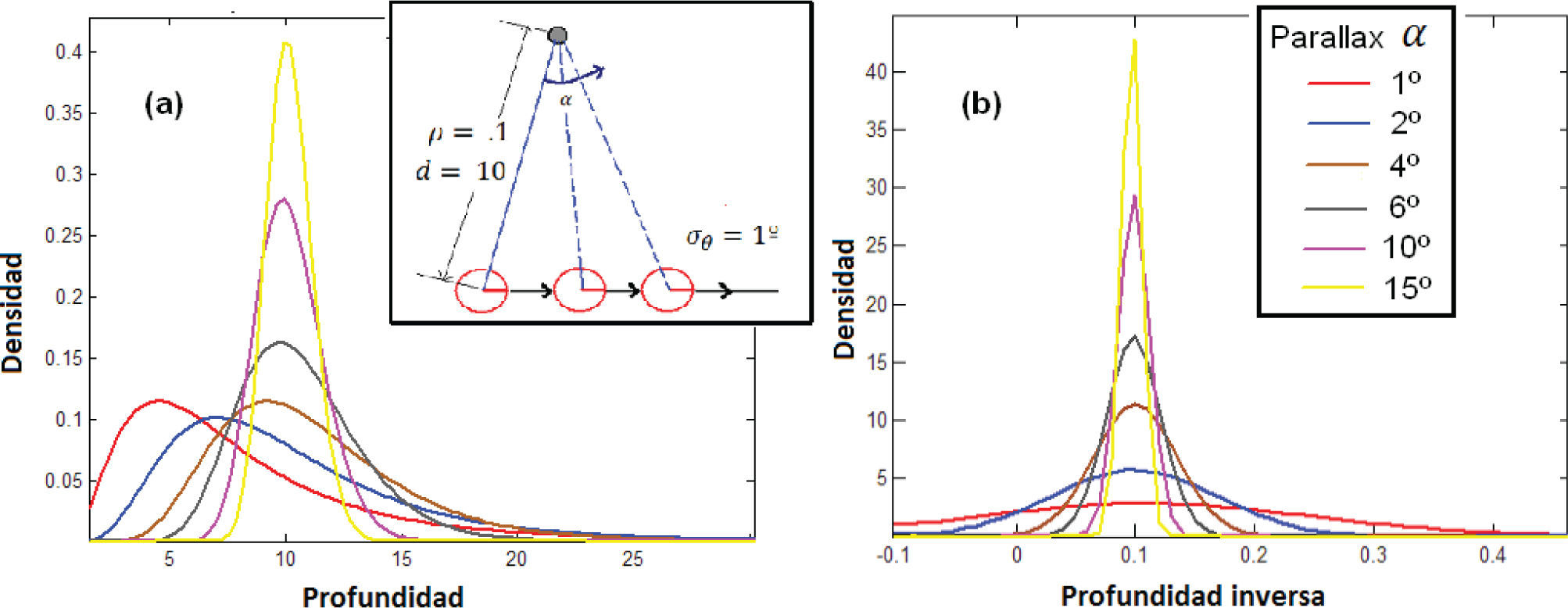
La figura 3 muestra la reconstrucción de un punto mediante mediciones angulares afectadas de ruido a diferentes paralajes, usando tanto la parametrización euclidiana (figura 3a), como la profundidad inversa (figura 3b).

Figura 3.

Simulación de la reconstrucción de un punto mediante observaciones con diferentes paralajes. La posición del vehículo es conocida. Se introduce un error de σ_θ = 1° (grados) en las mediciones angulares. Las graficas (a) y (b) muestran la evolución de la función de probabilidad para la profundidad d y la profundidad inversa ρ, mientras el paralaje de las observaciones crece: en (a), la función de probabilidad converge a una forma Gaussiana, pero las estimaciones iniciales son altamente no Gaussianas. En contraste, las funciones de probabilidad para la profundidad inversa (b) (la abscisa está en metros inversos) son notablemente Gaussianas incluso para pequeños paralajes

b)

Inicialización sin retardo

En el método presentado por Montiel et al. (2006) no existe una transición explícita de un estado “parcial” a uno “totalmente” inicializado, esto significa que las características son agregadas al mapa y expresadas mediante su representación final desde que son observadas por primera vez. En lo subsiguiente se referirá a esta propuesta como método de la profundidad inversa sin retardo (o PI-SR).

Para el método PI-SR, el valor inicial para ρ_i y su variancia inicial asociada σρ2, se determinan heurísticamente para cubrir una región de aceptación de 95%, es decir, un enorme rango de profundidad [d_min, ∞] codificado en su inversa ρ_i = 1/d_i, tal que ρ_ini = ρ_min/ 2, σ_ρ(ini) = ρ_min / 4, ρ_min = 1/d_min. Entonces una nueva característica ŷ_new, detectada en un instante k, se compone de manera que

donde x_υ, y_υ, θ_υ se toman directamente del estado actual xˆυ, ρ_ini es la profundidad inversa inicial y z_k es medición angular inicial.

El nuevo estado del sistema xˆ se compone simplemente agregando la nueva característica ŷ_new al final del vector de estados, tal como se muestra en la ecuación (5). Por ejemplo, para agregar una nueva característica en un mapa con 2 características, el nuevo vector resultaría

La matriz de covariancias del estado del sistema P, es expandida en el proceso de inicialización por

Donde J es el Jacobiano de la función de inicialización, σz2 es la variancia del sensor angular y σ_ρ(ini) es la variancia que representa la incertidumbre de la profundidad inversa inicial.

c)

Casos de prueba

El método de la parametrización inversa sin retardo es, sin duda, una buena opción para su implementación en sistemas de SLAM basados en sensores angulares, debido a su claridad y escalabilidad. Por otro lado, en experimentos basados en simulación, se encontró que bajo ciertas circunstancias los parámetros iniciales fijos ρ_ini y σ_ρ(ini) tienen que ser sintonizados manualmente para asegurar la convergencia del algoritmo.

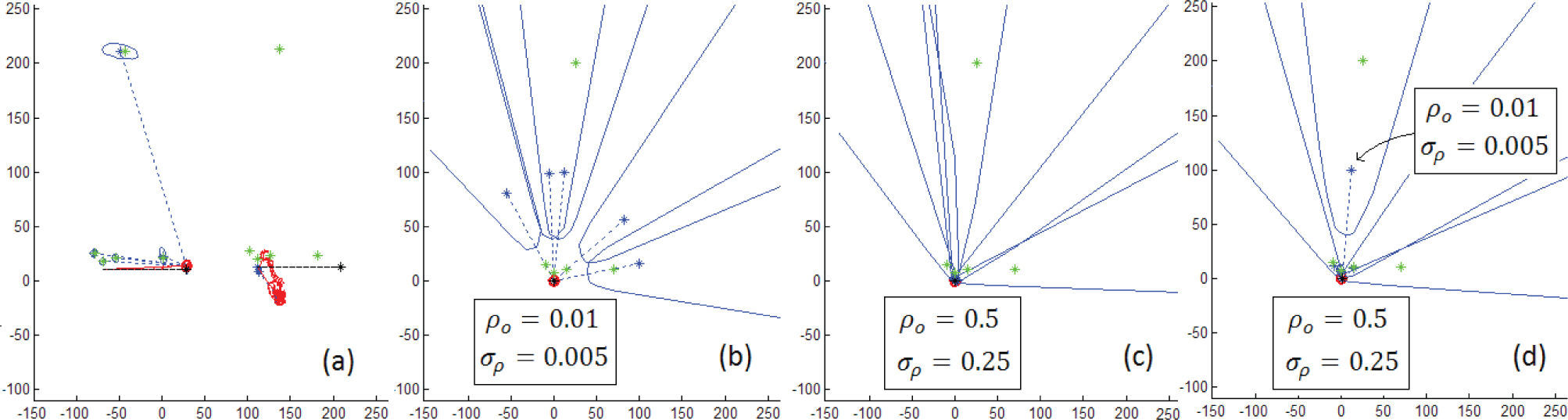
Considérese, por ejemplo, las pruebas experimentales ilustradas en la figura 4, en las cuales un vehículo equipado con odometría y un sensor angular (ambos con ruido), se desplaza por una línea recta (realizando SLAM) a través de un entorno, que contiene 5 características (4 cercanas a la trayectoria del vehículo y una más distante). El gráfico en la figura 4a ilustra tres casos encontrados en la estimación final del algoritmo, de izquierda a derecha: i) estimación final con una gran deriva (en rotación), ii) divergencia y iii) estimación correcta del algoritmo.

Figura 4.

Simulación del método PI-SR utilizando distintos parámetros iniciales de la profundidad inversa y su incertidumbre asociada (ρi_ni, σρ(i_ni)) para un vehículo desplazándose en línea recta a través de un entorno consistente en 4 características cercanas y una distante

Las pruebas consistieron en variar los parámetros iniciales (ρ_ini, σ_ρ(ini)) y observar el efecto en la estimación final, ejecutando 20 veces el algoritmo para cada caso. En el primer caso, (figura 4b) los parámetros iniciales fueron establecidos de manera que las características inicializaran a una distancia media entre el vehículo y la característica más distante (ρ_ini = 0.01, σ_ρ(ini) = 0.005). En este caso se encontró una gran deriva en las estimaciones finales para casi todas las ocasiones que se ejecutó el algoritmo.

En el siguiente caso, los valores iniciales fueron establecidos para inicializar las características de una posición cercana al vehículo (figura 4c) (ρ_ini = 0.5, σ_ρ(ini) = 0.25), aquí se encontró un deficiente porcentaje de convergencia (aproximadamente 50%), por lo que fue notoria la influencia de la característica más lejana, ya que al retirarla de la simulación (manteniendo los mismos valores iniciales) el porcentaje de convergencia se incrementó 80%.

Finalmente en el último caso (figura 4d) se utilizaron diferentes valores iniciales, dependiendo de la cercanía o lejanía de las características de acuerdo con el vehículo. Para las cuatro características cercanas se utilizaron valores iniciales ρ_ini = 0.5, σ_ρ(ini) = 0.25 y para la distante ρ_ini = 0.01, σ_ρ(ini) = 0.005. En este último caso se obtuvo una efectividad de 90%.

Con base en los resultados de las diferentes simulaciones realizadas, se puede inferir que la profundidad inversa inicial y su variancia asociada pueden tratarse previamente a su inclusión en el mapa (en lugar de utilizar valores preestablecidos), con tal de incrementar la efectividad del método.

Método por triangulación estocástica

En la sección anterior se observó que la sintonización manual de los parámetros iniciales mejora la efectividad del método PI-SR. Teniendo en cuenta este contexto, es razonable considerar la posibilidad de recolectar información acerca de la profundidad, previamente a la inclusión de las características en el mapa. En este sentido, la figura 5 muestra que unos cuantos grados de paralaje son suficientes para reducir significativamente la incertidumbre de la profundidad.

Figura 5.

Simulación que muestra el decremento de la incertidumbre en la profundidad de una característica con relación al incremento del ángulo de paralaje. Nótese que sólo unos grados de paralaje son suficientes para reducir considerablemente la incertidumbre en la estimación

La idea clave del método propuesto por los autores consiste en: i) estimar dinámicamente la profundidad inicial inversa ρ_ini de manera que ésta sea más consistente a su valor real y ii) incorporar directamente la incertidumbre relacionada con el proceso de estimación de ρ_ini en la matriz de covariancias del sistema cuando la característica es inicializada, en lugar de utilizar un valor inicial σ_ρ(ini).

En lo subsiguiente nos referiremos al enfoque propuesto como método por triangulación estocástica o (MTE).

a)

Puntos candidatos

Cuando una característica es detectada por primera vez, se almacena una parte del estado actual xˆ, la matriz de covariancias P y la medición del sensor. Estos datos λ_i se llaman puntos candidatos y están compuestos por

Los valores [x₁, y₁, θ₁] representan la posición actual del vehículo, [σ_1(x), σ_1(y), σ_1(θ)] representan sus variancias asociadas tomadas de la matriz de covariancias del estado P_k, y z₁ es la primera medición angular de la característica. En los instantes subsiguientes, la característica se rastrea hasta que se alcanza el umbral de paralaje mínimo α_min.

El paralaje α se estima utilizando (figura 6):

• i)

  la línea base de desplazamiento b.

• ii)

  λ_i y sus datos asociados.

• iii)

  el estado actual del vehículo xˆυ y la medición actual z_i.

Figura 6.

Parametrización del método MTE

b)

Estimación del paralaje

Cada ocasión que una nueva medición angular z está disponible para punto candidato λ_i, el ángulo de paralaje α se estima por

El ángulo β se determina mediante el vector direccional unitario h₁, y el vector b₁, definido por la línea base de desplazamiento b en la dirección de la trayectoria del vehículo.

El ángulo γ se determina de manera similar a β, pero utilizando el vector direccional unitario h₂, y el vector b₂, definido por la línea base de desplazamiento b en la dirección opuesta de la trayectoria del vehículo.

donde (h₁•b₁) es el producto escalar entre h₁ y b₁. El vector direccional h₁, expresado en marco de referencia absoluto W, apunta desde la locación del centro del vehículo a la dirección en donde la característica fue observada por primera vez, y se calcula utilizando los datos almacenados en λ_i.

El vector direccional h₂ expresado en el marco de referencia absoluto W se calcula de manera similar a h₁, pero utilizando la posición actual del vehículo xˆυ y la medición angular actual z_i.

b₁ es el vector que representa la línea base de desplazamiento del vehículo, entre la posición del centro del mismo, cuando la característica fue detectada por primera vez (x₁, y₁ almacenado en λ_i) y el centro de la posición actual del vehículo (x_v, y_v tomados de xˆυ). El vector b es el modulo de b₁ o b₂

c)

Inicialización en el estado y matriz de covariancias

Si el paralaje es mayor que un umbral (α > α_min) entonces λ_i es inicializado como una nueva característica ŷ_i. El umbral α_min puede ser establecido dependiendo la precisión del sensor angular. En el caso de la figura 5, donde σ_θ = 1° (típico valor en el caso de cámaras), se aprecia que la incertidumbre es considerablemente minimizada cuando α ≈ 10°.

Para cada nueva característica ŷ_new, los valores de x_i, y_i y θ_i se determinan de la misma manera que en (13). Con la diferencia de que en el método propuesto, la estimación inicial de ρ_i se determina por

La nueva característica ŷ_new se agrega al estado xˆ definida en (14).

En el método propuesto (MTE), la variancia σ_ρ de la profundidad inversa ρ se calcula dinámicamente por el proceso de inicialización (en lugar de una variancia predefinida heurísticamente como en el método PI-SR). En este sentido, las covariancias para la nueva característica ŷ_new son derivadas de la matriz de covariancias de errores de medición R_i y la matriz de covariancias del sistema P.

Por simplicidad R_i se define como una matriz diagonal (las covariancias cruzadas no se toman en cuenta) y está conformada por las variancias del sensor angular σ_z² (una por cada medición angular z₁ y z) y las variancias almacenadas en λ_i (σ_1(x), σ_1(y)) y σ_1(θ)). Nótese que el valor de σ_z es constante y no es almacenado previamente según se indica en (16).

La nueva matriz de covariancias del sistema, después de la inicialización, es

Donde J es el Jacobiano de la función de inicialización. Obsérvese que el método propuesto no implica la definición de una incertidumbre inicial para la profundidad σ_ρ(ini).

d)

Características distantes

Como es de esperarse, para ciertos tipos de entornos puede darse el caso de que características muy lejanas no produzcan paralaje (para trayectorias pequeñas con relación a la profundidad).

Agregar características cuya profundidad es sumamente incierta incide muy poco sobre la estimación de la locación x_v , y_v del vehículo, sin embargo, puede aportar información útil para la estimación de la orientación θυ.

En el método propuesto, si se desea incluir características distantes en el mapa, se puede considerar una línea base de desplazamiento mínima b_min, la cual se determina en función de las particularidades de la aplicación.

Entonces, en el caso de una característica distante, si b > b_min y no obstante α < α_min , ésta sería inicializada en el mapa como en el método PI-SR, pero utilizando valores iniciales ρ_ini, σ_ρ(ini) que tengan en cuenta la gran profundidad de la característica.

Un caso especial, en el cual una característica cercana no produce paralaje, se da cuando el vehículo se mueve exactamente en dirección de la característica (β ≈ 0°). En este trabajo se supone que se darán las condiciones necesarias para que se produzca paralaje en al menos una característica de las observadas a cada momento por el sensor.

En el caso de incluir características distantes en el mapa, y suponiendo que el vehículo no se mueve plenamente en la dirección de la característica (en nuestro trabajo se considera β > 20°), una posible forma de aproximar unos valores iniciales para ρ_ini, σ_ρ(ini) en función de α^min y ^b_min podría ser

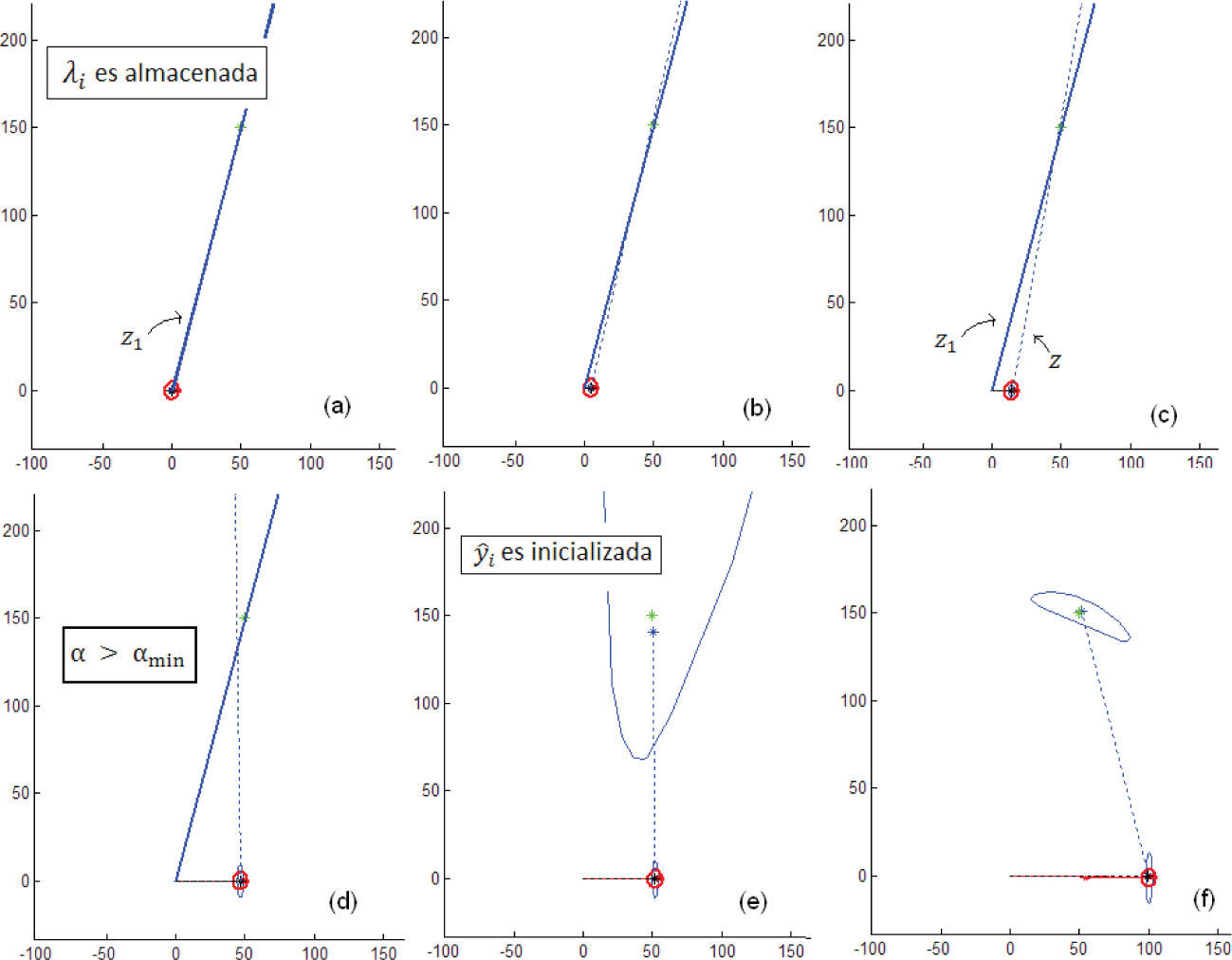
Resultados experimentales

a)

Simulaciones

La figura 7 muestra el proceso de inicialización de una sola característica por el método MTE; cuando un punto de referencia se observa por primera vez (figura 7a) se define un punto candidato λ_i. Mientras el vehículo se mueve realizando nuevas mediciones angulares, el paralaje α se estima repetidamente (figuras 7b, c y d). Si α > α_min (figura 7d) entonces se inicializa una nueva característica ŷ en el vector de estados del sistema y la matriz de covariancias (figura 7e). En esta simulación se utilizó α_min = 20° por claridad, mientras que en las simulaciones subsiguientes α_min = 10°.

Figura 7.

Proceso de inicialización mediante el método de la triangulación estocástica, MTE

En el entorno de pruebas ilustrado en la figura 4, el método MTE obtuvo 100% de efectividad. Es importante hacer notar que se realizaron numerosas pruebas mediante diversos entornos simulados, bajo distintas condiciones, cuyos resultados, por razones de espacio, no pueden mostrarse en este trabajo. Así pues, es muy importante resaltar que con el método propuesto también se presentaron numerosos casos de divergencia en las estimaciones del filtro. Sin embargo, el porcentaje de divergencia obtenido con el método MTE es en la mayoría de los casos menor con relación al porcentaje obtenido con el método PI-SR.

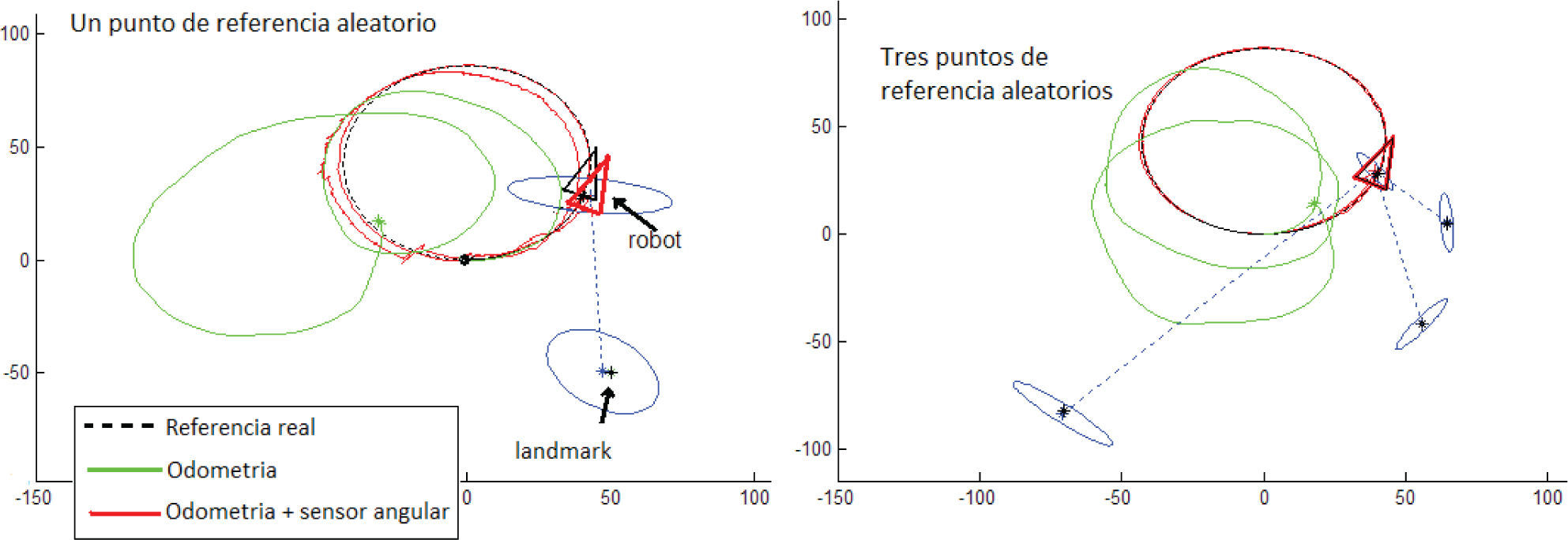
La figura 8 muestra resultados de la simulación del algoritmo MTE para una trayectoria circular. En este caso, se añadió a la odometría ruido gaussiano con una variancia de 0.01 (típico valor para sistemas basados en codificadores en las ruedas del robot). Para el sensor angular, se ha considerado una variancia σ_z = 5° (suponiendo poca precisión en el sensor). También se supone que el sensor angular puede rastrear los puntos de referencia sobre 360°. Obsérvese la mejora en la estimación de la trayectoria mediante el SLAM cuando se compara con la trayectoria estimada, utilizando únicamente la odometría. También puede observarse la mejora en la estimación de la trayectoria cuando se incluyen mayor número de características en el mapa.

Figura 8.

Simulación del algoritmo con puntos de referencia con posiciones aleatorias

b)

Experimentación con datos reales

El método propuesto por triangulación estocástica MTE, ha sido probado en distintos escenarios de SLAM con datos reales, obtenidos mediante distintos sensores angulares. Los resultados experimentales iniciales han sido reportados previamente por los autores en memorias de congreso (Munguía y Grau, 2007–2008).

SLAM con una sola fuente de sonido

El SLAM basado en sensores angulares usualmente se ha asociado con sistemas basados con visión artificial, probablemente porque las cámaras son, con diferencia, el sensor angular más usado en robótica. En este contexto el uso del sentido auditivo se ha explorado mucho menos en SLAM. En este caso, los autores proponen el uso de fuentes de sonido (artificiales o naturales) como puntos de referencia por el robot, para incluirlas como características del mapa en el proceso de SLAM.

En las simulaciones (sección anterior) se observó que una sola característica (observada de manera continua) es suficiente para corregir el error de la odometría de manera aceptable. Este hecho ha motivado a los autores a probar el algoritmo MTE en un robot real de construcción propia equipado con un sensor capaz de rastrear la única fuente de sonido.

En las simulaciones también se evidencia que el algoritmo trabaja mejor con un mayor número de características. Sin embargo, en una situación real, rastrear y discriminar entre varias fuentes de sonido, incrementa considerablemente la complejidad de la implementación. Existen diferentes propuestas en la literatura respecto al tratamiento de la problemática del sonido, sin embargo, están fuera del ámbito del presente trabajo.

Los experimentos consistieron en mover un pequeño robot móvil sobre una trayectoria predefinida, en modo de seguidor de líneas (para obtener una comparativa con una referencia real), mientras realizaba el seguimiento de una fuente de sonido.

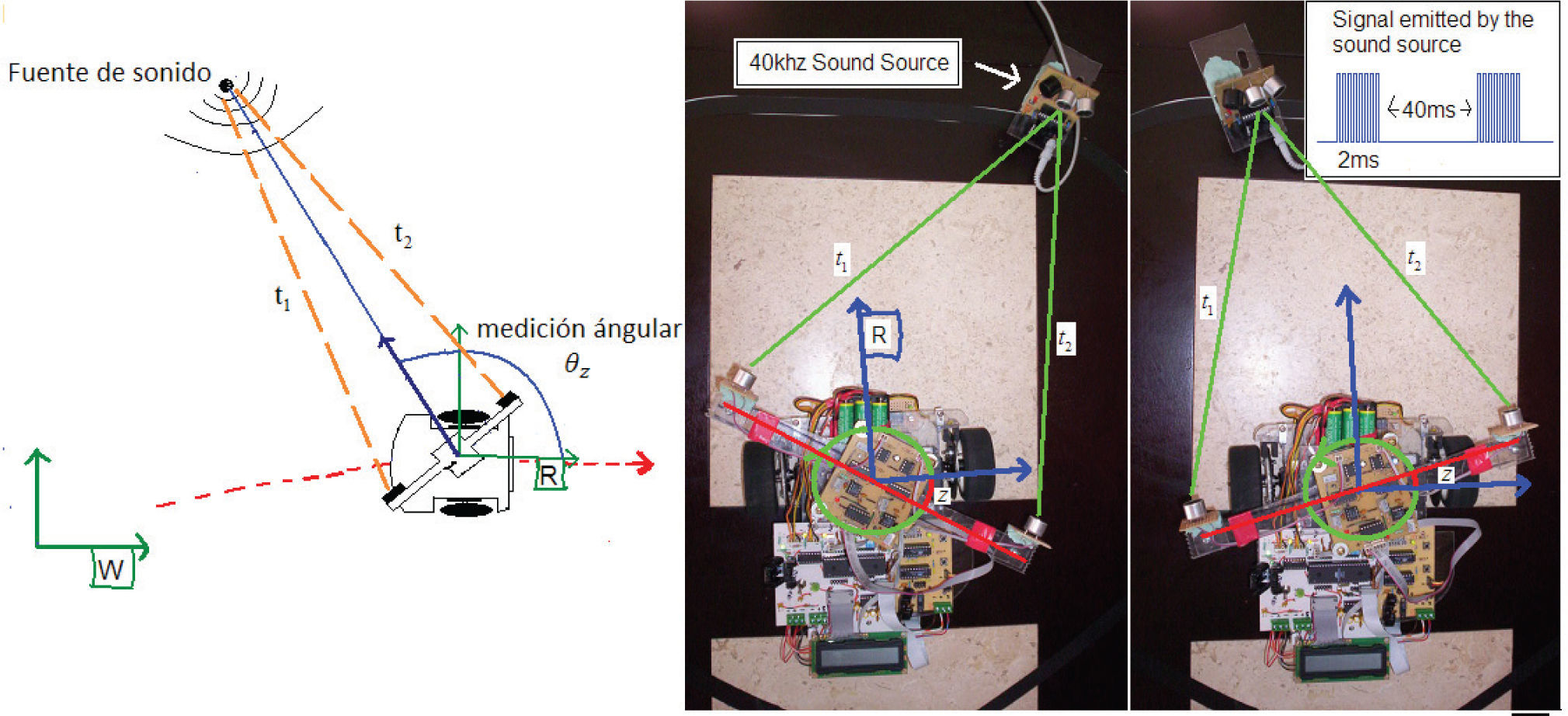
Para el sensor de sonido (figura 9), se ha desarrollado un cabezal rotatorio (de 360°), con dos receptores de ultrasonidos en sus extremos, los cuales reciben una señal estructurada de ultrasonidos emitida por una fuente. La diferencia de tiempos interaural (t₁ – t₂) se utiliza como retroalimentación para el controlador del servo del cabezal, el cual busca mantener siempre t₁ – t₂ = 0 tratando, de esta manera, de orientar el cabezal en dirección de la fuente de ultrasonidos. Con la implementación anterior, se obtuvo una modesta precisión angular de alrededor de ±15°.

Figura 9.

Con motivo de probar el método MTE con datos reales, se desarrolló un pequeño robot móvil diferencial (20 cm de eje), capaz de rastrear la dirección de la única fuente de ultrasonidos

La figura 10 muestra los resultados obtenidos con los datos capturados por los sensores del robot. Para una trayectoria en forma de óvalo (figura 10a) y para una trayectoria en forma de ocho (figura 10b). En el gráfico (b) se observa que después de 6 vueltas (alrededor de 24 metros de viaje) la trayectoria ha sido razonablemente bien recuperada con el algoritmo de SLAM, comparando las estimaciones y utilizando únicamente la odometría del robot.

Figura 10.

Estimaciones para dos trayectorias predefinidas para el robot: un ovalo (a) y un ocho (b). En ambos casos, después de varias vueltas, el error de la odometría es razonablemente bien limitado por el algoritmo de SLAM MTE.

SLAM Monocular

El SLAM monocular de 6-DOF, probablemente representa la variante más extrema del SLAM. En este caso, una webcam de bajo costo, desplazada libremente por su entorno, representa la única entrada sensorial del sistema (sin odometría ni sensado inercial o capacidad estéreo para la percepción de profundidad de manera directa). Para esta aplicación, un modelo de velocidad constante sin restricciones representa el movimiento de la cámara

siendo q((ω^w_k+Ω^w)Δt) el cuaternión definido por el vector de rotación (w^w_k+Ω^w)Δt. Para cada paso se supone una entrada incierta de aceleración lineal y angular con media cero y covariancia gaussiana conocida a^w y α^w, produciendo un impulso de velocidad lineal y angular: V^w = a^wΔt and Ω^w = α^wΔt. El estado de la cámara xˆ se define por

donde r^wc = [x, y, z] representa la posición del centro óptico de la cámara, q^wc = [q₀, q₁, q₂, q₃], representa, mediante un cuaternión, la orientación de la cámara y v^w = [v_x, v_y, v_z] y ω^w = [ω_x, ω_y ω_z] denotan las velocidades lineales y angulares, respectivamente. En este contexto una característica ŷ_i representa un punto i en una escena 3D definida por el vector de 6 dimensiones

el cual modela el punto 3D localizado en (figura 11)

donde x_i , y_i , z_i representa la posición del centro óptico de la cámara cuando la característica fue observada por primera vez, y θ_i, φ_i representa el acimut y la elevación (con respecto al marco de referencia global W) para el vector unitario m(θ_i, φ_i). La profundidad del punto d_i se codifica por su inversa ρi=1/di

Figura 11.

Parametrización en 6 grados de libertad (6 DOF)

Las diferentes posiciones de la cámara, conjuntamente con las posiciones de las características ya agregadas al mapa, se usan para predecir la posición de la característica h_i El modelo de observación de un punto ŷ_i desde una posición de la cámara define una línea expresada en el marco de referencia de la cámara como

h^c es observado por la cámara a través de su proyección en la imagen. R^cw es la matriz de transformación del marco de referencia global W al marco de referencia de la cámara C. La proyección se modela para una cámara de lente amplia. La búsqueda de las características se limita a regiones suscritas alrededor de la predicción h_i y con área definida por la matriz de innovación

donde H_i es el Jacobiano del modelo de observación con respecto al estado xˆ, P_k es la matriz de covariancias a priori del estado. Se suponen mediciones corrompidas por ruido Gaussiano con media cero y covarianza R. Si desea más detalles acerca de la adaptación del método MTE para su aplicación en SLAM monocular, consulte Munguía y Grau (2007).

Con el fin de validar experimentalmente el método MTE (en su variante de aplicación al SLAM monocular), se realizó una implementation del mismo en lenguaje MATLAB ©. Posteriormente se capturaron varias secuencias de video utilizando una cámara web de bajo costo. Durante la captura de los videos, la cámara web fue desplazada manualmente sobre trayectorias predefinidas (por ejemplo, tomando como referencia el contorno exterior de un escritorio). Después se ejecutó el algoritmo en modo fuera de línea, utilizando las secuencias de video capturadas previamente como señales de entrada.

Posteriormente se llevó a cabo una evaluación cualitativa del desempeño del algoritmo. Dicha evaluación consistió en comparar, mediante inspección, las estimaciones producidas por el algoritmo respecto a la trayectoria seguida por la cámara y la estructura tridimensional de la escena.

La figura 12 muestra resultados experimentales, para una secuencia de 790 fotogramas, capturados en un entorno en interiores (indoor), siguiendo una trayectoria similar a la curva frontal del escritorio (figura 13, izquierda). En este experimento se utilizó una cámara web Microsoft LifeCam Studio con interface USB. Esta cámara es capaz de adquirir video a color en alta resolución (HD), sin embargo, en estos experimentos se utilizaron secuencias de video en blanco y negro con una resolución de 424 × 240 pixeles, capturadas a 30 fotogramas por segundo.

Figura 12.

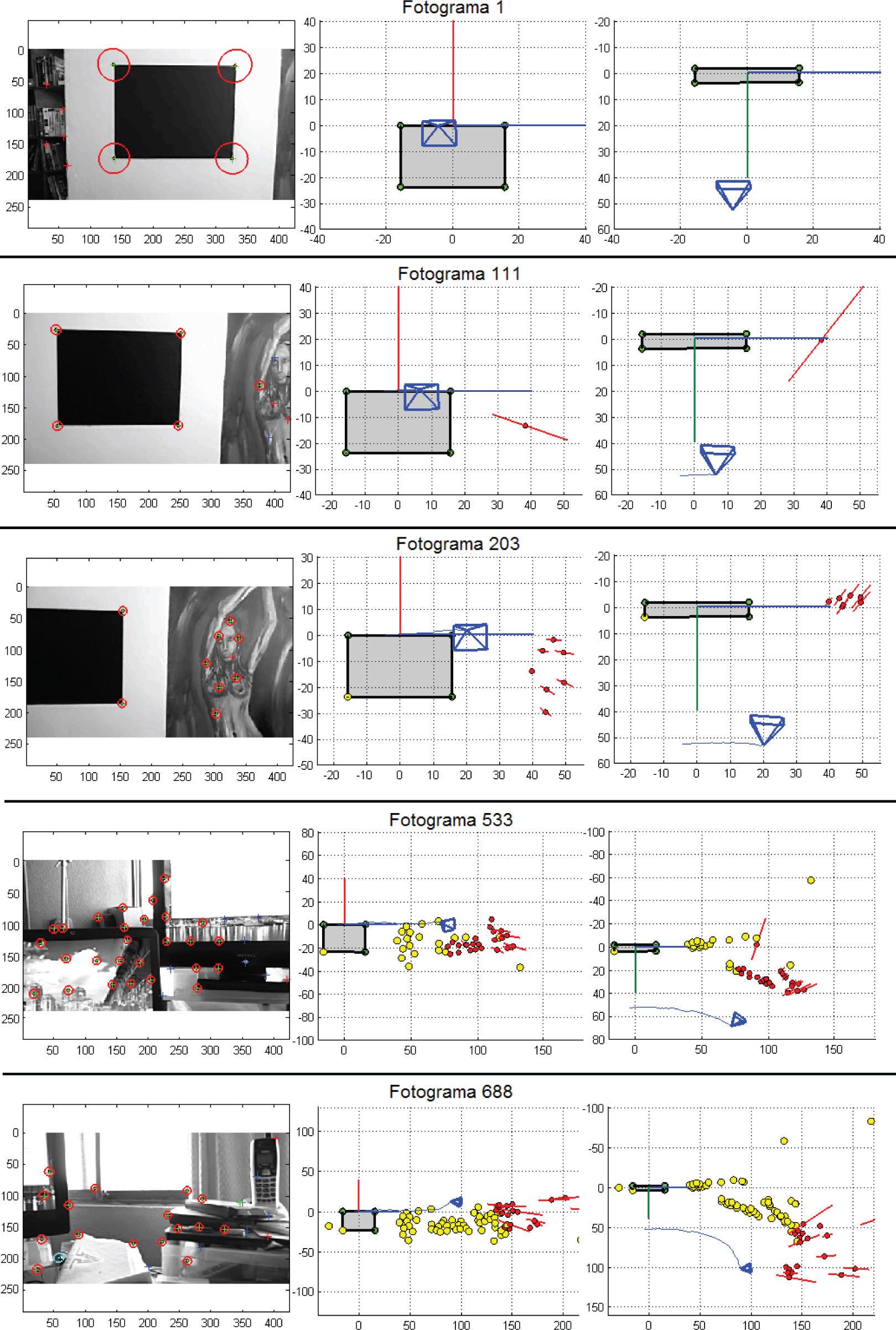
Estimación de la trayectoria de la cámara y la estructura de la escena a partir de una secuencia de video de 790 fotogramas, capturada en un entorno de escritorio. Se muestran los fotogramas 1, 111, 203, 533 y 688 (columna izquierda), así como la estimación del algoritmo para dichos fotogramas en una vista X-Y (columna central) y una vista X-Z (columna derecha)

Figura 13.

Imagen (compuesta) de la vista superior del entorno experimental (ilustración izquierda). Estimación, mediante el método MTE de la trayectoria de la cámara y la estructura de la escena a partir de 790 fotogramas (ilustración derecha). La escala de la gráfica se encuentra en centímetros. En esta figura se puede observar que tanto la trayectoria de la cámara como la estructura de la escena, fueron recobrados de manera satisfactoria. En ambas ilustraciones se agregan etiquetas para indicar la relación entre algunos objetos del entorno experimental y su correspondientes características del mapa

Una hoja de papel negra sobre un fondo blanco se utilizó como referencia métrica inicial (fotograma 1, figura 12). La posición de la referencia métrica inicial determina el origen del marco de referencia global del sistema. Encuentra más información acerca del procedimiento de inicialización en el SLAM monocular en Munguía y Grau (2007). En la figura 12, se puede observar cómo desde el primer fotograma son detectados algunos puntos candidatos (indicados en los fotogramas mediante una marca “+”). Sin embargo, la primera característica se inicializa en el mapa hasta el fotograma 111. En los fotogramas, las características del mapa están indicadas mediante marcas “+” circunscritas en elipsoides. Los elipsoides ilustran la incertidumbre en la predicción de la posición de las características en la imagen. Observe que en el fotograma 111 dos nuevos puntos candidatos han sido detectados (indicados en rojo), mientras que otros dos puntos candidatos se están rastreando (en azul). En ese momento (fotograma 111), el mapa está conformado por cinco características completamente inicializadas, cuatro de la cuales corresponden a la referencia métrica inicial y una que ha sido automáticamente inicializada en el sistema mediante el método MTE. En las gráficas que ilustran las estimaciones del algoritmo (columna central y derecha de la figura 12), se indica la incertidumbre de la profundidad de las características mediante líneas rojas graficadas en tres dimensiones.

En fotograma 203 (figura 12) se puede observar cómo dos características correspondientes a la referencia métrica han quedado fuera del campo de visión de la cámara, debido al movimiento translacional de la misma. En el mismo fotograma (203) se puede observar que otras características, correspondientes a una pintura localizada aproximadamente en el mismo plano que la referencia métrica inicial, han sido inicializadas en el mapa.

Así también, es posible observar que la incertidumbre en la profundidad de la primera característica inicializada en el mapa fue considerablemente minimizada. Al momento del fotograma 688 (figura 12), numerosas características han quedado fuera del campo de visión de la cámara (indicadas en amarillo), mientras que otras permanecen activas dentro del campo de visión de la misma (indicadas en rojo).

En la figura 13 se muestra desde una vista superior el entorno experimental (ilustración izquierda) así como las estimaciones para la trayectoria de la cámara y el mapa de características al final de la secuencia de video (fotograma 790), mediante una vista X-Z (ilustración derecha). En esta gráfica varios objetos se etiquetaron para ilustrar de mejor manera la reconstrucción de la escena. En este experimento, tanto la trayectoria de la cámara como la estructura de la escena, se reconstruyeron de manera satisfactoria a partir de la secuencia de video capturada por la cámara.

Conclusiones

El SLAM basado en sensores angulares ha recibido notable atención en años recientes por la comunidad robótica, debido principalmente a la versatilidad de las cámaras. Por otro lado, esta variante de SLAM requiere del uso de técnicas especiales de inicialización de características debido a su naturaleza parcialmente observable.

En este artículo se presentan diversos resultados producto de la investigación de los autores, respecto a la problemática del SLAM basado en sensores angulares. Particularmente se presenta un algoritmo llamado método por triangulación estocástica, el cual aborda el problema de la inicialización de nuevas características en el mapa. Dicho método está basado en la parametrización inversa de profundidad e implementa, mediante un retardo, una técnica de triangulación estocástica para definir una hipótesis para la profundidad inicial de las características.

En el SLAM basado en sensores angulares, el uso de una parametrización inversa para la profundidad de las características permite utilizar de manera directa un esquema estándar EKF en el proceso de estimación, simplificando de esta manera su implementación.

Por otro lado, en experimentos mediante simulaciones se observó que en ocasiones es necesario sintonizar manualmente los parámetros iniciales de la profundidad inversa para asegurar la efectividad de algoritmo. Este hecho motivó a los autores al desarrollo del método propuesto en el cual, se estiman de manera dinámica los parámetros iniciales de la profundidad inversa.

Se presentaron diversas simulaciones para demostrar la validez de la presente propuesta. De igual manera, se presentaron resultados experimentales obtenidos con el método propuesto para distintos escenarios de SLAM utilizando datos reales de sensores. Dichos escenarios experimentales consistieron en: i) un pequeño robot móvil capaz de rastrear la dirección de arribo de una fuente de ultrasonidos y ii) un contexto de SLAM monocular en 6 DOF, en el que una cámara web, capaz de moverse libremente por su entorno, representa la única entrada sensorial del sistema.

Es importante mencionar que un beneficio de los métodos sin retardo, reside en el hecho de que las características proveen información acerca de la orientación del sensor desde el principio. Por otro lado, en los métodos con retardo (como el propuesto en este trabajo) puede ser útil esperar hasta que el movimiento del sensor produzca algunos grados de paralaje (por tanto, recabando información de profundidad) con el objetivo de mejorar la robustez del sistema. Más aún, cuando se usan cámaras en entornos reales densos y dinámicos, el retardo puede utilizarse para rechazar características débiles antes de su inclusión en el mapa.

Al tenor de los resultados experimentales, se considera que el método propuesto es una buena opción para su implementación en sistemas de SLAM basados en sensores angulares.