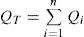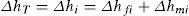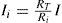En este trabajo se presenta el diseño de un controlador proporcional difuso (CPD), como una solución propuesta al problema de desacoplamiento sin contar con el modelo matemático del sistema y basándose únicamente en la información del error y los principios físicos del sistema. El CPD se aplica a un sistema de tuberías en paralelo, el cual por su dinámica natural se comporta como acoplado y mediante un conjunto adecuado de reglas difusas (basadas en el error entre la entrada y la salida) se logró como resultado un comportamiento desacoplado sobre el sistema. Se eligió este sistema por la importancia de cuidar y optimizar el uso del agua, ya que la escasez, el cambio climático y la contaminación afectan a este vital líquido. Además es importante resaltar que el problema no ha sido abordado desde el enfoque aquí propuesto, prescindiendo de un modelo matemático. Los resultados se presentan mediante simulaciones.
This paper presents the design of a Fuzzy Proportional Controller (FPC) as a proposed solution of the decoupling problem without the mathematical model of the system and based only on error information and the physical principles of the system. The FPC is applied in a parallel piping system, which by its natural dynamic behavior is coupled, and with a suitable set of fuzzy rules (based on the error between the input and output), such that the system is decoupled. This system was chosen in order to care and optimize the use of the water due to the drought, climate change, and pollution that affects this vital fluid. It is also important to note that the decoupling problem has not been approached without a mathematical model as in this paper. The results are shown by simulations.
El comportamiento dinámico de un sistema se ve afectado por las variables manipuladas (válvulas, interruptores, relevadores, potenciómetros, calefactores, ventiladores, etcétera). Los efectos de esas variables se pueden ver reflejados en una o más variables controladas del sistema (temperaturas, niveles, presiones, velocidad, concentraciones, posición, entre otras) que bajo ciertas condiciones se desean mantener en un valor determinado. Cuando en el sistema intervienen más de una variable de entrada y de salida se le conoce como un sistema MIMO (multiple input multiple output), en el cual está presente el problema de interacción o acoplamiento entre las variables (figura 1). En los sistemas MIMO una entrada puede afectar a más de una salida debido al acoplamiento, lo que puede tener el resultado de no alcanzar los objetivos de control. Cuando el sistema MIMO tiene el mismo número de entradas que salidas se le conoce como sistema regular.
Cuando el acoplamiento en un sistema no permite lograr los objetivos de control, una alternativa es que el sistema MIMO se pueda transformar en varios sistemas SISO (simple input simple output) donde sólo una entrada afecta una sola salida, a lo cual se le conoce como desacoplamiento regular (figura 2). Esta estructura es deseable en un gran número de aplicaciones donde la interacción entre las variables controladas y manipuladas afecta el control del sistema, tal como en los sistemas de calefacción, ventilación y aire acondicionado (o HVAC), procesos de cristalización de penicilina, columnas de destilación, entre otros.
El problema de desacoplamiento ha sido abordado desde diferentes enfoques: lineal (Orozco et al., 2012; Wang, 2003), difuso (AL-Niami y Mehdi,1993; Wang et al., 2011), adaptativo (Ren y Fan, 2005), entre otros. Estas soluciones están basadas en un modelo matemático del sistema a desacoplar, es decir, se tienen que conocer las ecuaciones dinámicas que aproximen, en la medida de lo posible, el comportamiento real del sistema. Sin embargo, esta tarea no siempre resulta fácil para el diseñador, pues cuando en el sistema interviene una gran cantidad de variables, obtener una representación es una tarea difícil. Además deben considerarse las características del sistema, es decir, si el sistema es no lineal o lineal, variante o invariante en el tiempo. Es importante resaltar que en los sistemas reales, existen procesos donde su dinámica es muy compleja o exhiben características altamente no lineales lo cual dificulta obtener un modelo matemático o satisfacer especificaciones de desempeño con métodos de control lineal convencional.
Una alternativa para alcanzar el desacoplamiento de un sistema complejo sin contar con un modelo matemático es basarse en la lógica difusa, ya que esta teoría acerca más la forma de hacer diseño de control con la forma de pensar humana a pesar de no contar con tal modelo y de no saber si el sistema es no lineal, variante en el tiempo, etcétera Así, si en un sistema real, existe un experto en el manejo del mismo sin tener una representación matemática y además el experto sabe cómo conseguir un comportamiento desacoplado, entonces, pueden plantearse un conjunto de reglas heurísticas que logren este objetivo de desacoplamiento.
Los trabajos relacionados con el problema de desacoplamiento basándose en lógica difusa, utilizan el modelo matemático del sistema para proponer un controlador difuso basado en el error y su derivada del error de la entrada con respecto a la salida que se desea. Algunos trabajos relacionados con esta idea fueron analizados por Chao et al. (2005) en la que realizaron una investigación sobre la aplicación del desacoplamiento difuso en un proceso de cristalización de penicilina, basado en el modelo matemático del sistema, el error y su derivada. Sus resultados de simulación muestran que el método de desacoplamiento difuso mejora el desempeño del control significativamente comparado con un control de desacoplamiento convencional. Demostraron además que el método de desacoplamiento difuso tiene robustez ante errores de modelado. Otro trabajo relacionado es el propuesto por Wang et al. (2011) que aplicaron el desacoplamiento difuso al control de una caldera, donde también se basaron en el modelo matemático del sistema, en el error y la derivada del error. Ellos propusieron el uso de dos controladores, un PID y un controlador difuso desacoplante; sus resultados de simulación indican que el esquema de control propuesto tiene buena habilidad de desacoplamiento, características dinámicas y robustez. Por otro lado, Delgado y Orozco (2011) proponen una solución al problema de desacoplamiento basado en la información de la señal del error de un sistema de tanques interconectados y proponen un conjunto de reglas difusas para el diseño de un controlador proporcional derivativo (PD) difuso, el cual desacopla parcialmente un sistema de tanques.
El problema de desacoplamiento también se ha aplicado para rechazar perturbaciones en los sistemas en lugar de analizarlos desde el punto de vista de entradasalida como se considera en el presente trabajo. Algunos trabajos de desacoplamiento difuso de perturbaciones han sido propuestos por Guo et al. (2008) y Therese et al. (2012), los cuales basan sus resultados en el conocimiento de un modelo matemático y el comportamiento del error, el primero considera el comportamiento del error en tres instantes de tiempo y el segundo en la integral del error absoluto y la integral del error absoluto del tiempo.
Todos los trabajos acerca del desacoplamiento difuso revisados anteriormente, basan sus resultados en el conocimiento de un modelo matemático descriptivo de la dinámica del sistema, en el error y su variación del error, por lo que, esto nos lleva a preguntarnos ¿qué pasa cuando no es posible obtener un modelo matemático?, ¿cómo se puede lograr el desacoplamiento cuando no es posible contar con el modelo matemático?
Este artículo propone una solución al problema de desacoplamiento prescindiendo del modelo matemático, para esto se considera un controlador difuso tipo Mamdani que desacopla el sistema basándose en los principios físicos que describen a ese sistema. Como caso de estudio se considera un sistema de riego por aspersión del cual el experto sólo debe conocer los principios básicos de continuidad y de pérdidas de carga.
Control con lógica difusaPara aplicar la teoría de control difuso (Passino y Yurkovich, 1998) al problema de desacoplamiento es necesario que exista conocimiento experto sobre el funcionamiento del sistema. En general si no existe este conocimiento la lógica difusa no puede aportar una solución. Cuando el conocimiento experto existe y se puede transcribir en reglas difusas, se permite emplear la lógica difusa prescindiendo de un modelo matemático del sistema. Cabe mencionar que el problema de desacoplamiento difuso, como se mostró en los antecedentes, en todos los casos está basado en un modelo matemático, en el error y su variación del error. Por lo tanto, aplicar la lógica difusa al problema de desacoplamiento se considera como una alternativa viable.
A continuación se describe el caso de estudio del sistema de riego en paralelo.
Caso de estudioEl sistema de riego en paralelo a considerar, es un sistema MIMO regular, consta de una tubería principal de la cual se desprenden 3 tuberías secundarias en forma paralela a la tubería principal y cada una de estas tuberías secundarias constan de una válvula proporcional de comportamiento lineal, la cual regula el flujo de agua (figura 3).
El sistema de la figura 3 se aproxima a los sistemas de riego por aspersión y distribución ampliamente utilizados a nivel agrícola, que pudiera ser un dispositivo móvil de riego, el cual propone como mejora que el sistema de riego se adapte a las necesidades de riego de diferentes cultivos, controlando la presión y el gasto en cada válvula. De esta manera se logra un mejor uso del agua y se favorecen los cultivos ya que sólo se administra el agua requerida.
Los sistemas de riego de distribución de agua cumplen con el principio básico de continuidad (Saldarriaga, 2007), el cual se representa en la ecuación 1.
dondeQT = caudal total
Qi = caudal a través de cada rama paralela
i = 1, 2, …, n es el número de ramas en paralelo.
Así mismo, la pérdida de carga total es igual a la pérdida de carga en cada una de las tuberías del sistema, lo cual se representa en la ecuación 1 (Saldarriaga, 2007).
dondei = i-ésima rama paralela
hji = pérdidas por fricción en el tramo j de la rama i
hmi = pérdidas menores en el accesorio m de la rama i.
Para entender mejor el sistema de referencia y poderlo simular en Matlab se estableció una analogía de este sistema a través de un circuito eléctrico, donde la corriente del circuito se comporta como el flujo de la tubería y las válvulas proporcionales lineales son potenciómetros lineales. El circuito que representa el sistema hidráulico se muestra en la figura 4.
El comportamiento del sistema real se representa por el circuito eléctrico mostrado en la figura 4, pues la división de corrientes en circuitos eléctricos se comporta de forma similar a la ecuación de continuidad 1 y la división de voltajes, a las pérdidas de carga de la ecuación 2. Para establecer la analogía del sistema de tuberías y el circuito eléctrico se considera que las ecuaciones de equilibrio que gobiernan el comportamiento de los sistemas eléctricos son las leyes de Kirchhoff de voltaje y corriente, las cuales establecen la siguiente ley de voltaje de Kirchhoff (ecuación 3): la suma algebraica de las caídas de tensión a lo largo de una trayectoria cerrada es cero.
Ley de corrientes de Kirchhoff: la suma algebraica de las corrientes en un nodo es igual a cero, en otras palabras, la suma de las corrientes que entran a un nodo debe ser igual a la suma de las corrientes que salen del mismo nodo, ecuación 4.
La regla divisora de voltaje determina cómo se dividirá la corriente que entra en los elementos del grupo de ramificaciones en paralelo. Para dos elementos en paralelo de igual valor, la corriente se dividirá equitativamente en el sistema de tuberías en paralelo, esto significa que si dos válvulas de las tuberías se abren de igual forma el flujo será el mismo en ambas.
Para los elementos en paralelo con valores distintos, entre más pequeña sea la resistencia mayor será la corriente de entrada, para el sistema de tuberías, si una válvula ofrece muy poca resistencia fluídica entonces el flujo será mayor. En la ecuación 5 se representa el valor de la corriente para un elemento en paralelo del circuito eléctrico:
dondeIi = corriente en la i-ésima rama paralela
RT = resistencia total en paralelo del circuito
I = corriente total
Ri = resistencia en la i-ésima rama paralela.
Ambos sistemas se caracterizan por comportarse de manera análoga, pues por ser sistemas de energía hidráulica y eléctrica, respectivamente, cumplen con el principio de conservación de la energía, la cual es una ley fundamental de la física.
En este trabajo se considera que en el sistema de tuberías, la bomba es la fuente de potencial fluídico, ya que impulsa al líquido a través de la tubería; en el circuito eléctrico esta energía la proporciona la fuente de voltaje. Una vez que fluye el agua en el sistema de tuberías, se establece un gasto deseado para cada rama paralela que depende directamente de la presión del fluido, la cual es igual para cada rama paralela, y de la apertura de la válvula, ésta última gobernante del paso del líquido. En el circuito eléctrico, esta energía de presión se representa como el voltaje presente en la rama paralela y el potenciómetro es el gobernante del paso de la corriente. Por lo tanto, se considera que la bomba proporciona un caudal constante, es decir, el voltaje del circuito es constante también. Si se desea disminuir el gasto en alguna de las ramas, se tendrá que cerrar la válvula correspondiente para lograrlo, pero por el principio de continuidad (ecuación 1), el fluido que deja de circular por la rama que tuvo una disminución, tendrá que ser absorbido por las demás ramas de cierta forma, afectando el gasto en ellas, lo que es visto como acoplamiento.
Si el objetivo de control es el desacoplamiento, es necesario determinar de qué manera se puede conseguir una dinámica del funcionamiento tanto de la bomba como de las válvulas, de tal manera que se modifiquen los gastos en las ramas paralelas sin afectarse entre sí. La propuesta de desacoplamiento mediante la lógica difusa basa su metodología a partir de un conocimiento experto sobre cómo manipular el sistema de tuberías y conseguir el objetivo de control regulando adecuadamente tanto la bomba como las válvulas, haciendo que el sistema tenga cambios en los flujos de cada una de las ramas paralelas sin afectarse entre sí.
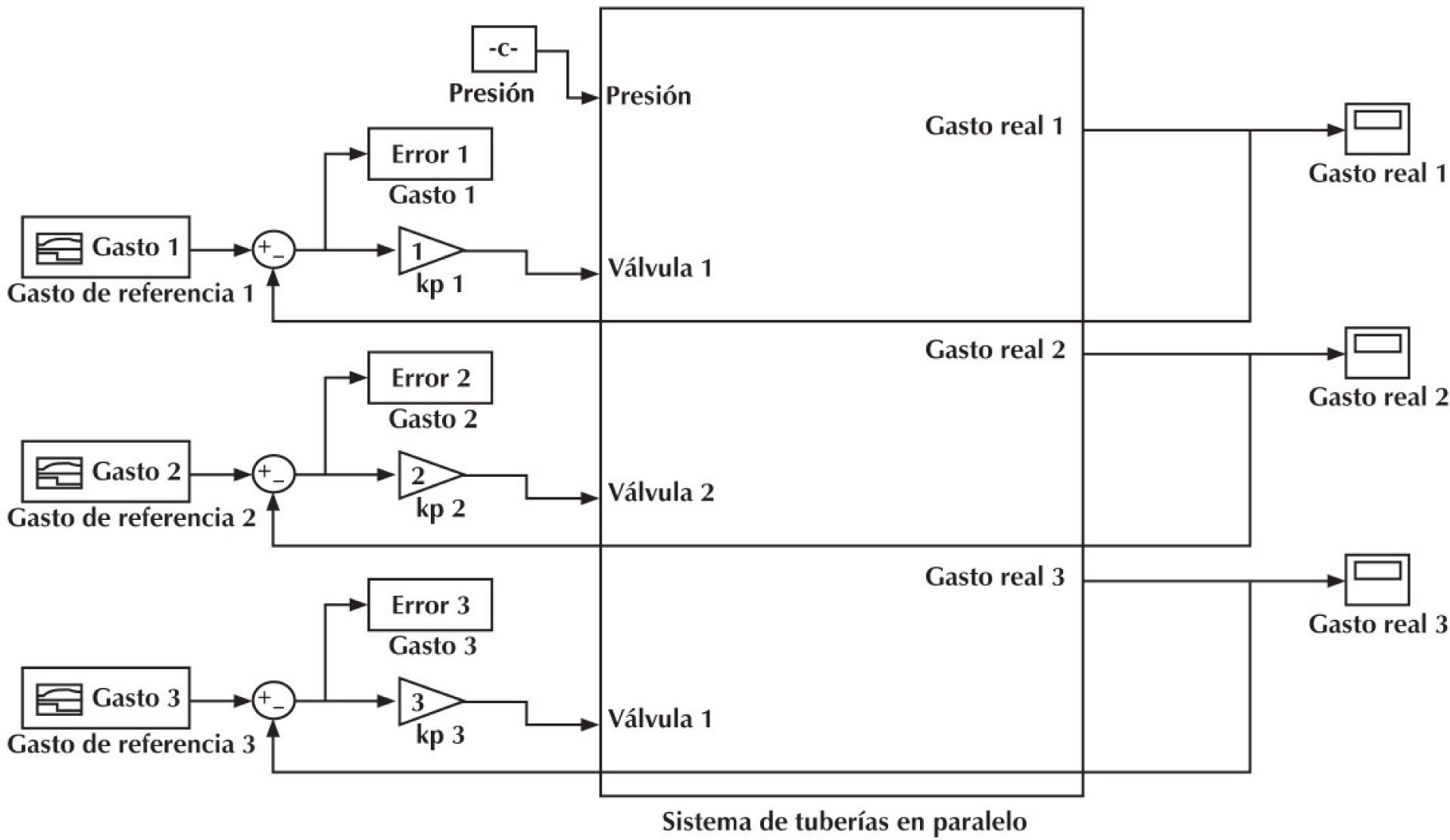
Por ejemplo, si se disminuye el gasto en alguna rama y se desea no afectar a las demás, la acción sobre el sistema será disminuir el gasto para que sólo satisfaga la demanda necesaria del sistema, de igual forma si la demanda aumenta, entonces el gasto debe aumentar para satisfacer lo necesario. Esta forma de control se asemeja a un controlador proporcional. Para verificar que este comportamiento desacoplado se podría lograr, se simuló en Matlab el sistema mostrado en la figura 4, el cual está representado en el bloque llamado “sistema de tuberías en paralelo” de la figura 5. En este diagrama se consideró un bloque de ganancia unitaria que representa un controlador proporcional; las entradas son señales de demanda de flujo aleatorias, es decir, existe variación en la demanda de flujo para ciertos lapsos de tiempo. El bloque que ingresa el valor de la presión es constante para cada rama paralela, que como ya se comentó en este sistema la presión es igual para cada rama. El controlador proporcional (P) determina el valor para cada válvula y la información del error entre el flujo deseado y el real es el conocimiento experto. Entonces, con esta información, es posible traducir este error en un controlador proporcional difuso (CPD) el cual puede conseguir el mismo objetivo de control.
De la simulación mostrada en la figura 5, se obtiene la base del conocimiento experto (error), el cual se verá con detalle en la sección 2.6, para no perder secuencia con el diseño del controlador difuso que a continuación se propone.
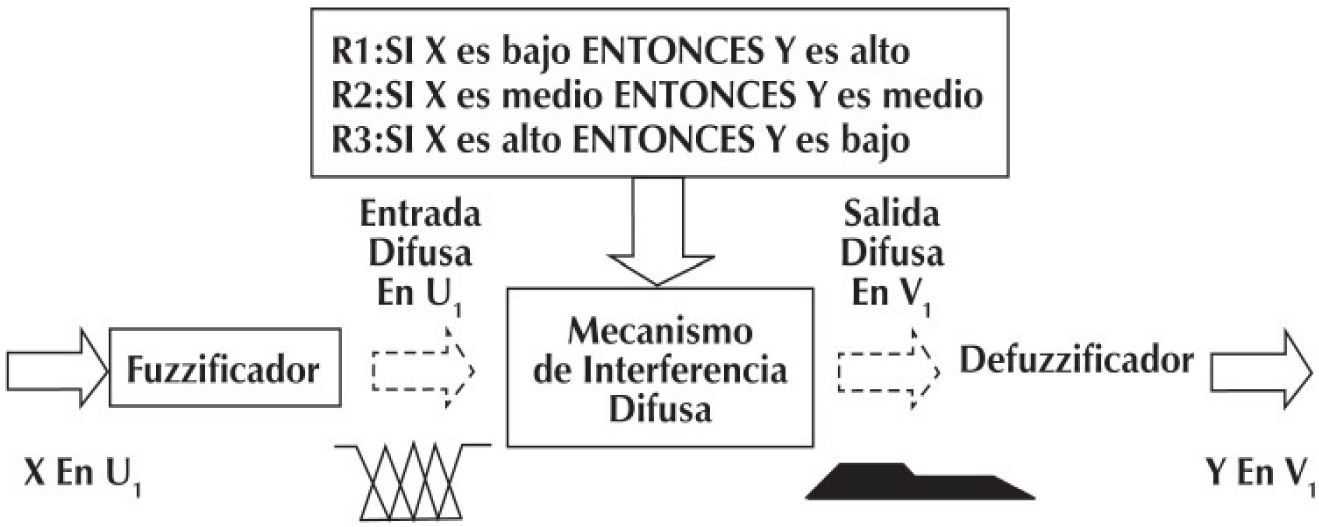
Sistema de control difuso tipo Mamdani para el sistema de riegoAl desarrollar un controlador difuso es posible prescindir de la rigidez matemática y transmitir el raciocinio humano a un sistema, en este caso el experto. El diagrama de bloques del control difuso que se utilizará es del tipo Mamdani, que se muestra en la figura 6, el cual está compuesto por el fuzificador, el mecanismo de inferencia, la base de las reglas y el defuzificador.
La entrada de un sistema de lógica difusa tipo Mamdani normalmente es un valor numérico adquirido, por ejemplo de un sensor, en este caso, y ese valor proviene de un valor real del gasto en alguna de las 3 válvulas. Para que este valor pueda procesarse en el sistema difuso se hace necesario convertirlo a una variable del lenguaje difuso que el mecanismo de inferencia pueda procesar. Estos valores difusos son los niveles de pertenencia de los valores de entrada a los diferentes conjuntos difusos en los cuales se ha dividido el universo de discurso.
Para definir un conjunto difuso, se utiliza cualquier función de membresía, sin embargo, existen funciones que son más utilizadas debido a su simplicidad matemática, entre ellas podemos mencionar las funciones de tipo triangular, trapezoidal y gaussiana, entre otras. El tipo de función de membresía a utilizar en este trabajo es de tipo triangular por su sencilla implementación, pudiéndose extender a otro tipo. Las funciones de membresía de las variables lingüísticas de entrada-salida del sistema de tuberías se describen a continuación.
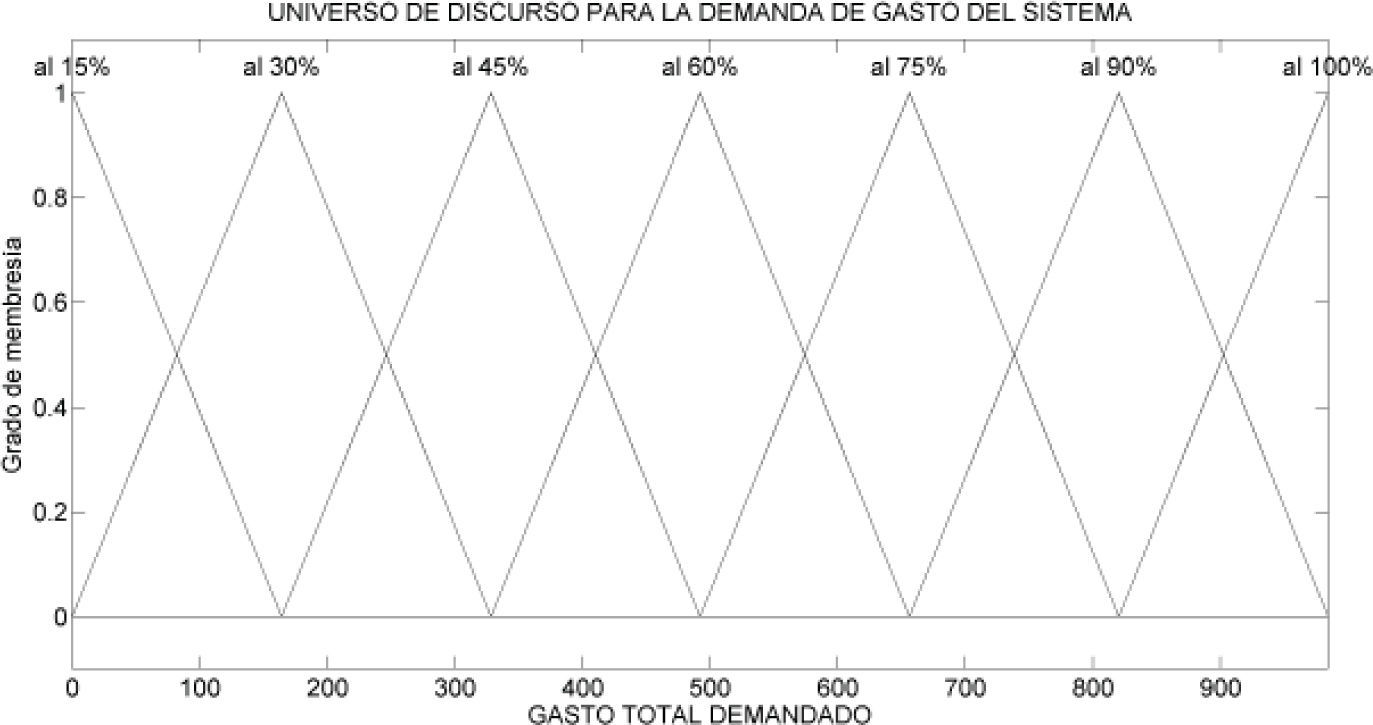
Consideremos como universo de discurso de la variable de entrada para el control del gasto de la bomba el flujo total demandado por el sistema. Para clasificar los conjuntos difusos del universo de discurso de esta variable de entrada, se proponen 7 conjuntos, los cuales se denotan como: demanda de gasto de 0 a 15%, demanda de gasto de 15 a 30%, demanda de gasto de 30 a 45%, demanda de gasto de 45 a 60%, demanda de gasto de 60 a 75%, demanda de gasto de 75 a 90% y demanda de gasto de 90 a 100%, los cuales se muestran en la figura 7.
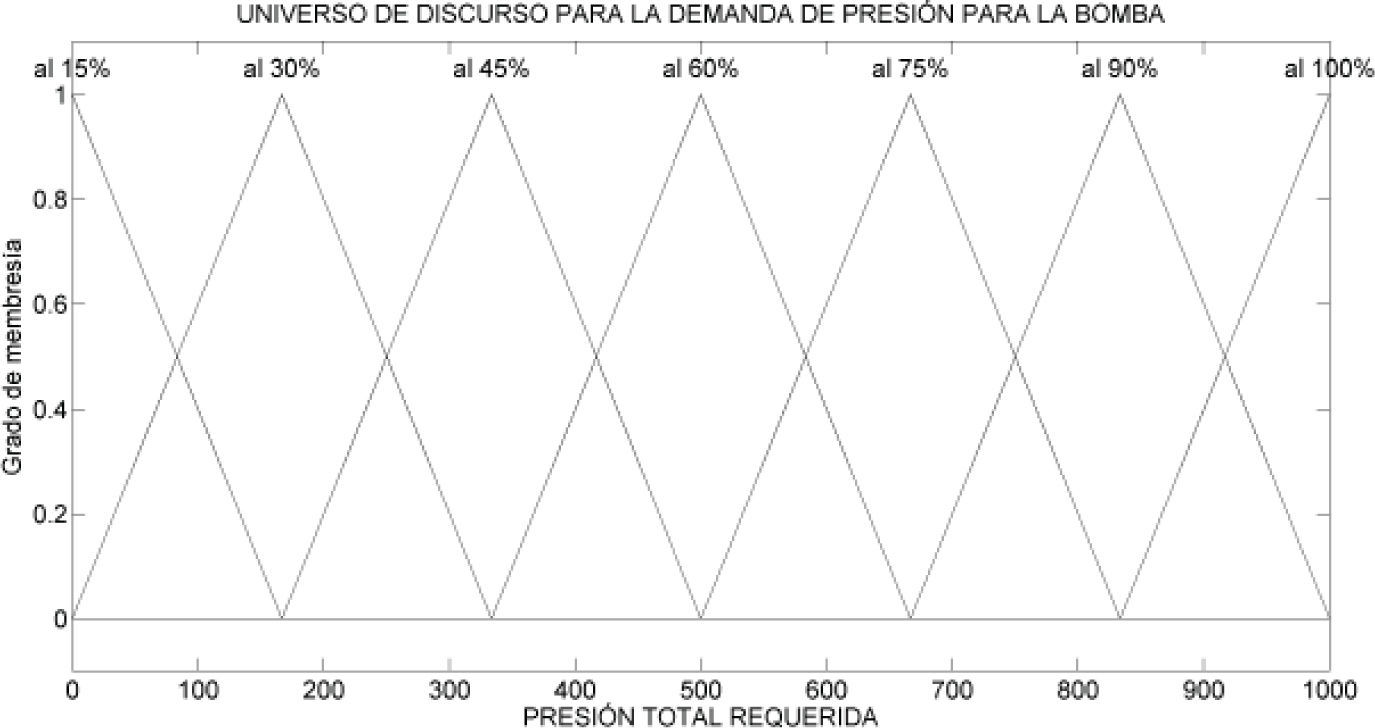
El universo de discurso de la variable de salida es la demanda de presión de la bomba. Para esta salida se proponen 7 conjuntos difusos los cuales son: demanda de presión del 0 a 15%, demanda de presión de 15 a 30%, demanda de presión de 30 a 45%, demanda de presión de 45 a 60%, demanda de presión de 60 a 75%, demanda de presión de 75 a 90%, demanda de presión de 90 a 100%. En la figura 8 se aprecian las funciones de membresía propuestas.
Ahora, se considera el universo de discurso del flujo demandado por la tubería gobernada por la válvula 1, es decir, el error del gasto 1. Se considera también una variable lingüística para clasificar los conjuntos difusos del universo de discurso de esta variable, la cual se divide en 7 conjuntos difusos: error negativo alto (NA), error negativo medio (NM), error negativo pequeño (NP), gasto ideal (FI), error positivo pequeño (PP), error positivo medio (PM) y error positivo alto (PA), vea la figura 9.
El universo de discurso de las variables lingüísticas de apertura de la válvula 1 proporcional son: abrir totalmente (AT), abrir medianamente (AM), abrir un poco (AP), mantener (M), cerrar un poco (CP), cerrar medianamente (CM), cerrar totalmente (CT). En la figura 10 se aprecia esta definición de variables lingüísticas.
La obtención de los universos de discurso para las válvulas 2 y 3 se hace de manera análoga a lo mostrado para la válvula 1.
Mecanismo de inferencia del CPDAsí, teniendo los diferentes niveles de pertenencia arrojados por el fuzificador, éstos deben ser procesados para generar una salida difusa. La tarea del sistema de inferencia es tomar los niveles de pertenencia y, apoyado en la base de reglas, generar la salida del sistema difuso. La base de las reglas es la manera que tiene el sistema difuso de guardar el conocimiento lingüístico que le permiten resolver el problema para el cual se diseñó, estas reglas son del tipo SI-ENTONCES (IF-THEN).
Para el CPD que controla la presión de la bomba, la base de las reglas se da en la tabla 1, la cual contiene siete conjuntos de entrada difusos y siete conjuntos de salida difusos.
Base de las reglas del CPD gasto-presión
| Salida: presión: P | ||||||||
|---|---|---|---|---|---|---|---|---|
| Bomba | 0 a 15% | 15 a 30% | 30 a 45% | 45 a 60% | 60 a 75% | 75 a 90% | 90 a 100% | |
| Entrada: demanda total de gasto: QT | 90 a 100% | 90 a 100% | 90 a 100% | 90 a 100% | 90 a 100% | 90 a 100% | 90 a 100% | 90 a 100% |
| 75 a 90% | 75 a 90% | 75 a 90% | 75 a 90% | 75 a 90% | 75 a 90% | 75 a 90% | 75 a 90% | |
| 60 a 75% | 60 a 75% | 60 a 75% | 60 a 75% | 60 a 75% | 60 a 75% | 60 a 75% | 60 a 75% | |
| 45 a 60% | 45 a 60% | 45 a 60% | 45 a 60% | 45 a 60% | 45 a 60% | 45 a 60% | 45 a 60% | |
| 30 a 45% | 30 a 45% | 30 a 45% | 30 a 45% | 30 a 45% | 30 a 45% | 30 a 45% | 30 a 45% | |
| 15 a 30% | 15 a 30% | 15 a 30% | 15 a 30% | 15 a 30% | 15 a 30% | 15 a 30% | 15 a 30% | |
| 0 a 15% | 0 a 15% | 0 a 15% | 0 a 15% | 0 a 15% | 0 a 15% | 0 a 15% | 0 a 15% | |
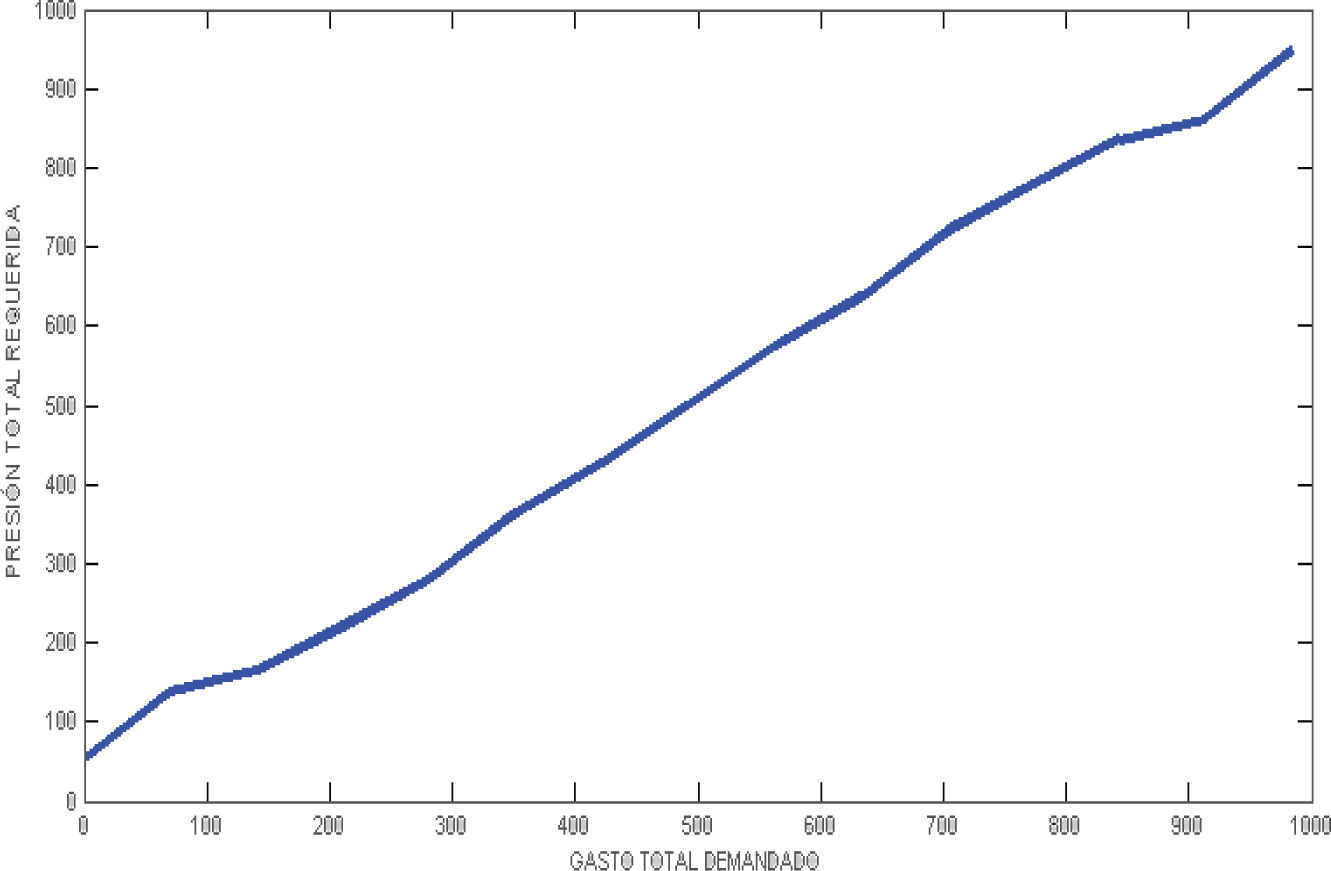
Donde QT, es el gasto que demanda el sistema y P es la presión requerida. La gráfica generada por esta base de reglas se muestra en la figura 11.
Se observa, que la demanda de gasto del sistema requiere de una presión en forma proporcional. Los rangos mostrados en la figura 11, se eligieron arbitrariamente, siendo la demanda máxima de gasto igual a 1000lts/min y la demanda máxima de presión igual a 1000kg/cm2.
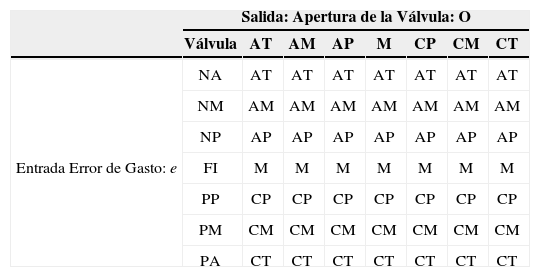
Para el CPD que controla el gasto en cada una de las ramas paralelas de la tubería, se tiene que la base de las reglas está dada en la tabla 2, la cual contiene siete conjuntos de entrada difusos y siete conjuntos de salida difusos.
Base de las reglas del CPD para la apertura de las válvulas
| Salida: Apertura de la Válvula: O | ||||||||
|---|---|---|---|---|---|---|---|---|
| Válvula | AT | AM | AP | M | CP | CM | CT | |
| Entrada Error de Gasto: e | NA | AT | AT | AT | AT | AT | AT | AT |
| NM | AM | AM | AM | AM | AM | AM | AM | |
| NP | AP | AP | AP | AP | AP | AP | AP | |
| FI | M | M | M | M | M | M | M | |
| PP | CP | CP | CP | CP | CP | CP | CP | |
| PM | CM | CM | CM | CM | CM | CM | CM | |
| PA | CT | CT | CT | CT | CT | CT | CT | |
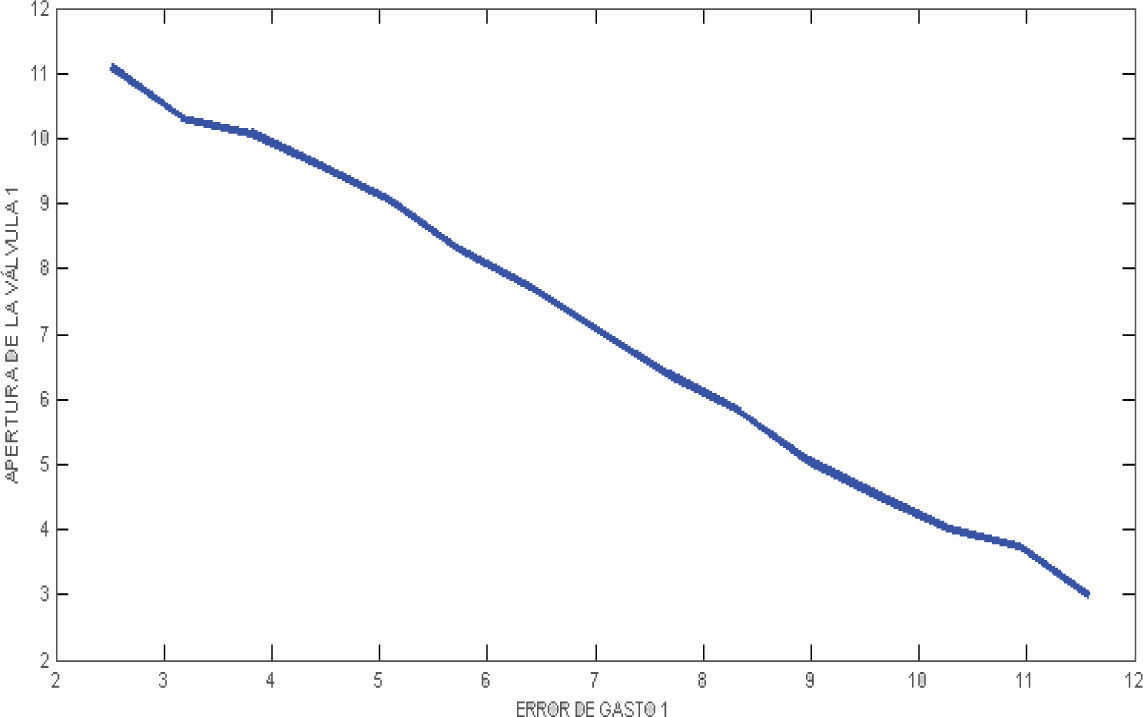
Donde e, es el error de gasto que demanda la rama paralela y O es la apertura de la válvula. La gráfica generada por la base de estas reglas se muestra en la figura 12.
Como se puede ver en la figura 12, si la demanda de flujo aumenta con respecto a un valor actual, entonces es necesario reducir el valor de la resistencia hidráulica, es decir, es necesario abrir la válvula de forma adecuada.
Método de defuzificación del CPDLa defuzificación es resultado del tipo de funciones de pertenencia y de la base de las reglas que están dadas en la tabla 1 y 2, respectivamente. En este trabajo se utilizó el método del centroide para la defuzificación.
Obtención del conocimiento expertoPara mostrar los resultados obtenidos en este trabajo, en la figura 13 se muestran entradas de referencia arbitrarias para cada rama paralela, las cuales muestran variaciones en diferentes lapsos de tiempo.
En la figura 13, se muestra la especificación de gasto propuesta para cada rama paralela. Se eligieron esas entradas para que el sistema se comportara como desacoplado, esto es, que ante variaciones de gasto en alguna rama paralela, el gasto de las demás ramas paralelas no se vea afectado. La tarea del experto es definir cómo es el comportamiento del sistema para cumplir con estas especificaciones. En la figura 14 se muestra la salida del experto, que es la salida de la figura 5 ante las entradas de la figura 13.
Claramente, se aprecia que el experto responde satisfactoriamente y es posible obtener información sobre cómo se comportan las válvulas y la bomba del sistema real, teniendo como objetivo de control el desacoplamiento, basándose en el error de la figura 5. Asimismo es posible traducir este conocimiento lingüístico a un CPD, utilizando la información del error como entrada y obteniendo como salida la posición de la válvula adecuada, así como la presión de la bomba.
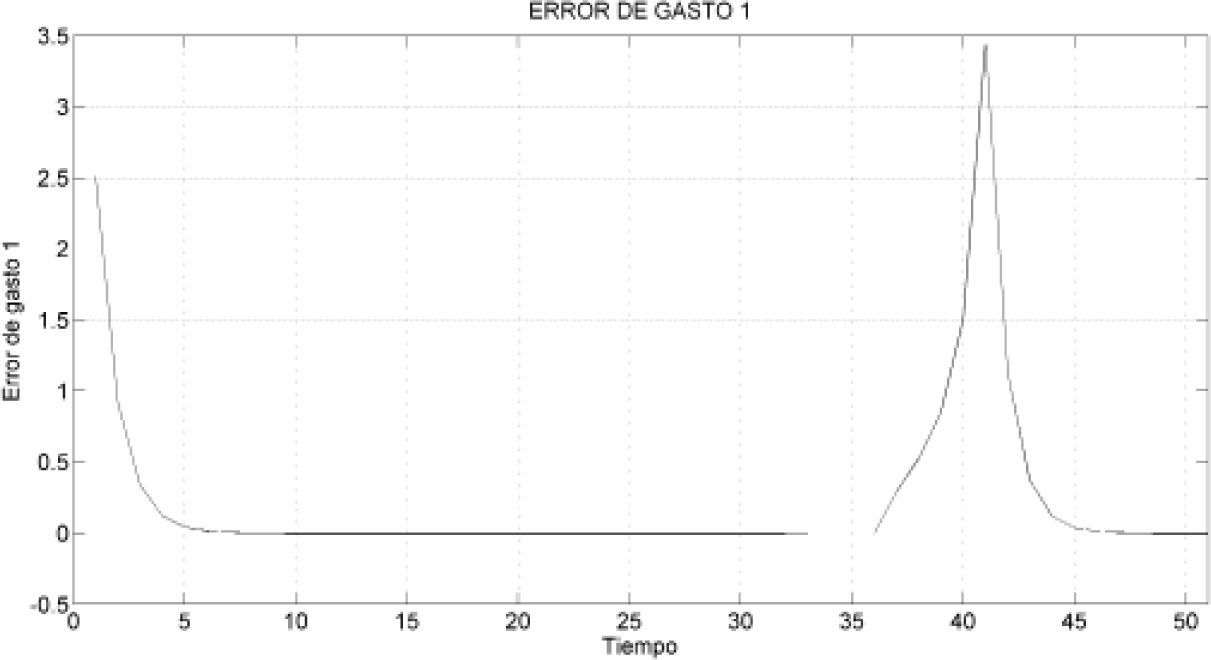
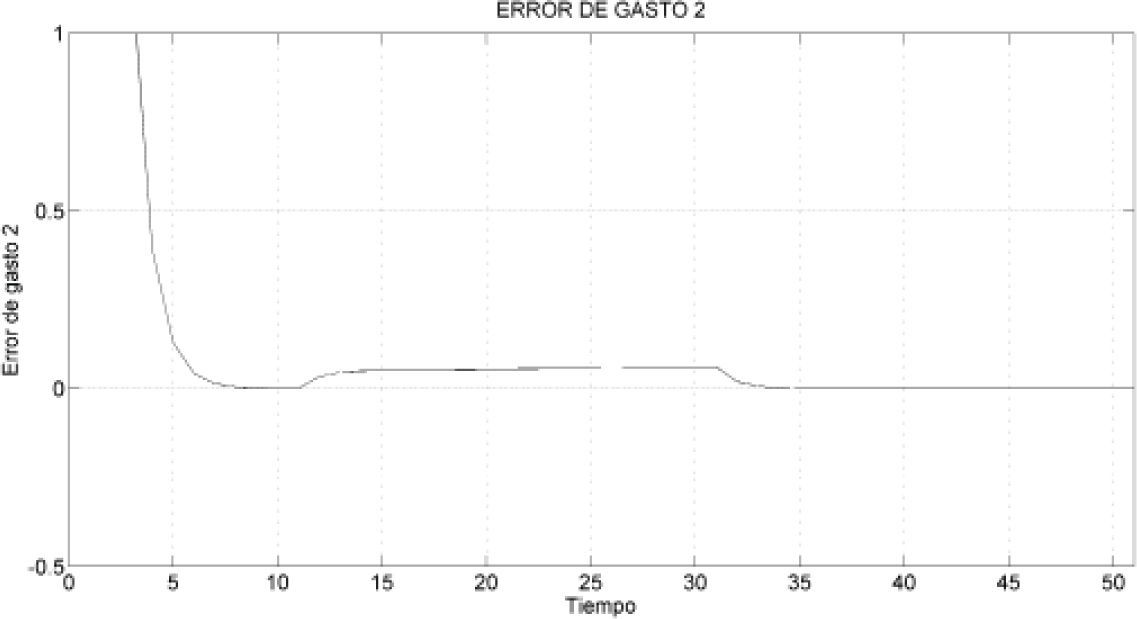
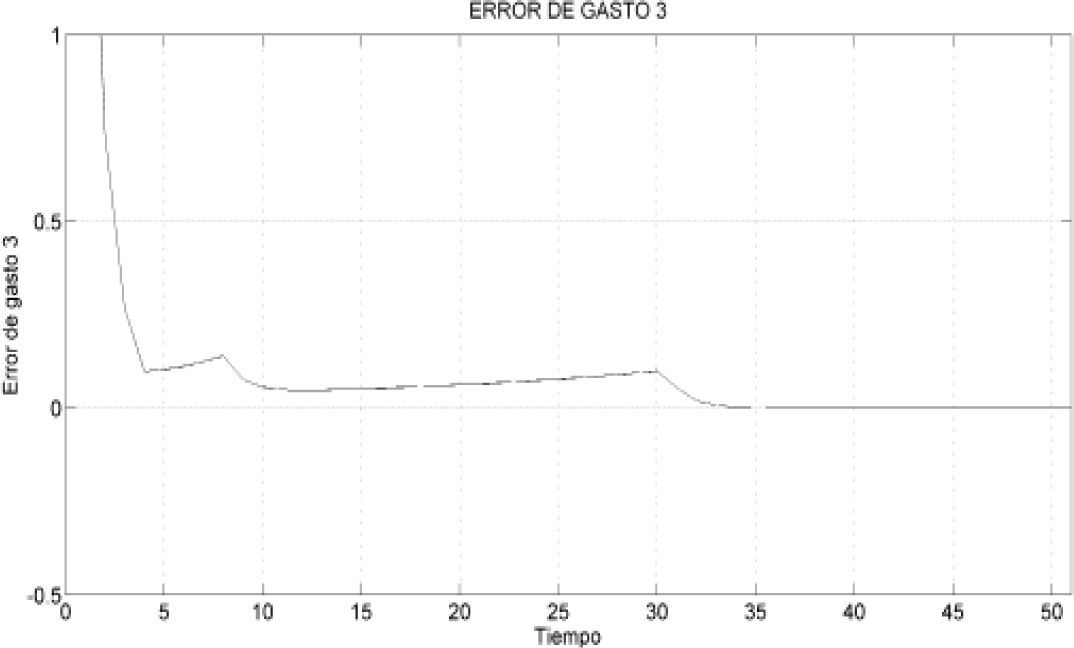
Información del expertoAnte las referencias de gasto para cada rama paralela que se muestran en la figura 13, el experto responde de manera satisfactoria, es decir, logra el desacoplamiento de los gastos. A continuación, en las figuras 15, 16 y 17, se muestra el conocimiento experto o error del sistema de la figura 5.
Con este conocimiento experto del comportamiento de cada tubería mostrado en las figuras 15, 16 y 17, es posible diseñar un controlador proporcional que consiga desacoplar el sistema.
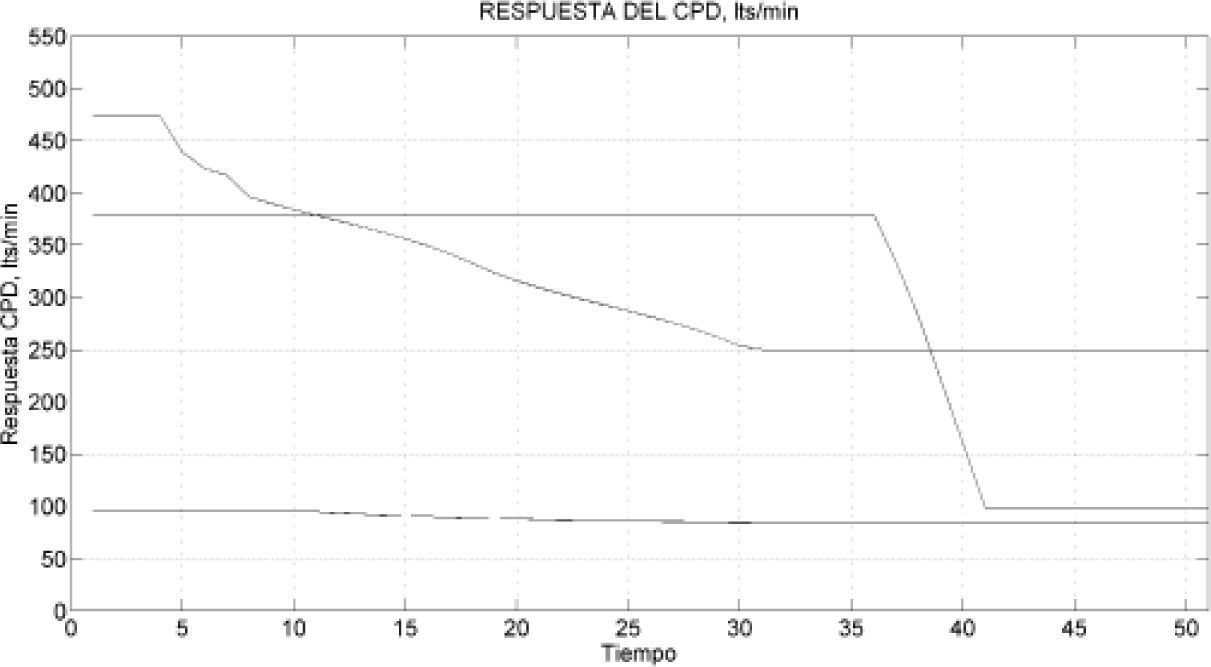
Resultados sobre desacoplamiento del CPDA continuación se muestra el resultado del CPD propuesto, en donde se aprecia claramente que el sistema está desacoplado (figura 18). Se puede observar cómo el CPD es robusto ante cambios en las entradas, ya que una entrada no afecta a las otras.
Las entradas de referencia muestran cambios de demanda de gasto en cada rama paralela mostrados en la figura 13; de esta manera, el experto P determina el comportamiento de las válvulas y la bomba, lo cual se aprecia en la figura 14, y por último, en la figura 18 se observa el buen funcionamiento del CPD propuesto, el cual logra el objetivo de desacoplamiento. También, en la figura 19 se muestra la demanda de gasto (presión determinada por el CPD propuesto).
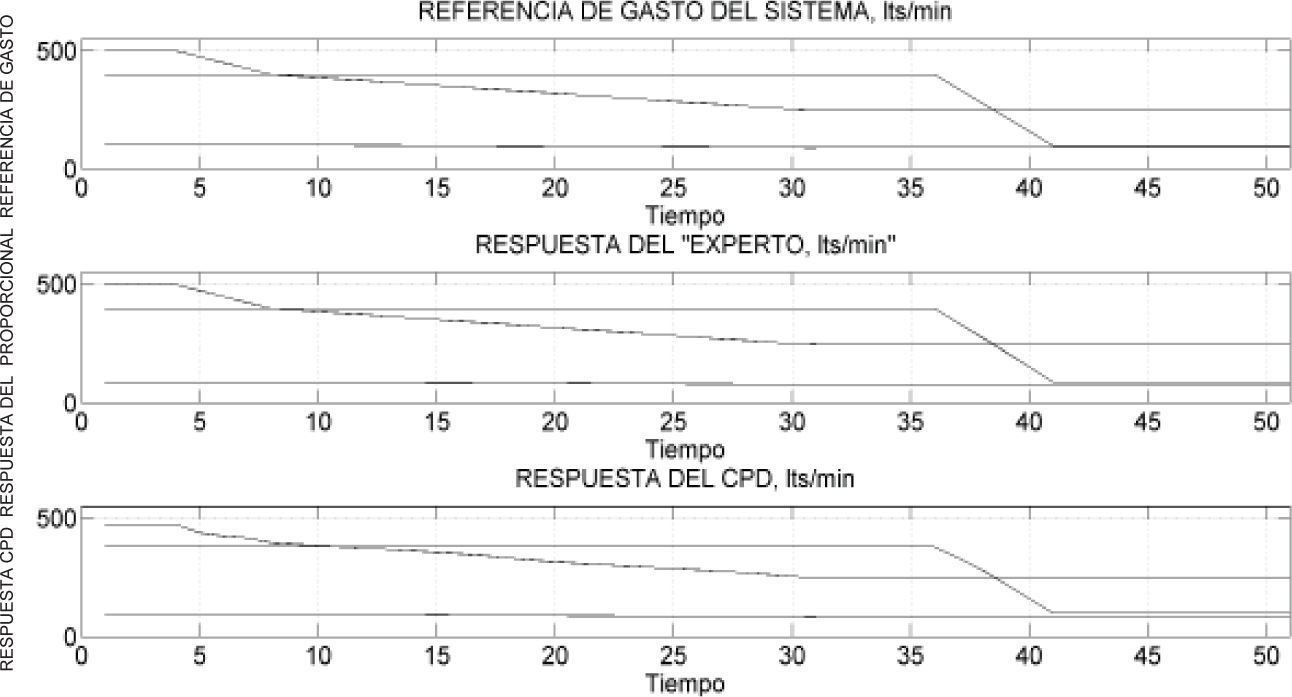
En la figura 19, se observa que la demanda de gasto requiere una presión proporcional suministrada por la bomba, es decir, la demanda de gasto se satisface en proporción a la demanda, así el sistema cumple con el objetivo de desacoplamiento, conseguido por el CPD. Por último, se muestran en la figura 20, las referencias de gasto para cada rama paralela, la respuesta del experto y el desempeño del CPD.
El diseño del CPD que logra el objetivo de desacoplamiento del sistema de riego está basado en la extracción de información del comportamiento desacoplado del sistema de referencia, que se controla por un control proporcional convencional, el cual determina el comportamiento de las válvulas y el comportamiento de la bomba para cumplir con el objetivo de control, el cual en este caso es el flujo deseado en cada una de las tuberías.
El CPD propuesto alcanza el objetivo de desacoplar el sistema a partir de un conocimiento experto del funcionamiento basado en el error entre el flujo deseado y el real. Lo anterior es importante porque implica que se puede aplicar esta metodología para otro tipo de sistemas, como los no regulares, variantes en el tiempo y otros.
ConclusionesSe diseñó un controlador proporcional difuso (CPD) a partir del conocimiento experto del error entre el flujo deseado y el real para desacoplar el sistema de riego en paralelo prescindiendo de un modelo matemático del sistema, obteniéndose un comportamiento satisfactorio comparado con el controlador proporcional. Es importante mencionar que la metodología propuesta se puede aplicar a otros sistemas siempre y cuando se cuente con la información del experto.
En general, la metodología que se propone en este artículo para lograr el desacoplamiento para un sistema dinámico con la técnica de lógica difusa sin contar con el modelo matemático, consiste en determinar de manera precisa las entradas y las salidas del sistema entendiendo que como entrada será la referencia a seguir y la salida correspondiente será el valor real de dicha variable. Cuando exista una diferencia entre una entrada y su respectiva salida se dice que existe un error, el cual se considera como el conocimiento experto y será la base para la construcción del sistema de inferencia. Posteriormente se define el rango de operación de todas las variables (entradas, salidas y el error), con el propósito de dividir este rango en la cantidad de conjuntos difusos que se deseen asignar a cada variable, la cantidad de conjuntos difusos afectará en el desempeño del sistema lo mismo que la cantidad de reglas difusas. Una vez hecho lo anterior, el objetivo del mecanismo de inferencia será llevar a cada variable de salida a su valor de referencia de entrada sin importar el acoplamiento interno entre las variables del sistema, así como comportamientos no lineales y la varianza en el tiempo, entre otros. El diseño del mecanismo de inferencia consiste en un conjunto de reglas que se basan en el conocimiento experto que relaciona a cada variable de entrada con su respectiva variable de salida.
Actualmente los trabajos en sistemas lineales, no lineales, difusos, invariantes en el tiempo logran desacoplar los sistemas basándose en el modelo matemático, es decir, deben conocerse las ecuaciones dinámicas que aproximen, en la medida de lo posible, el comportamiento real del sistema. Sin embargo, esta tarea no siempre resulta fácil para el diseñador, pues cuando en el sistema intervienen una gran cantidad de variables, obtener una representación será una tarea laboriosa. Por lo tanto, el enfoque que proponemos basado en la lógica difusa presenta una alternativa de solución viable al problema de desacoplamiento sin contar con el modelo matemático.
Este trabajo fue apoyado por el Consejo Nacional de Ciencia y Tecnología (CONACyT) y al Instituto Tecnológico de Aguascalientes.
Ingeniero mecánico por el Instituto Tecnológico de Aguascalientes, 2009. Fue becario de CO-NACYT en la maestría en ciencias en ingeniería eléctrica del Instituto Tecnológico de Aguascalientes. Actualmente está realizando estudios de doctorado en el Centro de Investigación y de Estudios Avanzados del Instituto Politécnico Nacional (CINVESTAV). Sus intereses de investigación se relacionan con el problema de desacoplamiento difuso de sistemas regulares y no regulares.
Citación estilo Chicago Delgado-Aguiñaga, Jorge Alejandro, Jorge Luis Orozco-Mora, Elvia Ruiz-Beltrán. Solución al problema de desacoplamiento mediante un controlador proporcional difuso de un sistema regular de riego con tuberías en paralelo. Ingeniería Investigación y Tecnología, XIV, 04 (2013): 523–536.
Citación estilo ISO 690 Delgado-Aguiñaga J.A., Orozco-Mora J.L., Ruiz-Beltrán E. Solución al problema de desacoplamiento mediante un controlador proporcional difuso de un sistema regular de riego con tuberías en paralelo. Ingeniería Investigación y Tecnología, volumen XIV (número 4), octubre-diciembre 2013: 523–536.
Estudió ingeniería electrónica en el Instituto Tecnológico de Aguascalientes de 1994 a 1998, en 2001 obtuvo el grado de maestro en ciencias en ingeniería eléctrica y en 2005 obtuvo el grado de doctor en ciencias en ingeniería eléctrica en el Centro de Investigación y de Estudios Avanzados del Instituto Politécnico Nacional (CINVESTAV). Sus investigaciones se relacionan con desacoplamiento de sistemas lineales, desacoplamiento con estabilidad, cambios en la estructura al infinito, sistemas variantes e invariantes en el Tiempo, control lineal y discreto, caracterización y control de producción microalgal entre otras áreas. Actualmente es miembro del cuerpo académico, Reconocimiento de señales y control, registrado ante PROMEP y es miembro de la Sociedad de Sistemas de Control del IEEE.
Recibió el grado de licenciatura en la Universidad Autónoma de Sinaloa en 2002. En 2004 recibió el grado de maestra en ciencias en ingeniería eléctrica en el Centro de Investigación y de Estudios Avanzados del Instituto Politécnico Nacional. (CINVESTAV); en 2007 obtuvo el grado de doctora en ciencias en ingeniería eléctrica en CINVESTAV. Las líneas de investigación que trabaja se relacionan con el modelado, análisis estructural, diagnosticabilidad, esquemas de detección y localización de fallas en sistemas de eventos discretos. También trabaja con el problema de control de sistemas de eventos discretos, verificación formal de software y sistemas de producción microalgal. Actualmente es miembro del cuerpo académico, Reconocimiento de señales y control, registrado ante PROMEP; es miembro de la Sociedad de Robótica y Automatización y de la Sociedad de Computación del IEEE.