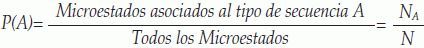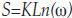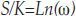La proteína de superficie del merozoíto MSP-1 está asociada al fenómeno de invasión de la malaria al glóbulo rojo, mientras que la proteína del antígeno EBA-140 interactúa con las sialo-glicoproteínas de la superficie de los eritrocitos. La identificación de péptidos de estas proteínas que se unan al HLA clase II es de vital importancia para el desarrollo de vacunas.
En nuestro trabajo se aplicó una teoría predictiva de unión al HLA clase II basada en la proporción S/k de la entropía, para la predicción del fenómeno de unión de péptidos de las proteínas MSP-1 y EBA-140 a la totalidad de secuencias de 20 aminoácidos de dichas moléculas. Se calcularon los valores de probabilidad, combinatoria y entropía de 948 secuencias nonámeras sobrelapadas de las proteínas MSP-1 y 732 de EBA-140. Se construyeron computacionalmente tres proteínas teóricas de 500 aminoácidos de longitud cada una, para aplicar la teoría de unión desarrollada en todos los péptidos nonámeros sobrelapados de las mismas.
Se predijo que para las dos proteínas del merozoíto estudiadas, 298 secuencias están asociadas al macroestado de unión y 1409 al macroestado de no unión. La predicción teórica desarrollada puede facilitar la selección de péptidos implicados en el desarrollo de vacunas. Para las tres proteínas construidas teóricamente se encontró que las secuencias 111, 84 y 72 son predichas como pertenecientes al macroestado de unión, mientras que las restantes, 381, 408 y 420 se predicen asociadas al macroestado de no unión.
Las predicciones evidencian un orden físico y matemático en la presentación antigénica, útil en el desarrollo de vacunas.
The MSP-1 merozoite surface protein is related to the invasion phenomenon of malaria to red cells, while the EBA-140 antigen protein interacts with the sialoglycoproteins on the surface of erythrocytes. The identification of peptides from both proteins that bind to HLA class II has a particular importance for the development of vaccines.
In the present work, a predictive binding to HLA class II theory, based on S/k proportion of entropy was applied, for the prediction of proteins MSP-1 and EBA-140 binding phenomenon to the totality of 20 amino acid sequences of both molecules. The probability, combinatory and entropy values were calculated for 948 and 732 nonamer overlapping sequences of MSP-1 and EBA-140, respectively. Three theoretical proteins of 500 aminoacids of lenght each were computationally built in order to apply the developed binding theory to all their nonamer overlapping peptides.
It was predicted that for the two studied merozoite proteins, 298 sequences are related to the binding macrostate and 1409 to the not-binding macrostate. The developed theoretical prediction can facilitate the selection of peptides during the process of vaccine development. For the three theoretical proteins built, it was found that 111, 84 and 72 are predicted as included into the binding macrostate, while sequences 381, 408, and 420 are predicted as related to the not-binding macrostate.
The predictions are an evidence of a physical and mathematical order in antigen presentation, which can be useful to the development of vaccines.
La malaria constituye un problema de salud pública a nivel mundial, afectando a casi 500 millones de personas al año y generando alrededor de 3.000.000 de muertes solamente en el continente africano(1,2). En este sentido, se han desarrollado gran cantidad de trabajos para conocer el proceso de invasión, que buscan establecer las interacciones ligando-receptor específicas durante todo el proceso, con el fin de desarrollar vacunas(3).
Dentro de los antígenos identificados como potencialmente útiles en el desarrollo de una vacuna contra la malaria, la más estudiada ha sido la proteína Mayor de Superficie del Merozoito MSP-1, sintetizada durante el desarrollo del esquizonte, la cual está presente en la superficie del merozoito como un complejo de fragmentos proteolíticos(4,5) al estar directamente involucrada en el proceso de invasión al glóbulo rojo. Investigaciones sugieren que tiene una importante función en las primeras etapas de dicha interacción, siendo por ello un activador de la respuesta inmunitaria humana. Trabajos en este área han demostrado que la activación de la respuesta humoral a diferentes regiones de la proteína disminuye la susceptibilidad a la malaria clínica(6-9). Por otro lado, la EBA-140, una de las proteínas del merozoíto de Plasmodium falciparum o antígeno de unión eritrocitaria, es también conocida como BAEBL o PfEBP-2; estudios de la localización subcelular sugieren que está localizada en los micronemas del complejo apical, cuyas proteínas interactúan con las sialoglicoproteínas de la superficie de eritrocitos sanguíneos(10,11).
La presentación de antígenos a los linfocitos T es mediada por el HLA: los linfocitos T CD4+ reconocen los péptidos presentados por el HLA clase II(12). La región central de unión de péptidos del HLA clase II se encuentra abierta en sus extremos y está formada por los dominios α1 y β1; dicha apertura explica la variabilidad en el tamaño de los péptidos presentados(13-17). De manera general se ha encontrado que una región central compuesta por nueve aminoácidos es fundamental para la unión(18).
Dada la importancia del HLA clase II en el proceso de activación antigénica resulta de gran utilidad determinar si existen péptidos de las proteínas asociadas a la invasión del eritrocito por parte del merozoíto que puedan ser reconocidos por dicha molécula. Recientemente se desarrolló una teoría para la predicción de péptidos a la región central del HLA clase II(19), con base en las teorías de probabilidad, combinatoria y entropía. Este trabajo partió de una abstracción físico teórica basada en la observación de la distribución de aminoácidos en la región central de unión como un fenómeno finito y probabilista donde la distribución de las probabilidades de aparición de grupos de aminoácidos en las diferentes posiciones permite estudiar matemáticamente las diferencias entre los péptidos de unión y no unión al HLA clase II. Al hacer grupos de aminoácidos, es posible hacer una abstracción de las particularidades de cada péptido para lograr una caracterización más general, y realizar una analogía con los macroestados de la mecánica estadística, en términos del número de posibles formas de organización de moléculas de un gas, que tienen ciertas características comunes por las que son incluidas dentro de un mismo macroestado. Con el fin de establecer el conjunto total de posibilidades del fenómeno, independientemente de la especificidad alélica, en dicho experimento se estudiaron no sólo péptidos sintéticos, naturales y promiscuos, tanto de unión como de no unión, sino lo que ocurriría en el caso de encontrar un péptido teórico con todos los aminoácidos iguales, así como un péptido teórico que presente todos los aminoácidos diferentes(19). De este modo fue posible establecer que los péptidos de unión se caracterizan por ciertas repeticiones y condiciones específicas, al ser estudiada la distribución de grupos de aminoácidos con base en las leyes de probabilidad y combinatoria. Esta caracterización probabilista permitió la evaluación de la autoorganización del sistema con base en la ley de la entropía, estableciendo diferencias matemáticas entre péptidos de unión y no unión con base en la relación S/k. Dicha teoría fue aplicada a 161 péptidos, con una eficacia del 100% en su capacidad de predicción de su estado de unión o no unión a la molécula de HLA II. Posteriormente también fue aplicada en la determinación de péptidos de unión al HLA clase II de las proteínas MSA-2 y AMA-1 de malaria, determinando péptidos que pueden ser útiles en el desarrollo de vacunas(20) así como a la proteína API m1 y a dos del HER-2/neu, mejorando medidas de desempeño de los métodos de predicción actuales (Rodríguez J, Bernal P, et al manuscrito en preparación).
Por medio de la probabilidad se puede cuantificar la ocurrencia futura de un evento(21,22), de esta forma la región central fue definida como compuesta por varios eventos probabilísticos con el fin de realizar cuantificaciones que den cuenta de la combinación de los aminoácidos en las secuencias y posteriormente evaluar la probabilidad de la secuencia, respecto a todas las posibles secuencias. La entropía ha recibido varias interpretaciones(23-26), el concepto análogo usado en esta teoría fue el enunciado por Boltzmann, en términos del número de microestados de un sistema equiprobable(23), en donde la entropía de un macroestado es proporcional al número de microestados o configuraciones en las que el macroestado se puede presentar; de esta forma se realiza una analogía entre los péptidos presentados por la región central y los macroestados y microestados de la mecánica estadística.
En la presente investigación se aplicará la teoría de predicción de unión de péptidos a la región central del HLA clase II(19), a los péptidos nonámeros sobrelapados de las 79 secuencias de 20 aminoácidos no sobrelapados que abarcan la proteína MSP-1 y a los péptidos nonámeros sobrelapados de las 61 secuencias de 20 aminoácidos no sobrelapados que abarcan la proteína EBA-140.
DefinicionesMacroestado: conjunto de secuencias que presentan alta unión o no unión al HLA clase II. Por lo tanto existen dos clases de macroestados, asociados a cada una de estas condiciones específicas(19).
Microestado: Toda secuencia específica de nueve aminoácidos(19).
Tipo de secuencia: Microestados que presenten el mismo valor en su combinatoria y su evaluación con los criterios definidos(19).
Probabilidad Laplaciana: La probabilidad de un tipo de secuencia A es definida como la cantidad de microestados Na asociados a este tipo de secuencia dividida entre el total de posibles microestados N(24,19):
Ley combinatoria para determinar la cantidad de microestados ω: De acuerdo con la metodología desarrollada por Rodríguez(19), cada posición del péptido tiene asociada un número de posibles aminoácidos. Para calcular el número de posibles microestados asociados a un tipo de secuencia se multiplican los valores asociados a cada posición, que dependen del número de posibles aminoácidos asociados a cada lugar, los cuales a su vez están determinados por el grupo al que pertenezcan y sus repeticiones en el tipo de secuencia. Para las cuantificaciones específicas ver tablas de criterios evaluadores y tablas de grupos de aminoácidos de la teoría realizada(19).
Entropía: En un sistema con microestados equiprobables la entropía se define de acuerdo con la ecuación 2:
Donde k es igual a la constante de Boltzmann, 1.38x10 23 (J/k), ω los posibles microestados y S el valor de la entropía¿'19, 23-25).
Proporción S/k: Despejando de la ecuación 2 se obtiene(19):
MATERIAL Y MÉTODOInicialmente se determinaron los péptidos nonámeros sobrelapados pertenecientes a secuencias no sobrelapadas de 20 aminoácidos, 79 correspondientes a la proteína MSP-1 y 61 a la EBA-140, así como los péptidos nonámeros sobrelapados de tres proteínas teóricas compuestas por 500 residuos cada una.
Posteriormente se aplicó la metodología desarrollada por Rodríguez(19) para determinar si las secuencias sobrelapadas pertenecen al macroestado de unión o no unión. Para ello inicialmente se define un espacio muestral, donde cada microestado es considerado como un posible evento. Luego se evaluó la probabilidad laplaciana de cada una de las secuencias, aplicando la ley de combinatoria (ver definiciones), para calcular los microestados equivalentes a partir de la cantidad de aminoácidos que tendrían la posibilidad de ocupar cada posición. El número de aminoácidos asociados a cada posición depende del valor del grupo al que pertenezca y sus repeticiones en el tipo de secuencia(19).
Para estos cálculos se realizaron cuatro pasos en donde se agrupan los 20 aminoácidos de forma específica, el procedimiento de cálculo para los pasos uno y tres es asignar a cada posición un número según el aminoácido encontrado en cada lugar dependiendo del conjunto en el que se encuentre; se realiza el mismo procedimiento con cada aminoácido que aparece consecutivamente, considerando además la disminución de sus posibilidades en la medida que van apareciendo aminoácidos de un mismo grupo y las repeticiones de un mismo aminoácido. Posteriormente para calcular la probabilidad laplaciana de un tipo de secuencia (ver definiciones), se multiplican dichos valores hallando el número de microestados asociados al tipo de secuencia(19). Partiendo del número de microestados posibles se realizaron los cálculos de entropía para cada tipo de secuencia aplicando la ley de Boltzmann (Ecuación 2).
La predicción teórica desarrollada se calcula con base en la proporción S/k, ecuación 3, y de los rangos mínimos y máximos asociados a los péptidos de alta unión; de esta forma se encontró previamente que las secuencias nonámeras con proporciones S/k entre 8,55 y 12,8 para los primeros pasos y entre 6,98 y 10,5 para los últimos pasos son predichas de unión al HLA clase II de acuerdo con la teoría desarrollada(19).
De este modo, una vez hallado el valor de la entropía de cada secuencia nonámera se determina el valor de la proporción S/k y se determina si se encuentra o no dentro de los rangos predichos de unión mencionados previamente (Ecuación 3).
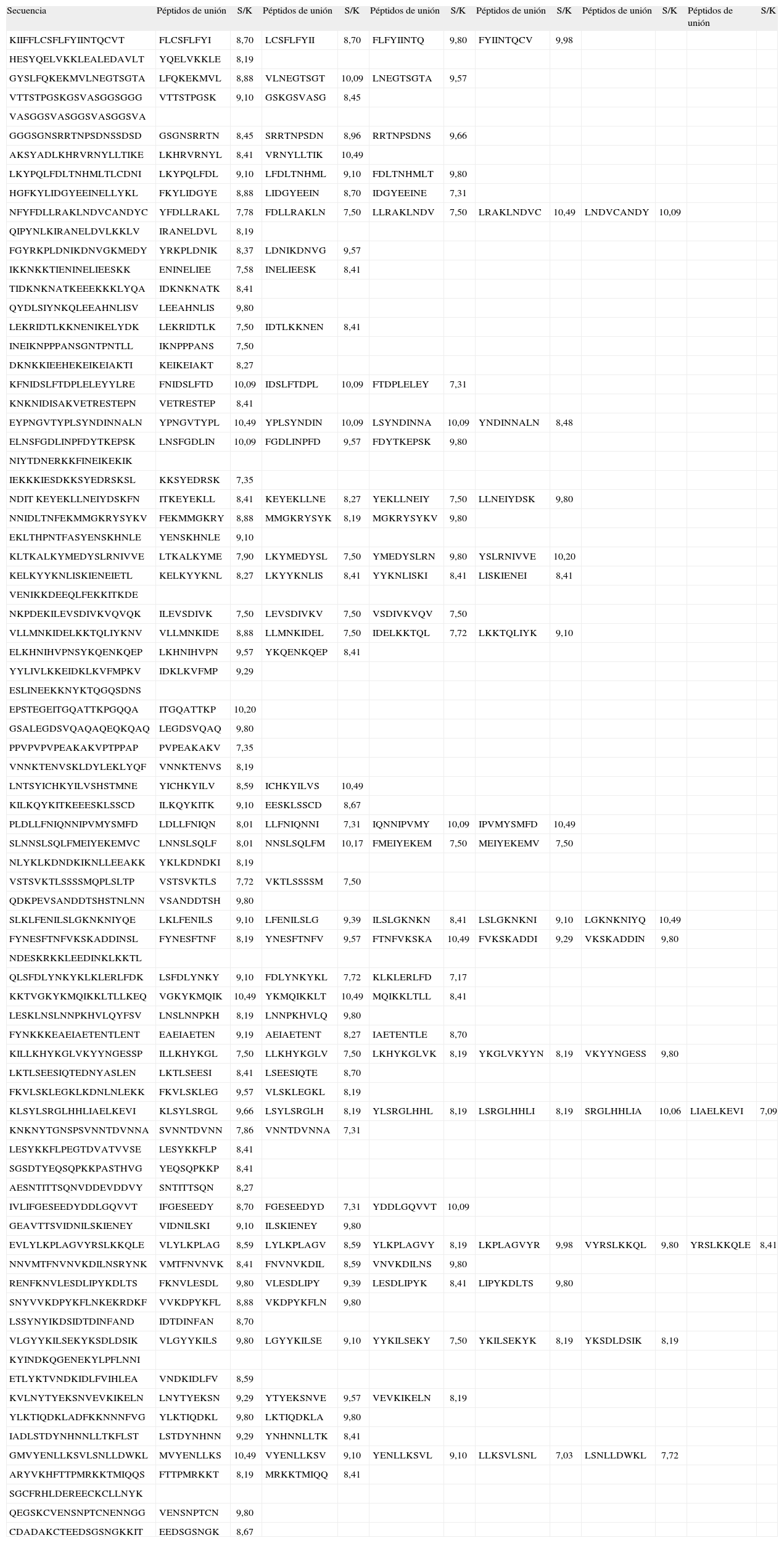
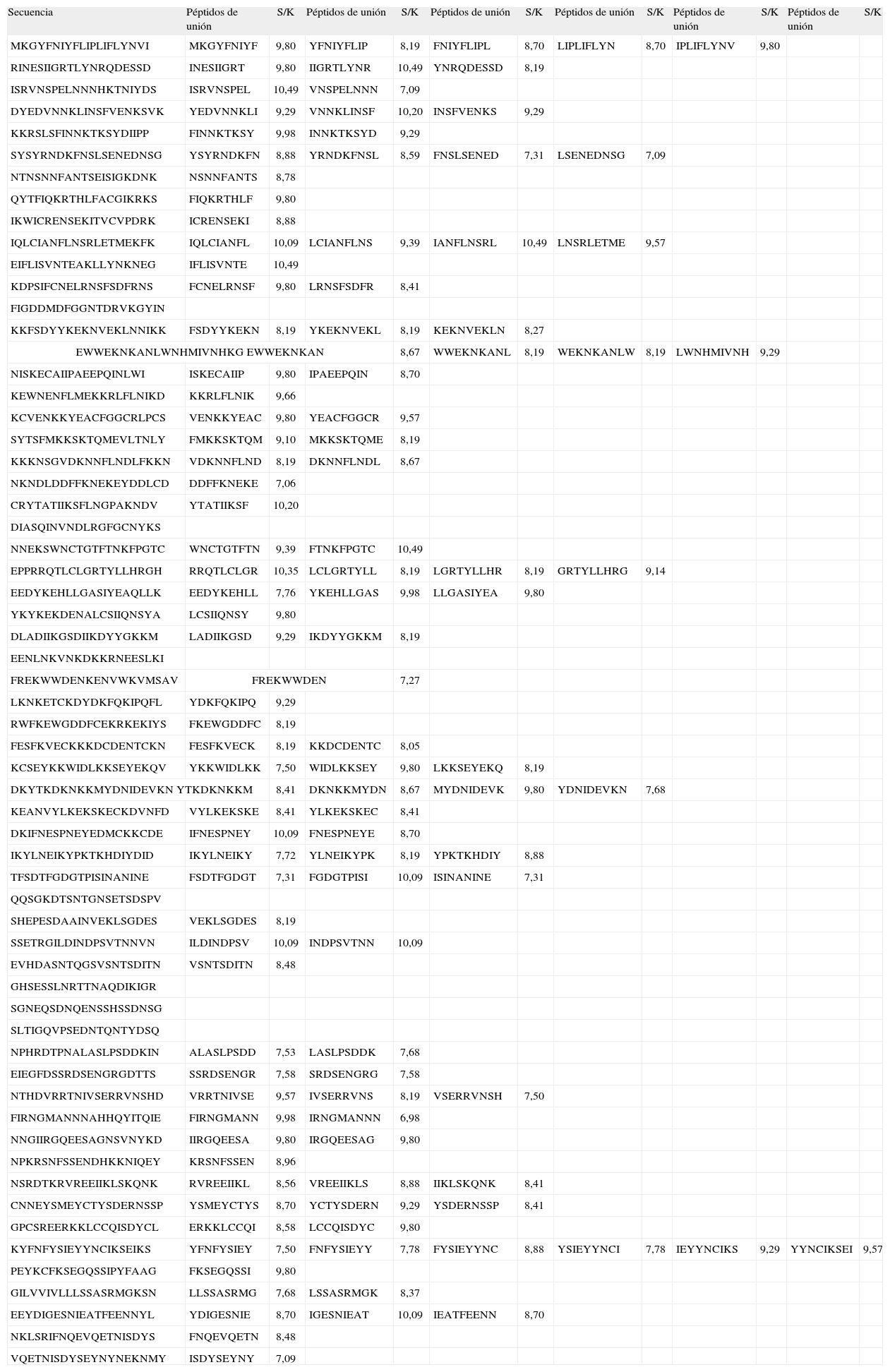
RESULTADOSDe los 79 péptidos de 20 aminoácidos analizados de MSP-1, se encontraron 179 secuencias nonámeras que corresponden al macroestado de unión, mientras que 769 corresponden al macroestado de no unión (Tabla I). De los 61 péptidos de 20 aminoácidos analizados para EBA-140, se encontraron 119 secuencias nonámeras que corresponden al macroestado de unión, mientras que 613 corresponden al macroestado de no unión (Tabla II). Las proporciones S/k de los péptidos asociados al macroestado de unión oscilaronentre 7,03 y 10,49 para MSP-1 y entre 6,98 y 10,49 para EBA-140 (Tablas I y II).
Péptidos no sobrelapados de 20 aminoácidos de la proteína MSP-1, y secuencias nonámeras predichas de unión correspondientes junto con sus valores de la proporción S/k
| Secuencia | Péptidos de unión | S/K | Péptidos de unión | S/K | Péptidos de unión | S/K | Péptidos de unión | S/K | Péptidos de unión | S/K | Péptidos de unión | S/K |
| KIIFFLCSFLFYIINTQCVT | FLCSFLFYI | 8,70 | LCSFLFYII | 8,70 | FLFYIINTQ | 9,80 | FYIINTQCV | 9,98 | ||||
| HESYQELVKKLEALEDAVLT | YQELVKKLE | 8,19 | ||||||||||
| GYSLFQKEKMVLNEGTSGTA | LFQKEKMVL | 8,88 | VLNEGTSGT | 10,09 | LNEGTSGTA | 9,57 | ||||||
| VTTSTPGSKGSVASGGSGGG | VTTSTPGSK | 9,10 | GSKGSVASG | 8,45 | ||||||||
| VASGGSVASGGSVASGGSVA | ||||||||||||
| GGGSGNSRRTNPSDNSSDSD | GSGNSRRTN | 8,45 | SRRTNPSDN | 8,96 | RRTNPSDNS | 9,66 | ||||||
| AKSYADLKHRVRNYLLTIKE | LKHRVRNYL | 8,41 | VRNYLLTIK | 10,49 | ||||||||
| LKYPQLFDLTNHMLTLCDNI | LKYPQLFDL | 9,10 | LFDLTNHML | 9,10 | FDLTNHMLT | 9,80 | ||||||
| HGFKYLIDGYEEINELLYKL | FKYLIDGYE | 8,88 | LIDGYEEIN | 8,70 | IDGYEEINE | 7,31 | ||||||
| NFYFDLLRAKLNDVCANDYC | YFDLLRAKL | 7,78 | FDLLRAKLN | 7,50 | LLRAKLNDV | 7,50 | LRAKLNDVC | 10,49 | LNDVCANDY | 10,09 | ||
| QIPYNLKIRANELDVLKKLV | IRANELDVL | 8,19 | ||||||||||
| FGYRKPLDNIKDNVGKMEDY | YRKPLDNIK | 8,37 | LDNIKDNVG | 9,57 | ||||||||
| IKKNKKTIENINELIEESKK | ENINELIEE | 7,58 | INELIEESK | 8,41 | ||||||||
| TIDKNKNATKEEEKKKLYQA | IDKNKNATK | 8,41 | ||||||||||
| QYDLSIYNKQLEEAHNLISV | LEEAHNLIS | 9,80 | ||||||||||
| LEKRIDTLKKNENIKELYDK | LEKRIDTLK | 7,50 | IDTLKKNEN | 8,41 | ||||||||
| INEIKNPPPANSGNTPNTLL | IKNPPPANS | 7,50 | ||||||||||
| DKNKKIEEHEKEIKEIAKTI | KEIKEIAKT | 8,27 | ||||||||||
| KFNIDSLFTDPLELEYYLRE | FNIDSLFTD | 10,09 | IDSLFTDPL | 10,09 | FTDPLELEY | 7,31 | ||||||
| KNKNIDISAKVETRESTEPN | VETRESTEP | 8,41 | ||||||||||
| EYPNGVTYPLSYNDINNALN | YPNGVTYPL | 10,49 | YPLSYNDIN | 10,09 | LSYNDINNA | 10,09 | YNDINNALN | 8,48 | ||||
| ELNSFGDLINPFDYTKEPSK | LNSFGDLIN | 10,09 | FGDLINPFD | 9,57 | FDYTKEPSK | 9,80 | ||||||
| NIYTDNERKKFINEIKEKIK | ||||||||||||
| IEKKKIESDKKSYEDRSKSL | KKSYEDRSK | 7,35 | ||||||||||
| NDIT KEYEKLLNEIYDSKFN | ITKEYEKLL | 8,41 | KEYEKLLNE | 8,27 | YEKLLNEIY | 7,50 | LLNEIYDSK | 9,80 | ||||
| NNIDLTNFEKMMGKRYSYKV | FEKMMGKRY | 8,88 | MMGKRYSYK | 8,19 | MGKRYSYKV | 9,80 | ||||||
| EKLTHPNTFASYENSKHNLE | YENSKHNLE | 9,10 | ||||||||||
| KLTKALKYMEDYSLRNIVVE | LTKALKYME | 7,90 | LKYMEDYSL | 7,50 | YMEDYSLRN | 9,80 | YSLRNIVVE | 10,20 | ||||
| KELKYYKNLISKIENEIETL | KELKYYKNL | 8,27 | LKYYKNLIS | 8,41 | YYKNLISKI | 8,41 | LISKIENEI | 8,41 | ||||
| VENIKKDEEQLFEKKITKDE | ||||||||||||
| NKPDEKILEVSDIVKVQVQK | ILEVSDIVK | 7,50 | LEVSDIVKV | 7,50 | VSDIVKVQV | 7,50 | ||||||
| VLLMNKIDELKKTQLIYKNV | VLLMNKIDE | 8,88 | LLMNKIDEL | 7,50 | IDELKKTQL | 7,72 | LKKTQLIYK | 9,10 | ||||
| ELKHNIHVPNSYKQENKQEP | LKHNIHVPN | 9,57 | YKQENKQEP | 8,41 | ||||||||
| YYLIVLKKEIDKLKVFMPKV | IDKLKVFMP | 9,29 | ||||||||||
| ESLINEEKKNYKTQGQSDNS | ||||||||||||
| EPSTEGEITGQATTKPGQQA | ITGQATTKP | 10,20 | ||||||||||
| GSALEGDSVQAQAQEQKQAQ | LEGDSVQAQ | 9,80 | ||||||||||
| PPVPVPVPEAKAKVPTPPAP | PVPEAKAKV | 7,35 | ||||||||||
| VNNKTENVSKLDYLEKLYQF | VNNKTENVS | 8,19 | ||||||||||
| LNTSYICHKYILVSHSTMNE | YICHKYILV | 8,59 | ICHKYILVS | 10,49 | ||||||||
| KILKQYKITKEEESKLSSCD | ILKQYKITK | 9,10 | EESKLSSCD | 8,67 | ||||||||
| PLDLLFNIQNNIPVMYSMFD | LDLLFNIQN | 8,01 | LLFNIQNNI | 7,31 | IQNNIPVMY | 10,09 | IPVMYSMFD | 10,49 | ||||
| SLNNSLSQLFMEIYEKEMVC | LNNSLSQLF | 8,01 | NNSLSQLFM | 10,17 | FMEIYEKEM | 7,50 | MEIYEKEMV | 7,50 | ||||
| NLYKLKDNDKIKNLLEEAKK | YKLKDNDKI | 8,19 | ||||||||||
| VSTSVKTLSSSSMQPLSLTP | VSTSVKTLS | 7,72 | VKTLSSSSM | 7,50 | ||||||||
| QDKPEVSANDDTSHSTNLNN | VSANDDTSH | 9,80 | ||||||||||
| SLKLFENILSLGKNKNIYQE | LKLFENILS | 9,10 | LFENILSLG | 9,39 | ILSLGKNKN | 8,41 | LSLGKNKNI | 9,10 | LGKNKNIYQ | 10,49 | ||
| FYNESFTNFVKSKADDINSL | FYNESFTNF | 8,19 | YNESFTNFV | 9,57 | FTNFVKSKA | 10,49 | FVKSKADDI | 9,29 | VKSKADDIN | 9,80 | ||
| NDESKRKKLEEDINKLKKTL | ||||||||||||
| QLSFDLYNKYKLKLERLFDK | LSFDLYNKY | 9,10 | FDLYNKYKL | 7,72 | KLKLERLFD | 7,17 | ||||||
| KKTVGKYKMQIKKLTLLKEQ | VGKYKMQIK | 10,49 | YKMQIKKLT | 10,49 | MQIKKLTLL | 8,41 | ||||||
| LESKLNSLNNPKHVLQYFSV | LNSLNNPKH | 8,19 | LNNPKHVLQ | 9,80 | ||||||||
| FYNKKKEAEIAETENTLENT | EAEIAETEN | 9,19 | AEIAETENT | 8,27 | IAETENTLE | 8,70 | ||||||
| KILLKHYKGLVKYYNGESSP | ILLKHYKGL | 7,50 | LLKHYKGLV | 7,50 | LKHYKGLVK | 8,19 | YKGLVKYYN | 8,19 | VKYYNGESS | 9,80 | ||
| LKTLSEESIQTEDNYASLEN | LKTLSEESI | 8,41 | LSEESIQTE | 8,70 | ||||||||
| FKVLSKLEGKLKDNLNLEKK | FKVLSKLEG | 9,57 | VLSKLEGKL | 8,19 | ||||||||
| KLSYLSRGLHHLIAELKEVI | KLSYLSRGL | 9,66 | LSYLSRGLH | 8,19 | YLSRGLHHL | 8,19 | LSRGLHHLI | 8,19 | SRGLHHLIA | 10,06 | LIAELKEVI | 7,09 |
| KNKNYTGNSPSVNNTDVNNA | SVNNTDVNN | 7,86 | VNNTDVNNA | 7,31 | ||||||||
| LESYKKFLPEGTDVATVVSE | LESYKKFLP | 8,41 | ||||||||||
| SGSDTYEQSQPKKPASTHVG | YEQSQPKKP | 8,41 | ||||||||||
| AESNTITTSQNVDDEVDDVY | SNTITTSQN | 8,27 | ||||||||||
| IVLIFGESEEDYDDLGQVVT | IFGESEEDY | 8,70 | FGESEEDYD | 7,31 | YDDLGQVVT | 10,09 | ||||||
| GEAVTTSVIDNILSKIENEY | VIDNILSKI | 9,10 | ILSKIENEY | 9,80 | ||||||||
| EVLYLKPLAGVYRSLKKQLE | VLYLKPLAG | 8,59 | LYLKPLAGV | 8,59 | YLKPLAGVY | 8,19 | LKPLAGVYR | 9,98 | VYRSLKKQL | 9,80 | YRSLKKQLE | 8,41 |
| NNVMTFNVNVKDILNSRYNK | VMTFNVNVK | 8,41 | FNVNVKDIL | 8,59 | VNVKDILNS | 9,80 | ||||||
| RENFKNVLESDLIPYKDLTS | FKNVLESDL | 9,80 | VLESDLIPY | 9,39 | LESDLIPYK | 8,41 | LIPYKDLTS | 9,80 | ||||
| SNYVVKDPYKFLNKEKRDKF | VVKDPYKFL | 8,88 | VKDPYKFLN | 9,80 | ||||||||
| LSSYNYIKDSIDTDINFAND | IDTDINFAN | 8,70 | ||||||||||
| VLGYYKILSEKYKSDLDSIK | VLGYYKILS | 9,80 | LGYYKILSE | 9,10 | YYKILSEKY | 7,50 | YKILSEKYK | 8,19 | YKSDLDSIK | 8,19 | ||
| KYINDKQGENEKYLPFLNNI | ||||||||||||
| ETLYKTVNDKIDLFVIHLEA | VNDKIDLFV | 8,59 | ||||||||||
| KVLNYTYEKSNVEVKIKELN | LNYTYEKSN | 9,29 | YTYEKSNVE | 9,57 | VEVKIKELN | 8,19 | ||||||
| YLKTIQDKLADFKKNNNFVG | YLKTIQDKL | 9,80 | LKTIQDKLA | 9,80 | ||||||||
| IADLSTDYNHNNLLTKFLST | LSTDYNHNN | 9,29 | YNHNNLLTK | 8,41 | ||||||||
| GMVYENLLKSVLSNLLDWKL | MVYENLLKS | 10,49 | VYENLLKSV | 9,10 | YENLLKSVL | 9,10 | LLKSVLSNL | 7,03 | LSNLLDWKL | 7,72 | ||
| ARYVKHFTTPMRKKTMIQQS | FTTPMRKKT | 8,19 | MRKKTMIQQ | 8,41 | ||||||||
| SGCFRHLDEREECKCLLNYK | ||||||||||||
| QEGSKCVENSNPTCNENNGG | VENSNPTCN | 9,80 | ||||||||||
| CDADAKCTEEDSGSNGKKIT | EEDSGSNGK | 8,67 |
Péptidos no sobrelapados de 20 aminoácidos de la proteína EBA-140, y secuencias nonámeras predichas de unión correspondientes junto con sus valores de la proporción S/k.
| Secuencia | Péptidos de unión | S/K | Péptidos de unión | S/K | Péptidos de unión | S/K | Péptidos de unión | S/K | Péptidos de unión | S/K | Péptidos de unión | S/K |
| MKGYFNIYFLIPLIFLYNVI | MKGYFNIYF | 9,80 | YFNIYFLIP | 8,19 | FNIYFLIPL | 8,70 | LIPLIFLYN | 8,70 | IPLIFLYNV | 9,80 | ||
| RINESIIGRTLYNRQDESSD | INESIIGRT | 9,80 | IIGRTLYNR | 10,49 | YNRQDESSD | 8,19 | ||||||
| ISRVNSPELNNNHKTNIYDS | ISRVNSPEL | 10,49 | VNSPELNNN | 7,09 | ||||||||
| DYEDVNNKLINSFVENKSVK | YEDVNNKLI | 9,29 | VNNKLINSF | 10,20 | INSFVENKS | 9,29 | ||||||
| KKRSLSFINNKTKSYDIIPP | FINNKTKSY | 9,98 | INNKTKSYD | 9,29 | ||||||||
| SYSYRNDKFNSLSENEDNSG | YSYRNDKFN | 8,88 | YRNDKFNSL | 8,59 | FNSLSENED | 7,31 | LSENEDNSG | 7,09 | ||||
| NTNSNNFANTSEISIGKDNK | NSNNFANTS | 8,78 | ||||||||||
| QYTFIQKRTHLFACGIKRKS | FIQKRTHLF | 9,80 | ||||||||||
| IKWICRENSEKITVCVPDRK | ICRENSEKI | 8,88 | ||||||||||
| IQLCIANFLNSRLETMEKFK | IQLCIANFL | 10,09 | LCIANFLNS | 9,39 | IANFLNSRL | 10,49 | LNSRLETME | 9,57 | ||||
| EIFLISVNTEAKLLYNKNEG | IFLISVNTE | 10,49 | ||||||||||
| KDPSIFCNELRNSFSDFRNS | FCNELRNSF | 9,80 | LRNSFSDFR | 8,41 | ||||||||
| FIGDDMDFGGNTDRVKGYIN | ||||||||||||
| KKFSDYYKEKNVEKLNNIKK | FSDYYKEKN | 8,19 | YKEKNVEKL | 8,19 | KEKNVEKLN | 8,27 | ||||||
| EWWEKNKANLWNHMIVNHKG EWWEKNKAN | 8,67 | WWEKNKANL | 8,19 | WEKNKANLW | 8,19 | LWNHMIVNH | 9,29 | |||||
| NISKECAIIPAEEPQINLWI | ISKECAIIP | 9,80 | IPAEEPQIN | 8,70 | ||||||||
| KEWNENFLMEKKRLFLNIKD | KKRLFLNIK | 9,66 | ||||||||||
| KCVENKKYEACFGGCRLPCS | VENKKYEAC | 9,80 | YEACFGGCR | 9,57 | ||||||||
| SYTSFMKKSKTQMEVLTNLY | FMKKSKTQM | 9,10 | MKKSKTQME | 8,19 | ||||||||
| KKKNSGVDKNNFLNDLFKKN | VDKNNFLND | 8,19 | DKNNFLNDL | 8,67 | ||||||||
| NKNDLDDFFKNEKEYDDLCD | DDFFKNEKE | 7,06 | ||||||||||
| CRYTATIIKSFLNGPAKNDV | YTATIIKSF | 10,20 | ||||||||||
| DIASQINVNDLRGFGCNYKS | ||||||||||||
| NNEKSWNCTGTFTNKFPGTC | WNCTGTFTN | 9,39 | FTNKFPGTC | 10,49 | ||||||||
| EPPRRQTLCLGRTYLLHRGH | RRQTLCLGR | 10,35 | LCLGRTYLL | 8,19 | LGRTYLLHR | 8,19 | GRTYLLHRG | 9,14 | ||||
| EEDYKEHLLGASIYEAQLLK | EEDYKEHLL | 7,76 | YKEHLLGAS | 9,98 | LLGASIYEA | 9,80 | ||||||
| YKYKEKDENALCSIIQNSYA | LCSIIQNSY | 9,80 | ||||||||||
| DLADIIKGSDIIKDYYGKKM | LADIIKGSD | 9,29 | IKDYYGKKM | 8,19 | ||||||||
| EENLNKVNKDKKRNEESLKI | ||||||||||||
| FREKWWDENKENVWKVMSAV | FREKWWDEN | 7,27 | ||||||||||
| LKNKETCKDYDKFQKIPQFL | YDKFQKIPQ | 9,29 | ||||||||||
| RWFKEWGDDFCEKRKEKIYS | FKEWGDDFC | 8,19 | ||||||||||
| FESFKVECKKKDCDENTCKN | FESFKVECK | 8,19 | KKDCDENTC | 8,05 | ||||||||
| KCSEYKKWIDLKKSEYEKQV | YKKWIDLKK | 7,50 | WIDLKKSEY | 9,80 | LKKSEYEKQ | 8,19 | ||||||
| DKYTKDKNKKMYDNIDEVKN YTKDKNKKM | 8,41 | DKNKKMYDN | 8,67 | MYDNIDEVK | 9,80 | YDNIDEVKN | 7,68 | |||||
| KEANVYLKEKSKECKDVNFD | VYLKEKSKE | 8,41 | YLKEKSKEC | 8,41 | ||||||||
| DKIFNESPNEYEDMCKKCDE | IFNESPNEY | 10,09 | FNESPNEYE | 8,70 | ||||||||
| IKYLNEIKYPKTKHDIYDID | IKYLNEIKY | 7,72 | YLNEIKYPK | 8,19 | YPKTKHDIY | 8,88 | ||||||
| TFSDTFGDGTPISINANINE | FSDTFGDGT | 7,31 | FGDGTPISI | 10,09 | ISINANINE | 7,31 | ||||||
| QQSGKDTSNTGNSETSDSPV | ||||||||||||
| SHEPESDAAINVEKLSGDES | VEKLSGDES | 8,19 | ||||||||||
| SSETRGILDINDPSVTNNVN | ILDINDPSV | 10,09 | INDPSVTNN | 10,09 | ||||||||
| EVHDASNTQGSVSNTSDITN | VSNTSDITN | 8,48 | ||||||||||
| GHSESSLNRTTNAQDIKIGR | ||||||||||||
| SGNEQSDNQENSSHSSDNSG | ||||||||||||
| SLTIGQVPSEDNTQNTYDSQ | ||||||||||||
| NPHRDTPNALASLPSDDKIN | ALASLPSDD | 7,53 | LASLPSDDK | 7,68 | ||||||||
| EIEGFDSSRDSENGRGDTTS | SSRDSENGR | 7,58 | SRDSENGRG | 7,58 | ||||||||
| NTHDVRRTNIVSERRVNSHD | VRRTNIVSE | 9,57 | IVSERRVNS | 8,19 | VSERRVNSH | 7,50 | ||||||
| FIRNGMANNNAHHQYITQIE | FIRNGMANN | 9,98 | IRNGMANNN | 6,98 | ||||||||
| NNGIIRGQEESAGNSVNYKD | IIRGQEESA | 9,80 | IRGQEESAG | 9,80 | ||||||||
| NPKRSNFSSENDHKKNIQEY | KRSNFSSEN | 8,96 | ||||||||||
| NSRDTKRVREEIIKLSKQNK | RVREEIIKL | 8,56 | VREEIIKLS | 8,88 | IIKLSKQNK | 8,41 | ||||||
| CNNEYSMEYCTYSDERNSSP | YSMEYCTYS | 8,70 | YCTYSDERN | 9,29 | YSDERNSSP | 8,41 | ||||||
| GPCSREERKKLCCQISDYCL | ERKKLCCQI | 8,58 | LCCQISDYC | 9,80 | ||||||||
| KYFNFYSIEYYNCIKSEIKS | YFNFYSIEY | 7,50 | FNFYSIEYY | 7,78 | FYSIEYYNC | 8,88 | YSIEYYNCI | 7,78 | IEYYNCIKS | 9,29 | YYNCIKSEI | 9,57 |
| PEYKCFKSEGQSSIPYFAAG | FKSEGQSSI | 9,80 | ||||||||||
| GILVVIVLLLSSASRMGKSN | LLSSASRMG | 7,68 | LSSASRMGK | 8,37 | ||||||||
| EEYDIGESNIEATFEENNYL | YDIGESNIE | 8,70 | IGESNIEAT | 10,09 | IEATFEENN | 8,70 | ||||||
| NKLSRIFNQEVQETNISDYS | FNQEVQETN | 8,48 | ||||||||||
| VQETNISDYSEYNYNEKNMY | ISDYSEYNY | 7,09 | ||||||||||
Para los 492 péptidos analizados en cada una de las proteínas teóricas, se encontró que 111, 84 y 72 corresponden respectivamente al macroestado de unión de cada una, mientras que las restantes 381, 408 y 420 respectivamente corresponden al macroestado de no unión (Tabla III). El porcentaje de unión respecto a la totalidad de péptidos corresponde al 22,2% para la secuencia teórica 1, al 16.8% para la 2 y al 14,4% para la 3.
Primera secuencia teórica generada y péptidos predichos de unión para esta secuencia
| SKHINLWSHPYMGMVRPNINIREITVSQPGYLRKSARFCYSSTTWNILRTNKGVLWCWGAKTYAHDLFRWPEGFEPWNTNMAMVTQPYFTWFNISQPHTMSRESLTCDMTISGLMWVPMINDINKATQDVSGQKCTTDIPMMENHGSDKSERDWPEYQNRLYDPYHCMEGIDYMPGDVRWGKGKGYWAGWQMSDFVTHNECLYIAHDLIFQGAYLDHIDCNDWIYTLDKFESKRHIMWDGRPWSVRSTWWVTKMDHMGMDAFLMVTLCYIWRHRPLQVCRVRVYGVCHMTWPFASLGALNGTIAINVLQNNTFNANSMNFLDRGPLNLGICKCQRRENRPLDLVKCCRVVMNDLNLKWVVVVWNGLQPPRLPNLAVNHCNWCIKPDCIRAGNYLGDYYKFIKKRPEKECHMAMPAIHYPKCEMQLHKNKYRLTHSHFHVIWQINKRGERRLFMWFHIWWNQYWRIMNLLCNVGTRHIDICMMHVKMWWNVMGLKCSTSNC |
|
Este es el primer trabajo donde se realiza una predicción de la totalidad de péptidos nonámeros de las proteinas MSP1 y EBA 140 de plasmodium falciparum que pueden unirse a la región central de unión al HLA clase II con base en una teoría basada en las leyes de probabilidad, combinatoria y entropía. Se determinó que existen 179 péptidos incluidos dentro del macroestado de unión y 769 que no se unen para la proteína MSP-1, mientras que se hallaron 119 péptidos asociados al microestado de unión y 613 al de no unión para el caso del antígeno EBA-140, péptidos que deberán ser sometidos a validación experimental. Además se predijeron péptidos de unión en tres proteínas teóricas, 111, 84 y 72 respectivamente, con base en la metodología implementada; con esto se corrobora una alta especificidad característica del fenómeno de unión, útil en la predicción de péptidos al HLA clase II, a partir de leyes físicas y matemáticas.
Existen cuantificaciones de la unión de péptidos al HLA en trabajos anteriores en predicción de unión de péptidos a partir de ANN (Artificial Neural Networks), programación lineal, o vectores de máquina(27-29). Tales métodos buscan patrones de unión caracterizando las posiciones y sus respectivos motivos; su generalización es limitada pues depende de la muestra usada. En contraposición, la teoría aquí utilizada no depende de la población de estudio al estar basada en una abstracción físico teórica que permite cuantificar desde teorías físicas y matemáticas la totalidad de posibilidades existentes de péptidos. Su aplicación permitirá una disminución significativa de los costos necesarios para la determinación de la capacidad de unión de péptidos con el método que Berzofsky denominó "de fuerza bruta"(30), el cual se basa en la evaluación in vitro de la capacidad de estimulación de respuestas en linfocitos T por parte de péptidos sobrelapados que son sintetizados en el laboratorio. La teoría planteada en este trabajo economiza tiempo y simplifica el procedimiento hasta ahora empleado, ya que permite evaluar todas las secuencias nonámeras sobrelapadas para cualquier secuencia proteica, sustituyendo la utilización de los procesos experimentales de ensayo y error por predicciones numéricas rigurosas, evitando la realización de un análisis experimental de la totalidad de las secuencias nonámeras sobrelapadas del MSP-1 y de EBA-140. Además, al estar basada en una inducción que incluye péptidos promiscuos, y el estudio de las secuencias peptídicas mediante representaciones numéricas de tipos de secuencias y no mediante la distribución de aminoácidos específicos, la teoría aplicada en este trabajo fue diseñada para obviar las especificidades alélicas y para detectar péptidos promiscuos, implicando un valor adicional de las predicciones realizadas, al abarcar individuos con diferentes alelos de HLA clase II.
Se ha evidenciado experimentalmente una relación entre la disminución del tamaño del péptido asociado a la molécula de HLA clase II y la pérdida de energía de unión(31-34); las interacciones de la región central muestran una compensación a la pérdida que puede ser suministrada por la adición de aminoácidos en posiciones de anclaje(35). Según esto y con base en el trabajo realizado, se sugiere que de acuerdo con la teoría física y matemática desarrollada, el procedimiento a seguir en búsqueda de péptidos útiles en la elaboración de vacunas, es inicialmente efectuar una predicción de los posibles péptidos naturales ó sintéticos nonámeros de unión, seguidamente realizar una contrastación experimental, posteriormente introducir aminoácidos que puedan cambiar los valores de los microestados, y por último hacer las pruebas experimentales de respuesta y memoria inmunológica. En el caso de las proteínas MSA-2 y AMA-1, ya se efectuó una predicción de los péptidos nonámeros de unión al HLA clase II con base en la metodología aplicada en este trabajo, determinando 35 posibles péptidos de unión para la proteína MSA-2 y 60 para la proteína AMA-1, resultados que pueden ser de utilidad en la selección de péptidos útiles para el diseño de vacunas contra la malaria(20).
La utilidad de esta teoría no se limita al diseño de vacunas contra la malaria. En otro trabajo se aplicó esta metodología a la proteína API m1 y a dos del HER-2/neu, observando que al comparar el desempeño de esta predicción respecto a los métodos de predicción de unión de péptidos de mayor cobertura alélica disponibles en línea, se obtienen los mayores valores de sensibilidad, exactitud y valor predictivo positivo (Rodríguez J, Bernal P, et al. Manuscrito en preparación).
Otras investigaciones desarrolladas desde una perspectiva física y matemática acausal han producido resultados efectivos en áreas como la biología molecular, la morfología celular y la morfología y fisiología cardiaca. En el caso de la inmunología se han desarrollado caracterizaciones del fenómeno de unión de la proteína MSP-1 al receptor de glóbulo rojo, realizadas con la teoría de conjuntos(36), y posteriormente con las teorías de probabilidad y entropía(37), que permiten una diferenciación matemática objetiva de péptidos de unión y no unión. Del mismo modo se realizó una caracterización del fenómeno de unión de péptidos nonaméricos al HLA clase II con la teoría de conjuntos(38). En esta línea de trabajo, también se desarrolló previamente una caracterización de péptidos de alta unión de la proteína EBA-140 (39), en el que se logró diferenciar péptidos de alta unión y de no unión con 100% de acierto para los casos estudiados; este resultado evidencia la existencia de un orden subyacente en el fenómeno de unión, que se puede caracterizar de una manera objetiva y reproducible a partir de leyes físicas y matemáticas.
Es así como la presente investigación hace parte de una serie de trabajos fundamentados en una teoría desarrollada(19), con la cual se simplifica el fenómeno de unión, en donde a partir de la representación numérica de tipos de secuencias y obviando la especificidad alélica, se hace posible predecir los péptidos de unión, viabilizando el desarrollo de vacunas en ausencia de ensayos de prueba y error experimentales. El descubrimiento de órdenes físicos y matemáticos acausales desde las actuales teorías fundamentales de la física(40), evita la necesidad del uso de grandes cantidades de datos experimentales.
Esta concepción acausal ha permitido obtener resultados en otros campos de la medicina, tales como la dinámica cardiaca, donde se realizó una nueva metodología de evaluación del Holter(41). Recientemente, Rodríguez(42) desarrolló un método diagnóstico de aplicación clínica de dicho examen con base en la determinación de órdenes entrópicos proporcionales entre regiones geométricas definidas dentro del atractor. Del mismo modo, el establecimiento de órdenes acausales permitió el desarrollo de diferentes métodos predictivos de la dinámica anual en Colombia de enfermedades como malaria, estudiada mediante el análisis probabilista de rangos de infectados(43), y dengue, mediante una analogía de la dinámica con una caminata al azar probabilista(44); en el primero se desarrolló una predicción con un 100% de acierto y en el segundo se realizó una predicción, que al ser comparada con los casos registrados por el INS se encontró como resultado un valor que corresponde al 90,4 % respecto al valor predicho. La aplicación de la ley de entropía al análisis de la dinámica de malaria en todos los municipios de Colombia permitió realizar predicciones semanales, estableciendo matemáticamente la aparición de brotes(45).
AGRADECIMIENTOSDedicamos este trabajo a nuestros hijos y al ahijado del primer autor, Joshua.
A los doctores Luis Eduardo Cruz y Miguel Martínez del departamento de fisiología y a la facultad de medicina de la Universidad Nacional por apoyar nuestras investigaciones.