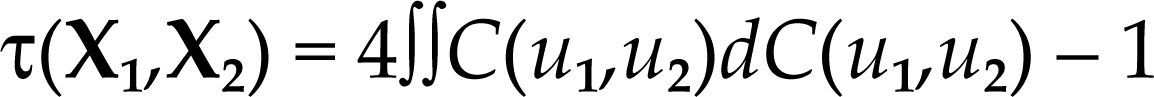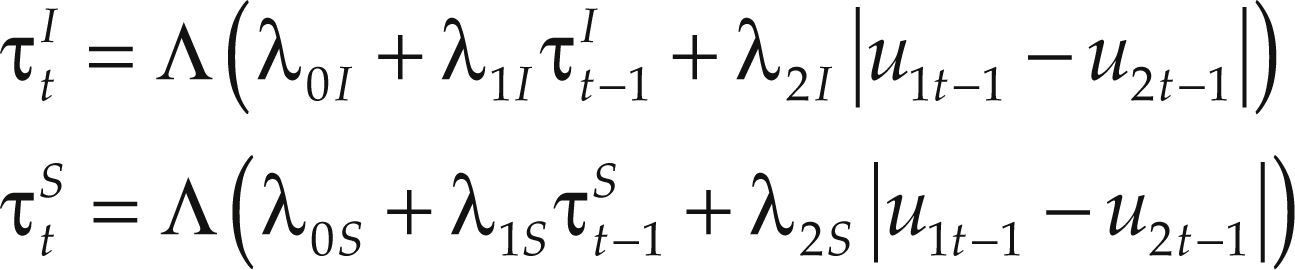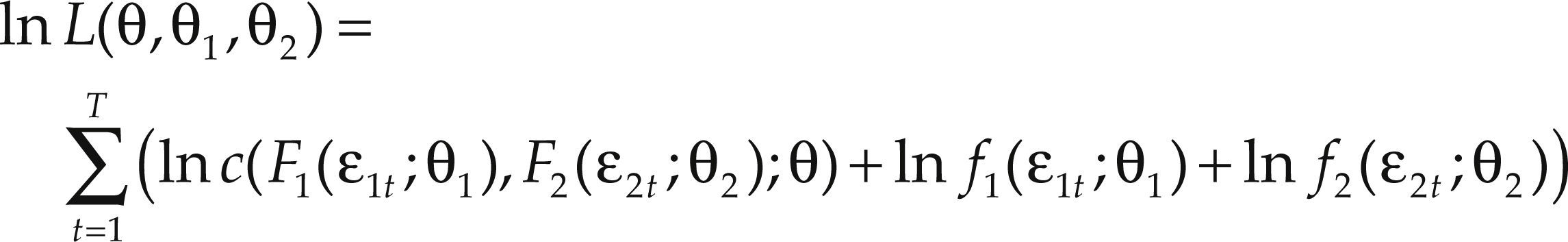Las investigaciones realizadas en torno a la relación entre el mercado financiero y el crecimiento económico se han concentrado en buscar el sentido de causalidad y una relación de largo plazo entre ellas, sin ser concluyentes en los resultados. Se observa que las herramientas utilizadas para estos propósitos asumen una distribución normal gaussiana bivariada, razón por la cual no se captan los efectos de dependencia asimétrica. El presente trabajo empleó la herramienta de cópula condicional-tgarch bivariada para determinar la dependencia condicional en colas entre los rendimientos mensuales del Índice de Precios y Cotizaciones (ipc) de la Bolsa Mexicana de Valores y las tasas de crecimiento del Indicador Global de la Actividad Económica (igae) durante el periodo de enero de 1993 a junio de 2015. Nuestros resultados sugieren la existencia de una relación de dependencia que no es uniforme en el tiempo; es mayor en momentos cercanos a crisis y se debilita posteriormente.
Research on the relationship between financial markets and economic growth has focused on finding their causal influence and long-term relationship with inconclusive results. The typical tools used for these purposes assume a bivariate Gaussian normal distribution, hence elements such as asymmetric dependence is not captured. The present work used the conditional bivariate copula-tgarch tool to determine the conditional dependence between the monthly returns of the Mexican stock exchange price index (ipc) and the index measuring the overall growth of economic activity (igae) for the January 1993 to June 2015 period. Our results suggest a dependence relationship that varies with time; it is higher in near crisis periods and weakens afterwards.
Uno de los sectores que tradicionalmente es estudiado para entender y, en algunos casos, caracterizar la dinámica de crecimiento económico de los países es el sector financiero. Esto se debe a que, en su mayoría, la teoría económica postula la existencia de una relación directa y positiva entre el desempeño de dicho sector y el crecimiento de la economía real en el corto y largo plazo. Esta relación ha sido estudiada y defendida desde inicios del siglo pasado. Como principales exponentes se encuentran los trabajos de Schumpeter (1911), Goldsmith (1969), McKinnon (1973) y Shaw (1973). En ellos se establece que elementos como la cantidad y calidad de instrumentos financieros disponibles, la presencia de intermediarios financieros, así como la estructura y desarrollo del mercado financiero, tenían un impacto positivo sobre el crecimiento económico. Por su parte, King y Levine (1993a, 1993b) muestran una relación empírica entre el sector financiero y el crecimiento al utilizar un modelo de crecimiento endógeno; en él señalan que altos niveles de desarrollo financiero están fuertemente asociados con mayores tasas de crecimiento de la producción, por lo que puede interpretarse como un indicador de crecimiento económico de largo plazo. El principal elemento de controversia es que dentro del desarrollo teórico y, sobre todo, en la validación empírica no se establece claramente la dirección de causalidad entre el desarrollo financiero y el crecimiento económico.
El estudio —tanto teórico como empírico— de la relación causal y/o de cointegración entre dichas variables ha tenido un crecimiento considerable en los últimos veinticinco años. Gran parte de la investigación se ha centrado en la búsqueda del sentido de causalidad, así como en una posible relación de largo plazo entre el mercado financiero y el crecimiento económico. Dentro de las herramientas más utilizadas con este fin se encuentran la prueba de causalidad en sentido Granger (1969, 1980, 1988) y el análisis de cointegración a partir de la metodología propuesta por Johansen (1988, 1991, 1995). Sin embargo, la evidencia empírica no ha sido concluyente respecto a la existencia de una relación de largo plazo entre las variables, el sentido unidireccional de la relación de causalidad o, incluso, la presencia de bidireccionalidad en la relación. Por una parte, los resultados de Fama (1990) sugieren que el comportamiento de la economía real causa el desempeño bursátil de Estados Unidos; por la otra, tanto los obtenidos por Schwert (1990) como los de Lee (1992) sugieren que la dirección de causalidad es la opuesta basándose en que, en principio, un mercado financiero desarrollado debiera propiciar el incremento en el ahorro nacional, así como la asignación eficiente de capital productivo. Lo anterior conduciría a un aumento en la tasa de crecimiento económico. Gran parte de los estudios realizados posteriormente se enfocan en esta última dirección como clave para el desarrollo económico de un país.
Los trabajos de Atje y Jovanovic (1993), Demirgüç-Kunt y Levine (1996) y Levine y Zervos (1998) muestran que el desarrollo del mercado de valores tiene una marcada correlación con el crecimiento real per cápita de la economía. Más aún, encuentran que tanto la liquidez del mercado de valores como el desarrollo de la banca pueden utilizarse como predictores del comportamiento real de la economía. Por su parte, Choi, Hauser y Kopecky (1999) sugieren que los rezagos del rendimiento del mercado accionario pueden ser utilizados para explicar el comportamiento futuro de la producción industrial.
Levine, Loayza y Beck (2000) hacen hincapié en el papel que desempeñan los intermediarios financieros para el desarrollo del mercado y su posterior efecto sobre la economía. Su estudio de causalidad sugiere que las reformas legales y contables que fortalecen los derechos de los acreedores y que, a su vez, refuercen el cumplimiento de contratos y la correcta aplicación de las prácticas contables promoverán el desarrollo de los intermediarios financieros. En consecuencia, esto se traduce en un impacto positivo sobre el desarrollo del mercado financiero y el crecimiento económico del país. En lo referente a la relación entre la estructura del mercado financiero y su impacto en el crecimiento económico, Demirgüç-Kunt y Levine (2001) hacen una recopilación de estudios que refuerzan la noción de que una correcta estructuración del mercado financiero promueve su desarrollo y, posteriormente, tiene efectos positivos sobre el crecimiento económico.
Para el caso de las economías emergentes, se destaca el trabajo de Mauro (2003), quien presenta un análisis de correlación entre el rezago de los rendimientos bursátiles y la producción económica de cuarenta y cinco mercados emergentes y veintiún desarrollados. Su estudio postula que existe una importante correlación entre dichas variables y que el grado de asociación es similar entre los dos grupos de economías. Destaca que elementos como la razón de capitalización-producto interno bruto (pib), el número de empresas listadas y de ofertas iniciales públicas, además de la regulación del mercado financiero, son fundamentales para entender el grado de correlación presente. Más recientemente, Cortés y Hernández (2014) proponen un modelo de efectos aleatorios en datos panel que utiliza cuatro variables para explicar el crecimiento económico per cápita de veintiséis países —trece de ellos latinoamericanos— dentro del periodo 2001-2011. Las variables que utilizan son: el crédito interno del sector bancario como variable proxy del desarrollo del sistema financiero, la formación bruta de capital fijo (como porcentaje del pib) como variable proxy de la inversión, la inflación y las exportaciones. Sus resultados indican que tanto el desarrollo del sector financiero como el nivel de inversión tienen efectos positivos de largo plazo sobre el crecimiento económico de los países emergentes.
Para el caso particular de economías latinoamericanas, Ruiz (2004) evalúa, a través de dos técnicas econométricas, la hipótesis de que el comportamiento de los agentes en los mercados de crédito, bonos y acciones, promueve el crecimiento económico para los casos de Argentina, Brasil, Chile, Colombia y México dentro del periodo 1945-1998. En un primer paso, se utiliza una estimación a través de mínimos cuadrados ordinarios para determinar el impacto específico de los mercados financieros en el crecimiento del producto per cápita de cada país. Posteriormente, con la finalidad de capturar efectos de externalidad intra e inter economías a partir de una estructura de crecimiento endógeno, se aplica el método de estimación Zellner-Schmidt para modelos que consideran un sistema de ecuaciones de regresión sin relación aparente (sure, Seemingly Unrelated Regression Equations). Su evidencia sugiere que existen efectos diferenciados en la contribución que tiene el sector financiero a la tasa de crecimiento para el caso de América Latina. Aunque sus resultados apoyan la idea de que, vistos de manera individual, los mercados financieros pueden jugar un papel significativo en el proceso de crecimiento de los países, se puntualiza que la interdependencia regional puede determinar la relevancia, y posiblemente la orientación causal, de dicha relación. En otras palabras, que los indicadores de mercados financieros internos tienden a presentar una mayor vinculación con el crecimiento económico si se considera el efecto de la interdependencia regional.
En lo referente a estudios de causalidad y cointegración, se destaca el trabajo presentado por Caporale, Howells y Soliman (2004), donde se emplea la metodología propuesta por Toda y Yamamoto (1995) para probar causalidad en sentido Granger entre el desarrollo del sector financiero y el crecimiento económico de Argentina, Chile, Grecia, Corea, Filipinas, Malasia y Portugal. A través de un modelo de vectores autoregresivos (var) encontraron evidencia de que el desarrollo del mercado bursátil impulsa el crecimiento económico de largo plazo para el caso de Chile, Corea, Filipinas y Malasia. Haciendo uso de la misma metodología, Guha y Mukherjee (2008) hallaron evidencia de causalidad bidireccional entre la capitalización del mercado de valores indio y el crecimiento económico del país.
Para el caso de la economía mexicana, resalta el trabajo de Rodríguez y López (2009), quienes realizaron un estudio de causalidad en sentido Granger y cointegración utilizando como variables al pib per cápita y la relación capital-trabajo para el periodo 1990-2004. Concluyeron que el desarrollo financiero tiene impacto positivo sobre el crecimiento económico, al tiempo que encontraron evidencia de causalidad bidireccional entre las variables. Por su parte, Tinoco, Torres y Venegas (2008) utilizan un modelo de corrección de error para efectuar un análisis de causalidad y cointegración con el fin de determinar la relación de corto y largo plazo entre el desarrollo del mercado financiero y el crecimiento económico mexicano en el periodo 1961-2003. No descubrieron evidencia de causalidad entre las variables, pero sus resultados sugieren que la regulación tiene un impacto negativo sobre el desarrollo del mercado financiero. Esto, en menor medida, tiene un impacto negativo sobre el crecimiento económico. También, a partir de un modelo de corrección de error, López y Rodríguez (2010) estudiaron la relación de causalidad y cointegración entre los índices del mercado accionario mexicano y el de volumen de la producción industrial. En contraste con los resultados de Tinoco, Torres y Venegas (2008), los autores hallaron una débil evidencia de causalidad en la dirección del mercado accionario hacia la producción industrial en el periodo 1987-2008. Otro contraste se presenta con los resultados de Ortiz, Cabello y De Jesús (2007), quienes, siguiendo el uso del modelo de corrección de error, encontraron evidencia de cointegración y de causalidad bidireccional entre la producción industrial y el mercado accionario para el periodo 1968- 2002. Brugger y Ortiz (2012) realizaron un estudio de causalidad y cointegración a través de un modelo de vectores autorregresivos entre los rendimientos bursátiles y el producto interno bruto de Argentina, Brasil, Chile y México para el periodo 1993-2005. Sus resultados indican causalidad unidireccional de la bolsa hacia el pib, así como una relación de largo plazo débil entre ellos.
Existen dos limitaciones importantes en las técnicas utilizadas para analizar la relación de dependencia entre variables aleatorias: el supuesto de normalidad de sus funciones de distribución y la obtención de una medida de correlación lineal y constante en el tiempo. Gran parte de las pruebas de causalidad en sentido Granger, cointegración y el cálculo de correlación asumen una distribución normal gaussiana bivariada por lo que están enfocadas típicamente en la media o varianza de las variables. No obstante, el empleo de la distribución gaussiana priva a la herramienta utilizada de captar características propias de las series de tiempo financieras: específicamente la dependencia asimétrica y, en caso de existir, elementos no lineales de la relación. A partir de un enfoque de administración de riesgos, y ante la constante presencia de periodos de crisis financieras, es necesario modelar la relación de dependencia en un entorno distinto al de la normal y enfocarse en la dinámica presentada en las colas.
Embrechts, McNeil y Straumann (2002) describen la problemática y malinterpretación del concepto de correlación cuando se aplica fuera del contexto de la distribución normal. Señalan que uno de los problemas principales cuando se construyen distribuciones multivariadas es que sean consistentes con las distribuciones marginales y la estructura de correlación dada. Por ello, enfatizan que herramientas como las cópulas ayudan a clarificar el término de dependencia. El uso de la modelación a través de éstas permite, sin la necesidad de asumir una función de distribución para las variables aleatorias consideradas, obtener una función de distribución conjunta de la cual se pueda cuantificar una medida del grado de dependencia entre ellas. Más aún, al tener la posibilidad de separar el comportamiento de los marginales, uno puede modelar las variables con la técnica econométrica que más convenga según sus características.
Como es ilustrado por Chollete, Heinen y Valdesogo (2009), las cópulas son de gran utilidad cuando se trabaja con series de tiempo financieras debido a que, además de permitir el análisis de la dependencia en colas, los parámetros estimados por esta herramienta pueden ser fácilmente adaptados a técnicas como simulaciones Monte Carlo para la administración de riesgos. Otra ventaja del uso de cópulas es que se puede evaluar si, en distintos periodos y ante la presencia de eventos extremos, el comportamiento de las colas se ve modificado por el cambio en la estructura de dependencia de las variables. Bajo un análisis de correlación estático esta dinámica no podrá ser capturada llevando, posiblemente, a conclusiones no del todo precisas. Es por ello que la herramienta utilizada deberá permitir la variación en tiempo de la medida de dependencia, situación que resulta posible trabajando con cópulas.
En suma, se puede observar que el análisis de cópulas se establece como una alternativa al estudio simple de correlación puesto que permite desarrollar un modelaje de la dependencia entre variables aleatorias y sus marginales, sin asumir una función de distribución, al tiempo que la medición del grado de asociación puede darse en un ambiente dinámico. El presente trabajo no busca aportar un caso más a la literatura del análisis de la dirección de causalidad entre los mercados real y financiero, ante la inconsistencia de los resultados presentados anteriormente. Son dos los principales objetivos: el primero es determinar, utilizando la herramienta de cópulas, el grado de dependencia entre el mercado financiero y el real de la economía mexicana, haciendo hincapié en el comportamiento de las variables ante la presencia de eventos extremos; el segundo es identificar qué sucede con dicha relación de dependencia a través del tiempo. Ambos resultados son de gran interés para la caracterización de la relación establecida y las consideraciones que tanto los participantes en el sector financiero como los del gobierno puedan llevar a cabo en periodos de crisis.
Con el fin de alcanzar los objetivos planteados, nuestro trabajo utiliza las cópulas condicionales para describir la función de distribución bivariada, así como una relación de dependencia en las colas entre las tasas de rendimiento en el mercado financiero y las tasas de crecimiento económico. El concepto de cópula condicional fue presentado por Patton (2001a, 2001b) e incluye, para cada variable individual, una función de densidad condicional variable en el tiempo, así como la dependencia condicional entre ellas. En trabajos subsecuentes, Patton (2006a, 2006b) desarrolló el modelo de cópula bivariada, que llamó cópula simétrica Joe-Clayton. Ésta utiliza un estimador de máxima verosimilitud de periodos múltiples para probar asimetría en la dependencia de las colas. Para identificar la evolución de las varianzas condicionales se emplea un modelo generalizado autorregresivo de heterocedasticidad condicional (garch, Generalized Autoregressive Conditional Heteroskedasticity) y con ello se busca capturar variaciones temporales a la estructura de dependencia presente en cada periodo. Esta modificación al modelo permite que los parámetros de la cópula varíen a través del tiempo y que, de esta manera, se pueda encontrar evidencia de cambios en la dependencia durante periodos de eventos extremos.
La metodología con cópulas no condicionales ha sido utilizada anteriormente por Rodríguez (2007), Okimoto (2008), Johansson (2011), Canela y Pedreira (2012) y Lorenzo y Massa (2013) para estudiar la relación entre mercados accionarios y evaluar la presencia de efectos de contagio o dependencia entre mercados. Sin embargo, no es de nuestro conocimiento la existencia de algún trabajo donde se analice la relación de dependencia en colas entre el sector financiero y el crecimiento económico. Por lo que, el presente trabajo, tiene como finalidad adicional atraer la atención académica hacia el uso de esta herramienta en el contexto de dependencia ante eventos extremos, considerando dicha dependencia en forma condicional, es decir, subordinada al tiempo. El artículo está estructurado como sigue: la segunda sección describe el concepto de cópula, mientras que la metodología utilizada se presenta en la tercera. La cuarta sección describe los datos y resultados obtenidos. Finalmente, la quinta sección expone las conclusiones.
CÓPULASUna copula bivariada C(u1,u2) es una función de distribución multivariada acumulada (fda) para dos variables uniformes sobre el intervalo unitario. El teorema de Sklar (1959) establece que si tomamos uj = Fj(xj) para j = 1,2 como la fda de una variable aleatoria continua univariada Xj, entonces C(F1(x1),F2(x2)) es una función de distribución bivariada para X(X1,X2) con distribuciones marginales Fj, j = 1,2. Inversamente, si F es una fda continua bivariada con marginales univariadas F1,F2, entonces existe una única cópula bivariada C tal que F(x1,x2) = C(F1(x1),F2(x2)).
Lo anterior permite el estudio de la dependencia de las dos variables a partir de sus distribuciones marginales. Las propiedades de las cópulas han sido estudiadas por varios autores, de entre los cuales destaca el trabajo de Nelsen (1999). La primera de ellas es que son invariantes ante transformaciones estrictamente positivas de variables aleatorias. La segunda propiedad es la consistencia entre el cálculo de las medidas de concordancia presente en los parámetros de las cópulas y medidas de dependencia como la tau de Kendall. Finalmente, la tercera propiedad consiste en el tratamiento que puede darse a la dependencia asintótica en las colas.
Dos puntos (x1,x2),(y1,y2) se dice que son concordantes si (x1 – y1)(x2 – y2) > 0 y discordantes si (x1 – y1)(x2 – y2) < 0. En forma similar, dos vectores aleatorios (X1,X2),(Y1,Y2) son concordantes si la probabilidad P[(X1 – Y1)(X2 – Y2) > 0] es mayor que la probabilidad P[(X1 – Y1)(X2 – Y2) < 0]; esto es, si X1 tiende a crecer con X2, por lo que la concordancia es una relación de dependencia. De igual forma, dos vectores son discordantes si ocurre lo contrario. La tau de Kendall mide las diferencias en probabilidad por lo que es una medida de concordancia:
Al trabajar con cópulas se tiene como ventaja la posibilidad de asociarlas con la tau de Kendall por medio de la siguiente relación:
Adicionalmente a la estimación de la tau de Kendall, el presente trabajo busca evidencia de dependencia asintótica en las colas de la distribución. Es decir, la medición del comportamiento de las variables aleatorias durante eventos extremos. En concreto, se emplean medidas que indican la probabilidad de que se observe un incremento (decremento) extremo en los rendimientos del índice accionario mexicano, dado que hay un incremento (decremento) extremo en la tasa de crecimiento económico en México. Es así que se definen los coeficientes de dependencia en colas inferior (τI) y superior (τS) como:
Existe independencia en las colas si los valores en [3] son cero, dependencia si los valores están entre cero y uno, y dependencia perfecta si son iguales a uno. Debido al enfoque que tienen en el comportamiento de las colas, en este estudio se utilizan las cópulas de Clayton y de Gumbel. En la primera existe el coeficiente de dependencia en cola inferior pero no el superior. En la cópula de Gumbel sucede lo opuesto, existe el coeficiente de dependencia en cola superior pero no existe el inferior. La cópula de Clayton bivariada es determinada por la siguiente ecuación:
con θϵ [–1,∞)\{0}. En este caso τI = 2–1/θ.
Por su parte, la cópula de Gumbel bivariada se define por la siguiente ecuación:
con θϵ [1,∞). Para este caso τS = 2 – 2–1/θ.
En nuestro estudio seguimos a Patton (2006a) y estimamos las dependencias en colas condicionales, es decir, dependientes del tiempo y suponiendo que la dinámica del comportamiento es la siguiente:
con Λ siendo la transformación logística utilizada para asegurar que los valores se mantengan entre cero y uno.
METODOLOGÍAPara evaluar la dependencia condicional en las colas entre el mercado accionario y el crecimiento económico de México, se toman los precios de cierre mensual del Índice de Precios y Cotizaciones (ipc) y el Indicador Global de la Actividad Económica (igae) en el periodo t, Pit, con i el ipc o el igae, y se calculan los rendimientos continuos por periodo:
Estas dos series de datos, de tasas continuas de crecimiento en el mercado financiero y en la economía, se tomarán como las dos variables a medir su dependencia. El modelo que describe el comportamiento para las distribuciones marginales es un modelo ar(1)-tgarch(1,1).
Las perturbaciones ¿it se distribuyen como una t de student estandarizada y se estiman los grados de libertad (v). El modelo presenta una ecuación para los rendimientos que, en este caso, se define como un proceso autorregresivo de orden uno, al depender los rendimientos del periodo de los mismos rendimientos en el periodo anterior, y una ecuación para la varianza (volatilidad al cuadrado) que sirve para describir la dispersión de los rendimientos continuos (en logaritmos).
Como se menciona en Tsay (2005), la inclusión de la volatilidad en los modelos permite describir ciertas características típicas de las series de tiempo financieras como son: 1) la probabilidad de tener rendimientos extremos superiores a los que se tendría si se supone una distribución normal, esto es, la distribución de probabilidades de los rendimientos presenta colas más anchas que una distribución normal, conocido como exceso de curtosis; 2) el efecto apalancamiento cuando existe una correlación negativa entre el rendimiento y la volatilidad en el sentido de que cuando el rendimiento baja la volatilidad aumenta, y 3) la relación temporal de la volatilidad que forma clusters, es decir, la volatilidad en un periodo depende de la volatilidad en periodos anteriores. Para capturar dichas características, así como la estimación de la ecuación de la volatilidad, se emplea un modelo tgarch (Thresholdgarch) introducido por Zakoian (1994) y Glosten et al. (1993), como una extensión a los modelos arch, desarrollados inicialmente por Engle (1982) y generalizados por Bollerslev (1986).
Finalmente, para la estimación de los parámetros se utilizó la siguiente función de verosimilitud en logaritmos:
donde c(F1(¿1t;θ1),F2(¿2t;θ2);θ) es la densidad de la cópula, mientras f1 y f2 son las densidades de las marginales de los rendimientos de cada variable y {θ,θ1,θ2} son el conjunto de parámetros.
DATOS Y RESULTADOSLos datos del estudio consisten en precios de cierre mensuales del ipc y de los datos mensuales del igae de enero de 19931 a junio de 2015. En el cuadro 1 se presentan los resultados obtenidos en las pruebas de raíz unitaria Dickey-Fuller Aumentada (dfa) y Phillips-Perron (pp) sobre los precios en logaritmos y sus diferencias (rendimientos).
Prueba dfa y pp para precios en logaritmos (niveles) y rendimientos (primera diferencia)
| Niveles | Diferencias | |||
|---|---|---|---|---|
| Probabilidad | Rezago | Probabilidad | Rezago | |
| dfa | ||||
| ipc | 0.68540 | 0 | 0.00000 | 0 |
| igae | 0.83422 | 13 | 0.00009 | 11 |
| pp | ||||
| ipc | 0.68540 | 0 | 0.00000 | 0 |
| igae | 0.77106 | 13 | 0.00000 | 11 |
Nota: se muestra la probalidad (p-value) de la prueba, así como el rezago óptimo considerando el criterio de información de Schwarz.
Se encuentra que las series de tiempo en logaritmos de los precios del ipc y del igae son integradas de orden uno, por lo que podemos trabajar con las diferencias —en nuestro caso los rendimientos—, validando así que las relaciones que se estimarán no son espurias.
Se calculan los rendimientos continuos mensuales como en la ecuación [7] y se presentan las estadísticas descriptivas en el cuadro 2.
Estadísticas descriptivas del rendimiento mensual del ipc y de la tasa de crecimiento económica continua mensual del igae
| ipc | igae | ||
|---|---|---|---|
| Media | 0.01229 | 0.00219 | |
| Desviación estándar | 0.07037 | 0.02905 | |
| Coeficiente de asimetría | –0.89230 | 0.06053 | |
| Curtosis | 6.23601 | 2.76496 | |
| Jarque-Bera | 153.06732 | 0.78344 | |
| p-value | 0.00000 | 0.67589 | |
| Correlación | 0.15906 | ||
| Tau de Kendall | 0.08511 |
La no normalidad de los rendimientos del ipc es confirmada mediante el estadístico de Jarque-Bera basado en la curtosis y el coeficiente de asimetría. No se puede rechazar la hipótesis de que la tasa de crecimiento económico mensual se distribuya como una normal. La correlación positiva es superior a 15%, establece dependencia lineal de los rendimientos del ipc y el igae, además de la confirmación de la concordancia medida por la tau de Kendall. Estas dos medidas nos indican que durante el periodo de estudio existió una relación positiva débil entre los rendimientos de ambos indicadores.
En el cuadro 3 se presentan los resultados de la estimación de la cópula de Clayton, ecuación [4], y la cópula de Gumbel con los rendimientos de las marginales, suponiendo un modelo ar(1)-tgarch(1,1) como en la ecuación [8]. Aparece la estimación de los diferentes parámetros, así como su p-value para la muestra completa. También se presenta el estimador de los grados de libertad de la distribución t estandarizada.
Resultado de las estimaciones de las cópulas Clayton y Gumbel cuando las marginales siguen un modelo tgarch
| Clayton | Gumbel | |||||||
|---|---|---|---|---|---|---|---|---|
| ipc | igae | ipc | igae | |||||
| Coeficiente | Probabilidad | Coeficiente | Probabilidad | Coeficiente | Probabilidad | Coeficiente | Probabilidad | |
| ϕ0 | 0.01120 | 0.00180 | 0.00184 | 0.23774 | 0.01198 | 0.00000 | 0.00324 | 0.00000 |
| ϕ1 | 0.04709 | 0.046221 | –0.42623 | 0.00000 | 0.03859 | 0.00237 | –0.46147 | 0.00000 |
| α0 | 0.00011 | 0.24426 | 0.00039 | 0.00008 | 0.00016 | 0.00000 | 0.00043 | 0.00000 |
| α1 | 0.13547 | 0.12621 | 0.06263 | 0.53362 | 0.16064 | 0.00000 | 0.08242 | 0.00100 |
| γ | –0.01354 | 0.88479 | 0.83961 | 0.07335 | 0.03976 | 0.01173 | 0.69124 | 0.00000 |
| β | 0.84477 | 0.00000 | 0.09034 | 0.38524 | 0.82388 | 0.00000 | 0.14129 | 0.00000 |
| v | 15.31420 | 0.1323 | 37.6361 | 0.8448 | 11.1568 | 0.00000 | 20.0032 | 0.00000 |
| λ0S | –3.26794 | 0.00000 | ||||||
| λ1S | 5.32520 | 0.00000 | ||||||
| λ2S | 2.04940 | 0.00000 | ||||||
| λ0I | –5.72408 | 0.00568 | ||||||
| λ1I | 7.01034 | 0.00014 | ||||||
| λ2I | 5.98095 | 0.05170 | ||||||
| Log1 | 976.60 | 976.88 | ||||||
| Akaike | –7.18800 | –7.19012 | ||||||
Nota: se muestra el estimador y el p-value para los parámetros de la ecuación de la media (panel superior), ecuación de la volatilidad (segundo panel), grados de libertad (v) y parámetros de la dependencia condicional.
El ajuste del modelo se realiza al verificar que los correlogramas de los residuales y de los residuales al cuadrado se comportan como ruido blanco. Esta condición se cumple en todos los casos. El ajuste para el modelo de Clayton presenta problemas, en tanto que hay varios parámetros que no son significativos y llevan, incluso, a tener signo contrario al esperado, como es el caso del parámetro γ en el ipc, que mide el efecto apalancamiento. En el caso del modelo Gumbel, todos los parámetros son estadísticamente significativos. Se confirma el efecto apalancamiento medido por el parámetro γ para el caso de los rendimientos del ipc al ser estadísticamente positivo.
Resulta importante señalar que el criterio de información de Akaike y la medida de verosimilitud (Logl) son muy parecidos para las dos cópulas. No obstante, como puede verse en el cuadro 3, ambos sugieren que la cópula Gumbel tiene una mayor bondad de ajuste. Estadísticamente, este resultado implica que las relaciones de dependencia vinculadas a la cola superior son más relevantes para explicar la relación de estas variables, que aquellas vinculadas con la cola inferior. Es decir, cuando la probabilidad de que los rendimientos en el mercado accionario aumenta debido a un incremento en la tasa de crecimiento económico, y viceversa.
Los parámetros de las ecuaciones de las medidas de dependencia en colas inferior τI (Clayton) y superior τS (Gumbel) también están presentes en el cuadro 3 y son utilizados para obtener las series de dependencia que se presentan en la gráfica 1.
En la gráfica 1 se muestra que durante el periodo de estudio la probabilidad de que ocurra un incremento en los rendimientos del ipc —dado que hay un incremento en la tasa de crecimiento económico (dependencia condicional superior) — es muy volátil, pasando de 5% el 12 de diciembre de 1999 a 74% en febrero de 2007 y con una media de 24%. Los periodos en los que la probabilidad de que ambos rendimientos suban son justamente antes de las crisis de 1994 y 2008. Como se puede observar en la gráfica que describe la evolución de la dependencia condicional superior, se presenta una tendencia positiva a partir de la segunda mitad de 1993, que termina en 1995, para cambiar a una tendencia a la baja hasta 1996. A partir de esa etapa, se presenta un comportamiento promedio del 15%. De manera similar, se observa una tendencia a la alza a partir del 2005 que termina durante el 2008 para convertirse en una decreciente hasta el 2009, periodo a partir del cual muestra una probabilidad promedio de 18 y 10 por ciento para el 2010. Es decir, en momentos posteriores a las crisis, la tendencia de que exista la probabilidad de un aumento en crecimiento económico debido a que hubo un aumento en el ipc (o viceversa), va en decremento.
Por otro lado, la probabilidad de que se observe un decremento en los rendimientos del ipc, en tanto que hay un decremento en la tasa de crecimiento económico (dependencia condicional inferior), es aún más volátil, pasando de 0.3 a 88 por ciento y con una media de 10%. Es decir, los picos de probabilidad son más importantes en comparación con la dependencia condicional superior. En el cuadro inferior de la gráfica 1 se puede advertir que, durante los periodos previos a las crisis, existe una probabilidad alta de que un mercado baje cuando el otro baja, misma que, durante las crisis y en periodos posteriores, comienza a disminuir. El ejemplo más notorio de este efecto se da a partir de inicios de la crisis del 2008. Para el caso de la crisis de 1994, este comportamiento se presenta en menor proporción.
El hecho de que tanto para la dependencia condicional superior como para la inferior se muestre un resultado similar, nos lleva a inferir que existía una dependencia entre el mercado financiero y el mercado real mexicano. Más aún, esta dependencia se vuelve más fuerte en periodos previos a las crisis de 1994 y del 2008. En periodos posteriores a ambas crisis, la dependencia se debilitó.
CONCLUSIONESLas investigaciones realizadas sobre la relación entre el mercado financiero y el crecimiento económico se enfocan en dos aspectos: la dirección de causalidad y una relación de equilibrio o de largo plazo. Se puede observar que los estudios son abundantes pero no concluyentes para determinar si el sistema financiero es un factor que impulsa el crecimiento económico, o si, por el contrario, el crecimiento económico influye en el desarrollo del mercado financiero o, si bien, existe una determinación de manera simultánea. De igual forma, la existencia de una relación de largo plazo entre dichas variables no queda probada de manera consistente. Típicamente, las herramientas utilizadas para estos propósitos son la prueba de causalidad en sentido Granger y el análisis de cointegración a partir de la metodología propuesta por Johansen. Gran parte de la aplicación de estas herramientas, así como el cálculo de correlación invariante en el tiempo, asumen una distribución normal gaussiana bivariada por lo que están enfocadas en encontrar evidencias sobre la media o varianza de las variables. No obstante, al utilizar este supuesto, se impide que la herramienta capte características propias de las series de tiempo financieras, específicamente la dependencia asimétrica. El presente trabajo se planteó dos objetivos: determinar el grado de dependencia condicional en colas entre el sector financiero y real de la economía mexicana, así como observar los cambios que sufre dicha relación de dependencia durante el periodo de enero de 1993 a junio del 2015.
El análisis de las series de tiempo de rendimientos mensuales del ipc, como era de esperarse, no cumple el criterio de normalidad, pero se ajusta a los hechos estilizados de las series de tiempo financieras. Por su parte, el análisis realizado a la serie de tiempo mensual de las tasas de crecimiento del igae no rechaza normalidad. Aunado a ello, ambas series se ajustan adecuadamente a los modelos de volatilidad condicional, estimados conjuntamente, por medio de la herramienta de cópulas utilizando un modelo tgarch para el tratamiento de las marginales. Nuestros resultados sugieren que los rendimientos en el mercado accionario mexicano mantienen una relación de dependencia con la tasa de crecimiento económico, pero esa relación no es uniforme en el tiempo. Existen momentos en los que ésta se fortalece y momentos en los que es menos intensa. Se debe destacar que la relación entre ambas series es más fuerte cuando se presenta un incremento en las tasas de crecimiento, que cuando se presenta un decremento. Lo anterior se justifica con la obtención de un mejor ajuste en el modelo Gumbel (dependencia en colas superiores) en comparación con el modelo Clayton (dependencia en colas inferiores). Una posible interpretación de este resultado es que durante periodos de expansión económica el sector financiero tiende a incorporar dicha dinámica para ampliar sus ganancias a través del flujo de capital excedente que pudiera generarse como resultado del crecimiento del sector real de la economía. En sentido contrario, en presencia de periodos de expansión del sector financiero, la economía real tiende a apoyarse en él para aumentar elementos como el consumo y la inversión en capital productivo.
Por último, se estimaron parámetros para observar el comportamiento de dependencia condicional en colas (inferior y superior). La evidencia encontrada en nuestro estudio sugiere que el comportamiento del mercado accionario está relacionado con el crecimiento económico y que existe una dependencia entre ellos que es más fuerte en momentos cercanos a crisis, cuando la probabilidad de que los rendimientos en el mercado accionario aumenten (disminuyan) debido a un incremento (decremento) en la tasa de crecimiento económico, y viceversa. Posterior a las etapas de crisis, esta relación se debilita, lo que nos permite inferir que los mercados realizan ajustes sin considerar, en la misma medida que antes, el desempeño del otro. Sugerimos —sin comprobar por el momento— que una posible explicación a este resultado puede darse por la presencia de un efecto de “aislamiento” entre los agentes de ambos sectores en periodos posteriores a las crisis. Ante la incertidumbre generada por estas, cada sector tratará de disminuir la dependencia con factores exógenos a ellos, por lo que se buscará una recuperación desde el interior del mismo, tratando de alejarse de las decisiones, planteamientos o políticas adoptadas por el otro. Con base en nuestros resultados, consideramos que un elemento fundamental para ampliar este estudio y ayudar tanto al diseño y ejecución de la política económica del país como al desarrollo de los mercados financieros es definir los factores endógenos que determinan en qué momento es más fuerte la relación entre ambos mercados, así como buscar en qué dirección se encuentra la relación; es decir, si el crecimiento económico afecta el mercado financiero o el mercado financiero determina el crecimiento económico, o ambas.