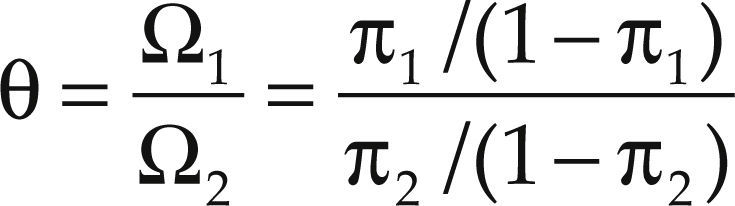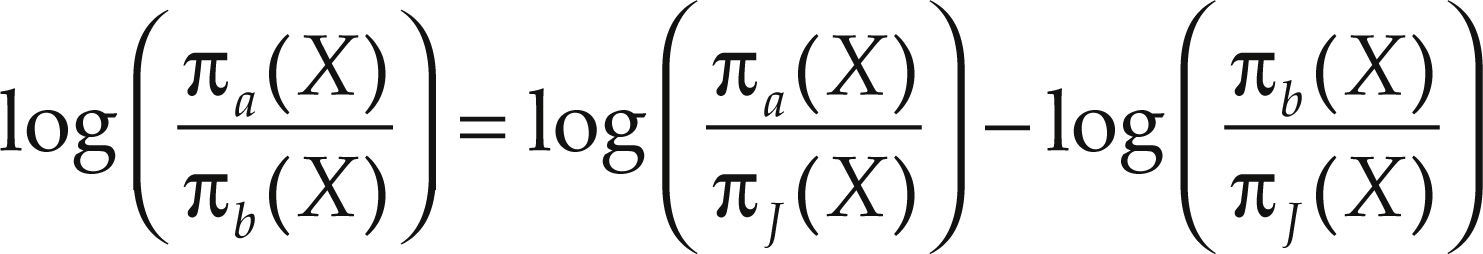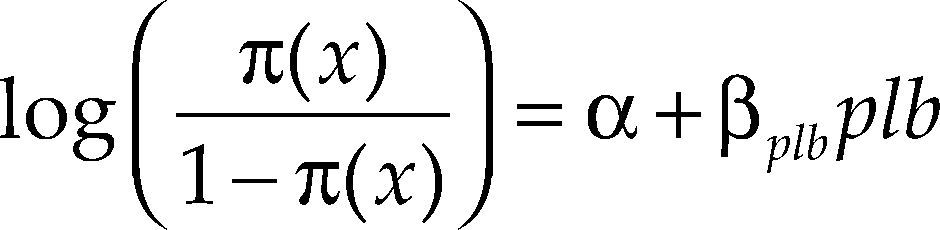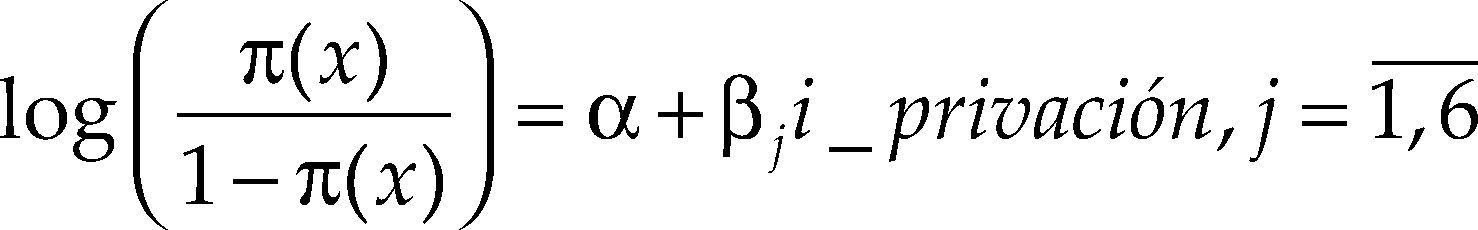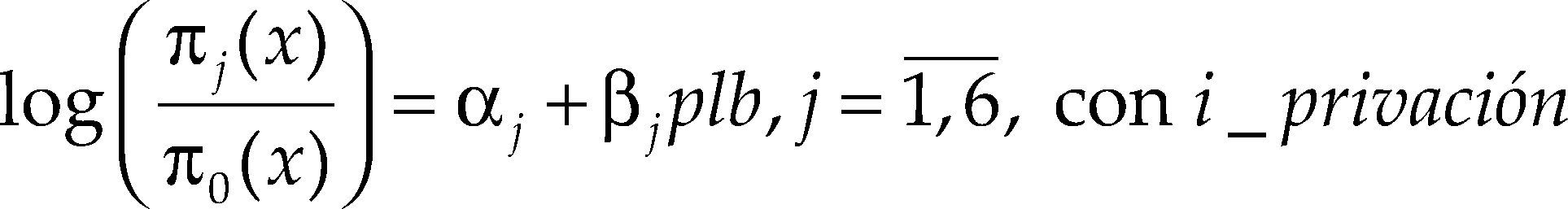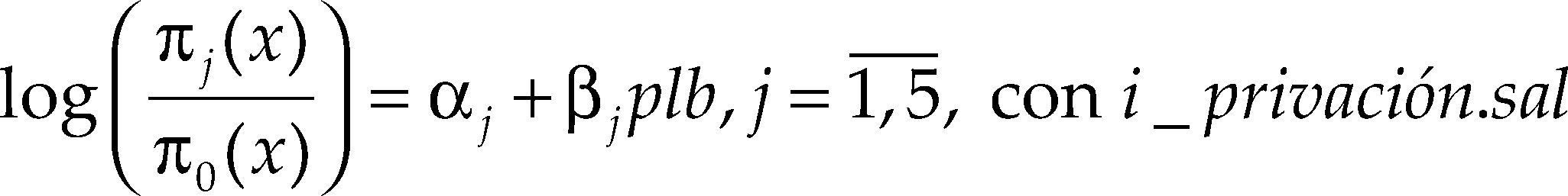La pobreza multidimensional en México requiere la ocurrencia simultánea de dos eventos: contar con un ingreso menor a un mínimo establecido en el espacio del bienestar y padecer al menos una carencia en el espacio de los derechos sociales. El Consejo Nacional de Evaluación de la Política de Desarrollo Social (Coneval) establece, bajo su postura teórica, que no es pertinente incluir al ingreso y las carencias en el cálculo de las medidas de profundidad; como si se tratase de espacios que funcionan de manera independiente. Se utilizan micro-regresiones con el fin de verificar la existencia empírica de asociación significativa entre ambos espacios, aunque ésta se presente en niveles diferenciados. Se sugiere, además, omitir la variable asociada a los servicios de salud para lograr una mejor visión de la relación entre las carencias de derechos sociales y el ingreso.
Multidimensional poverty measurement in Mexico require the simultaneous occurrence of two events: firstly, to have less income than an established minimum in the space of welfare, and secondly, to have at least one gap in the space of social entitlements. The Consejo Nacional de Evaluación de la Política de Desarrollo Social (Coneval) [National Council for the Evaluation of Social Development Policy] has established, under its own theoretical position, that is not appropriate to include income and gaps in the calculation of depth measurements; as if it were spaces that operate independently. In this paper, micro-regressions are used to verify the empirical existence of significant association between both spaces, although this is presented at different levels. The results suggest, also, to omit the variable associated with health services in order to achieve a better vision of the relationship between the gaps in social entitlements and income.
La conceptualización y la medición de la pobreza multidimensional en México han estado a cargo del Consejo Nacional de Evaluación de la Política de Desarrollo Social (Coneval) siguiendo los lineamientos establecidos en la Ley General de Desarrollo Social (lgds) del 2004. Se determinó que la perspectiva multidimensional de la pobreza en el país fuera realizada con base en dos enfoques: el espacio del bienestar y el espacio de los derechos sociales. El primero concierne al nivel de ingresos; el segundo, al acceso a un conjunto de derechos sociales básicos que es medido como un nivel de carencias.
Para el caso mexicano, en términos metodológicos la pobreza multidimensional requiere de la ocurrencia simultánea de dos eventos. Un individuo se clasifica como pobre multidimensional si su ingreso es menor a un mínimo establecido a través de la línea de bienestar, y padece al menos una de seis carencias (rezago educativo, acceso a servicios de salud, acceso a seguridad social, calidad y espacios de la vivienda, acceso a los servicios básicos de la vivienda y acceso a la alimentación).1 Sin embargo, la concepción teórica del Coneval (2009, p. 46) es que el ingreso no debe ser incluido en la medida de intensidad de la pobreza multidimensional.
La medida ofrecida por el Coneval sigue a la propuesta identificada como M0 en Alkire y Foster (2011a). En Alkire y Foster (2011b) pueden encontrarse detalles técnicos sobre la manera en que funciona la medida M0, tales como la elección del corte para definir a un pobre multidimensional o las posibles descomposiciones que pueden realizarse. El enfoque de necesidades básicas insatisfechas como un antecedente a la conceptualización multidimensional, y la familia de medidas multidimensionales de Bourguignon y Chakravarty son mostrados como elementos en la fundamentación de la medida M0 en Alkire y Santos (2013). Mientras que la robustez en los ordenamientos de los países tras calcular su M0 ante la elección de diferentes dimensiones y umbrales, así como distintas ponderaciones y cortes para ser definido como pobre multidimensional, pueden verificarse en Alkire y Santos (2014).
La principal motivación de este documento es que la medición mexicana de la pobreza multidimensional requiere de estudios más profundos que permitan conocer sus particularidades y las implicaciones de medir la pobreza de esta forma. Por ejemplo, Cohen y Saisana (2014) proponen un análisis a los diferentes componentes de su medida multidimensional, partiendo de la opinión de expertos en el tema, con el fin de obtener una medida que pueda representar mejor el fenómeno de la pobreza. Esto es importante debido a que la medición mexicana de la pobreza multidimensional se ha convertido en la base para la evaluación de programas, así como la identificación y focalización de áreas de atención prioritaria en el país. De esta forma, el interés radica en verificar la medición mexicana desde la perspectiva empírica, esto porque no se encontraron trabajos previos que planteen un análisis del alcance y limitaciones de la medida. En particular, aquí se aborda el supuesto de independencia entre los espacios de bienestar y de derechos sociales.
El Coneval parte de un trasfondo teórico que le conduce a establecer una postura de independencia entre el espacio de los derechos sociales y el del bienestar. Es válido suponer que el ingreso no debe afectar el acceso a ciertos derechos sociales que se consideran indispensables para garantizar una vida digna. De esta manera, el ingreso no debiera influir en el número de carencias que presente un individuo en el espacio de los derechos sociales ni viceversa. Además, se puede considerar que el alcance de las políticas públicas podría empezar a generar independencia de las carencias respecto del ingreso. Por ejemplo, la carencia en el acceso a los servicios de salud es una variable que considera el acceso al Seguro Popular, programa que ha contribuido a ampliar la cobertura sin necesidad de establecer un vínculo más sólido con el nivel de ingresos del individuo.
Este trabajo utiliza una técnica que permite examinar la asociación entre ambos espacios, así como la posibilidad de efectos diferenciados de acuerdo al conjunto de carencias que sean consideradas. Se eligió una metodología que permitiera brindar robustez al análisis estadístico; por ello, se propone el uso de modelos lineales generalizados (mlg), dado el carácter categórico de las variables involucradas en la definición de pobreza multidimensional, la cual es una aproximación también sugerida en Alkire et al. (2015, pp. 295-308). Los datos pueden ser obtenidos del Módulo de Condiciones Socioeconómicas (mcs) desarrollado por la Encuesta Nacional de Ingreso y Gasto de los Hogares (enigh).
El documento consta de tres secciones principales. La primera sección aborda la revisión de literatura que refiere a la correlación entre la pobreza de ingresos y las carencias de bienes y acceso a servicios básicos, así como a la posibilidad de describir al ingreso en función de un conjunto de características del hogar (o individuo), que usualmente reflejan el acceso a ciertos bienes y servicios básicos. Los detalles respecto a los mlg son presentados en la segunda sección. En la tercera sección se muestran los resultados obtenidos de aplicar mlg a los datos de pobreza multidimensional en México para 2012. Se cierra con unas breves reflexiones finales del ejercicio.
LA RELACIÓN ENTRE EL NIVEL DE PRIVACIÓN EN FUNCIÓN DEL INGRESOComo se explicó anteriormente, la definición mexicana de pobreza multidimensional requiere que el individuo sea pobre de ingresos y padezca al menos una carencia de seis en cuanto al espacio de los derechos sociales. El Coneval indica que, bajo su postura téorica conceptual, ambos espacios son independientes, esto se cumple al suponer que el ingreso y las carencias no se influyen mutuamente. Sin embargo, sería viable pensar en la asociación entre los espacios y en la posibilidad de que se afecten de manera diferenciada entre sí. Esto último sí es considerado por el Coneval cuando realiza ejercicios de estimación de áreas pequeñas, como los mapas de pobreza por ingresos de 2000 y 2005 a nivel municipal (Coneval, 2007) y las estimaciones de pobreza multidimensional a nivel municipal de 2010 (Coneval, 2011). Basta recordar que la técnica utilizada se basa en el método de Elbers, Lanjouw y Lanjouw (2003), en el cual, a partir de características sociodemográficas y económicas, es posible aproximar el nivel de ingresos del hogar.
La literatura ha encontrado que existen de medios a altos niveles de asociación entre la condición de pobreza de ingresos y la pobreza de bienes y servicios. Los documentos presentados a continuación tienen como fin mostrar que un índice formulado a través del acceso a ciertos bienes y servicios puede servir como una variable alternativa cuando no se cuenta con datos sobre ingreso. En ellos se plantea, desde diversas metodologías, abordar la relación entre el ingreso y el acceso a bienes, esto último usualmente representado como un índice de privación.
Una propuesta de elaboración de índices de privación es la de Nolan y Whelan (1996). Con datos de 1987 para Irlanda, eligieron 24 preguntas que contienen información sobre bienes y servicios que consideran indispensables. Haciendo uso de la técnica de análisis factorial (af) conforman cuatro índices: privación básica, privación secundaria (ocio), privación en el hogar y uno más a partir de todos los indicadores. Se analiza la relación entre el ingreso y este conjunto de índices a través de regresiones ordinarias, las cuales incorporan 15 variables explicativas, comprendiendo al ingreso y a características económicas, sociales y demográficas. Los cuatro índices reportan altos niveles de correlación con el ingreso; mientras que las cuatro regresiones (una para cada índice) sugieren que el ingreso es significativo, sobre todo respecto al índice agregado.
Klasen (2000) utiliza datos de 1993 para Sudáfrica con el fin de desarrollar, a partir de 14 variables, un índice de privación bajo el enfoque de capacidades de Sen. Su crítica se basa en la necesidad de ampliar la conceptualización de la pobreza más allá de los niveles limitados del gasto disponible de los hogares. El autor analiza la correlación entre los componentes del índice, el índice y el gasto; en todos los casos encuentra correlaciones positivas, lo cual no interpreta como una posibilidad de doble conteo, sino como una tendencia hacia la agrupación de ciertas características.2 Señala que la correlación entre el gasto y el índice es de 0.847, la cual se reduce a 0.503 cuando considera a los grupos más vulnerables de acuerdo al índice. También encuentra diferencias al momento de identificar a los más pobres usando las dos medidas, tanto en la focalización geográfica como de individuos beneficiarios; su sugerencia ante esto último es la de profundizar en este tipo de análisis.
El objetivo de Sahn y Stifel (2003) es verificar si un índice de privación funciona mejor que otros indicadores monetarios en las mediciones de bienestar. Con información referente a 11 países distintos, los autores se enfocan en salud y nutrición infantil como los principales funcionamientos (en la tipología de Sen). Cuentan con tres indicadores: un índice de privación formado mediante af, el gasto como un indicador monetario y, además, el gasto esperado a partir de características sociodemográficas del hogar. Los resultados señalan que países con alta correlación entre el gasto esperado y el reportado también presentan alta correlación entre el gasto y el índice. En otra etapa se explican los niveles de peso por edad en función del índice o del gasto esperado, además de varios controles (esto para cada país), encontrando que en zonas urbanas el índice tiene mayor capacidad explicativa que el gasto. Finalmente, se examina por quintiles el nivel nutricional estimado por el gasto y por el índice, resultando en mejores predicciones de la medida de bienestar cuando se usa el índice de privación. Aclaran que a pesar de la insuficiencia de la evidencia para decidir cuál es mejor, es posible decir que el índice está menos sujeto a errores que el gasto.
La propuesta de Stifel y Christiaensen (2007) es ligeramente distinta a las anteriores, ya que ofrece explicar el nivel de consumo en función de un conjunto de bienes, servicios y características de los individuos. A partir de una modificación de la técnica de Elbers, Lanjouw y Lanjouw (2003) usan datos de diversas fuentes para el periodo 1997-2003.3 Se pretende aproximar el consumo actual como función de un conjunto de características sociodemográficas y estimar niveles de bienestar futuros con la versión esperada de ese consumo.4 Las medidas de bienestar obtenidas por el consumo esperado se comparan contra las resultantes de usar otros indicadores, en particular, usan el índice ofrecido por Sahn y Stifel (2000), el consumo observado por las cuentas nacionales e índices basados en medidas no monetarias.5 La idea de estos autores es aproximar los niveles de bienestar cuando es difícil tener un conjunto grande de información recabada sobre ingreso o gasto, resaltando que el consumo puede ser descrito por un conjunto de características de los individuos.
Para Liverpool-Tasie y Winter-Nelson (2011) el acceso a ciertos bienes y servicios conduce a mejores mediciones de la pobreza, aunque la mayor dificultad recae en agrupar lo anterior en un solo índice. Los datos corresponden a 15 villas de Etiopía para el periodo 1994-2004. Se busca la relación entre un conjunto de bienes y el gasto a través del análisis econométrico; es decir, se calcula el ingreso a través de un índice de privación y otros controles sobre factores demográficos, temporales y geográficos. El siguiente paso es verificar la capacidad predictiva del modelo usando matrices de transición, dada la información tipo panel. Los autores encontraron mayor inestabilidad en la matriz de gasto, mientras que hogares con menores niveles de gasto tienden a presentar altos niveles en el índice de privación. Finalmente, resaltan que el índice captura mejor que el gasto la verdadera situación de pobreza de los hogares que son estructuralmente pobres.
Michelson, Muñiz y Derosa (2013) tienen un panel de datos para Malawi, Tanzania, Mali y Ghana, con el cual verifican la robustez de los resultados al usar diferentes metodologías para medir la pobreza. Calculan cuatro índices: el primero es el ingreso estructural obtenido por una regresión que incluye un conjunto de bienes y servicios y ciertas características demográficas; el segundo se obtiene por af; el tercero, por componentes principales (cp), y el cuarto resulta de aplicar af a una Encuesta Demográfica de Salud (dhs, Demographic Health Survey) que contiene menos información. La correlación de los índices con el nivel de ingreso original varía considerablemente entre países y en el tiempo. En cuanto a la capacidad predictiva usando matrices de transición, en los cuatro casos se obtienen resultados similares. Las diferencias más notorias se dan en las ordenaciones de la distribución de acuerdo a cada índice. Finalmente, muestran cinco correlaciones simples (una para cada índice y una para el ingreso), donde las variables explicativas fueron el género del jefe de hogar, la razón de dependencia y los meses de inseguridad alimentaria; las mayores correlaciones fueron encontradas al usar af, cp y el índice con la dhs.
En Alkire et al. (2015, pp. 295-310) se puede encontrar una interesante exposición sobre algunas aproximaciones econométricas que se han hecho respecto a las medidas de pobreza. Señalan que, en ocasiones, es de interés verificar mediante modelos econométricos los determinantes de la pobreza y el alcance de su efecto, particularmente se refieren a “micro” y “macro” regresiones. Las últimas se refieren a casos donde se plantea analizar a grupos, como estados, municipios, regiones; en este caso, la variable dependiente es alguna medida de pobreza (como las Foster-Greer-Thorbecke, fgt). Las micro-regresiones tienen como objetivo analizar las condiciones individuales, por lo que la variable dependiente es dicotómica, denotando si la persona cumple, o no, con la definición de pobreza. Estas últimas son precisamente el objetivo de este documento, y la metodología a emplear se describirá en la siguiente sección.
LOS MODELOS LINEALES GENERALIZADOSLos mlg extienden los modelos de regresión a modelos donde la respuesta es de tipo categórico.6 En el presente trabajo se hará énfasis en los modelos de respuesta binomial, dado el carácter categórico de las variables involucradas en el proceso de medición de la pobreza.
mlg para datos binariosSi la variable γ es de tipo binario, se tiene que E(γ) = P(γ = 1). Se denotará P(γ = 1) = π(X), donde X = (x1,…,xp), reflejando la dependencia de γ de los valores de los predictores. En adelante se considerará sólo una variable explicativa X. Usualmente, los datos binarios provienen de relaciones no lineales entre π(X) y X. En la práctica, las relaciones no lineales entre X y π(X) son generalmente monótonas, la curva más importante de este tipo corresponde a la formulación:
el cual es el definido como modelo de regresión logística.
Una posibilidad (odds) se define a partir de la probabilidad de éxito en una categoría de la variable X. Sea πi la probabilidad de éxito, entonces la posibilidad se escribe como:
Si Ωi> 1, la posibilidad de éxito es mayor que la de fracaso. Por ejemplo, si πi = 0.75, entonces Ωi = 3; de manera que la posibilidad de éxito es tres veces mayor la de fracaso. Así, el odds ratio o razón de posibilidades es:
Particularmente, cuando θ = 1 significa que las variables X y γ son independientes; por otro lado, θ > 1 indica que es más probable que los sujetos de la fila 1 tengan un éxito que los sujetos de la fila 2.
La posibilidad (odds, Ω) para la función logística es:
mientras que el logaritmo de la posibilidad tiene una relación lineal:
La regresión logística donde el componente aleatorio es de tipo binomial y la función enlace es la logit se conoce como modelos logit. El valor de π(X) deberá caer entre 0 y 1, mientras el logit puede ser cualquier número real. Para calcular los parámetros de este modelo, los programas computacionales utilizan máxima verosimilitud.7
Una forma de interpretar los parámetros de esta regresión es a través de las posibilidades. Considere lo siguiente:
en la que el lado derecho de la ecuación implica que cada unidad en que incremente X tendrá un efecto multiplicativo de exp(β) sobre Ω. Estas posibilidades también pueden obtenerse para incrementos en X mayores a la unidad. Particularmente, β puede interpretarse como log(θ) para las tablas de contingencia 2×2. Es posible extender el modelo logístico a múltiples variables explicativas:
donde la interpretación de los parámetros es análoga. Cuanto más se aleje βi de cero, mayor el efecto de xi, ya que las razones de posibilidades se encontrarán más lejos de uno. La significación de estos log θ se puede obtener con la prueba z. Una vez que se ha elegido el modelo es posible realizar algunas inferencias. La hipótesis de independencia es reflejada a través de la H0: β = 0 estableciendo que la X no tiene efecto sobre P(γ = 1).
Obtenidos los parámetros, es necesario verificar la calidad de ajuste, para ello se compara la verosimilitud del modelo particular contra la verosimilitud del modelo saturado. Las funciones de probabilidad para ambos modelos deben ser evaluadas en sus respectivos máximos estimados para obtener los valores de las verosimilitudes Lθ˜max;γ y Lθˆ;γ respectivas. Un estadístico que puede utilizarse es:
al cual se le puede aplicar el logaritmo, obteniendo:
cuanto mayor la diferencia, menos robusto es el ajuste del modelo particular. El estadístico más usual para medir la bondad de ajuste es la denominada devianza, siendo D = 2log(λ). La devianza también permite distinguir entre la bondad de ajuste de dos diferentes modelos particulares; se asociará la menor D al mejor modelo.
Los modelos logit son generalizables a modelos donde la variable respuesta cuente con más de dos opciones. Sea πj(X) = P(γ = j|X) para un conjunto de variables explicativas X, donde ∑jπjX=1 y se trata a los conteos de las J categorías de γ como una multinomial con probabilidades {π1(X),…, πJ(X)}. Los modelos logit emparejan, entonces, cada categoría respuesta a una categoría base, usualmente la primera o la última. El modelo:
describe simultáneamente los efectos de X sobre los J–1 logits. Estas J–1 ecuaciones determinan los parámetros para los logits con las otras categorías, dado que:
La ecuación que expresa los logit multinomiales directamente en términos de las probabilidades de respuesta es:
con αJ = 0 y βJ = 0. El denominador de la ecuación es el mismo para cada j, de manera que al final debe obtenerse ∑jπjX=1.
Análisis de varianza y covarianzaLa idea del análisis de varianza (Anova) es la de verificar si hay diferencia entre las medias poblacionales de distintos grupos. Siendo g el número de grupos a comparar y μ1,…, μg las medias de la variable respuesta de los respectivos grupos, la hipótesis nula del Anova es:
Así, el Anova puede considerarse como una prueba de independencia entre las variables respuesta y explicativa. Si se utilizan variables dicotómicas para representar a los diferentes grupos, el Anova es un caso particular de regresión. Las medias reportadas por los diferentes grupos pueden ser interpretadas como las probabilidades de presentar una determinada condición.
Para probar la hipótesis nula en el Anova se obtiene el estadístico F, el cual refleja la similitud entre las medias que se están comparando. El numerador de F es una estimación de la varianza poblacional basada en la variabilidad entre las medias de cada grupo. El denominador es la estimación de la varianza poblacional basada en la variabilidad existente al interior de cada grupo. Si las medias poblacionales son iguales, las medias muestrales también lo serán, y la diferencia puede atribuirse al azar. En el caso donde las medias son diferentes, el numerador será mayor que el denominador, por lo tanto F > 1. Cuanto mayor la diferencia entre medias, mayor el valor de F. De obtener en las pruebas un p-valor usualmente menor a 0.05, se rechaza la hipótesis de igualdad de medias.
En numerosas aplicaciones es útil comparar medias mientras se controla con una variable cuantitativa, dicha variable se denomina covariante, y a esta técnica se le conoce como análisis de covarianza (Ancova). Las covariables representan variables que ejercen un efecto sobre la dependiente al variar conjuntamente con las independientes. El Ancova puede considerarse también un caso particular de la regresión; de manera que si el término de interacción entre la explicativa y la covariante es significativo, entonces dicha covariante tiene un efecto sobre la variable respuesta.
RESULTADOS PARA LA POBREZA MULTIDIMENSIONAL DE MÉXICOUn individuo es pobre multidimensional en México si es carente en el espacio del bienestar y padece al menos una carencia en el espacio de los derechos sociales. El ingreso corriente total per cápita es el indicador asociado al primer espacio. Seis indicadores de carencias conforman el segundo espacio: rezago educativo, acceso a los servicios de salud, acceso a la seguridad social, calidad y espacios de la vivienda, servicios básicos de la vivienda y acceso a la alimentación.
En cuanto a ingresos, se presenta carencia si una persona cuenta con un nivel de ingreso que no es suficiente para adquirir los bienes y servicios básicos requeridos. Tales bienes y servicios se establecen en la denominada línea de bienestar (lb) definida por el Coneval; de manera que el individuo es carente en el espacio del bienestar cuando su ingreso es menor a la lb. Alguien es carente en el espacio de los derechos si al menos uno de ellos se ve limitado. Así, se construye el Índice de Privación Social (ips) como una combinación lineal unitaria de los seis indicadores asociados, por lo que un individuo es carente cuando su ips es mayor o igual a uno.
En el cuadro 1 se presentan los nombres de las variables a emplear a lo largo del documento, además de especificar su tipología. Los datos pueden ser obtenidos de los códigos ofrecidos en la página oficial del Coneval (excepto la variable ing.bc). En la muestra se indica para cada individuo si es pobre de ingresos y su ips. El análisis de la pobreza multidimensional en México es a nivel individual, ya que a pesar de que todos los miembros del hogar cuentan con el mismo ingreso, pueden presentar diferentes niveles de carencias.
Variables consideradas en la medición de la pobreza multidimensional
| Variable | Tipología |
|---|---|
| ic_rezedu | Dicotómica. Presenta la carencia de rezago educativo. |
| ic_asalud | Dicotómica. Presenta la carencia de acceso a servicios de salud. |
| ic_segsoc | Dicotómica. Presenta la carencia de acceso a seguridad social. |
| ic_cv | Dicotómica. Presenta la carencia en la calidad y espacios de la vivienda. |
| ic_sbv | Dicotómica. Presenta la carencia en los servicios básicos de la vivienda. |
| ic_ali | Dicotómica. Presenta la carencia en el acceso a la alimentación. |
| i_privación | Ordinal, de 0 a 6. ips. |
| i_privación.sal | Ordinal, de 0 a 5, se elimina la carencia ic_asalud del ips. |
| ictpc | Continua. Ingreso corriente total per cápita. |
| ing.bc | Continua. Transformación Box-Cox de ictpc. |
| plb | Dicotómica. Pobre de ingresos. |
Fuente: elaboración propia con base en información de Coneval.
En adelante, se hablará de carencias para referirse solamente a la condición de carencias en el espacio de los derechos sociales. El análisis aquí presentado parte de la definición de pobre multidimensional, es decir de los datos agregados, y no se busca ser exhaustivo, por lo cual no se desagreguen a menores niveles las definiciones de las carencias. En cuanto al espacio de bienestar, únicamente se usará la condición de pobreza de ingresos, esto porque es la variable con la cual se identifica a un potencial pobre multidimensional.
Si bien el ingreso no figura directamente en la definición de pobreza multidimensional es de interés incluirla en el presente documento. El ingreso corriente total se define como la suma del ingreso corriente monetario y no monetario.8 Posteriormente, el ingreso corriente total per cápita de cada hogar se ajusta por economías de escala y escalas de adulto equivalente cuando el tamaño del hogar es mayor a uno. Los datos del ingreso, variable ictpc, exhiben dos problemas de importancia considerable: reportes de cero ingreso y reportes de ingresos muy altos, de ahí que se haya añadió una transformación Box-Cox de esta variable.9
A continuación se plantearán modelos logit y logit multinomial, y posteriormente se realizarán los análisis de varianza y covarianza. Estos modelos de micro-regresiones aportarán información acerca de la asociación de las carencias y la condición de pobreza de ingresos de los individuos. Al utilizar esta técnica no se pretende establecer causalidad, más bien interesa verificar la existencia de correlación entre las variables y sus niveles diferenciados. Como sugieren Alkire et al. (2015, pp. 228-229), es importante verificar la asociación y eventual redundancia de las dimensiones elegidas en la conceptualización multidimensional.
Un primer paso podría ser establecer modelos logit donde la carencia se describa en función de la condición de pobreza de ingresos. Esto bajo el razonamiento de que son los bajos niveles de ingresos los que conducen a la manifestación de alguna carencia, por ejemplo, evitando la mejora de las condiciones de la vivienda. Por ello, se muestran los resultados de los seis modelos que siguen la siguiente ecuación:
Los parámetros que se obtienen son precisamente el logaritmo de las razones de posibilidades, log θ. Sin embargo, la interpretación más usual es a través de exp(βj) = θ, valores mostrados en el cuadro 2, siendo todos significativos con p-valor igual a cero en las pruebas z. Es posible ver que el menor valor se da en ic_asalud, lo que significa un menor nivel de asociación entre esa carencia y la pobreza de ingreso. La mayor asociación es encontrada en las variables que refieren a la vivienda y a la seguridad social.
Resultados de las regresiones logit con plb independiente
| Variable dependiente | exp(βplb) | Sig. | Variable dependiente | exp(βplb) | Sig. |
|---|---|---|---|---|---|
| ic_rezedu | 2.13 | *** | ic_cv | 3.83 | *** |
| ic_asalud | 1.33 | *** | ic_sbv | 3.63 | *** |
| ic_segsoc | 3.69 | *** | ic_ali | 3.19 | *** |
Nota: código para la significación (Sig.): ***: 0.001, **: 0.01, *: 0.05, -: 0.1.
Fuente: elaboración propia en R con base en información del mcs de la enigh 2012.
Posteriormente se realiza el análisis de varianza, donde la hipótesis nula sería que la probabilidad de presentar la carencia es la misma entre los grupos pobre y no pobre de ingresos. Es decir, H0: μcarencia(no pobre de ingresos) = μcarencia(pobre de ingresos). Dichas probabilidades se muestran en el cuadro 3; en todos los casos la prueba F resulta en el rechazo de H0, con p-valores iguales a 0.
Probabilidad de padecer las carencias entre grupos pobre y no pobre de ingresos
| Carencia | Categoría | Media: carencia | Carencia | Categoría | Media: carencia |
|---|---|---|---|---|---|
| ic_rezedu | plb = 0 | 0.139 | ic_cv | plb = 0 | 0.064 |
| plb = 1 | 0.256 | plb = 1 | 0.208 | ||
| ic_asalud | plb = 0 | 0.170 | ic_sbv | plb = 0 | 0.121 |
| plb = 1 | 0.214 | plb = 1 | 0.333 | ||
| ic_segsoc | plb = 0 | 0.454 | ic_ali | plb = 0 | 0.140 |
| plb = 1 | 0.754 | plb = 1 | 0.342 |
Fuente: elaboración propia en R con base en información del mcs de la enigh 2012.
El valor más alto se presenta en el caso de la carencia de acceso a la seguridad social. Ésta reporta una probabilidad del 75% de ser padecida cuando el individuo es pobre de ingresos, seguida de la carencia en la alimentación y los servicios básicos de la vivienda. Es interesante que la condición de no pobreza de ingresos reduce considerablemente la probabilidad de padecer la carencia de condiciones de la vivienda. Y, además, dada la alta proporción de individuos carentes de seguridad social, se tiene que aun cuando no se es pobre de ingresos hay una alta probabilidad de padecer dicha carencia.10
También es válido proponer que el ingreso estuviera actuando como una covariante y verificar si la probabilidad de la carencia varía con el nivel de ingreso del individuo pobre. Se agregan las variables ing.bc e interacción, esta última como plb*ing.bc. Los modelos logit pueden ahora escribirse como:
donde los parámetros βint representan el efecto de la covariante. En el cuadro 4 se reportan los p-valores asociados a las pruebas F de los términos de interacción de cada una de estas regresiones, para probar H0: βint = 0. Esto con el fin de identificar los casos en los que el nivel de ingresos de los pobres de ingresos sí tiene un efecto sobre la probabilidad de padecer cada carencia.
Significancia del término de interacción, Ancova
| Carencia | Sig. | Carencia | Sig. |
|---|---|---|---|
| ic_rezedu | *** | ic_cv | *** |
| ic_asalud | 0.52 | ic_sbv | *** |
| ic_segsoc | ** | ic_ali | *** |
Nota: código para la significación (Sig.): ***: 0.001, **: 0.01, *: 0.05, -: 0.1.
Fuente: elaboración propia en R con base en información del mcs de la enigh 2012.
De estos seis análisis de covarianza resaltan dos aspectos. Los resultados indican que el nivel de ingresos de aquellos que son pobres de ingresos sí afecta sobre la probabilidad de padecer las carencias, excepto para el acceso a los servicios de salud. En este caso, el nivel de ingresos de un individuo pobre de ingresos no tiene efecto sobre la probabilidad de padecer la carencia, potencialmente podría deberse a que el programa Seguro Popular ayuda a que una gran proporción de ellos cuente con el acceso a salud.11 Esto último implica que los servicios de salud, en años recientes, se otorgan sin importar la condición individual de trabajo o ingreso; lo cual provoca cierta independencia de este derecho respecto del ingreso, tal como lo supone Coneval. No obstante, esta observación debe tomarse con precaución, puesto que la carencia en el acceso a la seguridad social y el acceso a servicios de salud están altamente asociadas (como puede observarse en las definiciones del Anexo), y en la primera de ellas el ingreso sí ejerce un efecto sobre la probabilidad de padecer la carencia; esto por la alta incidencia de individuos pobres por ingresos que simultáneamente no cuentan con seguridad social.12
Como se mencionó previamente, en este documento no se pretende establecer el orden de la causalidad entre el ingreso y las carencias. Por ello, también se describirán seis modelos logit donde la pobreza de ingresos se describe ahora en función de cada carencia, de acuerdo con la ecuación:
Ya que la interpretación de los parámetros de estos modelos se realiza en términos de las razones de posibilidades, y éstas son independientes de cuál variable se use como respuesta, los parámetros son los mismos que se reportaron en el cuadro 2.13
A continuación se realiza el análisis de varianza, donde la hipótesis nula sería que la probabilidad de ser pobre de ingresos es la misma entre carente y no carente. Es decir, H0: μplb(no carencia) = μplb(carencia). Dichas probabilidades se muestran en el cuadro 5; en todos los casos la prueba F resulta en el rechazo de H0, incluso para ic_salud, con p-valores iguales a 0.
Probabilidad de pobreza de ingresos entre grupos carentes y no carentes
| Categoría | Media: plb | Categoría | Media: plb |
|---|---|---|---|
| ic_rezedu = 0 | 0.491 | ic_cv = 0 | 0.486 |
| ic_rezedu = 1 | 0.673 | ic_cv = 1 | 0.783 |
| ic_asalud = 0 | 0.514 | ic_sbv = 0 | 0.459 |
| ic_asalud = 1 | 0.585 | ic_sbv = 1 | 0.755 |
| ic_segsoc = 0 | 0.334 | ic_ali = 0 | 0.461 |
| ic_segsoc = 1 | 0.650 | ic_ali = 1 | 0.732 |
Fuente: elaboración propia en R con base en información del mcs de la enigh 2012.
El valor más alto se reporta para ic_cv, seguido de los servicios básicos de la vivienda y la alimentación, lo cual se interpreta como una fuerte asociación con la pobreza de ingresos. Puede deberse a que son dimensiones de los derechos sociales, en donde el ingreso tiene una fuerte relación con la condición de carencia, ya que la ayuda en las mejoras de la vivienda usualmente queda en manos de la familia, a diferencia del acceso a la educación, donde se promueve la asistencia a las escuelas públicas. Es importante notar que en todos los casos la presencia de carencias aumenta la probabilidad de ser pobre de ingresos, y sólo es ligeramente menor para el acceso a los servicios de salud.
Al igual que el ejercicio anterior, proponer que el ingreso actúa como una covariante es una opción a considerar en el estudio. Se agregan las variables ing.bc y de interacción, esta última como carencia*ing.bc. Los p-valores de las pruebas F del Ancova para los términos de interacción son todos iguales a cero. Anteriormente se dijo que el nivel de ingresos del pobre afectaba sobre la presencia de la carencia, con estos Ancova se muestra que también hay un efecto del nivel de ingresos sobre la carencia que refuerza la condición de pobreza de ingresos. Es decir, el nivel de ingresos de los individuos es un factor de suma importancia, a pesar de que éste no figura directamente en la medición de la pobreza multidimensional. Los resultados invitan a considerar al nivel de ingresos, y no solamente la condición de pobreza de ingresos, en las medidas a fin de poder establecer con mayor precisión la profundidad y severidad de la pobreza multidimensional en el país.
Para verificar la sensibilidad ante diferentes combinaciones de las carencias padecidas se propone utilizar diferentes carencias en las regresiones. Se inicia con un modelo como el siguiente:
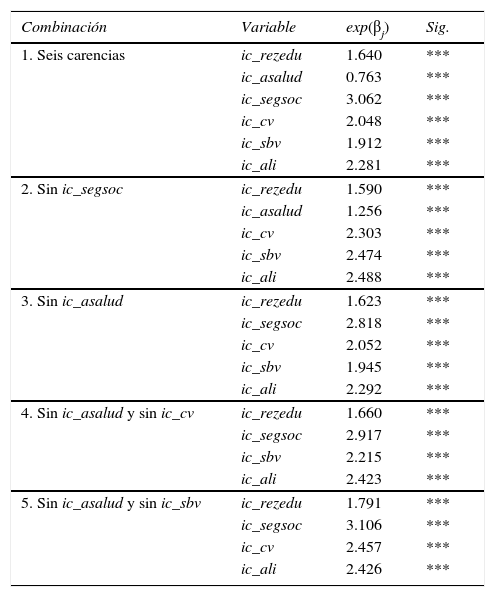
es decir, la pobreza de ingresos se expresa como función de las seis carencias, y luego se van omitiendo algunas otras a fin de comprobar cambios ante la consideración de distintas variables. En el cuadro 6 se presentan los resultados obtenidos de tal ejercicio.
Regresiones logit con diferentes combinaciones de variables
| Combinación | Variable | exp(βj) | Sig. |
|---|---|---|---|
| 1. Seis carencias | ic_rezedu | 1.640 | *** |
| ic_asalud | 0.763 | *** | |
| ic_segsoc | 3.062 | *** | |
| ic_cv | 2.048 | *** | |
| ic_sbv | 1.912 | *** | |
| ic_ali | 2.281 | *** | |
| 2. Sin ic_segsoc | ic_rezedu | 1.590 | *** |
| ic_asalud | 1.256 | *** | |
| ic_cv | 2.303 | *** | |
| ic_sbv | 2.474 | *** | |
| ic_ali | 2.488 | *** | |
| 3. Sin ic_asalud | ic_rezedu | 1.623 | *** |
| ic_segsoc | 2.818 | *** | |
| ic_cv | 2.052 | *** | |
| ic_sbv | 1.945 | *** | |
| ic_ali | 2.292 | *** | |
| 4. Sin ic_asalud y sin ic_cv | ic_rezedu | 1.660 | *** |
| ic_segsoc | 2.917 | *** | |
| ic_sbv | 2.215 | *** | |
| ic_ali | 2.423 | *** | |
| 5. Sin ic_asalud y sin ic_sbv | ic_rezedu | 1.791 | *** |
| ic_segsoc | 3.106 | *** | |
| ic_cv | 2.457 | *** | |
| ic_ali | 2.426 | *** |
Nota: código para la significación (Sig.): ***: 0.001, **: 0.01, *: 0.05, -: 0.1.
Fuente: elaboración propia en R con base en información del mcs de la enigh 2012.
El mejor de los cinco modelos, en términos de la devianza, es el que incluye las seis carencias, seguido del modelo donde sólo se elimina ic_asalud. Cuando se considera eliminar la carencia de salud y alguna de las variables de vivienda, el ajuste del modelo se reduce, lo cual tiene sentido debido a que las variables de vivienda captan elementos distintos. Lo anterior remite a la observación de Foster (2010), al decir que las carencias de la vivienda deberían reportarse en un subíndice ponderado y evitar brindarle doble peso a esta dimensión. Sin embargo, aun considerando los modelos 4 y 5 con su pérdida en la bondad de ajuste, son mejores que el modelo donde no se toma en cuenta la carencia de seguridad social.
Al momento se ha corroborado que la carencia ic_asalud podría ser omitida del ips, de manera que ahora se pueden contrastar otros dos modelos logit. Uno donde se utilice el ips original, i_privación, y otro donde se omita la carencia del acceso a los servicios de salud, i_privación.sal. Se elige describir la condición de pobreza de ingresos en función de las carencias, ya que los resultados previos sugieren que puede haber diferencias al considerar o no la variable ic_asalud. Estos modelos se escriben como:
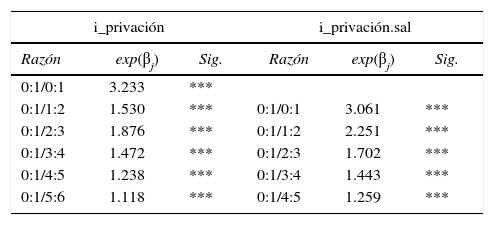
De los modelos se obtienen un conjunto de parámetros β, donde cada uno puede ser escrito como una razón de posibilidades θ. En el cuadro 7 se reportan los resultados de las razones y sus versiones logarítmicas, aplicando también las pruebas z a fin de verificar que son significativamente diferentes de cero.
Parámetros de las regresiones logit, ambos índices
| i_privación | i_privación.sal | ||||
|---|---|---|---|---|---|
| Razón | exp(βj) | Sig. | Razón | exp(βj) | Sig. |
| 0:1/0:1 | 3.233 | *** | |||
| 0:1/1:2 | 1.530 | *** | 0:1/0:1 | 3.061 | *** |
| 0:1/2:3 | 1.876 | *** | 0:1/1:2 | 2.251 | *** |
| 0:1/3:4 | 1.472 | *** | 0:1/2:3 | 1.702 | *** |
| 0:1/4:5 | 1.238 | *** | 0:1/3:4 | 1.443 | *** |
| 0:1/5:6 | 1.118 | *** | 0:1/4:5 | 1.259 | *** |
Nota: código para la significación (Sig.): ***: 0.001, **: 0.01, *: 0.05, -: 0.1.
Fuente: elaboración propia en R con base información del mcs de la enigh 2012.
De la columna i_privación, la posibilidad de que un no pobre sea no carente es 3.23 veces la posibilidad de que un pobre sea no carente; i.e., el individuo no pobre siempre presentará mayores posibilidades de tener menos carencias que el pobre. No obstante, la posibilidad de que un no pobre tenga cinco y no seis carencias es apenas 1.11 veces la posibilidad de que un pobre tenga cinco y no seis carencias. En ese caso, el individuo presenta un nivel tan alto de carencias que difícilmente saldrá de esa situación únicamente por la vía del ingreso. Del apartado con i_privación.sal, la posibilidad de ser no carente a carente, al pasar de no pobre a pobre de ingresos, es ligeramente menor. Pero ahora, la posibilidad de que un no pobre tenga una y no dos carencias es 2.26 veces la posibilidad de que un pobre tenga una y no dos carencias (contra el 1.53 obtenido con el otro índice).
Se proponen también modelos donde el nivel de carencias se expresa en función de la pobreza de ingresos. Así entonces, los modelos ahora describen al ips en función de plb, tomando la categoría cero como referencia:
Por lo tanto, en el cuadro 8 se exponen los coeficientes asociados a la variable plb que resultan de las regresiones logit multinomiales. En términos de la verosimilitud y la devianza, el mejor ajuste se logra con i_privación.sal.
Parámetros de los logit multinomial, ambos índices
| i_privación | i_privación.sal | ||||
|---|---|---|---|---|---|
| Categoría | exp(βj) | Sig. | Categoría | exp(βj) | Sig. |
| 1:plb | 3.233 | *** | |||
| 2:plb | 4.946 | *** | 1:plb | 3.061 | *** |
| 3:plb | 9.277 | *** | 2:plb | 6.891 | *** |
| 4:plb | 13.656 | *** | 3:plb | 11.728 | *** |
| 5:plb | 16.910 | *** | 4:plb | 16.925 | *** |
| 6:plb | 18.907 | *** | 5:plb | 21.312 | *** |
Nota: código para la significación (Sig.): ***: 0.001, **: 0.01, *: 0.05, -: 0.1.
Fuente: elaboración propia en R con base información del mcs de la enigh 2012.
Se observa que las posibilidades de presentar mayor número de carencias aumentan considerablemente ante la posibilidad de ser pobre de ingresos, para ambos índices. Es posible obtener las ecuaciones de regresión a partir de la ecuación [11] del marco metodológico, para conocer el cambio que hay entre dos categorías consecutivas y no sólo respecto de la categoría cero. En el cuadro 9 se muestran los parámetros correspondientes.
Resultados respecto a la categoría inmediata anterior, ambos índices
| i_privación | i_privación.sal | ||
|---|---|---|---|
| Categoría | exp(βj) | Categoría | exp(βj) |
| 2:1 | 1.530 | ||
| 3:2 | 1.876 | 2:1 | 2.251 |
| 4:3 | 1.472 | 3:2 | 1.702 |
| 5:4 | 1.238 | 4:3 | 1.443 |
| 6:5 | 1.118 | 5:4 | 1.259 |
Fuente: elaboración propia en R con base información del mcs de la enigh 2012.
Para i_privación, la pobreza de ingresos tiene un mayor efecto cuando se plantea pasar de dos a tres carencias; mientras que para i_privación.sal, el mayor efecto se presenta al pasar de una a dos carencias. Esto corrobora que el segundo índice captura mejor la relación entre los espacios de bienestar y derechos sociales, dado que la condición de pobreza de ingresos sí tiene efectos sobre el nivel de carencias de un individuo.
De los modelos logit multinomial del cuadro 8 pueden realizarse los análisis de varianza. La hipótesis nula es que la media del ips no varía entre los grupos pobre y no pobre de ingresos; es decir, H0: μIPS(no pobre de ingreso) = μIPS(pobre de ingreso). Lo anterior indicaría que la variable plb es independiente del ips; o bien, que los espacios del ingreso y los derechos sociales son independientes. No obstante, en ambos Anova se rechaza H0, y las medias difieren entre los grupos: la media del ips para quienes son pobres de ingresos es mayor, de acuerdo con el cuadro 10, considerando p-valores iguales a cero.
Una suposición válida sería que el nivel de ingreso pueda estar ejerciendo un efecto a través de su interacción con la variable pobreza de ingresos. En otras palabras, el nivel de ingreso, y no solamente la identificación de ser pobre, puede provocar variaciones en el nivel de carencias padecidas. Para verificar esta hipótesis se propone un modelo logit multinomial que agrega la interacción plb*ing. bc. Al realizar los Ancova a ambos modelos se encuentra que los términos de interacción son estadísticamente significativos con p-valores de cero.
De las regresiones realizadas, se observó que si bien los valores asociados a la interacción son bajos, son significativos, sobre todo en el apartado i_privación. sal. Es interesante mencionar que el ingreso, vía plb*ing.bc, sí tiene un efecto diferenciado entre pasar de un número menor a uno mayor de carencias, aunque para el ips original no resulta tan evidente como en el caso del índice modificado. Los términos de interacción con el mayor parámetro asociado resultan al pasar de tres a cuatro carencias, para ambos índices. Sin embargo, el incremento en el valor del parámetro más importante se da usando el índice modificado, al pasar de una a dos carencias, que es coincidente con lo anterior. Los términos de interacción, al resultar ser significativos, confirman que el ingreso es una variable que afecta al ips a través de su interacción con la variable que identifica al individuo como pobre por ingresos.
REFLEXIONES FINALESLa definición de pobreza multidimensional en México requiere que el individuo sea pobre de ingresos y presente al menos una carencia en el espacio de los derechos sociales. Lo anterior invita a preguntarse si existe algún nivel de asociación entre los derechos sociales y el ingreso, y por otro lado, si las carencias tienen el mismo nivel de asociación con el ingreso. Las preguntas anteriormente establecidas se intentan responder a partir de micro-regresiones, las cuales evalúan la condición de pobreza de un individuo en función de un conjunto de características. Los resultados señalan que sí hay asociación entre estos espacios; sin embargo, las carencias tienen influencias diferenciadas sobre la pobreza de ingresos.
En primer lugar, se formuló que cada carencia fuera explicada en términos de la pobreza de ingresos. Los parámetros encontrados confirman efectos diferenciados de la pobreza de ingreso al determinar las carencias. Las mayores asociaciones se dan en las variables de vivienda, seguridad social y alimentación, y la menor se encuentra en servicios de salud (si bien es significativa, es reducida). En el Ancova se encontró que el nivel de ingresos de los pobres de ingresos sí afecta sobre la probabilidad de presentar las carencias, excepto para el acceso a los servicios de salud. Esto último como un potencial efecto del programa Seguro Popular, sugiriendo con ello un cierto grado de independencia entre esta carencia y el ingreso.
Posteriormente, se formularon modelos donde la pobreza de ingresos se explica en términos de la presencia de cada carencia. Esto porque hasta el momento no se pretende establecer un orden de causalidad. Los Anova reportan que probabilidades de ser pobre ingresos varían según la carencia; siguiendo el patrón de los logit anteriores. Para el caso de ic_asalud las probabilidades son parecidas en ambos grupos; comparadas por ejemplo, con las de ic_cv. Al verificar si el nivel de ingresos establece algún efecto, se encuentra que tiene una interacción significativa estadísticamente con todas las carencias, incluso con la de ic_asalud.
Los resultados de esta etapa conducen a la necesidad de considerar el ingreso en la medición de la pobreza multidimensional. Por un lado se encuentra que el ingreso no tiene efecto sobre la carencia de servicio de salud, pero sí se encuentra que esta carencia interactúa con el ingreso reforzando la condición de pobreza de ingresos. Es decir, no se puede afirmar la independencia entre esta carencia y el ingreso, ya que es posible encontrar ciertos niveles de asociación, los cuales son estadísticamente significativos. Agregar al ingreso en la medición podría permitir encontrar medidas más próximas a la realidad de los individuos, ya que sería posible calcular medidas de profundidad de la pobreza en términos de cada una de las dimensiones; y es que la evidencia aquí mostrada sugiere que la asociación entre los espacios del bienestar y los derechos sociales existe y es de considerable importancia.
En otra etapa, se decidió explicar la condición de pobreza de ingresos en términos de la suma de las carencias, ips. Al realizar este análisis se encuentra que la omisión de la variable ic_asalud conduce a un modelo más robusto, de acuerdo con la devianza, y se incrementan los parámetros de las otras carencias. Omitir la variable ic_segsoc es lo que conduce al modelo menos adecuado en términos de su capacidad explicativa. La omisión de variables relacionadas con la vivienda reduce también la devianza, aunque en menor grado que ic_segsoc; y esto tiene sentido, pues las variables de la vivienda captan diferentes elementos.
A continuación se analizaron modelos donde la pobreza de ingresos se explica según el ips. Con todos los parámetros estadísticamente significativos, se encuentra que al padecer una carencia se incrementan las posibilidades de ser pobre de ingresos. Sin embargo, el siguiente valor alto en estas posibilidades varía según se elija al ips: usando el ips sin ic_asalud, aumenta de manera considerable la posibilidad de ser pobre de ingresos cuando se presentan dos carencias; en tanto que al usar el ips original, el aumento importante en la posibilidad se da al padecer tres carencias. Lo último puede explicarse por el efecto generado al omitir la variable del acceso a servicios de salud.
Otra aproximación es verificar si el nivel del ips puede explicarse por la condición de la pobreza de ingresos. Para ambas formas del ips, las posibilidades de contar con un mayor número de carencias aumentan con la posibilidad de ser pobre de ingresos. Los Anova, en este caso, plantean que la media del ips no varía entre los grupos pobre y no pobre de ingresos, lo cual se rechaza de manera contundente. Si se agrega el efecto covariante del ingreso surgen algunas observaciones interesantes. La interacción plb*ing.bc sí tiene un efecto diferenciado al incrementar el número de carencias, y es más evidente en el caso del ips sin ic_asalud.
Todas las pruebas realizadas en este documento apuntan a la viabilidad de omitir la variable de acceso a los servicios de salud en el análisis. Su eliminación en algunos modelos permitió evidenciar aún más la existencia de asociación entre la pobreza de ingresos y el nivel de carencias padecidas. Si bien las variables de la vivienda también exhiben algunos problemas, son menores en comparación. Estas cuestiones conducen a la necesidad de plantearse una forma alternativa de ponderar las dimensiones en el espacio de los derechos sociales. Lo anterior es una línea de investigación que se encuentra en proceso, ya que la mejora de la medición del nivel de carencias repercute en la medición de la pobreza multidimensional. Además, confirmar la asociación entre el ingreso y las carencias permite que los planes y programas de combate a la pobreza se enfoquen en la reducción de ambos, pues estos espacios interactúan, aunque con alcances diferenciados.
Centro de Investigaciones Socioeconómicas, Universidad Autónoma de Coahuila, Unidad Camporredondo (México).
Consejo Nacional de Evaluación de la Política de Desarrollo Social (Coneval, México).
Puede consultarse el Anexo para ver su definición; la discusión sobre la conveniencia de considerar estas u otras carencias no es un objetivo del presente documento.
Por ejemplo, los mayores niveles de privación tienden a presentar los menores niveles en capacidades y en gasto.
El documento de Elbers, Lanjouw y Lanjouw (2003) describe una técnica para la estimación de niveles de ingreso a escalas geográficas menores. La idea es combinar información nacional de los censos que no contienen la variable ingreso con encuestas de ingreso que no tienen representación a escalas administrativas menores a la nacional.
Las medidas de pobreza de la familia Foster-Greer-Thorbecke (fgt) (Foster et al., 1984) son las utilizadas como medidas de bienestar.
El documento de Sahn y Stifel (2000) analiza la pobreza y sus cambios en el tiempo para algunos países de África a través de un índice propuesto mediante análisis factorial. Por medidas no monetarias se refieren a asistencia escolar a nivel primaria y secundaria y la prevalencia de tallas bajas.
Se recomienda la revisión de Agresti (2002) y Agresti y Finlay (2009) para las secciones referentes a la metodología
Dado que las ecuaciones de verosimilitud son usualmente no lineales en β, se recurre a métodos iterativos, destacando el Newton-Raphson y el Fisher-Scoring.
Donde el primero considera remuneraciones por trabajo subordinado, ingreso por trabajo independiente (incluye autoconsumo), ingreso por renta de la propiedad, otros ingresos provenientes del trabajo y transferencias. El ingreso corriente no monetario comprende los pagos en especie, transferencias en especie (regalos en especie, se excluyen las transferencias que se dan por única vez) y no incluye renta imputada.
La muestra del mcs de la enigh 2012 cuenta con 870 reportes de cero ingresos y 674 de ingreso menor a 50 pesos mensuales; de estos 1 544 individuos, 1 432 son pobres multidimensionales. Además, al considerar ingresos mayores a 50 000 pesos mensuales se encuentran 180 casos (el mayor es de 508 700 pesos). Por lo tanto, tras realizar varias pruebas, se decidió utilizar únicamente la información referente a los individuos que contaran con un ingreso mensual entre 50 y 50 000 pesos. Esto con el fin de evitar un exceso de valores atípicos que pudieran sesgar los resultados. Los datos eliminados representan menos del 1% de la muestra total y el 1.30% de los pobres multidimensionales, lo que no implica una grave reducción de la muestra.
El 61.25% de la muestra padece la carencia de seguridad social, siendo la de mayor incidencia.
De hecho, el 78.2% de los pobres de ingresos no presenta la carencia, esto puede ser entendido cuando se considera el acceso al programa Seguro Popular para no ser registrado como carente.
El 39.8% de la muestra son individuos pobres de ingresos y con carencia en el acceso a la seguridad social, siendo este el caso de mayor incidencia.
En Agresti (2002, p.45) se especifica que una propiedad de las razones de posibilidades es que no cambian al establecer una u otra variable como respuesta.