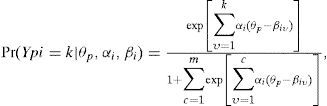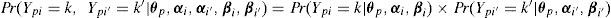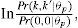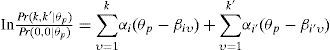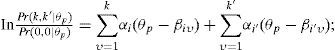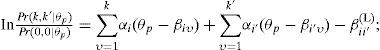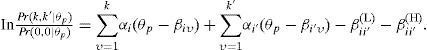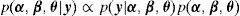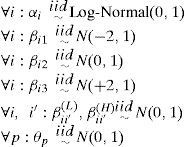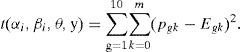Se describen el proceso y resultado de una validación psicométrica de un instrumento para estimar el nivel de las competencias de informática en estudiantes universitarios de nuevo ingreso. El nuevo instrumento, que se construyó a partir de un cuestionario existente (para una población anglófona), mide seis competencias a través de 45 ítems en los cuales los estudiantes expresan su grado de familiaridad con tareas concretas de cómputo. Los datos incluyeron las respuestas de dos cohortes de estudiantes de medicina (2 389 participantes, en total): la primera cohorte sirvió para seleccionar los ítems de la versión final del cuestionario; la segunda para una validación cruzada del nuevo instrumento. Se realizaron (a) análisis psicométricos basados en una variante del modelo del factor común y una nueva variante del modelo de crédito parcial generalizado, que da cuenta de dependencias locales entre los ítems y (b) análisis de ecuaciones estructurales para investigar las relaciones entre sí de las seis competencias. Los resultados psicométricos indicaron un buen ajuste a los modelos y mostraron adecuados valores para la fiabilidad y validez. El análisis estructural reveló relaciones de prerrequisito entre las habilidades. Los resultados fomentan el uso del instrumento para la evaluación for-mativa de los estudiantes.
This article informs on the process and the results of an instrument aimed at measuring the level of computer competencies in first-year university students. The new instrument, which was constructed from an existing questionnaire (originally for an English-speaking population), measures six competencies using 45 items in which students express their familiarity with specific computer tasks. Data included responses from two cohorts of medical students (for a total of 2 389 participants): Based on the results for the first cohort, items were selected for the questionnaire’s final version, which subsequently was evaluated in a cross-validation study on the second cohort. The analyses were based on (a) a variant of the common factor model and a novel variant of the generalized partial credit model that accounts for local item dependencies, and (b) structural equation modeling which examines the relations among the six abilities measured by the instrument. The psychometric results showed good fit of the models to the data and adequate reliability and validity indices. The structural analysis revealed prerequisite relations among the abilities. The results lend support to the instrument as a functional tool in the students’ formative evaluation process.
La competencia en computación se le considera fundamental en la formación profesional de prácticamente todas las disciplinas académicas. Un nivel superior de competencia en informática facilita al estudiante la búsqueda y aplicación efectiva de información y conlleva el uso racional de la tecnología para la solución de problemas.1, 2 Es en este contexto que varios autores advierten que un grado insuficiente de conocimientos y habilidades sobre computación puede convertirse en un obstáculo para los estudiantes y puede llevar a un bajo rendimiento académico.3, 4
Las variables que se han asociado con el nivel de competencias en computación incluyen, entre otras, aspectos relacionados con el nivel socioeconómico como el ingreso familiar y el tener computadora propia en casa.5, 6 Especialmente en las universidades públicas en los países en vías de desarrollo, que atraen estudiantes de distintos estratos socioeconómicos, existe el riesgo que una parte significativa de la población estudiantil carezca de las habilidades de cómputo requeridas para emprender y terminar exitosamente una carrera académica.
La Facultad de Medicina de la Universidad Nacional Autónoma de México (UNAM) constituye un ejemplo típico de la situación anteriormente descrita: Los aproximadamente 1 200 estudiantes que ingresan cada año académico a la facultad provienen de bachilleratos que exhiben una enorme variabilidad, tanto geográficamente como respecto al tipo y nivel de competencias que promueven y los estratos socioeconómicos de los estudiantes que recluían. A pesar de que el perfil de los aspirantes a ingresar a la Facultad de Medicina contempla, entre otros requisitos, conocimientos y habilidades básicas de computación e informática —y por lo tanto se puede suponer que todos los estudiantes durante su educación preparatoria fueron formados en este tema—, las experiencias de los profesores del primer año han enseñado que un grupo pequeño, pero significativo, de los estudiantes no dominan las herramientas informáticas elementales.
Por lo anterior, se considera conveniente disponer de un instrumento que permita conocer las habilidades de cómputo de cada estudiante de nuevo ingreso. Conforme al resultado proporcionado por tal instrumento, se puede ofrecer al estudiante un curso para remediar las carencias detectadas o, como mínimo, señalarle la necesidad de atender estas deficiencias. Varios autores han utilizado mediciones de las competencias relacionadas con el uso adecuado de la computadora y algunas fueron validadas en un estudio enfocado en la calidad psicométrica del instrumento.7-13 No obstante, dichos instrumentos se dirigen a poblaciones de habla inglesa (con excepción del instrumento de Joly y Ximenes-Martins,11 que está en portugués); instrumentos recientes para evaluar el nivel de las habilidades tecnológicas en estudiantes universitarios de habla hispana son escasos. En este artículo presentaremos el proceso y los resultados de la validación psicométrica de un nuevo instrumento que tiene este objetivo.
MétodoParticipantesDos cohortes de estudiantes participaron en el estudio: 1132 estudiantes (94%) de los que iniciaron la licenciatura en la Facultad de Medicina de la UNAM en el año académico 2010-2011 y 1 257 (85%) de los que iniciaron en el 2011-2012. La composición de la muestra de ambas cohortes resultó muy similar respecto del sexo (el 64% es mujer; el 36% hombre) y del tipo de escuela de procedencia (el 38% viene de un Colegio de Ciencias y Humanidades y el 43% de una Escuela Nacional Preparatoria, que pertenecen al subsistema de Educación Media Superior de la UNAM; el 19% proviene de una escuela privada o no incorporada a la UNAM). Respecto de la edad al momento de participar, los estudiantes de la primera cohorte fueron, en promedio, unos meses más jóvenes que los de la segunda (18 años y 10 meses vs. 19 años y 6 meses), lo cual se debe en gran parte a que la aplicación al primer grupo se realizó más temprano en el año académico que al segundo grupo (véase la sección de Procedimientos).
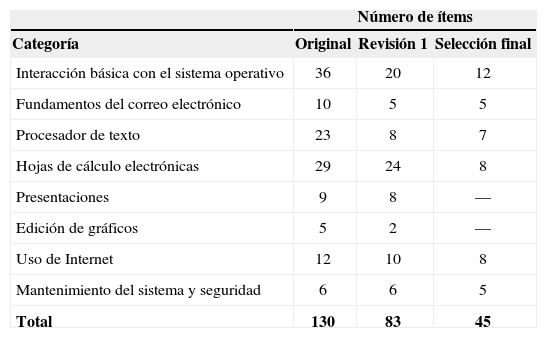
MaterialesComo punto de partida utilizamos el instrumento diseñado por Duvel y Pate,9 el cual se adaptó en varios aspectos para el presente estudio: (a) se realizó una traducción al español y posteriormente una retrotraducción al inglés, para verificar que se preservase el significado de los reactivos. (b) Un grupo de expertos revisó el instrumento traducido para evaluar su adecuación a nuestro medio; decidieron eliminar una de las siete escalas del instrumento original (el manejo de diskettes) debido a su obsolescencia y agregaron dos nuevas escalas: la elaboración de presentaciones y el mantenimiento y seguridad del sistema. (c) Se cambiaron el número de opciones de respuesta y se etiquetaron como “nada familiarizado”, “poco familiarizado”, “familiarizado”, “muy familiarizado”. Como resultado de este proceso, se obtuvo un instrumento conformado por ocho escalas y 130 reactivos (Tabla 1), el cual se aplicó a la muestra total de estudiantes (ambas cohortes).
Número de ítems para cada escala en distintas versiones del cuestionarios.
| Número de ítems | |||
|---|---|---|---|
| Categoría | Original | Revisión 1 | Selección final |
| Interacción básica con el sistema operativo | 36 | 20 | 12 |
| Fundamentos del correo electrónico | 10 | 5 | 5 |
| Procesador de texto | 23 | 8 | 7 |
| Hojas de cálculo electrónicas | 29 | 24 | 8 |
| Presentaciones | 9 | 8 | — |
| Edición de gráficos | 5 | 2 | — |
| Uso de Internet | 12 | 10 | 8 |
| Mantenimiento del sistema y seguridad | 6 | 6 | 5 |
| Total | 130 | 83 | 45 |
Versión original: la versión aplicada a los estudiantes. Revisión 1: quitando ítems con menos del 8% de respuestas en las dos categorías más bajas. Selección final: ítems seleccionados para la versión final del instrumento.
Para ambas cohortes, el instrumento se aplicó en la primera clase de la asignatura Informática Biomédica I. En el año académico 2010-2011 dicha asignatura se impartió en el primer semestre, por lo cual los estudiantes de la primera cohorte contestaron el instrumento en agosto del 2010; el siguiente año, la asignatura se impartió en el segundo semestre, de tal suerte que los datos de los estudiantes de la cohorte 2011-2012 se recopilaron en diciembre 2011. Previo a la administración del instrumento, se les informó a los estudiantes sobre el objetivo de su participación. El instrumento se aplicó en línea a través del módulo Cuestionario del software Moodle.14
Análisis de datosAnálisis previos. Al examinar la distribución de respuestas en cada ítem, se detectaron varios ítems con una distribución muy sesgada en el sentido de que casi todos los respondientes indicaron estar (muy) familiarizados con la tarea planteada. Por varias razones (incluyendo la escasa información que contribuyen y la violación de los supuestos de normalidad en los análisis con modelos lineales), decidimos eliminar de los análisis subsecuentes 47 de los 130 ítems que recibieron menos del 8% de respuestas (de las dos cohortes combinadas) en las dos categorías de respuesta más bajas. La columna “Revisión 1” de la Tabla 1 muestra más detalles.
Separación de cohortes para la validación cruzada. El proceso de validación de un instrumento típicamente implica una serie de decisiones tomadas en función de resultados de análisis intermedios de los datos (p. e., la eliminación/selección de ítems, modificaciones al modelo estadístico, etc.). Para reducir el peligro de la capitalización del azar, decidimos llevar a cabo el análisis en dos fases: en la primera, analizamos los datos de la cohorte de 2010-2011 de forma exploratoria; en función de los resultados obtenidos se seleccionaron los ítems para la versión final del instrumento y se decidió sobre algunas modificaciones en los modelos estadísticos. En la segunda fase (validación cruzada), se evaluó el instrumento final con los datos de la cohorte de 2011-2012. A menos que se indique lo contrario, todos los resultados que se presentan en la sección de Resultados se obtuvieron con la cohorte de 2011-2012.
Análisis psicométricos. Se llevaron a cabo análisis psicométricos para cada escala (excepto para Edición de gráficos, puesto que el número de preguntas en esta escala es insuficiente para cualquier análisis psicométrico, lo cual puede observarse en la Tabla 1). En particular, se realizaron dos tipos de análisis: (a) Después de asignar un valor numérico a las respuestas observadas de cada ítem (“nada familiarizado” = 0; “poco familiarizado” = 0.25; “familiarizado” = 0.75; “muy familiarizado” = 1), se aplicó el modelo del factor común, lo cual se considera una variante del modelo básico de la teoría clásica de los tests (TCT).15 Dentro de este enfoque, se calcularon índices de validez y fiabilidad de toda la escala tanto como índices psicométricos para cada ítem por separado. (b) Se ajustó el modelo de crédito parcial generalizado,16 el cual es un modelo en el marco de la Teoría de la Respuesta al Ítem (TRI). Mediante comprobaciones predictivas posteriores,17 se evaluó la bondad de ajuste del modelo y se identificaron ítems con mal ajuste. Nótese que el modelo del factor común es un modelo lineal, mientras que los modelos TRI especifican relaciones no lineales entre el constructo subyacente y las respuestas en los ítems.
Tanto el modelo del factor común como el modelo de crédito parcial suponen que no existan covarianzas residuales (significativas) entre los ítems, una vez eliminada la influencia del factor latente. Sin embargo, puesto que existen grupos de preguntas que se refieren a una misma subárea (p. e., los ítems en la escala de Hojas de cálculo que se refieren al uso de fórmulas), resultó necesario ampliar los modelos para tomar en cuenta dependencia local. Para remediar este problema, se amplió el modelo del factor común con parámetros de covarianza entre los términos residuales de pares de ítems particulares. El modelo de crédito parcial se amplió según las líneas sugeridas por Hoskens y De Boeck18 (Anexo 1).
Análisis de ecuaciones estructurales. Con el fin de investigar las relaciones entre las habilidades validadas en el análisis psicométrico, se realizaron análisis de ecuaciones estructurales.19, 20 Como modelo de medida, el cual relaciona las variables latentes con las variables observadas, se especificaron los mismos modelos mencionados arriba para el análisis psicométrico (lo cual entonces lleva a dos variantes de análisis). La parte estructural describe las relaciones de las variables latentes entre sí mediante funciones lineales y es idéntica en ambos análisis. La especificación del modelo -en la fase exploratoria- se guió por la plausibilidad de relaciones de prerrequisito entre las habilidades.
Cabe señalar que para los análisis lineales utilizamos el procedimiento PROC CALIS de SAS versión 9.2, con la estimación por máxima verosimilitud.21 Los análisis que incluyen el modelo de crédito parcial generalizado se realizaron dentro de un marco bayesiano (para una introducción de la evaluación y estimación de modelos psicométricos en una marco bayesiano, véase Revuelta).22 Para su ajuste se implementó un algoritmo de Metrópolis.23, 24 En el Anexo 1 se provee más detalles sobre dicho procedimiento bayesiano.
ResultadosAnálisis psicométricosEl análisis de los datos de la cohorte 2010-2011 (fase exploratoria) para los ocho ítems de Presentaciones mostró un mal ajuste al modelo del factor común tanto como al modelo de crédito parcial (utilizando los mismos criterios que se discuten a continuación para las otras escalas). Puesto que tampoco la eliminación de una parte de los ítems mejoró la bondad de ajuste de la escala, decidimos eliminar la escala completa del instrumento final. Para las seis escalas restantes seleccionamos los ítems que combinaron valores aceptables en los índices psicométricos y una justificación teórica más pertinente. En consideración de la funcionalidad ofrecida por un instrumento breve, decidimos limitar el número de ítems en la escala de Interacción básica a 12 y en las otras escalas a máximo ocho. El número de ítems en la versión final de cada escala, se muestra en la última columna de la Tabla 1. Los ítems, junto con algunos índices psicométricos, se encuentran en el Anexo 2.
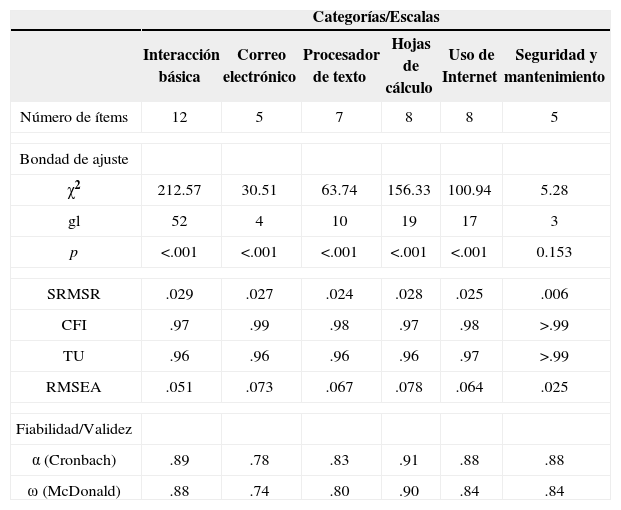
La Tabla 2 resume la información sobre la bondad de ajuste de las seis escalas retenidas y presenta índices de fiabilidad y validez basados en el modelo del factor común. En consideración de que la prueba de ji cuadrada, al evaluar la bondad de ajuste de un modelo de análisis factorial confirmatorio, casi siempre —y especialmente en muestras grandes— lleva a un rechazo (debido a que es un índice de ajuste exacto y ningún modelo estadístico es capaz de tomar en cuenta todos los aspectos de la realidad), es común presentar unos índices de bondad de ajuste aproximado: (a) el SRMSR (Standardized Root Mean Square Residual), para el cual se consideran aceptables valores menores de .08, y un valor de .05 o menor indica un excelente ajuste; (b) el CFI,25 para el cual se recomienda valores mayores a .95 para poder hablar de buen ajuste; (c) el TLI (Tucker-Lewis Index),26, 27 donde un buen ajuste requiere un valor mayor a .95; (d) el RMSEA,28 que con valores menores de .08 indica una bondad de ajuste aceptable y valores menores de .05 un ajuste excelente.29
Índices psicométricos para el modelo del factor común para cada escala (versión final, cohorte 2011-2012).
| Categorías/Escalas | ||||||
|---|---|---|---|---|---|---|
| Interacción básica | Correo electrónico | Procesador de texto | Hojas de cálculo | Uso de Internet | Seguridad y mantenimiento | |
| Número de ítems | 12 | 5 | 7 | 8 | 8 | 5 |
| Bondad de ajuste | ||||||
| χ2 | 212.57 | 30.51 | 63.74 | 156.33 | 100.94 | 5.28 |
| gl | 52 | 4 | 10 | 19 | 17 | 3 |
| p | <.001 | <.001 | <.001 | <.001 | <.001 | 0.153 |
| SRMSR | .029 | .027 | .024 | .028 | .025 | .006 |
| CFI | .97 | .99 | .98 | .97 | .98 | >.99 |
| TU | .96 | .96 | .96 | .96 | .97 | >.99 |
| RMSEA | .051 | .073 | .067 | .078 | .064 | .025 |
| Fiabilidad/Validez | ||||||
| α (Cronbach) | .89 | .78 | .83 | .91 | .88 | .88 |
| ω (McDonald) | .88 | .74 | .80 | .90 | .84 | .84 |
Los índices de bondad de ajuste: χ2: estadística ji cuadrada con sus grados de libertad (gl) y valor p asociado; SRMSR: Standardized Root Mean Square Residual; CFI: Bentler’s Comparative Fit Index; TLI: Tucker Lewis Index; RMSEA: Root Mean Squared Error of Approximation.
Dichos cuatro índices, evaluados en la muestra de validación cruzada, muestran un ajuste muy satisfactorio al modelo del factor común para las seis escalas. También el coeficiente α de Cronbach,30 que usualmente se interpreta como un índice de fiabilidad, tiene valores altos. La Tabla 2 incluye, además del coeficiente α, el coeficiente ω propuesto por McDonald,15 el cual goza de una interpretación más clara y que, si el modelo del factor común se ajusta, simultáneamente es un índice de fiabilidad y de validez interna. Los valores en estos dos índices son similares y cercanos o mayores a .80, lo cual se considera indicador de una fiabilidad/validez alta.
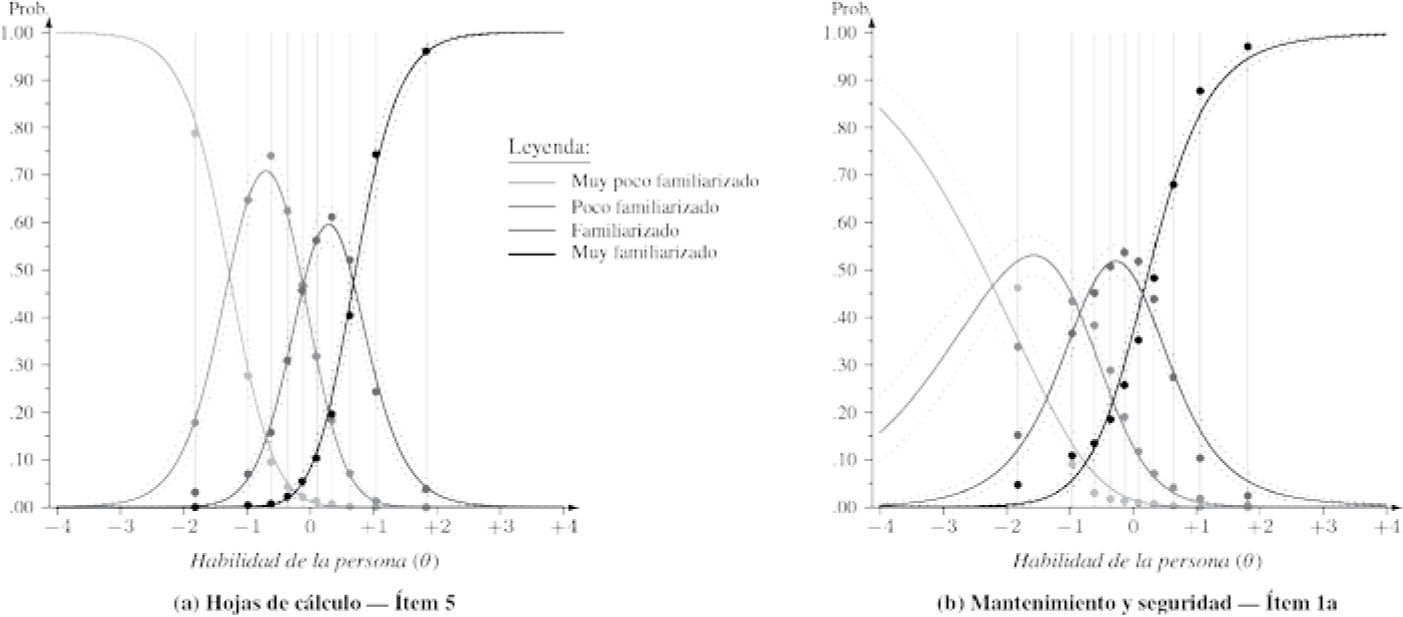
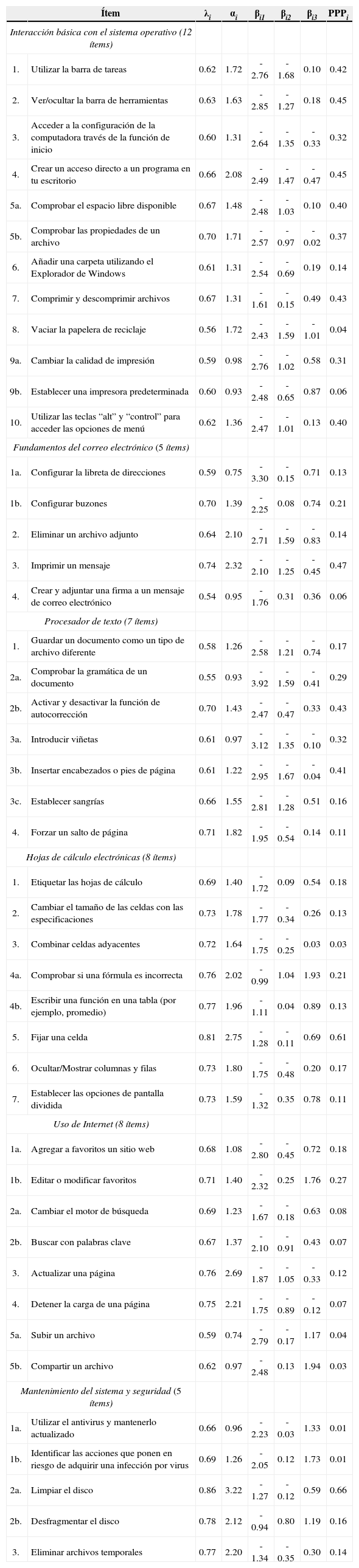
El ajuste al modelo de crédito parcial se evaluó a través de gráficas del tipo que se presentan en la Figura 1. Estas gráficas muestran, para un ítem en particular, la curva característica de las cuatro categorías de respuesta. Para evaluar la bondad de ajuste de los datos a estas curvas teóricas, dividimos los participantes en 10 grupos, conforme su decil para θ en la escala, y calculamos para cada grupo la proporción de respuestas en cada categoría. Por ejemplo, para la gráfica del panel izquierdo de la Figura 1, que muestra el ajuste para el ítem 5 de la escala Hojas de cálculo, calculamos que 79% de las personas del decil 1 (es decir, el grupo de nivel más bajo con un valor promedio de θ = -1.83) contesta “muy poco familiarizado”, 18% “poco familiarizado”, 3% “familiarizado” y 0.1% “muy familiarizado”. Dichas proporciones se representan mediante puntos gruesos, posicionadas en la abscisa según la media de θ del grupo. Evaluando las diferencias entre estas proporciones observadas y las probabilidades teóricas correspondientes (es decir, las distancias entre los puntos gruesos y las curvas características), se aprecia la bondad de ajuste del modelo a los datos. Para el ítem 5 de Hojas de cálculo, observamos que los puntos se encuentran por encima o muy cercanos a las curvas, lo cual es un argumento que apoya la hipótesis de buen ajuste.
Curvas características (curvas continuas) y proporción de respuestas observadas en 10 subgrupos de personas (puntos gruesos) para cada categoría de respuesta para (a) un ítem con buen ajuste (valor p de la comprobación predictiva posterior = 0.61) y (b) un ítem con (relativamente) mal ajuste al modelo de crédito parcial (valor p = 0.01). Las curvas punteadas indican el intervalo bayesiano de credibilidad de 90% para la probabilidad estimada por el modelo. Ambas gráficas se obtuvieron con los datos de la cohorte 2011-2012.
Como alternativa a la inspección visual de la bondad de ajuste llevamos a cabo contrastes estadísticos formales a través de comprobaciones predictivas posteriores (PPC);17, 22 para el caso actual definimos un estadístico que sigue la lógica que se acaba de describir en el párrafo anterior (en el Anexo 1 pueden observarse los detalles formales). Para el ítem representado en el panel izquierdo de la Figura 1, la PPC genera un valor p de .61, lo cual es evidencia a favor del modelo ajustado.
En el Anexo 2 se presenta para cada ítem, junto con sus parámetros de discriminación y de posición, el valor p resultado de la PPC. Con algunas excepciones, los valores p no resultan “significativos” y por lo tanto apoyan la hipótesis de un buen ajuste. Una de las excepciones es el primer ítem de la escala Mantenimiento y seguridad, (véase el panel derecho de la Figura 1). Su valor p es bajo (entre .01 y .02, el más bajo de todos los ítems) y efectivamente observamos en la gráfica que algunas de las proporciones observadas se encuentran fuera del intervalo de credibilidad de 90% de las curvas características. Al mismo tiempo, sin embargo, la inspección visual en este y otros ítems enseña que las discrepancias, aunque resultan formalmente significativas según la PPC, son pequeñas y no implican violaciones fuertes del modelo.
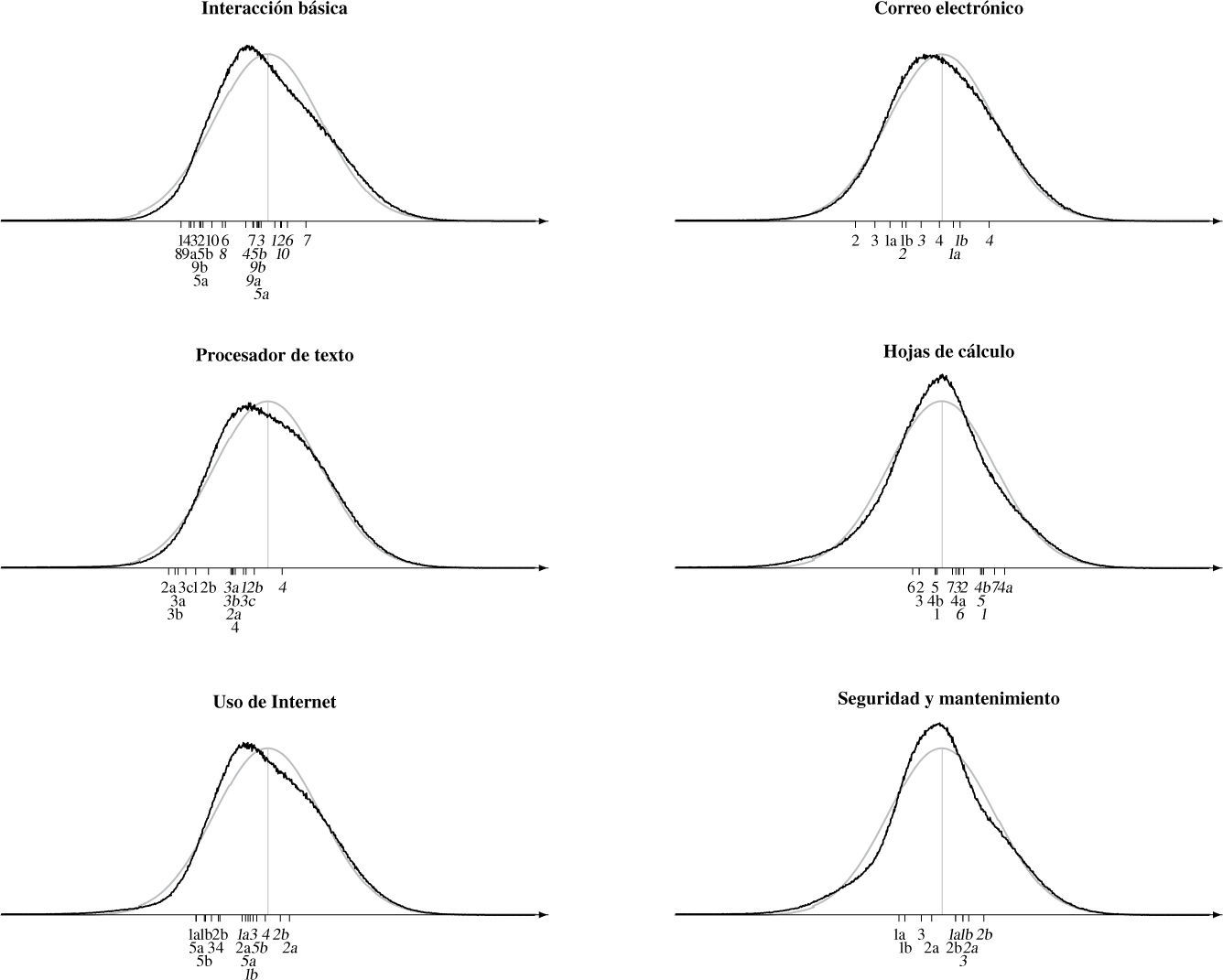
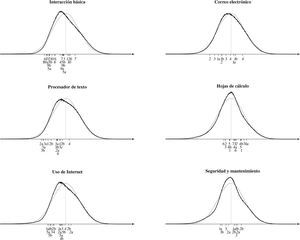
La Figura 2 muestra la distribución (posterior) del nivel estimado de las personas para las seis escalas, situándola en el mismo continuo que los grados de dificultad de los ítems. En este caso, definimos el grado de dificultad como el nivel θ que corresponde con una probabilidad de 50% de contestar en una de las dos categorías más altas (en letra normal), o bien, en la categoría más alta de “muy familiarizado” (letra cursiva). Es interesante señalar que las escalas Interacción básica, Correo electrónico, Procesador de textos y Uso de Internet son relativamente fáciles: Para cualquier ítem en estas escalas, una persona de nivel promedio tiene una probabilidad mayor de 50% para contestar que está familiarizada o muy familiarizada con la tarea planteada. Las escalas Hojas de cálculo y Mantenimiento y seguridad, al contrario, son más difíciles: los ítems se encuentran más en el centro de la distribución y una parte considerable de las personas no dominan las tareas en estos ítems.
Distribución posterior del nivel de las personas, relativo a la posición de los ítems para las seis escalas en la versión final del instrumento (cohorte 2011-2012). La posición de los ítems en la abscisa corresponde con el nivel que se requiere de una persona para tener una probabilidad de 50% de contestar este ítem en la categoría “familiarizado” o “muy familiarizado” (letra normal) o el nivel para una probabilidad de 50% de contestar en la categoría “muy familiarizado” (cursiva). El número de cada ítem corresponde con su número en el Anexo 2. La distribución normal estandarizada (en color gris) representa la distribución previa del nivel de las personas.
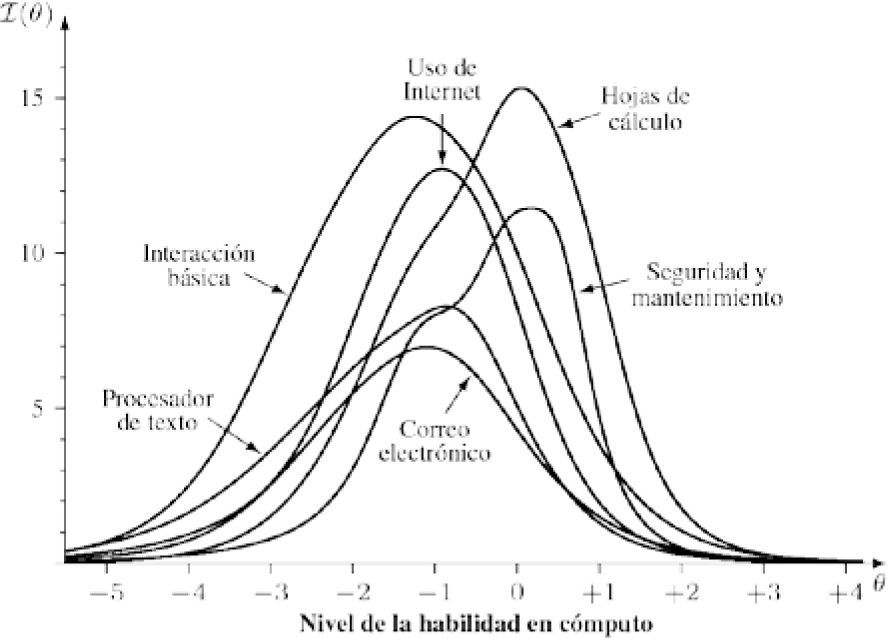
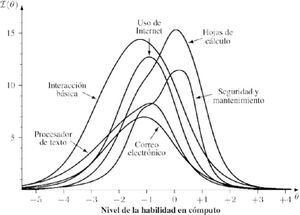
Para evaluar la fiabilidad en el contexto de modelos TRI, se examina la función de información, I(θ). La Figura 3 representa la función de información de cada una de las seis escalas en la versión final del instrumento. Se observa que para las escalas Interacción básica, Correo electrónico, Procesador de textos y Uso de Internet la función de información llega a su máximo cuando el nivel de la persona es bajo, mientras que la información en las escalas Hojas de cálculo y Mantenimiento y seguridad es máxima para niveles de habilidad promedio. Recuérdese que, al interpretar los resultados para la función de información, el error estándar de medida de θ es el inverso de la raíz cuadrada de I(θ). Por ejemplo, para las tres escalas con mayor número de ítems (Interacción básica, Hojas de cálculo y Uso de Internet), la información excede 10 en una parte importante del continuo, lo cual corresponde con un error estándar de medida de ± 0.3 (al estimar el nivel de la persona dentro de una distribución aproximadamente normal estandarizada). La información proveída por la escala de Mantenimiento y seguridad, aunque tiene solo cinco ítems, también es adecuada. Para las escalas de Correo electrónico y Procesador de textos, la función de información no alcanza la misma altura; sin embargo, todavía estiman el nivel de la persona en las zonas sensibles (para -2 ≤ θ ≤ 0) con un error estándar menor de 0.4.
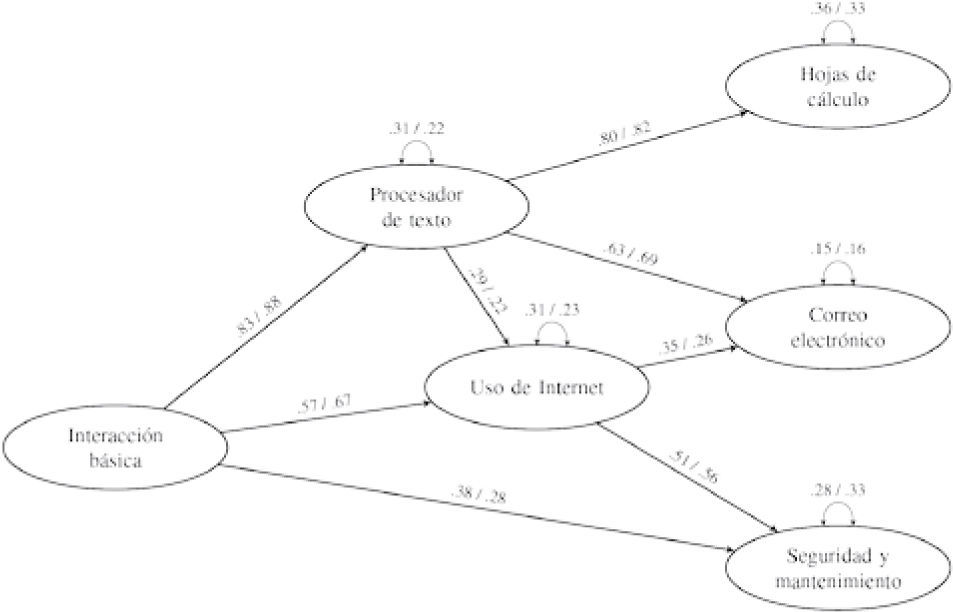
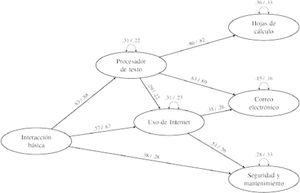
Análisis de ecuaciones estructuralesLa Figura 4 representa la parte estructural del modelo de ecuaciones estructurales ajustado a los 45 ítems de la versión final del instrumento (cohorte 2011-2012). Este modelo explica las correlaciones entre las seis habilidades asumiendo que (a) la habilidad Interacción básica influye directamente en las habilidades Procesador de texto, Uso de Internet y Mantenimiento y seguridad, (b) Procesador de texto influye directamente en Hojas de cálculo, Uso de Internet y Correo electrónico, y (c) Uso de Internet influye directamente en Correo electrónico y Mantenimiento y seguridad. Lo que llama la atención son los efectos fuertes de Interacción básica en Procesador de texto, y de Procesador de texto en Hojas de cálculo.
Representación gráfica de las relaciones estructurales entre las seis habilidades medidas en la versión final del instrumento. Las flechas unidireccionales indican efectos directos, las flechas bidireccionales varianzas residuales. Los números que preceden/siguen la diagonal son las estimaciones de los parámetros correspondientes utilizando como modelo de medida el modelo del factor común y el modelo de crédito parcial, respectivamente (cohorte 2011-2012). La varianza total de cada constructo iguala 1.
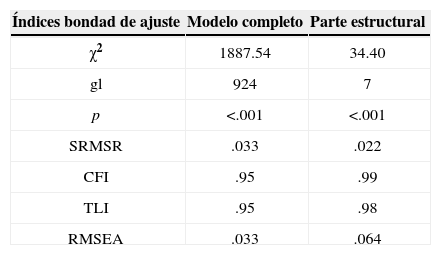
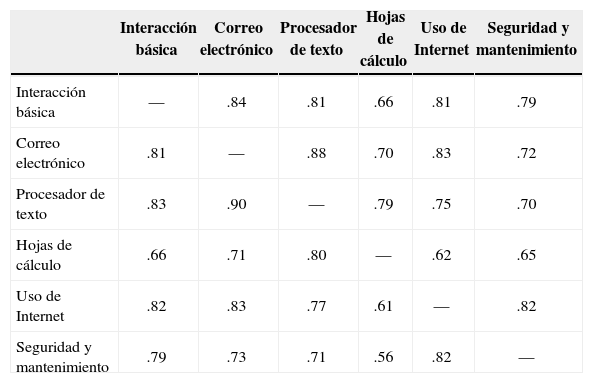
Los índices de bondad de ajuste aproximado para el modelo completo —el modelo de medida (en este caso, el modelo del factor común para cada escala) más el modelo estructural que se presenta en la Figura 4— resultan favorables (Tabla 3). También los índices parciales, que evalúan únicamente la bondad de ajuste de la parte estructural, apuntan a un ajuste aproximado satisfactorio. Este resultado se confirma en la Tabla 4 donde se aprecia que las correlaciones entre las habilidades derivadas del modelo en la Figura 4 son muy similares a las correlaciones en un modelo que no las restringe (la única excepción siendo la correlación entre Hojas de cálculo y Mantenimiento y seguridad, con una diferencia de .09 entre ambos tipos de correlaciones).
Indices de bondad de ajuste para el modelo de ecuaciones estructurales representado en la Figura 4.
| Índices bondad de ajuste | Modelo completo | Parte estructural |
|---|---|---|
| χ2 | 1887.54 | 34.40 |
| gl | 924 | 7 |
| p | <.001 | <.001 |
| SRMSR | .033 | .022 |
| CFI | .95 | .99 |
| TLI | .95 | .98 |
| RMSEA | .033 | .064 |
χ2: estadística ji cuadrada con sus grados de libertad (gl) y valor p asociado; SRMSR: Standardized Root Mean Square Residual; CFI: Bentler’s Comparative Fit Index; TLI: Tucker-Lewis Index; RMSEA: Root Mean Squared Error of Approximation.
Correlaciones entre las seis habilidades latentes medidas en la versión final del instrumento.
| Interacción básica | Correo electrónico | Procesador de texto | Hojas de cálculo | Uso de Internet | Seguridad y mantenimiento | |
|---|---|---|---|---|---|---|
| Interacción básica | — | .84 | .81 | .66 | .81 | .79 |
| Correo electrónico | .81 | — | .88 | .70 | .83 | .72 |
| Procesador de texto | .83 | .90 | — | .79 | .75 | .70 |
| Hojas de cálculo | .66 | .71 | .80 | — | .62 | .65 |
| Uso de Internet | .82 | .83 | .77 | .61 | — | .82 |
| Seguridad y mantenimiento | .79 | .73 | .71 | .56 | .82 | — |
La parte superior a la diagonal presenta las correlaciones bajo un modelo lineal en el cual las correlaciones no están restringidas; la parte inferior presenta las correlaciones para el modelo lineal que se encuentra gráficamente representado en la Figura 4.
La Figura 4 no sólo representa las estimaciones de los efectos cuando se utiliza el modelo del factor común como modelo de medida, sino también bajo el supuesto de que las respuestas en las preguntas siguen el modelo de crédito parcial. Aunque existen algunas diferencias entre las estimaciones en ambos modelos, las tendencias básicas son las mismas.
DiscusiónEn este trabajo realizamos estudios psicométricos con el fin de evaluar la validez interna de un instrumento para estimar el nivel de habilidades de cómputo de estudiantes que se encuentran en el primer año de su carrera académica. La versión inicial del instrumento se construyó a partir de un instrumento existente9 y aspiró medir ocho distintas habilidades a través de 130 ítems. Sin embargo, el análisis de los datos recopilados en una primera cohorte de estudiantes nos obligó a eliminar la medición de dos de las ocho habilidades, debido a que la escala incluyó pocos ítems o que la calidad psicométrica de los ítems era dudosa. La versión final del instrumento, que incluye seis escalas para un total de 45 ítems, mostró adecuados índices de fiabilidad y validez, los cuales posteriormente se confirmaron en una nueva cohorte de estudiantes, especialmente reservada para una validación cruzada.
El nuevo instrumento será utilizado para una evaluación diagnóstica de los estudiantes de nuevo ingreso en la Facultad de Medicina, con el fin de ofrecerles un curso remedial voluntario a aquellos que sean detectados con habilidades de cómputo insuficientes. De tal forma, el cuestionario contribuye a que todos los estudiantes cuenten con los prerrequisitos informáticos para los estudios de medicina.
Los análisis involucraron modelos de las dos corrientes principales de la psicometría. Aunque los resultados en grandes líneas convergen, el modelo de crédito parcial parece ser más exigente para los datos que el modelo del factor común, considerando que las PPCs para algunos ítems resultaron en un valor p significativo (mientras que los índices clásicos apuntaron a un buen ajuste). Sin embargo, con base en la inspección visual de la bondad de ajuste al modelo PCM (mediante gráficas como las en la Figura 1) decidimos conservar estos ítems en el cuestionario. En algún sentido, la aceptación del ítem en este caso es similar a la aceptación de un modelo de ecuaciones estructurales con una ji cuadrada que formalmente lo rechaza: en ambos casos se reconoce que el modelo no se ajusta perfectamente, pero que el ajuste aproximado es satisfactorio.
Llama la atención que el instrumento es relativamente poco sensible para los niveles altos de habilidad computacional: para la mayoría de las escalas, los grados de dificultad de los ítems son bajos (como muestra la Figura 2) y la función de información alcanza su máximo cuando la habilidad de la persona se encuentra por debajo de la media (Figura 3). Si el interés fuese discriminar entre sí estudiantes con habilidades sobresalientes, definitivamente el instrumento no sería el más adecuado. Sin embargo, como se mencionó anteriormente, el objetivo principal del instrumento es detectar a estudiantes con escasas habilidades computacionales, con el fin de remediar tempranamente posibles problemas, por lo cual es muy oportuno que el instrumento tenga máxima información para el lado negativo de la dimensión latente.
Una aportación interesante del presente estudio es que se examinaron las relaciones entre las seis habilidades medidas por la versión final del instrumento. Aunque en general es aventurado interpretar un modelo de ecuaciones estructurales en términos causales, es plausible interpretar las relaciones representadas en la Figura 4 como relaciones de prerrequisito: un alto nivel en una habilidad consecuente requiere un alto nivel en la(s) habilidad(es) antecedente(s). De esta forma, Interacción básica es un prerrequisito directo o indirecto de las otras habilidades; asimismo, dominar el Procesador de texto es prerrequisito para las cuatro habilidades restantes. Enfatizamos que este estudio es una primera aproximación al tema; hasta donde llega nuestro conocimiento, no existen otros estudios que han investigado o caracterizado las relaciones entre habilidades de cómputo en estos términos.
Cabe mencionar que, durante el periodo de investigación de este estudio, Peinado de Briceño y Ramírez31 publicaron los resultados de una validación de un instrumento similar dirigido a estudiantes de una universidad a distancia venezolana. Consideramos conveniente mencionar dos diferencias entre el enfoque de Peinado de Briceño y Ramírez y el nuestro. Primero, el instrumento que proponen estos autores venezolanos es el Inventario de Autoeficacia Computational (originalmente de Torkzadeh y Koufteros).32 Autoeficacia refiere a la creencia o percepción de una persona sobre sus propias habilidades y juega un papel significativo en (el cambio de) la conducta en un rango amplio del funcionamiento humano.33, 34 Por un lado, el diseño y el formato para responder a nuestro instrumento, lo convierte a una medición de autoeficacia, tal como el instrumento de Peinado de Briceño y Ramírez; por otro lado, aspiramos con nuestro instrumento detectar el nivel real de las habilidades de cómputo para que los estudiantes con un nivel insuficiente consideren actualizarse. Algunos estudios han investigado hasta qué grado la autoevaluación refleja diferencias reales entre habilidades tecnológicas; sin embargo, llegaron a hallazgos desacordes: McCourt-Larres, Ballantine, y Whittington35 y Sieber36 concluyeron que la relación es nula o insignificante, mientras que Katz y Macklin37 encontraron una correlación moderada. Los autores planeamos una investigación posterior en una nueva cohorte de estudiantes con el fin de comparar los niveles de cómputo estimados por el instrumento con observaciones directas en el aula de informática.
Una segunda diferencia con la validación por Peinado de Briceño y Ramírez31 se refiere al tipo de modelos psicométricos utilizados. Donde estos autores analizaron los datos con un modelo factorial exploratorio (de componentes principales), nosotros adoptamos un enfoque confirmatorio (aunque permitimos en la fase exploratoria modificaciones a los modelos psicométricos), examinando (a) la estructura interna de las escalas incluidas a priori en el instrumento a través de índices psicométricos clásicos y de la TRI y (b) las relaciones entre las seis competencias con modelos de ecuaciones estructurales. Además, la evaluación final del instrumento se cimentó en datos de una nueva muestra, aportando evidencia en el contexto de una validación cruzada.
ConclusiónLas habilidades computacionales son esenciales en el desarrollo del proceso de aprendizaje, porque es un saber transversal que impacta en todas las disciplinas e inclusive en la educación continua a lo largo de la vida profesional que conlleva una práctica reflexiva que favorezca el mejoramiento continuo en las ciencias de la salud. Además, son indispensables en asignaturas que utilizan una metodología de e-learning (aprendizaje electrónico) o blended learning (aprendizaje semipresencial) ya que sin habilidades mínimas en computación no es posible participar en ellas.
Como puede apreciarse, la estrecha relación entre las habilidades de computación y los aprendizajes que los estudiantes desarrollarán en su formación universitaria hacen evidente su inclusión en la estructura curricular. El progresivo dominio del manejo de información y las nuevas tecnologías permiten que los estudiantes cuenten con herramientas para hacer más efectivos sus aprendizajes en la totalidad de las asignaturas.
En este sentido, el presente trabajo aporta un instrumento con evidencia de validez, adaptado al español, que permite la evaluación formativa y sistemática de los estudiantes de primer ingreso a las Instituciones de Educación Superior. En particular, puede ser utilizado para realimentar a los estudiantes en su desempeño, así como a los profesores, a la propia institución y a las escuelas de Educación Media Superior.
Contribución de cada uno de los autoresIL realizó el análisis de datos y la elaboración de la parte mayor del manuscrito (texto y gráficos).
IMF y AMG participaron en el diseño del cuestionario aplicado, la recopilación y análisis descriptivos de los datos y la elaboración de algunas secciones del manuscrito (parte de la introducción y las conclusiones).
MSM enriqueció el texto con varios comentarios.
FinanciamientoNinguno.
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.
Presentaciones previasNinguna.
Modelo. Se describe la extensión del modelo de crédito parcial generalizado (GPCM) para tomar en cuenta dependencias locales entre los ítems. El GPCM original16 es un modelo para la probabilidad de que una persona p al contestar un ítem polltómico i con m + 1 opciones de respuesta graduadas (con valores 0…m), responda en la categoría k(0 ≤ k ≤ m). Dicha probabilidad se da por:
donde Ypi es la variable aleatoria asociada con la respuesta de la persona p en el ítem i, θp es el nivel de la persona p en el constructo bajo consideración, αi es el grado de discriminación del ítem i y βi = (βi1,…, βim) es un vector que contiene los grados de dificultad asociados con los respectivos umbrales del ítem i (que se definen por los pares de categorías de respuesta adyacentes). Nótese que, en el caso de k = 0, se define que la suma en el nominador iguala a 0.
Al considerar la probabilidad conjunta de dos o más respuestas de la misma persona, el GPCM original asume independencia local entre los ítems. Para dos ítems i e i′, esto implica:
para 0 ≤ k, k′ ≤ m.
En su artículo de 1997, Hoskens y De Boeck18 propusieron un marco teórico que organiza posibles causas por las que se invalide el supuesto de independencia local en modelos TRI y describieron cómo se puede adaptar el modelo para tomarlas en cuenta. Para la aplicación en este artículo, es importante mencionar el tipo de dependencia local que denominaron combinación constante, lo cual aplica especialmente en el caso de contenido compartido, es decir, cuando dos o más ítems de la escala hacen referencia a un subtema particular.
Aunque Hoskens y De Boeck elaboraron su método para el caso especial del modelo de Rasch, la aplicación de sus ideas al GPCM es bastante directa. Para simplificar la notación, escribiremos Pr(k, k′ | θp) en vez de Pr(Ypi = k, Ypi' = k′ | θp, αi, αi',βi, βi'). Hoskens y De Boeck consideran
lo cual es un logaritmo de momios, comparando la probabilidad del patrón de respuestas (k, k') con el patrón (0,0). En el caso de independencia local, se puede derivar de las Ecuaciones (1) y (2):
Para modelar dependencia local del tipo combinación constante en los ítems i e i′, que en nuestros datos tienen cuatro categorías de respuesta, Introducimos dos nuevos parámetros: βii′(L) y βii′(H). El primer parámetro entra en la ecuación si ambas respuestas caen en una de las dos categorías más altas (es decir, k,k′ ≥ 2), el segundo si ambas respuestas caen en la categoría más alta (es decir, k=k′ = 3). En específico, se distinguen los siguientes tres casos:
- (a)
si k < 2 o k′ < 2, entonces:
- (b)
si k ≥ 2 o k′ ≥ 2 y no k= k′ = 3, entonces:
- (c)
Los valores negativos para el parámetro βii′(L) aumentan la probabilidad de que la persona conteste en ambos ítems “familiarizado” o “muy familiarizado” (en comparación con el GPCM original). Los valores positivos reducirían dicha probabilidad. El parámetro βii′(H) tiene un efecto adicional y similar a la probabilidad de que la persona conteste en ambos ítems “muy familiarizado”. En los resultados se obtuvieron valores negativos para ambos parámetros en el análisis de todas las escalas.
Es posible extender el modelo más, según las mismas líneas, para Incorporar Interacciones de orden superior. No obstante, para el presente estudio consideramos únicamente Interacciones por pares entre los ítems; es decir, aunque son tres o más ítems de la escala que se refieren a un mismo subtema, el modelo solo Incluye la Interacción entre cada par de estos ítems.
Estimación. Se estimó el modelo en un marco bayeslano, considerando la distribución posterior de los parámetros, condicional a los datos. El teorema de Bayes relaciona la distribución posterior con la función de verosimilitud y la distribución previa:
donde α es un vector con los grados de discriminación de todos los ítems, β un vector con los umbrales de todos los ítems y los parámetros de Interacción (dependencia local), θ el vector de parámetros de todas las personas y y representa los datos observados.
La función de verosimilitud para el modelo se describió en los párrafos anteriores; para la distribución previa especificamos que cada parámetro fuera Independientemente extraída de la siguiente forma:
Se Implementó un algoritmo de Metropolis23, 24 con el fin de obtener una muestra de la distribución posterior. Se corrió el algoritmo con cuatro cadenas de Markov, inicializados con valores extraídos aleatoriamente de la distribución previa. Después de 5,000,000 Iteraciones, se evaluó la convergencia de las cadenas a través del estadístico Rˆ de Gelman y Rubín38 calculado sobre la última mitad de las cadenas; en todos los análisis, se obtuvo Rˆ<1.20 para cada parámetro.
Evaluación. Se evaluó la bondad de ajuste de cada ítem a través de comprobaciones predictivas posteriores (PPCs).17 Se utilizó como medida de discrepancia:
Para calcular el valor en t, se divide el grupo total de personasen 10subgruposde Igual tamaño, con base en θ; pgk es la proporción de personas en el grupo g que da la respuesta k al ítem i y Egk es la probabilidad, bajo el GPCM, de que una persona con θ igual a la media del grupo g responda en la categoría k. Si el ítem i no se incluye en un grupo de ítems con dependencia local, Egk se calcula a partir de la Ecuación (1); en el caso de que el ítem sí se afecte por la dependencia local con otros ítems, Egk se obtiene considerando todos los patrones de respuesta en los ítems en el grupo y calculando la probabilidad marginal de la respuesta k en el ítem i a través de la suma de las probabilidades entre todas las categorías de respuesta del (los) otro(s) ítem(s).
Cuestionario final. Ítems del cuestionario final con sus índices psicométricos.
| Ítem | λi | αi | βi1 | βi2 | βi3 | PPPi | |
|---|---|---|---|---|---|---|---|
| Interacción básica con el sistema operativo (12 ítems) | |||||||
| 1. | Utilizar la barra de tareas | 0.62 | 1.72 | -2.76 | -1.68 | 0.10 | 0.42 |
| 2. | Ver/ocultar la barra de herramientas | 0.63 | 1.63 | -2.85 | -1.27 | 0.18 | 0.45 |
| 3. | Acceder a la configuración de la computadora través de la función de inicio | 0.60 | 1.31 | -2.64 | -1.35 | -0.33 | 0.32 |
| 4. | Crear un acceso directo a un programa en tu escritorio | 0.66 | 2.08 | -2.49 | -1.47 | -0.47 | 0.45 |
| 5a. | Comprobar el espacio libre disponible | 0.67 | 1.48 | -2.48 | -1.03 | 0.10 | 0.40 |
| 5b. | Comprobar las propiedades de un archivo | 0.70 | 1.71 | -2.57 | -0.97 | -0.02 | 0.37 |
| 6. | Añadir una carpeta utilizando el Explorador de Windows | 0.61 | 1.31 | -2.54 | -0.69 | 0.19 | 0.14 |
| 7. | Comprimir y descomprimir archivos | 0.67 | 1.31 | -1.61 | -0.15 | 0.49 | 0.43 |
| 8. | Vaciar la papelera de reciclaje | 0.56 | 1.72 | -2.43 | -1.59 | -1.01 | 0.04 |
| 9a. | Cambiar la calidad de impresión | 0.59 | 0.98 | -2.76 | -1.02 | 0.58 | 0.31 |
| 9b. | Establecer una impresora predeterminada | 0.60 | 0.93 | -2.48 | -0.65 | 0.87 | 0.06 |
| 10. | Utilizar las teclas “alt” y “control” para acceder las opciones de menú | 0.62 | 1.36 | -2.47 | -1.01 | 0.13 | 0.40 |
| Fundamentos del correo electrónico (5 ítems) | |||||||
| 1a. | Configurar la libreta de direcciones | 0.59 | 0.75 | -3.30 | -0.15 | 0.71 | 0.13 |
| 1b. | Configurar buzones | 0.70 | 1.39 | -2.25 | 0.08 | 0.74 | 0.21 |
| 2. | Eliminar un archivo adjunto | 0.64 | 2.10 | -2.71 | -1.59 | -0.83 | 0.14 |
| 3. | Imprimir un mensaje | 0.74 | 2.32 | -2.10 | -1.25 | -0.45 | 0.47 |
| 4. | Crear y adjuntar una firma a un mensaje de correo electrónico | 0.54 | 0.95 | -1.76 | 0.31 | 0.36 | 0.06 |
| Procesador de texto (7 ítems) | |||||||
| 1. | Guardar un documento como un tipo de archivo diferente | 0.58 | 1.26 | -2.58 | -1.21 | -0.74 | 0.17 |
| 2a. | Comprobar la gramática de un documento | 0.55 | 0.93 | -3.92 | -1.59 | -0.41 | 0.29 |
| 2b. | Activar y desactivar la función de autocorrección | 0.70 | 1.43 | -2.47 | -0.47 | 0.33 | 0.43 |
| 3a. | Introducir viñetas | 0.61 | 0.97 | -3.12 | -1.35 | -0.10 | 0.32 |
| 3b. | Insertar encabezados o pies de página | 0.61 | 1.22 | -2.95 | -1.67 | -0.04 | 0.41 |
| 3c. | Establecer sangrías | 0.66 | 1.55 | -2.81 | -1.28 | 0.51 | 0.16 |
| 4. | Forzar un salto de página | 0.71 | 1.82 | -1.95 | -0.54 | 0.14 | 0.11 |
| Hojas de cálculo electrónicas (8 ítems) | |||||||
| 1. | Etiquetar las hojas de cálculo | 0.69 | 1.40 | -1.72 | 0.09 | 0.54 | 0.18 |
| 2. | Cambiar el tamaño de las celdas con las especificaciones | 0.73 | 1.78 | -1.77 | -0.34 | 0.26 | 0.13 |
| 3. | Combinar celdas adyacentes | 0.72 | 1.64 | -1.75 | -0.25 | 0.03 | 0.03 |
| 4a. | Comprobar si una fórmula es incorrecta | 0.76 | 2.02 | -0.99 | 1.04 | 1.93 | 0.21 |
| 4b. | Escribir una función en una tabla (por ejemplo, promedio) | 0.77 | 1.96 | -1.11 | 0.04 | 0.89 | 0.13 |
| 5. | Fijar una celda | 0.81 | 2.75 | -1.28 | -0.11 | 0.69 | 0.61 |
| 6. | Ocultar/Mostrar columnas y filas | 0.73 | 1.80 | -1.75 | -0.48 | 0.20 | 0.17 |
| 7. | Establecer las opciones de pantalla dividida | 0.73 | 1.59 | -1.32 | 0.35 | 0.78 | 0.11 |
| Uso de Internet (8 ítems) | |||||||
| 1a. | Agregar a favoritos un sitio web | 0.68 | 1.08 | -2.80 | -0.45 | 0.72 | 0.18 |
| 1b. | Editar o modificar favoritos | 0.71 | 1.40 | -2.32 | 0.25 | 1.76 | 0.27 |
| 2a. | Cambiar el motor de búsqueda | 0.69 | 1.23 | -1.67 | -0.18 | 0.63 | 0.08 |
| 2b. | Buscar con palabras clave | 0.67 | 1.37 | -2.10 | -0.91 | 0.43 | 0.07 |
| 3. | Actualizar una página | 0.76 | 2.69 | -1.87 | -1.05 | -0.33 | 0.12 |
| 4. | Detener la carga de una página | 0.75 | 2.21 | -1.75 | -0.89 | -0.12 | 0.07 |
| 5a. | Subir un archivo | 0.59 | 0.74 | -2.79 | -0.17 | 1.17 | 0.04 |
| 5b. | Compartir un archivo | 0.62 | 0.97 | -2.48 | 0.13 | 1.94 | 0.03 |
| Mantenimiento del sistema y seguridad (5 ítems) | |||||||
| 1a. | Utilizar el antivirus y mantenerlo actualizado | 0.66 | 0.96 | -2.23 | -0.03 | 1.33 | 0.01 |
| 1b. | Identificar las acciones que ponen en riesgo de adquirir una infección por virus | 0.69 | 1.26 | -2.05 | 0.12 | 1.73 | 0.01 |
| 2a. | Limpiar el disco | 0.86 | 3.22 | -1.27 | -0.12 | 0.59 | 0.66 |
| 2b. | Desfragmentar el disco | 0.78 | 2.12 | -0.94 | 0.80 | 1.19 | 0.16 |
| 3. | Eliminar archivos temporales | 0.77 | 2.20 | -1.34 | -0.35 | 0.30 | 0.14 |
λi: carga factorial estandarizada en el modelo del factor común; ai: grado de discriminación en el GPCM; βi1, βi2, βi3: grado de dificultad para los tres umbrales en el GPCM; PPPi: valor p predictivo posterior asociado con la PPC que evalúa la bondad del ajuste del ítem.
Los ítems con el mismo número (por ejemplo, 5a y 5b) pertenecen a un subgrupo en el cual se modela covarianza entre residuales o dependencia local. Los resultados se obtuvieron del análisis de los datos de la cohorte 2011-2012.