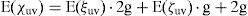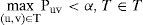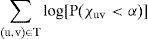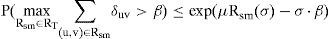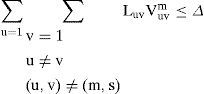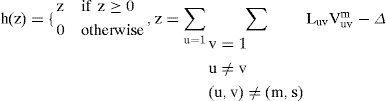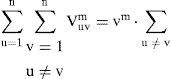Wireless Sensor Networks (WSN) is widely used as an effective medium to integrate physical world and information world of Internet of Things (IOT). While keeping energy consumption at a minimal level, WSN requires reliable communication. Multicasting is a general operation performed by the Base Station, where data is to be transmitted to a set of destination nodes. Generally, the packets are routed in a multi-hop approach, where some intermediate nodes are also used for packet forwarding. This problem can be reduced to the well-known Steiner tree problem, which has proven to be NP-complete for deterministic link descriptors and cost functions. In this paper, we propose a novel multicast protocol, named heuristic algorithms for the solution of the Quality of Service (QoS) constrained multicast routing problem, with incomplete information in Wireless Sensor Networks (WSN). As information aggregation or randomly fluctuating traffic loads, link measures are considered to be random variables. Simulation results show that the Hop Neural Networks (HNN) based heuristics with a properly chosen additive measures can yield to a good solution for this traditionally NP complex problem, when compared to the best multicast algorithms known.
It is well known that wireless sensor networks (WSN) is a self-organization wireless network system constituted by numbers of energy-limited micro sensors under the banner of Internet of Things (IOT). Nowadays, WSN is widely used as an effective medium to integrate physical world and information world of IOT [1-3]. A wireless sensor network consists of spatially distributed autonomous sensors to cooperatively monitor physical or environmental conditions, such as temperature, sound, vibration, pressure, motion or pollutants [4-6]. Multicast service is an efficient model. It can optimized the network resource and adapt to the bandwidth of wireless sensor network. Thus, the performance of the IOT will be improved [7-9]. The key service of the WSN is Multicast routing for the problem of multicast routing, generally we build a multicast tree with the least cost. And the cost of the Steiner tree is lowest, therefore, Sterner tree is regard as the best method to solve multicast correspondence [10-13]. In this paper, we present a kind of new multicast routing algorithm for application of Internet of things [14-17].
2The fundamental of Steiner treeBefore discussing the multicast algorithms, we need to introduce some notations [18-23]. A network is represented as a graph N=(VN,EN), where VN is the set of nodes and EN ⊂ VN x VN is the set of edges. The average number of edges that depart from a node is referred to as out degree. Over the set of edges we define the two functions delay Delay: EN → R+\{0} and cost Cost: EN →{1}.The delay and the cost of a path are defined as the sum of the delay or cost of all the edges of the path.
The multicast receivers are referred to as multicast group and Q ∈ VN is the source of the multicast group. Computing the Steiner Tree is an NP-complete problem [5-8]. The main contribution of this paper is the method to transform the original probabilistic link descriptors, which reduces the tree selection to a deterministic problem. Then we apply the HNN which then ensures fast convergence to a suboptimal solution.
3The packet transmission model for multicast routingWe model the network as a graph G(E, V, δuv,(u,v)∈E), where E denotes the set of edges, V the set of vertices and δuv is the descriptor of the link (u, v) ∈ E that can be delay, bandwidth or any other type of metric. The information source, typically a Base Station, is denoted by s ∈ V and the set of multicast nodes by M={m1. m2,…, mN} ⊂ V. We assume that equal transmission power is used by each node in the network
The probability of successfully packet reception is calculated by using the Rayleigh fading model as follows:
Where Θ is a hardware related threshold, σz2 represents the noise power, duv denotes the distance between node u and v, and γ is the path loss exponent.
We assume communication scheme where receiver nodes use acknowledgement packets (ACK), and we assume that the number of ACKs are not limited. Table I shows a sequence of packet transmissions between source node u and destination v, where v can either receive or fail to receive the data packet, which cases are denoted by 1 and 0 respectively. The ACK can also be decoded correctly by u or not. The communication ends when both packets are received correctly.
Let us denote the event of data reception followed by no ACK reception – first column – with ξ and the event of unsuccessful data reception – second column – with ζ. The corresponding distributions can be expressed as follows
Let us define χ as the random variable corresponding to the power consumption over the link (u, v) until successful data transmission
The expected value of the transmit power over link (u, v) then is
In this case the distribution of the delay δuv on link (u, v) can be calculated as follows:
4Multicast routing with incomplete informationBecause of incomplete information about the link states in the network, link metrics δ(u,v)are described by random variables. These link metrics are not additive thus the deterministic multicast tree search algorithms are not applicable. We transform the random link metrics into deterministic descriptors which can be fed to the traditional or heuristic algorithms. In order to do this, we introduce two types of common requirements for designing a multicast tree: a bottleneck type and an end-to-end additive type requirement.
We formulate the deterministic bottleneck Steiner tree problem as
where T is the set of all trees containing{s} □M, Puv is the transmitter power consumed during transmission, and α is the limit that we do not want to exceed in order to economize battery power.
The deterministic end-to-end additive type problem can be formulated as
Where Rsm is a path from s to m∈M in T, and Luv is an additive metric with QoS requirement β. Although no polynomial algorithm is known for finding Steiner trees but suboptimal algorithms exist. In the next subsections we extend the problem to the case of random link descriptors.
4.1Bottleneck type requirementWhen using random link descriptors, the optimal multicast tree problem for bottleneck measure is defined as follows
Ifχuv<α holds for the maximal χuv then it holds for all the values in the tree, which yields
Where we used the independence property of these random variables.
This results in the following objective function over additive measures:
Which is well suited for the later introduced HNN.
4.2End-to-end additive requirementIn the traditional multicast setting with incomplete information we search for a tree such that the probability that the delay of the longest route being smaller than β is maximal
The WSN setting requires us to also minimize the transmit power used by the network in order to prolong node life span.
To incorporate this additional constraint we define the following optimization problem, and by increasing the κ parameter in our algorithm we converge to the optimal tree:
In the optimal Steiner tree there are common links between paths for different multicast nodes, meaning that the random measures for different paths statistically dependent, which can be described by the joint distribution function.
We can use large deviation theory to approximate the previous probability
for all σ, where
and
The optimal σ value can be calculated by solving
for a given route from s to mjº
We are looking for the tree approximated by Equation (18) and our suboptimal solution will be the one with the minimal ∑(u,v)∈T Cuv for which
and translates Equation (17) into
which is in the form of the well-known Constrained Steiner Tree5, for which a Discrete Hop Neural Network (DHNN) based approximation is given in Section 5.
For a given β parameter then we can find better and better trees by increasing κ in an iterative or gradient fashion, which yields Algorithm 1.
Algorithm 1 find optimal tree for end-to-end requirement
Require: G, κ=0, β>1
Repeat
T=find tree with HNN (G,κ,β)
If T is found then
Decrease κ
Else
Increase κ
End if
Until no significant increase in performance
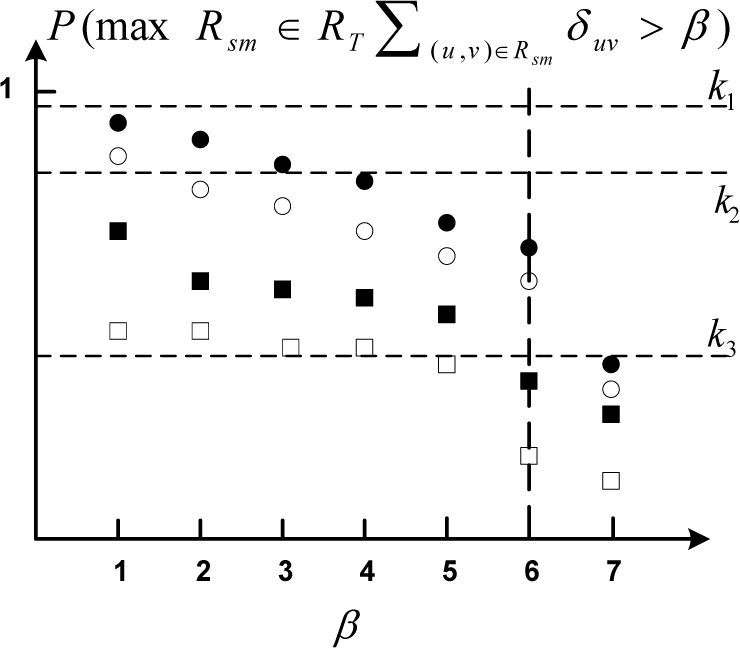
Figure 2 illustrates a case, when there are two sets of trees having equal longest path delay properties – from each set we choose based on the sum of transmit powers –. Assume that it is required that the probability of the longest route exceeding 6 is to be maximized. At the first step of the algorithm both of the routes can guarantee a longest delay of 6 with probability κ1, we can decrease κ. In the second step this holds again while in the third step there is only one tree below delay 6. This way we can determine the minimal value for κ for which there exists at least one tree.
5Solution by hop netIn this section we first describe the structure of the HNN that is capable of approximating the multicast tree for deterministic link measures.
Hop Networks in general have successfully been applied to combinatorial optimizations and solved many practical tasks 7-10. So this problem’s solution can be approximated by HNN5, 11-12 as well, based on the energy function proposed in 5, 11. We use DHNN, because it is reported to be computationally more effective 13-15. The energy function is a weighted linear combination of terms which are describing the objective function to be minimized E1m and the press of the constraint function subjected by the minimization task E5m. The feasibility of the solution is guaranteed by the neuron update selection rule, which ensures transitions to only valid candidate solutions. The HNN searches for routes and for a tree solution we use the union of the chosen routes. Thus we implicitly assume that the union of routes satisfying the constraints is a good Steiner tree. Every neuron represents an edge in the graph 5 and the neuron’s output variable is noted by Vuvm which is defined as
Cost and constraint terms: The cost value for the edge (u, v) ∈ RsM is noted by Cuv.
Note that the cost term is dependent on the edges previously elected in the multicast tree, so edge are reuse are preferred.
E5m is the term which presses the constraint function to be true. Luv>0 is the delay value on the link (u, v).
We use the same approach as [5] for dealing with inequality constraints; introduce a linear programming type neuron.
Neuron selection rule for DHNN: We initialize the network, that there is only one edge in the chosen path: Vuv=1, if (u, v)=(s, m) 0otherwise, □(u, v) □ Rsm. We update exactly 3 neurons for one discrete time step as follows: Selection A (edge splitting): choose an edge which is in the path (u, v) □ Rsm, choose two edges which are not in the path, but join at a common node and start and terminate at u and v. (u, w), (w, v) /□ Rsm. Selection B (edge joining): choose two edges which are in the path as (u, w), (w, v) □ Rsm, thus (u, v) /□Rsm.
Either A or B used, update the three neurons (flip Vuv, Vuw, Vwv triangle) if the state transition yields to a better energy state of the network. Use A and B alternatively until no state transition occurred. This selection rule ensures that if we started from a valid route we end up in a valid route from s to m. Cost and constraint terms for DHNN: The conventional energy function of the discrete Hop model is
We transform the neurons output variable to a column vector with elements of {−1,+1} for the DHNN structure. We treat treatVuvm an element of a series of matrices: from the mth matrix the element at the uth row and the vth column. We have N nodes in the graph and we read out Vm column wise, u, v=1, …, N
We define and ∑(u,v) ≠ (m,s) for the elimination of the terms “u=v” and” (u, v)=(m, s)” respectively by the multiplication with these matrices.
For the term E1m after the transformation the parameters of Equation (30) will be
Similarly for E5m the calculation can be done thus getting the parameters Wm,i, bm,i. The energy function of the HNN as in (30) is
6Performance analysisThe T1 and the T2 objective functions were evaluated by exhaustive search and the HNN based algorithm on a graph with the following parameters [8-13]: The size of the network N=8, the Rayleigh channel parameters were chosen to typical or better indoor environment: γ=3, g=1, θ=10, σ2=1. The positions of the nodes were randomly generated according to i.i.d. uniform distributions in the unit square. The group of the multicast nodes consisted 3 randomly chosen nodes. We have performed the exhaustive search by enumerating all the possible trees and evaluating the objective function on the trees. We have compared the results of the HNN algorithm to the exhaustive solution. For the T2 objective function. We have evaluated the performance given by the Chertoff bound and also the corresponding theoretical probability by performing convolutions on the known distributions.
The HNN algorithm can find almost always the optimal solution for the T1 objective function of the bottleneck problem [11-17]. This figure is typical in the sense that throughout the simulation runs we have seen the same behavior. For the T2 objective function the figures show the probability of meeting the delay constraint and the found tree’s energy consumption [18-23].
It can be seen in Figure 3 that the HNN algorithm can find almost always the optimal solution for the T1 objective function of the bottleneck problem. This figure is typical in the sense that throughout the simulation runs we have seen the same behavior [14-17].
In Figure 4 a case can be seen at β=4 that the HNN finds a solution that satisfies the delay constraint with a higher probability in the expense of larger transmit power [18-20].
It can be seen in Figure 5 for small β values it can happen that individual link measures approximated by the Chernoff bound could not give a positive probability of meeting the delay constraint; hence the HNN could not supply a valid tree [21-23].
7ConclusionWSN is widely used as an effective medium to integrate physical world and information world of IOT. While keeping energy consumption at a minimal level, WSN requires reliable communication. For networks sizes as small as 10 nodes exhaustive search is infeasible so heuristics are needed to approximate a good solution. We have shown that a HNN based heuristics with a properly chosen additive measures can yield to a good solution for this traditionally NP complex problem. Because of the conservativeness of the Chernoff approximation the delay bound is always met in the expense of consuming more transmit power.
This work is supported by “863” project plan of China (No.2007AA01Z188), National Natural Science Foundation of China (No.61170173 & No.60773073 & No.61202169 & No.61001174), Program for New Century Excellent Talents in University of China (No.NCET-09-0895), Key project of Ministry of Education of China (No.208010) Tianjin Natural Science Foundation (No. 10JCYBJC00500), Tianjin Key Natural Science Foundation (No. 13JCZDJC34600).