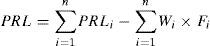Fuzzy Analytic Hierarchy Process for Risk Assessment to General-assembling of Satellite

Abstract

With a fuzzy analytic hierarchy process, the hierarchy of risk factors in satellite general-assembling process is established, based on which, the weights of various risk factors are determined one by one. Furthermore, the risk factors are quantitatively analyzed, and the comprehensive risk assessment model is established in the end. Taking a satellite model as an example, the risks in the satellite general-assembling process are assessed comprehensively, and the risk levels are quantitatively measured. The factors are sorted according to their impact capabilities to the overall risk level, and the key points of risk control for satellite general-assembling process is clarified. Results obtained from the analysis to risk sub-factors suggested that experience and techniques, narrow space and production rhythm are more detrimental to process risk than any other sub-factors. The results also show that the risk could be mitigated, provided that the effectiveness of engineering measures against deficiencies in the most influential (sub-)factors is maintained. The rationality and feasibility of the proposed method model is proved by the engineering application, which provide the effective technical support for the risk control in satellite general-assembling process.

1

Introduction

With the continuous development of the scientific technology, the function intensity of the spacecrafts, taking the satellite as the typical symbol, is improving continuously. The duration in orbit has been lengthened, and the orbital environment profile has become tougher, which proposes the strict requirement for the general-assembling process to assure the product without the slightest injury. Once there is any abnormal state appearing in the satellite general-assembling process, it is most likely to cause irreversible damage to the product, resulting in a huge irreparable economic loss. Thus, it is necessary to assess the safety level of the satellite general-assembling process, and to analyze the factors that affect the safety of the satellite general-assembling process, so as to take effective measures timely to control risks.

However, the satellite general-assembling process is complicated system engineering, reflected in the following facts that:

• (1)

  With limitation of operation space. There are many component, equipment, cable, and pipe of different systems assembled in the spacecrafts, with features of a high concentration, little open space, and poor visibility, some of which might even be in blind area.

• (2)

  With larger amount of manual work. There is little operation space in the spacecrafts, and the equipment, cable, and pipe are assembled with a high concentration, resulting in low mechanization and automation of spacecraft assembly. A large amount of work should be done manually, so human error is one of the main causes for the spacecrafts accidents [1].

• (3)

  With many procedures, and frequent cross-working. The general-assembling process involves the fitter assembling and installation, electricity installation, initiating explosive device installation, thermal control implementation, measurement of installation precision, sealing performance test, quality characteristics test, mechanical environment test and thermal vacuum test, including many procedures, and cross working. To complete all the work, many kinds of specialties and technologies should be applied and collaborated comprehensively, which proposes extremely high requirement to the procedures conversion.

It has been found that poor work conditions and strong restrictions for task are more detrimental to system risk of the satellite assembly process. It was also shown that ignoring organization when implementing the series of tasks could lead to significantly higher system risks.[1] However, limited research or practice has been performed considering quantification or semi-quantification to the impacts of the risk factors on the risk of satellite general-assembling process. Additionally and especially, various risk factors’ influences to the overall risk level should be considered due to the requirement of the features of tight coupling of many factors in the general-assembling process and the complexity of the satellite general-assembling process, so as to get the comprehensive measurement of the accident risk, and assure that the proposed method and model can be executed feasibly in the project. Thus, some analysis methods based on system engineering [2] would have advantages to explore the quantitative or semi-quantitative rules embedded in the qualitative argument we have obtained, by establishing hierarchical model and integrating multiple influential factors.

The main objective of this paper is to quantify the effect of multiple risk factors and risk control measures in satellite general-assembling process. Aiming at this, fuzzy Analytic Hierarchy Process (FAHP) is applied in the risk assessment of the satellite general-assembling process in this article. Taking a satellite model as an example, the risk analysis hierarchy model of the general-assembling is established, and then the safety level of the general-assembling process is comprehensively assessed. Also, the weights of various risk factors which are likely to cause accident are defined, and sensitivity analyses are performed to assess the effect of the most influential factors on the overall risk level. The results provide the references for taking the risk control measures in the general-assembling process.

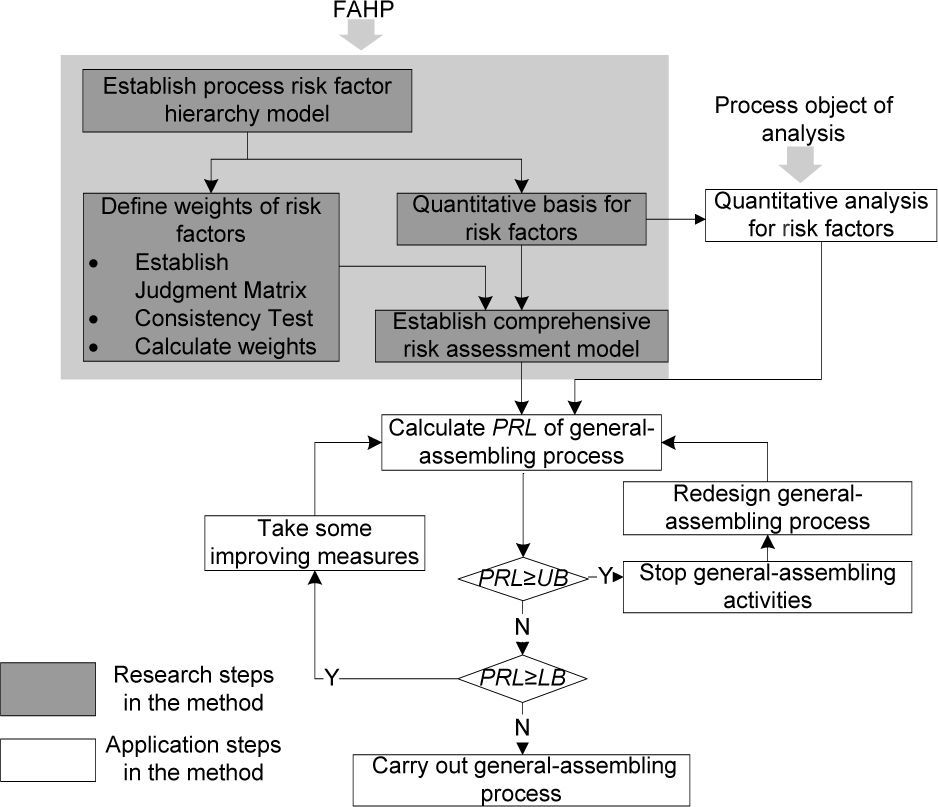
2

The safety assessment method in the satellite general-assembling process based on FAHP

The Analytic Hierarchy Process (AHP) [3] was proposed in 1970s by T. L. Saaty, an American expert in Operational Research. By the means of AHP, the non-quantitative events in system engineering are converted to quantitative analysis, which reduces the difficulty and working load of the analysis, and is widely applied in the fields of benefit analysis and risk assessment [4,5]. C. Lopez et al [6] proposes a multicriteria decision-making methodology by AHP, which will enable the prioritization of risks in Ambient intelligence (Aml) projects according to their level of threat. At present, there have been plenty of research that blend fuzzy logic, which is a popular method of incorporating uncertain parameters into the decision-making process, with analytic hierarchy process to form a model for risk assessment. Those risk assessment models are widely applied to multiple fields such as floor water invasion in coal mines [7], oil and gas offshore wells [8], electronic engineering [9,10], information technology projects [11], green initiatives in the fashion industry [12], food supply chains[13], and especially construction engineering related to such as railways, bridges, water plants, and power plants [14~17]. Most of the fuzzy-AHP methods suggest each risk factor in a hierarchical framework is expressed as a fuzzy number, which is a combination of the likelihood of a failure event and the associated failure consequence, and AHP is used to estimate weights required for grouping hazards.

The AHP and the Fuzzy Theory is combined in this article by a different means. Moreover, the FAHP is applied in the safety assessment of the satellite general-assembling process, which is not experienced so far. The method includes 4 procedures as follows:

• (1)

  Establish the risk factor hierarchy model;

• (2)

  Define the weights of risk factors;

• (3)

  Define the quantitative basis for risk factors;

• (4)

  Establish the comprehensive risk assessment model.

With the instructions of above procedures, the assessment flow of the calculation of the process risk level (PRL) is shown in Figure 1. Comparing the PRL with the upper bound (UB) and the lower bound (LB) of the comprehensive risk level of satellite general-assembling process, if

Figure 1.

Risk assessment flow of the satellite general-assembling process based on FAHP.

• •

  PRL≥UB, the general-assembling should be stopped, and the general-assembling system should be redesigned;

• •

  LB≤PRL<UB, improving measures should be taken, and then thePRL should be recalculated;

• •

  PRL<LB, the general-assembling process can be carried out.

3

Hierarchy model of risk factors

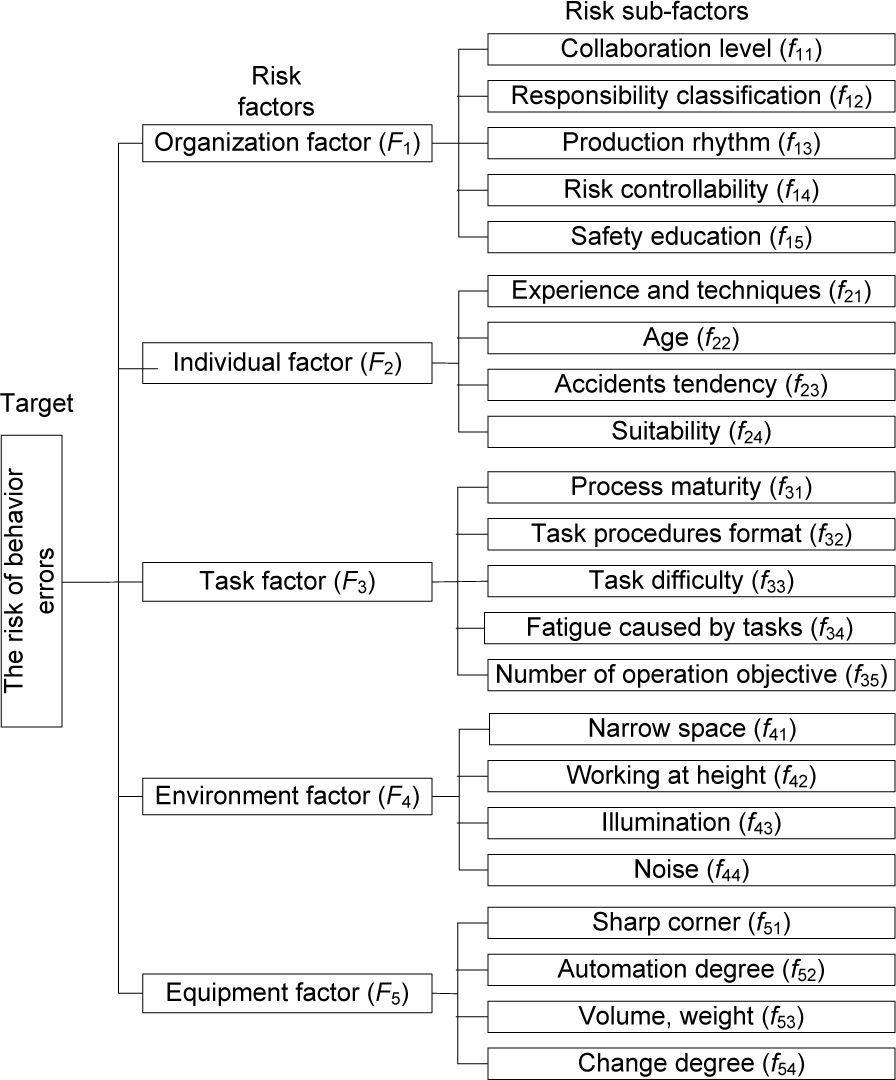
The identification of risk factors is the premise of risk assessment. According to the characteristics of satellite general-assembling process, with the combination of existing data and expert experience, the factors which might cause accident in the general-assembling process could be classified into 5 categories according to their sources, i.e. risk factors set F = {F₁, F₂, F₃, F₄, F₅ }, among which F₁ represents the organization factor, F₂ represents individual factor, F₃ represents task factor, F₄ represents environment factor, and F₅ represents equipment factor [18]. Each category of the above 5 categories also represents one sub-factor set, with the expression of f, i.e. F_i = { f_i1, f_i2, …, f_ij }, i =1, 2, …, 5. The risk factors in the satellite general-assembling process and the hierarchy is shown in Figure 2.

Figure 2.

The hierarchy of the risk factors in satellite general-assembling process.

In order to support the risk assessment and control, based on the hierarchy of the risk factors shown in Figure 2, a comprehensive risk assessment method is established with the application of FAHP, including the important procedures of the determination of weights of various risk factors, the quantitative analysis of risk factors, and the establishment of the comprehensive risk calculation model.

3.1

The determination of risk factor weight based on fuzzy mathematics

Based on the hierarchy model of risk factors, the weight is determined for each risk factor, based on fuzzy mathematics. It is achieved by taking 3 steps as follows.

Step 1: establishment of the judgment matrix.

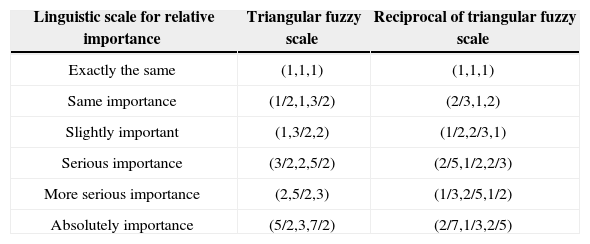
The values of various factors in the judgment matrix reflect the relative importance of various factors. If it is included in the measurement of the comprehensive risk level, the measurement result can be more reasonable. A fuzzy linguistic scale is present here, which is characterized by triangular fuzzy numbers for the comparison between two alternatives, so that the relative importance of various factors can be represented.

The definition to triangular fuzzy numbers is described as: given the F(R) as a full fuzzy set at R, then we take M as a triangular fuzzy number. If the membership function of M is described as μ_M, with p≤m≤q, then μ_M is represented as triangular, and triangular fuzzy number is usually noted briefly as M(p, m, q). One of the common fuzzy linguistic scale method [19] is adopted to comparison between risk factors and shown in Table 1.

Table 1.

Linguistic scale for relative importance.

Linguistic scale for relative importance	Triangular fuzzy scale	Reciprocal of triangular fuzzy scale
Exactly the same	(1,1,1)	(1,1,1)
Same importance	(1/2,1,3/2)	(2/3,1,2)
Slightly important	(1,3/2,2)	(1/2,2/3,1)
Serious importance	(3/2,2,5/2)	(2/5,1/2,2/3)
More serious importance	(2,5/2,3)	(1/3,2/5,1/2)
Absolutely importance	(5/2,3,7/2)	(2/7,1/3,2/5)

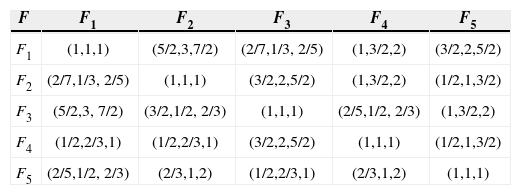
According to the risk factors hierarchy, through comparison of the importance of each pair of risk factors, the judgment matrix of the 5 categories of risk factors in the satellite general-assembling is shown in Table 2.

Table 2.

Judgment matrix for risk factor in general-assembling process.

F	F1	F2	F3	F4	F5
F1	(1,1,1)	(5/2,3,7/2)	(2/7,1/3, 2/5)	(1,3/2,2)	(3/2,2,5/2)
F2	(2/7,1/3, 2/5)	(1,1,1)	(3/2,2,5/2)	(1,3/2,2)	(1/2,1,3/2)
F3	(5/2,3, 7/2)	(3/2,1/2, 2/3)	(1,1,1)	(2/5,1/2, 2/3)	(1,3/2,2)
F4	(1/2,2/3,1)	(1/2,2/3,1)	(3/2,2,5/2)	(1,1,1)	(1/2,1,3/2)
F5	(2/5,1/2, 2/3)	(2/3,1,2)	(1/2,2/3,1)	(2/3,1,2)	(1,1,1)

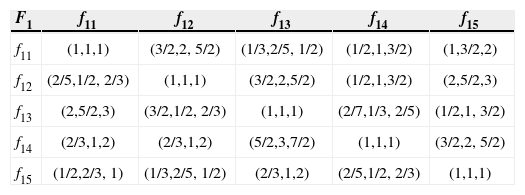
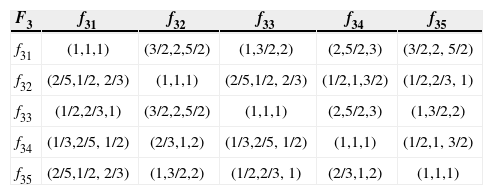
Similarly, the judgment matrix of risk sub-factors can be obtained respectively as Table 3 ~ Table 7.

Table 3.

Judgment matrix for sub-factor of organization.

F1	f11	f12	f13	f14	f15
f11	(1,1,1)	(3/2,2, 5/2)	(1/3,2/5, 1/2)	(1/2,1,3/2)	(1,3/2,2)
f12	(2/5,1/2, 2/3)	(1,1,1)	(3/2,2,5/2)	(1/2,1,3/2)	(2,5/2,3)
f13	(2,5/2,3)	(3/2,1/2, 2/3)	(1,1,1)	(2/7,1/3, 2/5)	(1/2,1, 3/2)
f14	(2/3,1,2)	(2/3,1,2)	(5/2,3,7/2)	(1,1,1)	(3/2,2, 5/2)
f15	(1/2,2/3, 1)	(1/3,2/5, 1/2)	(2/3,1,2)	(2/5,1/2, 2/3)	(1,1,1)

Table 4.

Judgment matrix for sub-factor of individual.

F2	f21	f22	f23	f24
f21	(1,1,1)	(2,5/2,3)	(1/2,1,3/2)	(1,3/2,2)
f22	(1/3,2/5,1/2)	(1,1,1)	(1/2,2/3,1)	(1/2,1,3/2)
f23	(2/3,1,2)	(1,3/2,2)	(1,1,1)	(1,3/2,2)
f24	(1/2,2/3,1)	(2/3,1,2)	(1/2,2/3,1)	(1,1,1)

Table 5.

Judgment matrix for sub-factor of task.

F3	f31	f32	f33	f34	f35
f31	(1,1,1)	(3/2,2,5/2)	(1,3/2,2)	(2,5/2,3)	(3/2,2, 5/2)
f32	(2/5,1/2, 2/3)	(1,1,1)	(2/5,1/2, 2/3)	(1/2,1,3/2)	(1/2,2/3, 1)
f33	(1/2,2/3,1)	(3/2,2,5/2)	(1,1,1)	(2,5/2,3)	(1,3/2,2)
f34	(1/3,2/5, 1/2)	(2/3,1,2)	(1/3,2/5, 1/2)	(1,1,1)	(1/2,1, 3/2)
f35	(2/5,1/2, 2/3)	(1,3/2,2)	(1/2,2/3, 1)	(2/3,1,2)	(1,1,1)

Table 6.

Judgment matrix for sub-factor of environment.

F4	f41	f42	f43	f44
f41	(1,1,1)	(1,3/2,2)	(3/2,2,5/2)	(2,5/2,3)
f42	(1/2,2/3,1)	(1,1,1)	(1,3/2,2)	(3/2,2,5/2)
f43	(2/5,1/2,2/3)	(1/2,2/3,1)	(1,1,1)	(1/2,1,3/2)
f44	(1/3,2/5,1/2)	(2/5,1/2,2/3)	(2/3,1,2)	(1,1,1)

Table 7.

Judgment matrix for sub-factor of equipment.

F5	f51	f52	f53	f54
f51	(1,1,1)	(3/2,2,5/2)	(1,3/2,2)	(1/2,1,3/2)
f52	(2/5,1/2,2/3)	(1,1,1)	(1/2,1,3/2)	(2/5,1/2,2/3)
f53	(1/2,2/3,1)	(2/3,1,2)	(1,1,1)	(1/2,1,3/2)
f54	(2/3,1,2)	(3/2,2,5/2)	(2/3,1,2)	(1,1,1)

Step 2: consistency test

In order to assure the consistency of the judgment matrix, the consistency test should be carried out to the judgment matrix. The test method described in Reference [20] is adopted, which is different from the conventional AHP test method, for which through calculation of the consistency ratio (CR) it is tested whether the judgment matrix has a satisfactory consistency. The test method used in this article goes like the following: If the latent roots λ of the judgment matrix composed of the triangular fuzzy number are between 0 and 1, it is concluded that the judgment matrix has the satisfactory consistency; if λ<0, it should be considered to readjust the values of factors of the judgment matrix, until the judgment matrix has the satisfactory consistency.

By the test method provided in Reference [20], it is shown that the above judgment matrix has the satisfactory consistency.

Step 3: weight calculation for risk factors

There are many calculation methods for FHAP weight [21]. An extent analysis method [22] is used to calculate and judge the weights of risk factors in this article. Through calculation, the fuzzy comprehensive values resulting from extended analysis to the 5 categories of risk factors in the satellite general-assembling process are shown as follows:

The following can be obtained through further calculation:

Finally, the weight vectors of the 5 categories of risk factors in general-assembling process are obtained, i.e.

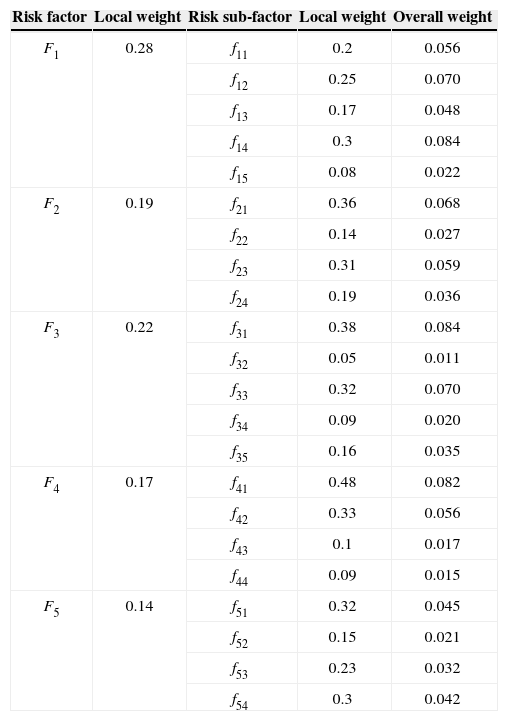
W_F = (0.28, 0.19, 0.22, 0.17, 0.14)^T.

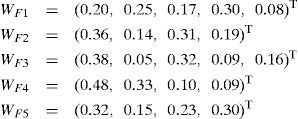
Similarly, the weight vectors of the risk sub-factors in the general-assembling process are obtained as follows:

The overall weight of the risk sub-factor equals to the product of local weight of this factor and the local weight of its “father factor”. The weights of the risk factors in the general-assembling process are shown in Table 8.

Table 8.

Weight table for risk factors in general-assembling process.

Risk factor	Local weight	Risk sub-factor	Local weight	Overall weight
F1	0.28	f11	0.2	0.056
		f12	0.25	0.070
		f13	0.17	0.048
		f14	0.3	0.084
		f15	0.08	0.022
F2	0.19	f21	0.36	0.068
		f22	0.14	0.027
		f23	0.31	0.059
		f24	0.19	0.036
F3	0.22	f31	0.38	0.084
		f32	0.05	0.011
		f33	0.32	0.070
		f34	0.09	0.020
		f35	0.16	0.035
F4	0.17	f41	0.48	0.082
		f42	0.33	0.056
		f43	0.1	0.017
		f44	0.09	0.015
F5	0.14	f51	0.32	0.045
		f52	0.15	0.021
		f53	0.23	0.032
		f54	0.3	0.042

3.2

Quantitative analysis for risk factors

Frequently those non-quantitative descriptive judgments can give but rough results, due to its subjectivity and ambiguity. In this case, in order to correctively measure the accident risk level in the general-assembling process, the risk factors needed to be quantified as much as possible. The characteristics of the general-assembling process and the human capacity of distinction among different levels, furthermore, the accuracy and efficiency of the risk assessment should be considered for the quantification of granularity of various risk factor levels in the satellite general-assembling process.

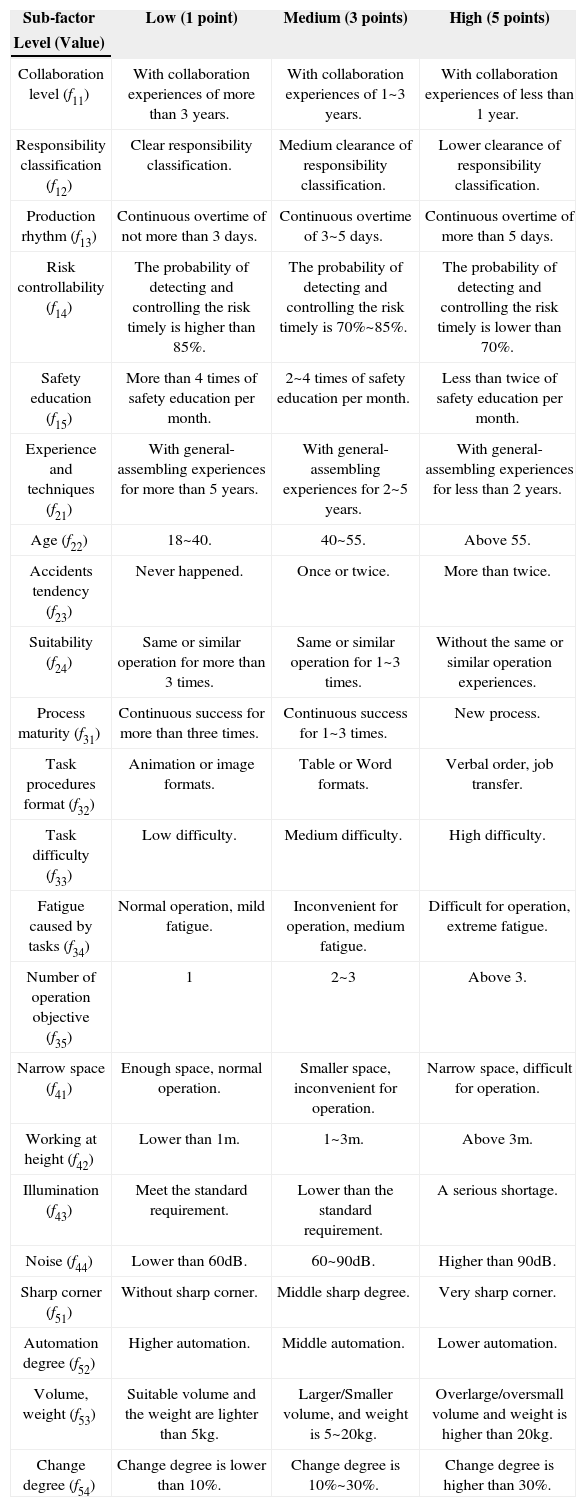
According to the characteristics of the satellite general-assembling, meanwhile, with the combination of existing data and experts experiences, a 3-leveled criteria [18], [23, 24] is taken to describe the risk factor level in the general-assembling process in this article, which is classified into three grades, according to the risk levels, i.e. low, medium, and high level. The quantitative assessment criteria are shown as Table 9.

Table 9.

The quantization table for the risk factors in general-assembling process.

Sub-factor	Low (1 point)	Medium (3 points)	High (5 points)
Level (Value)
Collaboration level (f11)	With collaboration experiences of more than 3 years.	With collaboration experiences of 1~3 years.	With collaboration experiences of less than 1 year.
Responsibility classification (f12)	Clear responsibility classification.	Medium clearance of responsibility classification.	Lower clearance of responsibility classification.
Production rhythm (f13)	Continuous overtime of not more than 3 days.	Continuous overtime of 3~5 days.	Continuous overtime of more than 5 days.
Risk controllability (f14)	The probability of detecting and controlling the risk timely is higher than 85%.	The probability of detecting and controlling the risk timely is 70%~85%.	The probability of detecting and controlling the risk timely is lower than 70%.
Safety education (f15)	More than 4 times of safety education per month.	2~4 times of safety education per month.	Less than twice of safety education per month.
Experience and techniques (f21)	With general-assembling experiences for more than 5 years.	With general-assembling experiences for 2~5 years.	With general-assembling experiences for less than 2 years.
Age (f22)	18~40.	40~55.	Above 55.
Accidents tendency (f23)	Never happened.	Once or twice.	More than twice.
Suitability (f24)	Same or similar operation for more than 3 times.	Same or similar operation for 1~3 times.	Without the same or similar operation experiences.
Process maturity (f31)	Continuous success for more than three times.	Continuous success for 1~3 times.	New process.
Task procedures format (f32)	Animation or image formats.	Table or Word formats.	Verbal order, job transfer.
Task difficulty (f33)	Low difficulty.	Medium difficulty.	High difficulty.
Fatigue caused by tasks (f34)	Normal operation, mild fatigue.	Inconvenient for operation, medium fatigue.	Difficult for operation, extreme fatigue.
Number of operation objective (f35)	1	2~3	Above 3.
Narrow space (f41)	Enough space, normal operation.	Smaller space, inconvenient for operation.	Narrow space, difficult for operation.
Working at height (f42)	Lower than 1m.	1~3m.	Above 3m.
Illumination (f43)	Meet the standard requirement.	Lower than the standard requirement.	A serious shortage.
Noise (f44)	Lower than 60dB.	60~90dB.	Higher than 90dB.
Sharp corner (f51)	Without sharp corner.	Middle sharp degree.	Very sharp corner.
Automation degree (f52)	Higher automation.	Middle automation.	Lower automation.
Volume, weight (f53)	Suitable volume and the weight are lighter than 5kg.	Larger/Smaller volume, and weight is 5~20kg.	Overlarge/oversmall volume and weight is higher than 20kg.
Change degree (f54)	Change degree is lower than 10%.	Change degree is 10%~30%.	Change degree is higher than 30%.

3.3

The establishment of the comprehensive risk assessment model

After the weights of the risk factors in the satellite general-assembling process and the quantitative analysis results of risk factors are obtained, the comprehensive risk assessment can be carried out, and the overall risk level can be obtained through calculation. The risk assessment model is shown as Formula 1.

Among which, i=1, 2,…n (n is the number of the risk factors); PRL_i is the weighted quantitative result of the risk factor number i; W_i is the overall weight of the risk factor number i; and F_i is the quantitative result of the risk factor number i.

The comprehensive risk assessment result is helpful for the decision maker to understand wholly the safety features of the process being analyzed. Because of the outstanding feature of quantification, it can be taken as the basis for the effectiveness analysis of the safety improving measures. Through the comparison of the risk level before and after taking improving measures, the effectiveness of the improving measures can be measured with the amount of the risk level changes.

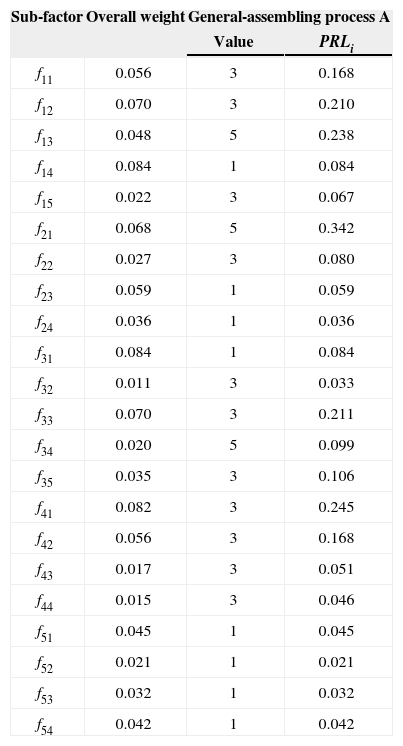
4

Case study

The general-assembling process of a satellite (represented as A) is regarding as the case study in this article. The quantitative result of its risk sub-factors are shown in Table 10.

Table 10.

Risk factors tabular statement for satellite general-assembling process A.

Sub-factor	Overall weight	General-assembling process A
		Value	PRLi
f11	0.056	3	0.168
f12	0.070	3	0.210
f13	0.048	5	0.238
f14	0.084	1	0.084
f15	0.022	3	0.067
f21	0.068	5	0.342
f22	0.027	3	0.080
f23	0.059	1	0.059
f24	0.036	1	0.036
f31	0.084	1	0.084
f32	0.011	3	0.033
f33	0.070	3	0.211
f34	0.020	5	0.099
f35	0.035	3	0.106
f41	0.082	3	0.245
f42	0.056	3	0.168
f43	0.017	3	0.051
f44	0.015	3	0.046
f51	0.045	1	0.045
f52	0.021	1	0.021
f53	0.032	1	0.032
f54	0.042	1	0.042

It is obtained from Formula 1 that PRL_A = 2.466.

Combined with existing data and expert experience, LB=2.00 and UB=2.50 are taken here. Because of the fact that LB≤PRL_A<UB, the general-assembling process A can be carried out after taking improving measures, and being verified.

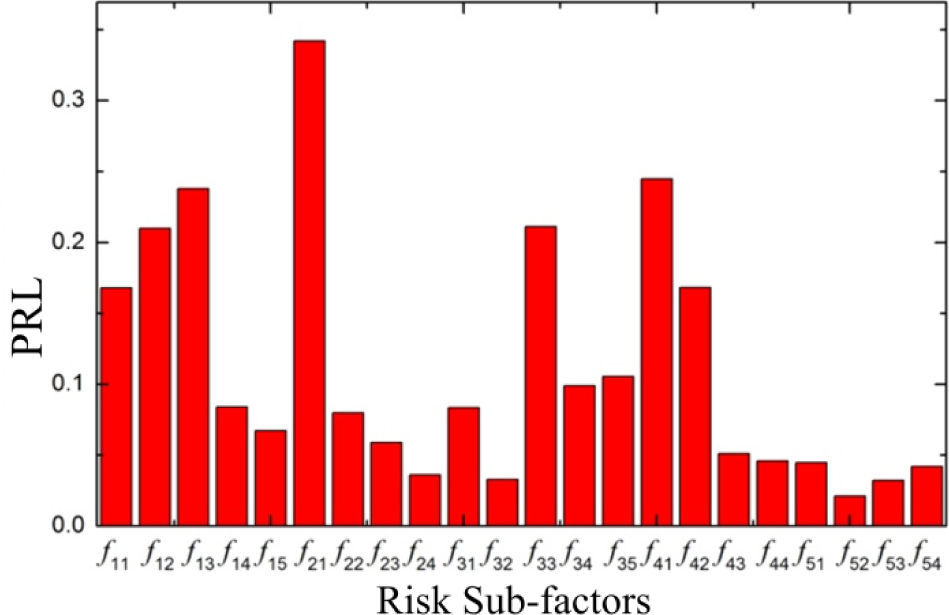
The weighted quantitative results of risk sub-factors in the general-assembling Process A are shown in Figure 3.

Figure 3.

The histogram of PRLs of risk sub-factors in the general-assembling process A.

It is shown in Figure 3 that the 3 risk sub-factors which are most influential to the general-assembling process A are experience and techniques (f₂₁), narrow space (f₄₁), and production rhythm (f₁₃), which are also shadowed in Table 10. These 3 risk sub-factors are all relative with either abilities of workers or work condition of general-assembling task. It has been well known that unfavorable work conditions add to the discomfort of assembly workers [25, 26], which proved to some degree that there should be a closer correlation between overall risk level and abilities of workers or work condition. Thus for risk mitigation, these 3 sub-factors above are more effective than any other factor. Accordingly, cost-effective risk mitigation efforts for satellite general-assembling should be targeted on those design and management practices that are most likely to reduce losses in a cost-effective manner.

Aiming at the issues identified, some feasible measures regarding the top 3 influential sub-factors are presented as a hypothesis for analysis. Based on them, sensitivity analyses are performed to assess the change in the contribution of the 3 sub-factors, as well as the effect of the measures enforcement on the system risk (say, the value of PRL).

The comparison for the top 3 contributing risk sub-factors in the general-assembling process A before and after taking improvement measures, and the corresponding improving measures are shown in Table 11. Using the improving measures, the estimated PRL value of the factors f₂₁, f₄₁ and f₁₃ would be decreased 80.1%, 66.5% and 79.8% individually.

Table 11.

The comparison table for the general-assembling process A before and after taking improving measures.

Comparison	General-assembling process A		Improving measures	General-assembling process A’
factors	Value	PRLi		Value	PRLi’
f21	5	0.342	Replaced by experienced staff	1	0.068
f41	3	0.245	Replaced by staff of small stature	1	0.082
f13	5	0.238	Decrease number of overtime	1	0.048

The risk level for the general-assembling process after the improvement (represented as _A’) is:

PRLA’ = 1.839 < LB.

After taking the improving measures, the risk of the general-assembling process A is decreased from 2.466 to 1.839, which meets the risk control requirement for general-assembling process. The general-assembling can be carried out.

5

Discussions and conclusions

Based on the actual engineering situations, the 22 risk sub-factors of 5 categories, which possibly cause accidents in the general-assembling process, are identified. The risk factor hierarchy for satellite general-assembling process is established. Based on this, with FAHP, a comprehensive risk assessment method is established, including the determination of the weights of risk factors, the quantitative analysis of risk factors, and the establishment of the comprehensive risk calculation model, etc. Taking a satellite model as an example, the risks in satellite general-assembling process are comprehensively assessed. The factors are sorted according to their influences on the overall risk level, and the key risk factors in the satellite general-assembling process are obtained, so as to assure the pertinence of the improvement measures, and the satellite safety. This method provides the theoretical principle for the transformation from hindsight to prognosis for the general-assembling accidents.

The results of case study showed that general-assembling process was relatively strongly related to experience and techniques (f₂₁, whose PRL is up to 34.2%), narrow space (f₄₁, whose PRL is 24.5%), and production rhythm (f₁₃, whose PRL is 23.8%), whereas the sub-factors such as suitability (f₂₄), task procedures format (f₃₂) and automation degree (f₅₂) proved to be much more weakly related to the overall risk level.

Additionally, after using the improving measures, the estimated PRL value of the top 3 influential sub-factors i.e. f₂₁, f₄₁ and f₁₃ would be decreased by a large margin (at a percentage between 67% and 80%), which means the improving measures are fairly effective.

All the variables were assessed with the engineering practice in China, including some empirical documentation, which means that a general empirical view might have contributed to the results. However, it should be noted that the relative comparison details about the relation between overall risk and each of its factors was reasonable and authentic.

It is shown from the application in actual cases that the risk assessment method, based on FAHP, is easy and effective in engineering application, which can provide technical support for the accident risk control in satellite general-assembling process. The method after appropriate modifications will be suitable for the risk assessment for the manufacturing process of other spacecrafts.