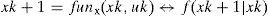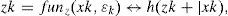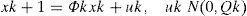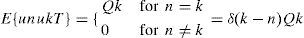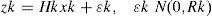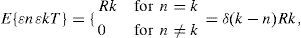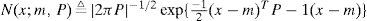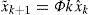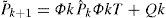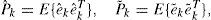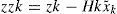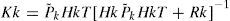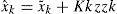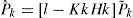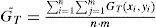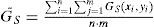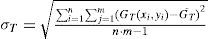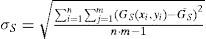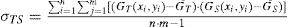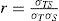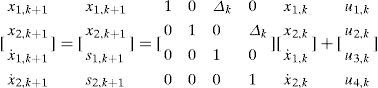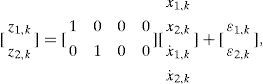This paper presents the performance of an adaptive location-estimation technique combining Kaiman filtering (KF) with vision assisting for wireless sensor networks. For improving the accuracy of a location estimator, a KF procedure is employed at a mobile terminal to filter variations of the location estimate. Furthermore, using a vision-assisted calibration technique, the proposed approach based on the normalized cross-correlation scheme is an accuracy enhancement procedure that effectively removes system errors causing uncertainty in real dynamic environments. Namely, according to the vision-assisted approach to extract the locations of the reference nodes as landmarks, a KF-based approach with the landmark information can calibrate the location estimation and reduce the corner effect of a location-estimation system. In terms of the location accuracy estimated from the proposed approach, the experimental results demonstrate that more than 60 percent of the location estimates have error distances less than 1.4 meters in a ZigBee positioning platform. As compared with the non-tracking algorithm and non-vision-assisted approach, the proposed algorithm can achieve reasonably good performance.
With the rapid increase in wireless communications, location-aware services have received a great deal of attention for commercial, public safety, and military applications [1]-[2]. Generally, most of location-estimation approaches are based on the received signal strengths (RSSs) in wireless network environment. For positioning systems based on RSSs in small areas, there are two major approaches for location estimation of a mobile terminal (MT) in wireless networks: one using wireless local area networks (WLANs) [3] and the other using wireless sensor networks (WSNs) [4]. The former approach is cost-effective, while the latter is energy-effective. In addition, for location estimation and tracking systems, a client-based deployment or an infrastructure-based deployment can be adopted. In terms of the applications of location-based services (LBSs) [5], one of the key challenges is the location accuracy. Nevertheless, in order to estimate an accurate location based on one of a client-based deployment or an infrastructure-based deployment, that location estimators only use RSS information is still a difficult problem for improving the location accuracy.
Traditionally, an accurate location can be improved with location tracking algorithms. The role of a tracking algorithm is to perform recursive state estimation, which is given by the state equation and the observation equation [6]. Furthermore, because Kaiman filtering (KF) algorithm is considered an optimal recursive computation of the least-squares algorithm, it has been introduced to enhance the accurate estimation of the location-estimation system [6]-[14]. That is, location-estimation techniques based on KF algorithm can be considered the optimal approach for the linear Gaussian model during location estimation and tracking. However, for location-tracking approaches, the dramatic change in speed in a short time may result in the corner effect and diminish location accuracy [7]. In addition, for wireless services in feature phones, most of LBS applications only use absolute approaches based on RSSs to infer the location of the MT [8]. Namely, to estimate an accurate location with absolute schemes is still a difficult problem for improving the location accuracy. Recently, a smartphone with multi-sensor systems and cooperative capabilities has become widely available. Specifically, a smartphone can offer more advanced computing ability and allows the user to run multi-task applications [13], [15]. Consequently, the portable navigation and tracking system (a smartphone or an MT) can combine with the diverse sensing capabilities. In other words, a location-estimation system combining with different devices can be considered an important technique to improve location accuracy. In addition, a landmark technique based on the RFID-assisted approach had been used to calibrate the location estimation, to overcome the corner effect of the dramatic time varying environments, and to enhance the system performance of the location accuracy [7]. Therefore, according to the features of smartphones, to combine the radio ranging scheme with video recording data is a natural choice for positioning systems to improve the location estimation of MTs.
This paper proposed an algorithm combining a location-tracking approach with a vision-assisted approach in a WSN environment. As compared with traditional location-estimation schemes, a vision-assisted scheme based on normalized cross-correlation (NCC) approach is proposed to detect landmark locations as a calibration technique, and then the technique is used to alleviate the corner-effect problem caused by filtering and tracking algorithms. By employing the proposed algorithm at the MT under a stationary environment, experimental results demonstrate that the proposed approach can achieve much better location accuracy in WSN environments. In short, the KF tracking approach based on a state space model is a minimum mean-square error (MMSE) estimator. The purpose of this paper is to investigate how to improve the corner effect caused by location tracking scheme. Thus, the accuracy of location estimations is close to an MMSE estimator based on a KF approach.
2Background2.1State and measurement modelsConsider the dynamic system described in state space form [10]. If the system is denoted by probability densities, the mathematical models for the system and measurement on the MT at time k can be taken by
State equation:
Observation equation:
where xk, funx (·), uk, zk, funz(·), and εk are the state vector, transition function, process noise with known distribution, observation vector, observation function, and observation noise with known distribution, respectively; f(xk+1|xk) and h(zk|xk) are the transition probability density function (PDF) and observation PDF, respectively. The hidden states xk disturbed by uk and the data zk disturbed by εk are assumed to be generated by functions funx (·) and funz(·), respectively. For the representation with the linear Gaussian model, the mathematical models of the linear dynamic system and of the measurement are denoted as a state space model by
State equation
Observation equation
where xk, Φk, uk, and Qk are the state matrix, state transition matrix, model noise matrix, and model noise covariance matrix, respectively; zk, Hk, εk, and Rk are the actual measurement matrix, measurement transition matrix, measurement noise matrix, and measurement noise covariance matrix, respectively. For these equations, uk and εk are zero-mean independent Gaussian vectors with covariance matrices Qk and Rk, respectively.
2.2Kaiman filteringLet the vector x=[x1,...,xn]T consist of independent components i=1,..., n. The PDF of x is the production of the individual PDF’s of x1,...,xn; N (x;m,P) is defined as Gaussian density for n dimensions; the n-dimension Gaussian density function is defined by
where x, m, and P are the argument, mean, and covariance, respectively. Furthermore, in this paper, the value of vector x(t) at a discrete time instant t=tk is denoted by xk; the estimate of x(t) at time t=tk given the observations up to time t=tj is denoted by a double-subscript notation with xk|y, and then three useful cases are denoted as follows: the one-step fixed-lag smoothing is xk|k+1=x⌣k, the best estimation is xk|k=xˆk, and the best one-step prediction is xk+1|k=x˜k+1. In terms of f(xk+1|xk)=N (xk+1;Φkxk,Qk), h(zk|xk)=N(zk;Hkxk,Rk) and Eqs. 1-6, the mathematical equations and phases of a KF algorithm are summarized as follows [6]-[7], [11].
2.2.1Prediction phase (time update phase)From k to k+1, the state prediction and prediction error covariance are obtained by
where ek|j≜xk|j-xk,ek|k≜xˆk-xk=eˆk,ek+k-1≜x˜k-xk=e˜k;xˆk,x˜k,eˆk|j,eˆk,, and e˜k are the state estimate matrix, state prediction matrix, state error matrix, estimation error matrix, and prediction error matrix, respectively; pˆk and p˜k are the estimation error covariance matrix and prediction error covariance matrix, respectively.
2.2.2Innovation phaseThe innovation that is based on the previous measurements is the difference between the actual measurement and the prediction. As a result, the innovation phase can be described by
where zzk and Kk are the innovation matrix and Kaiman gain matrix, respectively.
2.2.3Correction phase (measurement update phase)The state estimation and the estimation error covariance are updated as follows.
where I is the identity matrix. Therefore, Eqs. 8-14 of the KF algorithm fall into two group equations: time update and measurement update equations.
2.3Normalized cross correlation (NCC)In order to recognize the reference nodes (RNs) as landmarks along the test path, this paper combines a pattern recognition method with identifications (IDs) of RNs for calibrating the estimated location.
As is well known, the simplest area-based image-matching method is the NCC algorithm [16]. The NCC scheme is widely used in image-processing applications, and it is against the brightness difference between the image and template due to lighting condition. In this paper, the useful equations of the NCC approach are as follows.
where GT(x, y) and Gs(x, y) are the image masks of the grayscale of target window and search window, respectively; G¯TandG¯S are the means of the grayscale of target window and search windows, respectively; m and n are the numbers of rows and columns, respectively; στ and σs are the standard deviations of the image masks of the target window and search window, respectively. σTS is the value of cross correlation; r is the NCC value, and it can indicate that the most likely video frame or time passes through the landmarks.
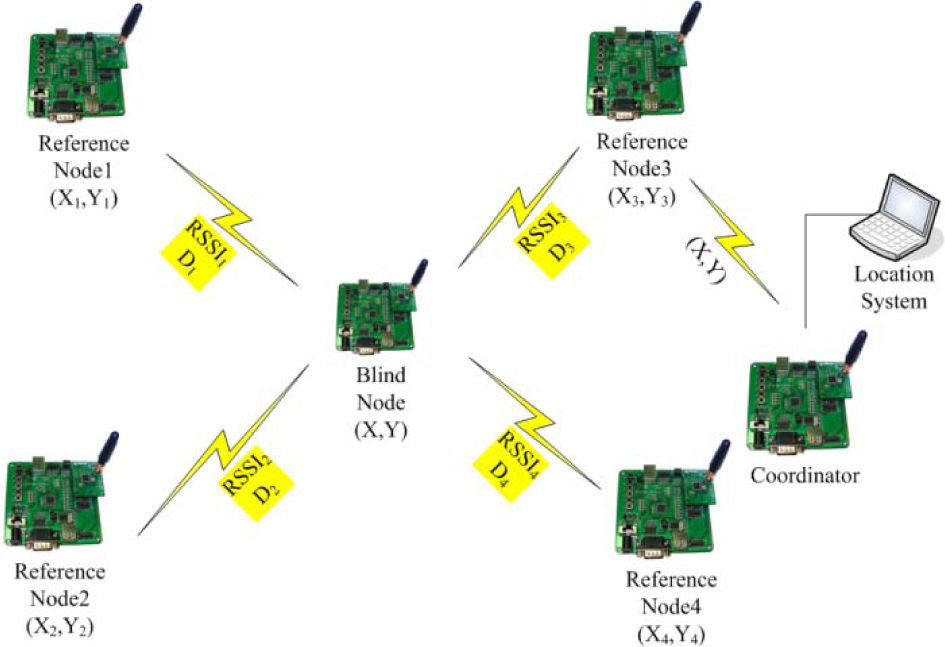
2.4ZigBee positioning system (ZPS)The ZigBee network is based on IEEE 802.15.4, which can exchange information during the route maintenance process with the features of low transfer rate, low power, and low cost. A simplified positioning system based on ZigBee network for location estimation is illustrated in Figure 1, where the RSS indicator (RSSI) is a measurement of the power of the received radio signal. This kind of ZigBee positioning system (ZPS) includes three type models (nodes): coordinator, reference node (RN), and blind node (BN). As shown in Figure 1, the coordinator is directly connected to a computer; RNs placed at a known position would send device IDs and coordinates to BNs. That is, an RN is a static node placed at a known position; a BN is a node collects signals from all RNs responding to the respective RSSI values of RNs for location estimation. When a BN receives signals from neighboring RNs, the distance between the BN and RNs can be calculated by the collecting RSSI samples and the path-loss model, and then the location of the BN can be obtained with well known coordinates of RNs. Afterward, the estimated location of the BN (MT) is sent to the coordinator through the WSN system for LBS applications.
3The proposed algorithmFor the approaches of incorporated measurement uncertainties in WSNs, one of the popular commercial ZPS systems is based on the CC2431 location engine developed by Texas Instruments (Tl) [17]. The TI CC2431 is a hardware location engine targeting low-power ZigBee applications in WSNs; it is used to estimate the locations of BNs in an ad-hoc wireless network with RSSI values from known RNs based on a centralized computation approach. In terms of the RSSI values, the TI CC2431 location engine outputs X and Y locations individually. Consequently, this paper focuses on location tracking approaches in terms of X and Y groups individually in twodimensional (2-D) coordinate system.
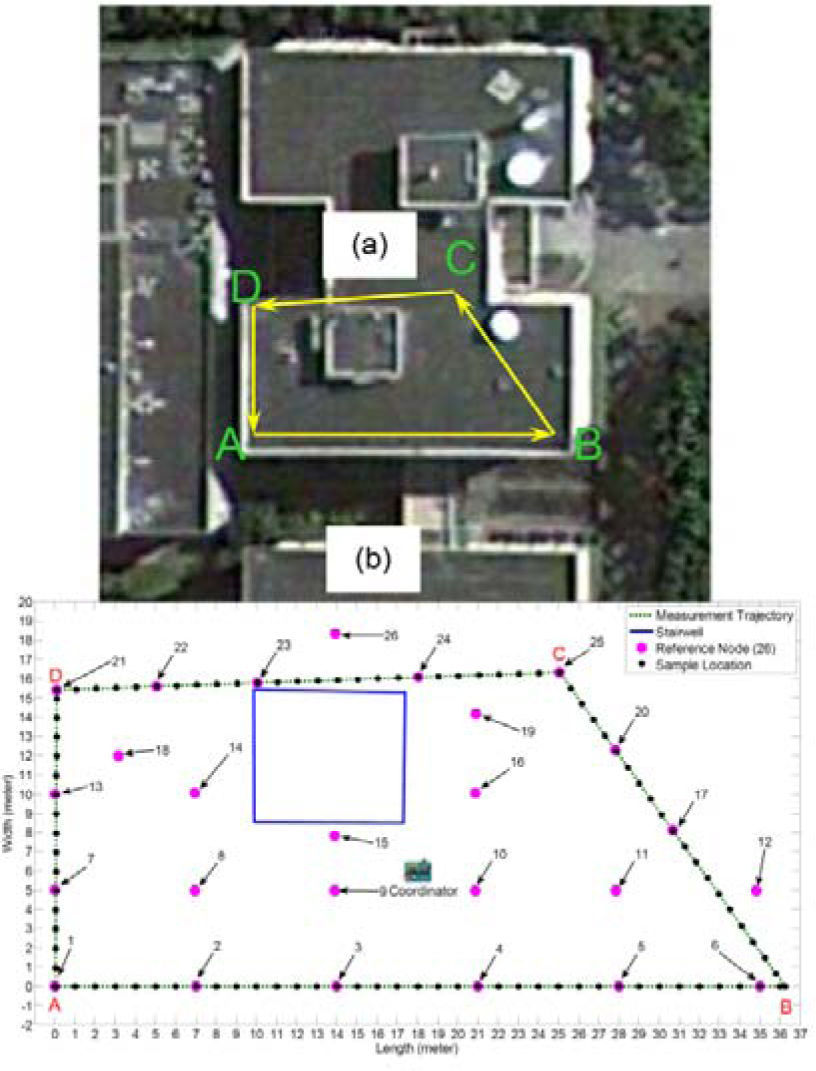
3.1Experiment setupThe experimental platform was located on the roof floor of a building (Center for Space and Remote Sensing Research, National Central University, Taiwan); the floor layout and experimental setup are shown in Figures 2 (a) and (b), respectively. In Figure 2(b), the sampled locations are denoted by black solid circle with 1 meter distance between each point; the coordinator located close to lower trajectory is denoted by
To improve the location accuracy with a tracking technique for location estimation, a location tracking approach can be formulated as a filtering problem [10]. For location-estimation techniques using tracking algorithms, the KF-based approach is introduced to enhance the accurate estimation of the location-estimation system [11]. In terms of filtering approach, although the state and measurement models are based on a 2-D model for a linear Gaussian system, the extension of the scheme to a three-dimensional (3-D) model is straightforward. For a 2-D model in this paper, the vector xk=[x1,k x2,kX-1,kX-2,k]T denotes the state of the MT at time k, where x1,k and x2,k are the locations in the X and Y directions; X-1,k=s1,k and X-2,k=s2,k are the speeds in the X and Y directions. For the motion model of the MT based on speed noise, by adding a random component to the MT, the 2-D model describing the motion and observing the location of the MT is taken as
where Δk is the measurement interval between k and k+1. As compared the Eqs. 3 and 5 with the Eqs. 21 and 22, uk=[u1,k u2,k u3,k u4,k]T is the process noise; zk,=[z1,k z2,k]T and εk=[ε1,k ε2,k]T are the observed information and measurement noise, corresponding to the MT at time k, respectively.
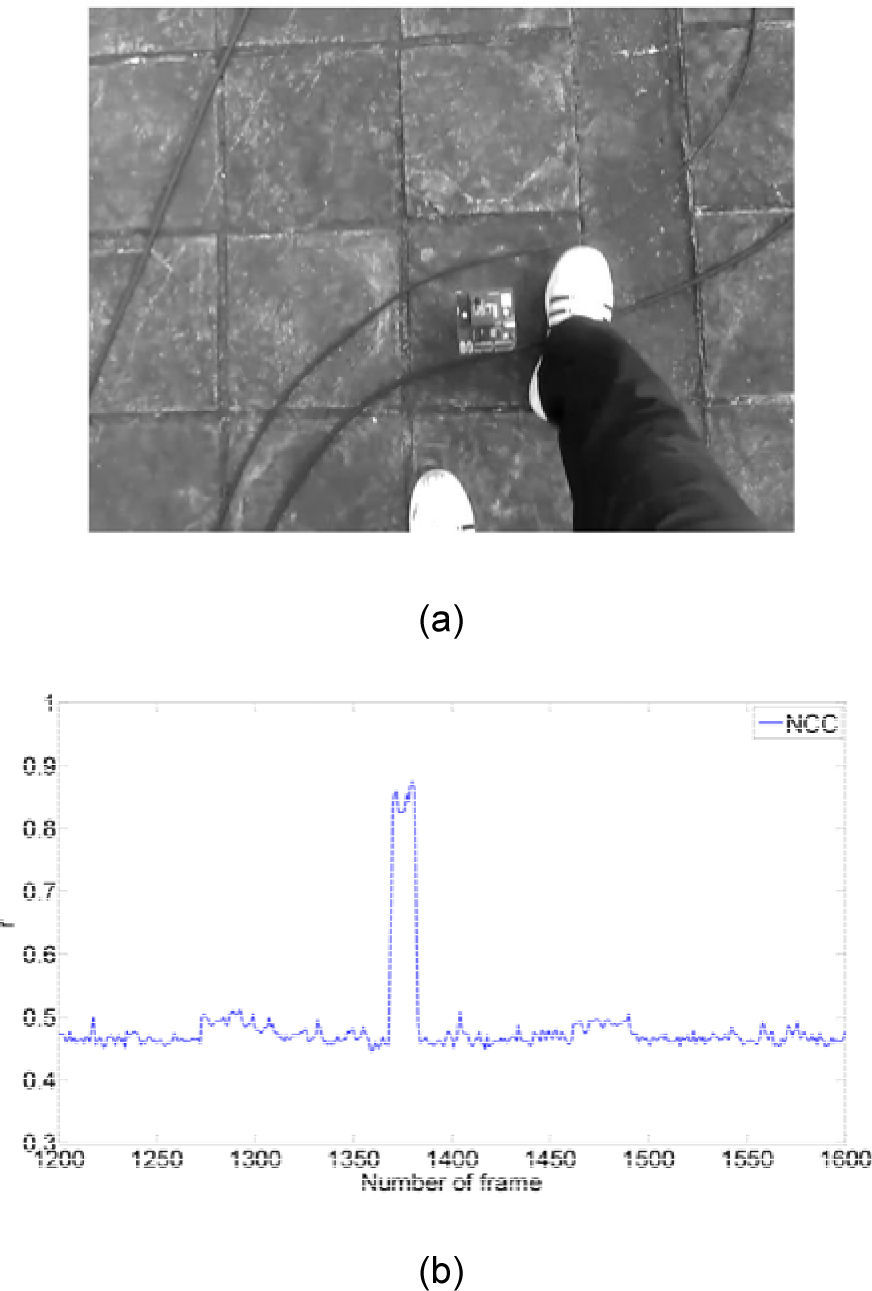
3.3Location estimation using vision assistingIn a WSN environment, the characteristics of signal propagation suffer from reflection, diffraction, scattering, and heavy shadow fading of the propagation effects, and the unstable RSSIs will affect the accuracy of location estimation. That is, as TI CC2431 location engine is fed with large fluctuation of RSSI information, the location accuracy will be reduced. To improve location accuracy, a simple technique employing landmark-assisted scheme is used to overcome the corner effect caused by the filtering and tracking method for dramatic time varying systems in different environmental conditions. That is, an MT (BN) can calibrate and modify its location based on sensing the landmark location. In this paper, the RNs as landmarks can be extracted from video characteristics by the NCC approach for location estimation. In addition, to reduce the energy consumption and prolong the lifetime of a smartphone using the NCC approach for location estimation, the proposed scheme allows the vision-assisted concept to operate two modes based on a threshold, where the two modes are the sleep mode and the active mode, and the threshold is in terms of RSSIs of the ZPS testbed. As illustrated in Figure 2, if an RSSI (path loss) is smaller than the threshold, the vision-assisted algorithm will enter the active mode. That is, only the BN is close to RNs, the video camera of the smartphone starts recording the path, and then the NCC approach is carried out for landmark detection. On the contrast, when an RSSI is larger than the threshold, the vision-assisted algorithm will enter the sleep mode, and the video camera stops recording the path. Figure 3 indicates a simple example about the vision-assisted scheme based on NCC approach. The experimental result demonstrates that an RN can be extracted and detected from video characteristics by the NCC approach as a landmark correctly.
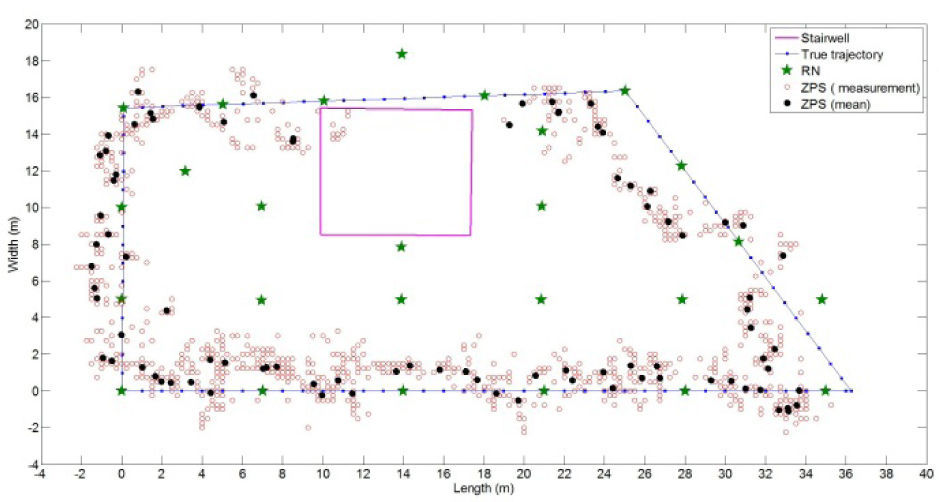
4Experimental results4.1ZigBee positioning systemFor wireless network systems, to estimate locations in wireless sensor networks, one of the popular commercial ZPSs using the TI CC2431 location engine in terms of the RSSI can obtain locations. In this paper, the experimental investigation combines TI CC2430/CC2431 ZPS platform with vision-assisted approach for location estimation and tracking. As an MT moved along the test path in Figure 2, the experimental results of location estimation using the Tl ZPS platform are illustrated in Figure 4, where the estimated locations are denoted by red hollow circles. In addition, as an MT locates at sample locations in Figure 2, the mean of the location estimation is denoted by black solid circles in Figure 4. To verify the performances of estimation results introduced by the proposed schemes, the location parameters are based on the estimated result from Tl ZPS testbed in Figure 4. Without loss of generality, it is assumed that the MT has a steady state in Eq. 21; Δk, the measurement interval (sampling time) between k and k+1, is set to one second. In addition, the model describing the observation location of the MT taken in Eq. 22 is based on Figure 4.
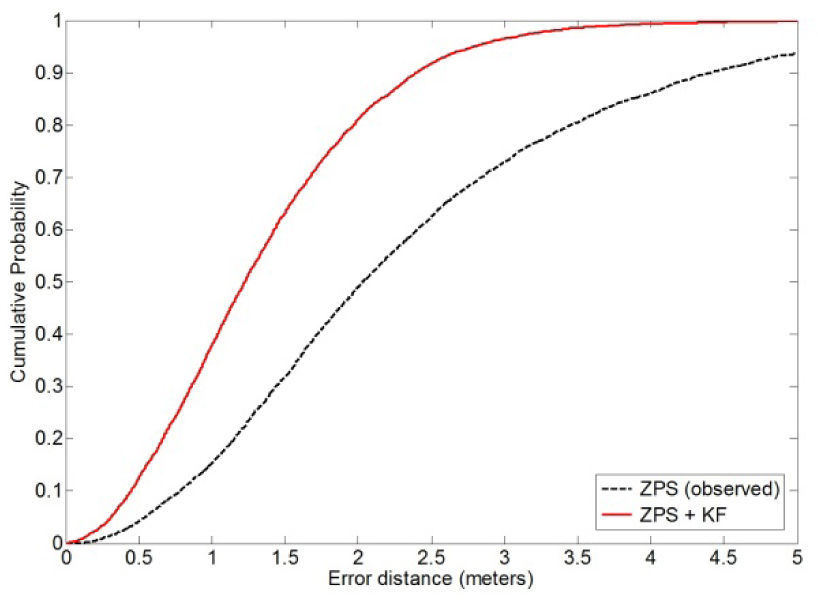
4.2Location estimation using Kaiman filteringIn terms of the cumulative distribution function (CDF) of the error distance, the simulation result of the location estimation of the tracking schemes is given in Figure 5. According to the results, the location accuracy of the tracking schemes is better than that of the non-tracking scheme. In fact, the KF algorithm is an optimal tracking scheme for the linear Gaussian model, and it usually gives the best linear estimator in a mean-square error sense. Therefore, the location accuracy of the KF tracking scheme can be considered an upper CDF bound for location-estimation systems in linear Gaussian environments.
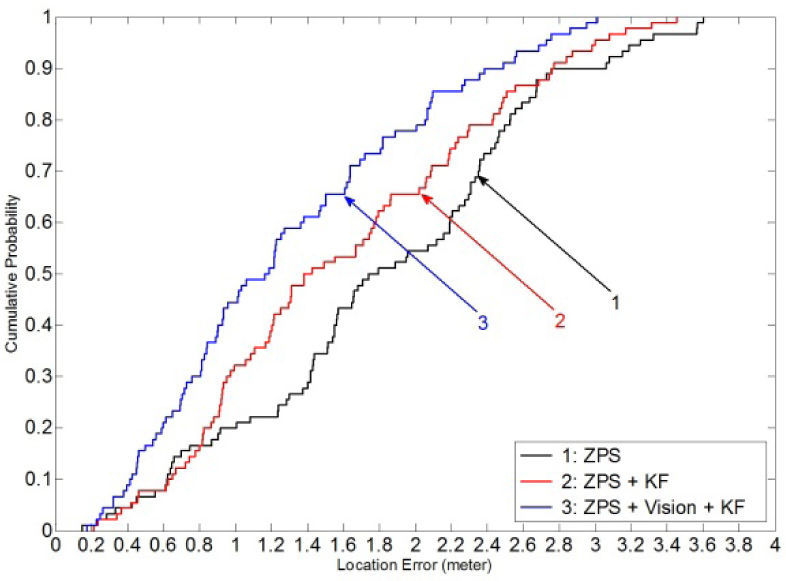
In addition, the location results in terms of the CDF of the error distance of the KF tracking method are given in Figure 6. The results demonstrate that more than 60 percent of the estimated locations with the Tl ZPS scheme have error distances less than 2.2meters; more than 60 percent of the estimated locations with the KF-based scheme have error distances less than 1.8meters. According to the experimental results in Figure 6, the location accuracy of the KF tracking algorithm is better than the ZPS non-tracking method. In other words, the KF-based approach can diminish the estimated errors compared with ZPS non-tracking method. In fact, the property of the KF-based method is a recursive minimum mean-squares state algorithm, so the location error of KF tracing algorithm is considered as an upper CDF bound for different location-estimation approaches in this paper.
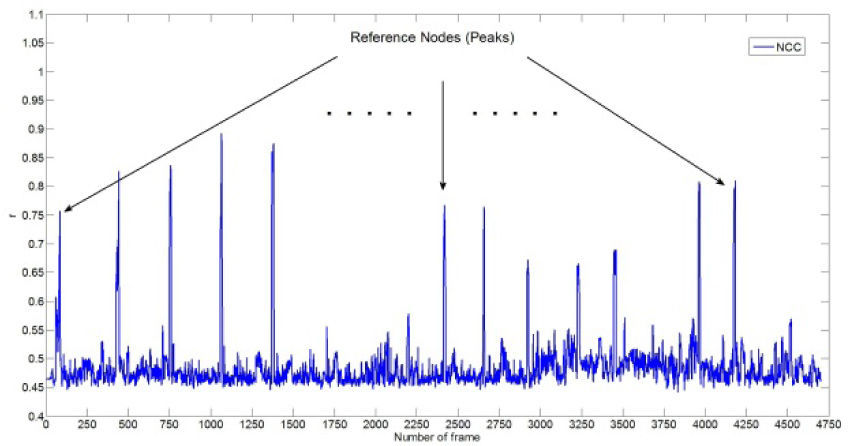
4.3Location estimation using vision assistingAccording to the experimental results, the threshold of RSSI values (path loss) of the ZPS platform is set to 60 for the TI CC2431 location engine in this paper. In Figure 2, if an RSSI value is larger than 60, the vision-assisted algorithm enters the sleep mode. On the contrast, when an RSSI value is smaller than 60, the vision-assisted algorithm enters the active mode, and then the NCC approach is carried out for landmark detection. Figure 7 indicates the experimental results using vision-assisted scheme based on NCC approach. The r values indicate that the most likely video frame or time passes through the landmarks. According to the experimental results in Figure 7, the threshold of the r values in the proposed NCC approach is set to 0.6 in this paper. Therefore, the results illustrate that the RNs can be detected as landmarks correctly. Furthermore, in terms of the CDF of the error distances in Figure 6, the experimental results also show that the KF tracking scheme uses the vision-assisted approaches based on NCC approach. It demonstrates that more than 60 percent of the estimated locations using the KF-based approach have error distances less than 1.4meters. In brief, Figure 6 indicates the comparison among the ZPS non-tracking, KF-based, and KF-based with the vision-assisted methods as an MT moves along a test path in Figure 2. In Figure 6, after using vision assistance, the experimental results illustrate that the location accuracies of the proposed positioning methods are better than the non-vision assisted positioning methods. The results show that the proposed vision-assisted scheme can provide a high degree of accuracy for location estimation and tracking. After combining the vision technique based NCC method with the KF-based algorithm, Figure 6 shows that the proposed tracking schemes can closely track locations of MTs. That is, with the vision-assisted method based on the NCC approach, the results show that the proposed algorithm could mitigate and overcome the dramatic time variance environments of the path more efficiently. In addition, the proposed location-tracking platform can be used in various applications in practice. For example, it can provide a continuous real-time positioning and tracking approach in indoor or outdoor environments when GPS signal is lock-lose. Therefore, a location-estimation system combining with different devices can be considered an important technique to improve location accuracy. In other words, a location-estimation scheme based on a location-tracking technique with a vision-assisting approach can be proposed to fuse the positioning information for multi-sensor positioning systems to improve the location estimation of MTs in LBS applications.
5ConclusionIn this paper, we have proposed a new technique with vision-assisted approach for location estimation and tracking in WSN environments. Using the KF-based approach, the MT can properly track variations of the location estimate obtained from the ZPS platform and improve the location accuracy. Furthermore, in terms of NCC procedures to match the images of RNs, the RNs extracted from video characteristics are as landmarks. Consequently, the KF tracking scheme with the RN information can calibrate the location estimation and alleviate the corner effect. Under a stationary environment, according to the experimental results about investigating and comparing the performance of the ZPS system, we conclude that the proposed scheme demonstrates much better accuracy as compared with the non-tracking scheme and the non-vision-assisted scheme. To sum up, the proposed scheme has good features of location accuracy, and it has been shown by experimental results that more than 60 percent of the location estimates have error distances less than 1.4 meters. As compared with the non-assisted schemes, the proposed location-tracking platform combining vision-assisted scheme with KF tracking approach in ZPS of WSNs is attractive for using in various LBS applications.
AcknowledgementsThis work was supported in part by the National Science Council of the Republic of China (R.O.C.) under Grants NSC 98-2221-E-008-097-MY2 and NSC 101-2218-E-033-007.