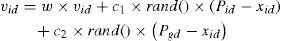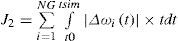A PSO Procedure for a Coordinated Tuning of Power System Stabilizers for Multiple Operating Conditions

Abstract

The problem of coordinated tuning stabilizers in multi-machine power systems is formulated here as a sequence of optimization problems. The design problem of stabilizers is converted to a nonlinear optimization problem with a multi-objective fitness function. The proposed method employs particle swarm optimization (PSO), an algorithm to search for optimal parameter settings of a widely used conventional fixed-structure lead-lag power system stabilizers (CPSSs). One of the main advantages of the proposed approach is its robustness to the initial parameter settings. In addition, the quality of the optimal solution does not rely on the initial guess. The robustness and performance of the newly designed controllers is evaluated in a large sixteen-machine power system subjected to different loading conditions in comparison with the genetic algorithm (GA) based PSSs design. The superiority of the controller designed is demonstrated through the nonlinear time-domain simulation and some performance indices studies. The results analysis reveals that the tuned PSSs with proposed objective function has an excellent capability in damping power system low-frequency oscillations.

1

Introduction

In the past three decades, the utilization of supplementary excitation control signals for improving the dynamic stability of power systems has received much attention. Nowadays, the CPSS is widely used by power system utilities. Power system stabilizers (PSSs) are auxiliary control devices on synchronous generators, used in conjunction with their excitation system by providing supplementary feedback stabilizing signals to provide control signals toward enhancing the system damping and extending power transfer limits [1–3]. Recently, several approaches such as optimization based techniques like genetic algorithms (GA), evolutionary programming, tabu search, simulated annealing and rule based bacteria foraging [4–11] have been applied to PSSs parameter optimization problem. These population based algorithms search procedures that incorporate random variation and selection operators. Appearing suitable for optimizing the PSS parameters, these approaches have long simulation time and degraded efficiency to obtain the global optimum solution when there is a large number of optimization parameters or when the system has a highly complex objective function (i.e., where parameters being optimized are highly correlated in large power system). In this paper, the PSO based PSS is proposed which is used for optimal tuning of the PSS parameters to improve optimization synthesis and the speed of the convergence. The PSO algorithm [12] is a derivative free promising algorithm for handling the combinatorial optimization problems. It has been proved theoretically that PSO algorithm converges to the optimal solution [13]. In addition, the PSO algorithm is robust i.e., the final solution quality does not strongly depend on the choice of the initial solution. Another strong feature of the PSO algorithm is that a complicated mathematical model is not required and the problem constraints can be easily incorporated [14].

In this study, the PSO is used to solve the problem of the PSSs design (PSOPSS) which is formulated as a multi-objective optimization problem. The multi-objective problem is concocted to optimize a composite set of two eigenvalue-based functions and the integral of the time multiplied absolute value of the error (ITAE)-based objective function. The effectiveness of the proposed PSOPSS is tested on a large scale multi-machine power system under different operating conditions in comparison with the GAPSS [11]. Results evaluation show that the designed PSSs with proposed method achieves good robust performance for damping lowfrequency oscillations under different operating conditions and is superior to the other methods.

2

Particle swarm optimization

Particle swarm optimization algorithm, which is tailored for optimizing difficult numerical functions and based on a metaphor of human social interaction, is capable of mimicking the ability of human societies to process knowledge. It has roots in two main component methodologies: artificial life (such as bird flocking, fish schooling and swarming); and, evolutionary computation [14]. The higher dimensional space calculations of the PSO concept are performed over a series of time steps. The population is responding to the quality factors of the previous best individual values and the previous best group values. This optimization technique can be used to solve many of the same kinds of problems as GA, and does not suffer from some of the GAs difficulties. It has been found also to be robust in solving problem featuring non-linearing, non-differentiability and high-dimensionality [14].

In the PSO technique a number of simple entities, the particles, are placed in the search space of some problem or function, and each evaluates the objective function at its current location. Each particle then determines its movement through the search space by combining some aspect of the history of its own current and best locations by those with one or more members of the swarm with some random perturbations. The next iteration takes place after all particles have been moved. Eventually the swarm as a whole, like a flock of birds collectively foraging for food, is likely to move close to an optimum of the fitness function [13]. In the PSO technique, the trajectory of each individual in the search space is adjusted by dynamically altering the velocity of each particle, according to its own flying experience and the flying experience of the other particles in the search space. The position vector and the velocity vector of the ith particle in the D-dimensional search space can be represented as: X_i = (x_i1,x_i2,…,x_iD) and V_i = (v_i1,v_i2…v_iD) respectively. According to the user defined fitness function, let us say the best position of each particle, which corresponds to the best fitness value (pbest) obtained by that particle at time, be P_i = (p_i1,p_i2,…,p_iD), and the global version of the PSO keeps track of the overall best value (gbest), and its location obtained, thus far from any particle in the population. Then, the new velocities and the positions of the particles for the next fitness evaluation are calculated using the following two equations [13, 14]:

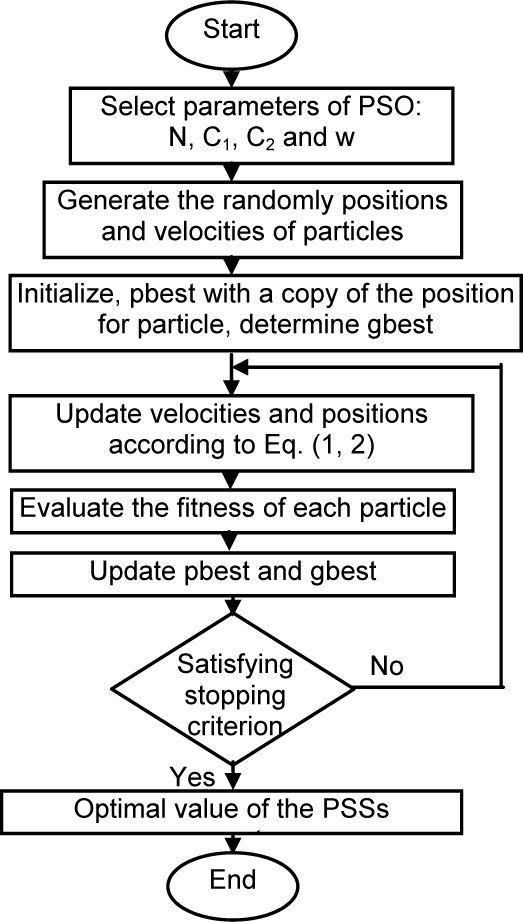
Where, P_id and P_gd are pbest and gbest. Here w is the inertia weight parameter which controls the global and local exploration capabilities of the particle. Constants c₁, c₂ are cognitive and social coefficients, respectively, and r₁r₂ are random numbers between 0 and 1. A larger inertia weight factor is used during initial exploration its value is gradually reduced as the search proceeds. Figure 1, shows the flowchart of the PSO algorithm.

Figure 1.

Flowchart of the PSO technique.

3

Problem formulation

3.1

Power system model

The aim of this study is to determine the parameters of power system stabilizers for damping oscillations. For this reason, appropriate modeling of the power system has a main role on better designing of stabilizers. To model the n-machine interconnected system, a set of differential algebraic equations is used and the model provided by assembling the models for each equipment such as generators, loads, controls etc. and connecting them appropriately via the network algebraic equations [15]. In this paper, the two-axis model [2], given in the Appendix, is used for time domain simulations and by linearizing the multi-machine power system around the operating points the simulation is done. The main objective of the PSS is increasing the rotor damping of a synchronous generator. By introducing appropriate supplementary control signals to the generator excitation system, this objective is achieved. Figure 2, shows a schema of a synchronous generator control components. The typical PSS block diagram used in this study is showed in Figure 3. The PSS operating function [3] is to produce a torque on the rotor of the machine involved in such a way that compensates the phase lag between the exciter input and the machine electrical torque. The dynamic compensator is made up to two lead-lag stages, an additional gain and a washout filter where Δω_i, is the deviation in speed from the synchronous speed, T_1i-T_4i are the lead-lag time constants, K_pss is the gain of the PSS and T_w is the washout time constant. The adjustable PSS parameters are the gain of the PSS, K_i, and the time constants, T_1i-T_4i which these time constants are usually not critical and they can range from 0.5 to 20 s. Hence, for each PSS, there are five parameters comprise of 4 time constants and a gain constant that should be determined to achieve optimal output. The output signal is fed as a supplementary input signal, V_pss to the regulator of the excitation system.

Figure 2.

Control diagram of synchronous machine.

Figure 3.

The structure of the PSS.

3.2

PSO based PSSs design

In this paper, for our optimization problem, the PSO is employed to minimize a multi-objective fitness function comprise of the ITAE-based and eigenvalue-based functions for the PSSs design problem. These objectives are defined as follows:

Where, σ_i, is the real part of the ith eigenvalue. Also, speed deviation (Δω), of the machines are considered for the evaluation of the j₂. The α₁ and α₂ are weighting factors and t_sim is the time range of simulation. The N_G is the number of machines and N_P is the total number of operating points for which the optimization is carried out. The value of σ₀ determines the relative stability in terms of damping factor margin provided for constraining the placement of eigenvalues during the process of optimization. By optimizing J₁, closed loop system poles are consistently pushed further left from the imaginary axis with simultaneous reduction in real parts. By optimizing J₂, the sum of deviation of speed in each generator speed response is getting minimized. The design problem can be formulated as the following constrained optimization problem, where the constraints are the PSS parameter bounds:

By employing the PSO, the proposed approach solves this optimization problem and search for optimal or near optimal set of the PSS parameters (K_i, T_1i−T_4ifor i=1,2,…,m where, m is the number of machines) [10].

4

Case study

In this study, the sixteen-machine five-area power system shown in Figure 4 is considered. The system comprises the five coherent groups representing a reduced model of the New England and New York interconnected system. Details of the system data are given in [16]. To assess the effectiveness and robustness of the proposed method over a wide range of loading conditions, five operating conditions (Table 1) without PSSs are considered.

Figure 4.

A New England–New York interconnected power system model.

Table 1.

Operating condition considered in the coordinated designing of the PSSs parameters.

Operating condition	Description
Base case	All lines in service
Case 1	Lines 33–34 are out of service
Case 2	Power generation at G6 increased 50%
Case 3	Lines 17–27 and 30–31 are out of service
Case 4	Lines 17–27 and 30–31 are out of service and Power generation at G8 and G10 increased 30%

4.1

PSO-based PSSs design

In the proposed method, we must tune the PSSs parameters optimally to improve the overall system dynamic stability in a robust way under different operating conditions and disturbances. For each PSS, the optimal setting of five parameters is determined by the PSO algorithm, i.e., 60 parameters to be optimized, namely K_i, T_1iT_2i,T_3i and T_4ifor i= 1, 2, …,12.

The optimization of the PSS parameters is carried out by evaluating the multi-objective function as given in Equation 5. In this work, in order to acquire better performance, number of particle, particle size, number of iteration, C₁, C₂, and C is chosen as 80, 60, 60, 2, 2 and 1, respectively. It should be noted that PSO algorithm is run several times and then optimal set of the PSSs parameters is selected. Results of the PSSs parameter achieved from the PSO algorithm are given in Table 2. The convergence rate of algorithm is illustrated in Figure 5.

Table 2.

Optimal PSSs parameters obtained by proposed method.

PSS number	K	T1	T2	T3	T4
G1	62.13	0.9037	0.0534	0.6332	0.4148
G2	197.7	0.7673	0.1747	0.4140	0.2492
G3	194.8	0.8147	0.1826	0.6761	0.7490
G4	126.62	0.6721	0.8259	0.8120	0.8544
G5	136.19	0.6690	0.2189	0.7219	0.9637
G6	198.37	0.6380	0.4256	0.9287	0.6872
G7	119.21	0.4391	0.2381	0.8901	0.5729
G8	128.07	0.7237	0.1584	0.8570	0.8297
G9	105.08	0.7803	0.9372	0.8173	0.2460
G10	174.77	0.6620	0.1454	0.9333	0.6595
G11	167.32	0.7904	0.1278	0.8422	0.8867
G12	116.73	0.8844	0.4280	0.8454	0.3693

Figure 5.

Variations of objective function.

4.2

Eigenvalue analysis

The PSSs were placed in all generators, except for the ones numbered as 13, 14, 15 and 16 in Figure 4. To assess the effectiveness and robustness of the proposed controller, a multiple of operating conditions according to Table 1 are considered and simulation studies are carried out for various fault disturbances and fault clearing sequences for two scenarios. The eigenvalues analysis from the two cases with proposed PSSs and from the base case without PSSs is depicted in Figure 6. Moreover, it is also clear that the system damping with the proposed PSO based tuned PSSs with multi-objective function has improved significantly.

Figure 6.

Eigenvalues of case study in three different operating conditions a) Without PSS-base case b) With PSS base case c) With PSS case 1.

4.3

Nonlinear simulation results

Scenario 1

In this scenario, by applying a three-cycle, three phase fault at bus 1, on line 1–2 the performance of the proposed controller under transient conditions is verified. The fault is cleared after 0.06 seconds and the original system is restored upon the clearance of the fault. The performance of the tuned multi-objective based PSSs is compared to that of the PSSs tuned using the GA for different operating conditions as given in Table 2. The speed deviations of generators G₃, G₈, G₁₀, G₁₂, G₁₃ and G₁₄ and the power flow on lines 1–30, 9–36, 9–30, 78 and 17–18 under the above conditions are shown in Figure 7. It can be seen that the PSOPSSs with multi-objective function achieves good robust performance and provides superior damping in comparison with the other methods.

Figure 7.

System response at scenario 1 with different operating conditions: Solid (PSOPSS) and dotted (GAPSS).

Scenario 2

In this scenario, another severe disturbance is considered for different loading conditions; that is, a five-cycle, three-phase fault is applied at bus 10, on line 10–11. The fault is cleared after 0.1 seconds and the original system is restored upon the clearance of the fault. The system response is shown in Figure 8. It can be seen that the proposed PSOPSSs have good performance in damping of the low frequency oscillations and stabilizes the system quickly.

Figure 8.

System response at scenario 2 with different operating conditions: Solid (PSOPSS) and dotted (GAPSS).

To demonstrate the performance robustness of the proposed method, two indices for system performance characteristics are defined as follows [3]:

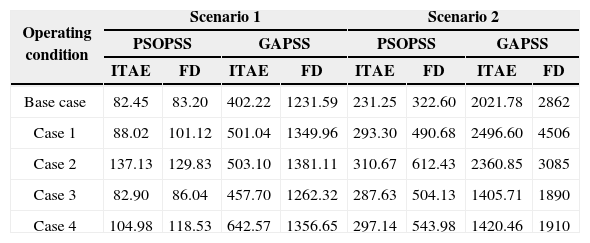
Where ω is the speed rotor; overshoot (OS); undershoot (US) and settling time (T_s) of all generators, speed deviations are considered for the evaluation of the ITAE and FD indices. The t_sim is the simulation time which is 10 seconds here. The lower the value of these indices is, the better the performance of system in disturbances. The results of evaluating these two indices for different operating conditions under various disturbances for PSOPSS in comparison with GAPSS are brought in Table 3. It can be seen that the value of these indices for the proposed method are much smaller than other methods. This demonstrates that the overshoot, undershoot, settling time and speed deviations of the machine are greatly reduced by applying the proposed stabilizers.

Table 3.

Values of ITAE and FD indices in different operating conditions at different scenarios.

Operating condition	Scenario 1				Scenario 2
	PSOPSS		GAPSS		PSOPSS		GAPSS
	ITAE	FD	ITAE	FD	ITAE	FD	ITAE	FD
Base case	82.45	83.20	402.22	1231.59	231.25	322.60	2021.78	2862
Case 1	88.02	101.12	501.04	1349.96	293.30	490.68	2496.60	4506
Case 2	137.13	129.83	503.10	1381.11	310.67	612.43	2360.85	3085
Case 3	82.90	86.04	457.70	1262.32	287.63	504.13	1405.71	1890
Case 4	104.98	118.53	642.57	1356.65	297.14	543.98	1420.46	1910

5

Conclusions

In order to improve the transient stability and damp the low frequency oscillations, robust PSSs design based on a multi-objective fitness function consist of a composite set of two eigenvalue based and the ITAE-based objective functions was proposed in large power systems. The design problem was formulated as a nonlinear optimization problem for multiple operating conditions. Then, the PSO algorithm was successfully applied to find the optimal solution of the design problem. The nonlinear simulation results under different operating conditions show the effectiveness of the proposed controllers and their ability to provide good damping of low frequency oscillations in comparison to the GAPSS method and the results demonstrated the superiority of the proposed method in solution quality. The ITAE and FD indices revealed that by using the proposed objective based function controllers, the overshoot, undershoot, settling time and power system oscillations are greatly reduced at various loading conditions.