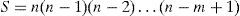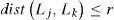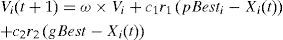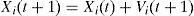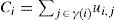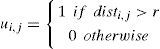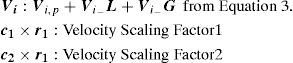Cell Assignment in Hybrid CMOS/Nanodevices Architecture Using a PSO/SA Hybrid Algorithm

Abstract

In recent years, substantial advancements have been made in VLSI technology. With the introduction of CMOL (Cmos\nanowire\MOLecular Hybrid), higher circuit densities are possible. In CMOL there is an additional layer of nanofabric on top of CMOS stack. Nanodevices that lie between overlapping nanowires are programmable and can implement any combinational logic using a netlist of NOR gates. The limitation on the length of nanowires put a constraint on the connectivity domain of a circuit. The gates connected to each other must be within a connectivity radius; otherwise an extra buffer is inserted to connect them. Particle swarm optimization (PSO) has been used in a variety of problems that are NP- hard. PSO compared to the other iterative heuristic techniques is simpler to implement. Besides, it delivers comparable results. In this paper, a hybrid of PSO and simulated annealing (SA) for solving the cell assignment in CMOL, an NP-hard problem, is proposed. The proposed method takes advantage of the exploration and exploitation factors of PSO and the intrinsic hill climbing feature of SA to reduce the number of buffers to be inserted. Experiments conducted on ISCAS'89 benchmark circuits and a comparison with other heuristic techniques, are presented. Results showed that the proposed hybrid algorithm achieved better solution in terms of buffer count in reasonable time.

1

Introduction

In recent years, we have witnessed a tremendous development in the field of VLSI. We have seen the appearance of novel nanodevices, nanocircuits, nano-crossbar arrays [1], manufactured by nano- imprint lithography [2], CMOS/nano co-design architectures [3], and, their applications [5], [1]. Likharev and his colleagues [3], [4], developed the idea of CMOL (Cmos\nanowire\MOLecular Hybrid) for nanoelectronic devices. One of the problems in CMOL based circuit design is cell assignment.

The CMOL cell assignment problem can be modeled as a special case of cell assignment problem on an FPGA, where one of the main objectives is to reduce the overall wire length. Whereas in CMOL, the goal is to place the connected cells close to each other with the constraint that these connected cells lie within a given radius from each other. Considerable amount of work has been done to tackle this problem. Strukov et al. proposed a deterministic algorithm [15], suitable for small circuits. Non-deterministic heuristic algorithms such as tabu search, particle swarm and simulated annealing have been widely used to solve a multitude of combinatorial optimization problems [20, 21, 22]. Xia Y. et al used genetic algorithm (GA) and laid the foundation to solve CMOL cell assignment problem using iterative heuristic algorithms [17]. The GA was able to find good solutions within acceptable time for circuits of varying complexity. Memetic algorithm (MA) an improvement of GA proposed by Z. Chu et al. [18], is a combination of GA and simulated annealing (SA). Another recent improvement proposed by Y. Xia et al. [19] combines Lagrangian relaxation (LR) technique and MA, hence the name LRMA, to solve the CMOL cell assignment problem. Higher quality solutions in terms of computational time and solution quality are reported with LRMA as compared to both GA and MA.

Ideas on combining strengths of different heuristics have been around for some time. In the past SA has been used effectively as a hybrid with other algorithms like tabu search (TS), genetic algorithm (GA) and simulated evolution (SimE) [11]. The basic idea of hybridization is to enhance the strengths and compensate for the weaknesses of two or more complementary approaches [10].

In this paper, the CMOL cell assignment problem using a hybrid of particle swarm optimization (PSO) technique and the simulated annealing (SA) algorithm is investigated. PSO, developed by Kennedy & Eberhart in 1995, is based on the social behavior of birds, fish and bees [12]. The strength of PSO lies in its simplicity of implementation and in achieving comparable and sometimes better results as compared to other heuristic techniques. PSO has been widely used in problems such as bandwidth minimization [9], FPGA cell assignment [13][8] and others.

In PSO, each particle carries a complete solution whose global best and the particle's personal best solution are updated only when the current solution improves, and this may lead to entrapment in a local minima. Simulated annealing (SA) algorithm is another widely used iterative heuristic algorithm. The powerful feature of SA is its intrinsic hill climbing capability. Therefore, SA is used in conjunction with the PSO algorithm for local minima avoidance. The proposed technique in [8], [9] is adopted for the CMOL cell assignment problem.

The rest of the paper is organized as follows: In Section 2, CMOL architecture is discussed. Problem formulation is given in Section 3. Section 4, discusses how PSO and SA are utilized to solve this problem. Implementation results are given in Section 5 and conclusions are drawn in Section 6.

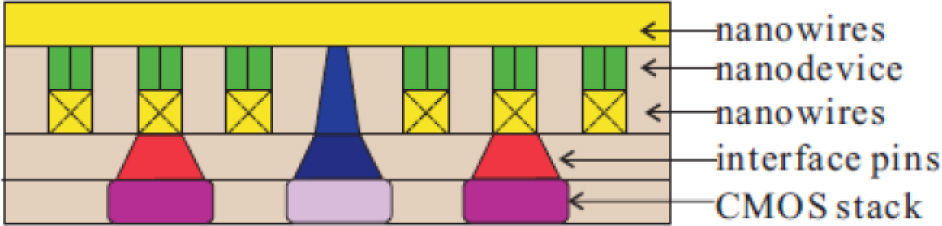
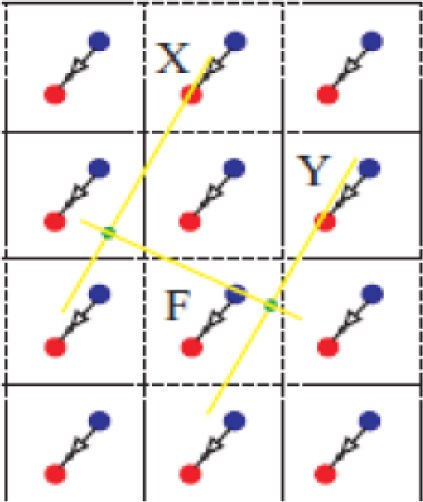
2

CMOL FPGA architecture

CMOL, developed by Likharev et al. [3], consists of nanodevices. These nanodevices can be any two terminal nanodevices, e.g., “latching switch” based on molecules with two metastable internal states. Figure 1 shows the basic structure of CMOL. The nanodevices are sandwiched between the two levels of perpendicular nano-imprinted nanowires. Logic functions are created by a combination of CMOS inverters and diode-like nanodevices as shown in Figure 2. In each cell there is a CMOS inverter, and nanowires are aligned such that one of their ends receive signal from the output of CMOS inverters. Those nanowires are OR'ed together with nanowires aligned with another (in orthogonal direction) according to the nanodevice configurations to give a wired-OR logic. This OR'ed signal goes to the inverter's input, which is on the CMOS stack to implement the required NOR-INV logic. For example, in Figure 2, X, Y and F are three signals connected with the three grayed cells' output pins. With the shown nanowire connections (lines) and “ON” nanodevices (dots), the logic expression is F=X+Y―.

Figure 1.

Generic CMOL circuit schematic side view.

Figure 2.

CMOL FPGA configuration example [4].

This cell assignment task poses a challenge for larger circuits. In this paper our goal is to investigate this problem as an optimization problem, while reducing the buffers, and finding a solution in reasonable CPU time.

3

Problem formulation

In computer-aided design (CAD) of digital systems, the assignment of cells to a given set of locations (in order to minimize a given cost function) is an NP-hard problem [11]. Even the simplest case of one dimensional assignment problem is hard to solve. In a 2-D array of n locations there are as many as the following arrangements for placing m cells.

Where m could be in multiples of thousands. Due to the aforementioned complexity and overtime work, designers have turned their attention to develop heuristic techniques to solve the assignment problem in order to find an optimal solution in polynomial time.

Given a collection of NOR/INV gates, and the collection of nets (the set of ports to be connected together), the CMOL cell assignment problem consists of finding suitable locations for each gate under the constraint of connectivity domain and a given cost function. Formally the problem can be restated as: For a set of gates G = g1,g2,g3,…gm and a set of netlists Γ = γ₁,γ₂,γ₃,…γ_m where γ_i = {fan - in_i, & fan - out_i} of g_i and given a set of slots or locations L = L₁,L₂,L₃,…,L_n where m ≤ n, the assignment problem is to assign each g_i ∈ G to a unique location L_j such that the objective is optimized. Positions are defined by the coordinate values (x_i,y_j) and the subset of G that represent inputs/outputs may be pre-assigned to fixed locations or constrained to certain positions.

Each CMOL cell can implement one inverter or one NOR gate with multiple fan-in, however, complying with connectivity constraint can be substantially harder if gates of high fan-in are allowed. Each CMOL cell can be connected to one of its proximity cell members; any violation of this constraint would impose further processing (i.e., buffer insertion) to satisfy connectivity. However, such process would cause more congestion to the already congested CMOL circuit and could result in substantial increase of timing delay. Mathematically, the “Connectivity Domain” can be defined as follows; given a gate and its netlist (g_i, γ_i) placed in location L_i, for any gate g_k ⊆ G and g_k in the netlist γ_i, the following Inequality should be satisfied.

Where L_k is the location of g_k. dist is the Manhattan distance, and r is CMOL connectivity radius. The objective of CMOL cell assignment is to satisfy the constraint inequality (2), and to minimize the distance between connected gates in circuit G. Failing to comply with CMOL constraint will result in an implementation that has more delay and area requirements.

4

Particle swarm optimization (PSO)

PSO which was proposed by Kennedy and Eberhart [13] is utilized in this work. A PSO algorithm consists of two main components, velocity and position. The velocity determines the rate at which a particle can change its position. In PSO, the non-determinism comes from the velocity component only. The discrete PSO as proposed by the original authors consists of the following two main equations:

In the above equations, ω is a constant to give certain weight to previous velocity, c₁ and c₂ are arbitrary constants, r₁ and r₂ are random variables of uniform distribution, pBest_i is the best solution of particle i so far, gBest is the overall global best solution among all particles. The pBest_i of a particle is the exploitation factor, while gBest helps in the exploration of solution space. This way, particles try not only to come closer to their own best solution, but also to the global best solution with a certain probability and weight factor.

In the proposed discrete PSO algorithm, each particle holds a complete solution which in our case is a 2-D grid representation of the assignment. For example, if the dimensions of a grid are 5 × 5, then the position of a particle is an assignment of cells to this grid of 25 elements with I/Os on the outer boundary of grid. Empty locations are denoted by −1. In the proposed formulation, the velocity is represented as a sequence of swaps [8][9]. For example, velocity V = (2,5); (4,7) represents swaps between cells 2 & 5 and 4 & 7, respectively. Swaps can only be performed between cells of the same types i.e., I/O with an I/O and Gate with a Gate. Hence, two velocity vectors are maintained and updated. Swapping between different logic types is not allowed. The current position of a particle X_i denotes the assignment of all cells within a grid. During initialization, the position X_i of each particle is initialized randomly and the velocity V_i is zero to control the total number of swaps, |V_i| = 0 → V_max.

The algorithm used in this work is shown in Figure 3. In the proposed algorithm [Compute VI/Oi,VLogici] and [Compute XI/Oi,XLogici] are computed using Equations (3) and (4) for each particle i respectively. Construct Xi=XI/Oi,XLogici means constructing a new grid based on updated positions of XI/Oi and XLogici.

Figure 3.

PSO algorithm.

Simulated annealing (SA) algorithm [11] is shown in Figure 4. It is invoked for each particle i if the global best solution does not improve for 10 iterations. It works by constructing a list of cells violating the connectivity constraint and then randomly swapping them with cells in the grid. The decision to make a swap is based on the condition given at line 15 in Figure 4, where “random” is a uniformly distributed random number. Hence, using SA, the movements of individual cell can be controlled in order to search for better solution.

Figure 4.

Simulated annealing (SA) algorithm.

4.1

PSO operators

In the context of cell assignment problem, the operators used in the discrete PSO equation 3 and 4, need to be defined. In order to subtract two vectors, let us say X – Y, the result of subtraction will be the number of swaps required so that vector Y becomes vector X. Therefore, the velocity is defined as the number of required swaps.

The complexity of this operation increases significantly when the problem size increases.

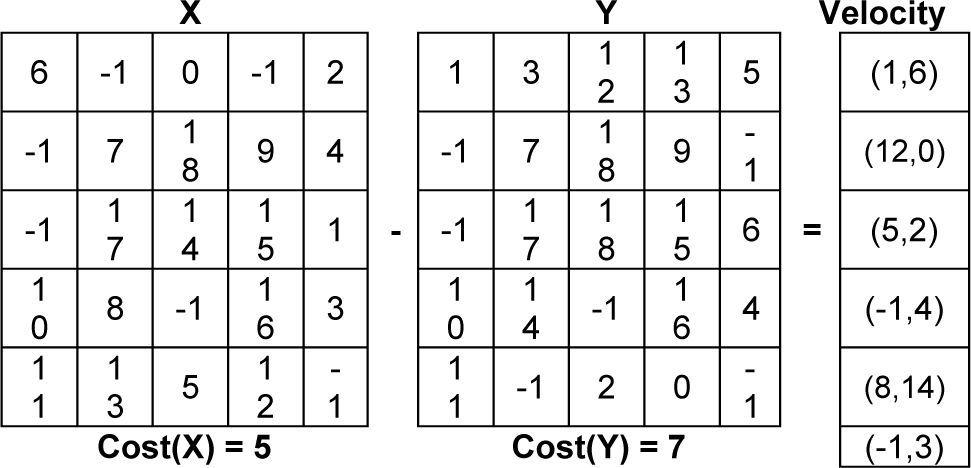
Therefore, the size of the resulting velocity is clamped to V_max to limit the number of swaps from becoming too large. The subtract operator is explained in Figure 5, as can be observed, |V| = 6 ⇒ six swaps have to be applied on grid Y so that Y = X. The velocity vector contains the sequence of swaps between corresponding cells.

Figure 5.

Subtraction b/2 two grids and their resultant velocity vector.

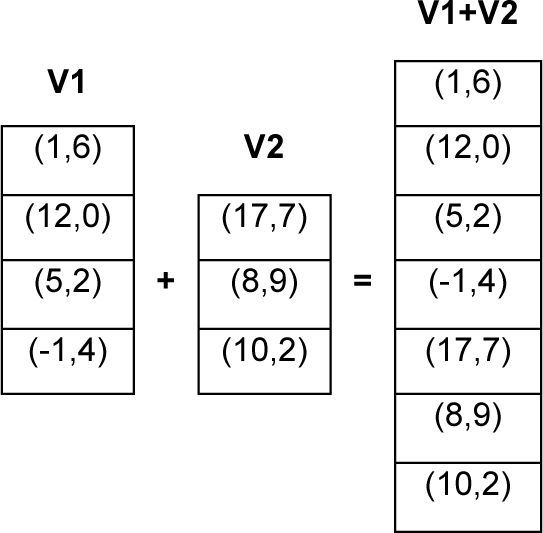
Multiplying a velocity ν by a constant c implies increasing the number of swaps if constant is > 1. Otherwise, the velocity vector is truncated. Then, if c > 1, then new swaps are added to the end of ν to increase its length by |ν| − c. The swaps to be added are extracted from the top of ν. Similarly, if c < 1, then swaps are truncated until the size of resulting velocity ≈ ν × c. The multiplication of velocity vector with a constant is illustrated in Figure 6 and the addition of two velocity vectors is shown in Figure 7.

Figure 6.

Scaling velocity by a constant.

Figure 7.

Addition of two velocity vectors.

Adding velocity to the current position X_i is performed by applying the swaps as given in the velocity vector to the position vector. The position vector X_i denotes the locations of all cells within a grid. For example, the arrangement of cells in two grids in Figure 5 can be a position vector X_i of a particle. Swaps are applied in the same order as given in the velocity vector.

4.2

PSO problem formulation

In the proposed DPSO algorithm, the position vector X is divided into two vectors X_logic and X_I/O. This is to make sure that no swaps can occur between an I/O and a logic Gate. Corresponding to it, the velocity vector V is also split into two vectors i.e., V_logic and X_I/O. To update the position and velocity of each particle, Equation 3 and 4 are applied twice with operators defined in Subsection 4.1. To evaluate the fitness of particle's new position, both X_logic and X_I/O are used to construct the complete position X.

In CMOL cell assignment problem, the solution is an arrangement of logic cell in two dimensional grid. The grid is constructed by computing the number of CMOL cells required for each benchmark circuit. The outer cells of the grid are reserved for I/O pins and the inner cells are reserved for logic gates. This is to make sure that the movements of cells are constrained to their respective domains. After initialization, the contents of each cell in a grid denote the I/O pin/logic gate number it is holding. Empty locations can be denoted by -1. An example of a sample solution is shown in Figure 5 for a small circuit.

4.3

Cost evaluation

The objective of cell assignment is to find cell assignments in a way such that all connections are satisfied. In CMOL assignment, as explained in Section 3, each cell has a connectivity radius and if

A cell is out of the radius then, an extra buffer(s) need to be inserted. Given that the cells in CMOL are already connected via pre-assembled nanowires, the optimization problem is to place the cells in order to eliminate the need to insert extra buffers. Therefore, a measure to capture the overall quality of the solution has to be defined. One simple approach is to calculate the number of nets that violate the connectivity domain constraint. The cost of each gate g ∈ G is given in Equation 5(b), where the cost of overall circuit is the sum of the costs of individual gates.

4.4

Particle's evolution

Each particle is randomly initialized with a unique solution. The best solution achieved by a particle during the course of iterations is its personal best solution. Global best solution is a best solution among the personal best solutions of all particles. Therefore, initially, each particle will have a different cost value. To change its position, each particle will either increase or decrease its velocity (number of swaps) in order to non-deterministically get closer to its personal best and the global best solution. As illustrated, the velocity in our case is the number of swaps required by a particle to move from one state to the other. Because the problem at hand requires the cells to be placed within each other's connectivity radius before making any swap, cost will be evaluated, as mentioned in Subsection 4.3, before and after the swap. If the cost is improved or in case the new cost is the same as the previous one, then if overall Manhattan distance is reduced swap is performed, otherwise, it will not. This way, only those swaps that will improve the cost function are made and others are ignored.

The intrinsic greedy nature of PSO algorithms allow them to converge very quickly, which may lead to local minima entrapment. Moreover, the PSO algorithm lacks the individual learning capability based on the fitness score of each cell. To address this simulated annealing (SA),- based local search algorithm is employed. SA has been used for a variety of problems and has its strength in the simplicity of its implementation. If SA is run for very long time, then it will give an optimal solution. In this algorithm K_max number of random swaps between I/Os or logic gates for each particle's solution are performed. To avoid local minima, the SA algorithm will accept a solution of increased cost with probability e−ΔhT. The initial temperature T is set to be 1.2. The cooling process is implemented using the relation T_new = αT_old. The value of α is fixed at 0.9.

4.5

An illustrative example

Let us consider an example of a simple benchmark circuit to elaborate the working principle of the proposed algorithm. For the sake of simplicity, our example has the following parameters, No. of Particles = 3, c₁ = c₂ = 1.5, ω = 0.2 and connectivity radius = 3. The considered circuit s27.blif has Total Gates = 19, Logic Gates = 11, I/O Gates = 8 and Grid Size = 5 × 5. The abbreviations used in the example are shown below along their definitions.

V_i,p: Previous velocity vector of particle i, computed using ω × V_i from Equation 3.

V_i−L: Personal best velocity vector of particle i computed using c₁r₁(pBest_i − X_i(t)) from Equation 3.

V_i−G: Global best velocity vector among all particles computed using c₂r₂(gBest − X_i(t)) from Equation 3.

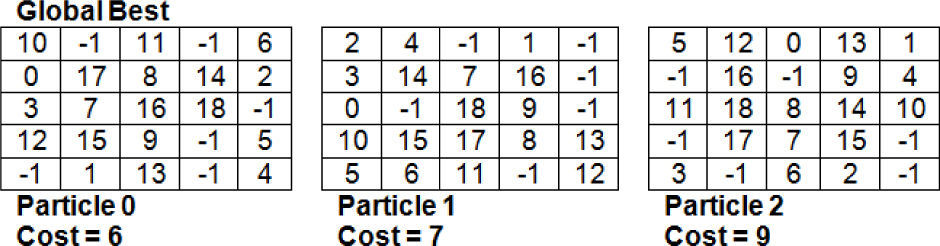
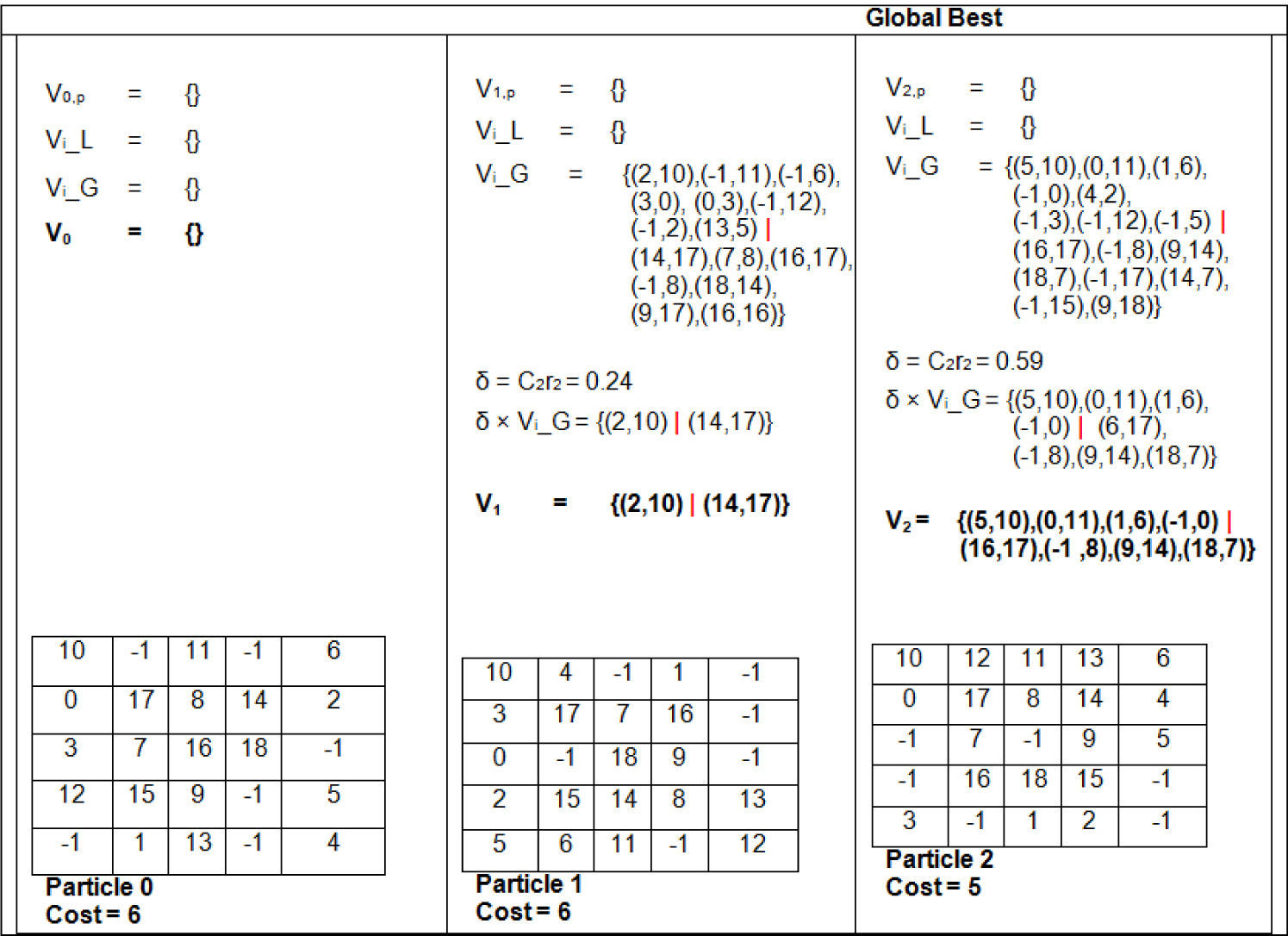
The state of three particles along their costs is shown in Figure 8. The initial velocities of all the particles are initialized to 0. It can also be observed that after initialization the best particle is Particle 0 and the local best solution of each particle is their current solution. We will now go through a few iterations to see how the particles evolve.

Figure 8.

Particles initial state.

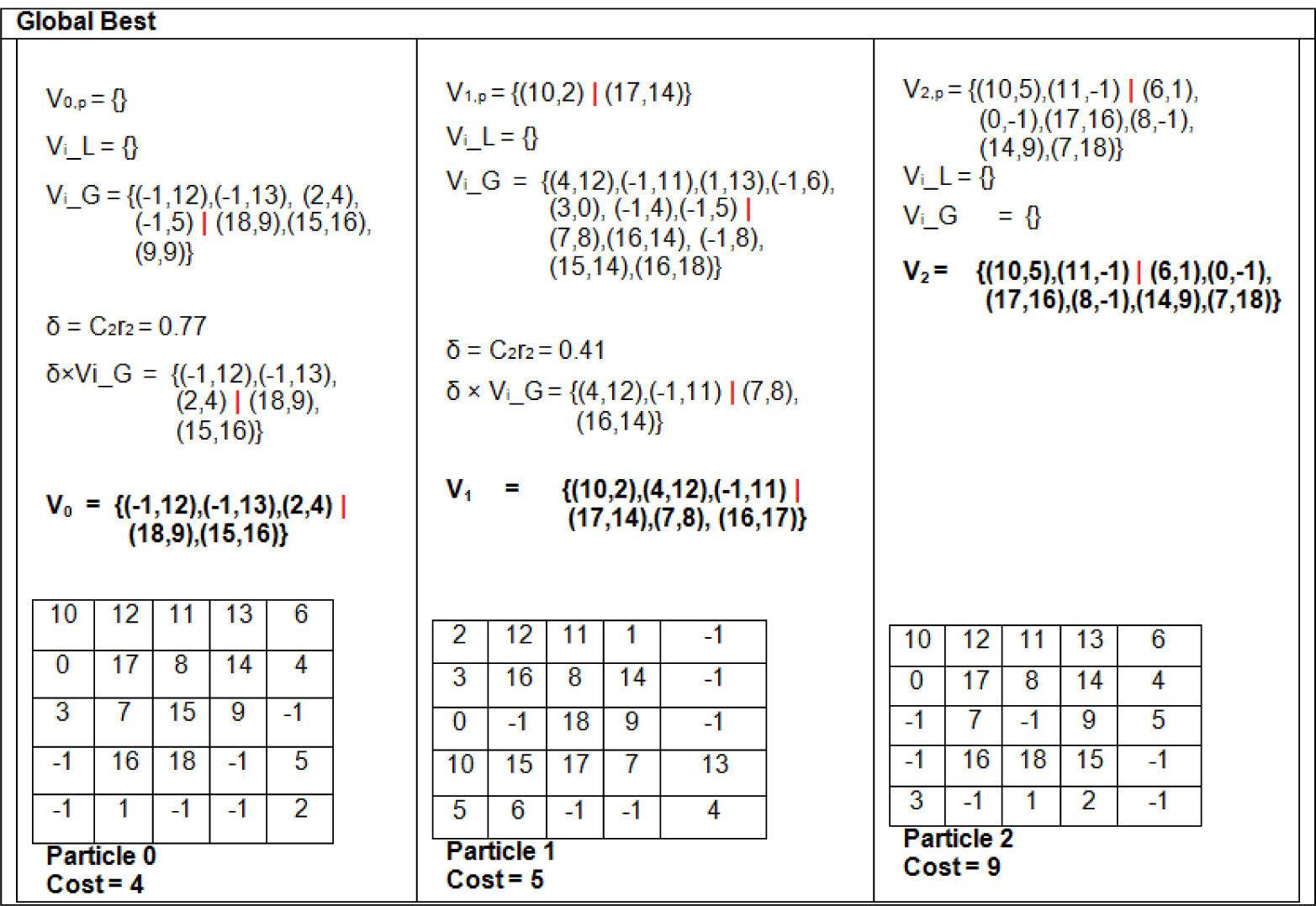
V_i−L is a set of swaps that are required by a particle to move from its current position to its local best position. V_i−G is a set of swaps that are required by a particle to move from its current position to the global best position. V_i−L and V_i−G are scaled by c₁ × r₁ and c₂ × r₂, respectively so that the new position may lie somewhere between particle's own best solution and the global best solution, which helps in exploiting the current and exploring the new solutions. Initially, |V_i−L| = |V_i,p| = |V_i−G| = 0 for all particles. After first iteration the particle's state is shown in Figure 9. The I/O swaps and logic swaps are separated by “|” in the velocity vectors. The solutions shown in Figure 9 are obtained by applying the swaps to the initial state of particles. Similarly, the solutions in Figure 10 were computed by applying the swaps mentioned before to the grids of Figure 9.

Figure 9.

Iteration l Swaps are applied to the initial state of particles.

Figure 10.

Iteration 2. Swaps are applied to the solutions in iteration 1.

For Particle 0 in iteration 1, all the velocity components are zero because initially, Particle 0 holds the global best solution. Therefore, no swaps are applied to Particle 0 and its position/solution remains unchanged after 1st iteration. For Particle 1 In iteration 1 velocity component w.r.t the global best solution is present and other velocity components are zero. The |V_i−G| = 15, for Particle 1, multiplying it by the scaling constant δ = 0.24 implies |V_i−G| = 2. Therefore, only two swaps are applied to the initial state of Particle 1 to get the new solution shown in Figure 9. Hence, after first iteration the global best particle is 2 with cost = 5.

Regarding the personal best solutions, for Particle 1 it remains unchanged because its own solution did not change in iteration 1. Particle 1's personal best solution is changed as its Cost_NEW = 6 < Cost_Initial = 7. Particle 2, which happens to be that the global best solution has also the new personal best solution.

After 2^nd iteration Particle 0 has the global best solution with Cost_NEW = 4, therefore its personal best solution is also updated. Particle 1's personal best solution is also updated with Cost_NEW = 5. Particle 2's new solution has Cost_NEW = 9 > Cost_Previous = 5, therefore its personal best solution is not updated, despite its current position is changed which has a greater cost as can be observed in Figure 10.

After 3^rd iteration, the global solution did not improve, therefore, it remains unchanged as achieved after 2^nd iteration. Only the personal best solutions of Particle 1 and Particle 2 are updated, because their new cost is 4. The, personal best for Particle 0 does not change as its Cost_NEW = 6 > Cost_Previous = 4.

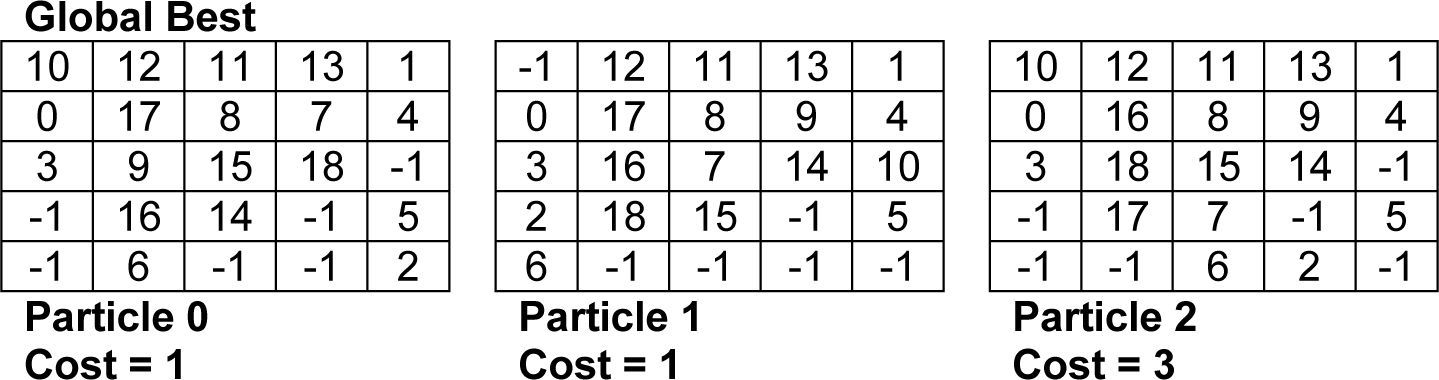
The discussed example is run for 10 iterations. The best solution is achieved after 9 iterations. The results produced after 9^th iteration are shown in Figure 12. The best cost/buffer count achieved after 10 iterations is 1.

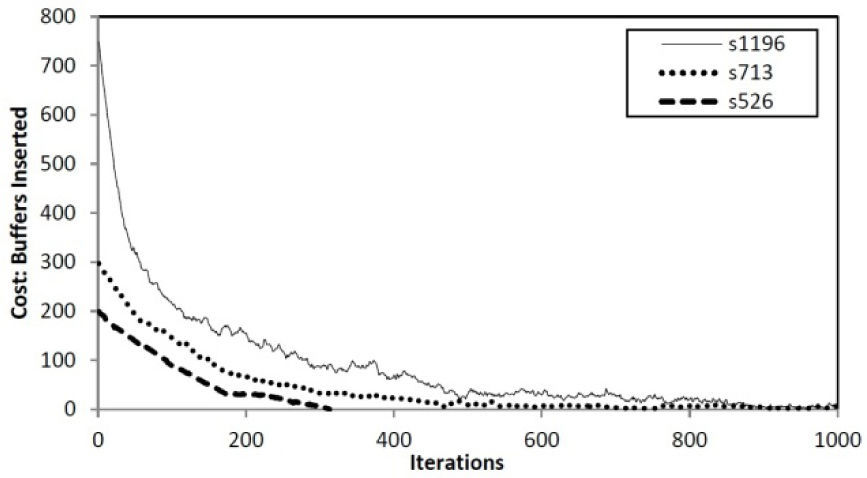
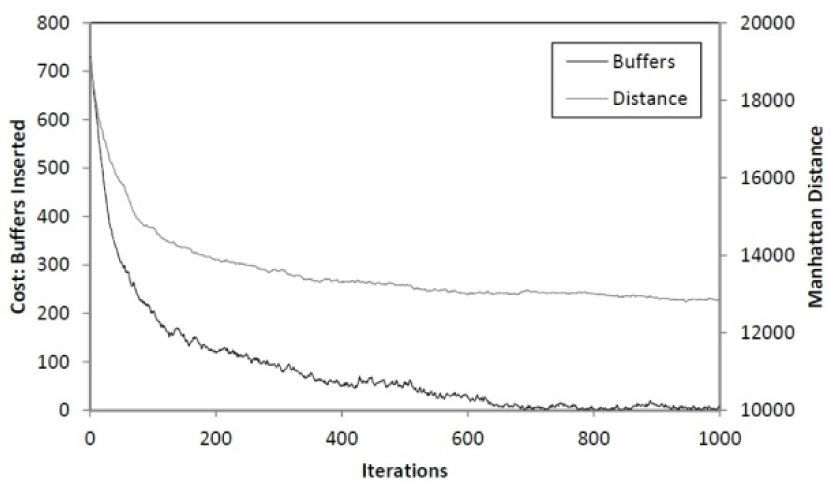
5

Implementation results

To evaluate the efficacy of the proposed algorithm ISCAS'89 benchmarks [14] have been used. These benchmark circuits are mapped to NOR-based gates, like CMOL layout, they consists only of NOR gates [7]. PSO is implemented using Perl scripting language and executed on a machine with 1.6 GHz Intel dual-core processor. The objective function used to solve the CMOL cell assignment problem is to reduce the number of buffers. Figure 13 shows the change in cost per iteration for few benchmark circuits of varying space complexity. Figure 14 explains the effect of buffers minimization cost function on the Manhattan distance.

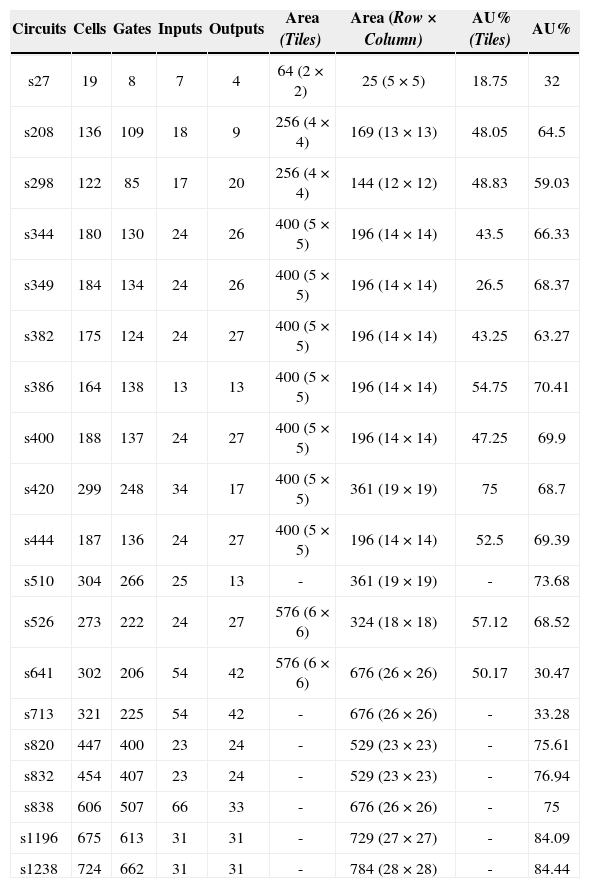
Table 1 shows the number of cells (i.e., NOR/INV logic gates), inputs and outputs of benchmark circuits used; Area (Tiles) is the area used by CM OLFPGA CAD 1.0 tool [15], while Area (Row × Column) is the area used in GA [17], MA [18], LRMA [19] and PSO. The algorithm is executed for a specific number of iterations. The heuristics stops when all the gate violations are removed or solution does not improve for a certain number of iterations. In this work if the global best solution in PSO algorithm does not improve for 10 iterations then SA is invoked for each particle and after that the PSO algorithm resumes. The PSO is stopped if the overall best solution does not improve for 50 iterations and results are reported. The median value of results obtained from 20 runs for each circuit is reported where each run uses different seeds for random numbers.

Table 1.

ISCAS'89 Benchmarks showing the number of cells to be placed including gates, inputs and outputs area is the size of CMOL 2-D grid. AU% is the fraction of utilized cells in CMOL grid.

Circuits	Cells	Gates	Inputs	Outputs	Area (Tiles)	Area (Row × Column)	AU% (Tiles)	AU%
s27	19	8	7	4	64 (2 × 2)	25 (5 × 5)	18.75	32
s208	136	109	18	9	256 (4 × 4)	169 (13 × 13)	48.05	64.5
s298	122	85	17	20	256 (4 × 4)	144 (12 × 12)	48.83	59.03
s344	180	130	24	26	400 (5 × 5)	196 (14 × 14)	43.5	66.33
s349	184	134	24	26	400 (5 × 5)	196 (14 × 14)	26.5	68.37
s382	175	124	24	27	400 (5 × 5)	196 (14 × 14)	43.25	63.27
s386	164	138	13	13	400 (5 × 5)	196 (14 × 14)	54.75	70.41
s400	188	137	24	27	400 (5 × 5)	196 (14 × 14)	47.25	69.9
s420	299	248	34	17	400 (5 × 5)	361 (19 × 19)	75	68.7
s444	187	136	24	27	400 (5 × 5)	196 (14 × 14)	52.5	69.39
s510	304	266	25	13	-	361 (19 × 19)	-	73.68
s526	273	222	24	27	576 (6 × 6)	324 (18 × 18)	57.12	68.52
s641	302	206	54	42	576 (6 × 6)	676 (26 × 26)	50.17	30.47
s713	321	225	54	42	-	676 (26 × 26)	-	33.28
s820	447	400	23	24	-	529 (23 × 23)	-	75.61
s832	454	407	23	24	-	529 (23 × 23)	-	76.94
s838	606	507	66	33	-	676 (26 × 26)	-	75
s1196	675	613	31	31	-	729 (27 × 27)	-	84.09
s1238	724	662	31	31	-	784 (28 × 28)	-	84.44

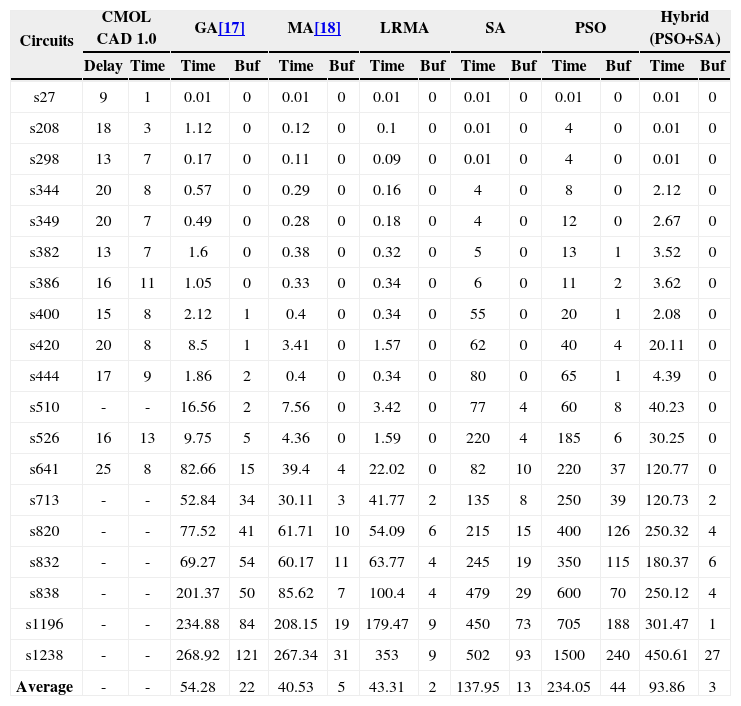
The connectivity radius is set to r = 12. The parameters are c₁ = c₂ = 1.5 and ω = 0.9 → 0.1 in PSO algorithm. SA used in our approach has initial temperature T = 1.2, =α = 0.9 and K_max = 50. Comparison is performed with CMOL FPGA CAD 1.0, GA, MA and LRMA. All algorithms except CMOL FPGA CAD 1.0 have population size of 24 and stopping criteria is based on non-improving cost in 50 iterations. Table 2 shows the final results obtained for ISCAS'89 benchmarks when r = 12; computation time (Time) is in seconds, (Buf) shows the number of inserted buffers to satisfy CMOL connectivity domain.

Table 2.

ISCAS'89 comparison with CMOL CAD, GA, MA and LRMA − (r = 12).

Circuits	CMOL CAD 1.0		GA[17]		MA[18]		LRMA		SA		PSO		Hybrid (PSO+SA)
	Delay	Time	Time	Buf	Time	Buf	Time	Buf	Time	Buf	Time	Buf	Time	Buf
s27	9	1	0.01	0	0.01	0	0.01	0	0.01	0	0.01	0	0.01	0
s208	18	3	1.12	0	0.12	0	0.1	0	0.01	0	4	0	0.01	0
s298	13	7	0.17	0	0.11	0	0.09	0	0.01	0	4	0	0.01	0
s344	20	8	0.57	0	0.29	0	0.16	0	4	0	8	0	2.12	0
s349	20	7	0.49	0	0.28	0	0.18	0	4	0	12	0	2.67	0
s382	13	7	1.6	0	0.38	0	0.32	0	5	0	13	1	3.52	0
s386	16	11	1.05	0	0.33	0	0.34	0	6	0	11	2	3.62	0
s400	15	8	2.12	1	0.4	0	0.34	0	55	0	20	1	2.08	0
s420	20	8	8.5	1	3.41	0	1.57	0	62	0	40	4	20.11	0
s444	17	9	1.86	2	0.4	0	0.34	0	80	0	65	1	4.39	0
s510	-	-	16.56	2	7.56	0	3.42	0	77	4	60	8	40.23	0
s526	16	13	9.75	5	4.36	0	1.59	0	220	4	185	6	30.25	0
s641	25	8	82.66	15	39.4	4	22.02	0	82	10	220	37	120.77	0
s713	-	-	52.84	34	30.11	3	41.77	2	135	8	250	39	120.73	2
s820	-	-	77.52	41	61.71	10	54.09	6	215	15	400	126	250.32	4
s832	-	-	69.27	54	60.17	11	63.77	4	245	19	350	115	180.37	6
s838	-	-	201.37	50	85.62	7	100.4	4	479	29	600	70	250.12	4
s1196	-	-	234.88	84	208.15	19	179.47	9	450	73	705	188	301.47	1
s1238	-	-	268.92	121	267.34	31	353	9	502	93	1500	240	450.61	27
Average	-	-	54.28	22	40.53	5	43.31	2	137.95	13	234.05	44	93.86	3

Figure 12.

Final arrangement of cells in grid after 10 iterations.

Figure 13.

Change in cost per iteration of few benchmarks.

Figure 14.

Change in cost and Manhattan distance per iteration of s1196.blif.

PSO solutions are more effective than those of CMOL CAD 1.0 in terms of delay and area utilization. The last two columns of Table 1 show that cell-based CMOL architecture has better area utilization AU% than that of tile-based architecture. Table 2 indicates that the tile-based approach is the most time consuming and the least effective in timing delay, it also fails to place big circuits.

The results achieved by hybrid PSO/SA algorithm, as shown in Table 2, are better than GA and MA in terms of number of inserted buffers for all benchmark circuits. It can also be observed that the overall solution quality and computation time by SA and PSO just for larger circuits is not encouraging. Hybrid algorithm produced results that are better in all performance comparison criteria. Comparing to LRMA, better results are achieved in terms of delay and number of inserted buffers for all benchmark circuits except for s832 ands1238, as they require more buffers in the proposed approach. The average time taken by PSO/SA hybrid is more as compared to other techniques due to the compute intensive operations of updating the velocity and position of each particle.

6

Conclusions

This paper discussed the implementation of a hybrid particle swarm optimization and simulated annealing heuristic for CMOL nano-hybrid cells assignment. The behavior of the problem was analyzed and a technique was engineered that utilized the exploration and exploitation features of PSO to solve the problem. In the proposed algorithm the PSO operators, like velocity and position update were defined in the context of assignment problem. Due to the inherent greedy nature of PSO algorithm, simulated annealing (SA) was used in hybrid to escape local minima entrapment. Implementation results illustrated that the proposed scheme achieved better results for most of the benchmarks as compared to other published techniques in previous studies.

Acknowledgments

The authors acknowledge King Fahd University of Petroleum & Minerals for all the support, and Dr. William N. N. Hung and Mr. Zhufei Chu for providing ISCAS'89 benchmark files. The authors also would like to thank Mr. Abdalrahman M. Arafeh for his help and support.