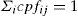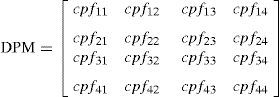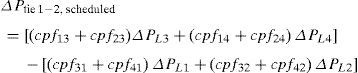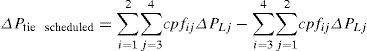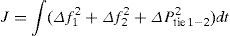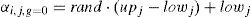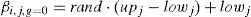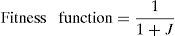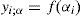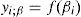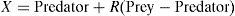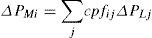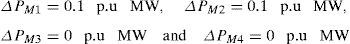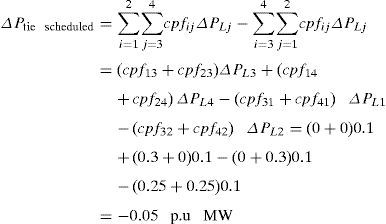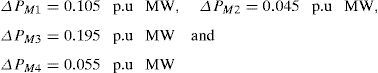In this paper, an artificial cooperative search (ACS) algorithm tuned adaptive network-based fuzzy inference system (ANFIS) controller for optimal gain tuning of load frequency control (LFC) operation in deregulated scenario has been offered. The conventional controllers for load frequency control operation are having fixed gain values intended for nominal operating conditions of the power system and they do not afford effective and efficient performance over a large range of operating scenarios in the deregulated environment. To progress the system performance to its near optimum for all probable operating circumstances of the power system, the controller gains have to be computed for the equivalent operating conditions by using the restructured parameters. For this intention, a controller based on an adaptive network-based fuzzy inference system seems to be the most excellent and valuable preference. The ANFIS is trained by off-line data obtained using a new optimization technique, artificial cooperative search optimization algorithm and the corresponding gains are updated in real-time as per the changing operating conditions. ACS is a swarm intelligence algorithm developed for solving numerical optimization problems. The swarm intelligence philosophy behind ACS algorithm is based on the migration of two artificial superorganisms as they biologically interact to achieve the global minimum value pertaining to the problem. To exhibit the competence and robustness of the projected ACS algorithm tuned ANFIS controller, the controller has been implemented on a two-area two-unit interconnected deregulated power system having one reheat unit and one non-reheat unit in each area. The simulation results exhibit the ability of the designed ACS algorithm tuned ANFIS controller for online LFC operation in deregulated environment.
Modern power systems are huge, interconnected and very composite in nature. These large interconnected power systems are composed of many number of control areas having coherent group of generators. All the control areas are interconnected by the tie-lines, which are used for energy exchange between the areas and enable inter-area backing during uncharacteristic conditions (Talaq & Al-Basri, 1999). For quality and trustworthy power supply to the consumers, it is vital to uphold the frequency and tie-line deviations within the prearranged value of the power system (Masiala, Ghribi, & Kaddouri, 2004). Lately, all over the world, the configuration of conventional electric power utilities are in a changeover state from vertical integrated configuration to deregulated configuration. In deregulated structure, the electric power utilities are split into three separate control companies as GENCO, the Generating Company, DISCO, the Distribution Company and TRANSCO, the Transmission Company respectively. The purpose of all the three utilities are controlled by a separate independent operator called as an Independent System Operator (ISO). For reliable operation, the ISO has a number of ancillary services, load frequency control being one of the important ancillary services (Bekhouche, 2002; Rakhshani & Sadeh, 2010a, 2010b).
During last decade, many techniques and approaches have been projected for design of LFC controllers (Jain, Chakrabarti, & Singh, 2013; Lakshmi, Fathima, & Muthu, 2016; Pandey, Mohanty, & Kishor, 2013; Shayeghi, Shayanfar, & Jalili, 2009). Most of the controller designs are based on the conventional approach. The conventional controllers are fixed gain controllers being designed for nominal operating conditions. Such type of controller designs does not integrate the different operating conditions of the operating power system and does not revise the parameters for computing their gain values. So, these controllers cannot afford enhanced performance (Hosseini & Etemadi, 2008). To overcome the above mentioned drawbacks and to improve the system performance, the design of an ANFIS-based controller gains added significance.
In recent years, different artificial intelligence techniques and swarm intelligence techniques have been implemented for obtaining optimal solution for LFC controllers in deregulated environment (Anilkumar & Venkataramana, 2012). In this paper, a new artificial cooperative search algorithm tuned adaptive network-based fuzzy inference system (ANFIS) controller for optimal gain tuning of load frequency control (LFC) in deregulated scenario has been offered to provide better performance. The artificial cooperative search algorithm is a new optimization algorithm designed for solving complex optimization problems. As the structure of ACS algorithm is simpler than the structures of other artificial intelligence algorithms, it is easily programmable and notably faster than the other algorithms. For purposes of examining the success of ACS algorithm in solving numerical optimization problems, 91 benchmark problems that have different specifications were tested by Civicioglu (2013). The success of ACS algorithm in solving the benchmark problems was compared to the successes obtained by PSO, SADE, CLPSO, BBO, CMA-ES, CK and DSA algorithms. The results obtained in the analysis demonstrate that the success achieved by ACS algorithm in solving numerical optimization problems is better incomparison to the other computational intelligence algorithms used in this paper. Hence ACS algorithm has been preferred for this paper. The ACS algorithm is used for obtaining the off-line training data. The performance of ACS tuned ANFIS controller is compared with the performance of ACS tuned controller based on integral square error criteria.
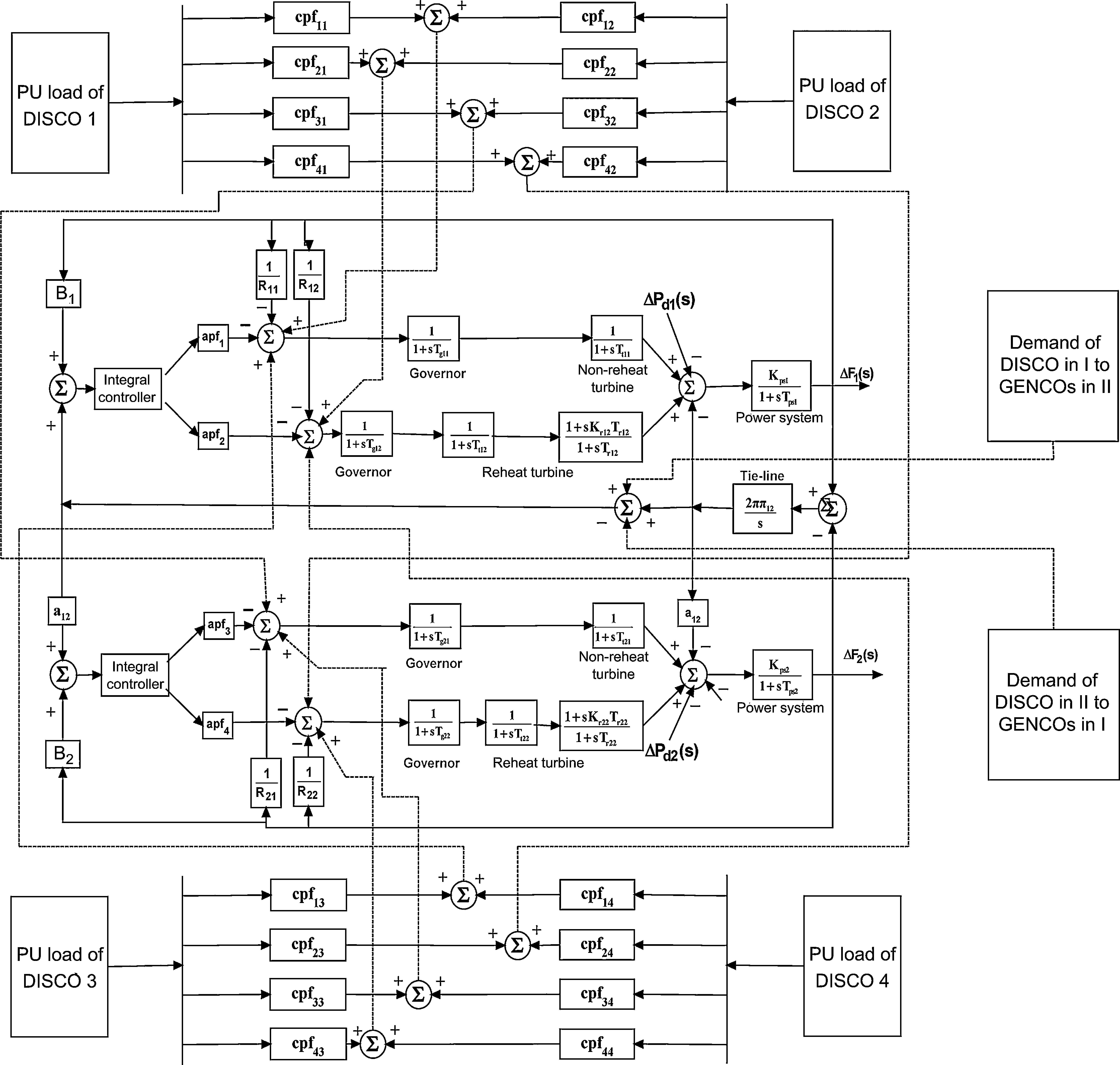
2Power system modelThe power system model in deregulated environment consists of the GENCOs and DISCOs which have a variety of combination of bilateral contracts among them. The bilateral power transfer contracts among the GENCOs and DISCOs can be realized in actual fact by using DISCO Participation Matrix (DPM). The DPM provides the particulars of the contracts which exist between the GENCO and DISCO. The number of rows present in DPM has to be equal to the number of GENCOs and the number of columns present in DPM has to be the same to the number of DISCOs in the deregulated environment. Each entry of DPM represents a fraction of the total load power contract between a DISCO and GENCO in the deregulated power system. The total sum of all the entries of DPM column is unity (Donde, Pai, & Hiskens, 2001).
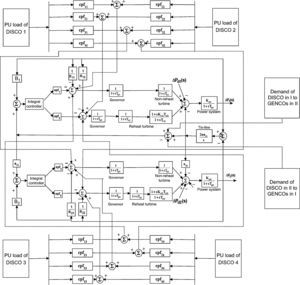
The projected deregulated system is a two-area system with two GENCOs and two DISCOs in each area. The block diagram of LFC model in deregulated scenario is given in Figure 1. The resultant DPM matrix can be expressed as given below, where ‘cpf’ represents the contract participation factor.
In DPM, the off diagonal entries symbolize the demand of DISCO in one area with the GENCO in another area. The expression for scheduled tie line power flow between the two interconnected areas is given by
The off diagonal blocks of the DPM are substituted in the above expression for the scheduled tie-line power flow as given below
The generalized expression for scheduled tie-line power flow can be written as
The optimal values of controller gains for the LFC of deregulated power system are calculated using Integral Square Error criterion. The objective function J for ISE is taken as (Bhatt, Roy, & Ghoshal, 2010).
3Integral gain optimization using ACS algorithmArtificial cooperative search algorithm (ACS) is a swarm intelligence algorithm developed for solving complex numerical optimization problems (Civicioglu, 2013). A genetic contact naturally prevails between diverse living things in natural world. The living kind concerned in genetic contact tries to achieve mutual benefits from the natural interaction. The habitation thought in ACS algorithm represents the search space concept that belongs to the associated problem.
In ACS algorithm, a superorganism consisting of arbitrary solutions of the associated problem corresponds to an artificial superorganism migrating to more fruitful feeding areas. ACS algorithm contains two superorganisms; α and β that have artificial sub-superorganisms equal to the dimension of the population (N). The dimension of the problem (D) is equal to the number of individuals within the associated sub-superorganisms. In ACS algorithm, α and β superorganisms are used for the finding of artificial Predator and Prey sub-superorganisms. The Predator sub-superorganisms in ACS algorithm can follow the Prey sub-superorganisms for a period of time while they migrate towards global minimum of the problem. When the iterative calculation process of ACS algorithm that is named as co-evolution process is considered, it can be seen that the two superorganisms looking for the global minimum of the related problem, establish mutual aid-based biological contact between each other. In ACS algorithm, the initial values of the individuals of ith sub-superorganism of α (i.e., α_(i,j)) and β (i.e., β_(i,j)) are defined by using (4) and (5);
where i=1, 2, 3, …, N, j=1, 2, 3, …, D and g=0, 1, 2, 3, …, max cycle. The ‘g’ value denotes the generation number expressing the co-evolution level containing the associated superorganisms. The rand shows a random number chosen from the uniform distribution with U∼[0 1]. The upj and lowj are the upper and lower limits of search space for jth dimension of the related problem. The fitness values are computed by using (6) and (7);The fitness value is obtained as follows:
where J is the objective function, i.e., integral square error given by (3).The biological interaction location, X, between Predator and Prey sub-superorganisms is modelled using Eq. (8);
where R is the scale factor that controls the speed of biological contact. The probabilistic character of ACS algorithm causes the super-organism that is determined as the predator to be changed in each generation. Therefore, ACS algorithm provides a cooperative/co-evolution process for both of the superorganisms. The proposed algorithm has been implemented with iteration count as the stopping criteria. The pseudo code of ACS algorithm is provided in (Civicioglu, 2013).For Load Frequency Control in a deregulated environment using ACS algorithm, to begin with, the random generated biological contact position X, i.e., the integral controller gain value, is used to calculate fitness value using the objective function, J. For each iteration, the sub-superorganism (α and β) values are obtained using (4) and (5). The predator and prey sub-superorganisms are determined in each generation by using α and β superorganisms. The biological contact position X, between predator and prey is updated using (8). The objective function J is calculated for each set of X using (3). The process is repeated until optimal integral gain, corresponding to global minimum objective function value is obtained. Iteration count is taken as the stopping criteria. For the proposed problem, the maximum iteration count has been assumed as 30.
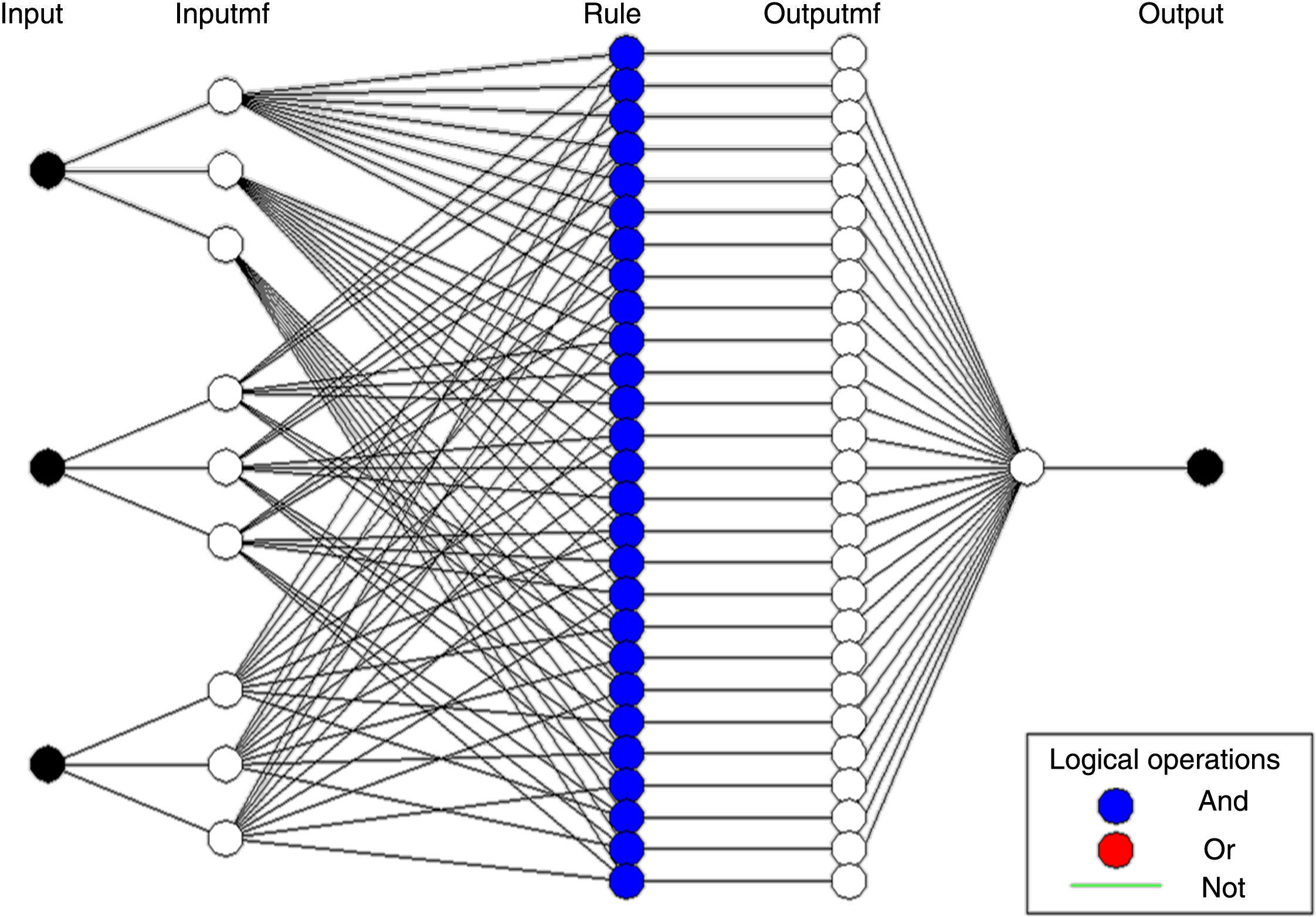
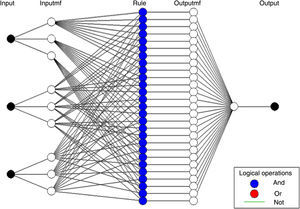
4Adaptive network-based fuzzy inference systemThe adaptive network-based fuzzy inference system (ANFIS) serves as a fundamental for constructing a set of fuzzy rules with appropriate membership functions to generate the prearranged input–output pairs (Jang, 1993; Lee, 1990). Various types of fuzzy rules have been projected in the earlier period (Jang, 1993; Kumar & Vani, 2014; Mosaad & Salem, 2014; Rao, 2012). Adaptive networks are evolving, dynamic networks, in which the topology changes in dependence of the dynamic state of the nodes, while the dynamics of the state depends on the topology. The output depends on the parameter pertaining to these nodes and the error values are minimized based on the parameter changes given by the learning rules. ANFIS is the fuzzy logic-based model that grasps the learning abilities of ANN to improve the intelligent system's performance using a former knowledge. Using a given input/output data set, ANFIS constructs a fuzzy inference system whose membership function parameters are tuned using back-propagation algorithm in combination with a least-squares type of method. This allows the fuzzy system to learn and model from these data. These techniques provide a method for the fuzzy modelling procedure to learn information about a data set, in order to compute the membership function parameters that best allow the associated fuzzy inference system to track the given input/output data as shown in Figure 2. This learning method works likewise to that of neural networks (Rajkumar, Ramachandaramurthy, Yong, & Chia, 2011). The ANFIS system has no limitations except the network should be feed forward type. Due to this minimal restriction, the adaptive network application has no bounds. An ANFIS controller in MATLAB Simulink is used to provide fast damping control for LFC operation.
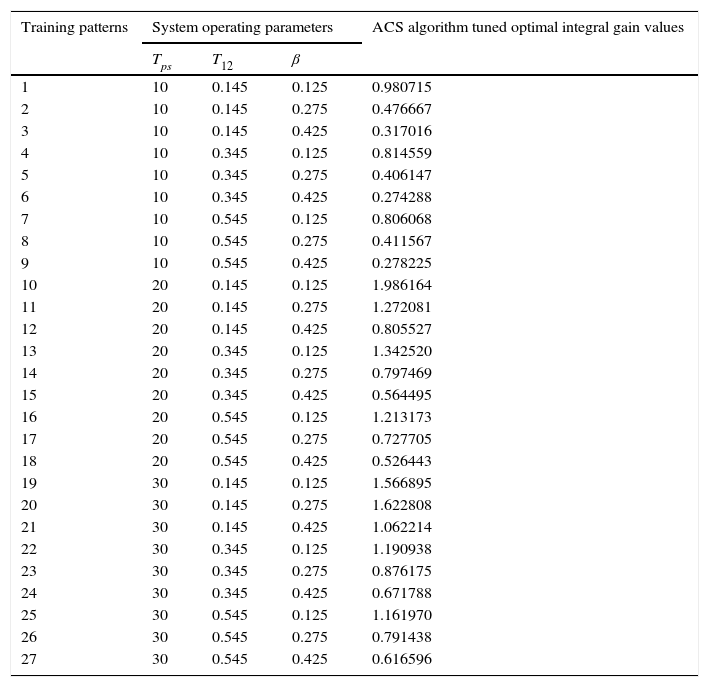
The performance of the fixed gain controller deteriorates with change in system operating conditions. To have preferred system performance, it is essential to take into account the performance of the system over an extensive range of operating conditions. In this paper, power system time constant Tps, synchronizing power coefficient T12 and frequency bias setting β which correspond to the system operating condition have been used as input to the ANFIS network. Three numbers of fuzzy membership functions have been used. Twenty seven different fuzzy rules have been framed for this controller. It uses a bell shaped fuzzy membership function. Twenty seven numbers of training samples have been used. The pattern for training are generated for diverse values of system parameters Tps, T12 and β. If the numbers of training patterns are large, the network training process will be very slow (Farzi, 2012; Jain et al., 2013). To overcome this drawback, only twenty seven different combinations of system parameters have been used. The calculated integral gain values for the twenty seven different power system operating condition patterns by using ACS algorithm are tabulated in Table 1 as follows.
ACS tuned optimal integral gain values for different operating conditions.
| Training patterns | System operating parameters | ACS algorithm tuned optimal integral gain values | ||
|---|---|---|---|---|
| Tps | T12 | β | ||
| 1 | 10 | 0.145 | 0.125 | 0.980715 |
| 2 | 10 | 0.145 | 0.275 | 0.476667 |
| 3 | 10 | 0.145 | 0.425 | 0.317016 |
| 4 | 10 | 0.345 | 0.125 | 0.814559 |
| 5 | 10 | 0.345 | 0.275 | 0.406147 |
| 6 | 10 | 0.345 | 0.425 | 0.274288 |
| 7 | 10 | 0.545 | 0.125 | 0.806068 |
| 8 | 10 | 0.545 | 0.275 | 0.411567 |
| 9 | 10 | 0.545 | 0.425 | 0.278225 |
| 10 | 20 | 0.145 | 0.125 | 1.986164 |
| 11 | 20 | 0.145 | 0.275 | 1.272081 |
| 12 | 20 | 0.145 | 0.425 | 0.805527 |
| 13 | 20 | 0.345 | 0.125 | 1.342520 |
| 14 | 20 | 0.345 | 0.275 | 0.797469 |
| 15 | 20 | 0.345 | 0.425 | 0.564495 |
| 16 | 20 | 0.545 | 0.125 | 1.213173 |
| 17 | 20 | 0.545 | 0.275 | 0.727705 |
| 18 | 20 | 0.545 | 0.425 | 0.526443 |
| 19 | 30 | 0.145 | 0.125 | 1.566895 |
| 20 | 30 | 0.145 | 0.275 | 1.622808 |
| 21 | 30 | 0.145 | 0.425 | 1.062214 |
| 22 | 30 | 0.345 | 0.125 | 1.190938 |
| 23 | 30 | 0.345 | 0.275 | 0.876175 |
| 24 | 30 | 0.345 | 0.425 | 0.671788 |
| 25 | 30 | 0.545 | 0.125 | 1.161970 |
| 26 | 30 | 0.545 | 0.275 | 0.791438 |
| 27 | 30 | 0.545 | 0.425 | 0.616596 |
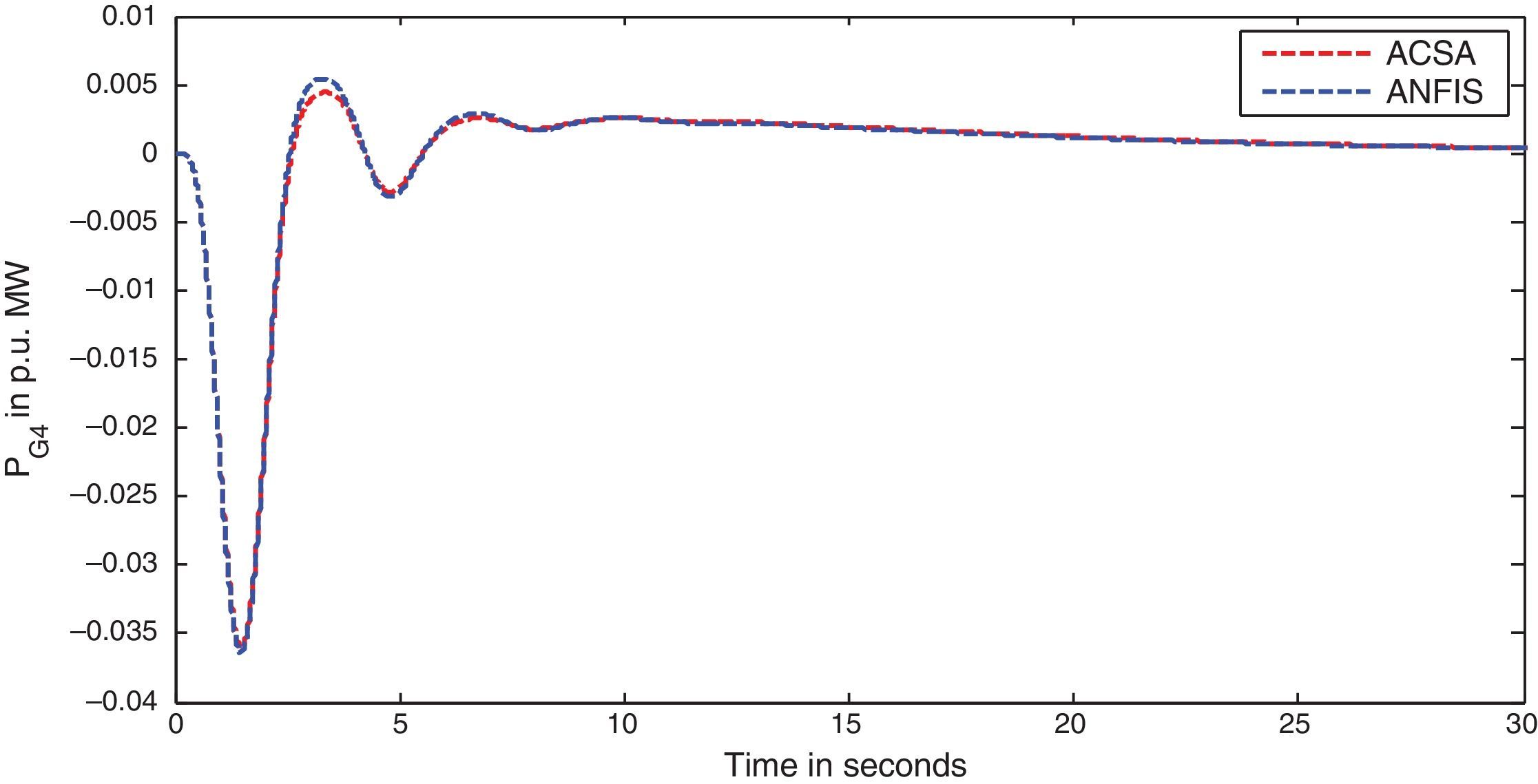
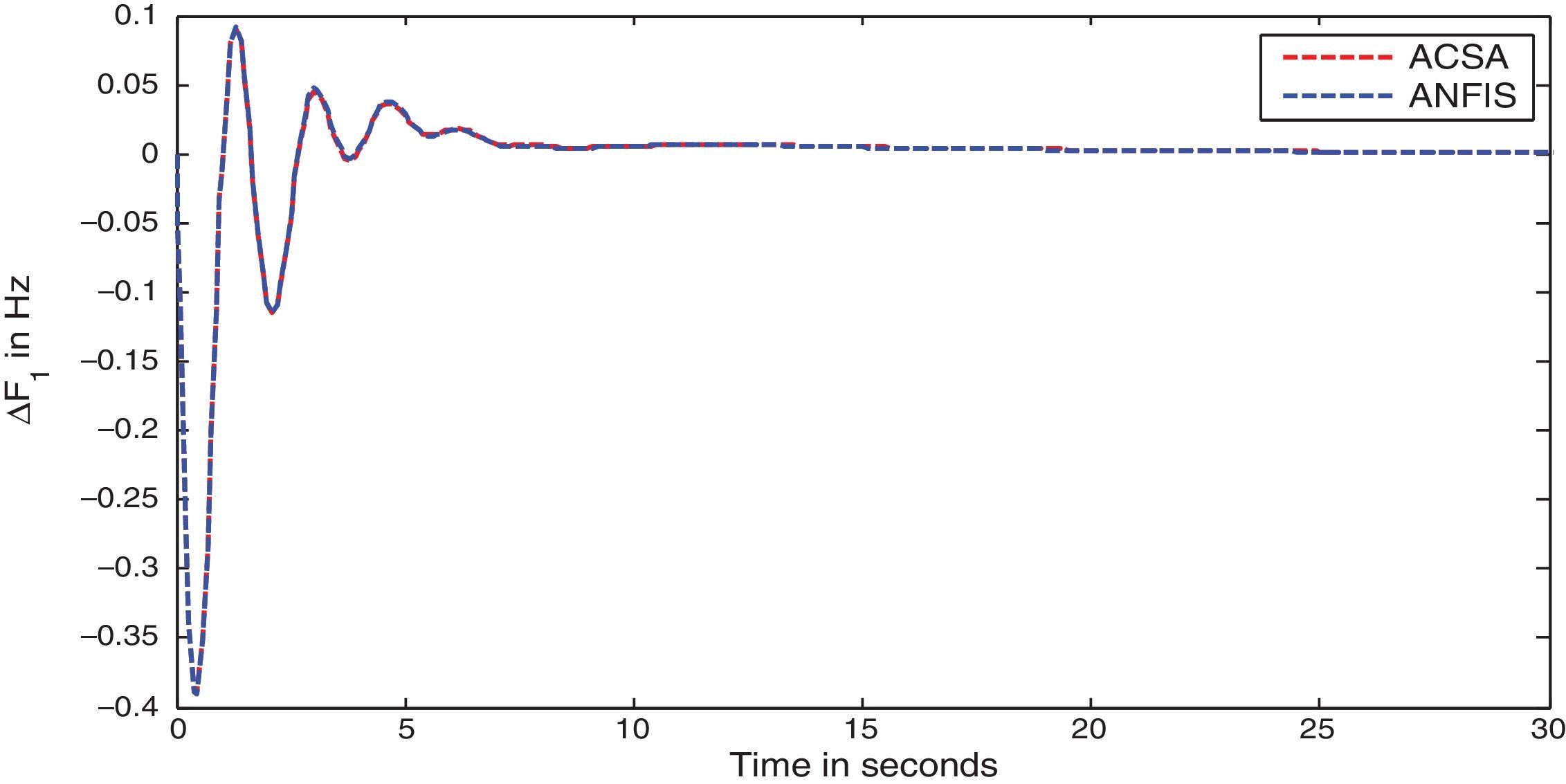
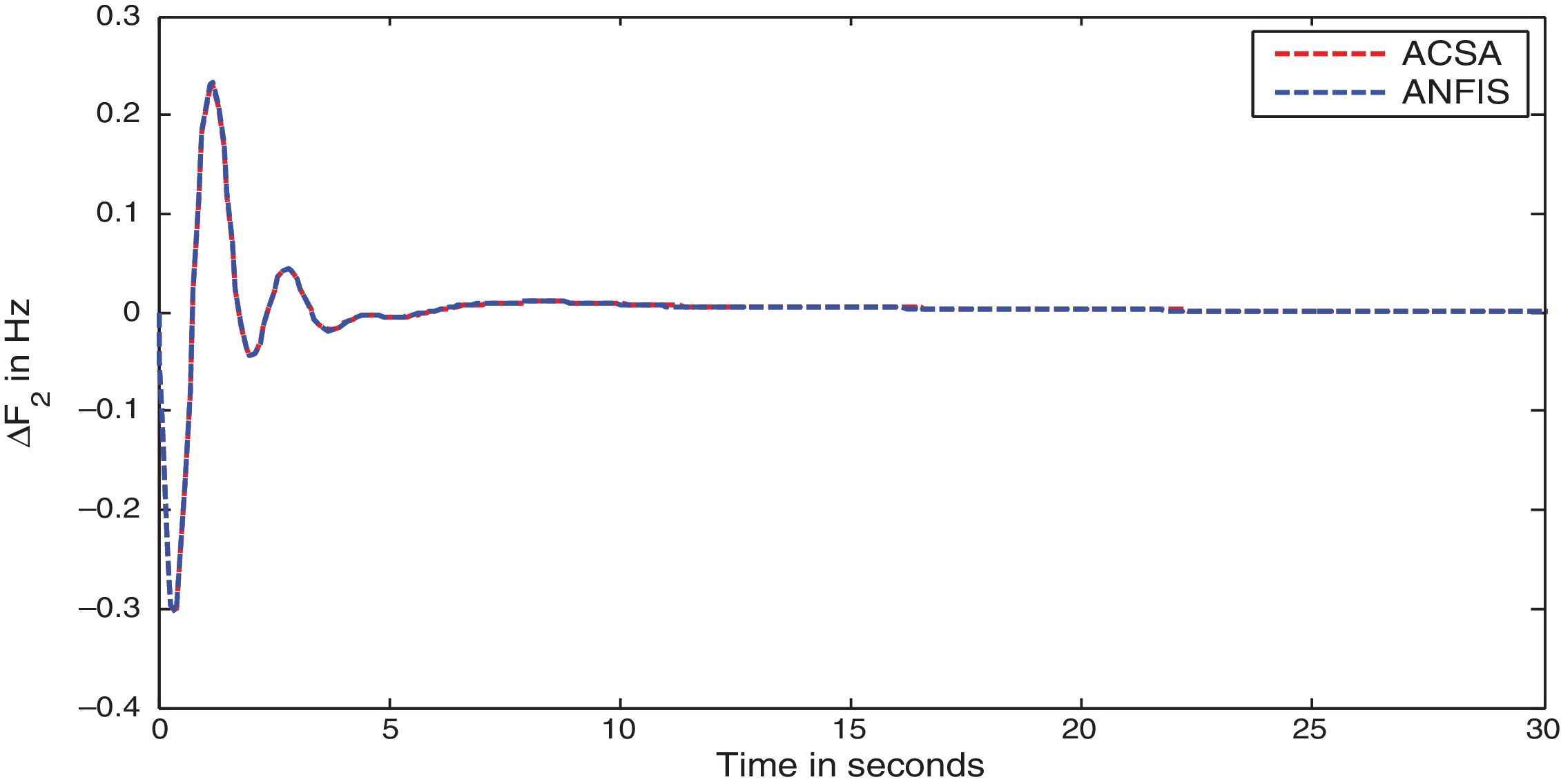
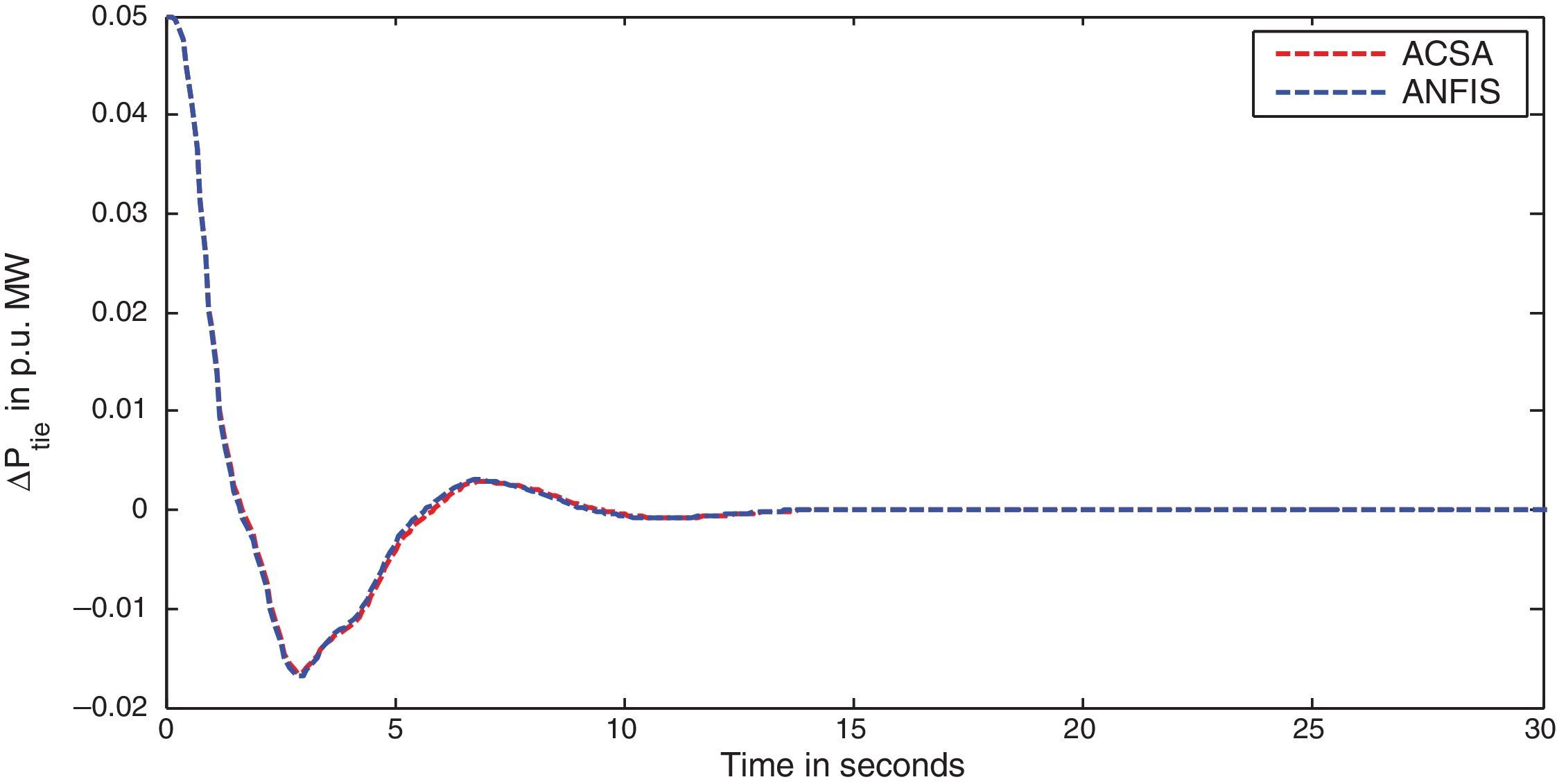
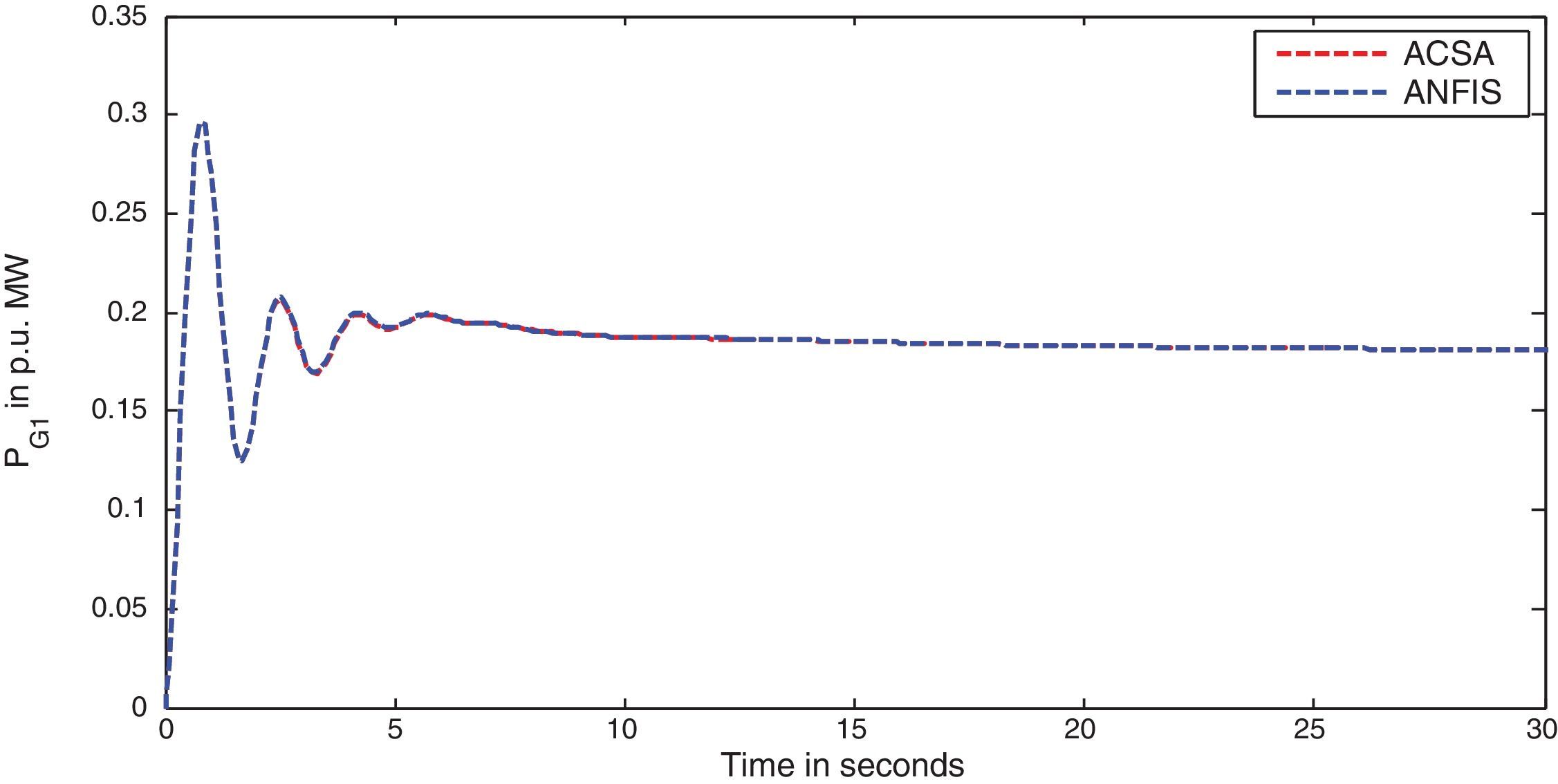
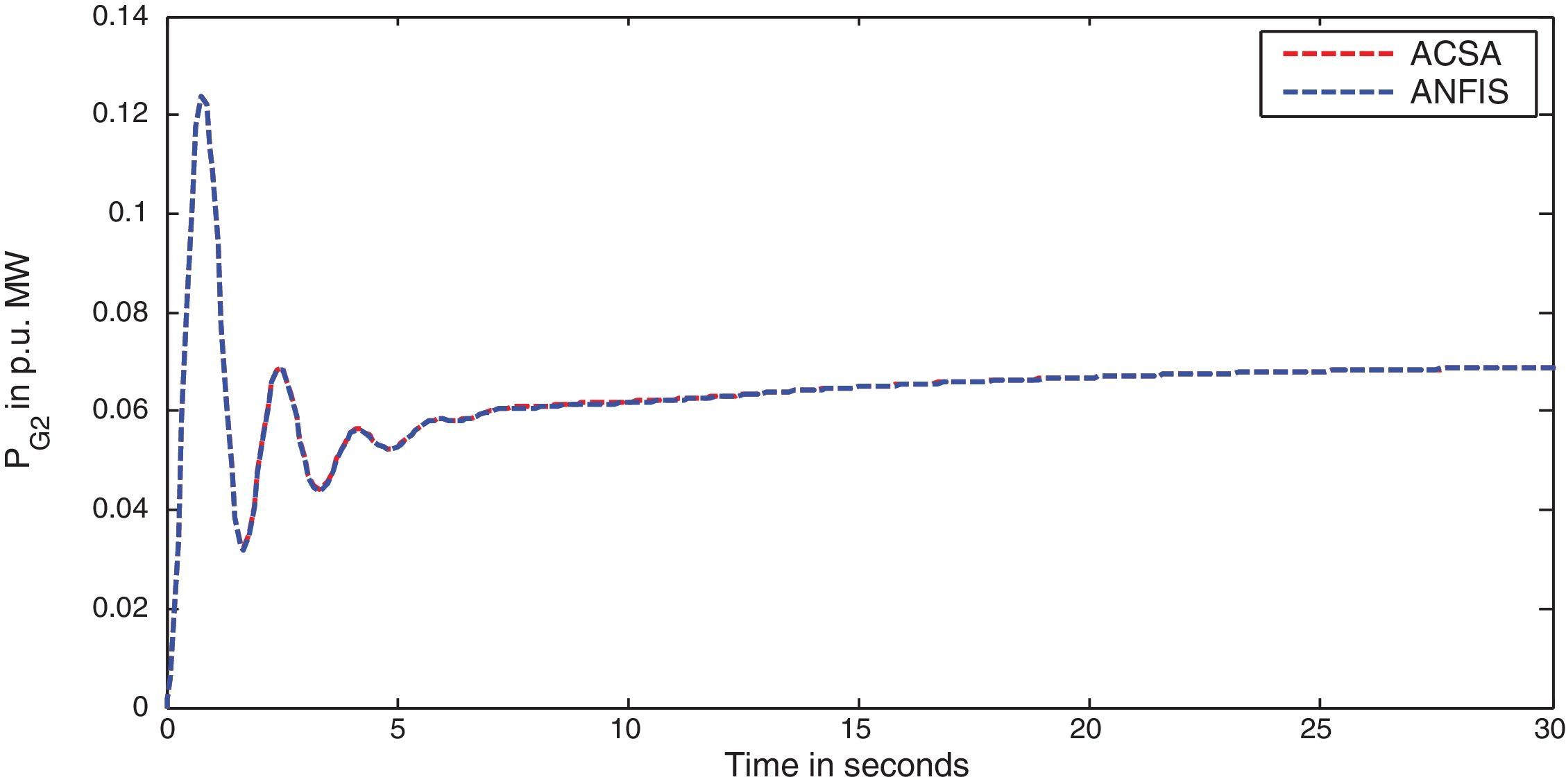
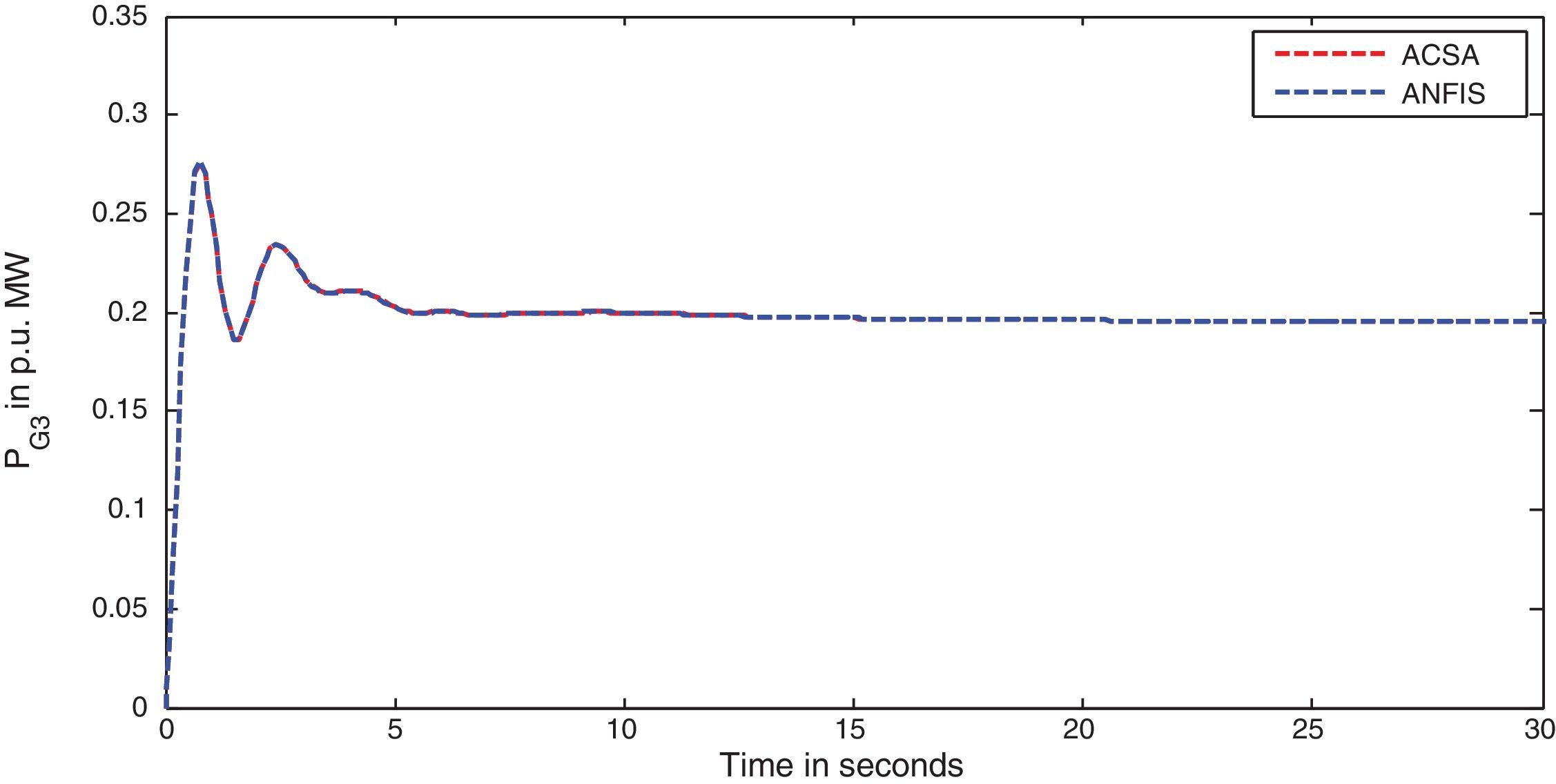
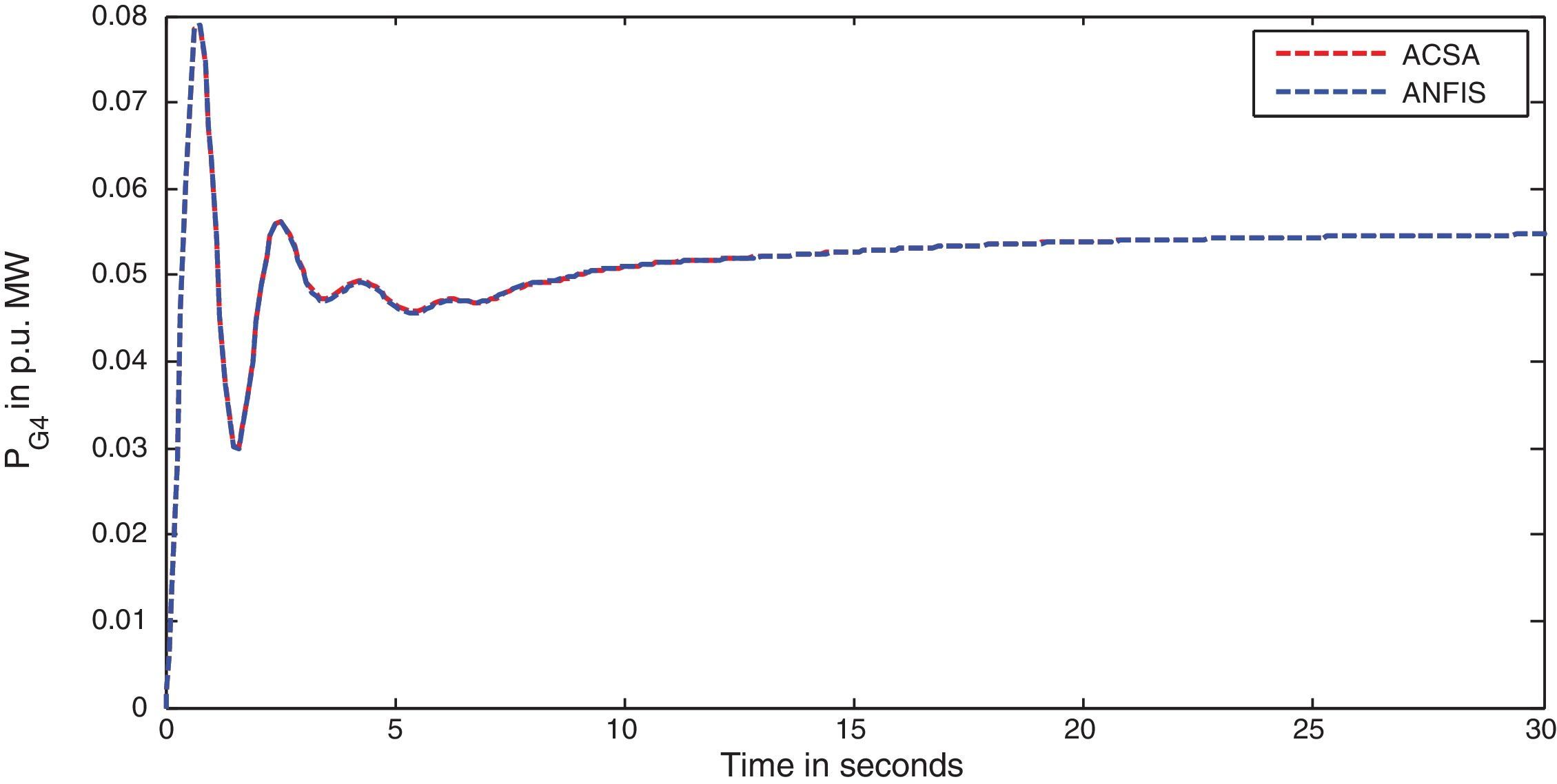
The two-area interconnected deregulated power system with one reheat and one non-reheat unit in each area as shown in Figure 1 is used to reveal the effectiveness of the projected ANFIS approach. The system parameters for the proposed power system model are given in (Donde et al., 2001; Ganapathy & Velusami, 2010) respectively. The following parameter variations, shown in Table 2 are considered for simulation and the corresponding optimal integral gain values obtained by ACS algorithm and ACS tuned ANFIS are given below. The simulation results for different deregulated contracts are also shown. Very slender degradation of oscillatory process is observed with ANFIS, as anticipated, due to the fact that ANFIS uses only three distinct signals namely system time constant Tps, synchronizing power coefficient T12 and frequency bias setting β, whereas ACS controller uses full state feedback (Djukanovic, Calovic, Vesovic, & Sobajic, 1997).
In this scenario, all the GENCOs take part equally in LFC operation. The participation factors are assumed to be identical as given: apf1=apf2=apf3=apf4=0.5. In this scenario, the variation in load is assumed to take place only in area-1, so only DISCO-1 and DISCO-2 claim the load. The per unit load demand of DISCO-1 and DISCO-2 are assumed to be 0.1p.u. MW. Therefore for this case, the entries in Disco Participation Matrix become modified as given below.
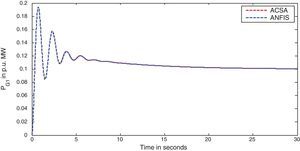
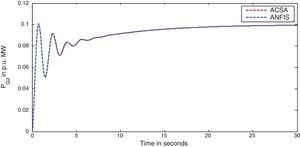
The generated power of each GENCO (ΔPMi) is expressed in terms of Contract Participation Factor (cpf) and load demand of DISCOs (ΔPLj) as given below
For this case,
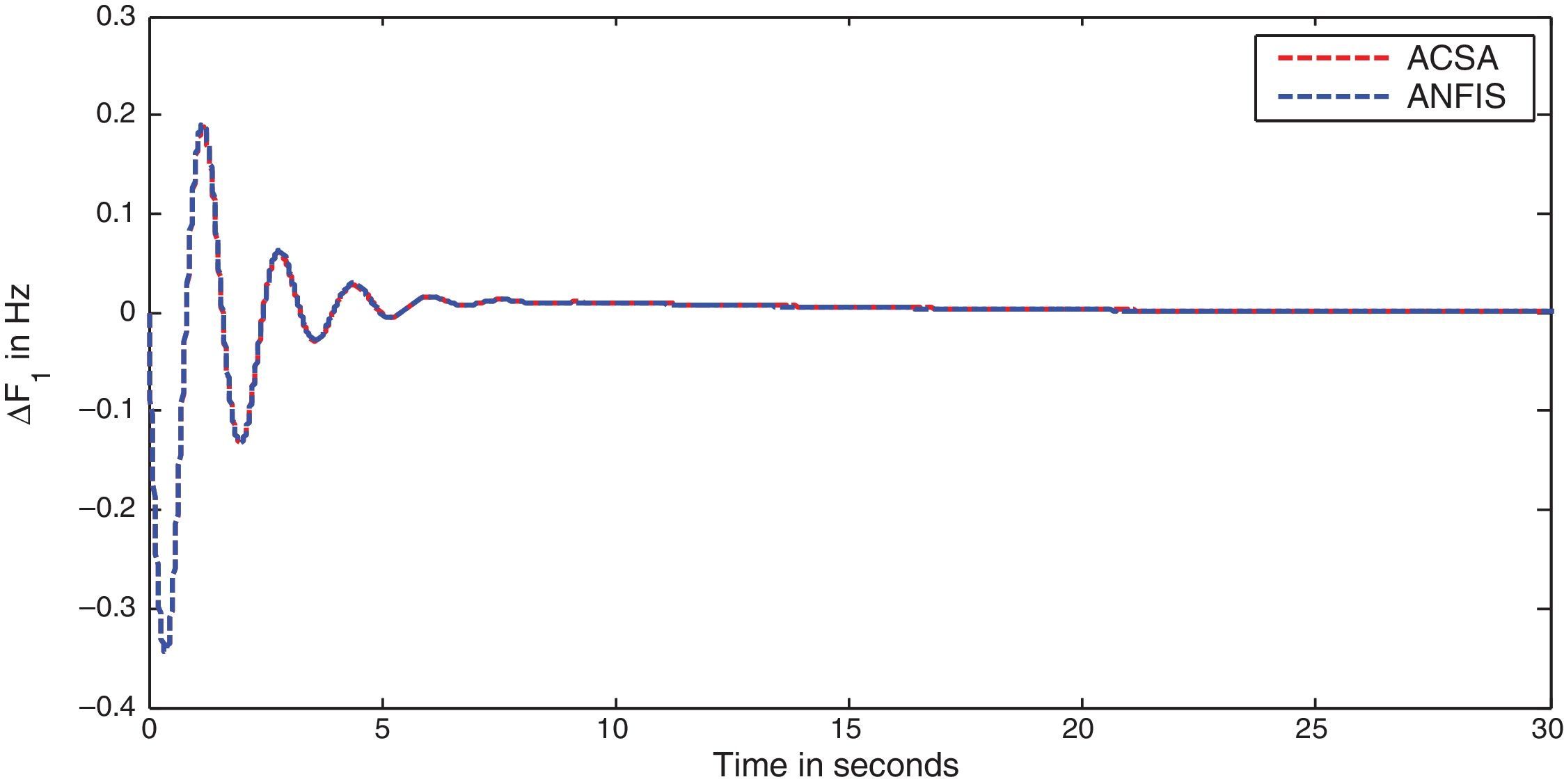
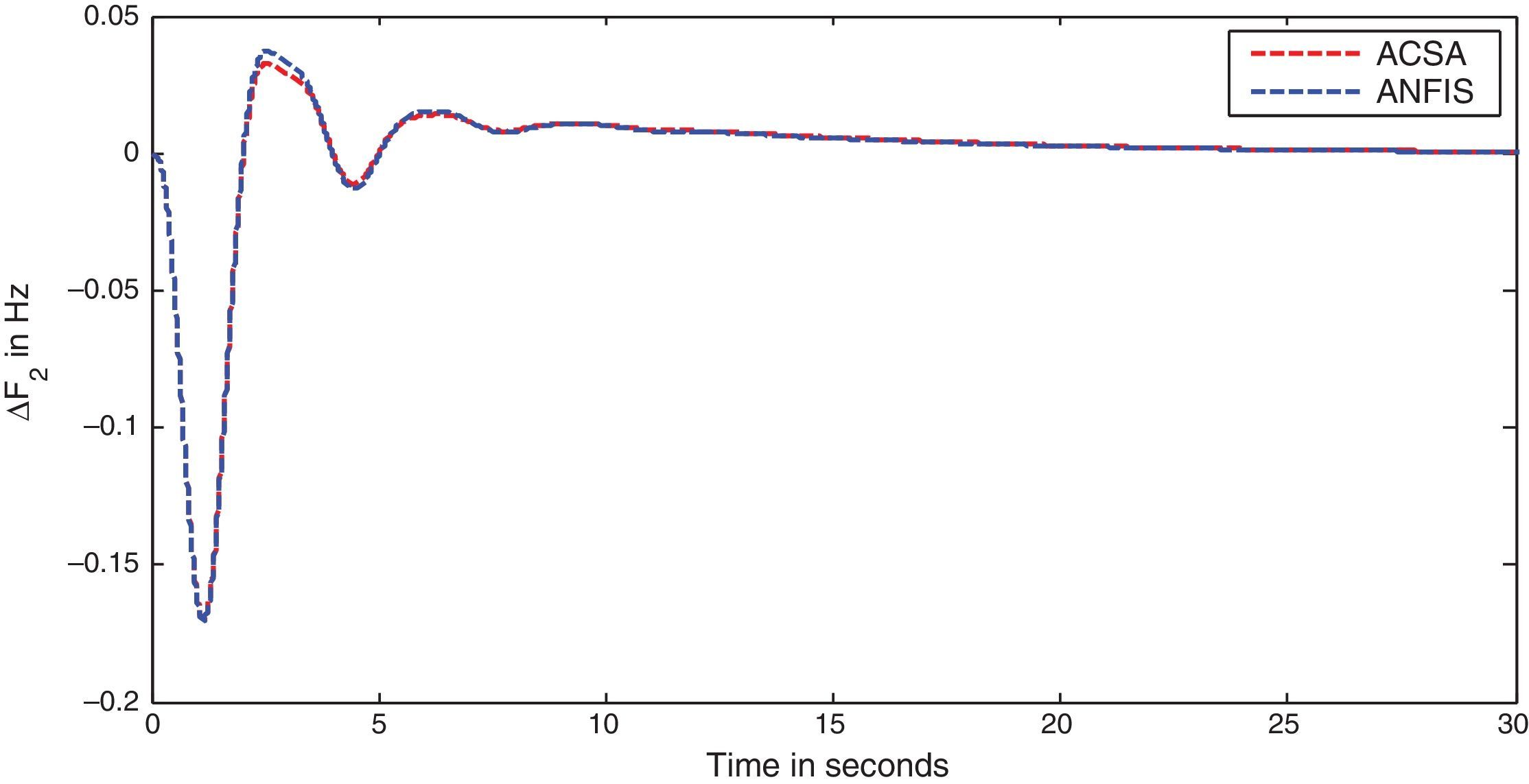
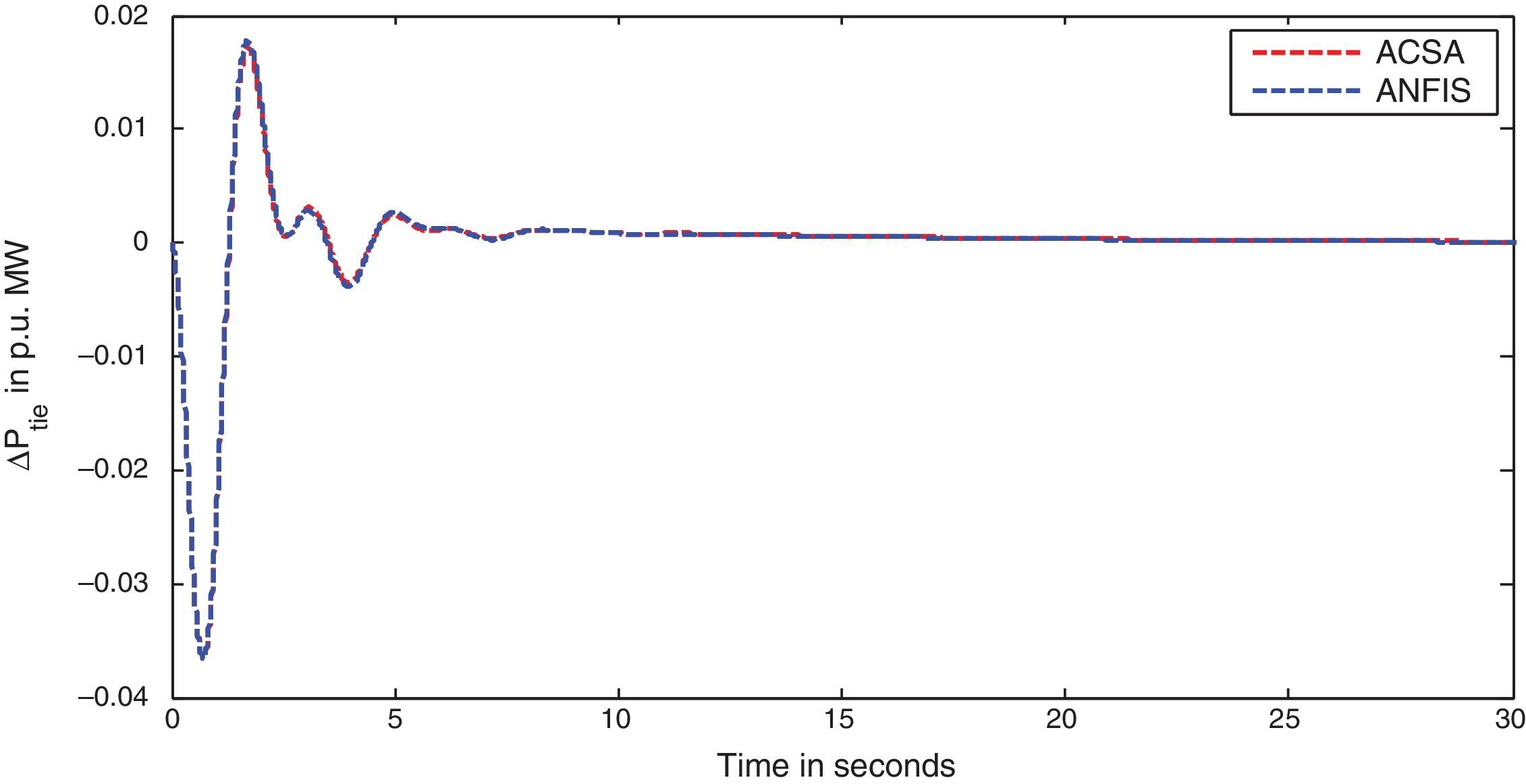
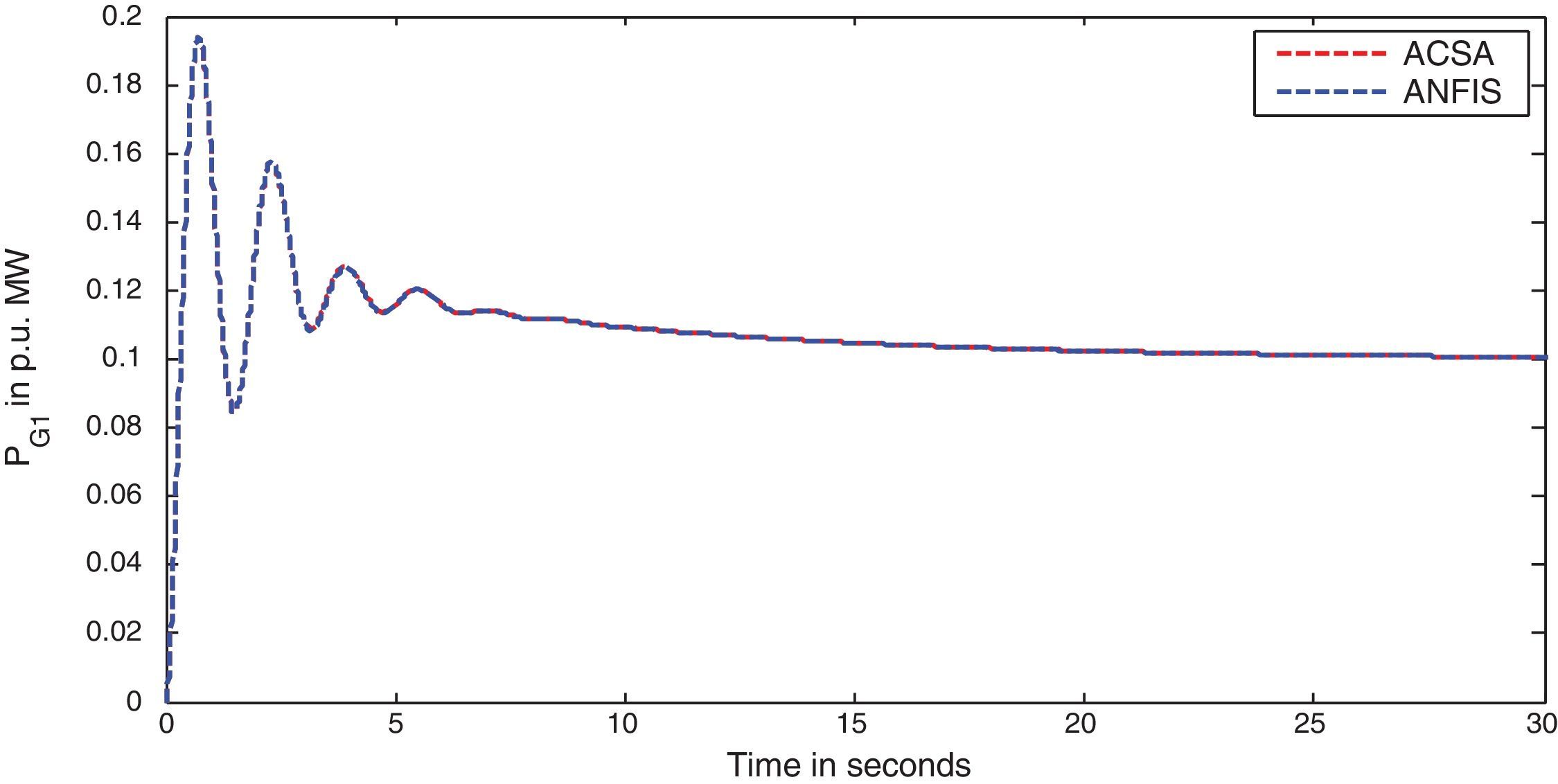
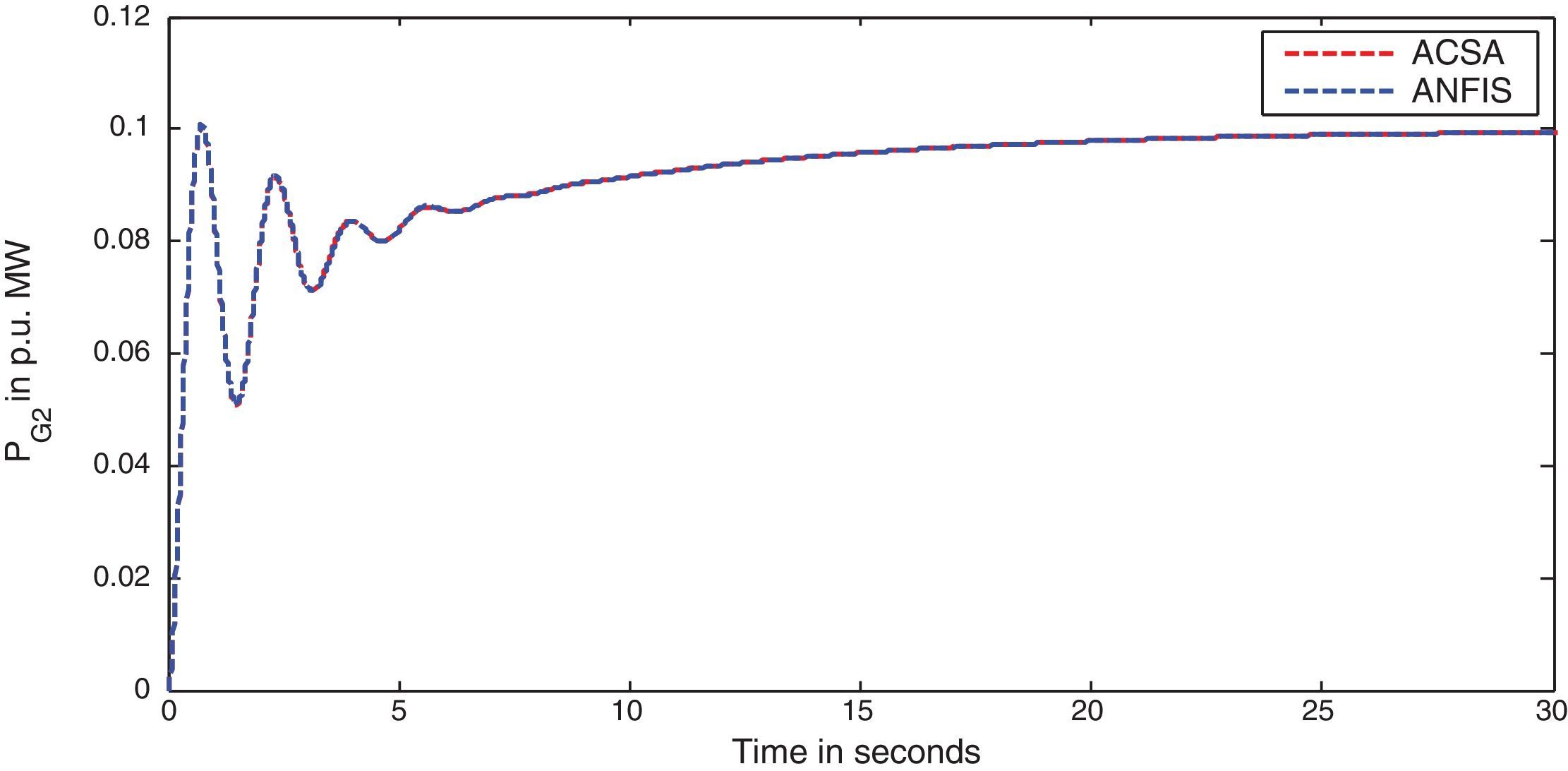
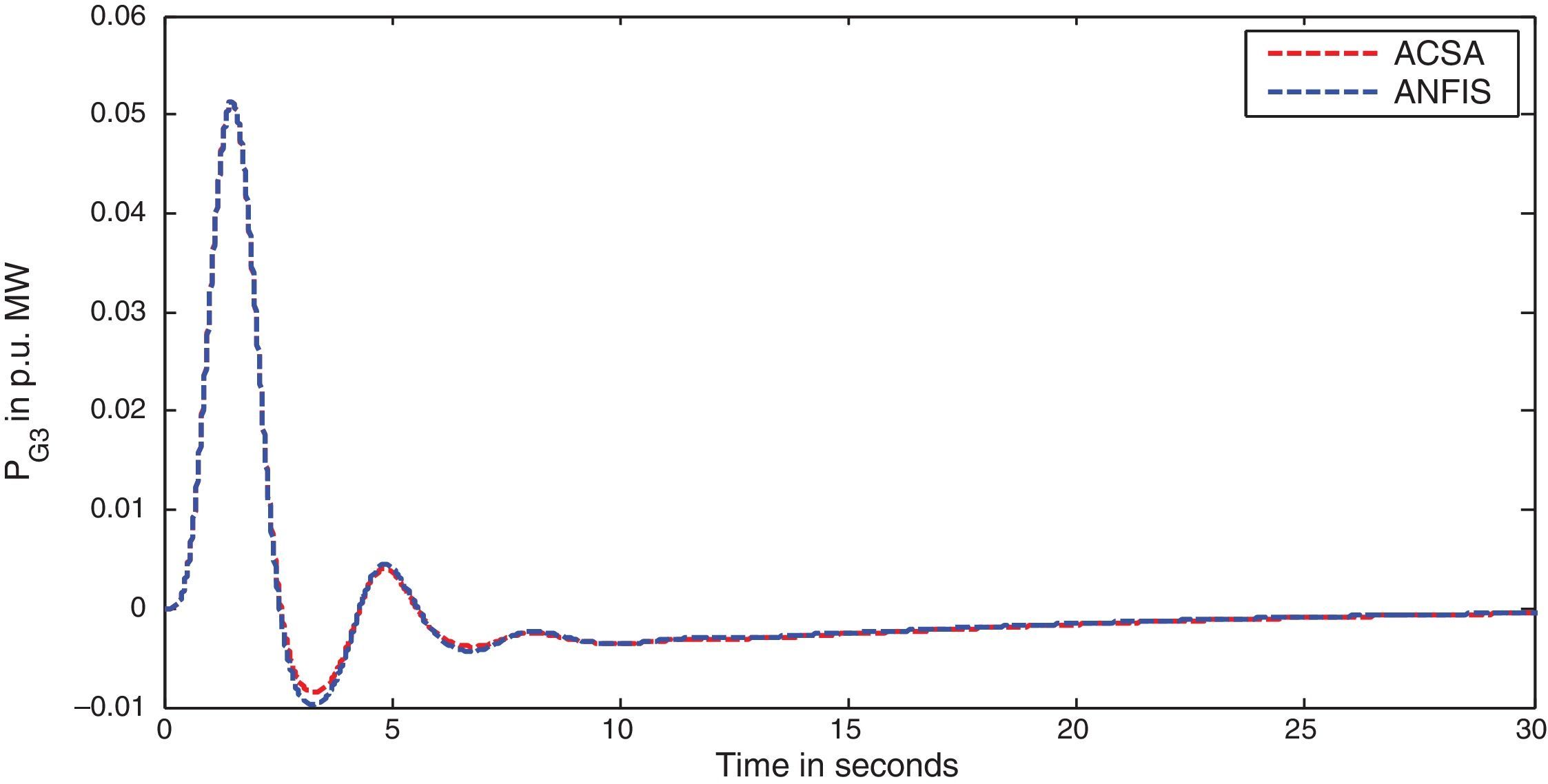
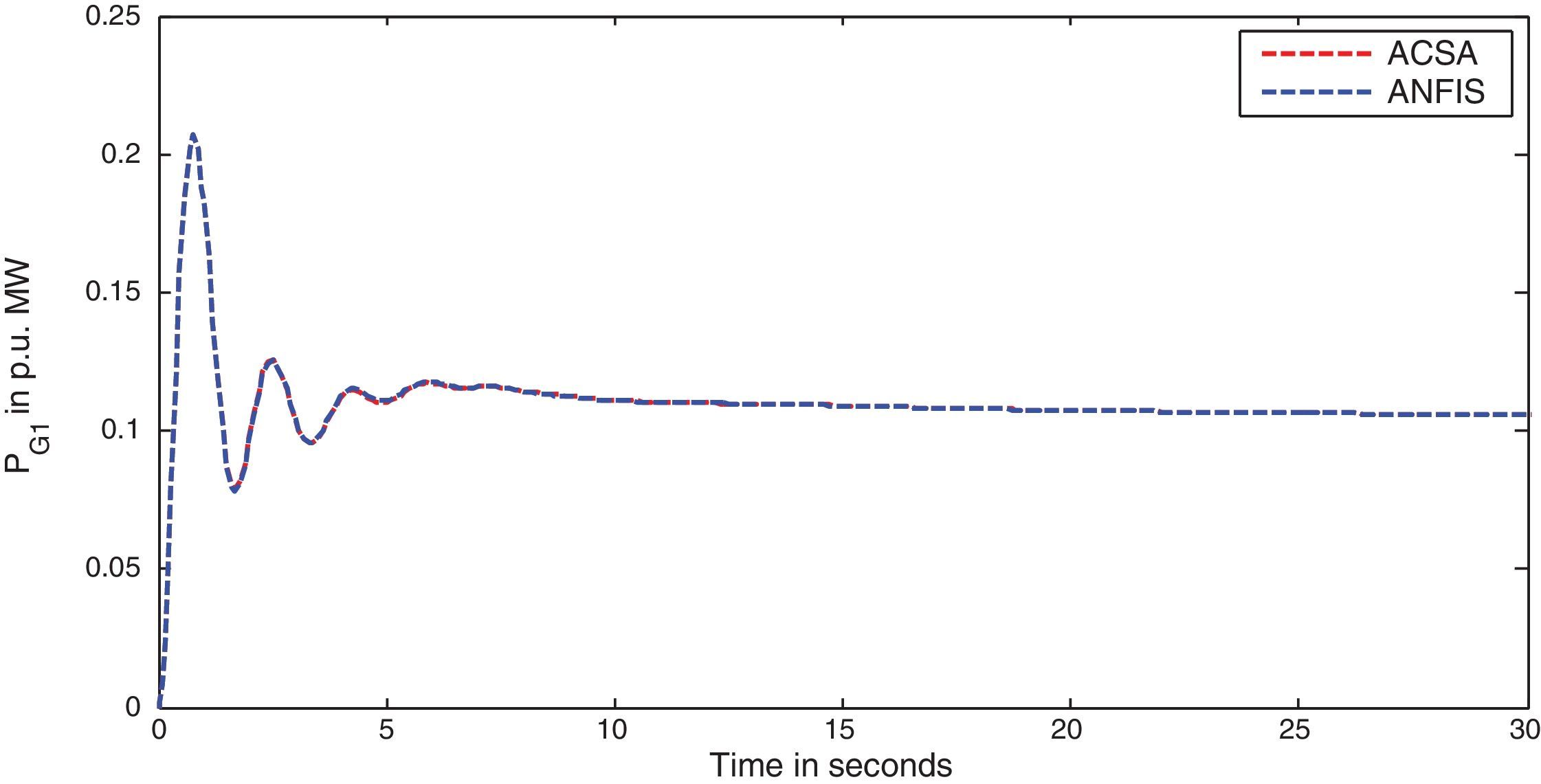
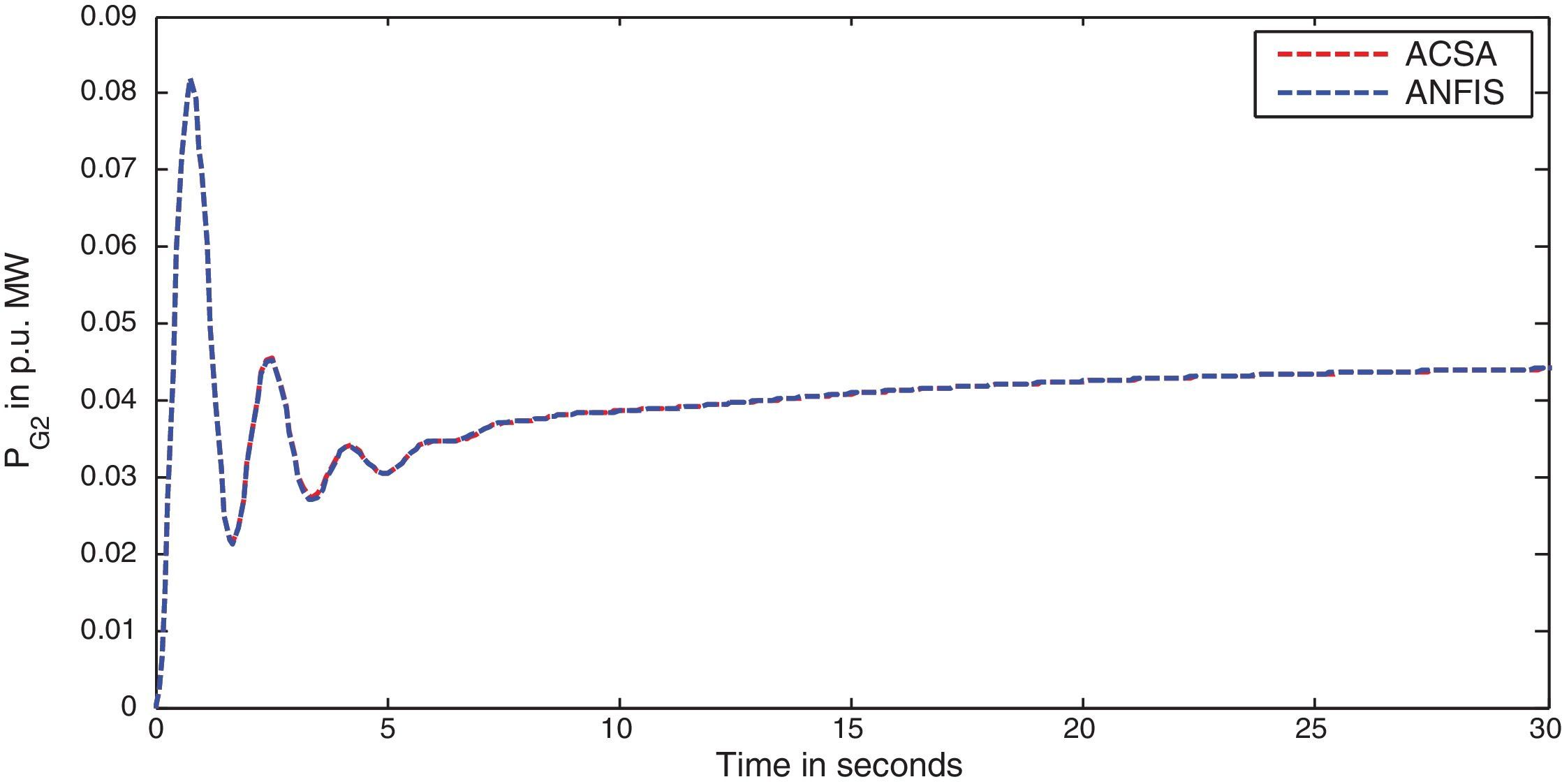
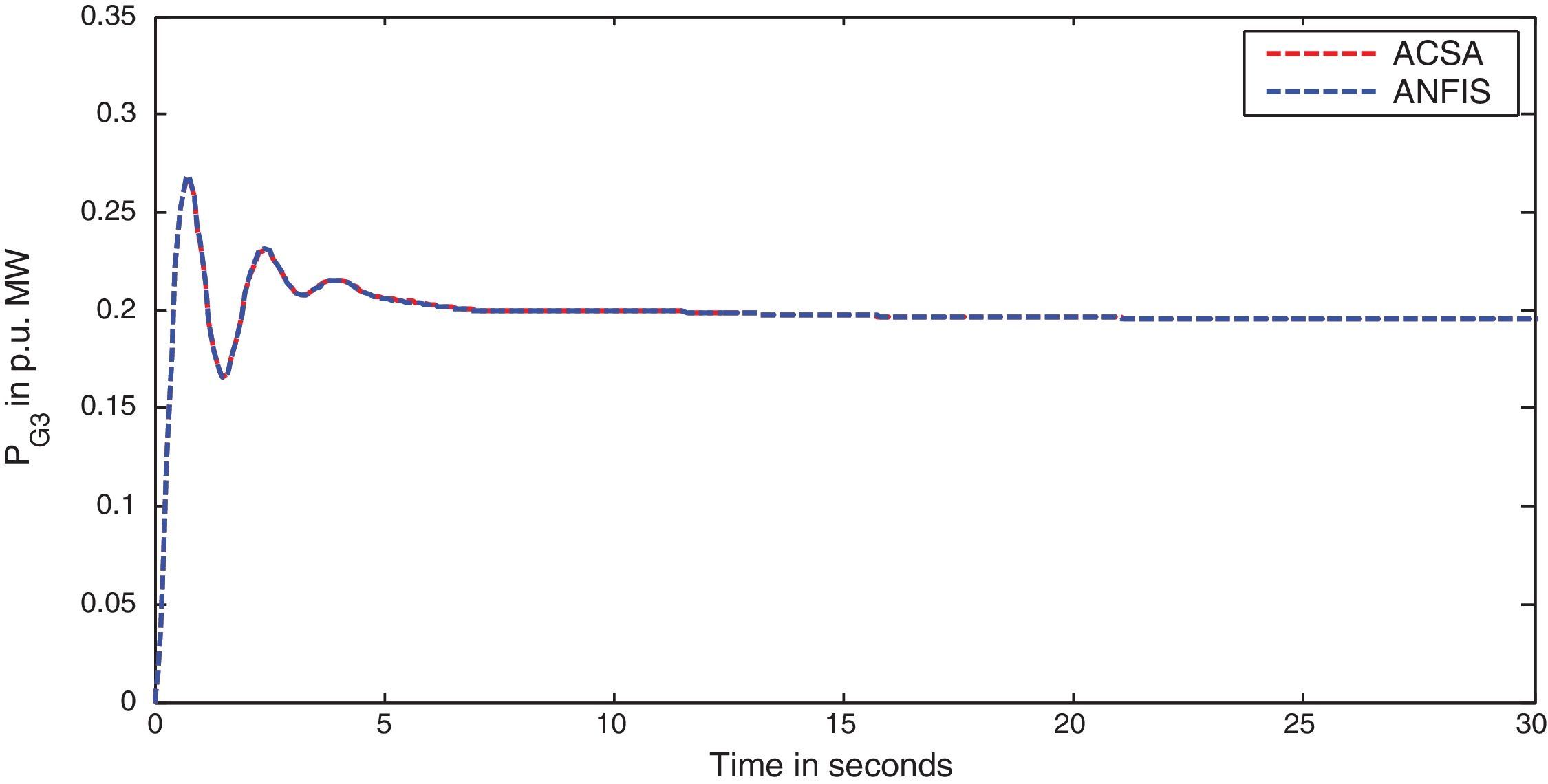
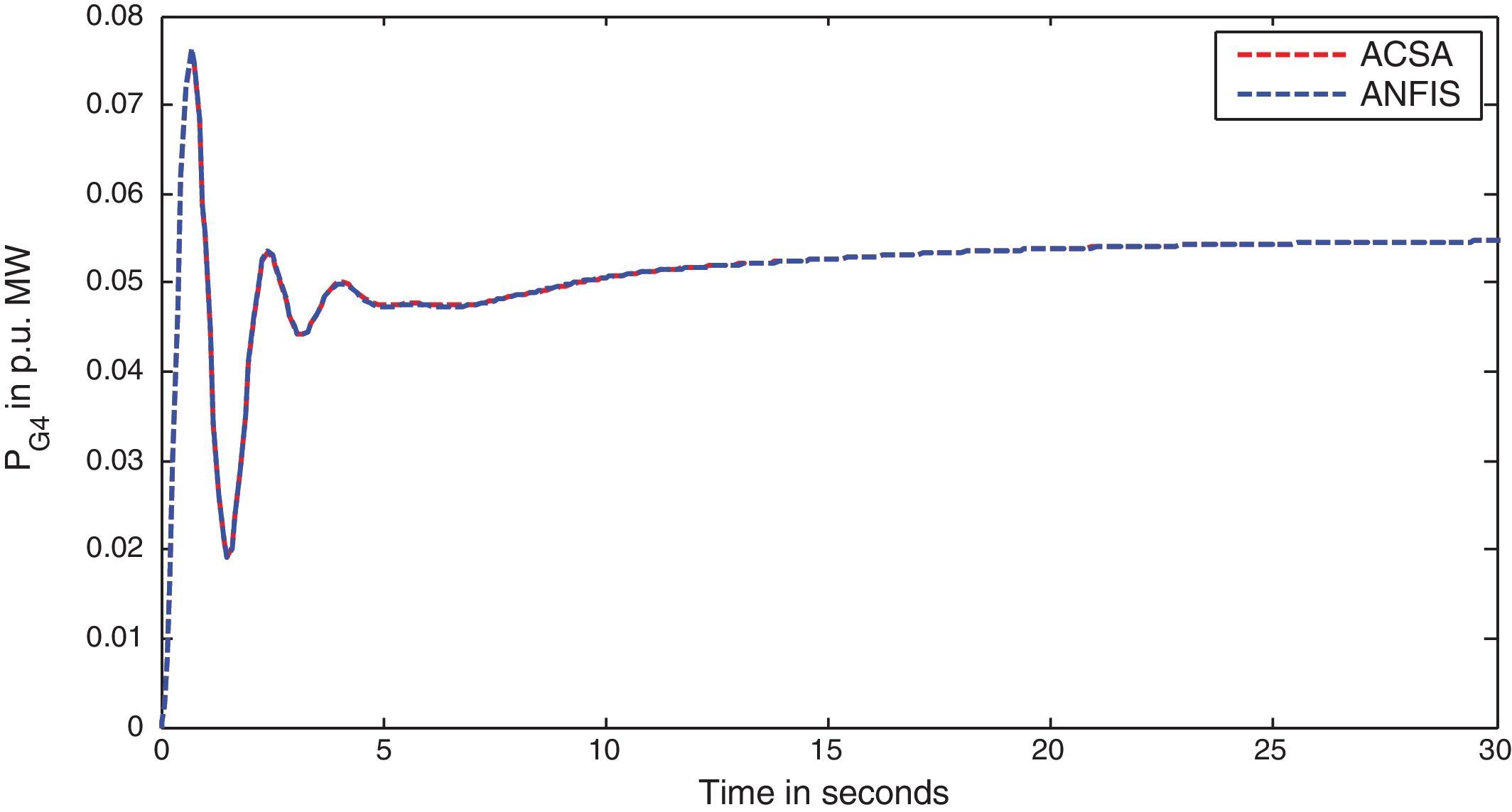
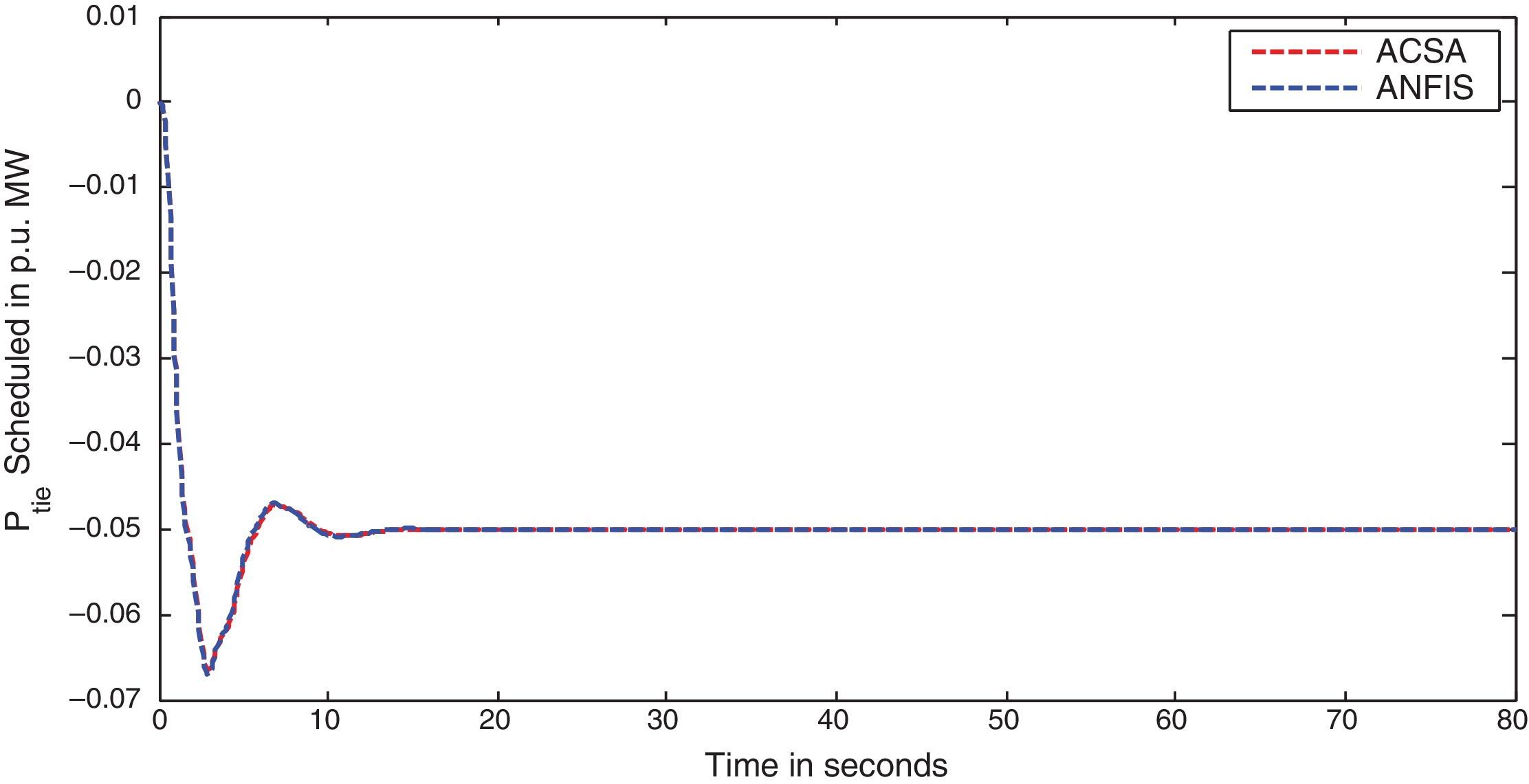
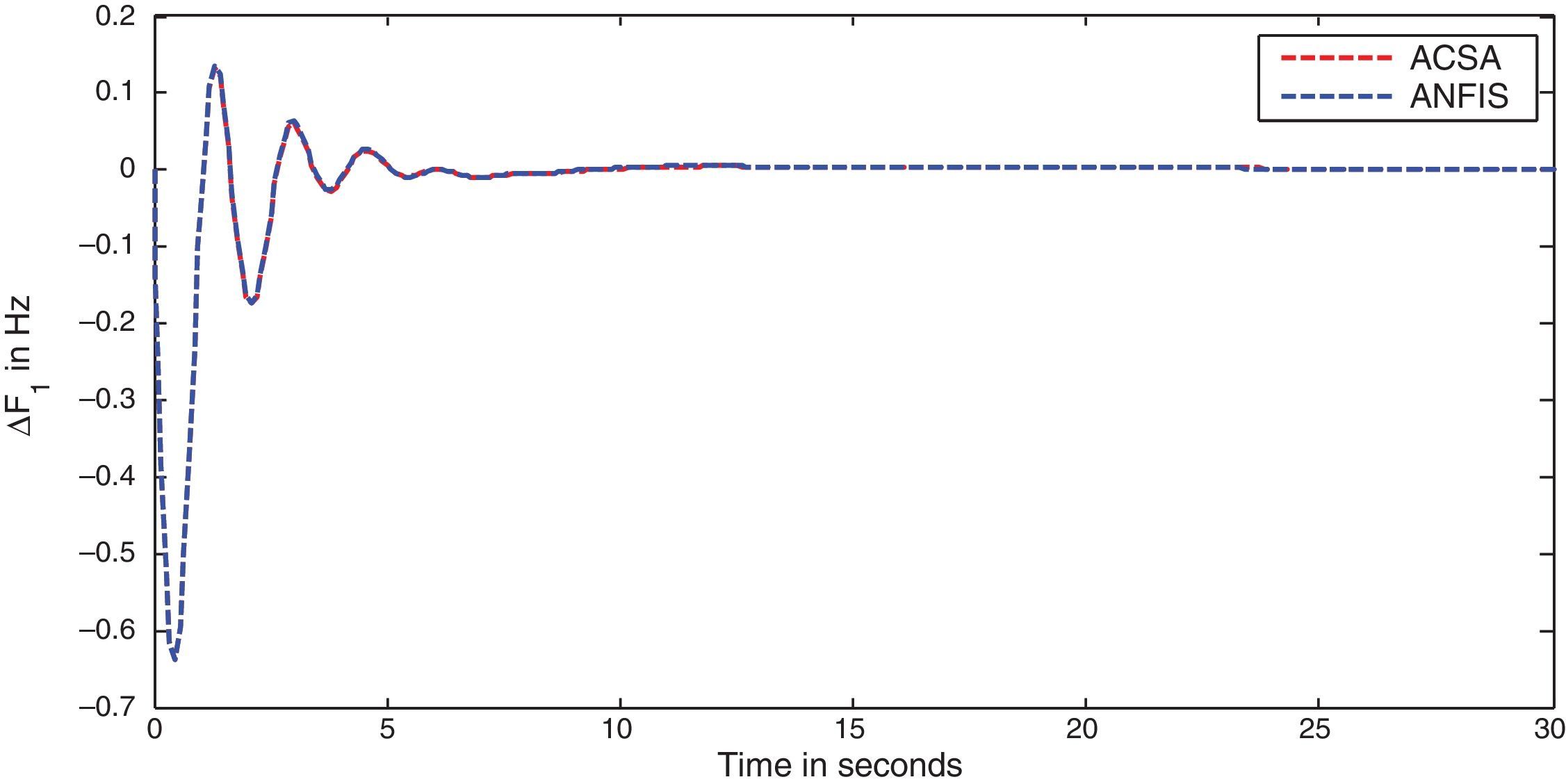
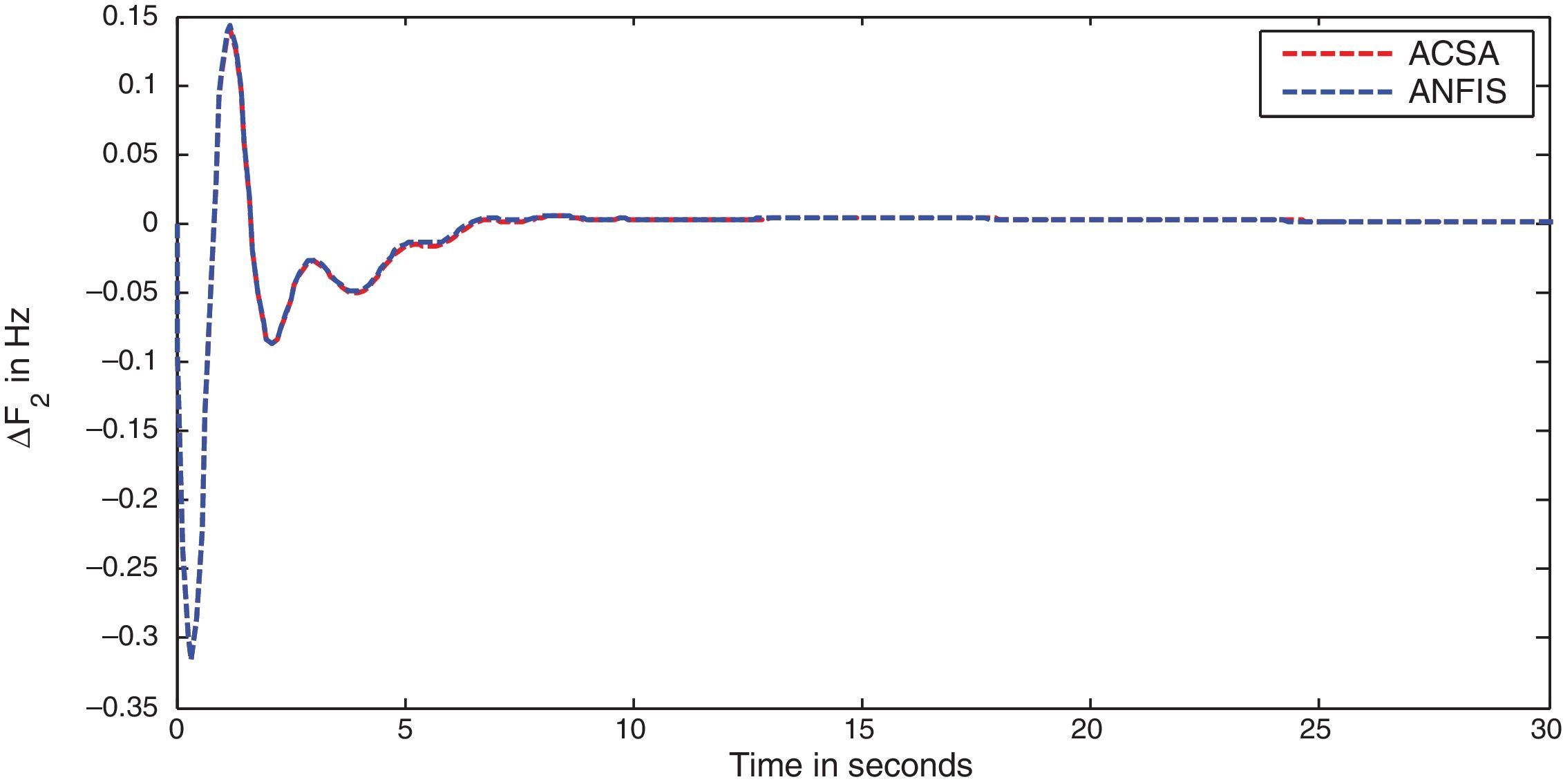
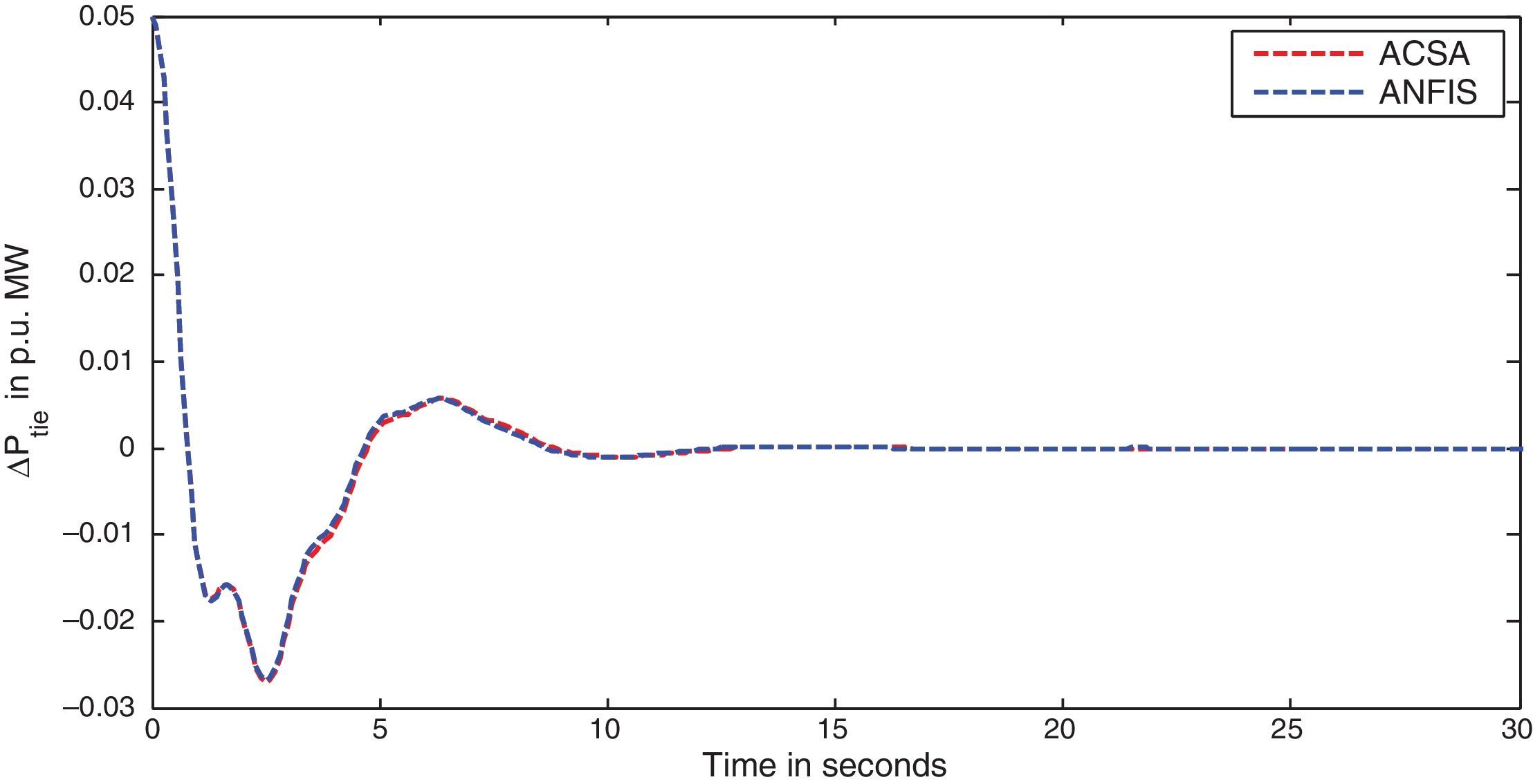
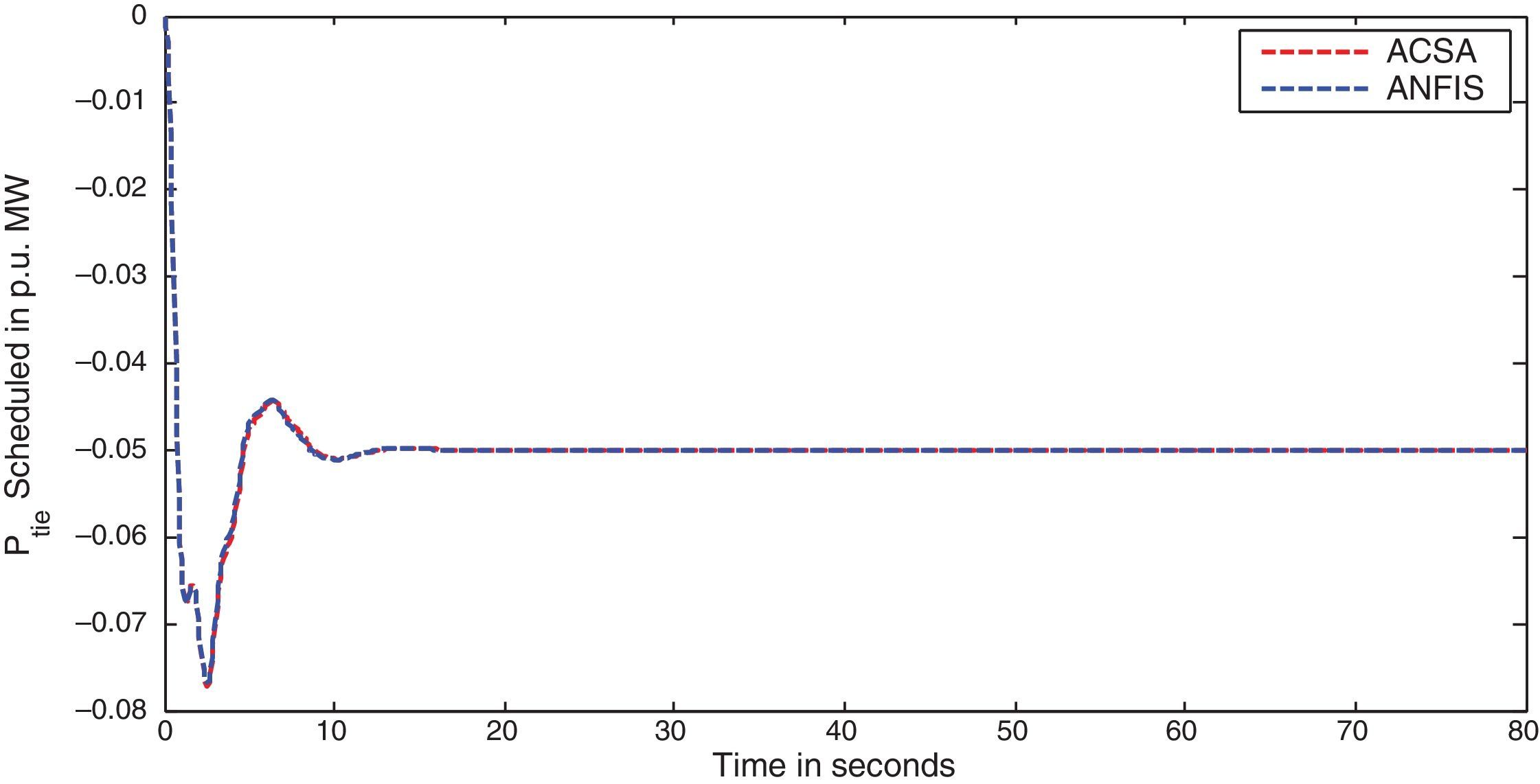
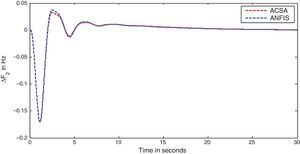
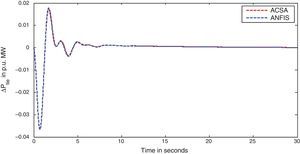
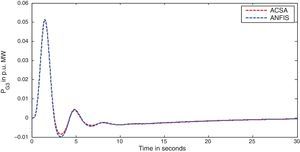
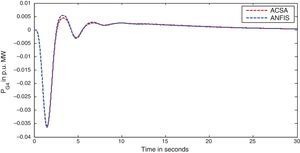
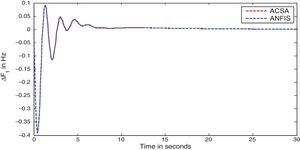
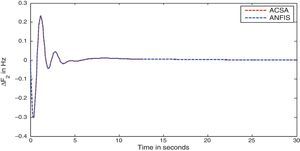
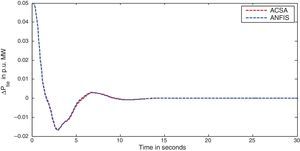
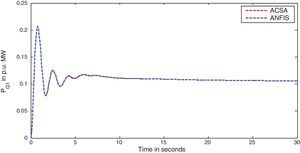
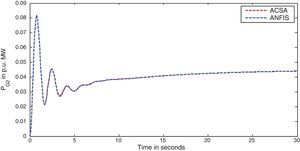
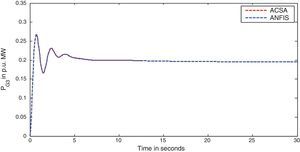
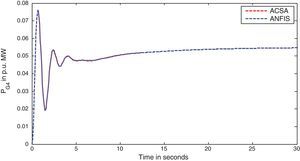
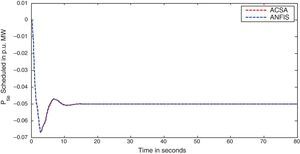
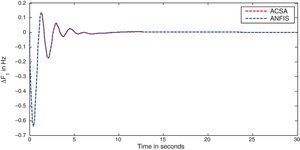
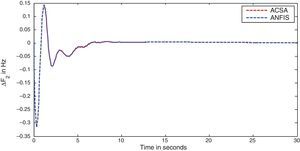
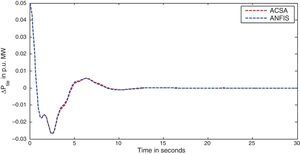
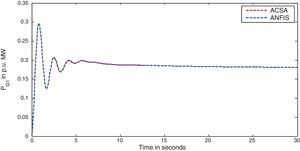
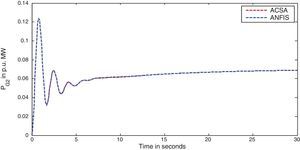
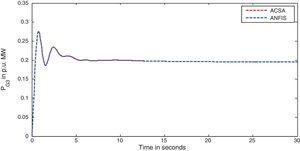
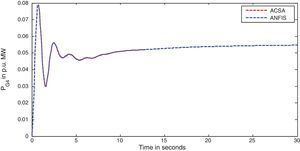
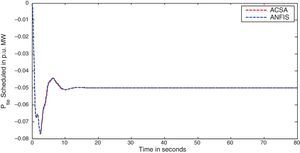
The simulation results for this scenario-1 are given in (Figs. 3–9).
5.2Scenario 2In this scenario, all the DISCOs in the system have contract with GENCOs in any other area as per the DPM. Each DISCO is assumed to claim 0.1p.u. MW power from the GENCOs. The area participation factors are assumed as apf1=0.75, apf2=0.25, apf3=0.5, apf4=0.5. Therefore the DPM becomes as shown below
The scheduled tie-line power from area 1 to area 2 is calculated from the values of the off diagonal elements of the DPM using the following expression,
The power generation of GENCOs (ΔPMi) are calculated using (9)
The simulation results for this scenario-2 are given in (Figs. 10–17).
5.3Scenario 3In this case, the existing contract is violated by DISCO 1 by demanding 0.1p.u. MW overload power than its actual contracted power. The additional uncontracted power will be provided by the GENCOs that are in the same area of the DISCO which violates the contract that is GENCO1 and GENCO2. The total load in area 1 is equal to the sum of load of DISCO 1, load of DISCO 2 and the uncontracted load, which is equal to 0.3p.u. MW. Similarly the load in area 2 is equal to the sum of the loads of DISCO 3 and DISCO 4 which is 0.2p.u. MW. The DPM is same as in scenario 2. The allocation of uncontracted load among the GENCOs is determined by the area participation factor. The simulation results for this contract violation scenario are given in (Figs. 18–25).
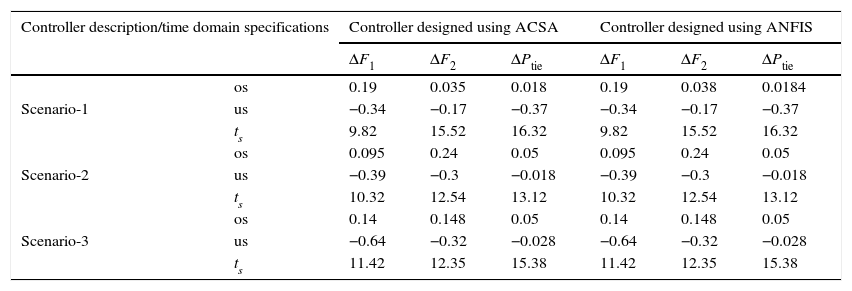
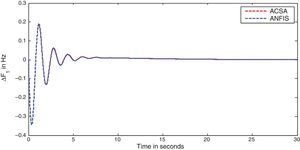
The area frequency deviations are measured in Hz, tie-line power deviations are measured in p.u. MW and settling time in seconds. Table 3 shows the comparison table of the system performance parameters. In scenario-1, the peak frequency overshoot in area-1 with controller designed using ACSA is 0.19Hz, which is almost identical to the frequency overshoot in area-1 with controller designed using ANFIS. The peak frequency overshoots in area-2 and tie-line power deviations with controller designed using ACSA are 0.35Hz and 0.018Hz respectively. The peak frequency overshoots in area-2 and tie-line power deviations with controller designed using ANFIS is also 0.035Hz and 0.018p.u. MW respectively. The overshoot for tie-line power deviations with both ACSA designed controller and ANFIS controller is approximately 0.018Hz. Similarly, the settling time for area frequency deviation and tie-line power deviations using ACSA designed controller and ANFIS controller is almost identical. This pattern of performance exists in scenario-2 and scenario-3 also. The ANFIS controller responses are similar to the responses of ACSA designed controller. This increases the overall efficiency of ANFIS controller for online application.
Comparison table of the system performance parameters.
| Controller description/time domain specifications | Controller designed using ACSA | Controller designed using ANFIS | |||||
|---|---|---|---|---|---|---|---|
| ΔF1 | ΔF2 | ΔPtie | ΔF1 | ΔF2 | ΔPtie | ||
| Scenario-1 | os | 0.19 | 0.035 | 0.018 | 0.19 | 0.038 | 0.0184 |
| us | −0.34 | −0.17 | −0.37 | −0.34 | −0.17 | −0.37 | |
| ts | 9.82 | 15.52 | 16.32 | 9.82 | 15.52 | 16.32 | |
| Scenario-2 | os | 0.095 | 0.24 | 0.05 | 0.095 | 0.24 | 0.05 |
| us | −0.39 | −0.3 | −0.018 | −0.39 | −0.3 | −0.018 | |
| ts | 10.32 | 12.54 | 13.12 | 10.32 | 12.54 | 13.12 | |
| Scenario-3 | os | 0.14 | 0.148 | 0.05 | 0.14 | 0.148 | 0.05 |
| us | −0.64 | −0.32 | −0.028 | −0.64 | −0.32 | −0.028 | |
| ts | 11.42 | 12.35 | 15.38 | 11.42 | 12.35 | 15.38 | |
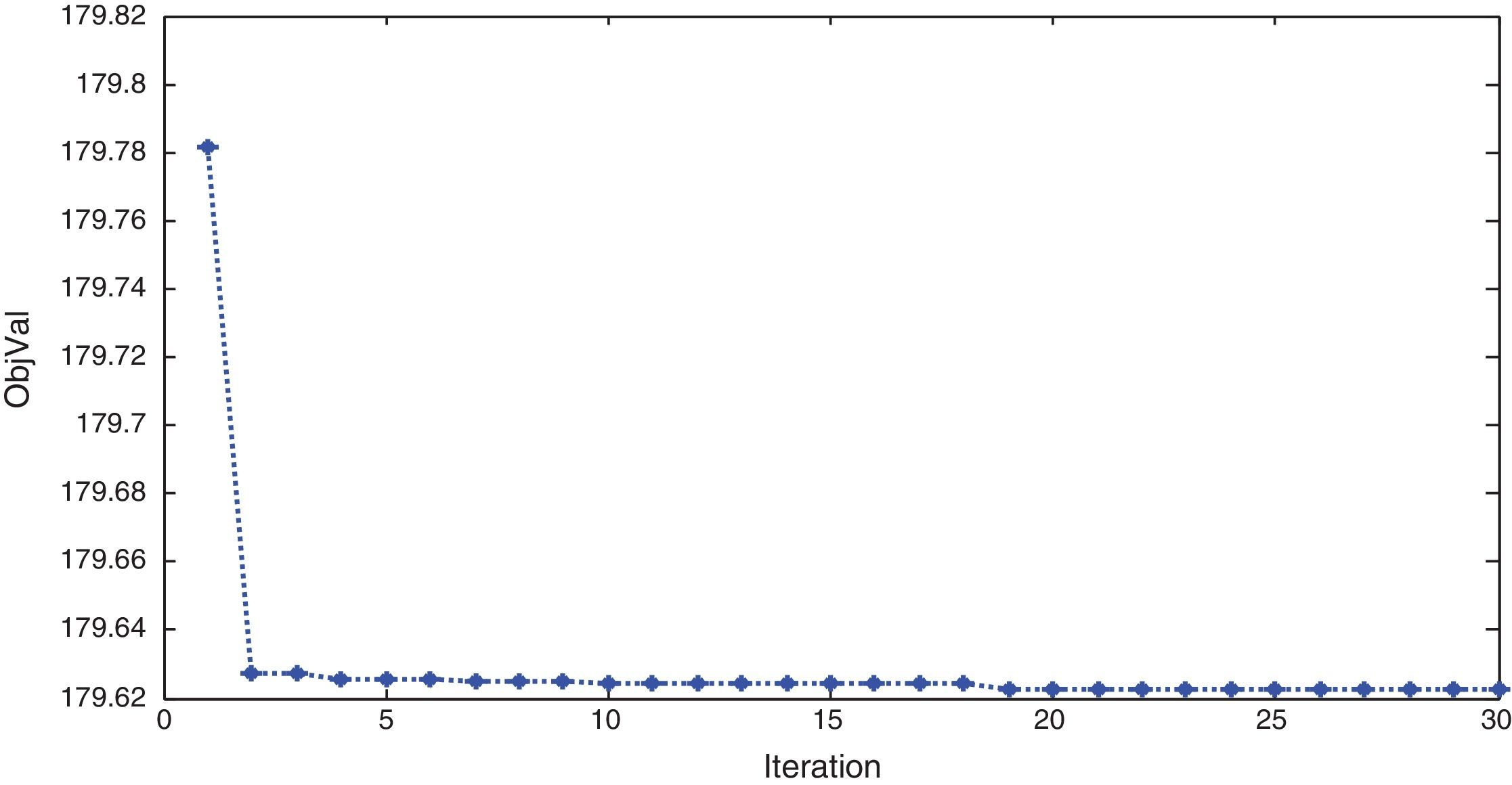
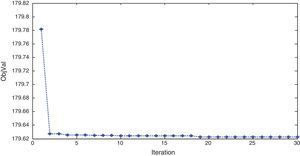
The simulation outcomes make known that the ACS tuned ANFIS controller responses are almost matching the responses of ACS tuned controller responses. Inspection of the objective function values reveals that the objective function values are to some extent equal when an ANFIS controller is used as compared to the ACS controller. The iteration graph i.e., Figure 26 shows that the ACS algorithm takes almost 15 iterations for convergence which takes approximately 30s. The ANFIS controller takes only a fraction of a second. This indicates the superior performance of ACS tuned ANFIS controller and its adaptability for online applications.
6ConclusionIn this paper, a new artificial cooperative search (ACS) algorithm tuned adaptive network-based fuzzy inference system (ANFIS) controller for optimal gain tuning of LFC operation in deregulated scenario has been productively implemented and tested on a two-area interconnected power system in deregulated scenario for a wide range of operating conditions. The artificial cooperative search algorithm is used for tuning the conventional controller integral gain values and also the integral gains at different operating conditions for ANFIS training. It has been observed that the responses of the system using ACS tuned controller and ACS algorithm tuned adaptive network-based fuzzy inference system controller are almost identical. The ANFIS tracks the operating condition and uses the updated parameters to compute the integral gain. The time taken for tuning is more in case of ACS tuned controller but, the response of ANFIS controller for different operating conditions is instantaneous. This makes the ACS algorithm tuned adaptive network-based fuzzy inference system controller more suited for online LFC operation in deregulated scenario than the other controllers. It has been obtained from the simulation results that the ANFIS-based controller and the ACS tuned controller are comparable for any given operating condition. Furthermore, it has been noted that ANFIS eliminates the need for switching between individual controllers as the operating condition changes thereby making the movement from one operating point to another smoother and automatic.
Conflict of interestThe authors have no conflicts of interest to declare.
Peer Review under the responsibility of Universidad Nacional Autónoma de México.