In this paper, we propose a carrier frequency offset (CFO) estimation scheme which is robust to the fractional CFO variation for orthogonal frequency division multiplexing (OFDM) systems. The proposed scheme first performs the envelope equalization process to convert the offset estimation problem to a carrier estimation problem, and then, estimates the integer and fractional parts of CFO by using periodogram of the received signal. Especially, in the estimation stage for fraction CFO, the ratio of the square-roots of periodograms is employed enlarging the estimation range of the stage than that of the conventional scheme. Numerical results demonstrate that the proposed scheme has better estimation performance than the conventional scheme for wider fractional CFO range in various channel conditions.
In wireless communication systems including wireless local area network (WLAN) [1], wireless metropolitan area network (WMAN), and digital video broadcasting (DVB) systems, the orthogonal frequency division multiplexing (OFDM) modulation has been widely used due to its high spectral efficiency and immunity to multipath fading [2]. However, the OFDM system is very sensitive to the carrier frequency offset (CFO) caused by Doppler shift [3] and oscillator instabilities [4]. Thus, the CFO estimation is one of the most important technical issues in OFDM systems.
Several schemes [5]-[8] have been proposed to estimate the CFO of OFDM signals. In [5], a CFO estimation scheme using a training symbol with two identical halves was proposed, whose estimation range equals to the subcarrier spacing. A novel CFO estimation scheme that utilizes a training symbol with more than two identical parts was proposed in [6], increasing the estimation range to twice that of the scheme in [5]. With the maximum-likelihood (ML) criterion, in [7], an optimal CFO estimation scheme was derived using the same training symbol as in [6].
Recently, in [8], an interesting CFO estimation scheme was proposed using an envelope equalization process (EEP) and periodogram operations. The scheme can be applied to a training symbol with arbitrary structure having the estimation range as large as the bandwidth of the OFDM signal by estimating the integer and fractional parts of the CFO (IFO and FFO) in each dedicated estimation stages, respectively. However, the performance of the scheme is very sensitive to the variation of the FFO distributed uniformly over [–0.5,0.5). Although the scheme in [8] employs an additional estimation stage to estimate the residual CFO (RFO), the performance sensitivity to the FFO variation still remains.
In this paper, we propose an improved periodogram-based CFO estimation scheme robust to the FFO variation for OFDM systems. The proposed scheme has wider FFO estimation range and numerical results demonstrate that the proposed scheme has better estimation performance than the conventional scheme in [8] for wider FFO range.
2System modelThe nth baseband OFDM sample xn of a training symbol can be expressed as
where ck is the data symbol for the kth subcarrier and N is the size of inverse fast Fourier transform (IFFT). Then, the nth received OFDM sample rn can be expressed as
where ε is the FO normalized by the subcarrier spacing whose integer and fractional parts are denoted by εI (εI ∈ {–N / 2, –N / 2+1,…, N / 2–1}) and εf (εf ∈ [–0.5,0.5)), respectively, hm is the channel coefficient of the mth path of the multipath channel with length of L, and wn is the zero-mean complex additive noise [9], [10].
At the receiver, we perform the EEP with a factor ρn defined by xn*/|xn|2 as in the scheme in [8], and then, the nth output sample r′n of EEP can be expressed as
where (·)*represents the complex conjugation and w′n=∑m=1L-1hmxn-mej2πεn/Nρn+wnρn. From Eq. 3, we can see that the CFO estimation problem is converted into the frequency (ε) estimation problem for a single tone complex sinusoidal signal, which is independent from the structure of the training symbol.
3Proposed schemeThe CFO estimation process of the scheme in [8] consists of three steps: IFO, FFO, and RFO estimation steps. In [8], the estimates εˆI,εˆf, and εˆr of the IFO, FFO, and RFO, respectively, are obtained as
and
respectively, where fk=-N2+k(k∈{0,1,…,N-1}) is the IFO candidate and |l(z)|2 is the periodogram of r′n defined by |I(z)|2=|∑n=0N-1r′ne-j2πzn/N|2. Then, the scheme in [8] yields estimate εˆ as εˆI+εˆf+εˆr.
Figure 1 shows the values of ε′f+εˆr as a function of ε-εˆI in the absence of channel and noise. From the figure, we can see that the scheme in [8] cannot estimate ε-εˆI even in the absence of channel and noise when ε-εˆI<-0.3 and 1.3<ε-εˆI (i.e., the estimation range of the FFO and RFO estimation scheme in [8] is -0.3≤ε-εˆI≤1.3).
εˆf+εˆr versus ε-εˆI for the scheme in [8].
Figure 2 shows the IFO metric normalized to N2 |h0 |2 as a function of fk and f ∈ [–N / 2, N / 2) for εI=1, εf=0.4, and N=8 when the noise is absent, where ‘º’ represents the IFO metric value corresponding to each integer fk. Since the FFO and RFO estimation range of the scheme in [8] is -0.3≤ε-εˆI≤1.3, the scheme in [8] requires an exact IFO estimate εˆI=1 to enable the FFO and RFO estimation scheme in [8] to compensate for the FO ε-εˆI. However, from the figure, we can see that the IFO metric value for fk=0 is as large as that for fk=1, and thus, the IFO metric Eq. 4 could yield an incorrect estimate under the influence of noise and channel. In this paper, we propose an FFO estimation scheme with a wide estimation range, allowing the FO to be compensated even though the IFO estimation step fails to provide a correct estimate, which would improve the overall CFO estimation performance.
Assuming that the channel is constant over one OFDM training symbol in the time domain and ignoring the noise term w′n, we can see that the channel coefficient h0 can be removed by taking the ratio of square roots of periodograms Is(εˆI) and Is(εˆI+1) as
where |Is (z)|2 is the periodogram of h0ej2πεn/N. Then, we can rewrite Eq. 7 as
Thus, we can obtain the estimate εˆ′f as
where M(εˆI)=Is(εˆI)/Is(εˆI+1) and ∠z represents the angle of a complex number z. Considering that –π≤∠z≤π for a complex number z, we can see that -N2≤εˆ′f=N2π∠1-M(εˆI)e-j2π/N-M(εˆI)≤N2, and thus, the estimation range of the proposed FFO scheme is obtained as [−N / 2, N / 2] in the absence of channel effect and noise. In the practical case, however, the proposed scheme would have the smaller estimation range than the ideal case of [−N / 2, N / 2] due to the fading channel and noise. For IFO and RFO estimation steps, we employ Eqs. 4 and 6, respectively.
4Numerical resultsThe estimation performance of the proposed and conventional [8] schemes are compared in terms of the frequency offset acquisition probability defined as the probability that the difference between ε and εˆI+εˆ′f (or εˆI+εˆf)is within the estimation range of the RFO estimation step -0.5~0.5. For simulations, we consider the OFDM symbols with 64 subcarriers and 8 guard interval samples and Rayleigh fading channels with an exponential power delay profile with four taps with an equal tap spacing of two samples. The power ratio of the first fading tap to the last fading tap is set to 20 dB. The channel coefficient is time varying with maximum Doppler shift of 266 Hz. The signal-to-noise ratio (SNR) is defined as σs2/σw2, where σs2 and σw2 are variance of the signal and noise components defined by E{|∑m=0L-1hmxn-m|2} and E{|wn|2}, respectively, and E {·} is the statistical expection.
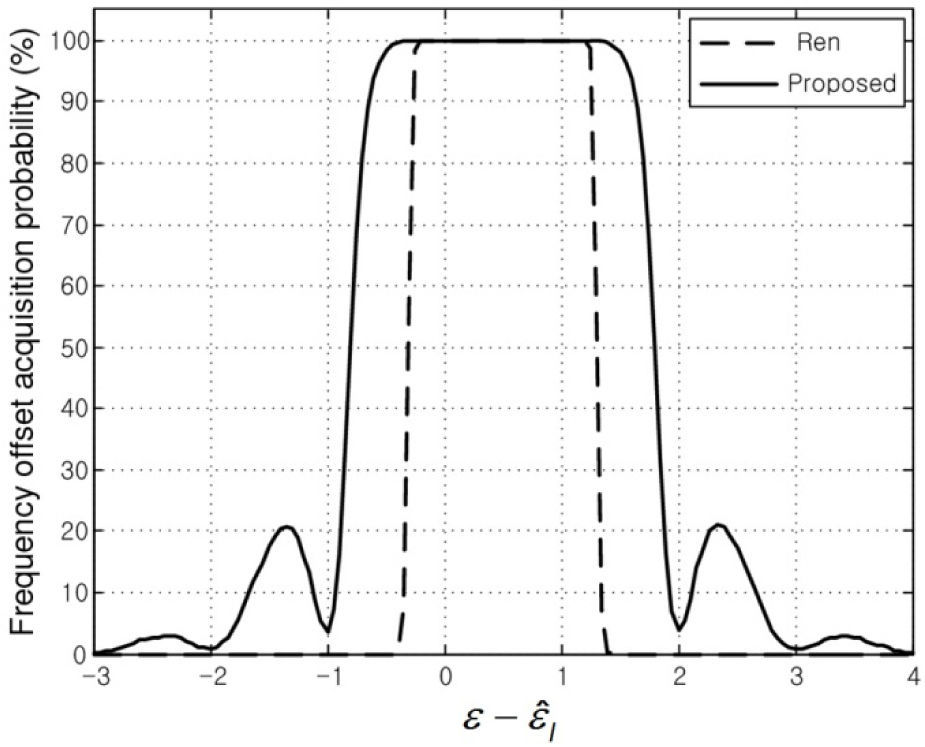
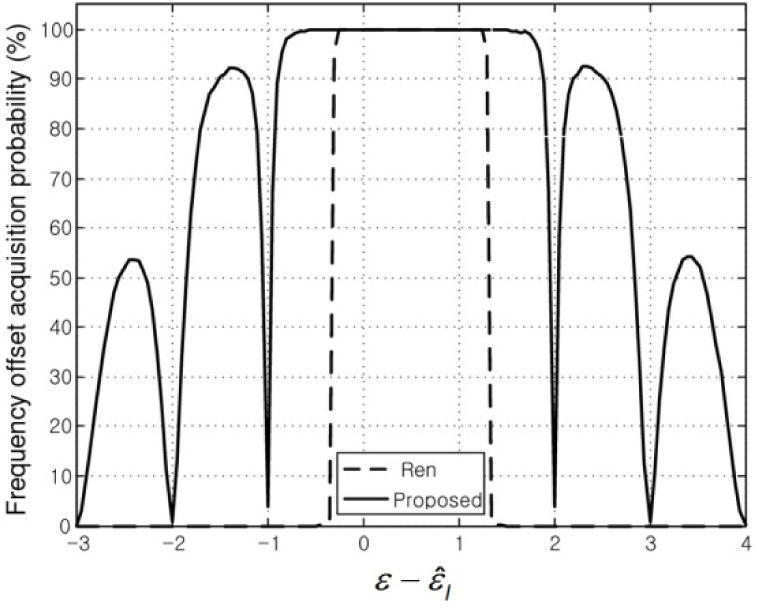
Figures 3 and 4 show the frequency offset acquisition probabilities of the proposed and conventional (denoted by Ren) schemes as a function of ε-εˆI over the additive white Gaussian noise (AWGN) channel, when SNRs are set to 5 and 25 dB, respectively. Also, Figures 5 and 6 show the frequency offset acquisition probabilities over the Rayleigh fading channels when SNRs are set to 5 and 25 dB, respectively. From the figures, we can see that the conventional scheme has the estimation range of -0.3≤ε-εˆI≤1.3, regardless of the channel and the value of SNR. On the other hand, the proposed scheme is found to have a better frequency offset acquisition probability in a wider range of ε-εˆI compared with the conventional scheme: Specifically, the proposed scheme always guarantees a reliable estimation performance in the range of -1<ε-εˆI<2, and moreover, in the range of ε-εˆI<-1 and 2<ε-εˆI, the frequency offset acquisition probability increases as the value of SNR increases.
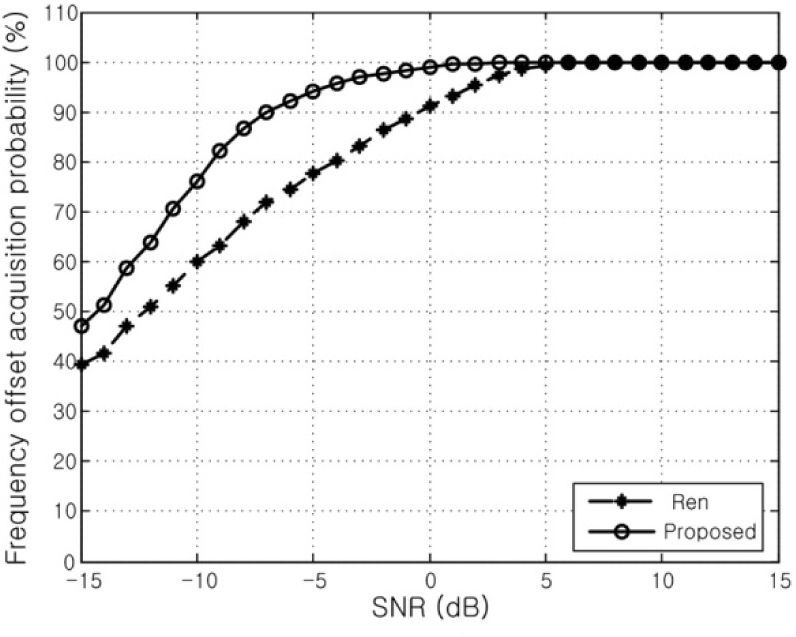
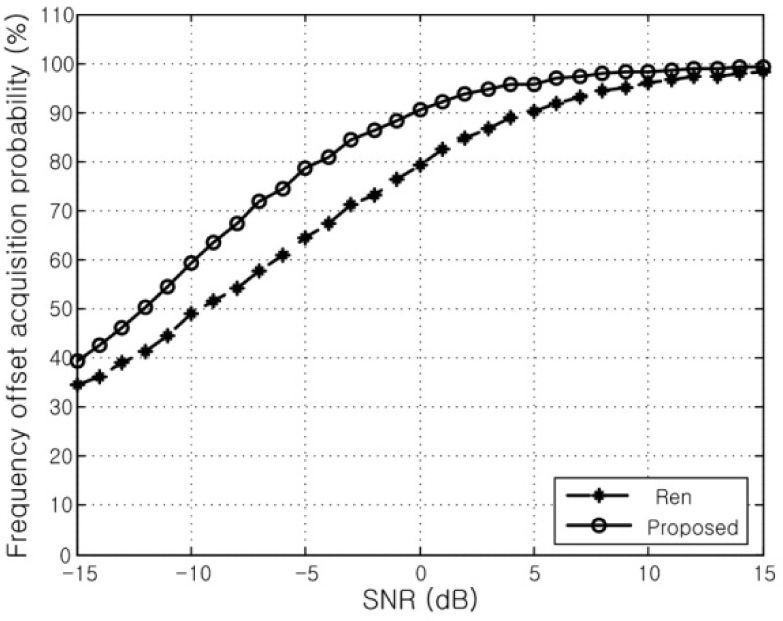
Figures 7 and 8 show the frequency offset acquisition probabilities of proposed and conventional schemes as the function of SNR over the AWGN and Rayleigh fading channels, respectively, when ε=1.3. From the figures, we also can see that the performance of the proposed scheme is better than that of the conventional scheme in the low SNR range and becomes similar as the value of SNR increases.
Since the ambient noise often exhibits impulsive non-Gaussian nature due to moving obstacles, car ignitions, and lightning in the atmosphere [11], we also compare the frequency offset acquisition of the proposed and conventional schemes in non-Gaussian noise environments. The non-Gaussian noise is often modeled as Cauchy noise [12]. Since the variance is not defined in Cauchy noise, we employ geometric SNR (G-SNR), which provides the characterization of the relative strength between the signal and noise [13] as G-SNR=σs2/(2Cγ2), where
C=explimb→∞(∑a=1b1/a-lnb)≅1.78 is the exponential of the Euler constant, and γ is the dispersion parameter, which is set to 1 in this paper.
Figures 9 and 10 show the frequency offset acquisition probabilities of the proposed and conventional schemes in non-Gaussian noise environments. From the figures, we can confirm that the proposed scheme has wider estimation range than the conventional scheme in non-Gaussian noise environments as well.
In this paper, we have proposed a periodogram-based CFO estimation scheme for OFDM systems. The FFO estimation step of the proposed scheme has the wider estimation range compared with that of the conventional scheme removing the effect of channel effectively. From numerical results, we have confirmed that the proposed scheme has better frequency offset acquisition probability performance than the conventional scheme for wider range of FFO.
AcknowledgementsThis research was supported by the National Research Foundation (NRF) of Korea under Grants 2012R1A2A2A01045887 and 2012R1A1A2004944 with funding from the Ministry of Education, Science and Technology (MEST), Korea, by the Information Technology Research Center (ITRC) program of the National IT Industry Promotion Agency under Grants NIPA-2012-H0301-12-1005 and NIPA-2012-H0301-12-2005 with funding from the Ministry of Knowledge Economy (MKE), Korea, and by National GNSS Research Center program of Defense Acquisition Program Administration and Agency for Defense Development.










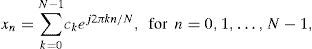





![εˆf+εˆr versus ε-εˆI for the scheme in [8]. εˆf+εˆr versus ε-εˆI for the scheme in [8].](https://static.elsevier.es/multimedia/16656423/0000001100000002/v2_201505081627/S166564231371530X/v2_201505081627/en/main.assets/thumbnail/gr1.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)











