The recent researches on the tracking of binary offset carrier (BOC) modulated signals have been studied focusing on resolving the ambiguity problem caused by the multiple side-peaks in BOC autocorrelation. In this paper, we propose a novel unambiguous BOC tracking scheme with an improved tracking performance by using partial-pulses of BOC signals. Firstly, we observe that a sub-carrier consists of two partial rectangular pulses referred to as partial-pulses, and then, generate multiple partial-correlations composing the BOC autocorrelation. Finally, a correlation function with no side-peak is constructed by combining the partial-correlations, and then, a delay lock loop employing the proposed unambiguous correlation function adjusts the phase of the local BOC signals. From numerical results, it is confirmed that the proposed scheme provides a better tracking performance than the conventional schemes in terms of the tracking error standard deviation.
Driven by the increasing demand for more precise location-based services [1], [2], new GNSSs including European Galileo and modernized global positioning system (GPS) employ the binary offset carrier (BOC) modulation to provide a higher positioning accuracy than the phase shift keying (PSK) modulation used in the conventional GPS [3]-[6]. The BOC modulated signal is generated by multiplying a pseudorandom noise (PRN) code with a sub-carrier of sine- or cosine-phased square wave, denoted as BOCsin(kn, n) or BOCcos(kn, n), respectively: Here, k represents the ratio of the chip period Tc of the PRN code to the period of the sub-carrier, and n denotes the ratio of Tc−1 to 1.023 MHz [7], [8].
Due to a sharp main-peak of BOC autocorrelation, the BOC signals offer a better tracking performance than the PSK signals. However, the BOC autocorrelation has multiple side-peaks around its main-peak, and thus, the tracking loop might be locked on one of the multiple side-peaks, causing a biased tracking result, which is referred to as the ambiguity problem [9]. Thus, several unambiguous tracking schemes [10]-[12] have been proposed to provide unambiguous correlation functions by removing side-peaks. A correlation function with no side-peak was firstly proposed for BOCsin(n, n) in [10] by subtracting the correlation between the received BOC and local PRN signals from the BOC autocorrelation. Then, in [11], specially designed local signals with a tunable parameter κ are employed to provide unambiguous correlation functions for BOCsin(kn, n). In [12], an interesting scheme applicable to both BOCsin(kn, n) and BOCcos(kn, n) was proposed based on a combination of sub-correlations of the BOC autocorrelation, which exhibits a better tracking performance than the schemes of [10] and [11]; However, the scheme of [12] has focused only on cancellation of correlation side-peaks without considering the tracking performance improvement.
The motivation of the paper comes from the fact that the effect of a tracking error can be reduced by sharpening the correlation main-peak [3]. Thus, in this paper, we address an unambiguous tracking scheme remove the side-peaks and improve the tracking performance by generating an unambiguous correlation function with a main-peak sharper than those of the conventional unambiguous correlation functions. We interpret a sub-carrier pulse as a sum of two partial pulses, and then, generate 4k partial-correlations composing BOC autocorrelation. In the first stage, we generate an unambiguous correlation function with a low and narrow main-peak by combining four partial-correlations out of 4k partial-correlations. In the second stage, we generate multiple unambiguous correlation functions with the same main-peak width by combining the correlation function obtained at the first stage with partial-correlations, and then, construct an unambiguous correlation function with a high and sharp main-peak by increasing the height of the main-peak. Moreover, the proposed scheme not only provides an improved tracking performance but also is applicable to both BOCsin(kn, n) and BOCcos(kn, n).
The rest of this paper is organized as follows. In Section 2, we describe the BOC signal model and its partial-correlations. Section 3 proposes an unambiguous correlation function with a higher and sharper main-peak. In Section 4, tracking performances of unambiguous tracking schemes are compared in terms of the tracking error standard deviation (TESD). Finally conclusion is presented in Section 5.
2Signal modelInterpreting that a sub-carrier pulse is the sum of two rectangular pulses (referred to as partial-pulses), we can express the baseband equivalent of BOC signal as
where S is the signal power, ci ∈ {−1,1} is the ith chip of a PRN code with period T, pα (t) is the unit rectangular pulse over [0, α], and Tc is the chip period of the PRN code. In addition, csc(t)=∑l=04k−1hlPTst−iTc−lTs is the square wave sub-carrier, Ts=Tc/4k=14kn×1.023MHz is the duration of a partial-pulse, and hl ∈ {−1,1} is the sign of the lth partial-pulse: For BOCsin(kn, n) and BOCcos(kn, n), hl is specified as −12ki+l2 and −12ki+l2, respectively, where X is the smallest integer not smaller than x and X is the largest integer not larger than x. We can also see that there exist 4k partial-pulses in a chip period Tc. We assume that every chip of the PRN code is an independent random variable taking on +1 and −1 with equal probability and the code period T is sufficiently large compared with the chip period Tc.
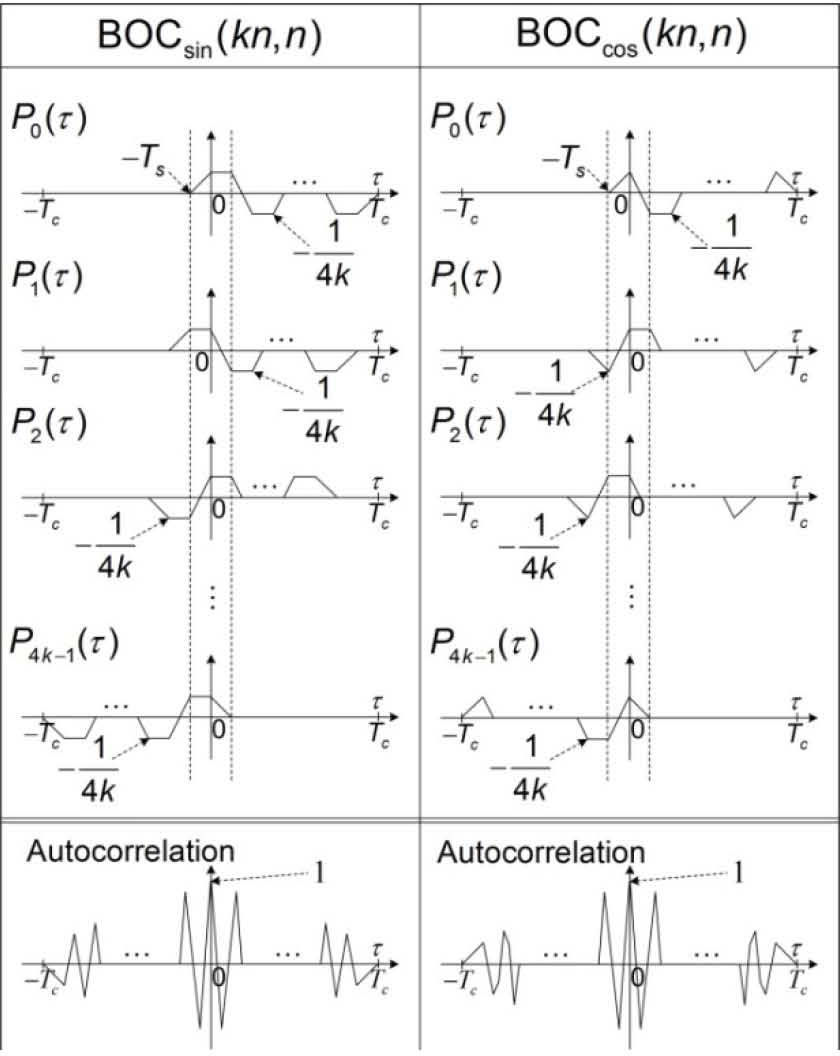
The normalized BOC autocorrelation can be expressed as
where
is a triangular function and
is the lth partial-correlation function. Figure 1 shows partial-correlations Pl(τ)l=04k−1 and autocorrelations for BOCsin(kn, n) and BOCcos(kn, n). From the figure, we confirm that the BOC autocorrelation is the sum of the partial-correlations.
3Proposed correlation functionWe generate an unambiguous correlation function with a high and sharp main-peak in two stages. The first and second stages are described in Figures 2 and 3, respectively, for BOCsin(kn, n).
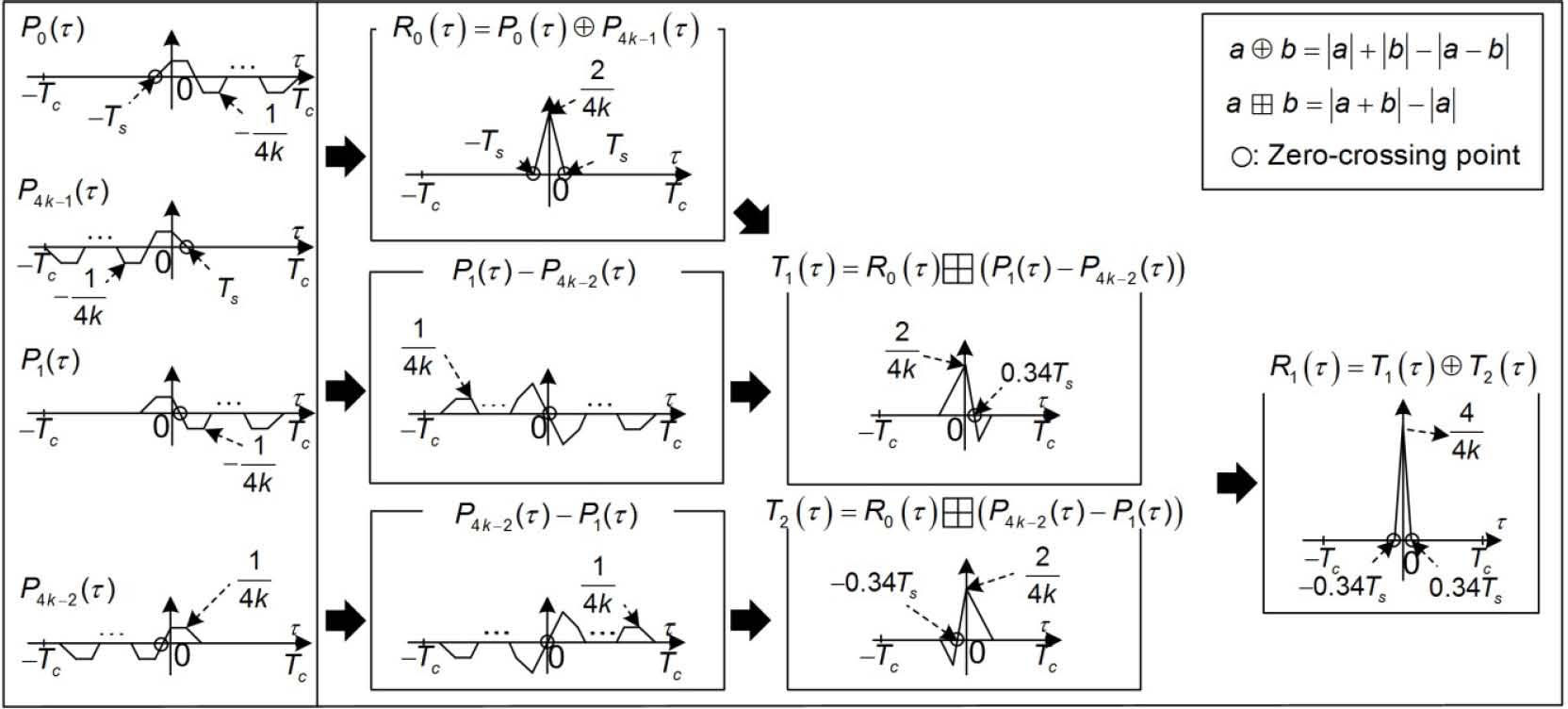
In the first stage, we combine P0(τ) and P4k−1(τ) as
to generate an unambiguous correlation function R0(τ) with no side-peak, where a⊕b≜a+b−a−b. From Figure 2, we can observe that the main-peak width of R0(τ) is determined by the location of a zero-crossing point nearest to τ = 0 in P0(τ) and P4k−1(τ). Thus, to generate an unambiguous correlation function with a narrow main-peak, we combine R0(τ) with P1(τ)−P4k−2(τ) and P4k−2(τ)−P1(τ) as
where a⊞b≜a+b−a. For example, the zero-crossing points nearest to τ = 0 for T1(τ) and T2(τ) are 0.34Ts for BOCsin(kn, n), which is obviously much narrower than the main-peak width Ts of the scheme of [12]. Then, we combine T1(τ) and T2(τ) as
yielding an unambiguous correlation function with a low and narrow main-peak; however, R1(τ) does not contain sufficient signal energy required for reliable tracking since R1(τ) is generated by using only four partial-correlations out of 4k partial-correlations, which causes a significant energy loss in the tracking process.
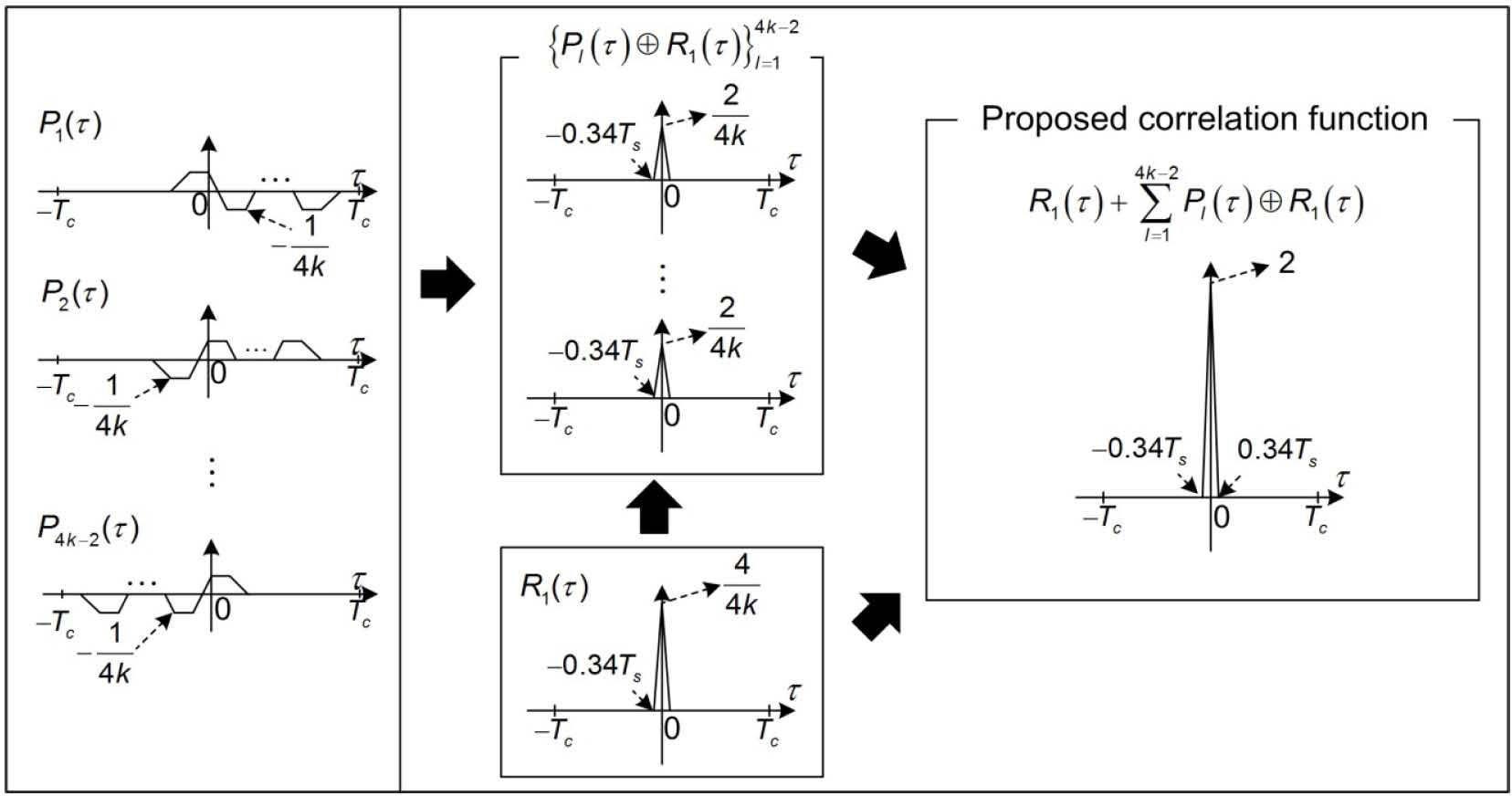
Thus, in the second stage we construct multiple unambiguous correlation functions by using additional combination of Plτ⊕R1τl=14k−2, and then, increase the height of a low and narrow main-peak as
yielding an unambiguous correlation function with a high and sharp main-peak as shown in Figure 3. The value of the main-peak is always two since its value can be calculated as 4/(4k) +(4k−2)×2/(4k), where 4/(4k) comes from R1(τ) and (4k−2)×2/(4k) comes from ∑I=14k−2Plτ⊕R1τ. It should be noted that the proposed two-stage method is also directly applicable to although the proposed method is described for BOCsin(kn, n) only.
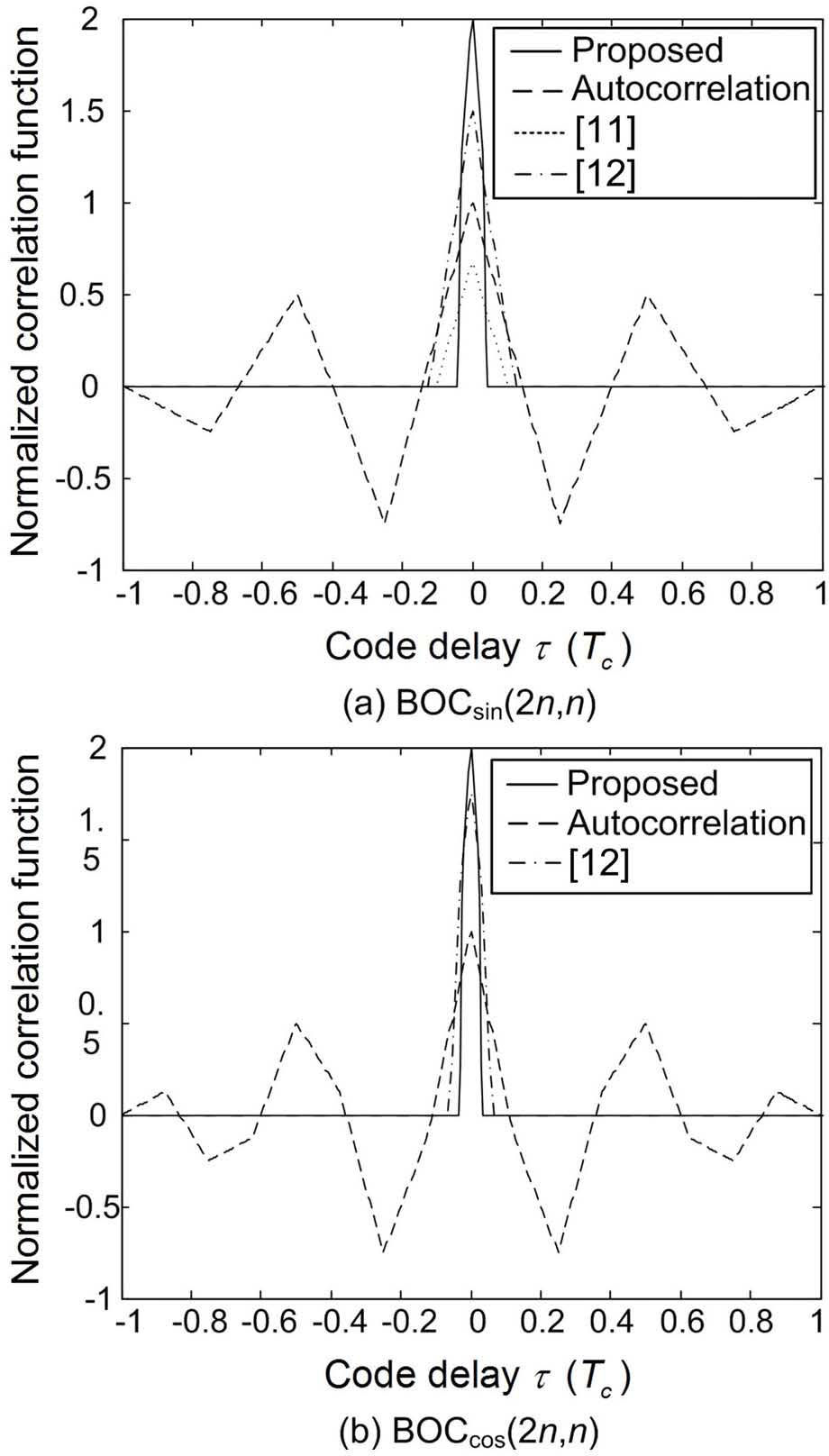
Figure 4 shows the normalized correlation function of the proposed and conventional schemes for BOCsin(2n, n)and BOCcos(2n, n): Here, it should be note that the schemes of [10] and [11] are dedicated to BOCsin(n, n)and BOCsin(kn, n), respectively, and the tunable parameter κ is set to 0.3 which guarantees the best performance [11]. From the figure, we can see that the proposed correlation function has a main-peak sharper than those of the conventional correlation functions. Specifically, the normalized height of the main-peak of the proposed correlation function is two regardless of the value of k The main-peak widths are 0.68Ts and 0.5Ts for BOCsin(kn, n) and BOCcos(kn, n), respectively. It is straightforward to show that the absolute slope of the main-peak of the proposed correlation function for BOCsin(kn, n) is 23.52k, and is larger than the absolute slope 8k–4 of the main-peak of the correlation function in [12]. Moreover, the proposed correlation function for BOCcos(kn, n) has an absolute slope 32k of the main-peak, which is larger than the absolute slope 16k–4 of the main-peak of the correlation function of [12].
As the main-peak width of the proposed correlation function is narrower than those of the conventional correlation functions, the available code tracking range of the proposed correlation function is smaller than those of the conventional correlation functions in [10] and [11].; however, the absolute slope of the main-peak of the proposed correlation function is much larger than those of the conventional correlation functions. Thus, we can anticipate that the proposed correlation function will offer a performance improvement over the conventional correlation functions.
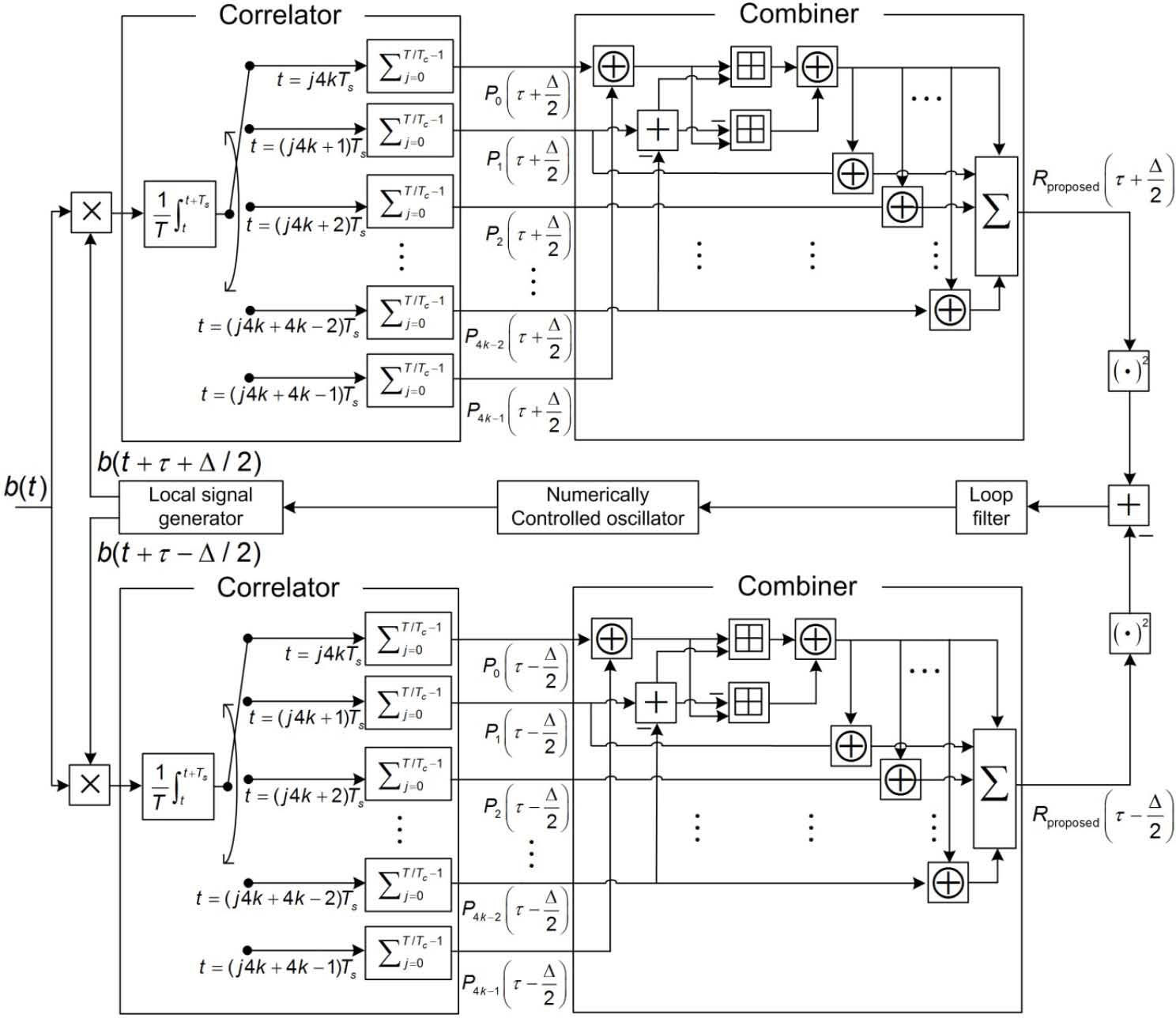
Figure 5 illustrates a delay lock loop (DLL) structure of the proposed noncoherent BOC signal tracking scheme, where τ represents the phase difference between the received and locally generated BOC signals and Δ is the early-late spacing. In the correlator, the received BOC signal b(t) is first multiplied with the early version of the locally generated BOC signal bt+τ+Δ2 (late version bt+τ−Δ2)), and then, correlated every Ts seconds, yielding partial-correlations of early version {Pl(τ+Δ2)}l=04k−1 (late version {Pl(τ−Δ2)}I=04k−1). Then, in the combiner, partial-correlations of early version {Pl(τ+Δ2)}l=04k−1 (late version {Pl(τ−Δ2)}I=04k−1) are combined as in Eq. 8 to produce the proposed correlation function of early version Rproposedτ+Δ2 (late version Rproposedτ−Δ2)).Finally, in the tracking process, the discriminator output
is applied to the loop filter to drive the numerically controlled oscillator (NCO), which advances or delays the clock of the local signal generator until τ becomes zero.
4Numerical resultsTracking performances of the proposed and conventional schemes are compared in terms of TESD: Here, the TESD is defined as σG2BLTl where σ is the standard deviation of D(0), BL is the bandwidth of the loop filter, Tl is integration time, and G=dDτdτ|τ=0 is the discriminator gain [14]. We assume the following parameters for simulations: Galileo E1-B PRN code with period T = 4 ms, Tl = T, Δ = Ts/4, BL = 1Hz, κ = 0.3 for the scheme of [11], and Tc−1=1.023MHz.
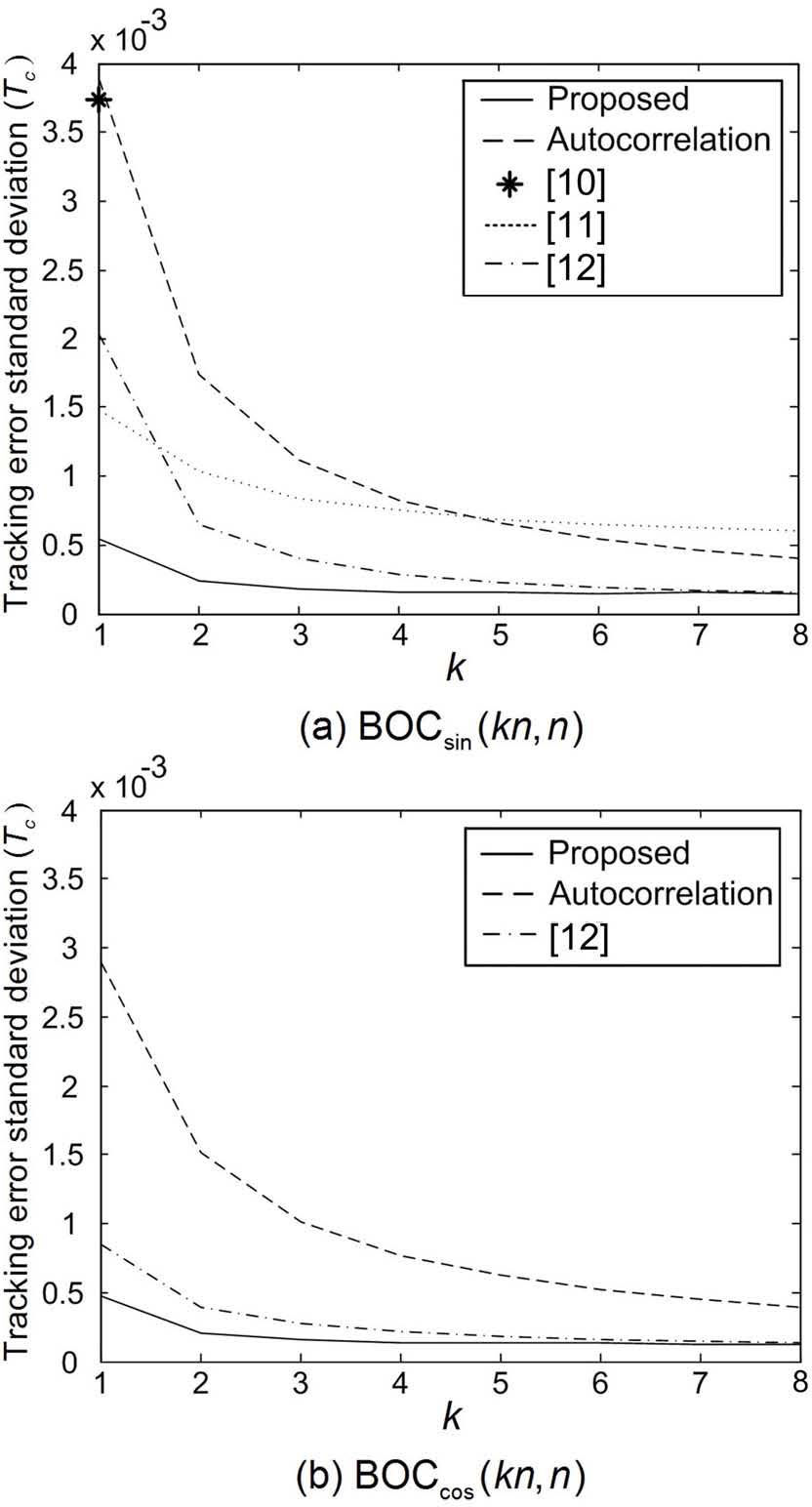
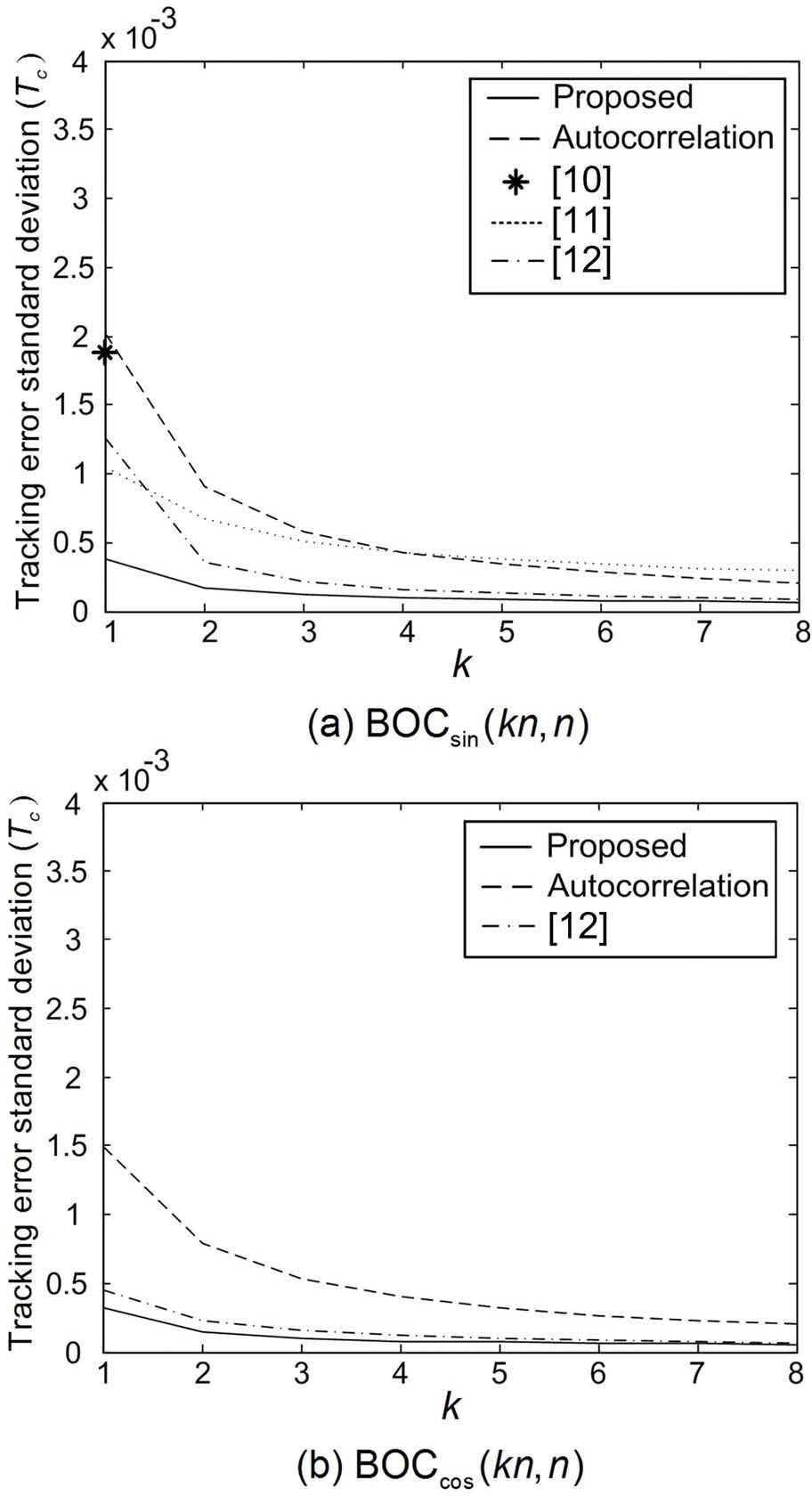
Figures 6 and 7 show the TESD of the tracking schemes with the proposed and conventional correlation functions as a function of k when the carrier-to-noise ratio (CNR) is 30 and 35 dB-Hz, respectively: Here, the CNR is defined as S/N0 where N0 is the noise power spectral density. From the figures, it is clearly observed that the proposed correlation function provides a better TESD than the conventional correlation functions. Although the TESD of the conventional correlation functions becomes smaller as the value of k increases, the proposed correlation function always provides the best performance due to its sharp main-peak.
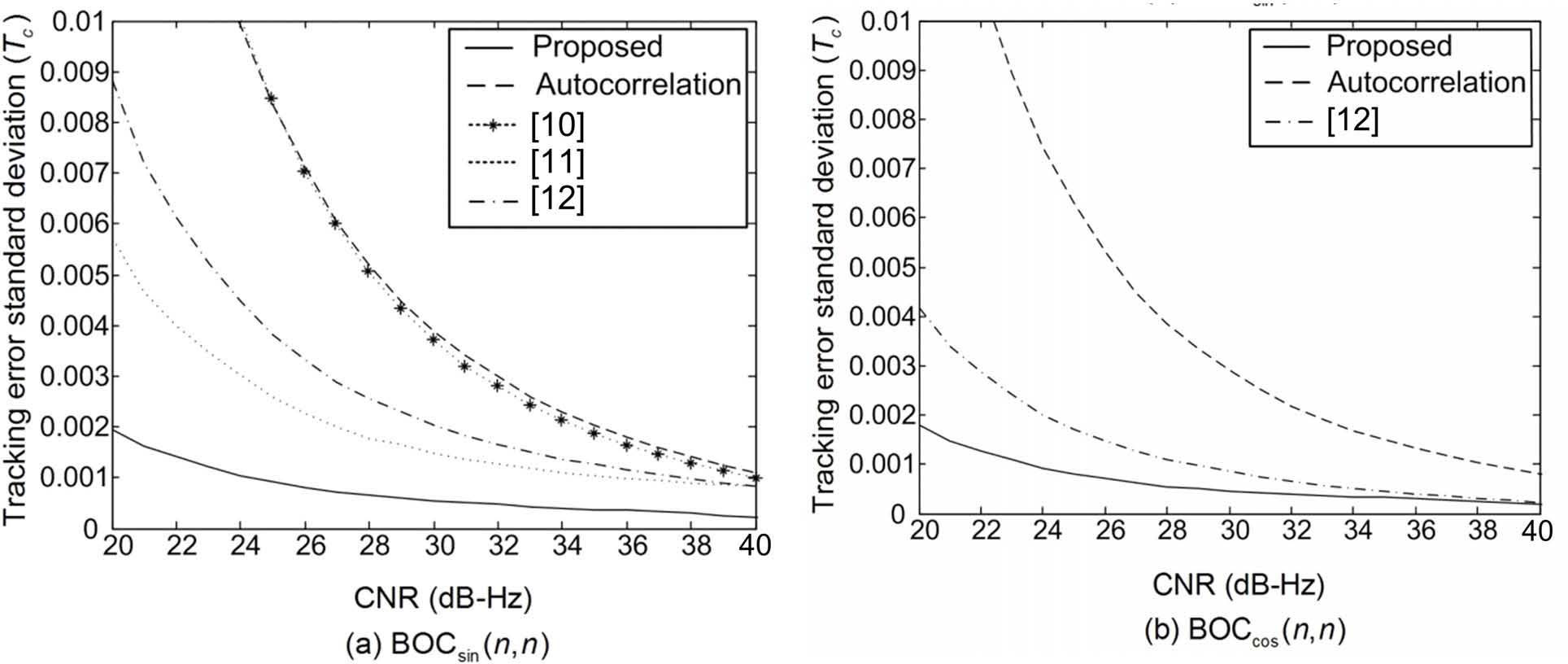
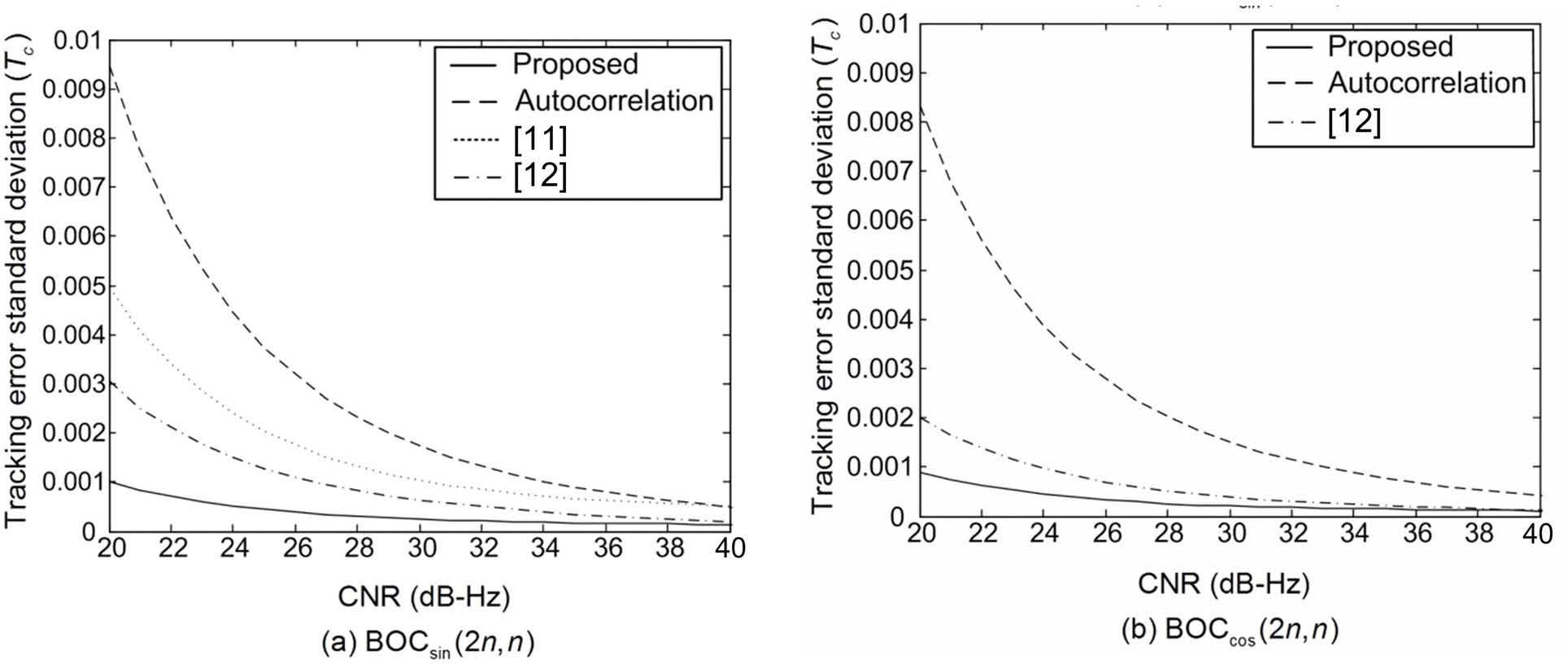
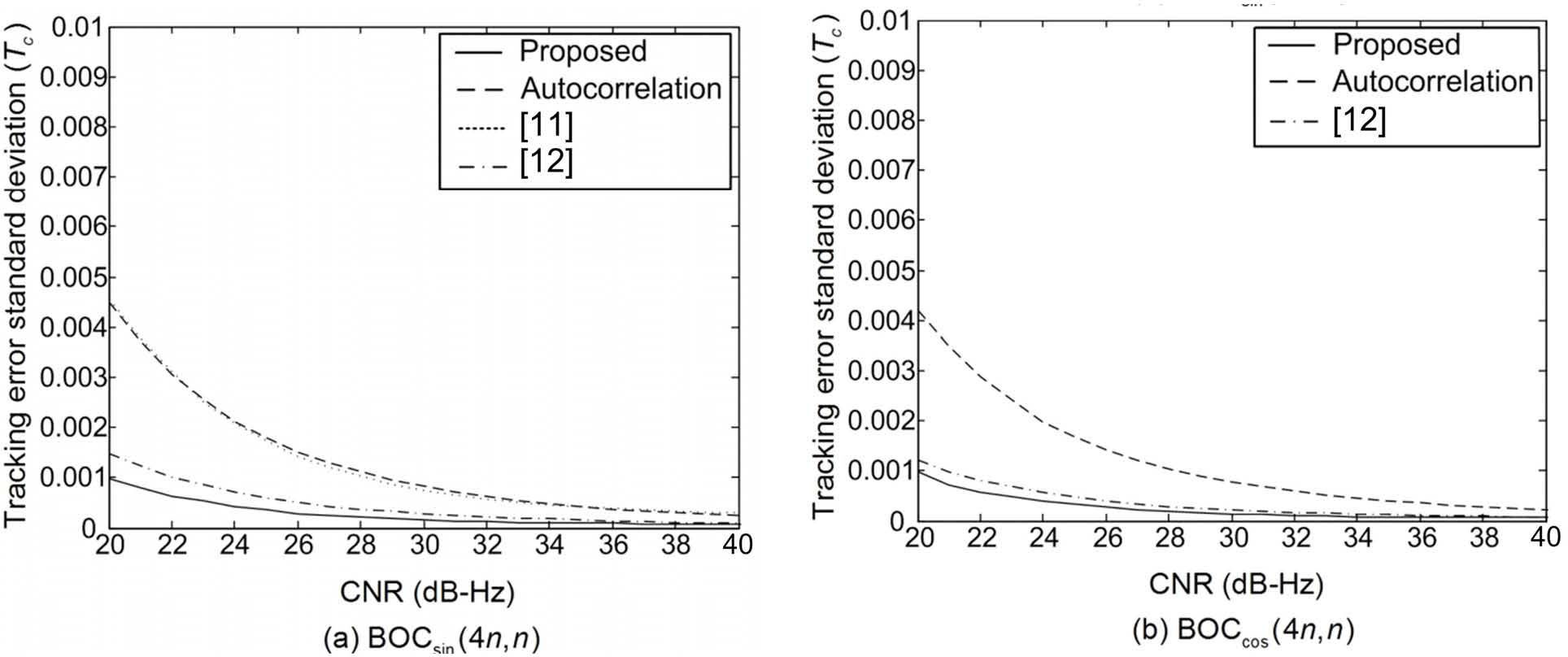
Figures 8-10 show the TESD of the tracking schemes with the proposed and conventional correlation functions as a function of CNR when k = 1, 2, and 4, respectively. From the figures, we can confirm that the proposed correlation function also provides a significant performance improvement over the conventional correlation functions in the CNR range of 20 ~ 40 dB-Hz of practical interest.
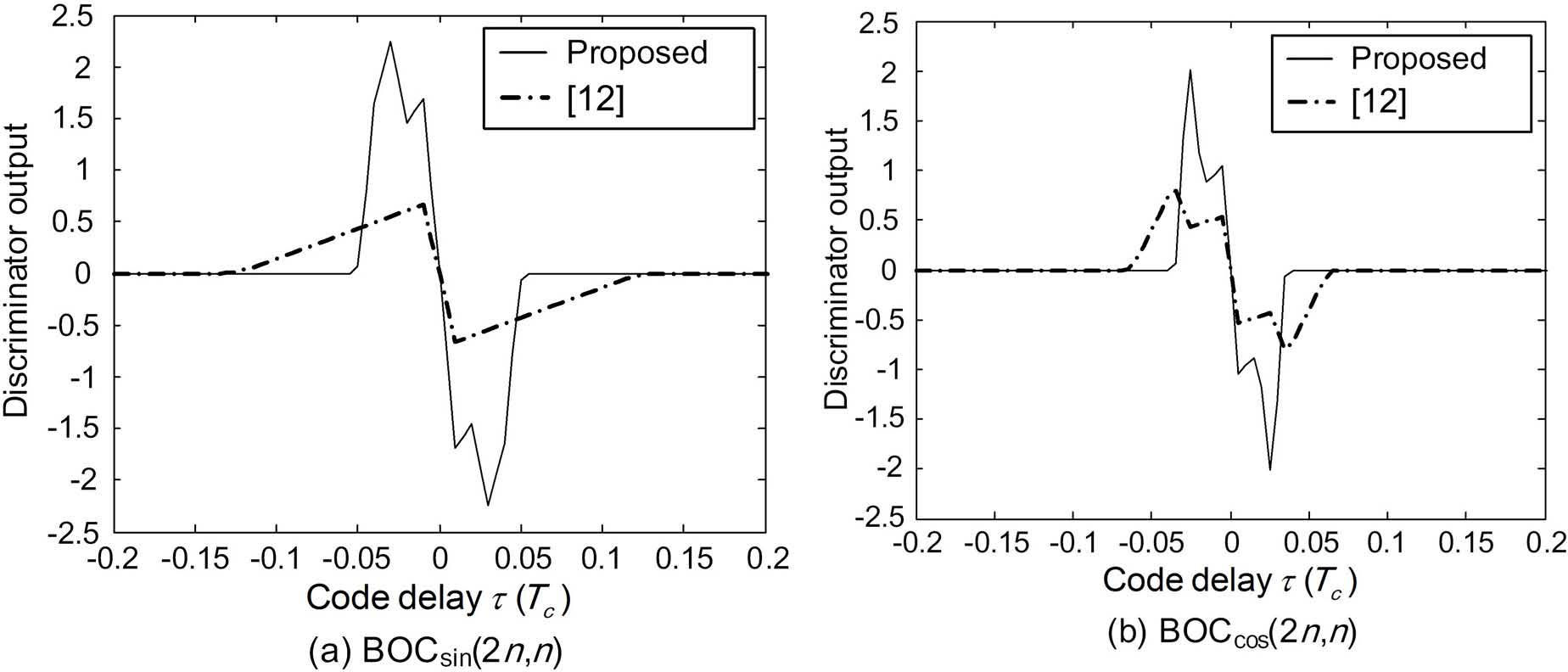
We would like to stress that the improved performance of the proposed scheme comes from the fact that the discriminator output of the proposed correlation function has a much higher slope (i.e., the discriminator gain) than that of the conventional one as shown in Figure 11. It should be also observed that the proposed scheme has the same tracking range, which is defined as the range of the linear part around τ = 0, as that of the conventional one of [12].
Discriminator outputs of the proposed and conventional scheme of [12] for BOCsin(2n, n) and BOCcos(2n, n).
In this paper, we have proposed an unambiguous tracking scheme using partial-pulses by generating an unambiguous correlation function with a high and sharp main-peak. The proposed scheme not only removes the side-peaks completely but also provides an improved tracking performance compared with the conventional schemes. Specifically, we have generated 4k partial correlations using partial-pulses, and then, produced an unambiguous correlation function with a low and narrow main-peak based on the combination of four partial-correlations in first stage. In second stage, we have generated an unambiguous correlation function with a high and sharp main-peak using the correlation function obtained at the first stage and partial-correlations. The numerical results have demonstrated that the proposed scheme provides a better tracking accuracy than the conventional schemes in terms of the TESD.
This research was supported by the National Research Foundation (NRF) of Korea under Grant 2014R1A5A1011478 and by the Convergence Information Technology Research Center (C-ITRC) support program supervised by the National IT Industry Promotion Agency (NIPA) under Grant NIPA-2014-H0401-14-1009 with funding from the Ministry of Science, ICT and Future Planning (MSIP), Korea, and by Priority Research Centers Program through the NRF of Korea under Grant 2009-0093828 with funding from the Ministry of Education, Science and Technology.




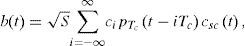
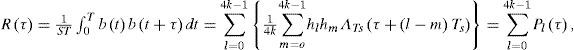
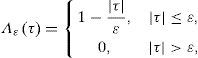
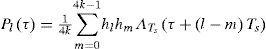



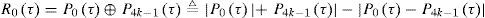
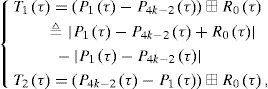
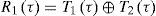
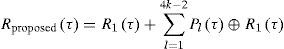

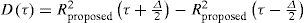






![Discriminator outputs of the proposed and conventional scheme of [12] for BOCsin(2n, n) and BOCcos(2n, n). Discriminator outputs of the proposed and conventional scheme of [12] for BOCsin(2n, n) and BOCcos(2n, n).](https://static.elsevier.es/multimedia/16656423/0000001200000006/v2_201505081706/S1665642314716700/v2_201505081706/en/main.assets/thumbnail/gr11.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)