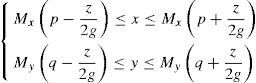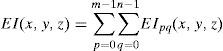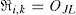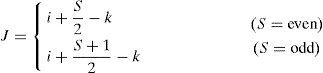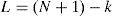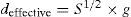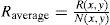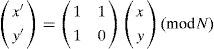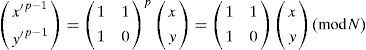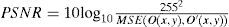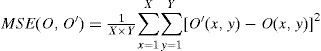In this paper, a three-dimensional (3D) image security system combines the use of the smart pixel mapping (SPM) algorithm and the Fibonacci transformation technique is proposed. In order to reconstruct orthoscopic 3D images with improved image quality, a smart pixel mapping process is adopted. Based on the SPM-based computational integral imaging (CII) system, the depth-converted elemental image array (EIA) is obtained for increasing the quality of the reconstructed image. In the encryption process, the depth-converted EIA is scrambled by the Fibonacci transformation (FT) algorithm. Meanwhile, the computational integral imaging reconstruction (CIIR) technique is used to reconstruct the 3D image in the image reconstruction process. Compared with conventional CII-based 3D image encryption methods, the proposed method enable us to reconstruct high-resolution orthoscopic 3D images at long distance. To demonstrate the effectiveness of the proposed method, some numerical experiments are made to test the validity and the capability of the proposed 3D image security system.
With the growth of the Internet and the increase of the requirement for image transmission, image encryption and watermarking are becoming more and more important [1]. Recently, Image encryption technology based on optics is an effective measure to ensure the information security and has gained great interest in the rapid development of communication technologies. Optical encryption methods own many intrinsic advantages, such as high speed and difficulty of unauthorized access [2]. Integral imaging (II) is a three-dimensional (3D) imaging technique which comprises of two optical processes: pickup process and reconstruction process [3-4]. In the pickup process, the light rays emanating from 3D images pass through the lenslet array is recorded as a two-dimensional (2D) elemental image array (EIA) with a different perspective of a 3D image. In the reconstruction process, by back-propagating light rays of the EIA through the lenslet array, the 3D image is reconstructed at the location where it was picked up. However, II systems work in their conventional configuration degrade quality of the reconstructed 3D scenes due to the lens refraction. The computational integral imaging (CII) [5-9] becomes an important part of II. In CII, the reconstructed process is accomplished on computers, and no physical noise is produced.
In recent years, image encryption methods based on II have been proposed for practical applications. Piao et al. [10] proposed an image encryption using II and pixel scrambling techniques. In this method, pixels of the cover image were scrambled with the pixel scrambling technique and elemental images (EIs) for this scrambled image are picked up through a lenslet array, the image reconstructed by applying the computational integral imaging reconstruction (CIIR) technique. The experimental results implied this method provided high robustness.
In 2013, Kim et al. [11] presented a 3D image encryption method based on II and maximum length cellular automata (CA). In this method, the picked-up EIA was encrypted by the 2D maximum length CA. The 3D image reconstruction algorithm also based on CIIR. This method has given a secure and robust encryption algorithm.
Recently, Li et al. [12] have proposed a 3D image encryption system combined the use of CII system and complemented maximum length CA. In this method, a 3D image was optically picked-up by a lenlet array, the picked-up EIA was then encrypted by the complemented maximum length CA. This method utilized the complemented CA to improve the security of the encrypted image. However, in the image reconstruction process, the quality of reconstructed image will degrade due to the interference of adjacent pixels in CIIR.
Basically, the CIIR technique allows us to reconstruct 3D images at any distance from the virtual pinhole array (VPA) by pixels superposition, according to computationally simulating geometrical optics. However, the qualities of the reconstructed images degrade due to the interference of adjacent pixels in the reconstruction process. Also, the resolution of 3D reconstructed images is dramatically degraded as the distance from the VPA increases. To overcome these problems, in this paper, we propose a modified CII method based on smart pixel mapping (SPM) [13-15] and pixel average algorithm for reconstructing orthoscopic 3D images with enhanced quality of the image. To demonstrate the usefulness of this proposed method we carry out some experiments and the results are shown.
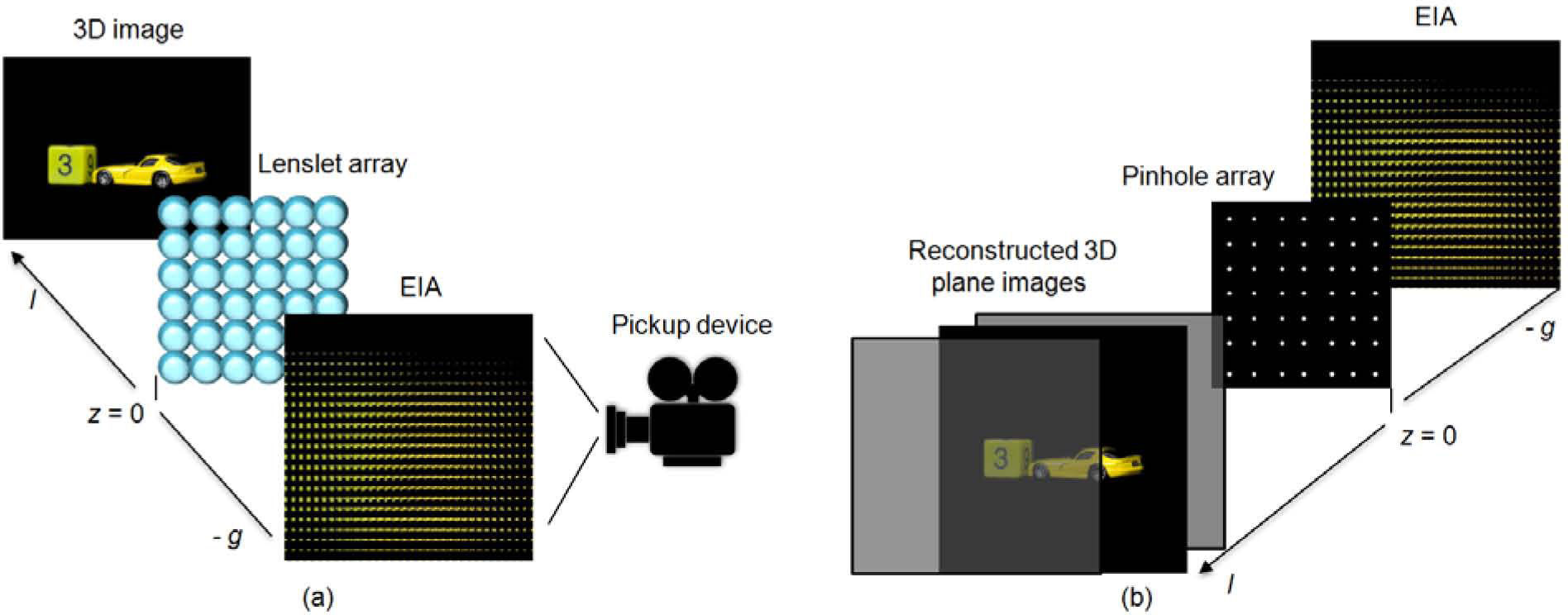
2Review of CII system for 3D image pickup and reconstructionThe principle of 3D image encryption using CII is that it is possible to obtain the 3D image encryption of interest. That is, we can encrypt 3D image effectively and speedily. The schematic diagram of CII system composed of the optical pickup and computational reconstruction parts is shown in Figure 1. Figure 1 (a) illustrates an optical pickup system, in which intensity and direction information of the rays coming from a 3D image through a lenslet array is optically recorded as a form of 2D EIA representing different perspectives of a 3D image in the pickup process.
Figure 1 (b) represents a computational reconstruction system, the 3D plane images are computationally reconstructed by the captured EIA via digital simulation of ray optics called CIIR at an arbitrary distance from a virtual pinhole array. Let Epq be the p-th row and the q-th column elemental image, and EIpq(x,y,z) be the inversely magnified image of the elemental image Epq at the location (x, y, z). In order to reconstruct a plane image, EIs are inversely mapped to an output plane located in longitudinal distance z. The inverse mapped image EIpq (x,y,z)can be represented in terms of elemental image Epq at the distance z is written as
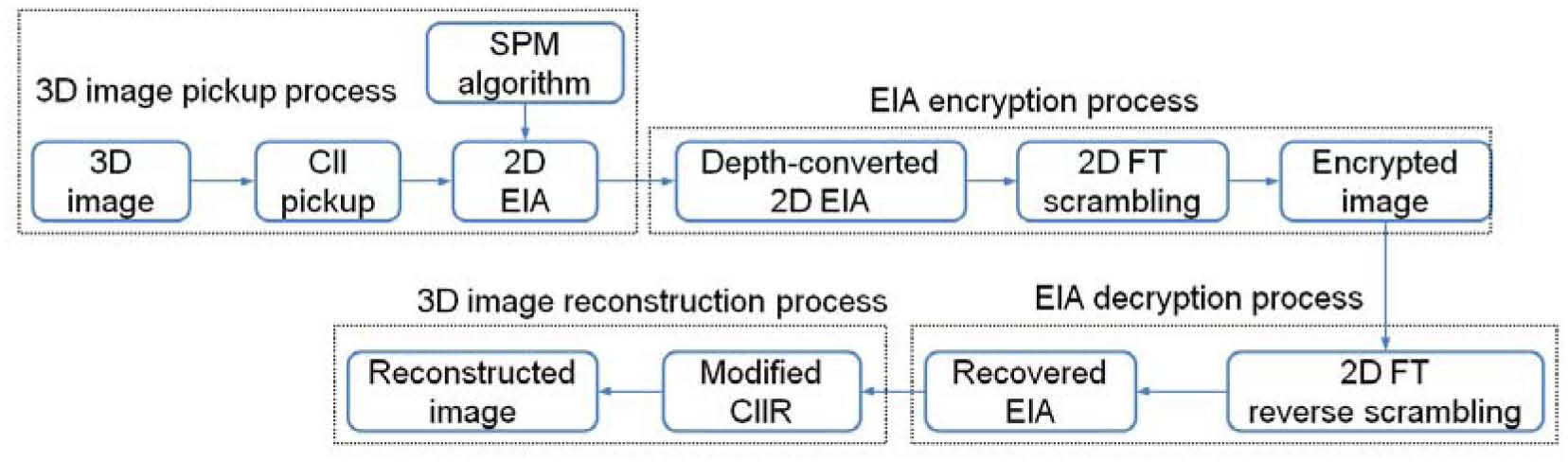
where Mx and My are the sizes of elemental image Epq in x, y directions, respectively. The reconstructed 3D image at the (x, y, z) is the summation of all inversely mapped EIs and given bywhere m and n indicate the number of EIs in the x and y directions, respectively.3Proposed methodFigure 2 shows the flowchart of the proposed encryption method. The image encryption process is mainly divided into the following parts: First, the 3D image is optically picked-up by a lenslet array. Then, the obtained 2D EIA is converted by the SPM algorithm. Finally, the generated depth-converted EIA is scrambled by the 2D FT algorithm. The image decryption is the reverse process of the encryption. The encrypted image is first inversely scrambled by the 2D FT technique. The 3D image is reconstructed by the depth-converted EIA via the improved CIIR technique.
3.1Proposed SPM-based CII methodImage reconstruction based on conventional CIIR, the quality of the reconstructed image is degraded by interference between pixels due to the magnification factor. This causes the noise superposition of intensity information from adjacent pixels when the magnified elemental images (EIs) are overlapped on the output plane. Thus as the magnification factor increases, the interference strength of pixels increases. The magnification factor M = l/g, the l represents the distance between the VPA and the reconstructed plane image, the g represents the distance between the EIA and VPA. In this study, we seek to reduce the interference in CIIR by the SPM algorithm.
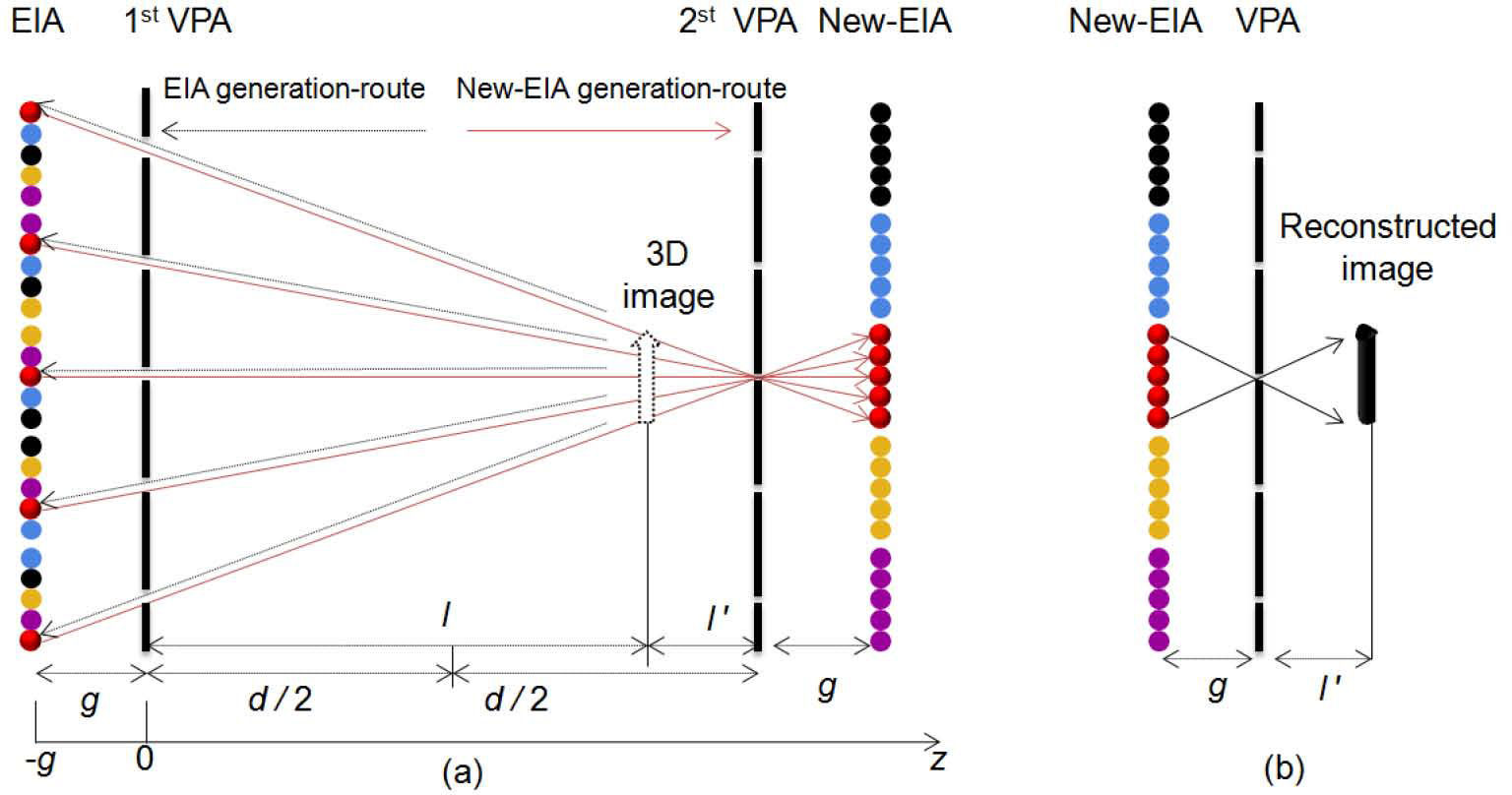
The principle of the SPM-based CII method is illustrated in Figure 3. To obtain the modified EIA, in this method, two VPAs are used. The first VPA locates at z = 0, and the second VPA locates at z = d. The (i, k)th modified elemental image ℜi,k can be expressed as
Here, let O be the original EIA. S and N represent the number of the EIs and the number of pixels each elemental image, respectively. The subscripts i and J represent corresponding elemental image of the modified EIA and original EIA, respectively, and the k and L are the pixel number of the corresponding elemental image. The effective distance of SPM-based CII is obtained from the following equation:
If we consider the EIA consists five EIs and each of EIs has five pixels, the relation of pixel mapping is shown in Figure. 3 (a), using the Eq. 4, the modified elemental image ℜ3k is obtained by the equation: ℜ3k= ϕ (O11, O22, O33, O44, O55), ‘ϕ’ represents a relation of pixel mapping, k ∈ (1,2,3,4,5).
To demonstrate the reduction of the pickup distance, we suppose that light rays coming from the 3D image and pass through the first VPA to form an EIA located at z = -g, as shown in Figure 3 (a). Then, the rays of the recorded EIA pass through the first VPA and second VPA, respectively, to form a modified EIA. The modified EIA is computationally recorded in the location z = d + g. Using the modified EIA, the 3D image is reconstructed at the distance z = l’ as shown in Figure 3 (b). The plane image reconstructed distance of the proposed method has been reduced, compared with the conventional CIIR algorithm.
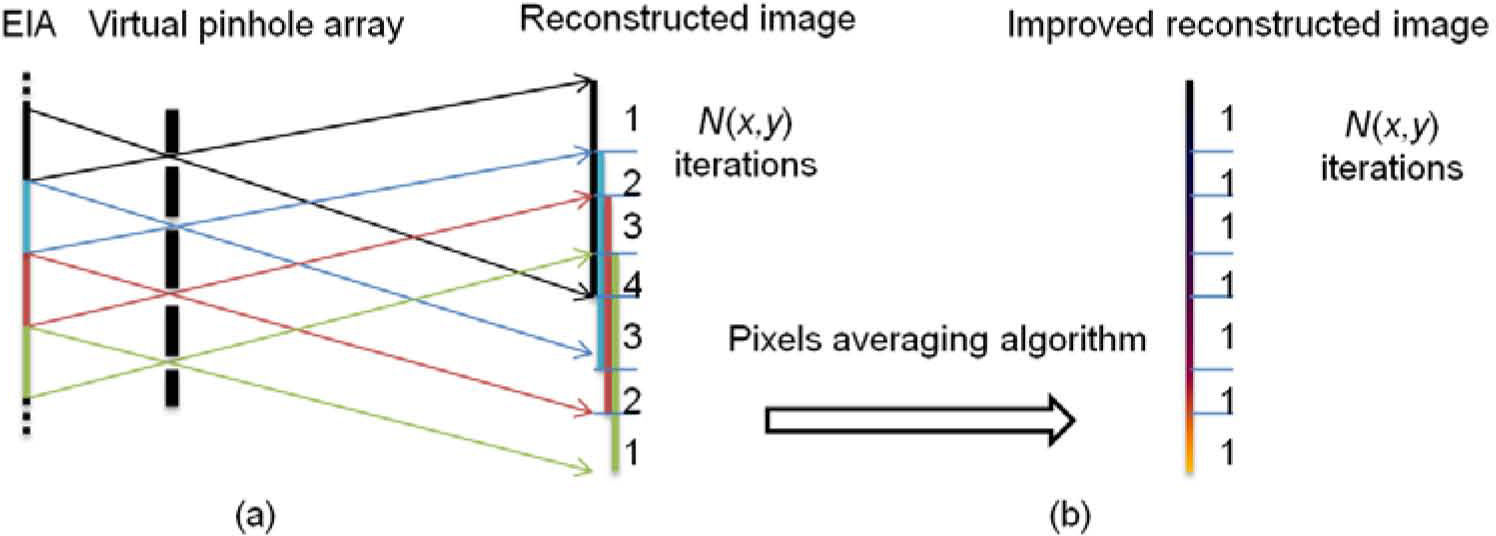
In conventional CIIR, each elemental image is projected through a VPA and magnified by a magnification factor M, as depicted in Figure 4 (a), each magnified and projected elemental image is superimposed on the reconstruction plane. Because of the magnification for each inversely mapped elemental image, pixel superposition occurs for the magnification factor.
To further avoid the blur noise of interference caused by the pixel overlapping in CIIR. In this work, the pixel average algorithm is presented. As shown in Figure 4 (b). For each pixel, we calculate the iterative times N(x,y), and the pixel averaged plane image can be derived from
where R(x,y) represents the reconstructed plane image by SPM-based CIIR, N(x,y)is the iterative times.3.2Two-dimensional Fibonacci transformThe Fibonacci numbers are named after Leonardo of Pisa, who was known as Fibonacci [16,17]. The sequence 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,…, and each subsequent number is the sum of the previous two. The sequence Fn=Fn-1+Fn−2 (n ∈ 2,3,...), and the seed values F0 =0,F1 = 1. The 2D Fibonacci transformation (FT) for the plane image transformation can be rewritten as:
where x,y ∈ {0,1,2,...,N−1}, N is the size of plane image pixels.
The 2D FT can be used for image encryption due to the Fibonacci series exist periodicity. If there exists an inter p such that Eq. 8, the period of Fibonacci transformation ρN=p.
If the transformation period of FT for the 2D EIA is p and the encrypted image is obtained by scrambling ρx times. The 2D EIA can be decrypted by transformation times of p − ρx.
4Experiments and resultsTo test the feasibility of the proposed method, computational experiments are performed with some 3D objects “car1” with the size of 70 mm × 30 mm × 25 mm, “car2” with the size of 65 mm × 25 mm × 15 mm and “elephant” with the size of 75 mm × 45 mm × 65 mm locate at z = l. The lenslet array used in this experimental setup is composed of 30 × 30 lenslets. The interval between the lenslets is 1.08 mm and the gap g between the EIA and the lenslet array gives 3 mm. We use the pickup system of CII as shown in Figure 1 (a) and capture the 2D EIA of 3D image “car1” with a resolution of 900 × 900 pixels is shown in Figure 5 (a). The first experiment is the case when the pickup distance z = 96 mm. Using the SPM algorithm of Figure 3 (a), the depth-converted EIA is obtained and it is shown in Figure 5 (b). Then, we use the 2D FT scrambling algorithm to encrypt the 2D depth-converted EIA. Figure 5 (c) and (d) show the scrambled images after 5 and 24 scrambled times, respectively.Figure 5 (e) shows the recovered depth-converted EIA with the right key: ρx = 24. If the scrambled time ρx is incorrect and the corresponding reconstructed image at the distance z = 96 mm as shown in Figure 5 (f). Figure 5 (g) and (h) show the reconstructed 3D plane images with the wrong pickup distance z = 60 mm, and right key (ρx= 24, z = 96 mm), respectively. Figure 5 (i)-(l) shows the reconstructed images which locate different position with the incorrect scrambled time ρx and wrong pickup distance z. Under the same conditions, Figure 6 shows the experimental results with other 3D images. Figure 6 (a) and (b) show the original 3D image “car2” and the obtained depth-converted EIA with the proposed method. Figure 6 (c) and (d) show the encrypted and decrypted image of “car2”. Figure 6 (e)-(f) shows the corresponding results with the 3D image “elephant”.
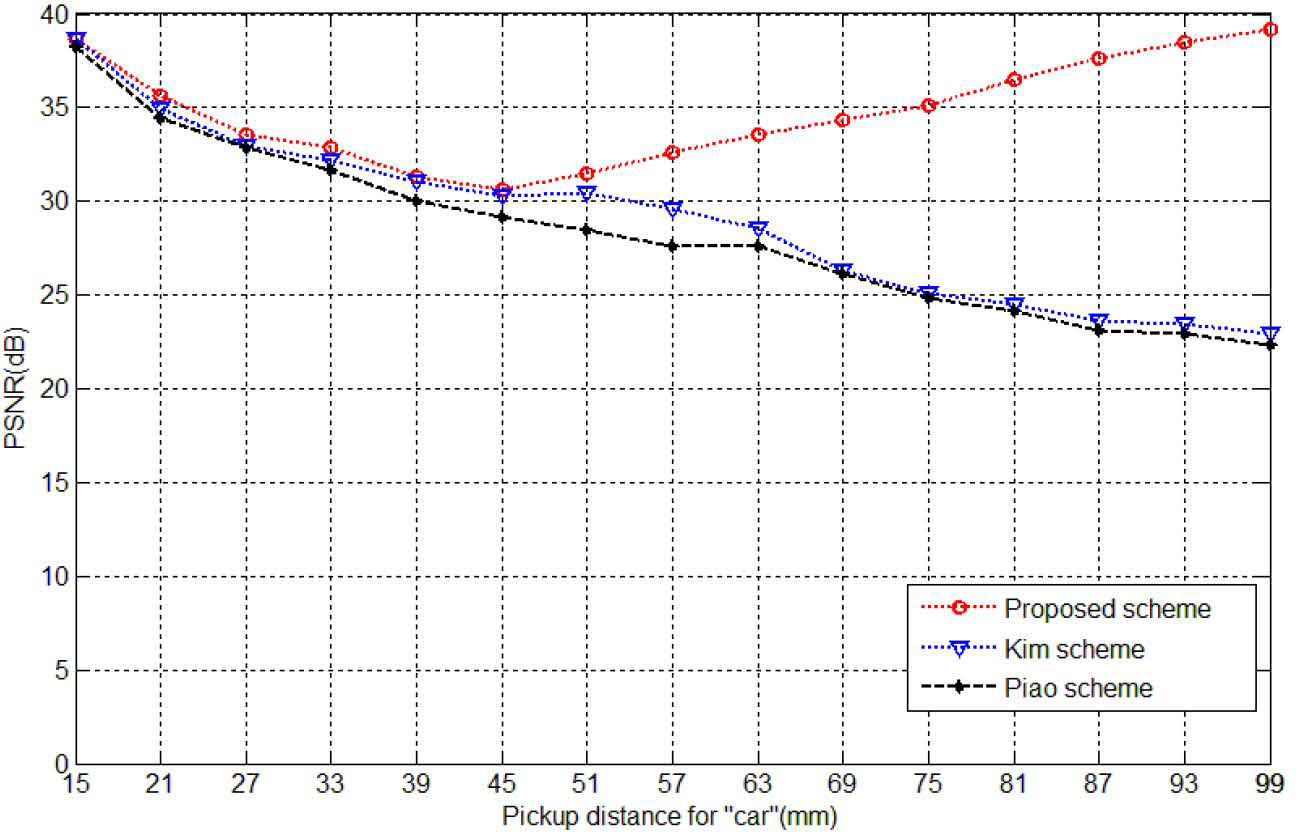
To verify the improvement of the proposed method, we compared the qualities of the plane images reconstructed from the decrypted EIAs produced by the proposed scheme, the Kim et al. (2013) scheme and the Piao et al. (2009) scheme, respectively, in the different pickup distances z. For convenience, we only use the 3D image “car1as the test image. Figure 7 (a) shows the reconstructed plane images using the depth-converted EIA of the proposed method with the different pickup distances. Figure 7 (b) and (c) show the reconstructed plane images using CIIR-based EIA of the Kim et al. scheme and the Piao et al. scheme, respectively. In visually comparing the reconstructed plane images based on the proposed scheme against the conventional CIIR methods, the conventional CIIR-based reconstructed plane images qualities obviously decreased along with the increase of distance z. However, our proposed method can effectively remedy this disadvantage.
To quantitatively evaluate the proposed method, the peak signal-to-noise ratio (PSNR) is employed as an image quality measure. The PSNR in a high value corresponds to a great similarly between the recovered image and the original image. The PSNR is defined as
and the mean-square error (MSE) is given by
where O' (x,y) represents the recovered image, O(x,y) stands for the original image and X × Y denotes the size of the image.
Figure 8 displays the PSNR values of the reconstructed plane images of the three kinds of encryption methods with the different pickup distances. From the PSNR values are represented in Figure 8, we can see that the PSNR of the reconstructed plane images with the proposed scheme can provide high value, even though the pickup distance is increased. However, the PSNR values of the conventional CIIR-based methods, the Kim et al. scheme and the Piao et al. scheme, obviously decreased along with the increase of pickup distance z. In other words, the quality of the recovered image of the proposed method has greatly improved compared with the conventional methods.
To further evaluate the performance of the proposed encryption method, we comparatively analyze the characteristics of the robustness against noise attacks for three kinds of encryption methods: the proposed scheme, the Kim et al. (2013) scheme and the Piao et al. (2009) scheme with the same pickup distance of z = 96 mm, respectively. Here, Gaussian noise as a common data loss attack is tested. In this work, Gaussian noise with zero-mean and variances of 0.1 and 0.5 are assumed to be equally added to each of the encrypted images and the corresponding reconstructed plane images are shown in Figure. 9.
Figure 9 (a) shows the reconstructed images of the proposed scheme after Gaussian noise attack with variances of 0.1 and 0.5. Figure 9 (b) and (c) show the reconstructed images of the Kim et al. scheme and Piao et al. scheme, respectively. To quantitatively evaluate the proposed method, we calculate the PSNR value between the test plane image and the plane image reconstructed from the encrypted image attacked by Gaussian noise attack. The PSNR values of the reconstructed images in Figure 9 are recorded in Table 1. The values of PSNR in Table 1 indicate that the proposed method has averagely improved 5.16 dB and 8.95 dB more than the Kim et al. scheme and the Piao et al. scheme, respectively. In other words, the proposed method has been increased 31.85% and 58.24% compared with Kim et al. scheme and the Piao et al. scheme, respectively.
Figure 10 shows the reconstructed 3D plane images under the speckle noise attack with the variance 0.1 and 0.5. Figure 10 (a)-(c) shows the reconstructed plane images of the proposed scheme, the Kim et al. scheme and the Piao et al. scheme with the variances 0.1 and 0.5. From the experimental results are presented in 1, we can see that the proposed encryption scheme has provided high robustness compared with the Kim et al. scheme and the Piao et al. scheme. The PSNR results of the reconstructed plane images in Figure 10 are recorded in Table 2.
The values of PSNR in Table 2 indicate that the proposed method has averagely improved 68.82% and 75.78% more than the Kim et al. scheme and the Piao et al. scheme, respectively. From the simulation results, we can see that the robustness of the proposed scheme outperforms the conventional encryption methods.
5ConclusionIn conclusion, an effective method of three-dimensional (3D) image encryption for a computational integral imaging (CII) system has been presented. A smart pixel mapping (SPM) and pixels averaging algorithm based CII reconstruction method for eliminating superposition interference of neighboring pixels, increasing the quality of reconstructed images. In this paper, we utilize two-dimensional (2D) Fibonacci transform (FT) to encrypt the depth-converted EIA, because the FT-based encryption method is a free data loss in encryption and decryption. To test the proposed method, we have performed the experiments and the experimental results show that this proposed method can improve the quality of reconstructed images compared to the conventional CIIR-based encryption methods.
This work was supported by a Research Grant of Pukyong National University (2013 year). Here, we appreciate for Editors/Reviewers’ warm work earnestly, thank you very much for your comments and suggestions.