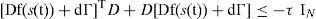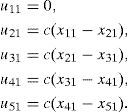Chaotic Synchronization in Nearest-Neighbor Coupled Networks of 3D CNNs

Abstract

In this paper, a synchronization of Cellular Neural Networks (CNNs) in nearest-neighbor coupled arrays, is numerically studied. Synchronization of multiple chaotic CNNs is achieved by appealing to complex systems theory. In particular, we consider dynamical networks composed by 3D CNNs, as interconnected nodes, where the interactions in the networks are defined by coupling the first state of each node. Four cases of interest are considered: i) synchronization without chaotic master, ii) master-slave configuration (directed ring), iii) open ring configuration (a path), and iv) directed path configuration. In addition, an application to chaotic communication networks is given.

Resumen

En este trabajo se estudia numéricamente la sincronización de redes neuronales (CNNs) en arreglos acoplados con arreglos cercanos. Usando la teoría de sistemas complejos se logra la sincronización de múltiples CNNs. En particular, consideramos redes dinámicas compuestas por 3D CNNs, como nodos de la red, donde las interacciones en las redes se definen por el acoplamiento del primer estado de cada nodo de red. Se consideran cuatro casos de interés: i) sincronización sin maestro caótico, ii) configuración maestro-esclavo (anillo dirigido), iii) configuración de anillo abierto (camino) y iv) configuración de camino dirigido. Además, se da una aplicación a redes de comunicación caótica.

1

Introduction

Generally, a chaotic oscillator is a nonlinear deterministic system that possesses complex similarity to random behavior, continuous broadband power spectrum, and sensitive dependence on initial conditions, see e.g. [1–5]. Synchronization of chaotic systems have been developed and thoroughly studied over the past two decades, see e.g. [6–17] and references therein. It is a topic of both theoretical and practical interests. Because of its applications in communications, cryptography, neural networks, etc. For example, in engineering, mainly in the design of chaotic secure/private communication systems, see e.g. [18–26].

On the other hand, a complex dynamical network can be defined as a set of interconnected nodes, each node is considered a basic element with behavior depending on the nature of the network. These classes of structures have been observed in computer sciences, economy, biology, physics, chemistry, engineering, and social sciences, see e.g. [27–29].

Nowadays, synchronization is required in complex dynamical networks with many coupled identical nodes. The scenario where the connected nodes have chaotic behavior is particularly interesting. Synchronization in complex dynamical networks has direct applications in different fields, see e.g. [24, 30–47]. Some interesting studies on artificial neural networks are reported in [48, 49]. In particular, Cellular Neural Networks (CNNs) exhibit chaotic dynamics, and so on, synchronization of CNNs becomes an important area of study. For example, CNN has broad applications in image and video signal processing, robotic, and biological visions [50]. In addition, synchronization of CNNs in different arrangements is very interesting by its possible application for security communication of encrypted information in a network of multiple users. Chaos plays a fundamental roll in the storage and retrieval of information in artificial and natural neural networks. Chaos has been observed and studied in CNNs [51, 52], in particular, some works on chaotic networks synchronization of CNNs with different coupling topologies can be consulted in [24, 39, 40, 43, 44].

Promising results on chaotic synchronization of coupled 3D CNNs in irregular arrays has been shown in [50]. However, the synchronization in nearest-neighbor coupled networks has direct application to chaotic communication systems.

The main goal of this paper is to synchronize multiple chaotic 3D CNNs (as interconnected nodes), that conform nearest-neighbor dynamical networks. This goal is achieved by appealing to results from complex systems theory. We arrange the chaotic 3D CNNs in nearest-neighbor coupled arrays in four scenarios: without chaotic master node, as a directed ring, as an open ring (path), and as a directed path. Finally, we present an application to chaotic communication in directed path coupled networks.

The organization of this paper is as follows: In Section 2, we describe the 3D CNN mathematical model to be used as fundamental node to construct the nearest-neighbor coupled networks. In Section 3, a brief review on synchronization in complex dynamical networks is given. In Section 4, we show the design of nearest-neighbor dynamical networks constructed using interconnected 3D CNNs and the synchronization in such networks. In Section 5, an application to encrypted chaotic network communications is presented. Finally, some concluding remarks are given in Section 6.

2

3D CNN as fundamental node to be used to construct networks

Consider the following three-dimensional (3D) continuous time CNN [52],

where S_i is a monotone differentiable function which is bounded above and below. T = (T_ij) is a 3x3 matrix, called weighting matrix or connection matrix describing the strength of connections among neurons and I_i is a constant vector. In [52] it has been shown that under certain conditions the model Equation 1 exhibits chaotic behavior. The simplified mathematical model of a 3D CNN to be used to construct the nearest-neighbor dynamical networks, is given by [52]:

where x ∈ R³ is the state vector, and

The values for weighting matrix Equation 3 are given by: T₁₁ = 1.49, T₁₂ = 2, T₁₃ = 1, T₂₁ = -2, T₂₂ = 1.7, T₂₃ = 0, T₃₁ = 4, T₃₂ = -4, and T₃₃ = 2. The 3D CNN model defined by Equations 2 and 3 generates a chaotic attractor, see Figure 1. where the chaotic attractor (double-scroll type) of the 3D CNN is projected onto the (x₁, x₂, x₃)-space, when we have used the initial conditions x₁(0) = 0.14, x₂(0) = -0.5, and x₃(0) = 0.1.

Figure 1.

Chaotic attractor of 3D CNN projected onto the (x₁, x₂, x₃)-space.

Next, we show the arrangements for nearest-neighbor dynamical networks by using as coupled chaotic nodes to 3D CNNs defined by Equations 2 and 3.

3

Synchronization of complex dynamical networks

3.1

Complex dynamical networks

We consider that complex dynamical networks are composed by N identical nodes, linear and diffusively coupled through the first state of each node. Each node constitutes a N-dimensional dynamical system, described as follows

where x_i = (x_i1, x_i2,…,x_iN)^T ∈ R^N is the state vector of the node i, u_i ∈ R^N is the input signal of the node i, and is defined by

the constant c > 0 represents the coupling strength, and Γ ∈ R^NxN is a constant 0-1 matrix linking coupled states. Assume that Γ = diag(r_1,r_2,…, r_N) is a diagonal matrix with r_i =1 for a particular i and r_j = 0 for j ≠ i. This means that two coupled nodes are linked through their i-th state. Whereas, A = (a_ij) ∈ R^NxN is the coupling matrix, which represents the coupling configuration in Equations 4 and 5. If there is a connection between node i and node j, then a_ij = 1; otherwise, a_ij = 0 for i ≠ j. The diagonal elements of coupling matrix A are defined as

Let suppose that the dynamical network, Equations 4 and 5, is connected in the sense that there are no isolated clusters. Then, the coupling matrix A is a symmetric irreducible matrix. In this case, zero is an eigenvalue of A with multiplicity 1 and all the other eigenvalues are strictly negatives [45, 46]. Synchronization state in complex dynamical networks, Equations 4 and 5, can be characterized by the nonzero eigenvalues of the coupling matrix A. The complex dynamical network, Equations 4 and 5, is said to achieve (asymptotically) synchronization, if [45]:

The diffusive coupling condition in Equation 6 guarantees that the synchronization state is a solution, s(t) ∈ Rⁿ, of an isolated node, that is

where s(t), can be an equilibrium point, a periodic orbit or, a hyperchaotic attractor. Thus, stability of the synchronization state,

of complex networks in Equations 4 and 5, are determined by the dynamics of an isolated node, i.e. the nonlinear function f (and its solution s(t)), the coupling strength c, the inner linking matrix Γ, and matrix A. In this work we choose Γ = [1,0,…,0], with this liking matrix, we can guarantee at least network sinchronization of the first state of all nodes. Network synchronization among the first states of the nodes is enough to achieve the final goal of the chaotic synchronization that is the transmission of encrypted information. If we want to achieve network synchronization of all states of the nodes, then we should use all states of the nodes as signal timing, rather than just the first state.

3.2

Synchronization conditions

Theorem 1 [45, 46] Consider the dynamical network inEquations 4and5. Let

be the eigenvalues of its coupling matrixA.Suppose that there exists a NxN diagonal matrixD > 0 and two constantsd¯ < 0 and τ > 0, such that

for alld¯, whereI_N ∈ R^N×Nis an unit matrix. If, moreover,

then, the synchronization state,Equation 9, of dynamical network inEquations 4and5is exponentially stable.

Since λ₂ < 0 and d¯, inequality in Equation 12 is equivalent to:

Synchronizability of dynamical network in Equations 4 and 5 with respect to a specific coupling configuration can be characterized by the second-largest eigenvalue (λ₂) of coupling matrix A.

3.3

Nearest-neighbor coupled networks

The coupling configurations commonly studied in synchronization of complex dynamical networks are the so-called: globally coupled networks, nearest-neighbor coupled networks, and star coupled networks. In this work, we concentrate on the synchronization in nearest-neighbor coupled networks with identical nodes (3D CNNs). In the sequel, we will show the particular arrangement of the coupling matrix for this class of complex dynamical networks. A nearest-neighbor coupled network consists of N nodes arranged in a ring, where each node i is adjacent to the neighbor nodes i ± 1, i ± 2,…,i ± K/2 where K is even, with coupling matrix defined by:

and the second largest eigenvalue given by:

For a fixed K, λ₂ decreases to zero as N goes to infinity

condition in Equation 15 implies that the networks no synchronize if N is too large.

4

Synchronization of 3D CNNs in nearest-neighbor networks

In this section, first, we show the particular arrangements of nearest-neighbor dynamical networks, considering four coupling scenarios: nearest-neighbor networks without chaotic master, directed ring, open ring (path), and directed path, by using the 3D CNN-node (Equations 2 and 3) as fundamental node (see Figure 2). Finally, we show synchronization in the designed dynamical networks.

Figure 2.

a) Nearest-neighbor coupled network, b) directed ring coupled network, c) open ring (path) coupled network, and d) directed path coupled network.

The complex dynamical networks to be constructed with N coupled 3D CNNs Equations 2 and 3, take the following form (according to Equations. 4 and 5),for i = 1,2,…,N, with input signals defined by

If the input signals (Equation 17) are u_i1 ≡ 0 for i = 1,2,…,N, then we have the original set of N uncoupled 3D CNNs (Equations 2 and 3), which evolve according to their own dynamics, and of course, the uncoupled N nodes are not synchronized. In particular, for the networks in Equations. 16 and 17, we consider N = 5 and Γ = diag(1,0,0) from Equation 5, that is, we have five 3D CNN-nodes composing the (nearest-neighbor) dynamical networks to be synchronized.

Let us rewrite explicitly, the arrangements of the (nearest-neighbor) dynamical networks (Equations 16 and 17) for five nodes. The first 3D CNN-node is given by:

the second one is described by

the third one by means of

the fourth one by

and the fifth one as

In the sequel, we present four nearest-neighbor connection topologies for networks with five 3D CNN-nodes, in the four cases: nearest-neighbor networks without chaotic master node, directed ring, open ring (path), and directed path.

Case 1 (Network without master node): Five uncoupled chaotic 3D CNN-nodes (Equations 2 and 3) to be synchronized in a dynamical network in a nearest-neighbor configuration without master node, see Figure 2(a).

The coupling matrix (Equation 14) for this case with K = 2, is given by

and the second largest eigenvalue is:

For synchronization purpose, we have designed the input signals u_i1 = g(x_i1; c), i = 1, 2,…,5 to construct the mentioned arrangement, that explicitly are given by:

To construct the nearest-neighbor coupled network without master node shown in Figure 2(a), we use Equations 18 and 22, with input signals from Equation 23. We take the initial conditions: x₁₁(0) = 0.14, x₁₂(0) = 0.5, x₁₃(0) = 0.1, x₂₁(0) = 0.15, x₂₂(0) = 0.6, x₂₃(0) = 0.2, x₃₁(0) = 0.16, x₃₂(0) = 0.7, x₃₃(0) = 0.05, x₄₁(0) = 0.13, x₄₂(0) = 0.4, x₄₃(0) = x₅₁(0) = 0.12, x₅₂(0) = 0.45, and x₅₃(0) = 0.3. With d = −1 d we can stabilize to zero all the states of a single (isolated) node. With d¯=-1, we can obtain from Equation 13, c ≥ 0.7236, for the computer simulations we have used the coupling value c = 70. With these values the Theorem 1 guarantees synchronization in the network with five chaotic 3D CNN-nodes. Figure 3, shows chaos synchronization in the first state of five 3D CNN-nodes, x_i1, i = 1,…,5, and the chaotic attractor corresponding to new chaotic collective behavior in the dynamical network (Equations 18 to 22) with input signals (Equation 23), projected onto the (x_11,x₁₂, x₁₃)-space. Figures 4 and 5, show the phase diagrams of the second and third states, from these figures we can see that the second and third states do not synchronize.

Figure 3.

Synchronization in the first state (x_i1, i = 1,…,5) of five chaotic 3D CNNs in nearest-neighbor configuration without master node, and the new chaotic attractor of the collective behavior in the network, projected onto the (x_11,x₁₂, x₁₃)-space.

Figure 4.

Phase diagrams of the second state (x_i2, i = 1,…,5) of five chaotic 3D CNNs in nearest-neighbor configuration without master node, and the new chaotic attractor of the collective behavior in the network, projected onto the (x_11,x₁₂, x₁₃)-space.

Figure 5.

Phase diagrams of the third state (x_i3, i = 1,…,5) of five chaotic 3D CNNs in nearest-neighbor configuration without master node, and the new chaotic attractor of the collective behavior in the network, projected onto the (x_11,x₁₂, x₁₃)-space.

Case 2 (Directed ring): Five uncoupled chaotic 3D CNN-nodes (Equations. 2 and 3) to be synchronized in a nearest-neighbor network with directed ring configuration, see Figure 2(b).

To construct the proposed arrangement, we have used the coupling signals x_i1, i = 1,…,5 for the five 3D CNN-nodes. For this purpose, we have designed the input signals u_i1 = g(x_i1; c), i = 1,…,5, that explicitly are given by:

Now, by using Equations 18 to 22 with input signals (Equation 24) among chaotic 3D CNN-nodes, we have constructed the nearest-neighbor network with directed ring configuration shown in Figure 2(b) to be synchronized. For this network, the corresponding coupling matrix is given by

with eigenvalues: λ₁ = 0, λ₂ = -0.691 + 0.9511j, λ₃ = -0.691 – 0.9511j, λ₄ = -1.809 + 0.5878j, and λ₅ = -1.809 – 0.5878j. Matrix A is no longer symmetric, however their nonzero eigenvalues have negative real part, so Theorem 1 still holds. Initial conditions and the constants d¯ and d are the same as in previous case, and with coupling value c = 70. With these values the Theorem 1 guarantees chaos synchronization in the dynamical network with five 3D CNN-nodes. The Figure 6. shows chaos synchronization in the first state of five CNN-nodes, i.e., x_i1, i = 1,…,5, and the chaotic attractor of the collective behavior imposed by the master node 1 in the dynamical network, projected onto the (x_11,x₁₂, x₁₃)-space.

Figure 6.

Synchronization in the first state (x_i1, i = 1,…,5) of five chaotic 3D CNNs in nearest-neighbor network with directed node configuration, and the new chaotic attractor of the collective behavior in the network, projected onto the (x_11,x₁₂, x₁₃)-space.

Case 3 (Open ring (path)): Five uncoupled chaotic 3D CNN-nodes (Equations 2 and 3), to be synchronized in a nearest-neighbor network with open ring (path) configuration, see Figure 2(c).

To construct the proposed arrangement, we have used the coupling signals x_i1, i = 1,…,5 for the five 3D CNN-nodes. For this purpose, we have designed the input signals u_i1 = g(x_i1; c), i = 1,…,5, that explicitly are given by:

Now, by using Equations 18 to 22 with input signals (Equation 25) among chaotic 3D CNN-nodes, we have constructed the nearest-neighbor network with open ring (path) configuration, shown in Figure 2(c) to be synchronized. For this network, the corresponding coupling matrix is given by:

with eigenvalues: λ₁ = 0, λ₂ = -0.382, λ₃ = -1.382, λ₄ = -2.618, and λ₅ = -3.618. Initial conditions and the constants d¯ and d are the same as in previous case, and with coupling value c = 70. With these values the Theorem 1 guarantees chaos synchronization in the dynamical network with five 3D CNN-nodes. Figure 7. shows chaos synchronization in the first state of five CNN-nodes, i.e., x_i1, i = 1,…,5, and the chaotic attractor of the collective behavior imposed by the master node 1 in the dynamical network, projected onto the (x_11,x₁₂, x₁₃)-space.

Figure 7.

Synchronization in the first state (x_i1, i = 1,…,5) of five chaotic 3D CNNs in nearest-neighbor network with open ring configuration, and the new chaotic attractor of the collective behavior in the network, projected onto the (x_11,x₁₂, x₁₃)-space.

Case 4 (Directed path):Five uncoupled chaotic 3D CNN-nodes (Equations 2and3,) to be synchronized in a nearest-neighbor network with directed path configuration, seeFigure 2(d).

To construct the proposed arrangement, we have used the coupling signals x_i1, i = 1,…,5 for the five 3D CNN-nodes. For this purpose, we have designed the input signals u_i1 = g(x_i1; c), i = 1,…,5, that explicitly are given by:

In this case, u₁₁ = 0 because the node 1 is the master node, i.e. it does not receive any input signal from any other node of the network; the role of the node 1 is to drive to other nodes. Now, by using Equations 18 to 22 with input signals (Equation 26) among chaotic 3D CNN-nodes, we have constructed the nearest-neighbor network with open ring (path) configuration, shown in Figure 2(d) to be synchronized. For this network, the corresponding coupling matrix is given by

with eigenvalues: λ₁ = 0, λ₂ = λ₃ = λ₄ = λ₅ = -1. Matrix A is no longer symmetric, however their nonzero eigenvalues have negative real part, so Theorem 1 still holds. Initial conditions and the constants d¯ and d are the same as in previous case, and with coupling value c = 70. With these values the Theorem 1 guarantees chaos synchronization in the dynamical network with five 3D CNN-nodes. Figure 8, shows chaos synchronization in the first state of five CNN-nodes, i.e., x_i1, i = 1,…,5, and the chaotic attractor of the collective behavior imposed by the master node 1 in the dynamical network, projected onto the (x_11,x₁₂, x₁₃)-space.

Figure 8.

Synchronization in the first state (x_i1, i = 1,…,5) of five chaotic 3D CNNs in directed path configuration, and the new chaotic attractor of the collective behavior in the network, projected onto the (x_11,x₁₂, x₁₃)-space.

Remark 1:It is important to mention that an exact synchronization was only achieved in the first state in the four cases (i.e., in second and third states, the synchronization is approximate, that is, the synchronization error is approximately to zero).Figures 4and5, show the phase diagrams of the second and third states for the first case of study. From these figures we can see that the second and third states do not synchronize. This behavior of the second and third states is repeated in the next three cases of study.

5

Encrypted chaotic communications

In this final section, we apply the synchronization of five chaotic 3D CNNs with directed path configuration (Fig. 2(d)), to secure communication of confidential information. In particular, we construct a chaotic communication network system to transmit a encrypted pulse train as information. The purpose is to send the pulse train, from a transmitter (chaotic 3D CNN-node 1) to each receiver (3D CNN-nodes N₂, N₃, N₄, and N₅) via public channels.

Figure 9. shows the chaotic communication scheme to transmit hidden messages from node N₁ (transmitter) to the four remote receivers. The transmission is achieved by using chaotic switching technique, see e.g. [2, 4, 10-14]. In this technique, a binary signal m(t) is used to modulate one parameter of transmitter (node N₁). According to the value of m(t) at any given time t; the transmitter has either the parameter value p or p’. For example, if is a ‘0’ bit for transmission, then the transmitter has the parameter value p, otherwise the parameter value is p’. So, m(t) controls a switch whose action changes the parameter values between p and p’ in the transmitter, while the remote receivers have all time the parameter value p. The synchronization error e_i+1(t) = x_i;1(t) - x_i+1,1(t), i = 1, 2, 3, 4 decides if the received signal corresponds to a ‘0’ or ‘1’ bit. Thus, when transmitter and each receiver synchronize (i.e., e_i(t) = 0, i = 2, 3, 4, 5) can be interpreted as a ‘0’ bit, and when transmitter with the receivers no synchronize (i.e., e_i(t) ≠ 0, i = 2, 3, 4, 5) will be interpreted as a ‘1’ bit. The diference between p and p’ must be small so the transmitter node does not lose its chaotic behavior, but big enough to produce a momentaneous lose of synchrony with the other nodes of the network (receivers). This momentaneous lose of synchrony can be detected in the synchrony error. The correct value of p’ is selected experimentally.

Figure 9.

Chaotic communication network system to transmit encrypted image messages.

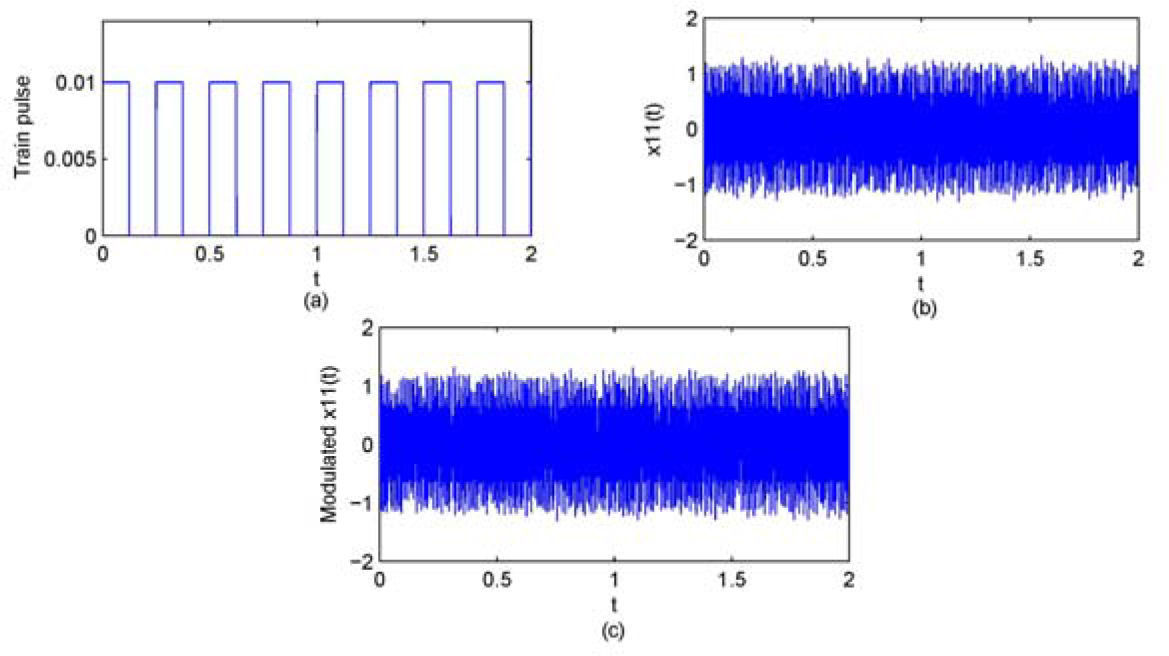
In this work, to transmit an encrypted train pulse via chaotic switching, let T₁₁ be the parameter to be modulated in the 3D CNN (Equation 18) node N₁. The binary information m(t) is adding to T₁₁ as follows, T₁₁(t) = T₁₁+r·m(t), where r = 0:01. Let us consider the train pulse shown in Figure 10(a) as the confidential message to be transmitted. In Figure 10(b), the first state of node N₁ without transmission is showed. Figure 10(c) illustrates the train pulse transmission through an insecure channel in the communication network, when the parameter T₁₁ in the transmitter (node N₁, Equation 18) is switched between T₁₁ = 1.49 (to encode a ‘0’ bit) and T’₁₁ = 1.5 (to encode a ‘1’ bit). At the remote receiver ends, the synchronization error detection e_i(t) = x_i;1(m(t)) - x_i+1,1(t), i = 1, 2, 3, 4 is achieved for the recovered binary sequence m’(t) after a low-pass filtering stage. Finally, from m(t), the recovered train pulse message is shown in Figure 11. The rule to obtain the binary sequence m’(t) is based on the synchronization error detection e_i(t), i = 2; 3; 4; 5 for each bit period to assign a ‘0’ or ‘1’ bit, as follows: when in the receiver ends we have e_i(t) ≠ 0, then is a ‘1’ bit and when e_i(t) = 0, then is a ‘0’ bit. Note that, an eavesdropper (in any public channel of the communication network system) will obtain the encrypted image shown in Figure 10(c), constructed from the transmitted chaotic signal x₁₁ (m(t)).

Figure 10 (a).

Train pulse m(t) to be transmitted, (b) first state of the transmitter node N₁ without transmission, (c) first state of the transmitter node N₁ modulated with the message and transmitted through public channel.

Figure 11.

Synchronization error in each receiver node.

In the sequel, by using the same chaotic communication network system (see Figure 9), we illustrate the encrypted image transmission. Previously, in the encryption process, the image message is converted to a binary sequence, to obtain m. Figure 12 shows the image message to be sent to set of remote receivers, Figure 13, shows the chaotic encrypted image message, and Figure 14, the recovered image message from m’ by the nodes N₂, N₃, N₄, and N₅. If we use a different node to transmit the message only the subsequent nodes will recover the message, in Table 1 a relation of this is shown. If we want to transmit a message to a prior node, we will need another directed path network in the opposite direction in order to have a full duplex connection.

Figure 12.

Original image message (“mime”) to be sent.

Figure 13.

Chaotic encrypted image message through insecure channel.

Figure 14.

Recovered image message (“mime”).

Table 1.

Transmission scheme.

Transmitter node	Receiver nodes
N1	N2, N3, N4 and N5
N2	N3, N4 and N5
N3	N4 and N5
N4	N5
N5	None

6

Concluding remarks

In this paper, we have presented the synchronization of multiple coupled chaotic 3D CNNs. We have achieved synchronization in the designed of a nearest-neighbor complex networks in four scenarios, without chaotic master node, in a directed ring configuration, open ring (path) configuration and directed path configuration. It was shown that, in the three last presented cases, the synchronization in second and third states is only approximate, while the first state is synchronized, in the first scenario the syncronization is complete. In addition, based on synchronization of multiple 3D CNNs in nearest-neighbor coupled networks we have presented an application to chaotic communications to transmit a train pulse as messages, from a single transmitter (node N₁) to remote multiple receivers (nodes N₂, N₃, N₄, and N5) via public channels. We also give an example transmitting an image.

Acknowledgments

This work was supported by the CONACYT, México under Research Grant No. 166654, and by UABC, México under Research No. 474.