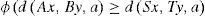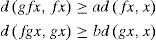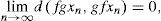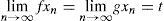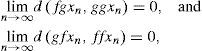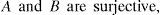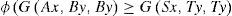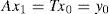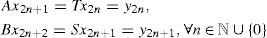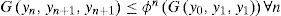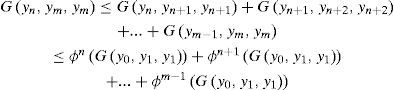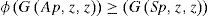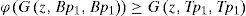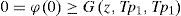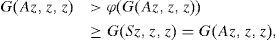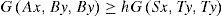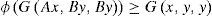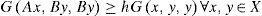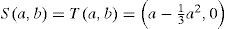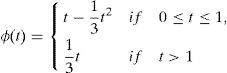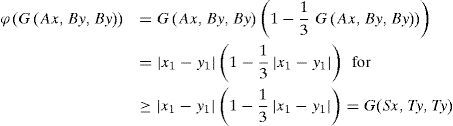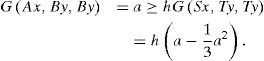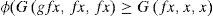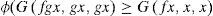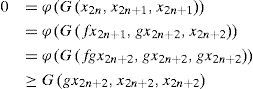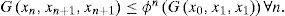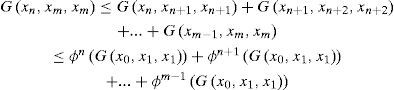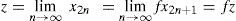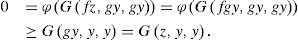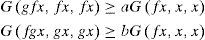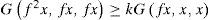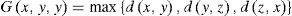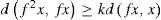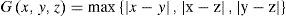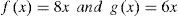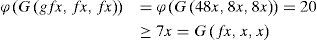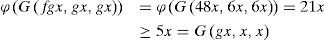Common Fixed Points of Expansive Mappings in Generalized Metric Spaces

Abstract

In this paper, we establish a common fixed point theorem for expansive mappings by using the concept of weak compatibility in the setting of G -metric spaces. This result generalizes the result of Ahmed [2] from 2-metric spaces to G -metric spaces by removing the condition of sequential continuity of the mappings. Further, we generalize and extend the theorem of Şahin and Telci [20] to G -metric spaces and thereby extending the theorem of Wang et al. [23] for a pair of mappings to G -metric spaces. Some comparative examples are constructed which illustrate the obtained results.

1

Introduction

Fixed point theory has gained impetus, due to its wide range of applicability, to resolve diverse problems emanating from the theory of nonlinear differential equations and integral equations [24], game theory relevant to military, sports and medicine as well as economics [3]. A metrical common fixed point theorem is broadly comprised of conditions on commutativity, continuity, completeness and contraction besides suitable containment of range of one map into the range of the other. For proving new results, the researchers of this domain are required to improve one or more of these conditions. With a view to accommodate a wider class of mappings in the context of common fixed point theorems, Sessa [21] introduced the notion of weakly commuting mappings which was further generalized by Jungck [4] by defining compatible mappings. After this, there came a host of such definitions which are scattered throughout the recent literature whose survey and illustration (upto 2001) is available in Murthy [11]. A minimal condition merely requiring the commutativity at the set of coincidence points of the pair called weak compatibility was introduced by Jungck [6] in 1996. This new notion was extensively utilized to prove new results.

Mustafa and Sims [16] introduced the G-metric spaces as a generalization of the notion of metric spaces. Mustafa et al. ([12]-[15], [17]) obtained some fixed point theorems for mappings satisfying different contractive conditions. Abbas and Rhoades [1] initiated the study of common fixed point in G-metric spaces.

In 1984, Wang et al. [23] presented some interesting work on expansion mappings in metric spaces which correspond to some contractive mappings in [18]. Rhoades [19] and Taniguchi [22] generalized the results of Wang [23] for pair of mappings. Later, Khan et al. [9] in 1986 generalized the result of [23] by making use of the functions. Kang [7] generalized these results of Khan et al. [9], Rhoades [19] and Taniguchi [22] for expansion mappings. In 2009, Ahmed [2] established a common fixed point theorem for expansive mappings by using the concept of compatibility of type (A) in 2-metric spaces. The theorem proved by Ahmed [2] was the generalization of the result of Kang et al. [8] for expansive mappings. Recently, Şahin and Telci [20] presented a common fixed point theorem for expansion type mappings in complete cone metric spaces which generalizes and extends the theorem of Wang et al. [23] for a pair of mappings to cone metric spaces.

The purpose of this paper is to generalize the results of Ahmed [2] to G-metric spaces by removing the condition of sequential continuity of the mappings. In order to prove the results, a more generalized concept of weak compatibility in G-metric spaces have been used instead of compatibility of type (A) used by Ahmed [2] in 2-metric spaces. Also, we extend the results of Şahin and Telci [20] to G-metric spaces thereby extending the theorem of Wang et al. [23] for a pair of mappings to G-metric spaces.

2

Preliminaries

Consistent with Mustafa and Sims [16], the following definitions and results will be needed in the sequel.

Definition 2.1

(G -Metric Space [16])

Let X be a nonempty set and let G: X × X × X→R⁺ be a function satisfying the following properties:

• (1)

  G (x, y, z) = 0 if x = y = z

• (2)

  0 < G (x, x, y) for all x, y ∈ X with x ≠y,

• (3)

  G(x, x, y) ≤ G(x, y, z) for all x, y, z ∈ X with z ≠ y,

• (4)

  G(x, y, z) = G(x, z, y) = G(y, z, x) = ...(symmetry in all three variables)

• (5)

  G(x, y, z) ≤ G(x, a, a) + G(a, y, z) for all x, y, z, a ∈ X (rectangle inequality).

Then the function G is called a G-metric on X, and the pair (X, G) is called a G-metric space.

Definition 2.2

([16])

Let (X,G) be a G-metric space and let {x_n} be a sequence of points of X, a point x ∈ X is said to be the limit of the sequence {x_n} if limn,m→∞Gx,xn,xm=0 and we say that the sequence {x_n} is G-convergent to x. Thus, if {x_n}→x in a G-metric space (X, G), then for any ε > 0, there exists a positive integer N such that G(x, x_n, x_m) < ε, for all n, m ≥ N.

It has been shown in [16] that the G-metric induces a Hausdorff topology and the convergence described in the above definition is relative to this topology. The topology being Hausdorff, a sequence can converge at most to one point.

Proposition 2.1

([16])

Let (X, G) be a G-metric space, then the following are equivalent:

• (1)

  {x_n} is G-convergent to x.

• (2)

  G(x_n, x_n, x)→0 as n→∞.

• (3)

  G(x_n, x, x)→0 as n→∞.

• (4)

  G(x_m, x_n, x)→0 as n→∞.

Definition 2.3

([16])

Let (X,G) be a G-metric space, a sequence {x_n} is called G-Cauchy if for every ε > 0, there is a positive integer N such that G(x_n, x_m,x_l) <ε, for all n,m,l ≥ N, that is, if G(x_n, x_m,x_l) →0, as n, m,l →∞.

Proposition 2.2

Let (X,G) be a G-metric space. Then the following statements are equivalent:

• (1)

  The sequence {x_n} is G-Cauchy,

• (2)

  For any,ε >0, there exists N ∈ℕ such that G(x_n, x_m,x_m) < ε, for all m, n ≥ N.

Definition 2.4

([16])

Let (X, G), (X′, G′) be two G-metric spaces. Then a functionf : X → X′ is G -continuous at a point x ∈ X if and only if it is G-sequentially continuous at x, that is, whenever {x_n} is G-convergent to x, {f(x_n)} is G-convergent to f(x).

Definition 2.5

([16])

A G-metric space (X, G) is called symmetric G-metric space if G(x, y, y) = G(y, x, x) for all x, y ∈ X.

Definition 2.6

([16])

A G-metric space (X, G) is said to be G -complete (or complete G-metric space) if every G-Cauchy sequence in (X, G) is convergent in X.

Matkowski [10] considered the set φ of all real functions ϕ :[0,∞) →[0, ∞) satisfying the following conditions:

• (i)

  ϕ is non-decreasing and upper-semicontinuous from the right at 0,

• (ii)

  (ii) ϕ(t) < t for each t > 0 and ϕ(t) = 0 ⇔t = 0.

Lemma 2.3

([10])

Let ϕ [0,∞) → [0, ∞) be a function satisfying the conditions (i) and (ii). Then limn,m→∞ϕnt=0 where ϕⁿ(t) denotes the composition of ϕⁿ (t) with n-times.

Ahmed [2] proved the following common fixed point theorem for expansive mappings in 2-metric spaces:

Theorem 2.4

Let A, B, S and T be mappings of a complete 2-metric space (X, d) into itself such that A and B are surjective. Suppose that one of the mappings A, B, S, T is sequentially continuous and the pairs {A, S} and {B, T} are compatible mappings of type (A). If there exists ϕ∈φ such that the inequality

holds, then A, B, S and T have a unique common fixed point.

Later, Şahin and Telci [20] in 2010 proved the following common fixed point theorem for expansion type of mappings in complete cone metric spaces.

Theorem 2.5

Let (X, d) be a complete cone metric space and P be a cone. Let f and g be surjective self-mappings of X satisfying the following inequalities:

for all x in X, where a, b >1. If either f or g is continuous, then f and g have a common fixed point.

Definition 2.7

(Compatible Mappings[4])

Two self mappings f and g on a metric space (X, d) are said to be compatible if

Whenever x_n is a sequence in X such that

for some t ∈ X.

Definition 2.8

(Compatible Mappings of type (A) [5])

Two self mappings f and g on a metric space (X, d) are said to be compatible of type (A) if

whenever x_n is a sequence in X such that limn→∞fxn=limn→∞gxn=t for some t ∈ X.

Definition 2.9

(Weakly compatible mappings [6])

Two self mappings f and g on a metric space (X, d) are said to be weakly compatible if they commute at coincidence points. Compatible maps are weakly compatible but the converse is not true.

The following lemma asserts that the concept of weak compatibility is more general than the concept of compatibility of type (A). So, in our result we shall make use of this more generalized notion of compatibility called as weak compatibility.

Lemma 2.6

[5]

Let A and S be self-mappings of compatible of type (A) of a metric space (X, d). If Ax = Sx for some x ∈ X, then ASx = SAx.

3

Main Results

Let A, B, S and T be mappings from G-metric space (X, G) into itself satisfying the conditions:

for each x,y ∈ X, where ϕ.∈.φ

Since, A and B are surjective, one can choose a point x₁ in X for an arbitrary point x₀ in X such that

For a point x₁, there exists a point x₂ in X such that Bx₂ = Sx₁ = y₁ Inductively, one can define a sequence (y_n) in X such that

where ℕ is the set of all positive integers

We, now prove a common fixed point theorem for expansive mappings in G -metric spaces by using the concept of weak compatibility.

Theorem 3.1

Let A, B, S and T be mappings of a complete symmetric G -metric space (X, G) into itself satisfying the condition (1). Suppose that the pairs {A, S} and {B, T} are weakly compatible mappings. If there exists ϕ ∈ φ such that the inequality (2) holds, then A, B, S and T have a unique common fixed point.

Proof

First, we have to prove that the sequence (y_n) defined above is a G- Cauchy sequence. Clearly, we have

Therefore, by lemma 2.3, G(y_n, y_n+l, y_n+l)→0 as

Consider,

Using Lemma 2.3, we obtain G(y_n, y_m, y_m)→0 as m,n→∞. Thus, {y_n} is a G- Cauchy sequence. Since (X,G) is a complete G-metric space, it yields that (y_n) and hence any subsequence thereof, converge to z ∈ X.

So, (Ax_2n),(Bx_2n+l),(Sx_2n) and (Tx_2n+1) converge to z ∈ X. Since A(X) is a complete G-metric space, so there exists a point p ∈ X such that Ap = z.

Now, using inequality (2), we have (ϕG(Ap, Bx_2n+2, Bx_2n+2)) ≥ G (Sp, Tx_2n+2, Tx_2n+2) letting n → ∞, we have

That is, 0 = ϕ (0) ≥ G(Sp, z, z). This proves that Sp = z. Since A and S are weakly compatible mappings, therefore ASp = SAp ⇒A_z=Sz. Now, since B(X) is also a complete G-metric space. So, there exists a point p₁ ∈ X such that Bp₁ = z.

Now, consider

ϕ (G(Ax_2n+1, Bp₁, Bp₁)) ≥ G(Sx_2n+1, Tp₁,Tp₁) letting n → ∞, we get

Recalling that Bp₁= z, we obtain

This implies that Tp₁ = z. Since B and T are weakly compatible mappings, therefore, BTp₁ = TBp₁⇒Bz = Tz.

Now, we have to show that Az = z and Bz = z. Let us suppose that G(Az, z, z) > 0. So, using the inequality (2) and the fact that ϕ(t) < t for all t > 0, we have

which is a contradiction. So, G(Az, z, z) = 0. That is, Az = Sz = z.

Similarly, let us suppose that G(Bz, z, z)>0. Therefore, by using the fact that the G-metric space X is symmetric and Az = Sz = z, we get G(Bz, z, z) > ϕ(G(Bz, z, z)) = ϕ(G(Az, Bz, Bz)) which is ≥ G(Sz, Tz, Tz) = G(Az, Bz, Bz) = G(Bz, z, z), a contradiction. So, G(Bz, z, z) = 0. This proves that Bz = Tz = z. Therefore, Az = Bz = Sz = Tz = z. It follows that z is the unique common fixed point of A, B, S and T.

As a corollary of the previous theorem, we have the following.

Corollary 3.2

Let A,B,S and T be mappings of a complete symmetric G-metric space (X,G) into itself satisfying the condition (1). Suppose that the pairs {A, S} and {B, T} are weakly compatible mappings. Assume that there exists h > 1 such that

for all x,y ∈ X. Then A, B, S and T. have a unique common fixed point.

Proof

By taking ϕt=th, where h >1 in Theorem 3.1, we get the proof of the Corollary 3.2.

Corollary 3.3

Let A and B be mappings of a complete symmetric G-metric space (X, G) into itself satisfying the condition (1). If there exists ϕ ∈ φ such that the inequality

Holds, then A and B have a unique common fixed point.

Proof

If we put S = T = i_X (the identity mapping on X) in Theorem 3.1, we obtain the proof of the Corollary 3.3.

Corollary 3.4

Let A and B be mappings of a complete symmetric G-metric space (X, G) into itself satisfying the condition (1). Assume that there exists h >1 s.t

Then, A and B have a unique common fixed point.

Proof

By taking ϕt=th where h > 1 in Corollary 3.3, we obtain the proof of the Corollary 3.4.

Remark 3.1

Theorem 3.1 is more general than Corollary 3.2 as shown in the following example.

Example 3.1

Let X ={(a, b):a,b∈[0,1]} and G be the G-metric on X defined by G(x, y, z) = max{|x−y |,||x−z|,|y−z|}, where d is the metric on X defined by d((a₁, b₁), (a₂,b₂)) = |a₁ − a₂ | + |b₁−b₂|

for all (a₁, b₁),(a₂, b₂)∈ X. Define A, B, S, T : X→X A(a, b)=B(a, b)=(a,0), by

for each (a, b) ∈ X. Then it is easily seen that A and S are weakly compatible mappings. Consider,

then ϕ ∈φ Further, we see that

all x = (x₁, x₂), y = (y₁, y₂)∈X. Therefore, all the hypothesis of Theorem 3.1 are satisfied.

However, condition (4) is not satisfied. Indeed, for x = (0, 0), y = (a, 0), 0 < a ≤; 1 and h > 1, we have

This implies that h < 1, which yields a contradiction.

Now, we prove a common fixed point theorem for expansive mappings in G-metric spaces, which in turn extends the results of Şahin and Telci [20].

Theorem 3.5

Let (X, G) be a complete G-metric space. Let f and g be surjective self mappings of X satisfying the following inequalities:

for all x∈X, where ϕ∈φ If either f or g is continuous, then f and g have a common fixed point.

Proof

Let x₀∈ X be arbitrary. Due to the reason that the mappings f and g are surjective mappings, there exists points x₁∈f⁻¹(x₀) and x₂∈g⁻¹(x₁). Continuing in this way, we obtain the sequence {x_n} with x_2n+1∈ f⁻¹(x_2n) and x_2n+2∈ g⁻¹ (x_2n+1).

Note that if x_n = x₊₁ for some n, then x_n is a common fixed point of f and g. Indeed, if x_2n = x_2n+1 for some n ≥ 0, then x_2n is a fixed point of f.. On the other hand, we have from inequality (6) that

This implies that G(x_2n+1, x_2n+2+2, x_2n+2) = 0. So, by the property of a G-metric, we have x_2n+1=x_2n+2. Therefore, x_2n is a common fixed point (5), we obtain x_2n+1 is a common fixed point of f and g. So, let us suppose that x_n ≠ x_n+1 for all n.

Clearly, we have

Now, we have to prove that {x_n} is a G-Cauchy sequence. For this, we need to show that G(x_n, x_m, x_m)→ 0as m,n →∞. Let n, m ∈ℕ with m > n,

Using lemma 2.3, we obtain G(x_n,x_m,x_m)→0 as m,n →∞. Hence, {x_n } is a G-Cauchy sequence in X. Since X is G-complete, there exists a point z ∈ X such that limn→∞xn=z. Now, we consider that f is continuous. Since x_2n = fx_2n+1, so we have

and so z is a fixed point of f. Since g is surjective, therefore there exists y ∈ X such that gy = z. Now, using inequality (6), we have

This implies that G(z, y, y) = 0 which further implies that z = y. Therefore, z is a common fixed point of f and g. Similarly, by considering the continuity of g, it can be proved that f and g have a common fixed point and this completes the proof.

Corollary 3.6

Let (X, G) be a complete G-metric space. Let f and g be surjective self-mappings of X satisfying the following inequalities

for all x in X, where a, b > 1. If either f or g is continuous, then f and g have a common fixed point.

Proof

Take ϕt=th, where h = max{a, b}>1 in inequalities (5) and (6) of Theorem 3.5, we get the proof.

Corollary 3.7

Let (X, G) be a complete G-metric space. Let f be a surjective self-mapping of X satisfying the following inequality

for all x in X, where k > 1. If f is continuous, then f has a fixed point.

Proof

Putting f = g and k = min{a, b} in Corollary 3.6, we get Corollary 3.7.

Remark 3.2

Taking

for usual metric space (X, d) in the corollary 3.7, we obtain the following result of Wang et al. [23].

Corollary 3.8

Let (X, d) be a complete metric space and let f be a surjective self-mapping of X satisfying the following inequality

for all x in X, where k > 1. If f is continuous, then f has a fixed point.

We now give the following example in support of our Theorem 3.5.

Example 3.2

Let X = [0, ∞) and ϕ:[0, ∞) → [0, ∞) defined by ϕt=t2 Define a G-metric on X by

Define the surjective self mappings f, g : X → X by

for all x in X Then we have

and

hold for all x in X Thus, inequalities (5) and (6) are satisfied and hence all the hypothesis of Theorem 3.5 are satisfied. Clearly, x = 0 is a common fixed point of f and g.

Acknowledgment

The first author, Junior Research Fellow (No. F. 2-16/2011 (SA-I) gratefully acknowledges the University Grants Commission, Government of India for financial support.