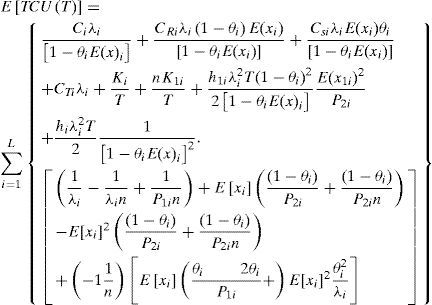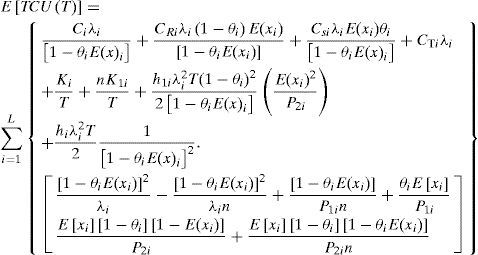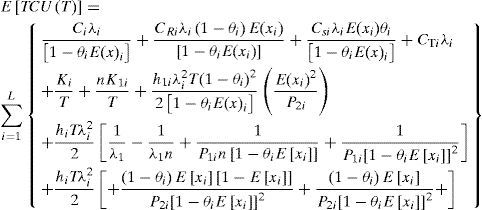This paper is concerned with determining the optimal common production cycle policy for a multi-item economic production quantity (EPQ) model with scrap, rework and multiple deliveries. The classic EPQ model considers the optimal replenishment quantity of single product under a perfect production assumption and a continuous inventory issuing policy. However, in real life production planning, manufacturing firms often plan to have multiple products made in turn on a single machine in order to maximize the machine utilization. Also, dealing with random defective items during the production run seems to be an inevitable task, and the multi-delivery policy is commonly adopted for distributing finished items to customers. In this study, we assume a portion of nonconforming items is scrap and the other portion of them can be reworked and repaired in the same production cycle with additional cost. The objective is to determine an optimal common production cycle time that minimizes the long-run average cost per unit time for such a specific multi-item EPQ model with scrap, rework and multi-delivery policy. Mathematical modeling and analysis is used and a closed-form optimal common cycle time for multi-item production planning is obtained. A numerical example is provided to demonstrate the practical usage of research result.
The economic production quantity (EPQ) model [1] considers the optimal replenishment quantity of single product under a perfect production assumption and a continuous inventory issuing policy. However, in real life production planning manufacturing firms often plan to have multiple products made in turn on a single machine in order to maximize the machine utilization. Burinskii and Fursova [2] studied the time variation of probability distributions of inventory levels in a multi-item supply system. Gaalman [3] proposed a multi-item production smoothing model using an aggregation technique that makes use of the structural properties of the inventory-production model. Aggarwal [4] indicated that multi-item inventory control may be simplified by grouping items into subgroups with a common order cycle for all the items in each group. The methods provided in the literature for determination of the order cycle values are either suboptimal or computationally inefficient. He proposed a procedure which finds the optimal values and is also computationally efficient. Dellaert [5] considered a problem of production control in situations in which several types of products are produced on one machine and in which only the ordered goods can be produced. He assumed the demand is stochastic and depends on the average delivery-time and proposed two decomposition methods: a method based on queuing theory and a method for discrete demand and discrete service-times. Both methods were compared with a cyclic production strategy. Studies related to various aspects of multi-item production planning and optimization issues have since been extensively conducted [6-14].
In practical production environments, dealing with random defective items produced seems to be one of the inevitable tasks. Shih [15] examined inventory models where the proportion of defective units in the accepted lot is a random variable with known probability distributions. Optimal solutions to the amended systems were developed. Comparisons with the traditional models were also presented via numerical examples. Makis [16] investigated the optimal lot sizing and inspection policy for an economic manufacturing quantity (EMQ) model with imperfect inspections. He assumed that the process could be monitored through inspections, and that both the lot size and the inspection schedule were subject to control. It was assumed that the in-control periods are generally distributed and the inspections are imperfect. Using Lagrange’s method and solving a nonlinear equation, a two-dimensional search procedure was proposed to find the optimal lot sizing and inspection policy. Many studies have also been carried out to address different aspects of imperfect production systems and quality assurance issues during past decades [17-25].
Unlike EPQ model adopts continuous inventory issuing policy, periodic multi-delivery policy is often used for distributing finished items to customers. Hahm and Yano [26] determined the frequencies of production and delivery of a single component with the objective of minimizing the long-run average cost per unit time. Their cost includes production setup costs, inventory holding costs at both the supplier and the customer, and transportation costs. For their proposed model, it was proved that the ratio between the production interval and delivery interval must be an integer in an optimal solution. They used these results to characterize situations in which it is optimal to have synchronized production and delivery, and discussed the ramifications of these conditions on strategies for setup cost and setup time reductions. Viswanathan [27] examined the integrated vendor-buyer inventory models with two different strategies that had been proposed in the literature for the problem: one where each replenishing quantity delivered to the buyer is identical and the other strategy where at each delivery all the inventory available with the vendor is supplied to the buyer. He showed that there is no one strategy that obtains the best solution for all possible problem parameters. His study presented the results of a detailed numerical investigation that analyzed the relative performance of the two strategies for various problem parameters. Hoque and Goyal [28] studied an optimal policy for the single-vendor single-buyer integrated production– inventory system. Their model assumed that the successive batches of a lot are transferred to the buyer in a finite number of unequal and equal sizes. The successive unequal batch sizes increase by a fixed factor. The capacity of the transport equipment used to transfer batches from the vendor to the buyer is limited. The objective was to minimize the total joint annual costs incurred by the vendor and the buyer. Additional studies were conducted to address various aspects of periodic or multiple deliveries issues [29-37]. This paper is concerned with determining the optimal common production cycle policy for a multi-item economic production quantity (EPQ) model with scrap, rework and multiple deliveries. Since little attention has been paid to this area, this paper is intended to bridge the gap.
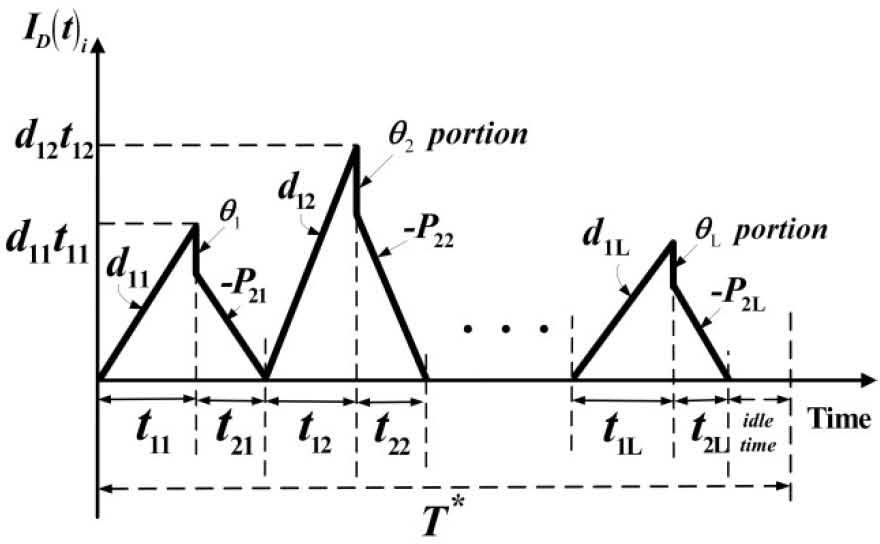
2Description and Mathematical ModellingA multi-item EPQ model with scrap, rework and multiple deliveries is examined in this paper. Consider that L products are made in turn on a single machine with the purpose of maximizing the machine utilization. All items made are screened and inspection cost for each item is included in the unit production cost Ci. During production process for each product i (where i = 1, 2, …, L), an xi portion of nonconforming items is produced randomly at a rate di. Among these nonconforming items, a θi portion is considered to be scrap items and the other portion can be reworked and repaired at a rate of P2i right after the end of regular production process in each cycle with an additional cost CRi. Under the normal operation, the constant production rate P1i for product i must satisfies (P1i-di-λi)>0, where λi is the demand rate for product i per year, and di can be expressed as di= xiP1i. Unlike classic EPQ model assumes a continuous issuing policy for meeting product demands, this study adopts a multi-delivery policy. It is assumed that finished goods for each product i can only be delivered to customers if whole production lot is quality assured in the end of rework process for each product i. Fixed quantity n installments of the finished batch are delivered at a fixed interval of time during delivery time t3i (refer to Figure 1).
Other cost parameters used in this study include: disposal cost CSi per scrapped item, unit holding cost hi, production setup cost Ki, unit holding cost h1i for each reworked item, the fixed delivery costK1i per shipment for product i, and unit shipping cost CTi for product i. Additional notation includes
t1i = production uptime for product i in the proposed EPQ model,
t2i = the rework time for product i in the proposed EPQ model,
H1i = maximum level of on-hand inventory for product i when regular production ends,
H2i = maximum level of on-hand inventory in units for product i when rework process ends,
T = common production cycle length, a decision variable,
Qi = production lot size per cycle for product i,
n = number of fixed quantity installments of the finished batch to be delivered to customers in each cycle, it is assumed to be a constant for all products,
tni = a fixed interval of time between each installment of finished products delivered during t2i, for product i.
I(t)i= on-hand inventory of perfect quality items for product i at time t,
ID(t)I = on-hand inventory of defective items for product i at time t,
TC(Qi) = total production-inventory-delivery costs per cycle for product i,
E[TCU(Q)] = total expected production-inventory-delivery costs per unit time for L products in the proposed system.
E[TCU(T)] = total expected production-inventory-delivery costs per unit time for L products in the proposed system using common production cycle time T as the decision variable.
The on-hand inventory of defective items during uptime t1i and the reworking time t2i is illustrated in Figure 2.
One can obtain the following formulas directly from Figures 1 and 2:
Total delivery costs for product i (n shipments) in a cycle are:
Holding costs for finished products during the t3, where n fixed-quantity installments of the finished batch are delivered to customers at a fixed interval of time, are (see [29]).
Total production-inventory-delivery cost per cycle TC(Qi) for L products, consists of the variable production cost, setup cost, rework cost, fixed and variable delivery cost, holding cost during production uptime t1i and rework time t2i, and holding cost for finished goods kept during the delivery time t3. Therefore, total TC(Qi) for or L products are
To take the randomness of defective rate x into account, by applying the expected values of x in the cost analysis and substituting all variables from equations (1) to (9) in Eq. (10), the following expected E[TCU(Q)] can be obtained:
where E[T] = Qi[1 − θiE(xi)]/λi,
Replacing Qi with T, one can convert Eq. (11) into Eq. (12) as follows (see Appendix for details)
Let E0i, E1i denote the following:
Equation (12) becomes
3Determining Optimal Common CycleIf the expected cost function E[TCU(T)] is convex, then one can locate its minimum point and hence find the optimal common production cycle time. Differentiating Eq. (15) with respect to T gives
Eq. (17) is resulting positive for Ki, n, K1i, and T are all positive. Hence, E[TCU(T)] is a convex function for all T different from zero. The optimal common production cycle time T* can be obtained by setting first derivative of E[TCU(T)] equal to zero.
With further derivations one obtains
4Numerical ExampleConsider a production schedule is to produce five products in turn on a single machine using a common production cycle policy. Production rate P1i for each product is 58000, 59000, 60000, 61000, and 62000 respectively, and annual demands λi for five different products are 3000, 3200, 3400, 3600, and 3800 respectively. Random defective rates xi during production uptime for each product follow the uniform distribution over the intervals of [0, 0.05], [0, 010], [0, 0.15], [0, 020], and [0, 0.25] respectively. Among the defective items θi portion is scrap items where θi for five different products are 0, 0.025, 0.050, 0.075, 0.100 respectively and additional disposal costs are $20, $25, $30, $35, and $40 per scrapped item. The other portion of nonconforming items is assumed to be repairable at the reworking rates P2i of 1800, 2000, 2200, 2400, and 2600 respectively, with additional reworking costs of $50, $55, $60, $65, and $70 per reworked item. Other parameters used include
Ci = unit manufacturing costs are $80, $90, $100, $110, and $120 respectively.
hi = unit holding costs are $10, $15, $20, $25, and $30 respectively.
Ki = production set up costs are $3800, $3900, $4000, $4100, and $4200, respectively.
h1i = unit holding costs per reworked are $30, $35, $40, $45, and $50 respectively.
K1i = the fixed delivery costs per shipment are $1800, $1900, $2000, $2100, and $2200.
CTi = unit transportation costs are $0.1, $0.2, $0.3, $0.4, and $0.5 respectively.
n = number of shipments per cycle, in this study it is assumed to be a constant 4.
The optimal common production cycle time T* = 0.6066 (years) can be computed by Eq. (19), and applying Eq. (15) one obtains the expected production-inventory-delivery costs per unit time for L products, E[TCU(T* = 0.6066)] = $2,015,921.
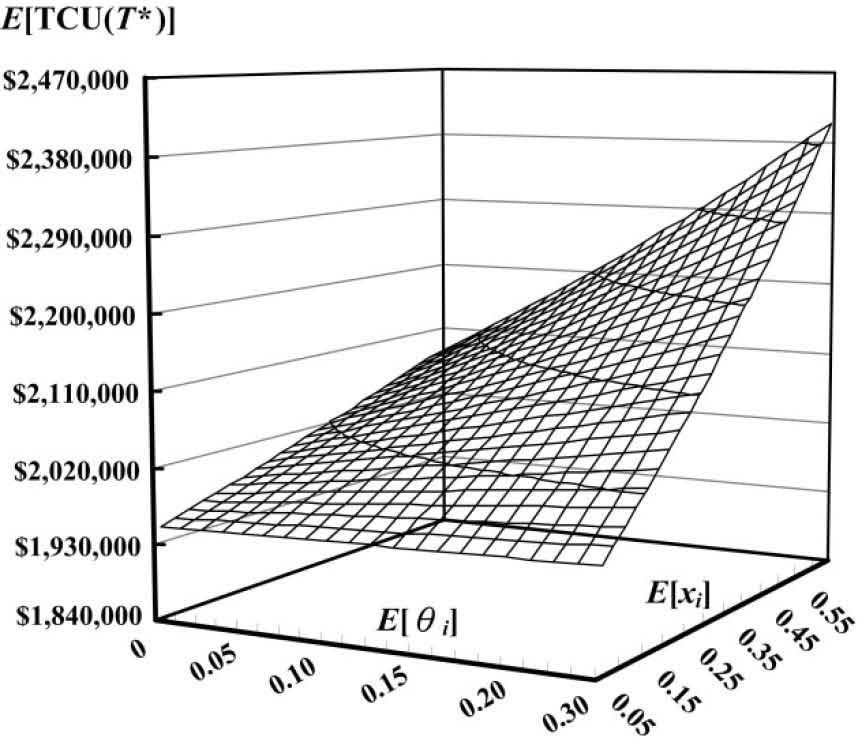
Variation of average defective rate and average scrap rate effects on the optimal system cost E[TCU(T*)] are illustrated in Figure 3.
One notes that as the average random defective rate E[xi] increases, the expected system cost E[TCU(T*)] increases significantly; and as the average scrap rate E[θi] increases, the expected system cost E[TCU(T*)] increases slightly.
5ConclusionsClassic EPQ model determines replenishment lot size for single product with perfect production situation and under a continuous inventory issuing policy. However, in real life production environment, for the purpose of maximizing machine utilization production planners often have multiple products produced in turn on a single machine. During the production process, due to various uncontrollable factors it is inevitable to produce nonconforming items. Sometimes, a portion of nonconforming items can be reworked and repaired with additional cost. Also, the delivery of finished goods to outside clients is commonly done under a practical periodic multi-shipment policy. Therefore, it is important for management to look into effect of rework and multi-delivery policy on the common cycle decision of the multi-item production system. Because little attention has been paid to this area, this paper is intended to bridge the gap.
Mathematical modeling is used in this study and an optimal common cycle time for such a specific EPQ model is obtained. Effects of scrap and the reworking of defective items on the expected system cost are investigated. The research results are intended to assist management in the fields to better plan and control such a realistic multi-item production system. For future study, an interesting topic will be to consider imperfect rework effects on the on the common cycle time for the same model.
Authors greatly appreciate National Science Council of Taiwan for supporting this research under grant number: NSC 102-2410-H-324-005.






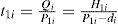
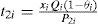
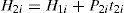
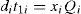
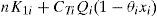
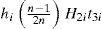
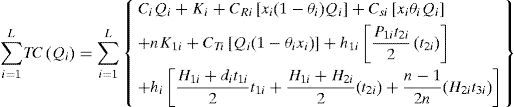
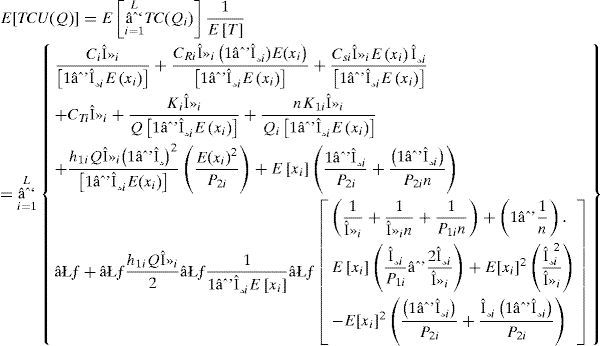
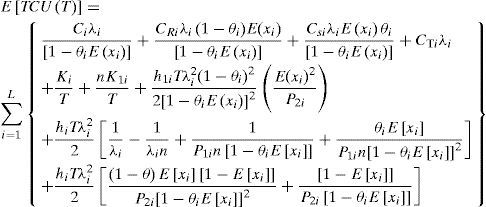
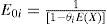
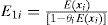
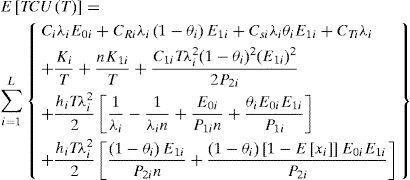
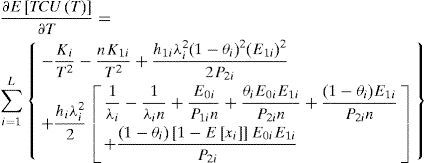
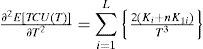
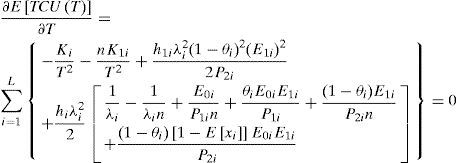
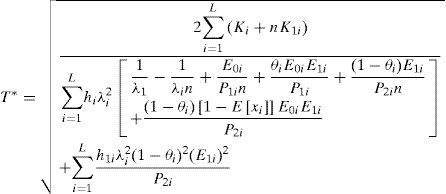
![Variation of average defective rate and average scrap rate effects on the system cost E[TCU(T*)]. Variation of average defective rate and average scrap rate effects on the system cost E[TCU(T*)].](https://static.elsevier.es/multimedia/16656423/0000001200000003/v2_201505081651/S1665642314716414/v2_201505081651/en/main.assets/thumbnail/gr3.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)