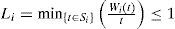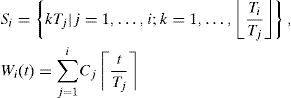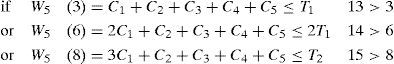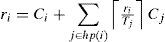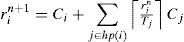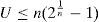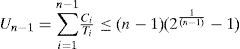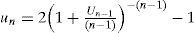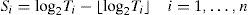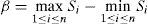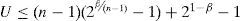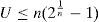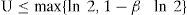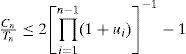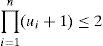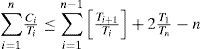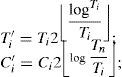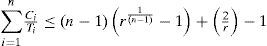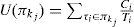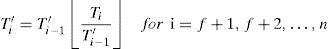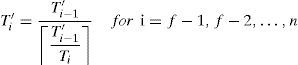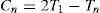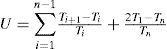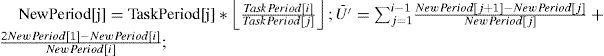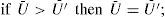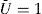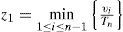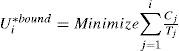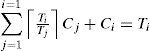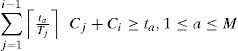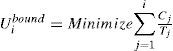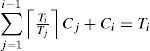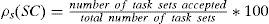Schedulability conditions are used in real-time systems to verify the fulfillment of the temporal constraints of task sets. In this paper, a performance analysis is conducted for the best-known real-time schedulability conditions that can be used in online admission control on uni-processor systems executing under the Rate-Monotonic scheduling policy. Since Liu and Layland introduced the Rate-Monotonic scheduling algorithm, many research studies have been conducted on the schedulability analysis of real-time periodic task sets. However, in most cases, the performance of the proposed schedulability conditions were compared only against the Liu and Layland test and not against the remaining schedulability tests. The goal of this paper is to provide guidelines for system designers in order to decide which schedulability condition provides better performance under different task characteristics. Extensive simulation experiments were conducted to evaluate the inexact schedulability conditions and compare their performance and computational complexity.
Las condiciones de planificabilidad son utilizadas en los sistemas de tiempo real para verificar el cumplimiento de las restricciones temporales de los conjuntos de tareas. En este artículo se presenta un análisis del desempeño de las condiciones de planificabilidad mas conocidas y que pueden ser usadas como control de admisión en línea en sistemas monoprocesador que se ejecutan con la política de planificación rate-monotonic. Desde que Liu y Layland propusieron el algoritmo de planificación R-M, se han llevado a cabo muchos proyectos de investigación acerca del análisis de planificabilidad de conjuntos de tareas periódicas de tiempo real. Sin embargo, en la mayoría de los casos, el desempeño de las condiciones de planificabilidad ha sido comparado tan solo con la prueba de Liu y Layland y no consideran al resto de las condiciones de planificabilidad. El objetivo de este artículo es el de proporcionar una guía a los diseñadores de sistemas para que puedan decidir qué condición de planificabilidad presenta un mejor desempeño con diferentes características de las tareas. Se llevaron a cabo extensos experimentos de simulación para evaluar a las condiciones inexactas de planificabilidad, así como para comparar su desempeño y complejidad computacional.
In a real-time system, the scheduling algorithm decides an order of execution of the tasks and the amount of time allowed to each task in the system so that no task (for hard real-time systems), or a minimum number of tasks (for soft real-time systems), misses their deadlines. To verify if a scheduling policy guarantees the fulfillment of the temporal constraints of a task set, real-time systems designers use different exact or inexact schedulability conditions (also known as schedulability tests). The schedulability condition indicates if a given task set can be scheduled with a given scheduling algorithm such that none of the tasks in the set miss their deadlines. When a new task is created in a dynamic real-time system, an online admission control mechanisms that uses a schedulability test guarantees predictability if the new task is admitted. Examples of these kind of systems are those with quality-of-service (QoS) requirements, such as multimedia systems [1][2], communication services [3][4], and automated flight control [5]. Other examples are found on the scheduling of real-time traffic over networks [6][7], or in open systems environments [8][9].
Exact schedulability tests usually have high-time complexities and may not be adequate for online admission control if the system has a large amount of tasks or a dynamic workload. In contrast, most of the inexact schedulability tests provide low-complexity sufficient schedulability tests, which are suitable for using in online admission control mechanisms to decide the acceptance of the newly arrived tasks in the system. If a task set does not satisfy a sufficient schedulability test, it is not known if the task set can be feasibly scheduled using a given scheduling policy. For this reason, it is important to determine which inexact schedulability test provides a better performance, given the specific task set parameters.
The rate-monotonic scheduling algorithm assigns priorities proportionally to the task activation rates. Many other scheduling algorithms have been proposed, such as the earliest deadline first (EDF) [10] that allows a better use of the computational resources. However, because RM introduces low-computational overhead, is simple to implement and is predictable. It is widely used on most realtime operating systems and is supported by most real-time systems standards.
Liu and Layland first introduced the rate-monotonic algorithm along with a sufficient schedulability test[10]. They introduced the concept of achievable utilization factor to derive a low complexity test that is used to determine the schedulability of independent, periodic and preemptable task sets executed on one processor.
The schedulability test introduced by Liu and Layland for RM states that a task set will not miss any deadline if the utilization factor of the task set, defined as U=∑i=1nCiTi, is not greater than n(21n-1) where Ci and Ti are the computation requirement and period of the task τi, respectively, and n is the number of tasks. Unfortunately, this condition fails to identify many schedulable task sets when the system is heavily loaded.
After Liu and Layland’s seminal work, many researchers, motivated by the low overhead and simplicity of RM, developed new tests that improved the test proposed by them. The improvement on these new tests was due to the introduction of additional timing parameters in the schedulability analysis, and in some cases, also to the transformation of the task sets.
When comparing the inexact schedulability conditions, the problem of evaluating their performance with respect to either the pessimistic Liu and Layland test or the exact schedulability test, becomes an important issue. The effectiveness of the schedulability test is measured in terms of the acceptance ratio. The higher the acceptance ratio, the better the test, which means that more tasks sets are schedulable. When the ratio is equal to one, it means that the schedulability condition finds as many schedulable task sets as those found by the exact condition.
Comparing the inexact schedulability conditions, using a rigorous analytical approach, is not easy because each schedulability condition considers different task set parameters. Furthermore, some of them are based on algorithms, that is, transforming the original task set into an equivalent one. Consequently, the acceptance ratio of a given test is affected by the characteristics of the task set parameters. For these reasons, our aim is to evaluate the performance of the schedulability conditions through extensive simulations.
In this paper, we surveyed the inexact schedulability conditions that can be used in online admission control when the system is comprised of periodic and preemptable real-time tasks, using the rate-monotonic scheduling algorithm. We analyzed the best-known inexact schedulability conditions for one processor that exists in the literature. We also conducted extensive simulation experiments to evaluate and compare their performance in terms of the acceptance ratio and the computational complexity. Based on the results provided by the experimental evaluations, we provided guidelines to help system designers to decide, given a particular task set parameters and load conditions, which schedulability tests provide better or worst performance, and how they compare with each other under these different characteristics.
To the best of our knowledge, no previous comparative analysis of the RM schedulability conditions has been conducted for real-time scheduling on one processor. Most of the published schedulability conditions compared their performance only against the schedulability condition introduced by Liu and Layland, and just a few of them compared their performance against each other.
The rest of this document is organized as follows: In Sections 2 and 3, an overview of the real-time scheduling theory and schedulability analysis of real-time systems is introduced. In Section 4, the schedulability conditions for RM on one processor are introduced, and in Section 5, extensive simulation experiments conducted to test and compare the performance of the inexact schedulability conditions are described. Finally, the conclusions appear in Section 6.
2Real-time systems schedulingA real-time system is composed of several concurrent activities that are normally implemented as tasks. To schedule these tasks, real-time operating systems use scheduling algorithms to decide the order of execution of the tasks and the amount of time assigned to each task.
Scheduling algorithms of general-purpose operating systems are nondeterministic because the correctness of the system does not depend on the order in which every task is executed. In these operating systems, the scheduler is intended to provide optimal performance, optimal usage of resources, and fairness in resource assignment. In contrast, in real-time operating systems, the scheduler must restrict the nondeterminism associated with the concurrent system, and must provide the means to predict the worst-case temporal behavior of the task set.
A real-time scheduling algorithm provides an ordering policy for the execution of the tasks (as in the non-real-time scheduling algorithm). A given real-time scheduling algorithm may produce feasible or infeasible schedules. In a feasible schedule, every job for a given task set always completes by its deadline. In contrast, in an infeasible schedule, some jobs may miss a few of their deadlines. A set of jobs is schedulable according to a given scheduling algorithm if, when using the algorithm, the scheduler always produces a feasible schedule. The criterion used to measure the performance of the scheduling algorithms for real-time applications is their ability to find feasible schedules of the given application whenever such schedules exist. A hard real-time scheduling algorithm is optimal if, for any feasible task set, it always produces feasible schedules [11].
The scheduling algorithms can be classified as static and dynamic. In a static scheduling algorithm, all scheduling decisions are provided a priori. For a given set of timing constraints, a table is constructed indicating the starting and completion times of each task, such that, no task misses its deadline. This approach is highly predictable, but when the parameters of the tasks change, the table must be recomputed and the system restarted.
In dynamic scheduling algorithms, the scheduling decisions are taken at run-time based on the priorities of the tasks. These priority values are used to decide the execution order of the tasks. Priority values can be assigned statically or dynamically, depending on the dynamic scheduling algorithm. If static priorities are used, the priority of each task remains fixed during the complete execution of the system, whereas if dynamic priorities are used, the priority of a task is allowed to change at any moment.
As mentioned before, Liu and Layland [10] introduced the first real-time scheduling algorithms for a single processor (rate-monotonic and earliest deadline first), and developed their corresponding schedulability analysis. RM assigns the highest priority to the task with the smallest period, and EDF assigns priorities to the tasks considering the proximity of each instance of a task with its deadline, so that the task with the closest relative deadline receives the highest priority. Liu and Layland demonstrated that RM and EDF are optimal for fixed and dynamic priority algorithms, respectively.
2.1System modelIn this paper, we consider a real-time system composed of a set of n real-time tasks τ={τ1,τ2...,τn} on one processor under rate-monotonic. A task is usually a thread or a process within an operating system. The parameters that define a task τi are: the execution time Ci, the period Ti, and the deadline Di. We will consider that only periodic tasks can be executed in the system, and we will consider that Ti=Di. Each periodic task τi is composed of an infinite sequence of jobs. The period Ti of the periodic task τi is a fixed time interval between the release times of consecutive jobs in τi. Its execution time Ci is the maximum execution time of all the jobs in τi. The period and execution time of the task τi satisfies that Ti>0 and 0<Ci≤Ti=Di, (i=1,..., n). The utilization factor of the task τi is defined as ui=ciTi. The utilization factor of the task set, denoted as U, is the sum of the utilization of the tasks in the set, that is, U=∑i=1nCiTi. We will consider that a job in τi that is released at time t, must complete within Di, that is, it must complete within the time interval (t, t+Di]; where Di is the relative deadline of the task τi. The release time of the first job in each task τi is called the phase of τi, and is denoted as θi.
We use H to denote the least common multiple of Ti, for i=1, 2,..., n. A time interval of length H is called the hyperperiod of the task set.
In the model used in this paper, the following restrictions also apply
A1 The tasks are independent. That is, the arrival of a job of task τi is not affected by the arrival of any job of the other task τj≠i.
A2 It is assumed that all tasks in the system can be preempted at any time.
A3 The cost of the context switch of the tasks is considered negligible.
A4 No resources, other than the CPU are shared among the tasks.
3Schedulability testsA schedulability test defines a mathematical condition that is used to verify whether the task set meets its temporal restrictions for a given scheduling algorithm. The inputs of the test are the temporal parameters of the task set.
A test is said to be sufficient in the sense that a task set is schedulable if it satisfies the test. However, if the task set does not satisfy the sufficient test, it is not known whether the task set can be schedulable using that scheduling algorithm. A test is said to be necessary if all schedulable task sets satisfy the test. Otherwise, if a given task set satisfies the test, we cannot say that it is schedulable. Exact tests provide a necessary and sufficient condition. The inexact schedulability tests provide only a sufficient (but not necessary) schedulability condition.
Schedulability tests depend on the scheduling algorithm chosen and the knowledge of the parameters of the task set. The schedulability test in dynamic scheduling algorithms can be performed off-line or online. If the test is executed off-line, there must be complete knowledge of the set of tasks that are to be executed in the system along with the timing constraints imposed on every task (e.g., deadlines, precedence restrictions, execution times) before the execution of the system. In this case, the arrival of new tasks is not allowed while the system is executing, and the tasks cannot change their timing constraints.
In contrast, if the scheduling test is performed online, new arrivals are allowed at any time and the tasks can change their timing constraints during the execution of the system. In this test, the scheduler decides dynamically, by means of an admission control mechanism, if the acceptance of these new tasks will not cause other tasks to miss their deadlines.
The utilization bound Û, for a given real time scheduling algorithm, is the value such that any task set, whose utilization factor is no larger than Û, is schedulable under that scheduling algorithm.
Utilization-based schedulability conditions verify if the utilization of the task set does not exceed the utilization bound (that is, U≤Û).
We classify the inexact tests in accordance with the parameters used as follows
Non-period-aware schedulability conditions. These schedulability conditions derive the utilization bound using information about the number of tasks or the utilization of the tasks in the system. The tests based on the utilization found in the literature are:
- -
The Liu and Layland condition (LL) introduced in [10].
- -
Increasing Period condition (IP) [12].
- -
Utilization Oriented condition (UO) developed by Y. Ohet al.[13].
Period-aware schedulability conditions. Some variants of the utilization-based conditions use additional information from the task set in order to derive the utilization bound. In these conditions, the value of the periods of the tasks is included in the analysis. According to the way they derive their schedulability bounds, these conditions can be further classified as closed-form period-aware conditions and non-closed-form period-aware conditions:
- -
Closed-form period-aware conditions: Period Oriented (PO) [14], Conditions based on Harmonic Chains [15-17] andCRMB[18].
- -
Non-closed-form period-aware conditions: T-Bound andR-Bound[19], Algorithms ofChen, Mok and Kuo[20],Sr andDCT[17], and conditions that use linear programming techniques, such as thePSUB[21] andLP conditions [1].
In this section, we review the best-known schedulability conditions found in the literature for rate-monotonic on one processor.
4.1Exact schedulability conditions for rate-monotonicAfter Liu and Layland derived the RM scheduling algorithm along with its inexact condition, many necessary and sufficient tests for RM on one processor have been proposed [20] [22-27]. In this section, we will review two of them.
4.1.1Exact schedulability condition based on processor’s demand (LE)One of the first exact conditions was proposed by Lehoczky et al.[22]. In this test, the total demand of the processor time by a job in a critical instant is computed, along with the total demand of the processor time for all the higher priority tasks. Then, the test checks if this demand can be met before the deadline of the job. The LE scheduling condition is formally defined in Theorem 1 [22].
Theorem 1(LE Condition). Let τ={τ1, τ2,…,τn} be a task set with n tasks and T1≤T2≤...≤Tn. τi can be schedulable under RM if and only if,
Where
The entire task set can be schedulable under RM if and only if
It can be observed that the computational complexity of the LE condition is pseudo-polynominal [22].
The function Li(t) is monotonically decreasing since tTit is strictly decreasing except at a finite set of values called rate-monotonic scheduling points. When t is a multiple of one of the periods Tj, for 1≤j≤i, the function has a local minimum [22]. Consequently, only a search over these local minimum values (the multiples of Tj≤Ti, 1≤j≤i) is needed, to determine if τi can meet its deadline.
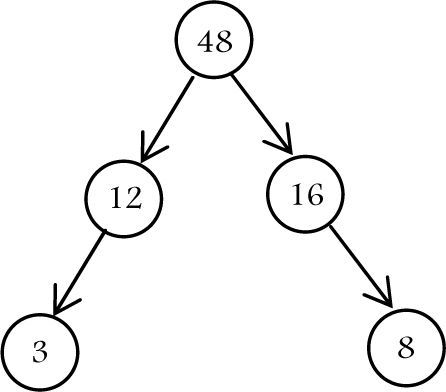
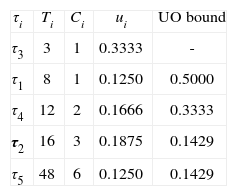
Example 1.Table 1 shows a task set τwith five tasks, including its timing constraints: Ci, Ti, ui and U=∑{j=1,..,i}ui. In order to verify if this task set is schedulable under the RM algorithm, we will use the exact LE condition.
We first sort the task set by the ascending period values. Thus, τ′1=(3,1),τ′2=(8,1),τ′3=(12,2),τ′4=(16,3) and τ′5=(48,6). To determine if the task set is schedulable we just need to check if τ′5 fulfills its timing constraint. The set of scheduling points is S5={3, 6, 8, 9, 12, 15, 16, 18, 21, 24, 27, 30, 32, 33, 36, 39, 40, 42, 45, 48}.
Task τ′5 is schedulable if any of the following Equations hold (for Di=Ti):
…
or W5(45)=15C1+ 6C2+ 4C3+ 3C4+ C5≤15T1 44≤45
or W5(48)=16C1+ 6C2+ 4C3+ 3C4+ C5≤T5 46≤48
From the previous analysis, note that W5(t)≤t≤T5(t=45 and t=48). Therefore, we can conclude that the task set shown in Table 1 is schedulable under the RM algorithm.
4.1.2Exact schedulability condition based on the task’s response timesJoseph and Pandya introduced an exact schedulability condition in [23] for fixed priority scheduling. In this test, the response time of each task ri is obtained, and if ri≤Di, then task τi meets its deadline.
This test starts by obtaining the response time of the highest priority task, using the following Equation
Where hp(i) is the set of tasks with a higher priority than the task τi. Given that ri appears on both sides of the Equation, a possible solution was proposed by Audsley et al. in [24]. The solution is obtained by the following iterative process:
Iterations described in Equation 3 can start considering ri0=∑k=1iCk. It is easy to note that rin+1≥rin. If rin≥Di, then task τi will miss its deadline. However, if rin+1=rin, the iterative process will conclude, meaning that τi is schedulable.
The response time analysis has evolved to include offsets, blocking, fault tolerance, and release jitter [24].
The exact schedulability analysis is time-consuming due to its high computational complexity. Therefore, it is not suitable for online schedulability analysis.
4.2Liu and Layland (LL) schedulability conditionIn [10], Liu and Layland defined the critical instant for a task as the instant at which a request for that task will have the largest response time, and showed that if all the tasks meet their deadlines at their critical instants, then the task set is feasible. The worst-case phasing occurs when θ1=θ2=…=θn (e.g. θi=0 for all i).
Liu and Layland introduced the concept of utilization factor in [10] and defined it as the fraction of the processor time spent in the execution of the task set. Further, they defined that a task set is said to fully utilize the processor according to a given scheduling algorithm if the set of tasks can be feasibly scheduled and that any increase in the execution time of any of the tasks will make the task set infeasible with respect to that algorithm. For a given fixed-priority scheduling algorithm, the least upper bound of the utilization factor is the minimum of the utilization factors over all the sets of tasks that fully utilize the processor.
In order to derive the least upper bound for the rate monotonic algorithm, Liu and Layland showed that the worst-case situation occurs when the task set fully utilizes the processor, all tasks start simultaneously (that is, at its critical instant) and the relationship among the periods is such that ∀i=2,…,n; T1<Ti<2T1. Under this worst-case scenario, Liu and Layland found the least upper bound by minimizing the total utilization with respect to the period values.
The Liu and Layland condition (LL) is formalized in Theorem 2 [10].
Theorem 2 (LL condition). A set of tasks τis schedulable under the RM algorithm if the following condition is satisfied
If the condition of Theorem 2 is not satisfied, that is, U>n(21n-1), then it is not known whether the task set is schedulable under Rate-Monotonic.
It is important to note that the LL condition depends only on the number of tasks in the system [29]. The computational complexity of the LL condition is O(n).
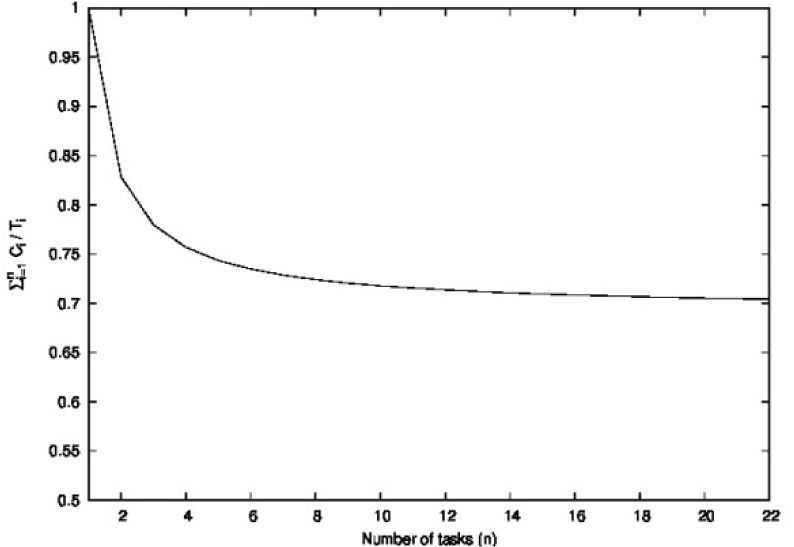
Figure 1 shows the processor utilization factor under the LL schedulability condition. It can be observed that when the number of tasks tends to infinity, the minimum achievable utilization factor tends to ln(2)=0.6931.
Leung and Whitehead, in [28], generalized the results provided by Liu and Layland and proved that the Deadline monotonic (DM) algorithm is optimal for the fixed-priority scheduling model. In the DM scheduling algorithm, task deadlines can be smaller than its periods (Di≤Ti).
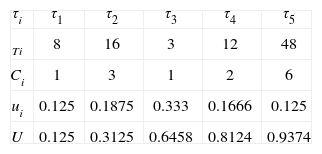
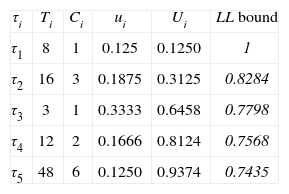
Example 2. After applying the LL condition to the task set shown in Table 1, we can conclude that tasks τ1, τ2, and τ3 can be feasibly scheduled, but adding τ4 and τ5 violates the LL condition, as shown in Table 2.
LL condition applied to the TS of Table 1.
| τi | Ti | Ci | ui | Ui | LL bound |
| τ1 | 8 | 1 | 0.125 | 0.1250 | 1 |
| τ2 | 16 | 3 | 0.1875 | 0.3125 | 0.8284 |
| τ3 | 3 | 1 | 0.3333 | 0.6458 | 0.7798 |
| τ4 | 12 | 2 | 0.1666 | 0.8124 | 0.7568 |
| τ5 | 48 | 6 | 0.1250 | 0.9374 | 0.7435 |
The IP condition was introduced by Dhall and Liu [12] and was proposed to be used together with the multiprocessor algorithms rate-monotonic next fit and rate-monotonic first-fit. In order to determine the tasks that can be assigned to each processor, the IP condition takes into account both the utilization of the task set assigned to a processor and the utilization of the new task. The IP schedulability condition is defined in Theorem 3 [12]:
Theorem 3(IP condition). Let τ={τ1, τ2,…,τn} be a set of n tasks with T1≤T2...≤Tn and let
If the following condition is met
Then the set of tasks can be feasibly scheduled under the RM algorithm. When n → ∞, the minimum utilization of task τn approaches to (2e−u - 1).
This condition requires an ordering of the periods of the tasks. Because of this ordering, its complexity is O(n log n). As it can be noticed, this condition is based on the utilization and the number of tasks in the system.
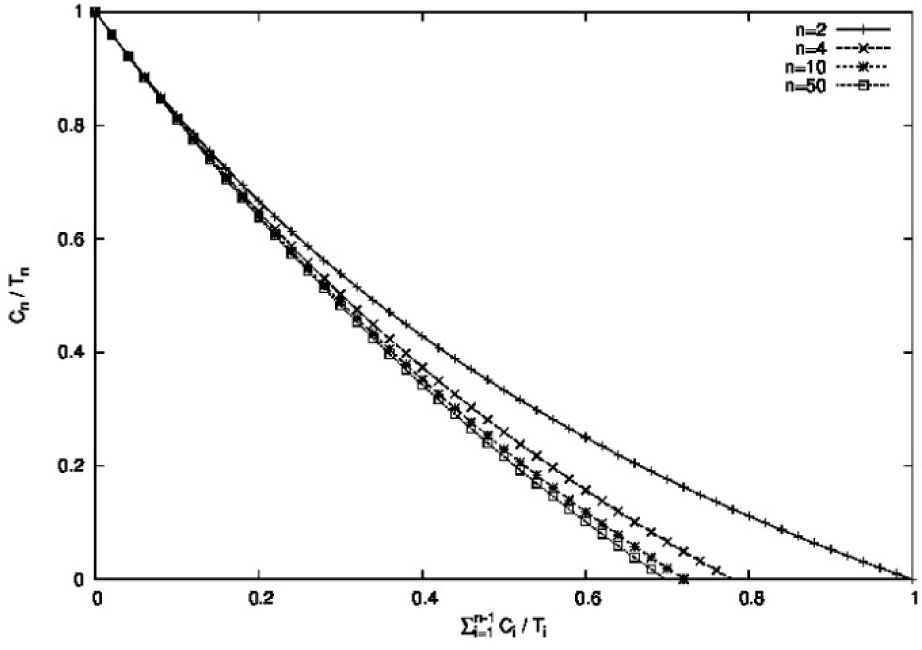
Figure 2 shows the performance of the IP condition, where the utilization of task τn is a function of the (n-1) tasks already in the system. The different curves illustrate different values for the number of tasks (n). The area under the curve denotes the feasibility area for this test.
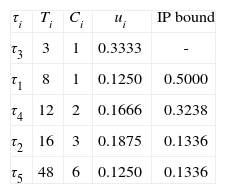
Example 3. In this example, we will show the performance of the IP schedulability condition using the task set described in Table 1. To use this condition, tasks must be sorted in the nondecreasing order of their periods. After applying the IP condition, we note, in Table 3, that while tasks τ3, τ1, τ4, and τ5 are identified as schedulable, the IP condition fails to identify task τ2 as schedulable.
IP condition applied to the TS of Table 1.
| τi | Ti | Ci | ui | IP bound |
| τ3 | 3 | 1 | 0.3333 | - |
| τ1 | 8 | 1 | 0.1250 | 0.5000 |
| τ4 | 12 | 2 | 0.1666 | 0.3238 |
| τ2 | 16 | 3 | 0.1875 | 0.1336 |
| τ5 | 48 | 6 | 0.1250 | 0.1336 |
Burchard et al.[14] introduced the period oriented condition to be used by the rate monotonic small tasks (RMST) and rate monotonic general tasks (RMGT) multiprocessor algorithms. To be able to use the PO condition, it is necessary to know the values of the periods of the tasks in the system. The PO condition is formally defined in Theorem 4 [14]:
Theorem 4(PO condition). Given a set of tasks τ={τ1, τ2,…,τn}, Siand β are defined as follows:
and
(a) if β<(1 – 1/n) and the total utilization satisfies that
then the task set is schedulable on one processor under RM.
(b) if β≥(1 - 1/n) and the total utilization satisfies that
Then the task set is schedulable on one processor under RM.
From Equation 7 it can be observed that Si is a function that goes from zero (when the period Ti is a power of two) to one (when the period Ti is the next power of two), and it measures the logarithmic distance of the period of task τi from a power of two (where 0.5 means that the period is logarithmically in the middle of two powers of two). Therefore, β measures how logarithmically equidistant the periods of all tasks are from a power of two. When β=0, Ti+1=2αTi ∀I=1,2,…,n. and ∀α∈N, and α>0.
As β approaches to zero, the utilization bound tends to one, independent of the number of task. On the other hand, as β approaches to one, the utilization bound approaches the LL condition.
A simpler version of Equation 9 of the PO condition is defined in Corollary 1 [14].
Corollary 1 (PO condition). Given a set of tasks τ={τ1, τ2,…,τn} and given β (as defined in Theorem 4), if the total utilization satisfies that
then the task set can be feasibly scheduled on one processor under RM.
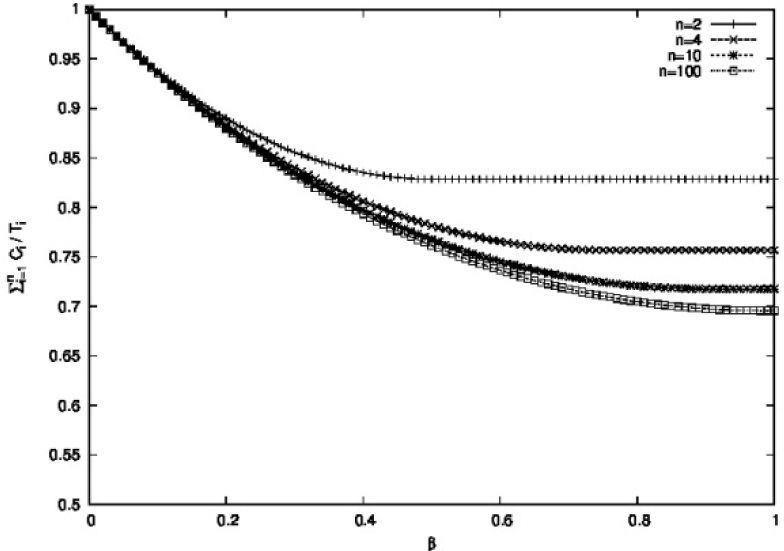
Figure 3 shows the performance of the PO condition. Each curve shows, for a given number of tasks, the relationship between β and the utilization of the task set. The area under the curve denotes the feasibility area for this test. It can be observed that when the number of tasks is large and the value of β=1, then the minimum achievable utilization is approximately 69%, similar to the result provided by the LL condition.
Example 4. The first step on applying the PO condition to the task set described in Table 1 involves calculating the Si values using Equation 7, and sorting them in the nondecreasing order. The obtained values are Si={S1=0, S2=0, S3=0.5849, S4=0.5849, S5=0.5849}, and β=0.5849 (from Equation. 8). Because β<(1 – 1/n) (0.5848<0.8), Corollary 1 can be used to check the schedulability of the task set. given that 0.9375>0.6931, the PO condition fails to identify the task set as schedulable.
4.5Utilization oriented (UO) schedulability conditionY. Oh et al. [13] introduced a schedulability condition based on the values of tasks utilization ui. Oh et al. derived their schedulability condition from the worst-case scenario identified by Liu and Layland [10], but instead of minimizing the total utilization with respect to the period values, they derived their schedulability condition as a function of the individual task utilization [13].
The UO condition was proposed to be used in the fate-monotonic-first-fit-decreasing-utilization (RM-FFDU) multiprocessor algorithm and is defined in Theorem 5 [13].
Theorem 5 (UO Condition). Let τ={τ1, τ2,…,τn−1} be a task set of (n-1) tasks, feasibly scheduled under RM. A new task τn can be feasibly scheduled along with the (n-1) tasks already in the system (on one processor under RM), if the following condition is met:
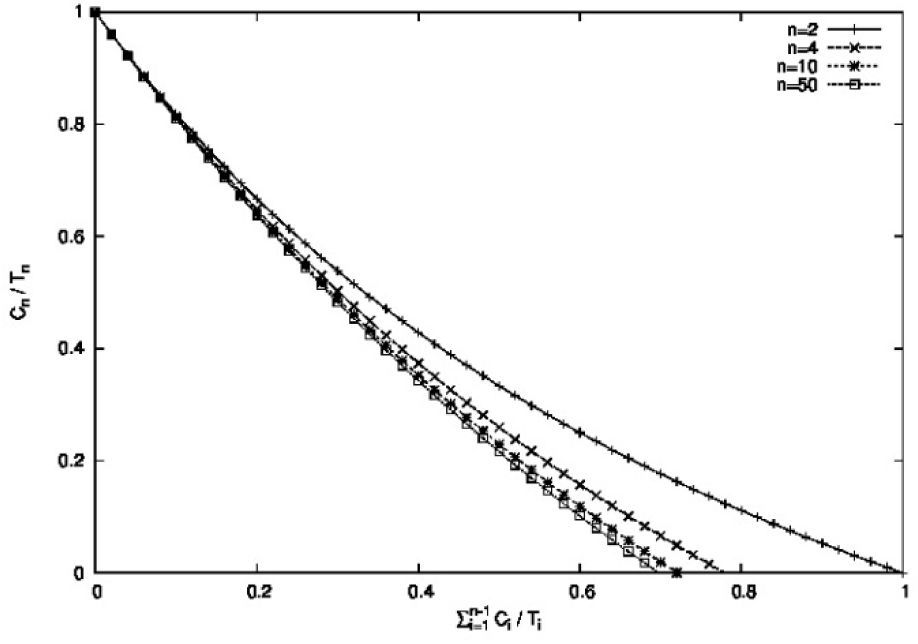
Figure 4 shows the UO utilization bound for different values of n, where the x-axis denotes the utilization of the (n-1) tasks already in the system, and the y-axis denotes the utilization of task τi. The area under each curve denotes the feasibility area for this test. Note that this condition takes into account the number of tasks and the individual utilization of the tasks. The complexity of this condition is O(n).
Bini et al. [29] introduced the Hyperbolic Bound (HB) condition, a schedulability test similar to the one provided by the UO condition. The HB condition is expressed in Theorem 6 [29].
Theorem 6 (HB Condition). Let τ={τ1, τ2,…,τn} be a set of n periodic tasks, where each tasks τi is characterized by a processor utilization ui. Then, τis schedulable by the RM algorithm if
It is clear that Equation 13 can be derived from Equation 12. Bini et al. extended the HB condition to include resource sharing and aperiodic servers.
Example 5. After using the UO condition to verify the schedulability of the task set described in Table 1, we find that tasks τ1,τ2 and τ3 are proved to be schedulable, but the UO condition fails to identify tasks τ4 and τ5 as schedulable, as shown in Table 4.
UO condition applied to the TS of Table 1.
| τi | Ti | Ci | ui | UO bound |
| τ3 | 3 | 1 | 0.3333 | - |
| τ1 | 8 | 1 | 0.1250 | 0.5000 |
| τ4 | 12 | 2 | 0.1666 | 0.3333 |
| τ2 | 16 | 3 | 0.1875 | 0.1429 |
| τ5 | 48 | 6 | 0.1250 | 0.1429 |
Lauzac et al. [30] developed the T-Bound and R-Bound schedulability conditions to be used as an admission control for RM scheduling on uniprocessor systems, and extended their results to be used as an admission control for the multiprocessor systems. While discussing the LL schedulability condition, we noted that the worst-case scenario occurs when all the tasks start simultaneously and the relationship among the periods is such that the ratio between any task periods is less than two. Liu and Layland showed in [10] that under this scenario, the computation times used to derive the least upper bound are:
Ci=Ti+ 1 – Ti (i=1, …, n – 1) and Cn=2T1 – Tn
If the total utilization U=∑i=1nCiTi is rewritten using these computation times, a new schedulability bound for RM can be derived. This bound is shown in Lemma 1 [30].
Lemma 1. Given a task set τof n tasks ordered by increasing periods, and the restriction that the ratio between any task periods is less than 2 τ is schedulable if
The T-Bound condition uses the ScaleTaskSet algorithm to transform the original task set into an equivalent task set where the ratio between the maximum and minimum periods is less than 2 (that is, r=Tmax/ Tmin<2). Using this transformed task set, the condition verifies its schedulability through Equation 14. As stated in Lemma 2 [30], if the transformed task set is feasibly scheduled under RM then the original task set is also feasible.
Lemma 2. Let τbe a given periodic task set, and let τ′be the transformed task set after applying the ScaleTaskSet algorithm to τ. If τ′ is schedulable on one processor under RM, then τ is also schedulable.
ScaleTaskSet (In: τ, Out: τ′)
Begin
Sort the task set in τby increasing period;for (i=1 to n-1) do
Sort the task set in τ′by increasing period; return (τ′);
end
Algorithm 1ScaleTaskSet Algorithm.
The ScaleTaskSet algorithm is defined in Algorithm 1 and the T-Bound condition is formally defined in Theorem 7 [30].
Theorem 7 (T-Bound condition). Consider a periodic task set τ, and let τ′be the transformed task set after executing the ScaleTaskSet algorithm to τ. If Equation 14 holds for τ′, then the task set τcan be feasibly scheduled on one processor under RM.
It is important to note that the T-Bound condition uses the value of the periods T′1,…,T′n, derived by the ScaleTaskSet algorithm. However, in order to provide an admission control criterion that does not depend on the periods of all the tasks, Lauzac et al. [30,19] derived the R-Bound schedulability condition, which uses the relationship between the largest and the smallest period values in the task set. The R-Bound schedulability condition is defined in Theorem 8 [19].
Theorem 8 (R-Bound condition). Consider a periodic task set τ, and let τ′be the transformed task set after applying the ScaleTaskSet algorithm to τ. If,
Where r=Tn′T1′, the task set τ can be feasibly scheduled on one processor under RM.
Because the T-Bound condition uses more information about the task set, it outperforms the R-Bound condition. However, Lauzac et al. showed in [19] that when r is close to one, the performance of the R-Bound condition is similar to the performance of the T-Bound condition. The complexity of the T-Bound and R-Bound conditions is O(n log n).
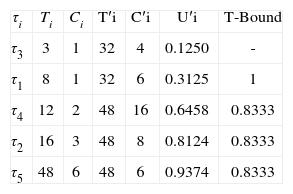
Example 6. Before applying the T-Bound condition to the task set described in Table 1, we first need to generate a transformed task set using the ScaleTaskSet algorithm. Then, according to Theorem 7, if the transformed task set is schedulable under RM, the former task set is also schedulable. Table 5 shows the values of the periods and the execution times of the transformed tasks. It can be noted that under the T-Bound condition tasks τ1,τ2, τ3 and τ4 are proved to be schedulable, whereas the T-Bound condition fails to identify task τ5 as schedulable.
T-Bound applied to the TS of Table 1.
| τi | Ti | Ci | T′i | C′i | U′i | T-Bound |
| τ3 | 3 | 1 | 32 | 4 | 0.1250 | - |
| τ1 | 8 | 1 | 32 | 6 | 0.3125 | 1 |
| τ4 | 12 | 2 | 48 | 16 | 0.6458 | 0.8333 |
| τ2 | 16 | 3 | 48 | 8 | 0.8124 | 0.8333 |
| τ5 | 48 | 6 | 48 | 6 | 0.9374 | 0.8333 |
Kuo and Mok [15] extended the results provided by Liu and Layland [10], by relating the achievable utilization factor to the number of harmonic chains found in a task set. A harmonic chain is a list of numbers (periods) wherein each number divides every number after it [20].
Kuo and Mok [15] developed the harmonic chain (HC) condition, in which a periodic task set τwill find a feasible schedule if its utilization factor is no larger than k(21k-1), where k is the size of the harmonic base of τ.
The harmonic chains found in the task set conform the harmonic base of a task set. The definition of harmonic base is described as follows:
Definition 1 (Harmonic Base of τ). Let S be the set of periods (positive numbers) of a set of periodic tasks τ. a subset H of S is said to be a harmonic base of the task set τif there is a partition, say Γ, of S into |H| subsets such that:
- 1.
Each member of H is the smallest element in exactly one member of the partition Γ, and
- 2.
If x and y are two elements in the same member of the partition Γ, then either x divides y or y divides x.
Each subset in the partition Γ is called a harmonic chain [15].
In order to explain the HC condition, we will use the following example:
Let T be a task set where every task is defined as τi=(Ti, Ci). We have T={τ1=(3, 1), τ2=(5, 1), τ3=(15, 2), τ4=(20, 3), τ5=(60, 8) }. Let P be the set of periods from T, such that P={3, 5, 15, 20, 60}. The subset H={3,5} is a harmonic base of P because there exists a partition Γ in |H| subsets, namely Γ={{3,15}, {5,20,60}}, such that:
- (1)
each member of H is the smallest single element of the partition Γ, and
- (2)
for each par of elements within the partition Γ, one element divides the other.
The harmonic chains condition is formally defined in Theorem 9 [15].
Theorem 9 (HC condition). Let τbe a set of periodic tasks and let k be the size of the harmonic base of τ. If the utilization factor is no larger than k(21k-1), then τ is schedulable by a preemptive fixed priority scheduler.
A polynomial time algorithm can solve the problem of computing the harmonic base of a periodic task set. From Theorem 9, it can be observed that when the size of the harmonic base is small, the utilization bound is large. For instance, for k=1, though the utilization may be as high as 100%, the task set is guaranteed to be schedulable. Note that the HC condition is similar to the LL condition when the periods of all tasks are relative primes 1
Example 7. The task set described in Table 1 has two harmonic chains: Γ={{8, 16}, {3, 12, 48}}, as shown in Figure 5. After applying the HC condition, we concluded that this condition identifies tasks τ1, τ2, τ3, and τ4 as schedulable, since their total utilization is not higher than 2(212-1). Task τ5 violates the HC condition because ∑i=15ui>2(212-1), therefore, it is not identified as schedulable.
The harmonic chains in the TS of Table 1.
Kuo et al. [16] developed the Root condition and demonstrated that a task set can be feasibly scheduled as long as the utilization of the task set is no larger than R(21R-1), where R is the number of roots in the task set. The concept of root is defined next [16].
Definition 2. Let τ={ τ1,τ2..., τn } be a periodic task set. Task τi is a root in τ if there does not exist any task period in τ, which is larger than and divisible by the period of the task τi.
In order to explain the concept of root, we will use the example described in the previous subsection:
Let τ be a task set where every task is defined as τi=(Ti, Ci). We have τ={ τ1=(3, 1), τ2=(5, 1), τ3=(15, 2), τ4=(20, 3), τ5=(60, 8) }. Let P be the set of periods from τ, such that, P={3, 5, 15, 20, 60}. The harmonic base of P is Γ={{3, 15}, {5, 20, 60}}. From the harmonic base of P we can observe that 60 is a value such that there does not exist any task period in P, which is larger than and divisible by 60.
The Root condition is defined in Theorem 10 [16].
Theorem 10 (Root condition). Suppose that the task set {τ1,τ2,τi-1 } is schedulable. Let R be the number of roots in the task set τ={τ1,τ2,τi-1,τi } If the total utilization factor of τis no larger than R (21/R – 1), then τis schedulable.
Because the number of roots could be much less than the number of tasks, and the size of its harmonic base, it is expected that the Root condition improves the acceptance ratio of the LL and HC conditions. This can be observed in Corollaries 2, 3 and 4 [16].
Corollary 2. Let τbe a set of periodic tasks. If τis guaranteed to be scheduled according to the LL condition, then τis guaranteed to be scheduled according to the Root condition.
Corollary 3. Let τbe a set of periodic tasks. If τis guaranteed to be scheduled according to the HC condition, then τis guaranteed to be scheduled according to the Root condition.
Corollary 4. There exists a task set that is guaranteed to be scheduled according to Root condition, but not according to the LL and HC conditions.
An important feature of the root condition is that it was developed to be used incrementally for online admission control.
Example 8. In this example, we will show the performance of the root condition. As described in the previous example, the task set from Table 1 has two harmonic chains: Γ={{8,16}, {3,12,48}}. However, it has only one root, R=48, as shown in Figure 5. Therefore, after applying the root condition, we observe that tasks τ1,τ2,τ3, τ4, and τ5 are identified as schedulable, since their total utilization is no larger than 1 (1(21/1 - 1)).
4.9Sr and DCT schedulability conditionsHan and Tyan [17] introduced two polynomial-time schedulability tests that transform the task periods into a special pattern where all the periods belong to a single harmonic chain. According to Theorem 9, when k=1 (which means there is only one harmonic chain in τ), the transformed task set τ′ is schedulable if its total utilization is less than or equal to 1. Han and Tyan proved that if τ′is schedulable under RM, then the original task set τis also schedulable under RM. The transformed task τ′ set must satisfy the Condition 1 [17].
Condition 1. τ′i≤τi for all i=1, 2,…, n, and τ′i evenly divides τ′i+1 denoted as τ′i|τ′j, (thus, τ′i≤τ′i+1 for all i=1, 2,…, n.
The schedulability of the transformed task set τ′is defined in Theorem 11 [17].
Theorem 11. Given a task set τ, if there exists another task set that satisfies condition 1 and Uτ′=∑i=1nCiTi≤1, then τ is schedulable by RM
In order to apply the results provided by Theorem 11, the problem is, given a task set τ, how to find (in polynomial time) another task set that satisfies condition 1 and whose utilization Uτ′ is as small as possible. Han and Tyan proposed, in [12], the Sr and DCT algorithms to find such τ′.
Input:τ={τi=(Ci,Ti)|1≤i≤n}, whereτisa periodic task set and Ti≤Tj,∀I≤j;
Output: Task set τ′and Φτ (r);
begin
for (i=1 ton) doli=Ti2log(TiT1);
sort (l1, l2,…,ln) into nondecreasing order
and remove duplicates, let (k1, k2…, ku) be
the
resulting sequence;
for (i=1 ton) do put τi into subset πli ;
;for (j=1 tou) do
compute Φτ (ku)=Φτ (T1);
for (j=u-1 down-to 1) do
Φτ(kj)=kj+1kjΦτ(kj+1)-U(πkj)
findr* suchthat
Φτ(r*)=minr∈{k1,k2…,ku) Φτ(r);
for (i=1 ton) doT′i=r*.2⌊log(Tir*)⌋;
return Φτ(r*) and τ′;
End
Algorithm 2Sr Algorithm.
4.9.1Sr AlgorithmThe first algorithm proposed is called the Sr Algorithm (Specialization operation). In this algorithm, each period Ti of the task set τis transformed into another period Ti′=r⋅2logTir, where r is a real number chosen from the range (T12,T1]. Because T′i≤T′i for all i and T′i≤T′j for all i<j, the transformed period values belong to a single harmonic chain. Furthermore, because T′i≤T′i for all i, we have that Uτ′=∑i=1nC′iT′i≥Uτ=∑i=1nCiTi. To minimize the total utilization increase Δ=Uτ′-Uτ the value of r should be carefully chosen. The Sr algorithm, reproduced in Algorithm 2, finds the best value for r, and then derives the new periods T′i, for all i, using the best r.
The Sr algorithm first computes li=Ti2log(Ti/T1), for 1≤i≤n, where T12
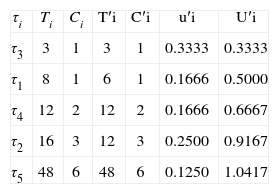
Example 9. In this example, we will show the performance of the Sr schedulability condition. The first step in the Sr algorithm is to find the li values to obtain the special base of r. After computing the li values and removing duplicates, we have k1=2 and k2=3. Next, we need to find the value of r* using Φτ*=Φτ(r*)=min{T12
Sr and DCT Applied to the TS of Table 1.
| τi | Ti | Ci | T′i | C′i | u′i | U′i |
| τ3 | 3 | 1 | 3 | 1 | 0.3333 | 0.3333 |
| τ1 | 8 | 1 | 6 | 1 | 0.1666 | 0.5000 |
| τ4 | 12 | 2 | 12 | 2 | 0.1666 | 0.6667 |
| τ2 | 16 | 3 | 12 | 3 | 0.2500 | 0.9167 |
| τ5 | 48 | 6 | 48 | 6 | 0.1250 | 1.0417 |
Input:=τ={τi=(Ci,Ti)|1≤i≤n }, where τ is a periodic task set and Ti≤Tj,∀I<j ;
Output: Task set τ′ ;
Begin
min_f=-1; min_utilization=∞;
for (f=1 to n) do {
Zf=Tf
for (i=f+1 to n) Zi=Zi-1⋅TiZi-1 ;
for (i=f-1 down-to 1) doZi=Zi+1Zi+1Ti ;
utilization ∑i=1nCiZi;
if utilization<min utilization then
min utilization=utilization;
min _ f;
for (i=1 to n) doT′i=Zi ;
endif
end
4.9.2DCT algorithmThe second algorithm proposed by Han and Tyan in [17] is called the DCT algorithm. The idea behind the DCT algorithm is the following. For each f, 1≤f≤n,T′f=Tf, and recursively, Ti, for each i>f, is transformed to the largest integral multiple of T′i-1 that is less than or equal to Ti. That is,
Similarly, Ti, for i<f, is recursively transformed to the largest divisor of T′i-1 that is less than or equal to Ti. That is,
The value of f that results in the minimum utilization increase will be the final index of Ti whose transformed value of T′i will be fixed at Ti. The DCT algorithm is described in Algorithm 3. The complexity of the DCT condition is O(n2).
Example 10. In this example, we will show the performance of the DCT schedulability condition. After applying the DCT algorithm to the task set shown in Table 1, we found that when f=3, a minimum utilization increase=1.0417 is obtained, which corresponds to the transformed task set τ′ shown in Table 6. Using Theorem 11 to verify the feasibility of this task set, we conclude that tasks τ1, τ2, τ3, and τ4 are proved to be schedulable, because their total utilization is no larger than 1. However, task τ5 is not identified as schedulable by the DCT condition given that U′5>1. It can be observed that for the task set described in Table 1, the Sr and DCT conditions produce identical results.
Han and Tyan showed in [17] that the DCT condition provides a better performance than the Sr condition. Han extended the DCT and Sr conditions to be used in the multiframe task model in [31].
4.10Chen, Mok, and Kuo AlgorithmsChen, Mok, and Kuo [20] developed three polynomial-time algorithms with the aim to improve the performance of the LL and HC conditions.
On Algorithm 1 (reproduced in Algorithm 4), a task set τ is transformed into another task set in which the ratio of any Ti and Tj (for all i ≠ j) is no larger than two. A new utilization bound U is calculated for the transformed task set, using Theorem 12 [20]. The task set τ can be feasibly scheduled under RM if its total utilization is less than or equal to U. The complexity of the Algorithm 1 condition is O(n2).
Theorem 12. Let τ={τ1, τ2,..., τn}be a set of periodic task. Let T→ be the array of the periods of the task set. If T1<T2<...n<2T1, then the utilization bound U for the task set is obtained when,
Example 11. In this example, we will show the performance of the Algorithm 1 condition. From the task set described in Table 1, we compute the periods of the transformed task sets and their respective total utilization. Therefore,τ′1=[6,8] and U′1=0.8333;τ′2=[8,12,12] and U′2=0.8333;τ′3=[12,15,16,16] and U′3=0.8167; and τ′4=[48,48,48,48,48] and U′4=1. Because the minimum of these utilization values is used as the schedulability bound, we have U′=0.8167; therefore, tasks τ1, τ2, τ3, and τ4 can be schedulable. The Algorithm 1 condition fails to identify task τ5 as schedulable because U′5>U.
Input: TaskPeriod[n] in nondecreasing order;
Output: Utilization bound U;
var NewPeriod: array[1…n] of integer;
begin
U=1;
for (i=2 to n) do
begin
for(j=1 to i) do
end
return (U¯);
end
Algorithm 4 Algorithm 1 of Chen, Mok, and Kuo.
The second algorithm, proposed by Chen, Mok, and Kuo [20], is named Algorithm 2, and is not included in our comparison. This algorithm introduce a strategy to compute, with higher efficiency, the size of the harmonic base from a set of tasks, which is better than the bound obtained using the HC condition. The complexity of the Algorithm 2 condition is O(n2). The Algorithm 2 condition is based on Lemma 3 and Lemma 4 [20].
Chen et al. proved in [20] that there is a smallest m, 1≤m≤n, and an array T→m=[T1,T2,…,Tm] with total utilization U′, reduced from T→ (the array of periods of the task set), such that U′≤U.
Lemma 3. Let U=Um. If Ti divides Tj,1≤i≤j≤m, then U ofT→ equals of U ofT′→=[T1,T2,…,Ti-1,Ti+1,…,Tn].
The definition of Lemma 4 is given next.
Lemma 4. Let U=Um. Consider Tj and Tk in T→m,tm=tjTj+rj=tkTk+rk. If tjTj≤tkTk and ek≤αjkej, then U is equal to the minimum utilization factor of all extreme task sets T→′=[T1,T2,…,Tki-1,Tk+1,…,Tn].
The Algorithm 3 condition is an improvement on the Algorithm 2 condition. In this condition, T→reduced is a reduced array from T→ where some periods are deleted according to Lemma 3. Then, all the extreme task sets of T→reduced are generated. The utilization bound provided by the Algorithm 3 condition is equal to the minimum utilization factor of all the extreme task sets of T→reduced. The Algorithm 3 condition is described in Algorithm 5. The complexity of the Algorithm 3 condition is O(n3).
Input: TaskPeriod[n] in nondecreasing order;
var TaskPeriod1: array[1… n] of integer; [reduced task pattern]
TaskPeriod2: array[1…n] of integer; [further reduced task pattern]
Begin
;for (i=1 to n) do
TaskPeriod1=reduced task pattern of TaskPeriod, in nondecreasing order;
TaskPeriod2=task pattern from TaskPeriod1 with T=TiT T for each element T, in nondecreasing order;
U′¯ utilization factor calculated from TaskPeriod2 using
Theorem 12;
if U¯>U′¯ then U¯=U′¯ ;
end for
return (U¯);
end
Algorithm 5. Algorithm 3 of Chen, Mok, and Kuo.
Theorem 13. Let T→=[T1,T2,…,Tn].
U=mini=1nU′i, 1≤i≤n, where U′i is the minimum utilization factor of all extreme task sets of the reduced array T→=[T1,T2,…,Ti].
Example 12. In this example, we will show the performance of the Algorithm 3 condition. From the task set described in Table 1, we have T→=[3,8,12,16,48]. The reduced task set is T→reduced=[3,8]. Transforming the reduced task set into a further reduced task sets by using the Algorithm 3 and calculating its utilization using Theorem 12, we obtain the minimum utilization factor of the extreme task set as U=0.8333, which means that the task set comprised of tasks τ1, τ2, τ3, and τ4 is identified as schedulable. However, if task τ5 is included, the task set is not schedulable because U′5>U.
4.11CRMB schedulability conditionLu et al. introduced the Conditional RM Bound (CRMB) schedulability condition in [18]. This condition extends the results provided by Lauzac et al. in [19] by using the relative period values in the task set.
Lauzac et al. showed in [19] that the schedulability bound used by the R-Bound condition is ln r+2/r – 1 when the number of tasks approaches to infinity. If z1 is the smallest period ratio in the task set and is defined as z1=T1/Tn=1/r, the schedulability bound can be rewritten as 2 z1 – ln z1- 1.
Using the same worst-case scenario identified by Liu and Layland [10], where Ti<2T1, and defining z2 as the largest period ratio in the task set (that is, z2=Tn – 1/Tn), Lu et al.[18] improved the schedulability bound provided by Lauzac et al. to 2 z1+1/z2+(ln z2 – ln z1) – 2.
In order to derive a schedulability bound for the case when some period values are less than or equal to Tn/2, Lu et al. defined the virtual period of a task [18].
Definition 3(Virtual Period). A virtual period of τi, denoted by vi, is the ready time of the critical job of τi. That is, vi=TnTi Ti where a critical job is defined as
Definition 4(Critical Jobs). The critical jobs are defined specifically at time Tn, the largest period in a task set. At Tn, the current jobs of all tasks, excluding J1,n, are called the critical jobs of the system. Note that every task except τn has a critical job, and that the critical jobs are identified at time Tn.
The smallest and the largest values among all virtual periods, z1 and z2, respectively, must be redefined in order to be used for the general case. These values are defined as follows:
The values of z1 and z2 are then used to derive the schedulability bound for the general case. The CRMB schedulability condition is formally defined in Theorem 14 [18].
Theorem 14. (CRMB condition) Let τbe a task set with n periodic tasks. Suppose z1=min1≤i≺n-1viTnandz2=min1≤i≤n-1viTn. Then τ is RM schedulable if U≤CB(z1,z2)=2 z1+1/z2+(ln z2- ln z1) − 2.
The CRMB schedulability condition achieves a higher schedulability bound if the difference between z1 and z2 is small. For instance, when the period values belong to a single harmonic chain, z1=z2=1, the CRMB bound is 1. In [18], Lu et al. introduced a system design methodology to explore and adjust task periods using the CRMB schedulability condition, in order to achieve a higher utilization bound.
Example 13. In this example, we will show the performance of the CRMB schedulability condition using the task set of Table 1. First, we need to obtain the virtual period values of the task set described in Table 1. In this case, all tasks have virtual periods equal to their real periods. Next, we find the z1 and z2 values, where z1=1 and z2=1. Using Theorem 14, we obtain that CB(z1,z2)=1. Therefore, the task set τ described in Table 1 can be feasibly scheduled under RM according to the CRMB schedulability condition, because U=0.9375≤CB(z1, z2)=1.
Using z1 and z2 values, Lu et al. derived, in [26], an exact test for RM on one processor. The complexity of the CRMB schedulability condition is O(n).
4.12LP schedulability conditionsLee et al.[1] introduced two linear programming formulations for calculating the utilization bounds for a given set of period options (T1, T2, …, Tk), where k is the number of period options (1≤k≤n) in the set, the periods of the tasks are (T1, T2, …, Tn), and Ti<Tj for all i<j.
These schedulability conditions have a high computational complexity, and therefore, are not practical in online admission control. However, according to Lee et al.[1], these schedulability conditions are suitable for use in many practical real-time applications, in which the finite set of frequencies (periods) corresponds to the predetermined QoS options that the applications can choose, as in the audio and control applications. Thus, the utilization bound can be calculated off-line using the finite set of periods, and then a QoS manager can use this bound online to determine the schedulability of the dynamically arriving task.
The first of the schedulability conditions, introduced in [2], is called exact linear programming formulation (LpExact condition). The second one, called approximated linear programming formulation (LpApprox), proposes a simpler formulation and is almost as accurate as the exact linear programming formulation. The experimental evaluation conducted in [1] showed that the LpExact condition outperforms the LpApprox condition. The complexity of the LP schedulability conditions is exponential [32].
4.12.1Exact linear programming formulation (LpExact)In order to calculate the tight bound U*bound, the tight level-i bounds Ui*bound (1≤i≤k) need to be calculated first. U*bound provides the system-level bound, whereas the level-i bound Ui*bound provides the schedulability bound of only the level-i task τi that uses the period Ti. Ui*bound is called tight level-i bound, that is formally defined in Theorem 15 [1].
Theorem 15. The minimum utilization U*=∑j=1iCjTj among those of all level-i barely schedulable task sets is the tight level-i bound Ui*bound.
To calculate the level-i bound, all possible combinations of the execution times that make the task set barely schedulable are considered. A task set is barely schedulable if it is schedulable with the given execution time values, but a slight increment in any of its execution times makes the task set unschedulable. If a task set is level-i barely schedulable, the level-i task τi is schedulable, and the processor is fully utilized by the level-i and the higher priority tasks during the interval [0, Ti]. It is possible to formulate a linear programming problem using a finite number of constraints. These constraints check the processor time demand only at the arrival times of the task instances (since the demand of the processor time changes only at those times) to determine the execution time values that make the level-i task set barely schedulable and to obtain its schedulability bound. The optimization problem to calculate the level-i bound Ui*bound is formulated in Theorem 16 [1].
Theorem 16. The tight level-i boundUi*bound is the solution for the following linear programming problem, where Tj, 1≤j≤i are fixed coefficients and Cj, 1≤j≤i are free variables,
Subject to
Where ta, 1≤a≤M are the series of all the arrival instants of the higher priority tasks in [0,Ti].
Theorem 16 assures only the schedulability of the level-i task τi. The tight system-level bound U*bound is given by the minimum of the level-i bounds, as stated in Theorem 17 [1].
Theorem 17 (LpExact condition). The minimum of the tight level-i (1≤i≤k) bounds, that is, mini=1kUi*bound, is the tight (largest sufficient) system-level U*bound.
Example 14. In this example, we will show the performance of the LpExact schedulability condition using the task set of Table 1. To use these conditions, we first sort the tasks by a nondecreasing order of their period values. To illustrate the LpExact condition, Figure 6 shows the linear programming problem formulation for U3*bound. Using Theorem 16 we obtain all level-i bounds, that is, U1*bound=1, U2*bound=0.9167, U3*bound=0.875, U4*bound=0.875, and U5*bound=1. According to Theorem 17, the system-level bound U*bound is equal to 0.875. Because the total utilization of τis greater than U*bound, the LpExact condition fails to identify the task set τ as schedulable under RM.
4.12.2Approximate Linear Programming Formulation (LpApprox)The main drawback of the exact linear programming formulation is its complexity. With a large number of period options, there can be a very large number of arrival instants resulting in a huge number of constraints.
In the LpExact condition, most of the constraints are used to check the processor time demand at all arrival instants to avoid the potential idle times. However, the idle times tend to occur late in the interval [0,Ti] when the processor is heavily loaded. This means that checking only at the last arrival of each task before t=Ti can avoid most of the potential idle times. The LpApprox condition just checks those last arrival times, resulting in a simpler linear programming formulation. This approximated formulation has only one constraint at each level and thus, the total number of constraints used to calculate the level-i bound Uibound is i, as can be observed in Theorem 18 [1].
Theorem 18. The solution for the following linear programming problem, Uibound, is a sufficient level-i bound.
Subject to
WhereTiTaTa,1≤a≤i-1, 1≤a≤i –1 is the last arrival instant of task τabefore Ti.
As in the tight system-level, a sufficient system-level bound can be found by taking the minimum of the level-i bounds, as expressed in Theorem 19 [1].
Theorem 19(LpApprox condition). The minimum of the sufficient level-i (1≤i≤k) bounds, that is, mini=ikUibound, is the sufficient system-level Ubound.
Example 15. In this example, we will show the performance of the LpApprox schedulability condition using the task set shown in Table 1. Figure 6 shows the linear programming problem formulation for U3bound. However, unlike the exact formulation that uses all the constraints shown in Figure 6, the LpApprox condition only uses the constraints 1, 4, and 5. Using Theorem 16, we obtain all level-i bounds, that is, U1bound=1, U2bound=0.9167, U3bound=0.875, U4bound=0.875, and U5bound=1. According to Theorem 18, the system-level bound Ubound is equal to 0.875. because the total utilization of τis greater than Ubound, the LpApprox condition fails to identify the task set τas schedulable under RM.
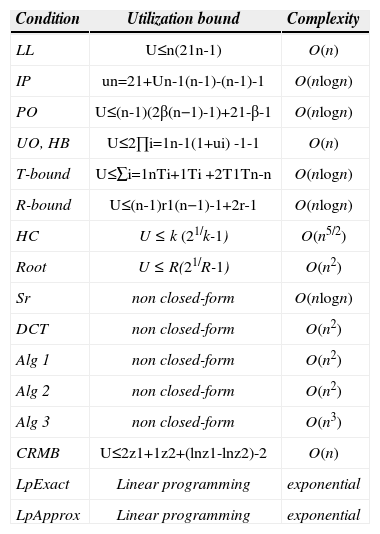
4.13Characteristics of the schedulability conditionsA summary of the inexact schedulability conditions for RM on one processor, discussed in this section, is shown in Table 7. It can be noted that the LP and Algorithm 3 schedulability conditions have the highest complexity, whereas the LL, UO, and CRMB schedulability conditions have the lowest complexity.
Comparison of the RM inexact schedulability conditions.
| Condition | Utilization bound | Complexity |
|---|---|---|
| LL | U≤n(21n-1) | O(n) |
| IP | un=21+Un-1(n-1)-(n-1)-1 | O(nlogn) |
| PO | U≤(n-1)(2β(n−1)-1)+21-β-1 | O(nlogn) |
| UO, HB | U≤2∏i=1n-1(1+ui) -1-1 | O(n) |
| T-bound | U≤∑i=1nTi+1Ti +2T1Tn-n | O(nlogn) |
| R-bound | U≤(n-1)r1(n−1)-1+2r-1 | O(nlogn) |
| HC | U≤k (21/k-1) | O(n5/2) |
| Root | U≤R(21/R-1) | O(n2) |
| Sr | non closed-form | O(nlogn) |
| DCT | non closed-form | O(n2) |
| Alg 1 | non closed-form | O(n2) |
| Alg 2 | non closed-form | O(n2) |
| Alg 3 | non closed-form | O(n3) |
| CRMB | U≤2z1+1z2+(lnz1-lnz2)-2 | O(n) |
| LpExact | Linear programming | exponential |
| LpApprox | Linear programming | exponential |
To evaluate the performance of the inexact schedulability conditions discussed in this paper, we tested every condition using a sample s of task sets that are schedulable under rate monotonic. We define the acceptance ratio ρ of a schedulability condition SC for a sample s, as the ratio of the number of tasks identified as schedulable by the schedulability condition and the total number of task sets:
Because all task sets in s are schedulable under RM, an exact condition will have an acceptance ratio equal to 100. If ρs(SC) approaches 100, then the performance of SC approaches the performance of the exact test for s.
With the purpose of evaluating the performance of the schedulability conditions under different characteristics of the task sets, we conducted our experiments using four different schemes of generation of the task sets in s.
The solution of the linear programming problems formulated by the LpExact condition was obtained using the lp_solve package [33].
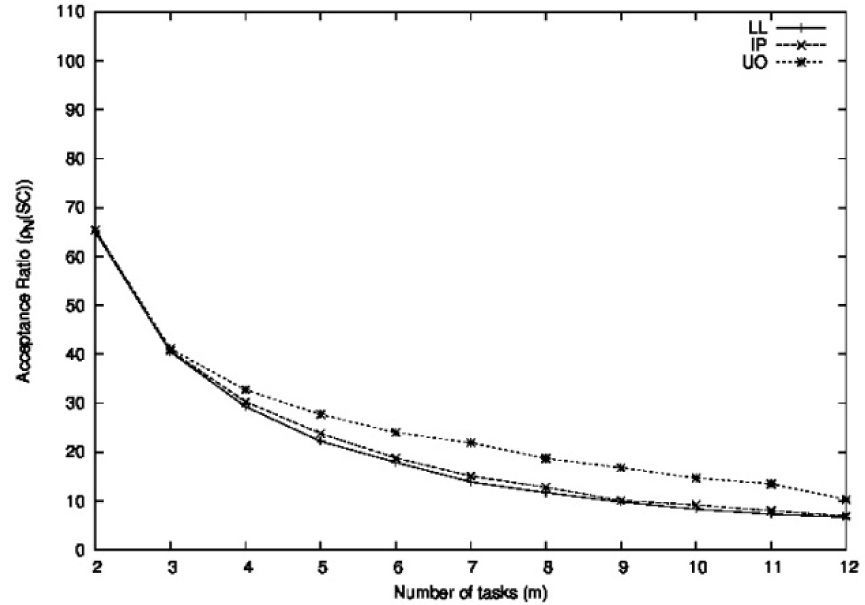
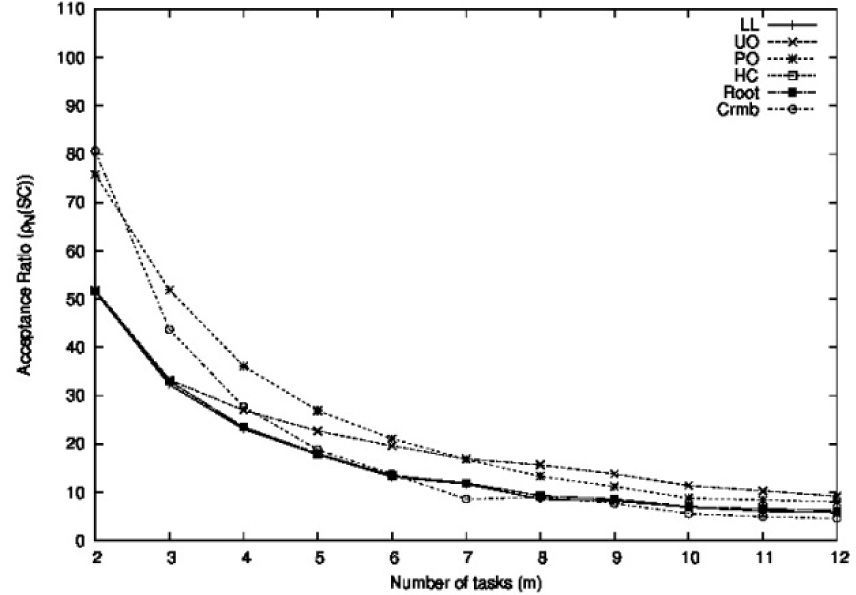
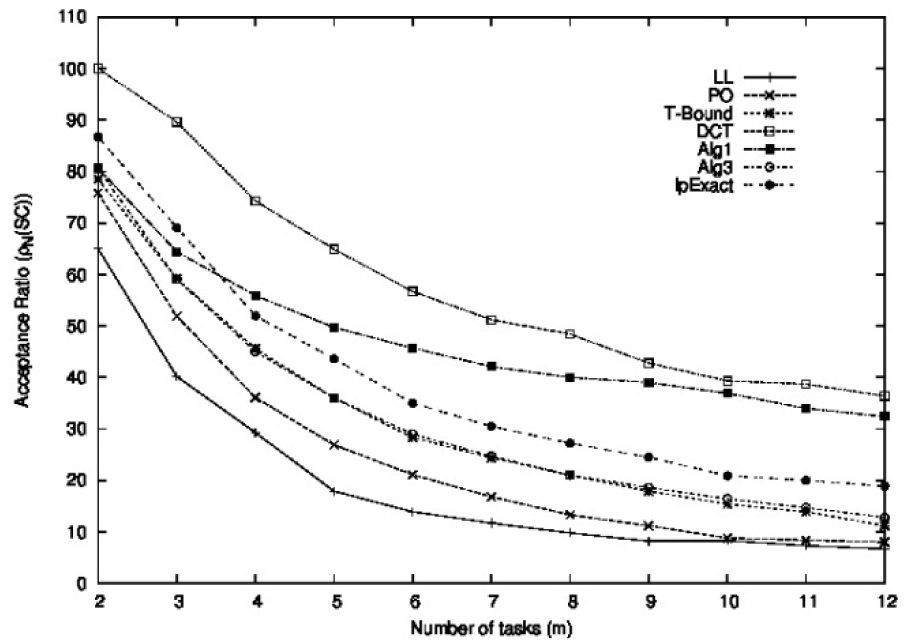
5.1Performance as a function of the number of tasksThe goal of this experiment was to evaluate the performance of the schedulability conditions as a function of the number of tasks. We generated eleven samples of task sets denoted as N2, N3, …, N12. Each sample Nm was conformed by 1,000 sets of m tasks. The total utilization of each task set and the periods of the tasks were uniformly distributed in the range [0.7, 0.95] and [100, 500], respectively. The maximum utilization of each task, denoted by α, followed a uniform distribution in the range [0.01, 0.3]. The execution times of the tasks were generated with values 1≤Ci≤αTi. Figures 7, 8, and 9 show the acceptance ratios obtained as a function of the number of tasks for these conditions in their respective groups.
Figure 7 shows the acceptance ratios obtained for he closed-form non-period-aware schedulability conditions. For these conditions, the performance decreases rapidly as the number of tasks increases. For each number of tasks, the acceptance ratios always satisfy the relation ρN(UO)>ρN(IP)>ρN(LL). This result is a consequence of the amount of timing information of he tasks used by each of the schedulability conditions. It is important to note that the improvement achieved by these conditions with respect to the LL condition is marginal (that is, maller than 8%).
Figure 8 shows the acceptance ratios obtained for the closed-form period-aware schedulability conditions where we also included the UO and LL conditions.
From this experiment, it can be observed that the PO and the CRMB are the conditions with better performance for small number of tasks (m<4). However, for m>4, only the PO and the UO conditions showed some performance improvement over the LL condition (less than 4%). These poor results can be explained by the fact that this experiment was designed without considering any relationship among the periods of the tasks, and since these conditions include the period in their analysis, it is clear that they cannot take advantage of this extra information.
Figure 9 shows the acceptance ratios obtained for the non-closed-form period-aware schedulability conditions, where we also included the PO condition and the LL condition. Due to the differences in the approaches used to derive their schedulability bounds and their resulting behaviors, these schedulability conditions can be differentiated as follows
- •
Schedulability condition based on linear programming. TheLpExact schedulability condition has the second best acceptance ratio for very small task sets (form<4, only lower than that of theDCT condition). For the larger task sets(that is, m≥4), its performance decreases faster than the performance of theDCT and the Algorithm 1 conditions, showing the third best acceptance ratio among all non-closed-form period-aware conditions. However, it is important to recall that the computational complexity of this condition is exponential.
- •
Schedulability conditions based on the transformation of the original task set (T-Bound, Algorithm 1, Algorithm 3 andDCT). It can be noted from Figure 9 that for every number of tasks, the acceptance ratio of these schedulability conditions was substantially better than the acceptance ratio of the closed-form schedulability conditions. TheDCT condition showed the best performance among all non-closed-form period-aware conditions form<6, with a clear improvement over the performance of the Algorithm 1 condition. However, for large number of tasks, their performance tended to be similar. On the other hand, the performance of the Algorithm 1 was always better than that of the Algorithm 3 and theT-Bound conditions. The Algorithm3 and the T-Bound conditions always obtained very similar performances, at least 6% better than theLL condition for large number of tasks.
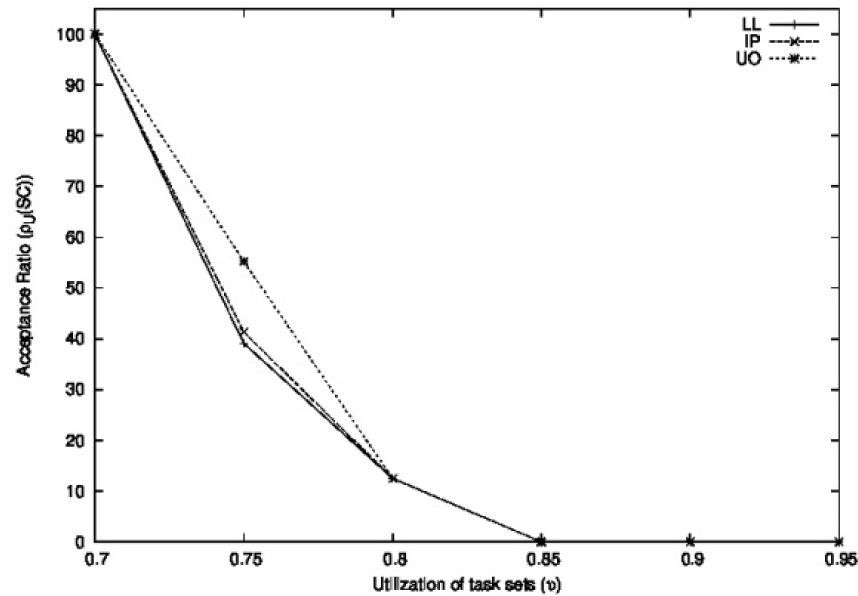
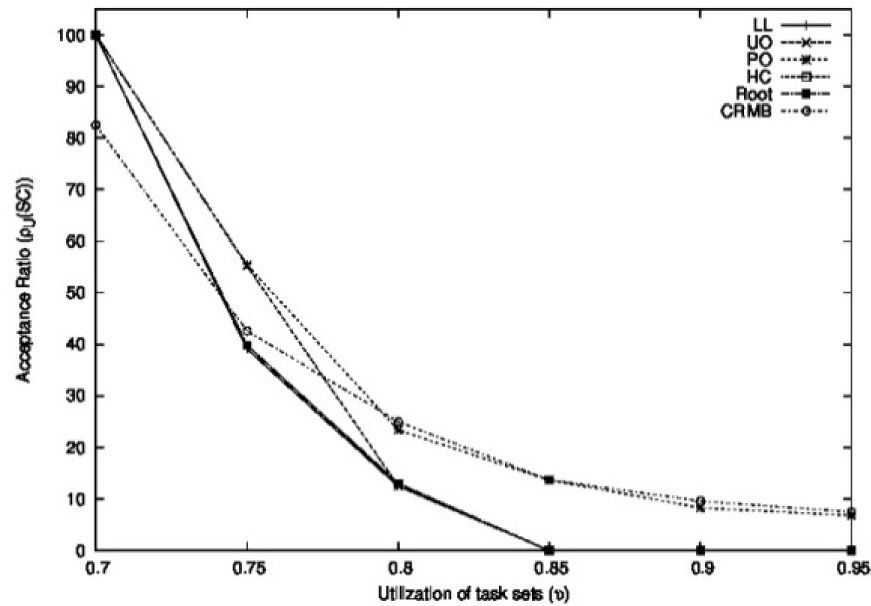
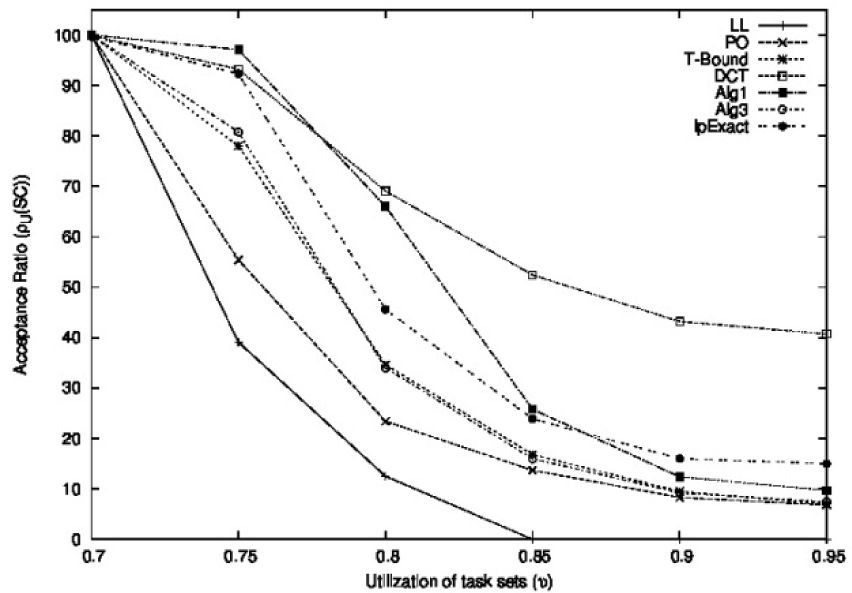
The goal of this experiment was to evaluate the performance of the schedulability conditions as a function of the total utilization of the task sets. We generated several samples of task sets denoted as Uυ, where the total utilization υ of each sample was set to 0.7, 0.75, 0.8, 0.85, 0.9, and 0.95. The maximum utilization of each task, denoted by α, followed a uniform distribution in the range [0.01, 0.3]. Each sample Uυ was conformed by 1,000 task sets. The periods of the tasks were uniformly distributed in the range [100, 500] and the execution times of the tasks were generated with values 1≤Ci≤α Ti. The number of tasks was uniformly distributed in the range [2,9]. Figuress 10, 11, and 12 show the acceptance ratios obtained as a function of the utilization of the task sets for the schedulability conditions.
Figure 10 shows the acceptance ratios obtained for the closed-form non-period-aware schedulability conditions. We can observe that the acceptance ratios of these conditions satisfy the relation ρU(UO)>ρU(IP)>ρU(LL). The performance of theUO is clearly better than the IP and the LL conditions in the range 0.7<υ<0.8.
Figure 11 shows the acceptance ratios obtained for the closed-form period-aware schedulability conditions, where we also included the UO and the LL conditions. We can observe from Figure 11 that the PO condition showed the best performance among the closed-form period-aware conditions for υ<0.8, improving upon the LL condition for all values of υ. For υ≥0.75, the CRMB condition showed an acceptance ratio similar or better than the PO condition. However, the acceptance ratio of the CRMB condition was poorer than that of the LL condition for υ=0.7. The HC and the Root conditions showed similar acceptance ratios as that of the LL condition for all the values of υ.
Figure 12 shows the acceptance ratios obtained for the non-closed-form period-aware schedulability conditions, where we also included the PO and the LL conditions. We can observe from Figure 12 that all non-closed-form conditions showed a significant performance improvement with respect to the closed-form conditions, and that the DCT condition yielded the best acceptance ratio among all the non-closed-form period-aware conditions. When compared with the other conditions, the DCT condition showed an increasingly better performance when the utilization of the task sets increased.
The Algorithm 1 and the LpExact conditions also showed a good performance, even improving on the DCT condition for υ≤0.75. However, their performance decreased rapidly as the utilization of the task sets increased.
The Algorithm 3 and the T-Bound conditions showed the worst performance among all the non-closed-form conditions, with results close to the PO condition for υ≥0.85.
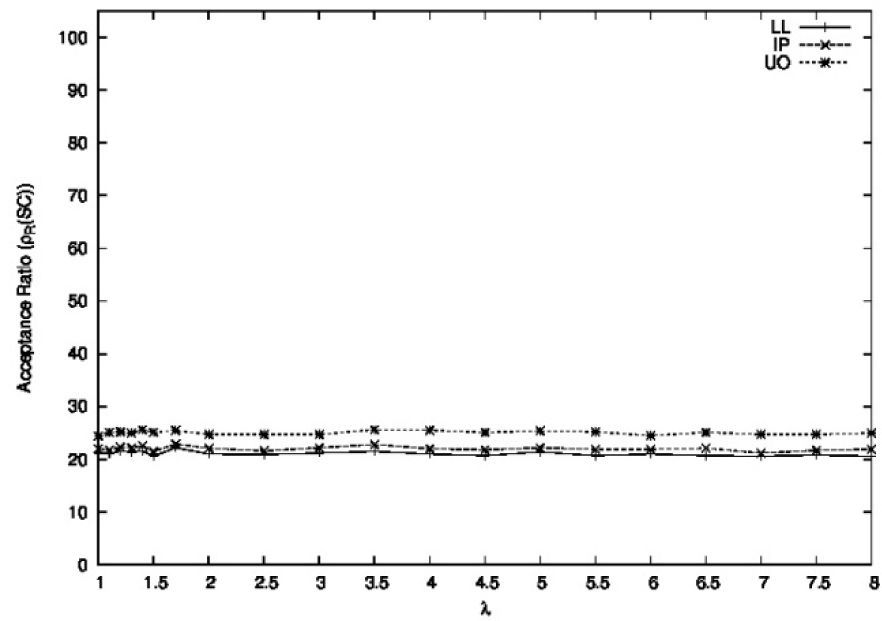
5.3Performance as a function of the period ratioThe goal of this experiment was to evaluate the performance of the schedulability conditions as a function of the period ratio. We define the period ratio as the ratio of the maximum and minimum period values in a task set. We generated several samples Rλ, where λ is a constant with values in the range [1, 8] used to derive the periods of the tasks. For each task set, we randomly generated an initial period value T1 in the range [100, 300]. After T1 was generated, the periods of the remaining tasks were generated in the range T1≤Ti≤λT1. The total utilization of every sample and the maximum utilization α of each task followed a uniform distribution in the range [0.7, 0.95] and [0.01, 0.3], respectively. The execution times of the tasks were generated with values in the range 1≤Ci≤αTi. The number of tasks was uniformly distributed in the range [2,9]. Every sample Rλ was composed of 1,000 task sets. Figures 13, 14, and 15, show the performance as a function of the period ratio for the schedulability conditions.
Figure 13 shows the acceptance ratios obtained for the closed-form non-period-aware schedulability conditions. It can be noted that for all the values of λ, the acceptance ratios satisfy the relation ρR(UO)>ρR(IP)>ρR(LL). The UO condition showed the best acceptance ratio among these conditions, with a small performance improvement with respect to the IP and the LL conditions, whereas these two conditions (IP and LL) yielded similar acceptance ratios. It is important to note that all closed-form non-period-aware conditions showed a constant acceptance ratio for all the values of λ.
Figure 14 shows the acceptance ratios obtained for the closed-form period-aware schedulability conditions, where we also included the UO and the LL conditions. We can observe that all the closed-form period-aware schedulability conditions yielded an acceptance ratio of 100 for λ=1. In addition, all of them decreased their performance sharply for the interval 1<λ<2, and for λ>2, their performance was constant with the small variations.
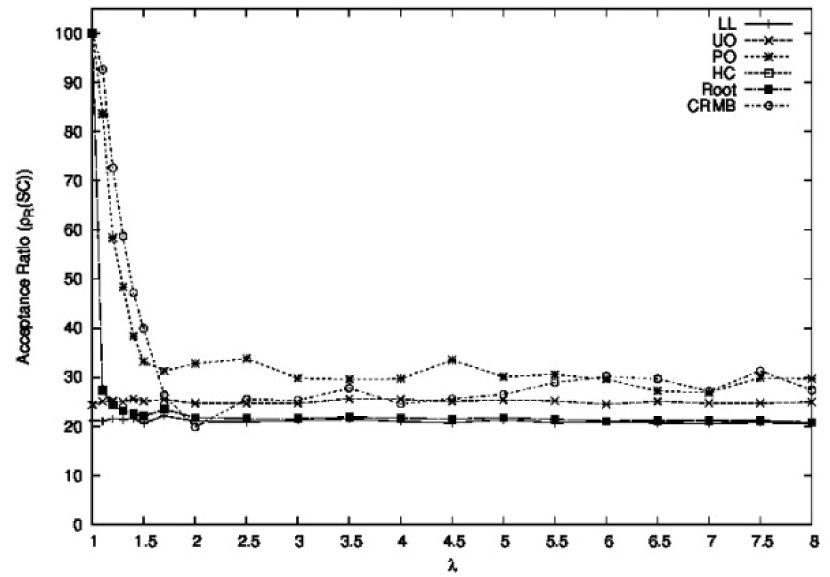
The PO condition was the best or second best of all the closed-form period-aware conditions for all values of λ. The CRMB condition showed the best performance among all the closed-form period-aware conditions for λ≤1.5. However, its performance was the worst of all the closed-form period-aware conditions for λ=2, but improved for λ>2, being among the best conditions for λ≥4.5. Finally, the root and the HC conditions showed a performance similar to that of the LL condition for all values of λ.
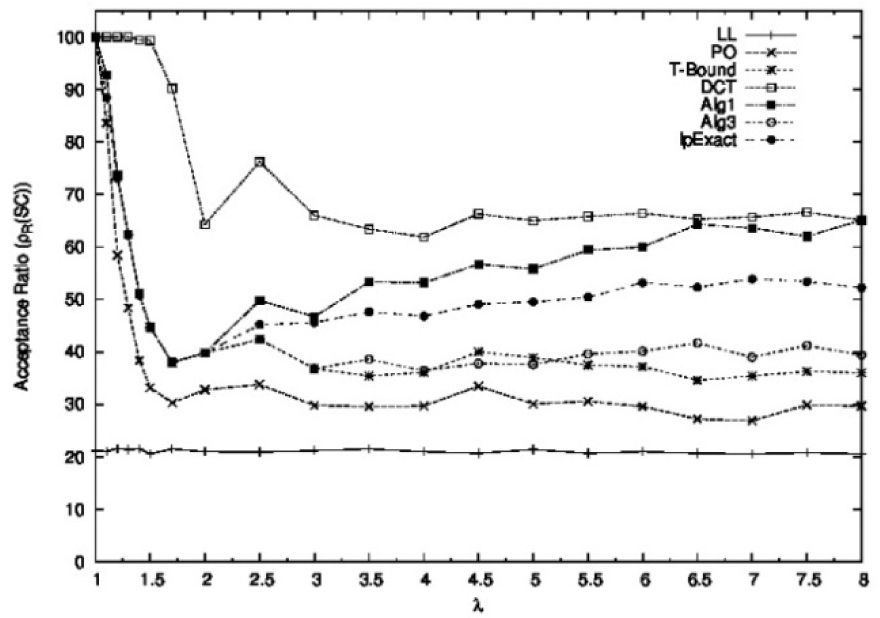
Figure 15 shows the acceptance ratios obtained for the non-closed-form schedulability conditions, where we also included the PO and LL conditions. From Figure 15, we can observe that all non-closed-form conditions clearly outperformed the remaining conditions.
The DCT condition showed the best acceptance ratio among the non-closed-form schedulability conditions for all the values of λ. It should be noted that for λ<1.5, the acceptance ratio of the DCT condition is almost equal to 100. On the other hand, forλ>2, its acceptance ratio is almost constant.
The Algorithm 1, the Algorithm 3, and the T-Bound conditions showed a fairly good performance for small λ values (λ≤1.2). These three conditions showed identical acceptance ratios for λ<2. This can be explained by the fact that they transform the original task set into another task set where all period values satisfy the relation Tmax/Tmin<2. However, for λ>2, ρR(Algorithm 1)>ρR(Algorithm 3)≥ρR(T-Bound), and for λ>1.5, the Algorithm 1 condition showed the second best acceptance ratio among all the conditions.
The LpExact condition showed a good performance for the small values of λ (λ≤1.2), whereas for λ>1.5, its acceptance ratio was the third best among all the schedulability conditions.
It is important to note that the acceptance ratios of all the conditions remain stable for λ>2.
5.4Performance as a function of tasks in the harmonic chainThe objective of this experiment was to evaluate the performance of the schedulability conditions as a function of the percentage of tasks that are part of a harmonic chain. We generated nine samples of task sets HCk conformed by 1,000 task sets, where k is a value in the range [20, 100] that denotes the percentage of tasks that are part of the harmonic chain. Only one harmonic chain in every task set was generated. The utilization of every sample and the maximum utilization α of each task was uniformly distributed in the range [0.7, 0.95] and [0.01, 0.30], respectively. The execution times of the tasks were generated with values 1≤Ci≤αTi. The number of tasks was uniformly distributed in the range [5, 9].
The period values of the tasks were generated as follows. The initial period T1 was obtained using a uniform distribution in the range [20, 100]. Once T1 was derived, the period of each task was generated using Ti=Ti–1*f, where f was randomly generated in the range [2, 3], until the defined percentage of tasks in the harmonic chain was reached. If this percentage was k<100%, the remaining period values were generated such that they did not belong to the harmonic chain. Figures 16, 17, and 18 show the obtained acceptance ratios as a function of the percentage of tasks that are part of a harmonic chain.
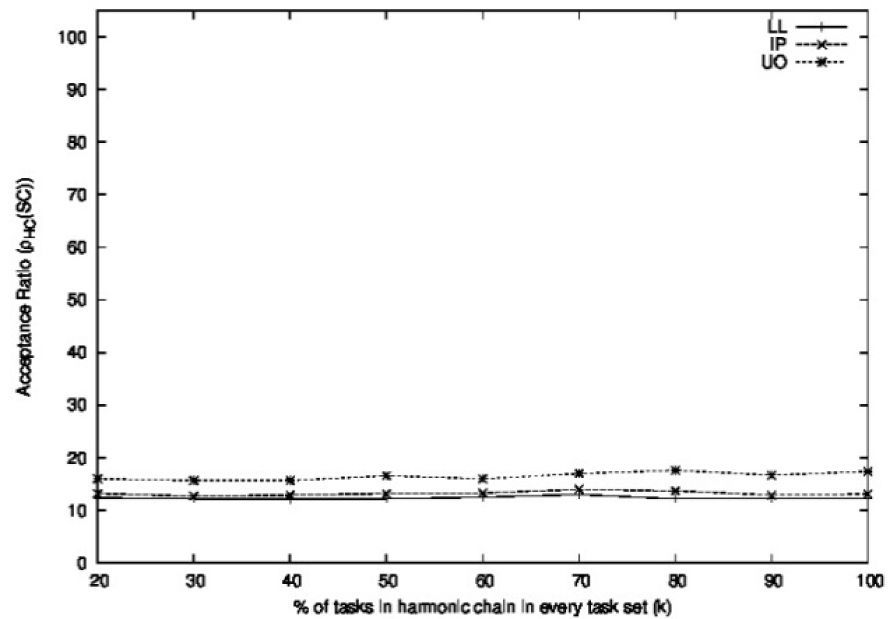
Figure 16 shows the acceptance ratios obtained for the closed-form non-period-aware schedulability conditions. We can observe that their acceptance ratios satisfy the relation ρHC(UO)>ρHC(IP)>ρHC(LL) for every value of k. The UO condition is slightly better than the IP and the LL conditions, whereas the acceptance ratio of the IP and the LL conditions are very close to each other. From these results, it is clear that none of these conditions benefit from including tasks that are part of a harmonic chain.
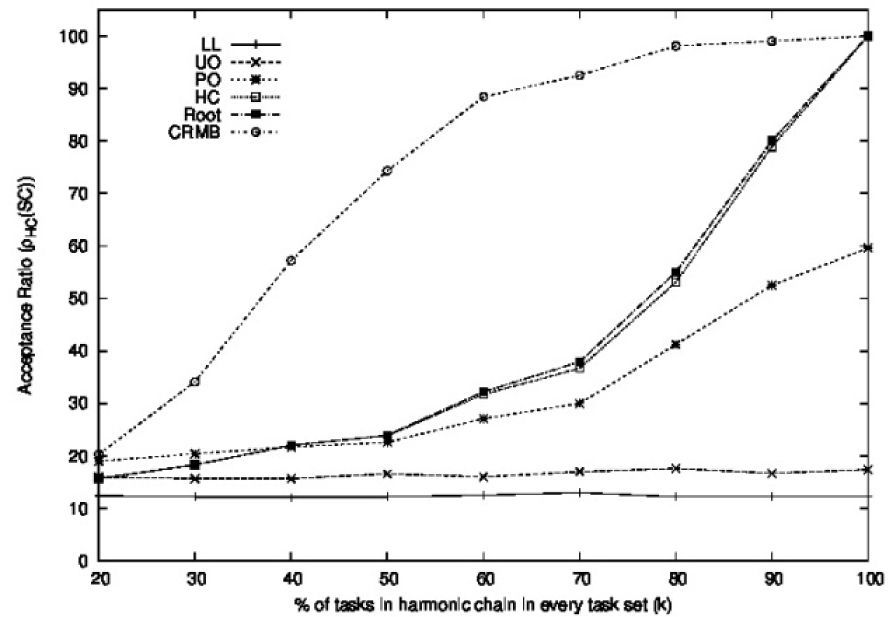
Figure 17 shows the acceptance ratios obtained for the closed-form period-aware schedulability conditions, where we also included the UO and the LL conditions. We can observe that in most cases, their acceptance ratios satisfy the relation ρHC(CRMB)>ρHC(PO)>ρHC(Root)>ρHC(HC). It can be observed that the CRMB condition had an acceptance ratio significantly better than that of the remaining closed-form period-aware conditions, showing an excellent performance for k≥60. As discussed previously, the acceptance ratio of the CRMB condition was equal to 100 when all the tasks were in a harmonic chain. The HC and the root conditions showed a very similar performance, only lower than that of the CRMB condition. The PO condition showed a performance similar to the HC and the root conditions for values of k≤50, but much lower than the HC and the root conditions for higher values of k.
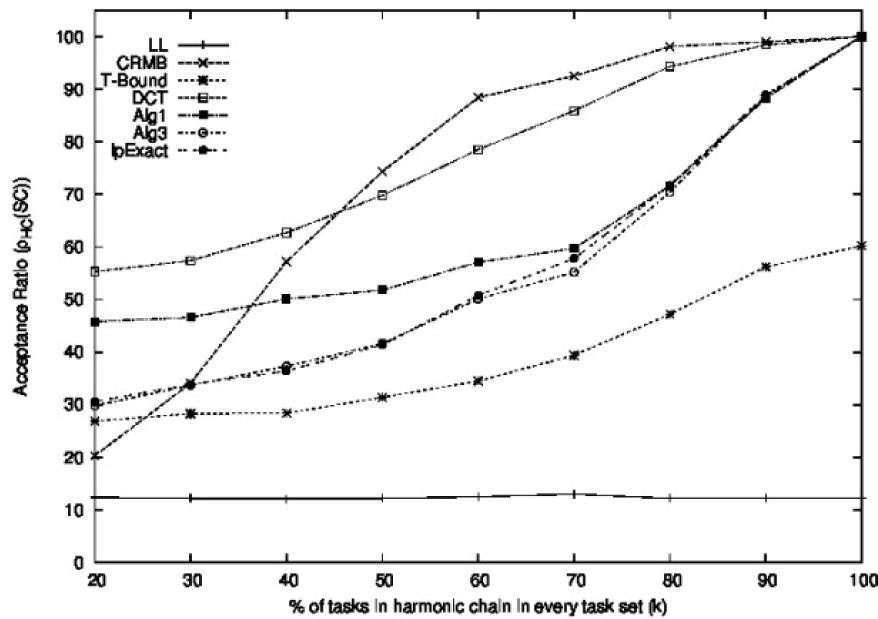
Figure 18 shows the acceptance ratios obtained for the non-closed-form period-aware schedulability conditions, where we also included the CRMB and the LL conditions. We can observe that the DCT condition showed the best performance among the non-closed-form period-aware conditions. Nevertheless, its performance was not as good as the performance of CRMB condition for k≥50.
The Algorithm 1, the Algorithm 3, and the LpExact conditions showed a similar performance for k≥60. However, the Algorithm 3 and the LpExact conditions showed a lower acceptance ratio for values of k smaller than 60. The T-Bound condition showed the worst performance among these schedulability conditions. It is interesting to poin out that the DCT, Algorithm 1, Algorithm 3, LpExact, and CRMB conditions yielded an acceptance ratio equal or close to 100 for k=100.
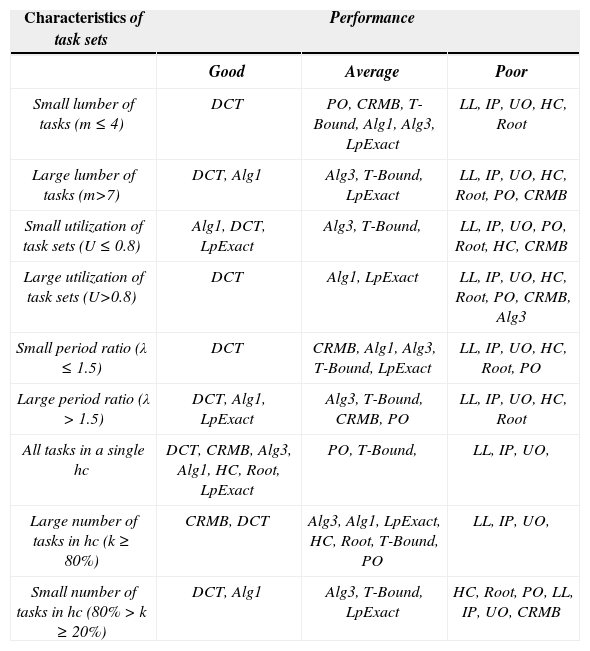
5.5Comparison of performances of the schedulability conditionsA comparison of the relative performance of the inexact schedulability conditions for RM on one processor is shown in Table 8. The aim of this comparison is to summarize the results of the experiments conducted in this section. Designers of real-time applications can use the comparison shown in Table 8 to determine which schedulability condition may be used in certain situations, taking into account the characteristics of the task set.
Relative performance of the RM inexact schedulability conditions.
| Characteristics of task sets | Performance | ||
|---|---|---|---|
| Good | Average | Poor | |
| Small lumber of tasks (m≤4) | DCT | PO, CRMB, T-Bound, Alg1, Alg3, LpExact | LL, IP, UO, HC, Root |
| Large lumber of tasks (m>7) | DCT, Alg1 | Alg3, T-Bound, LpExact | LL, IP, UO, HC, Root, PO, CRMB |
| Small utilization of task sets (U≤0.8) | Alg1, DCT, LpExact | Alg3, T-Bound, | LL, IP, UO, PO, Root, HC, CRMB |
| Large utilization of task sets (U>0.8) | DCT | Alg1, LpExact | LL, IP, UO, HC, Root, PO, CRMB, Alg3 |
| Small period ratio (λ≤1.5) | DCT | CRMB, Alg1, Alg3, T-Bound, LpExact | LL, IP, UO, HC, Root, PO |
| Large period ratio (λ>1.5) | DCT, Alg1, LpExact | Alg3, T-Bound, CRMB, PO | LL, IP, UO, HC, Root |
| All tasks in a single hc | DCT, CRMB, Alg3, Alg1, HC, Root, LpExact | PO, T-Bound, | LL, IP, UO, |
| Large number of tasks in hc (k≥80%) | CRMB, DCT | Alg3, Alg1, LpExact, HC, Root, T-Bound, PO | LL, IP, UO, |
| Small number of tasks in hc (80%>k≥20%) | DCT, Alg1 | Alg3, T-Bound, LpExact | HC, Root, PO, LL, IP, UO, CRMB |
It can be noted that the non-closed-form period-aware conditions yield better performance than the closed-form conditions.
6Conclusions and future workMany real-time applications demand efficient and low-cost schedulability tests for online admission control. In this paper, we surveyed the best-known exact and inexact schedulability conditions for rate monotonic executing on one processor. Extensive simulation experiments were conducted to evaluate the performance and computational complexity of the inexact schedulability tests. In our simulation experiments, the schedulability tests were evaluated for different number of tasks, utilization factors, and different period ratios. Additional experiments were conducted considering task sets with harmonics chains.
The comparative analysis done in this paper showed that for all the experiments conducted, the schedulability conditions using the non-closed-forms schedulability tests derive a better performance than those that use the closed-forms schedulability tests.
Among all the non-closed-form schedulability conditions, we observed that, in general, the DCT condition showed the best performance. This performance can be explained by the fact that the DCT condition transforms the period set into another period set where all the tasks belong to a single harmonic chain.
We believe that the decision of choosing one schedulability test over another for a particular real-time application should not depend only on its performance; it should also be take into consideration the characteristics of the tasks and their computational complexity.
As part of our future research, we plan to extend this study to include schedulability tests for aperiodic, resource-sharing tasks, and multiple processors.