Cognitive radios (CRs) have been recently emerging as prime candidates to enhance spectral efficiency by exploiting spectrum-aware systems which can reliably monitor licensed users’ activities. CR users monitor such activities by performing spectrum sensing to detect potential white spaces. However, this process of local sensing might be a challenging task in fading environments. The inefficiency of spectrum sensing might cause interference to licensees if they are miss-detected by CR users. Thus, cooperative spectrum sensing is proposed as a means to combat fading and improve the detection performance. However, the detection performance does not improve by such cooperation when low-SNR environment is considered. In this paper, cooperative spectrum sensing with PSO-based threshold adaptation is presented to address the aforementioned problem. Simulation results show that the detection performance with PSO-based adaptive detection threshold is improved, particularly, in low-SNR environment.
As wireless communication technology grows rapidly, the demand for spectrum is increasing consequently in order to support more wireless services. However, the limited radio resources become a great barrier to meet the increasing demand for spectrums. A survey is carried out by Federal Communication Commission (FCC) to investigate the spectrum usage efficiency in a temporal and geographical area variation [1]. This survey indicated the that current the licensed spectrum usage is often mostly under-utilized. Due to this fact, cognitive radio (CR) is proposed as one of the most promising solutions to support the increasing need for spectrum by occupying these under-utilized licensed spectrum segments.
CR is defined as a radio which is able to adapt and learn from its surrounding radio environment and adjust its network parameters to optimize the utilization of the spectrum while providing flexibility in wireless access [1]. In other words, CR is a technology which is capable of detecting and accessing the under-utilized spectrums efficiently. In order to perform this capability, four important functions are proposed for CR systems, namely, spectrum sensing, spectrum decision, spectrum sharing and spectrum mobility [2]. During CR operation, spectrum sensing will first be performed to detect all available under-utilized spectrums, also known as spectrum holes or white spaces[3]. After detecting all the white spaces, the function of spectrum decision-making will be performed to select the best white space for instantaneous transmission. The spectrum sharing function in CR provides coordination or scheduling for sharing of spectrum bands with other secondary users (SUs) and/or CR users. Lastly, the spectrum mobility function allows SU to smoothly release the spectrum band back to its owner, also known as primary user (PU), once detected and move to another available white space.
In reality, PU signals could be shadowed and faded, hence causing rapid fluctuation in signal strength, as indicated in many studies [2][4][5]. Local spectrum sensing by a single SU might not be able to determine the presence of PU signal accurately due to potential fading and shadowing effects. To tackle this issue, cooperative spectrum sensing is proposed [2][4]. The cooperative spectrum sensing techniques show promising improvement in detection performance [6][7]. However, the cooperative sensing can hardly provide improvement to the detection performance in low-SNR environment as can be observed in [7].
In this paper, performance investigations for local spectrum sensing and cooperative spectrum sensing are carried out under different radio environments, i.e., Additive White Gaussian Noise (AWGN) and Rayleigh fading channels. Energy detection-based spectrum sensing is adopted in this paper due to its implementation simplicity. Also, an OR-rule hard decision fusion scheme is used to realize cooperative sensing while maintaining low communication overhead in comparison to soft fusion schemes. Finally, a cooperative spectrum sensing with PSO-based threshold adaptation is proposed to address the drawback of inefficient performance of cooperative spectrum sensing in low-SNR scenario.
The rest of this paper is organized as follows. Section 2 provides an overview on energy detection-based spectrum sensing technique. In Section 3 cooperative spectrum sensing is explained. Section 4 presents cooperative spectrum sensing with PSO-based threshold adaptation and its performance evaluation. Finally, several concluding remarks are drawn in Section 5.
2Energy detector-based local spectrum sensingIn energy detection, the PU signal is first received and sampled. From the sampled received signals by SU, two hypotheses can be deduced as given below:
H0: PU does not exist.
H1: PU does exist
Based on the two hypotheses above, the received signal for the i-th SU can be expressed as follows [8]
where yi(t) is the signal received by i-th SU, x(t) is the PU signal, ni(t) is the AWGN noise received by i-th SU and hi is the channel gain. To determine whether H0 or H1 is true, the energy of the received signal, yi(t), is estimated from the licensed channel of interest within an observation period or sensing period, T, and then a test/decision statistic is obtained. According to [8], the decision statistic, Zi, obtained from the energy detector for the i-th SU is given as
Where yi,k=yi(k/2W) and N0 is the one-sided noise power spectral density. The decision statistic for the i-th SU, Zi, obtained from the energy detection is found to have chi-square distribution [8] and can be characterized as [9]
Where m=TW, that is the time-bandwidth product of the energy detector. For simplicity, m is assumed to be an integer value. From Equation 3, χ2m2 represents a central chi-square distribution with 2m degrees of freedom whereas χ2m2(2γi) represents a noncentral chi-square distribution with 2m degrees of freedom and a noncentrality parameter of 2γi for H1 where γi is the instantaneous SNR received at the i-th SU.
In general, the probability of false alarm and probability of detection for the i-th SU are, respectively, given as
Where λi is the detection threshold for the i-th SU. Hence, from Equations 3 and 4, the closed-form expression for probability of detection over AWGN channel can be obtained from [9] as
where Qm (a, b) refers to the generalized Marcum Q-function defined:
The probability of missed detection is simply defined as
On the other hand, using Equations 3 and 5, the probability of false alarm over AWGN channel is obtained as [9]:
Where Γ(.) and Γ(.,.) are the complete gamma function and the upper incomplete gamma function, respectively. It was noted that Equation 9 is independent of γi; the instantaneous channel SNR.
For fading channels, the probability of detection, Pd,i, for the i-th SU over fading channels can be, respectively, given as [6]
Where fγi (x) is the PDF for γi which varies with different fading models. However, the probability of false alarm will remain the same as in Equation 9 because it is independent of γi. When the PU signal experiences scattering imposed by the environment, the PU signal undergoes multipath fading. Due to this phenomenon, the faded PU signal is described by Rayleigh distribution. Therefore, γi would have an exponential distribution and thus the probability of detection over Rayleigh fading channel can be found as [9]
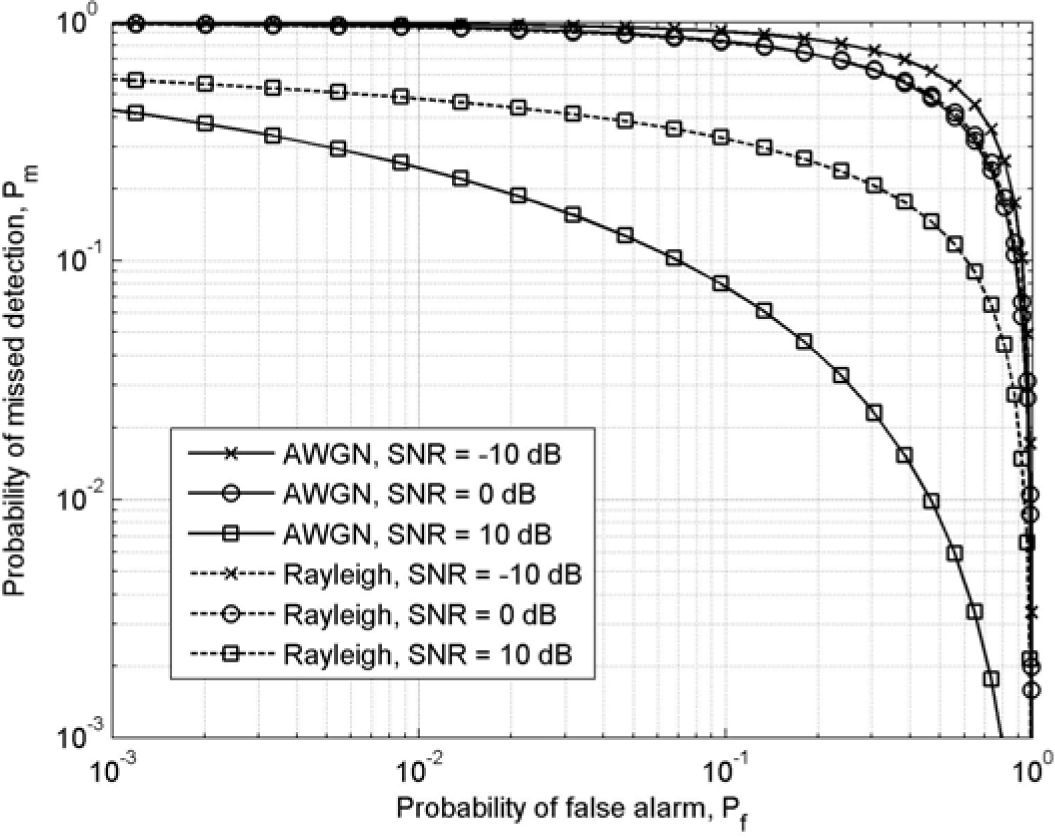
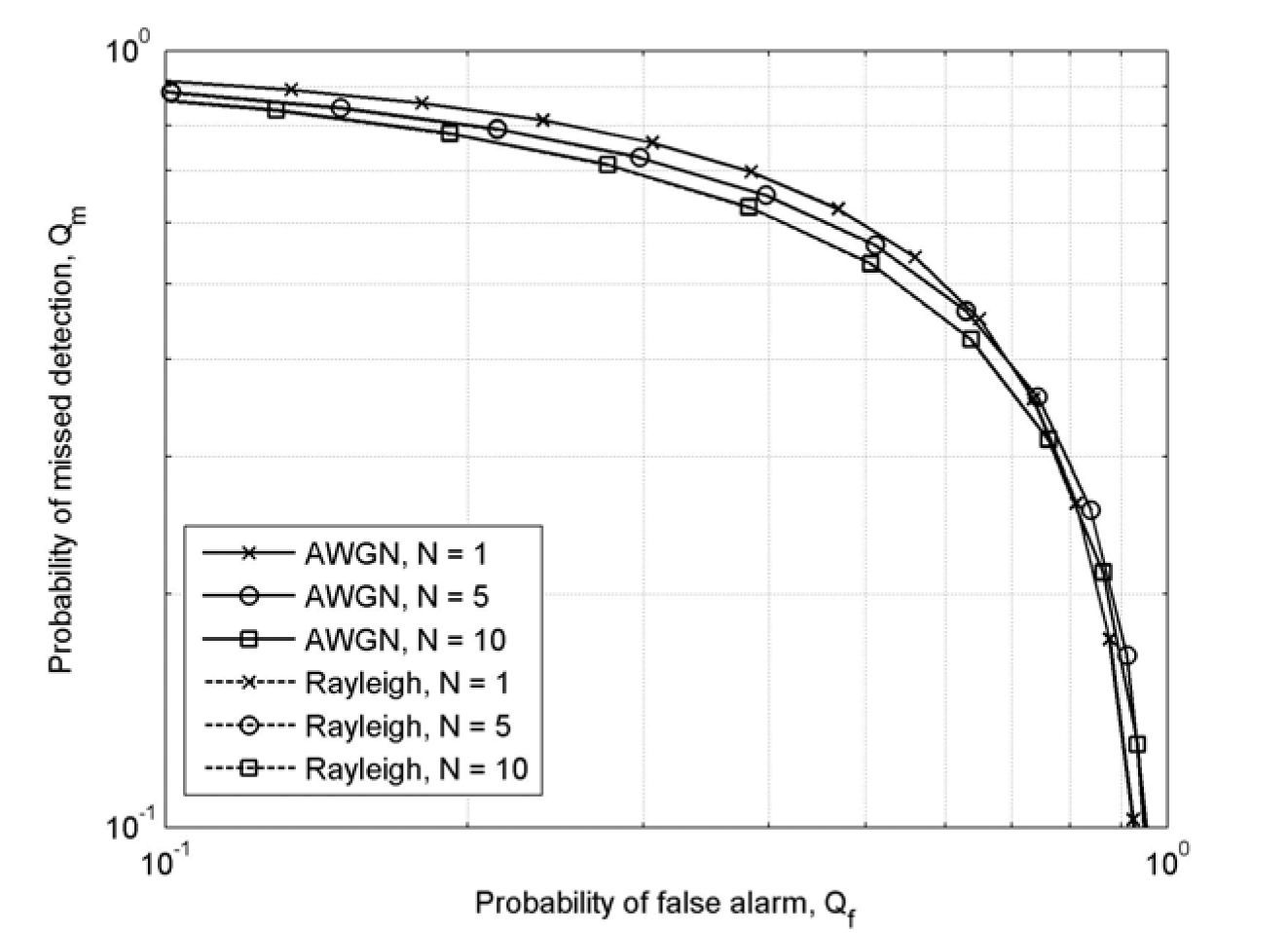
Figure 1 shows the complementary ROC curves for local spectrum sensing under AWGN and Rayleigh fading channels for different SNR values. It is observed that the probability of detection decreases diminishingly for a fixed probability of false alarm under both AWGN channel and Rayleigh fading channel when SNR decreases.
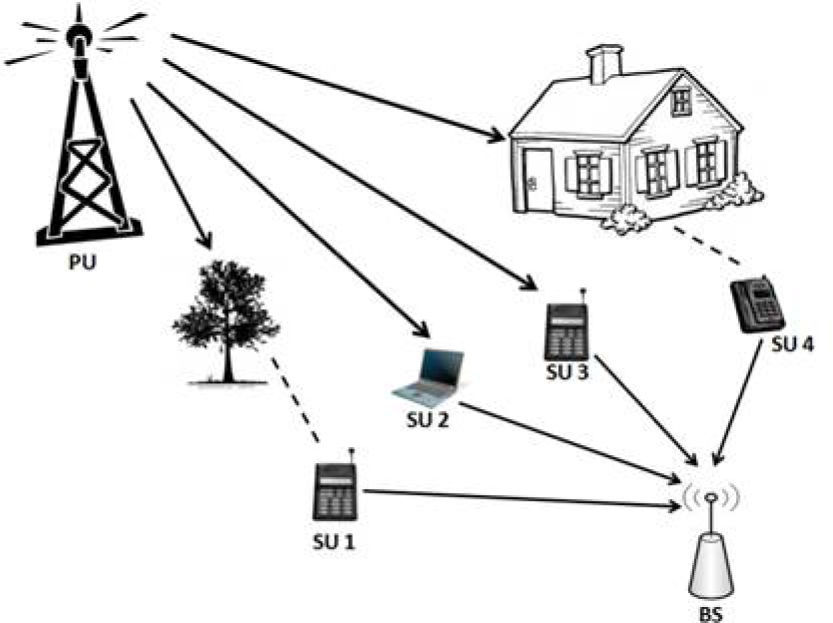
3Cooperative spectrum sensingA simple operating cognitive radio network (CRN) is illustrated in Figure 2. Each SU performs spectrum sensing to detect the presence of PU signal. When the PU signal undergoes deep fading and shadowing, the signal strength varies at different times and locations depending on the channel conditions represented by the corresponding noises and gains imposed.
Figure 2 shows different sensing scenarios by multiple SUs where some SUs may be able to reliably detect the PU signal such as SU 2 and SU 3 while others such as SU 1 and SU 4 may not able to detect it due to intermediate blocking obstacles. This observation leads to the idea of cooperative signal detection which involves collaboration among all SUs in a CRN to improve the detection performance. In cooperative spectrum sensing, each SU sends the sensing information to the SU base station and the base station makes a global final decision.
Many decision fusion schemes are proposed in the literature. One of the well-known decision fusion schemes is the so-called one-out-of-N rule or OR-rule, where N is the total number of cooperating SU. In this hard decision fusion scheme, all cooperating SUs send their local sensing decisions to a common fusion center for final decision fusion. A final decision corresponds to H0 is deduced if all N collaborating SUs indicated that the PU is absent whereas that corresponds to H1 is made if there is at least one out of N SUs reports that the PU is present. Assuming that all decisions are independent, the probability of detection, the probability of missed detection, and the probability of false alarm of cooperative spectrum sensing denoted by Qd, Qm and Qf, respectively, can be defined as [10]:
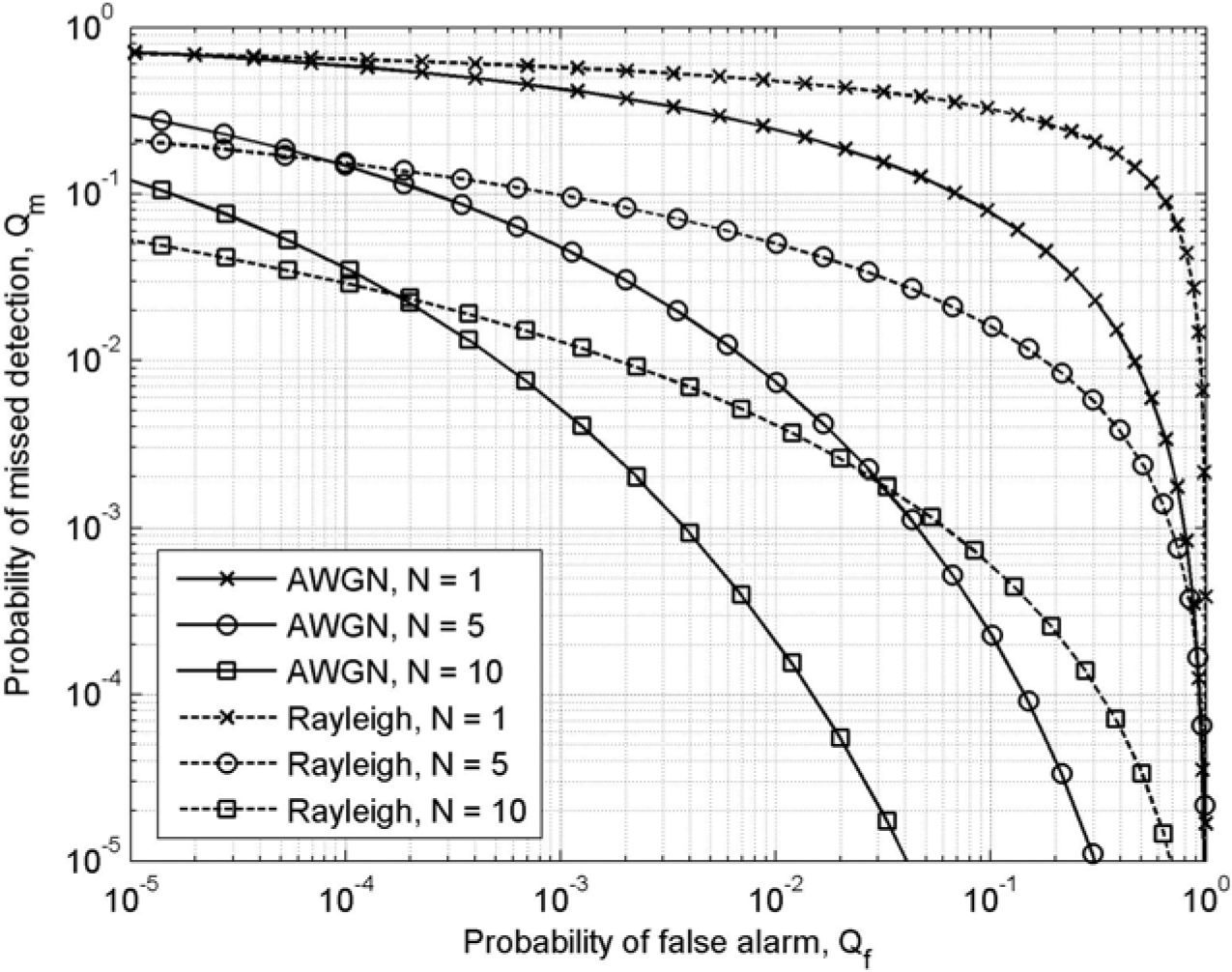
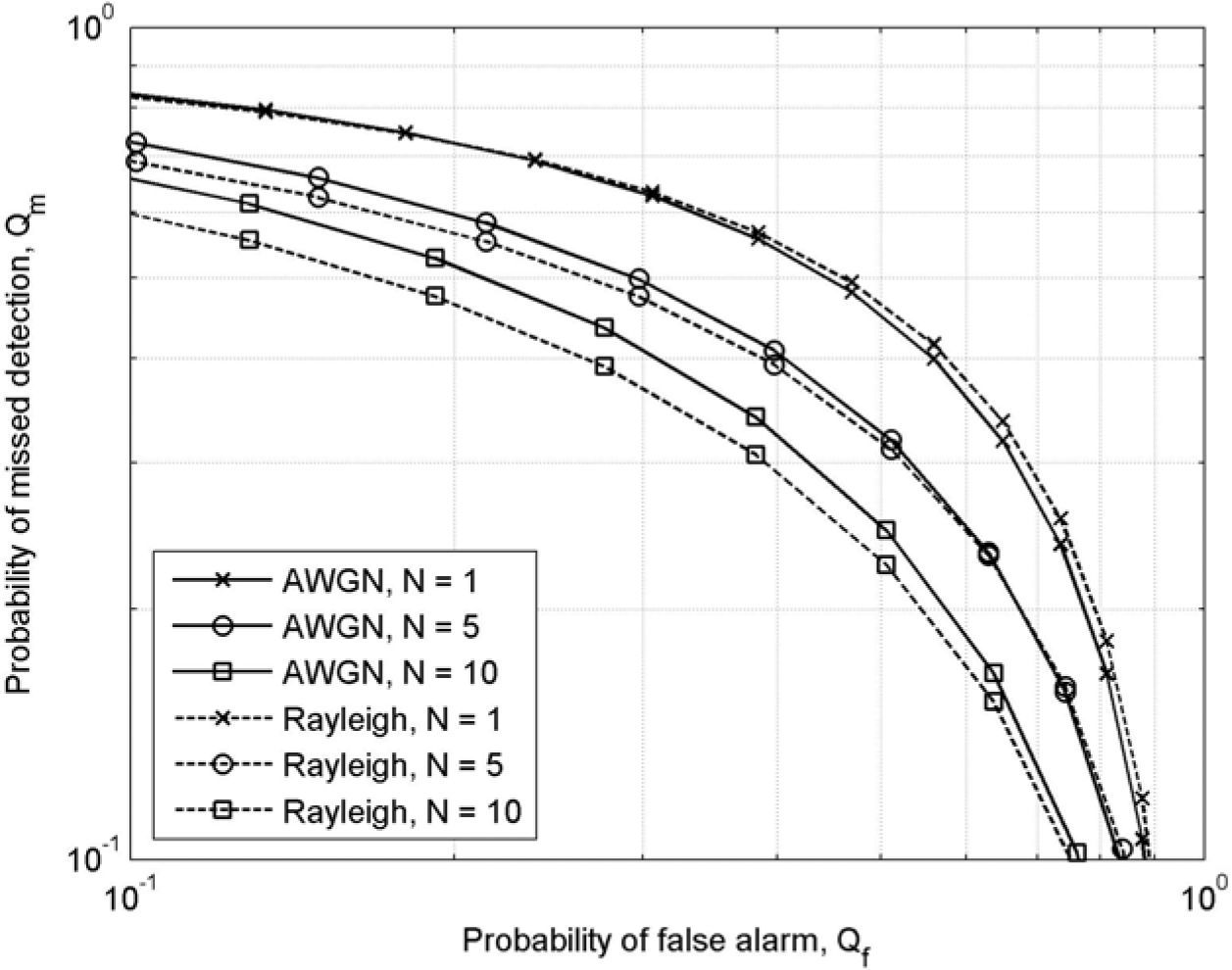
Figures 3, 4 and 5 illustrate the detection performance of cooperative spectrum sensing using OR-rule under AWGN and Rayleigh fading channel at different SNR values (i.e., 10 dB, 0 dB, and -10 dB). Under both AWGN and Rayleigh fading channels, it can be seen that the detection performance of cooperative spectrum sensing was greatly improved at high-SNR value (i.e., 10 dB) where the greater the number of cooperating SUs, the greater the improvement observed on the complementary ROC curve. However, Figure 4, shows that the improvement of detection performance did not improve significantly with the increased cooperation among SUs in medium-SNR scenario (i.e., SNR=0 dB). Even more noticeable, in low SNR (i.e., SNR=-10 dB), the cooperative spectrum sensing (e.g., N=5 or N=10) did not provide any improvement in comparison to the detection performance of local sensing (i.e., N=1), as depicted in Figure 5.
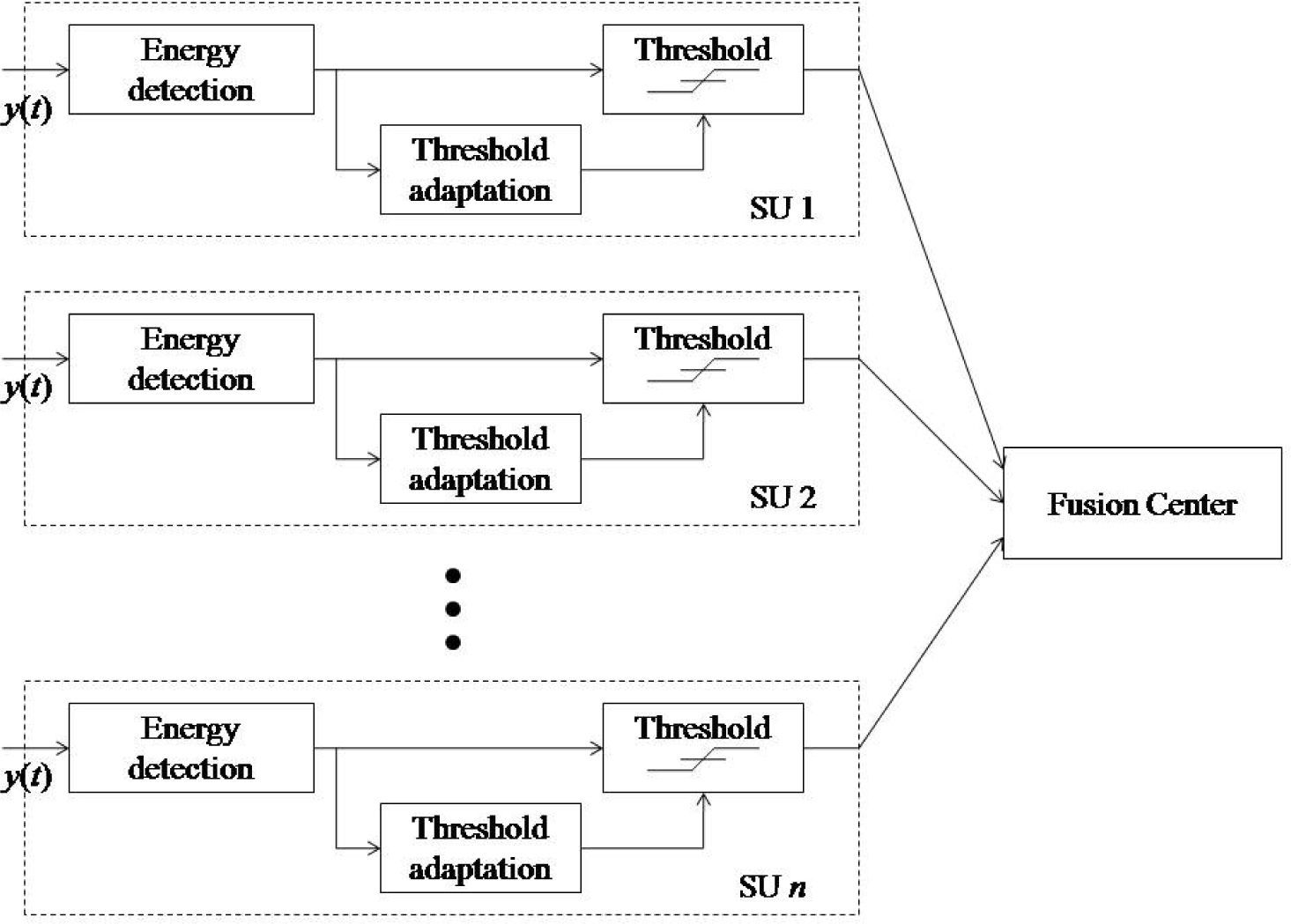
As mentioned in Section 3, the cooperative spectrum sensing did not provide significant improvement to the detection performance in low-SNR environment. In order to tackle this issue, this paper presents a cooperative spectrum sensing technique armed with PSO-based threshold adaptation. Figure 6 illustrates a simple block diagram for the proposed scheme.
Assuming that each SU is capable of estimating SNR at its receiver; each SU will perform local spectrum sensing and will calculate its own decision statistic. Then, every SU will run its PSO evolutionary processes to search for an optimal detection threshold such that high probability of detection and low probability of false alarm are jointly attained. The calculated decision statistic by each SU will be then compared with the optimized threshold and the corresponding decisions made by all SUs will be sent to an OR-rule common fusion center for developing a final global decision on PU availability.
4.1Problem formulation for threshold adaptationTo optimize the detection performance in an SNR-varying environment, low probability of missed detection and low probability of false alarm must always be jointly maintained. This is because minimizing the probability of missed detection makes the PU more protected against potential SU transmissions whereas minimizing the false alarm probability allows SUs to efficiently utilize the unused bands of spectrum. Therefore, the decision threshold has to be adaptively adjusted to satisfy the aforementioned two conflicting requirements for various channel conditions. The overall performance objective of the whole CRN can be put into a single optimization problem of minimizing the total sensing error given by [11]:
Where δ is a weighting constant ranging in (0, 1) for the probability of missed detection relative to that of false alarm. Because low probability of false alarm and high probability of detection are desired, a constraint has to be imposed to the threshold. In this paper, probability of false alarm is limited to the range of [0.001, 0.1]. It is reasonable to impose a maximum limit to the probability of false alarm so that low probability of false alarm can be maintained. A minimum limit is also imposed because a very low probability of false alarm would imply that that the probability of detection is also very low, thus imposing a minimum limit to the probability of false alarm could preserve a reasonable probability of detection. Hence, the optimization problem becomes
4.2Particle swarm optimizationParticle swarm optimization (PSO) is a population-based random search algorithm developed by Kennedy and Eberhart in 1995 based on swarm behavior of bird flocking and fish schooling [13][14]. In PSO, a population, also known as swarm, is initially created based on the search space of a given optimization problem. Each member in the swarm, also referred to as particle, is distributed randomly within the predefined search space. This population will randomly ‘fly’ through the search space to look for the global optimum. The trajectory of each particle is influenced by the best position personally found so far, which is called personal best (pbest), and the best position found by the entire swarm, named as global best (gbest). The velocity-update and position-update equations for each particle are given as [13][14]:
Where vij(t) denotes the velocity of i-th particle in j-th dimension at t-th iteration, c1 and c2 are referred as acceleration constants, r1 and r2 are uniformly distributed random values ranging in [0, 1]. yij(t) is referred as pbest, which is the best position found by the i-th particle in j-th dimension so far by the t-th iteration whereas ŷj(t) is referred as gbest, which is the best position found by the entire swarm in j-th dimension so far at the t-th iteration. xij(t) denotes the position of i-th particle in j-th dimension at t-th iteration. Another parameter, so-called maximum velocity, Vmax is imposed to limit the velocity of each particle to ensure exploration within the search space. A pseudocode of PSO is shown in Figure 7 for a given minimization problem [12]. In this paper, the performance objective of CRN is to minimize the total sensing error. Thus, the fitness function to be optimized by PSO is the objective function in Equation 15 and each particle represents a potential setting of the decision threshold.
Pseudocode for PSO algorithm [12].
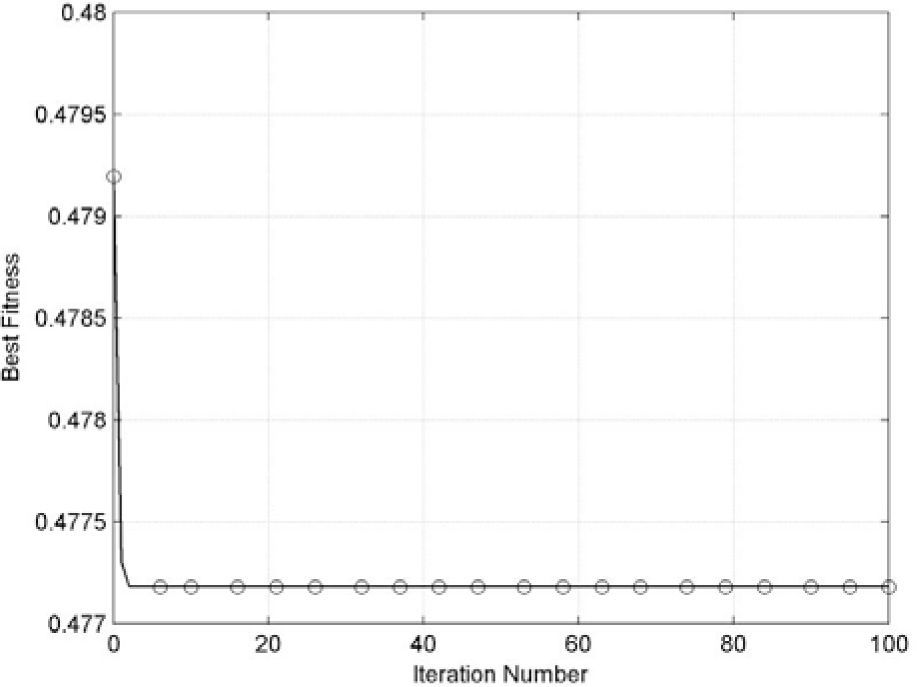
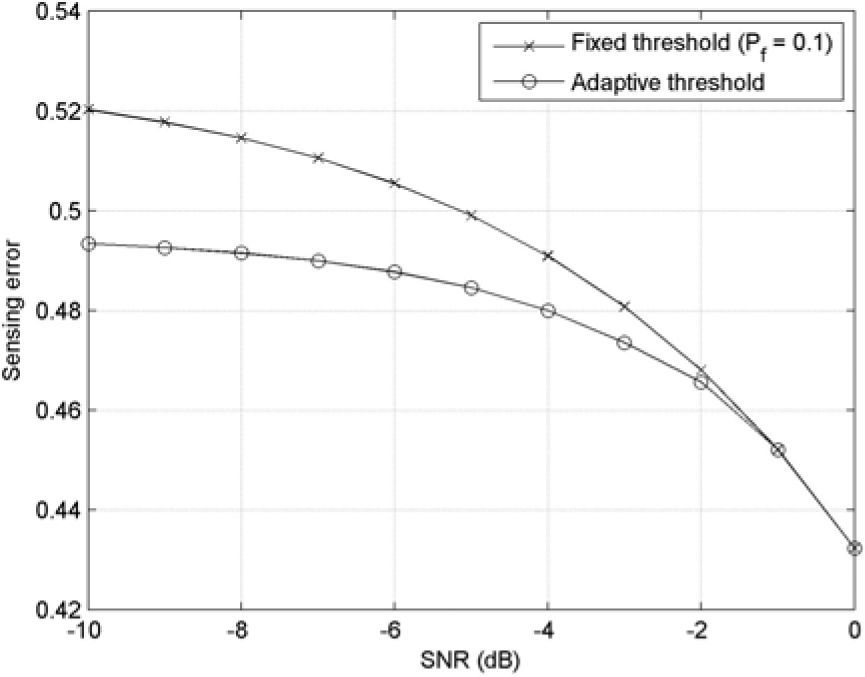
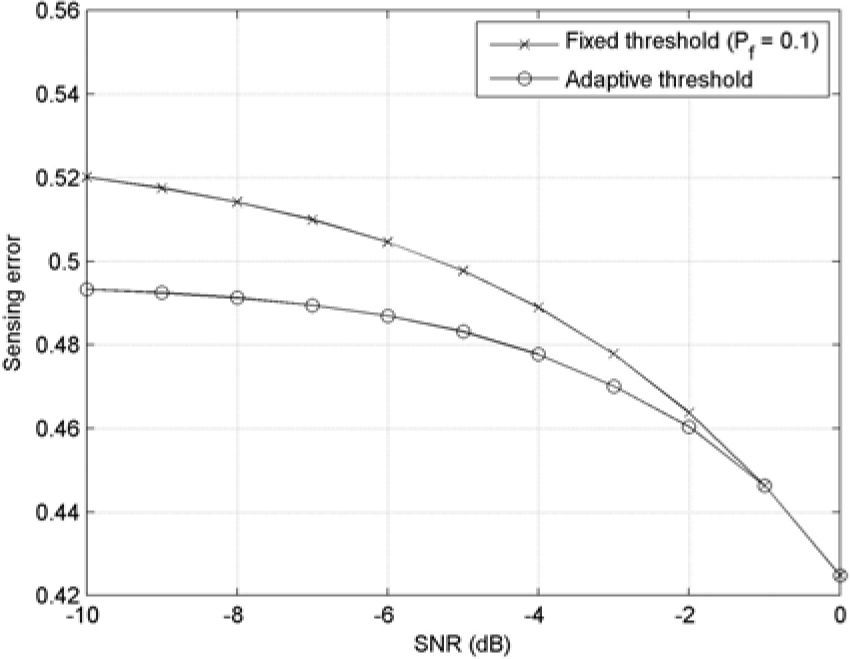
In this section, m is set to 10, δ is set to 0.5 as in [15], and SNR varies from -10 dB to 0 dB with a step size of 1 dB. In the PSO algorithm, the search space is set to the threshold values correspond to the constraint of the probability of false alarm stated in the Equation 16, Vmax is set as the difference between the minimum and maximum search space boundaries, c1 and c2 are both set to 2 as in [13][14], and the number of particles is set to 10. The PSO evolutionary operation runs for 100 iterations and to be repeated for 100 times to perform averaging (i.e., number of realizations=100) for each step increase in SNR. The convergence performance of PSO for AWGN channel, for instance, with SNR=0 dB is depicted in Figure 8. It can be observed that the PSO algorithm is able to converge within the first 10 iterations, which is extremely fast. This implies that the computational time of the proposed PSO algorithm is sufficiently short to meet the real-time requirements. The similar convergence performance of the proposed PSO-based cooperative spectrum sensing scheme can be observed at different SNR values and for channels encountering Rayleigh fading. This convergence performance confirms the effectiveness of employing a PSO-based threshold adaptation at the receiver of every SU which is observed by the fast processing speed of the optimization algorithm. Next, we are interested to show the improvement on the detection performance at the common fusion centre of a CRN employing PSO-based threshold adaption at its CR nodes. Remember that the main objective of employing PSO for dynamic adaption of CR/SU receiver’s threshold is to minimize the overall sensing errors of cooperative SUs in low-SNR environment. Consider the SNR range of PU signal at SU receivers from -10 dB to 0 dB. Figure 9 depicts the detection performance represented by the probability of sensing error versus SNR for cooperative network of 5 SUs (i.e., N=5) for AWGN channel. Figure 10 shows the detection performance for the same number of SUs but with assuming Rayleigh channels. For the two cases in Figures 9 and 10, it can be observed that the probability of sensing error is minimized by using threshold adaptation at the SUs’ receivers in comparison to the case of using static threshold setting based on a given probability of false alarm; Pf=0.1. The static threshold setting is basically obtained from Equation 9 for AWGN and Rayleigh fading channels, respectively, given a fixed probability of false alarm. Interestingly, the probability of sensing error is continually decreasing as the SNR goes lower for both AWGN and Rayleigh channels. This observation makes the proposed idea of employing PSO-based threshold adaption a good choice, in particular, in low-SNR scenarios. In addition, since minimizing the overall sensing error requires joint minimization of missed detection and false alarm probabilities, this approach provides a balanced compromise between PU protection demands and SU willingness to opportunistically access available unused spectrum bands or white spaces.
5ConclusionIn this paper, the detection performance for local spectrum sensing and cooperative spectrum sensing using OR-rule under AWGN and Rayleigh fading channel are evaluated. It was demonstrated that the cooperative spectrum sensing can hardly improve the detection performance in low-SNR environment. Thus, cooperative spectrum sensing with PSO-based threshold adaptation has been proposed to address the aforementioned drawback. The PSO threshold adaption algorithms are implemented at the receivers of CRN. The aim of improving the detection performance of CRN in low-SNR environment was realized by minimizing the overall sensing error; that is, by the joint minimization of probability of false alarm and probability of missed detection at the common fusion centre of CRN. Computer simulations showed that the performance of the proposed scheme is superior to that with fixed threshold and provide lower sensing errors in low-SNR environment. It was also observed that the gain of decreasing the sensing error increases as the SNR goes lower. Thus, these interesting findings confirmed the efficiency of employing PSO-based adaptive thresholds to improve the sensing performance of CRN in deteriorated channel conditions.






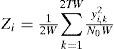
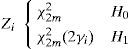

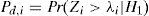
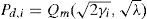
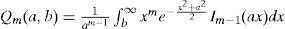
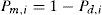
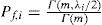
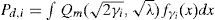
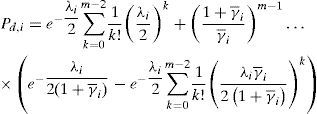



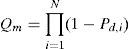
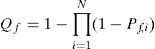




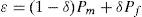

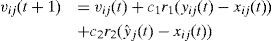
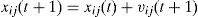
![Pseudocode for PSO algorithm [12]. Pseudocode for PSO algorithm [12].](https://static.elsevier.es/multimedia/16656423/0000001100000003/v2_201505081636/S1665642313715529/v2_201505081636/en/main.assets/thumbnail/gr7.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)


