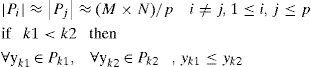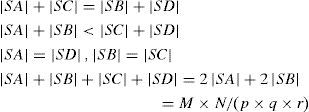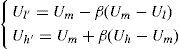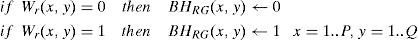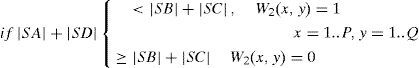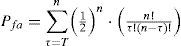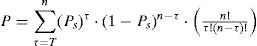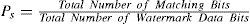Cropping Resilient Watermarking Based on Histogram Modification

Abstract

This paper proposes a watermarking scheme robust against most common geometric and signal processing operations, for applications that require an accurate detection of the owner watermark even if the digital image suffers intentional and non-intentional attacks. The proposed scheme is based on two modifications introduced in two 2D histograms. In the first modification a selected region of a 2D histogram, composed by red and green (R-G) color components, is modified according to the watermark bit sequence; while in the second modification another 2D histogram, composed by blue (B) and filtered red (R) components, is partitioned into several blocks to embed the watermark data bits. The experimental results show fairly good robustness against several geometric distortions, common signal processing operations and some quite aggressive combined attacks. A watermark robustness comparison with the related works and an analysis of the embedding method from the watermark robustness point of view are provided, in order to explain the robustness improvement of the proposed algorithm, especially against rotation and cropping attacks. The ROC curves also provided to show the desirable detection performance of the proposed method. Comparisons with the previously reported methods, based on different techniques, are also provided

Resumen

En este artículo se propone un esquema de marca de agua robusto contra operaciones de tipo geométrico así como de procesamiento avanzado de señales, orientado a aplicaciones que requieren una detección precisa de la marca de agua aun cuando la imagen sufre de ataques intencionales o no intencionales. El esquema propuesto se basa en un par de modificaciones introducidas en dos histogramas bidimensionales. En la primera de ellas, una región seleccionada de un histograma bidimensional, conformado por las componentes de color rojo y verde (R-G), se modifica de acuerdo a la secuencia de marca de agua; mientras que en la segunda modificación, otro histograma bidimensional compuesto por la componente azul (B) y una versión filtrada de la componente de color rojo (R) es particionado en varios bloques para insertar los bits de la marca de agua. Los resultados experimentales muestran una buena robustez ante diversas distorsiones geométricas, operaciones de procesamiento avanzado de señales y algunos ataques combinados algo agresivos. La robustez de la marca de agua obtenida del algoritmo propuesto y de otros trabajos relacionados, así como un análisis del método de inserción desde el punto de vista de robustez, correspondiente al método propuesto en este trabajo, son proporcionados para explicar la mejoría en la robustez del algoritmo propuesto contra ataques de rotación y recorte. Las curvas ROC también se proporcionan para mostrar las características de operación deseables del método propuesto, así como los resultados de comparación del método propuesto con otros esquemas propuestos previamente en la literatura, los cuales emplean técnicas de inserción y detección diferentes a la propuesta en este trabajo.

1

Introduction

During the last three decades the use of digital image, video and audio technologies in home computers and open networks, have dramatically grown; because they are easy to use and the digital files can be efficiently stored. However digital objects may be copied, manipulated or easily converted between several formats without any control, which can cause intellectual property damages to the owner of digital material.

This fact suggests the necessity to develop some efficient methods for solving these problems. The watermarking technique is considered as a suitable solution for copyright protection and authentication of digital materials, however, if there is a synchronization loss between the watermark embedding and detection stages the watermark cannot be properly detected. This problem is mainly due to geometric distortions, such as cropping, rotation, scaling and any affine transformations, which are common in practice. Thus, during the last two decades, numerous watermarking methods have been proposed that are robust against common signal processing such as: JPEG compression and filtering etc.; however, relatively few of these methods provide enough robustness against geometric distortions [1-11]. Some of them propose the use of image histograms as the watermark-embedding domain [8-11] because, if the watermark is embedded into this geometric invariant domain, it should survive to most geometric transformations. In this way, in [8] an exact histogram specification is used to embed the watermark into the images, while in [9] the histogram-specification method proposed in [8] is extended to chromatic histograms and the watermark sequence is embedded in the chromatic plane of a color image. The authors of [10] proposed a watermark embedding method into a color histogram using the constrained Earth Mover Distance (EMD), to optimize the image modification according to a target histogram. Almost all previous works based on histogram modification show watermark robustness against geometrical distortion; however they cannot provide enough robustness against common signal processing techniques; as well as to some combinations of geometric attacks and common signal processing operations. Only the histogram-oriented watermarking algorithm (HOWA) proposed in [11] shows watermark robustness against some combined attacks of geometrical modification and common signal processing. However, the HOWA presents some vulnerability to the cropping and rotation attacks and also to combined attacks involving these geometrical distortions.

In this paper we propose a color image watermarking method for copyright protection, in which the watermark should be detected even if the image to be protected suffers intentional attacks. The proposed scheme is based on the embedding of a same watermark pattern into two 2D-histograms obtained from a color image, such that the resulting watermark is robust against common signal processing operations, geometric distortions and combined attacks of common signal processing, such as JPEG compression, and geometric distortions, including cropping with high cropping rate. In the first histogram modification, a 2D color histogram composed by the R and G color components, an adequate region is selected and modified according to the binary watermark pattern. This R-G 2D histogram modification is carried out, mainly, to be robust against the geometrical distortions such as: cropping, rotation, scaling, shearing, among others. In the second modification, another 2D color histogram, composed by B and filtered R color components, is used. This histogram is dynamically partitioned in blocks, modifying the pixel values of each block according to the watermark sequence. This modification is carried out to be robust against the JPEG compression and other common signal processing operations, in a similar form as the HOWA [11]. The experimental results show the robustness against several geometric distortions including cropping and rotation, common signal processing operations and combined attacks composed by geometrical distortions and common signal processing operations. Comparison results are also given to show that the proposed method provides better performance than previously reported methods.

This paper is organized as follows: In Section 2, the histogram-oriented watermarking algorithm (HOWA) proposed by Lin et al. [11] is roughly described. In Section 3 the proposed algorithm is described in detail. The evaluation and experimental results as well as the robustness analysis of the HOWA and the proposed algorithm together with the analysis of the detector capability are provided in Section 4. Finally the conclusions are given in Section 5.

2

Histogram-oriented watermarking algorithm

In the histogram-oriented watermarking algorithm (HOWA) proposed in [11], an original color image is represented by using the YUV color space, therefore each pixel has three values (y, v, u). Firstly, the luminance component Y and a chrominance component V are filtered by a circular smoothing filter to get the filtered components Y_f and V_f. This operation compensates an effect of the JPEG compression and as a consequence the embedded watermark can be robust to such compression method. The pixels of the original image are segmented into p groups using Y_f values, which must satisfy the following conditions:

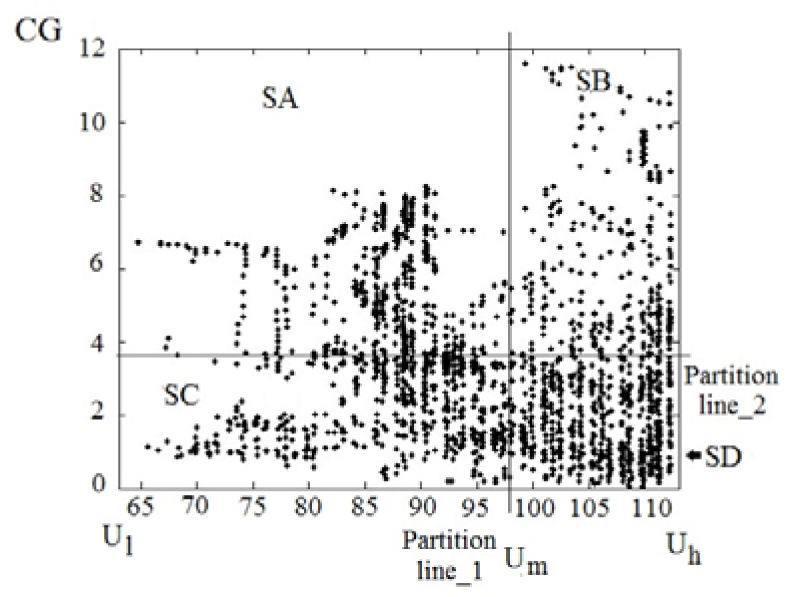
where |P_x| means the number of elements of group P_x, M×N are the total number of pixels of the image and y_k is the value of a pixel belonging to the group P_k. Later, each group P_i, i = 0,1,…,p-1 is segmented into q bands with v_f values using the same conditions mentioned above. Here the p×q bands D_i,j, i = 0,1,…,p−1, j = 0,1,…q−1 are obtained and furthermore each band is segmented into r blocks according to the U values, getting in total p×q×r blocks denoted by B_i,j,k, i = 0,1,…p−1, j = 0,1,…,q−1, k = 0,1,…r−1. The conditions used for this segmentation are also the same as Eq. (1), therefore the value (y_i,v_j,u_k) of a pixel belonging to the block B_i,j,k and the value (y_i’,v_j’,u_k’) of another pixel which belongs to B_{i’,j’,k’} satisfies the inequalities: y_i≤y_i’ if i<i’, v_j≤v_j’ if j<j' and u_k≤u_k’ if k<k’.

The distribution of pixels belonging to each block B_i,j,k can be expressed by the 2D histogram using the composite gradients (CG) and the U values of the pixels as shown by Figure 1. The CG(x,y) is composed by the horizontal, vertical and two diagonal gradients of Y_f(x,y) [11]. Each block B_i,j,k is partitioned dynamically into four sub-blocks SA, SB, SC and SD, by two partition lines: a line-1 denoted also as U_m and a line-2. Adjusting these partition lines, satisfy the initial conditions given by

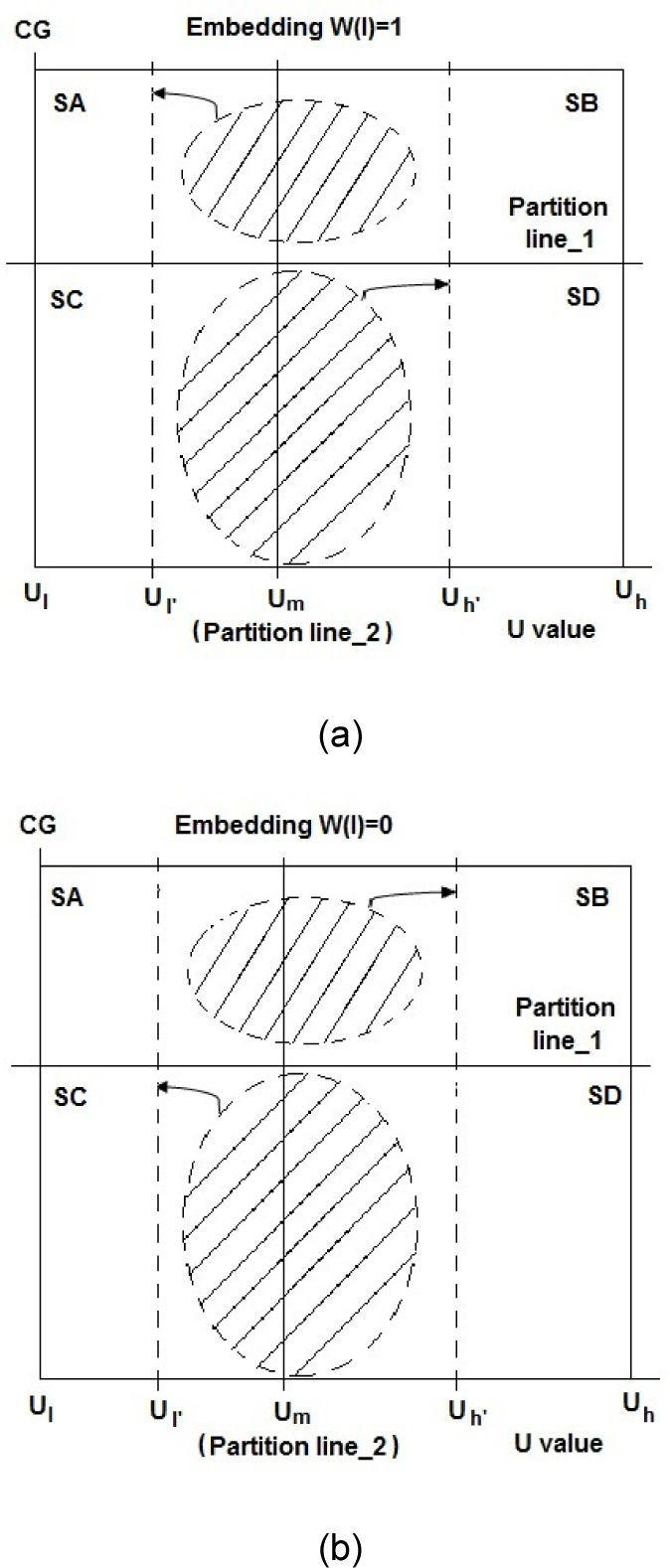
where |SX| is the number of pixels in the sub-block SX.

Figure 1.

Distribution of pixels in a block B_2,1,3 in U-CG plane together with sub-blocks and two partition lines.

In the embedding process of the HOWA, each bit of the watermark sequence is embedded into each block of B_i,j,k, i = 0..p-1, j = 0..q-1,k = 0..r-1 therefore the watermark length n is equal to the number blocks (p×q×r). In [11], p=16, q=2, r=4 are used, so the watermark length is equal to n=128. The l-th watermark bit w_l is embedded into the B_i,j,k block, where i = [l/qr], j = [(l/iqr)/r] and k = l=iqr-jr where [.] means a downward truncation operation. Depending on the watermark bit, the distribution of pixels in the sub-blocks is modified to satisfy a specific condition given by: if |SA| + |SD|>|SB| + |SC| then w_l = 1, otherwise w_l = 0. To obtain this specific pixel distribution in each block without causing visual distortion, two factors 0<α, β≤1 are introduced in HOWA. The factor α determines the amount of pixels that move between sub-blocks and β determines the amount of value that is added to or subtracted from the original U value of the pixels in the sub-blocks used to realize this movement [11]. Figure 2 depicts the movement of pixels to modify the pixel distribution in a block, according to the embedding watermark bit. The interval [U_l’, U_h’], where the movements of pixels are performed, is defined using the factor β, which is given by [11].

Figure 2.

Pixel movement of a block according as the embedding watermark bit. (a) Embedding W(l)=1; (b) embedding W(l)=0.

In HOWA the watermark embedding causes the modification of only the U values then the watermarked color image is constructed using the watermarked U and the original Y and V components. Figure 3 shows the pixel distribution in the U-CG plane of an original block and the corresponding watermarked block when a watermark data bit ‘0’ is embedded together with their respective histograms of the U component.

Figure 3.

Pixel distributions of a given block (B_1,1,3) before/ after embedding a watermark data bit ‘0’. (a) Original block, (b) histogram of the original U values, (c) watermarked block, and (d) histogram of the watermarked U values. (α = 0.9, β = 0.5 are used for easy comprehension).

In the watermark extraction process, the watermarked color image is segmented into p×q×r blocks B_i,j,k, i = 0..p−1, j=0..q−1, k=0..r−1, using the same condition given by Eq. (1) and then each block is partitioned dynamically into four sub-blocks SA, SB, SC and SD to satisfy Eq. (2). Depending on the distribution of pixels in the sub-blocks, the watermark bit (0 or 1) is extracted from each block as follows: if |SA| + |SD|>|SB| + |SC| then the extracted watermark bit is equal to ‘1’ and otherwise it is equal to ‘0’.

3

Proposed algorithm

The proposed algorithm consists of three stages: watermark generation, embedding and detection stages which are described in the next sub-sections.

3.1

Watermark generation

The security of the proposed algorithm strongly depends on the pseudo random number generator (PRNG) used to generate the watermark sequence. Several PRNG have been proposed in the literature during the last several years, among them, the PRNG called “Cilia” [12] appears to be a suitable choice. The “Cilia” with two λ-bit keys, is a (z, z³ / 2^2λ-1) - secure PRNG [12], has been tested using several crypt-analytical attacks such as: iterative guessing attack, backtracking attack, input based attack, permanent compromise attack, key search attack among others [12]. According with the reported results the most efficient attack on Cilia generation mechanism with two unknown λ-bit keys should have a complexity of about z=2^2λ steps. Thus for a λ = 128 the complexity of attacking the Cilia mechanism is equal to z = 2²⁵⁶ steps, which is generally impossible, for any attacker, to be carried out.

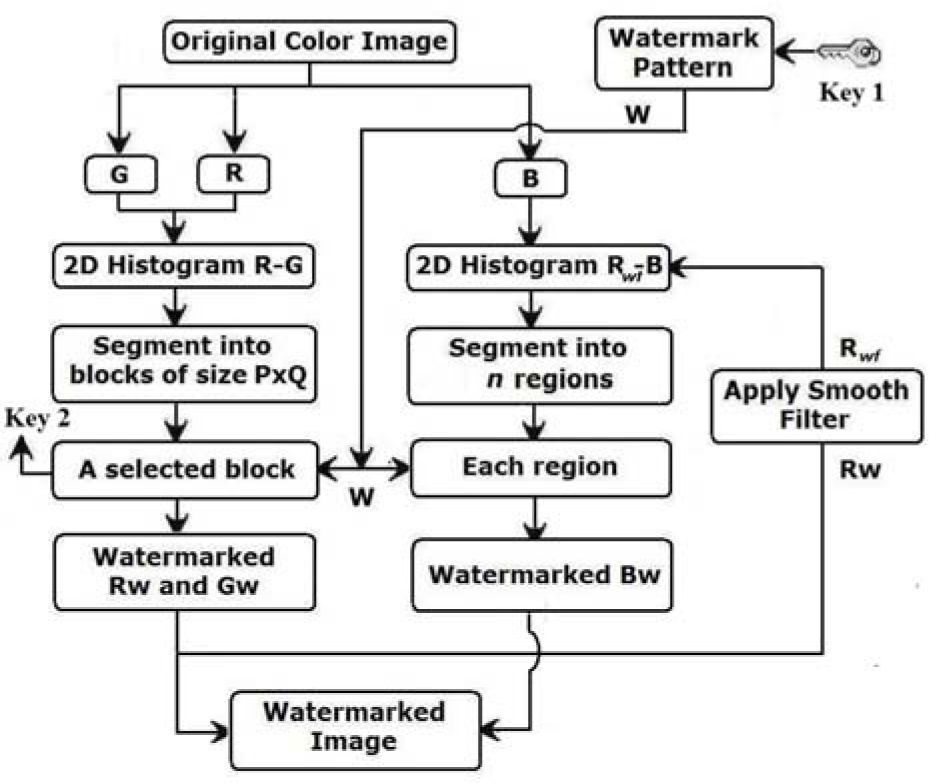
3.2

Watermark embedding

In computer graphics and photography, a color histogram is a representation of the color distribution in an image, derived by counting the number of pixels of each color. These representations can be structured as two-dimensional (2D) or three-dimensional (3D). Figure 4 shows an example of a 2D R-G color histogram. In this paper, we use two different 2D color histograms to embed with a same binary watermark sequence W. The embedding process comprises two strategies in order to modify the R, G and B color components.

Figure 4.

Example of a 2D R-G color histogram, (a) 2D color histogram obtained from original image (b).

The diagram of the embedding process is shown in Figure 5 and details of each modification of the 2D histograms are described in following sub-sections.

Figure 5.

Illustration of the watermark embedding process.

3.2.1

Modification of the 2D R-G histogram

This process is described in the following steps:

• 1)

  Decompose the original color image I in its three components R, G and B; and then using the R and G components, compute a 2D R-G color histogram denoted by H_RG.

• 2)

  Using the user's secret key ω₁ and the Cilia PRNG, generate the binary watermark sequence W with length n. Reshape the watermark sequence W in a pattern W_r of size n = P × Q (where P and Q are any integers).

• 3)

  Segment the histogram H_RG in blocks of size n = P×Q (P and Q are any integers) and select an adequate block BH_RG to embed the watermark sequence. The principal condition for an adequate block is that the value of almost all pixels in such block must be non-zero. There are many blocks that satisfy this condition; among them one block is selected randomly, whose block number will be provided as the user's key ω₂ in the detection stage. The pixel value of BH_RG(x,y) is modified according to the watermark bit W_r(x,y), as follows:

  
  Several situations may arise: If W_r(x,y) = 0 and BH_RG(x,y) = 0, as well as W_r(x,y) = 1 and BH_RG(x,y) ≠ , it is not necessary to modify the values of BH_RG(x,y). However if these conditions are not satisfied, BH_RG(x,y) must be modified. In the upper case of Eq. (4), BH_RG(x,y) must be forced to zero, distributing its value as uniformly as possible among its four neighbors. In the lower case, BH_RG(x,y) must be forced to be non-zero, which can be achieved subtracting one from its largest neighbor and adding it to BH_RG(x,y). This embedding method ensures the watermark imperceptibility, because the modified values are assigned to the neighbor pixels, so that causes slight changes in the image colors, remaining the total number of pixels unaltered with respect to the original ones.

• 4)

  Once the histogram H_RG has been modified, all pixel values are restored and watermarked components R_w and G_w are obtained. Figure 6 shows an example of original and watermarked 2D R-G color histograms versions.

  
  

  Figure 6.

  Example of original and watermarked 2D R-G color histograms from Lena image. (a) Original 2D color histogram. (b) Watermarked 2D color histogram.

3.2.2

Modification of the 2D B and filtered R_wf histogram

After the watermarked components R_w and G_w are obtained, we proceed with the B component modification using the second strategy, which is based on a 2D histogram composed by the B and filtered R_w components (2D B-R_wf). This embedding method is similar to that used in the HOWA [11]. The principal differences respect to that work are: in our proposed algorithm B components are modified instead of U components as in HOWA have done and the dynamic segmentation of the sub-block to embed a watermark bit is carried out in the 2D R_wf−B instead of the 2D CG-U proposed in HOWA. This second strategy is described as follows:

• 1)

  Apply a circular smooth filter [13] to R_w component and obtain the filtered component R_wf to effectively reduce the variability of the coefficients of R_w as a consequence of the JPEG compression with different quality factors.

• 2)

  Divide the 2D histogram composed by R_wf and B components into n regions h_i, i = 1…n, of the same number of pixels in each one, then |h_i|≈|h_j|, i≠ j, i, j = 1…n, where n is the watermark length.

• 3)

  Furthermore each 2D sub-histogram h_i is partitioned dynamically into four sub-blocks SA, SB, SC and SD using two partition lines in a similar way as in Figure 1. The condition used for segmentation is the same proposed by HOWA [11].

• 4)

  The i-th watermark bit is embedded into the i-th sub-histogram h_i, modifying the pixel values of the B component. According to the watermark bit value, the distribution of h_i is modified as follows: if W_r(x,y) = 1, some pixels in SB and SC are moved into SA and SD respectively: (|SA| = |SA| + α|SB|, |SD| = |SD| + α|SC|), otherwise if W_r(x,y) = 0 inverse reciprocal movement is applied (|SB| = |SB| + α|SA|, |SC| = |SC| + α|SD|). In the same way as in HOWA [11], two factors α and β are introduced to control the watermark imperceptibility and robustness. The details have been explained in previous section. This process changes only the interior distribution of sub-histogram h_i, but the global distribution among sub-histograms is not changed. Hence an adequate selection of the factors α and β is necessary to get the balance between the watermark imperceptibility and robustness.

• 5)

  Once all sub-histograms hi, i = 1…n, are modified to embed all watermark bits, the component B is restored to get the watermarked component B_w. Finally, the watermarked image I_w is constructed using the obtained three watermarked components R_w, G_w and B_w.

3.3

Detection process

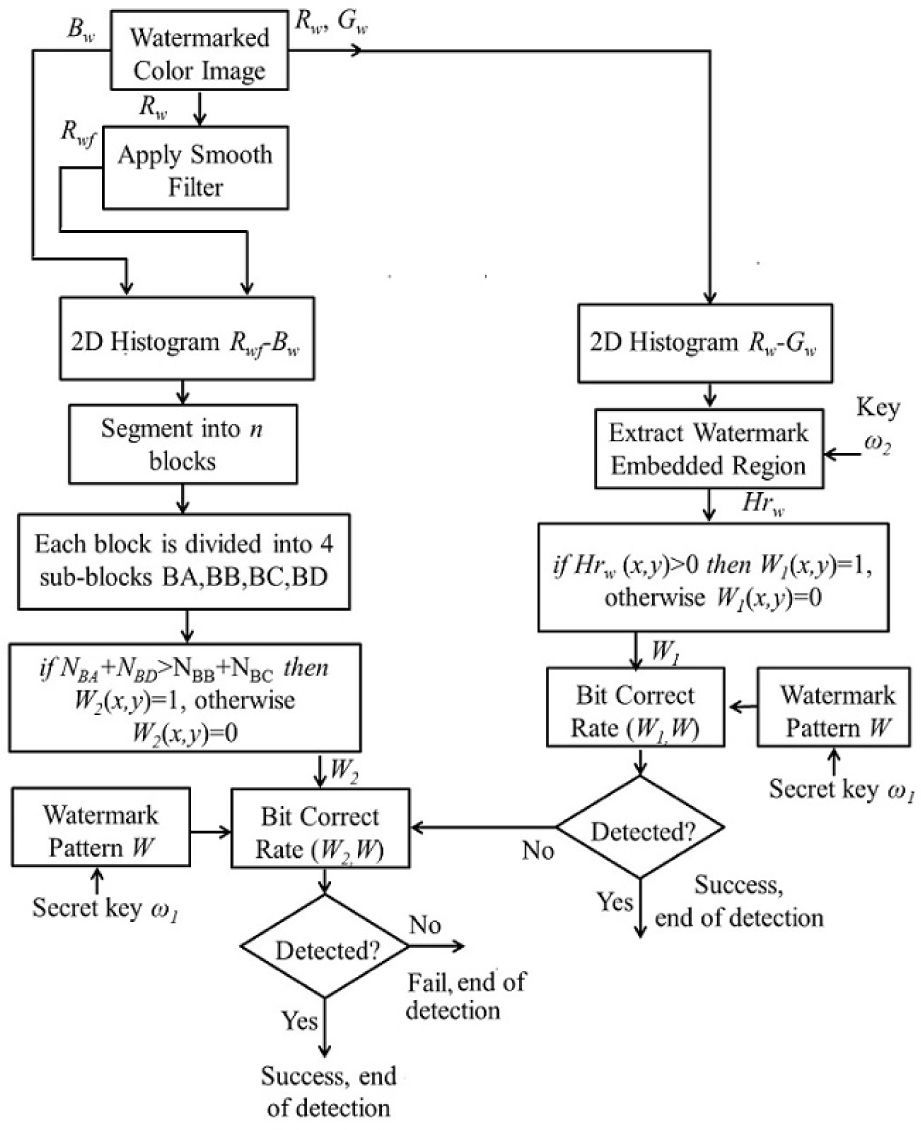
The detection process is shown in the diagram shown in Figure 7, which can be described as follows:

• 1)

  Obtain the R_w, G_w, and B_w components from the watermarked image I_w and generate the 2D R_w−G_w watermarked histogram H_RwGw using R_w and G_w, which is segmented into blocks of size n=P×Q.

• 2)

  Using the user's key ω₂ extract the region Hr_W, in which the watermark was embedded. From this region, the watermark pattern W₁ is extracted according to the following condition: if Hr_W(x,y)>0 then W₁(x,y) = 1, otherwise W₁(x,y) = 0, x = 1,…, P, y=1,…,Q.

• 3)

  Apply the circular smooth filter to R_w component to obtain the filtered component R_wf. Next the histogram composed by the R_wf and B_w components is segmented into n sub-histograms h_i, i = 1… n, using the same condition defined in the embedding process, which is |h_i|≈|h_j|, i≠j, i, j = 1 …n.

• 4)

  Divide dynamically each h_i into four blocks SA, SB, SC and SD, using the same condition defined in the embedding stage, which is given by Eq. (2).

• 5)

  Count the number of pixels in these four blocks, and according to the number, the i-th watermark bit of the second watermark W₂ is extracted. The condition for watermark bit extraction is given by Eq. (5).

  

• 6)

  Once the two watermark patterns W₁ and W₂ are extracted, the bit correct rates (BCR) between the corresponding extracted watermark W_{g (g = 1,2)} and the original watermark W are calculated. If the BCR between W₁ and W is greater than the predefined threshold T_N, BCR (W₁, W) > T_N, then the watermark is detected and the detection process is done, otherwise the quality of the W₂ is evaluated. The BCR of W₂ respect to W is compared with the same threshold value T_N. Then if the BCR (W₂, W) > T_N, the watermark is detected otherwise the image is considered as un-watermarked image. The order of evaluation of the two watermark sequence W₁ and W₂ can be inverted. That means the evaluation of W₂ can be followed by the evaluation of W₁ getting the same results. The selection of the threshold value is provided in 4.1.

Figure 7.

Illustration of the watermark detection process.

4

Experimental Results

From the watermark imperceptibility and robustness points of view, a set of color images with size 512 × 512 are used to evaluate the performance of the proposed scheme.

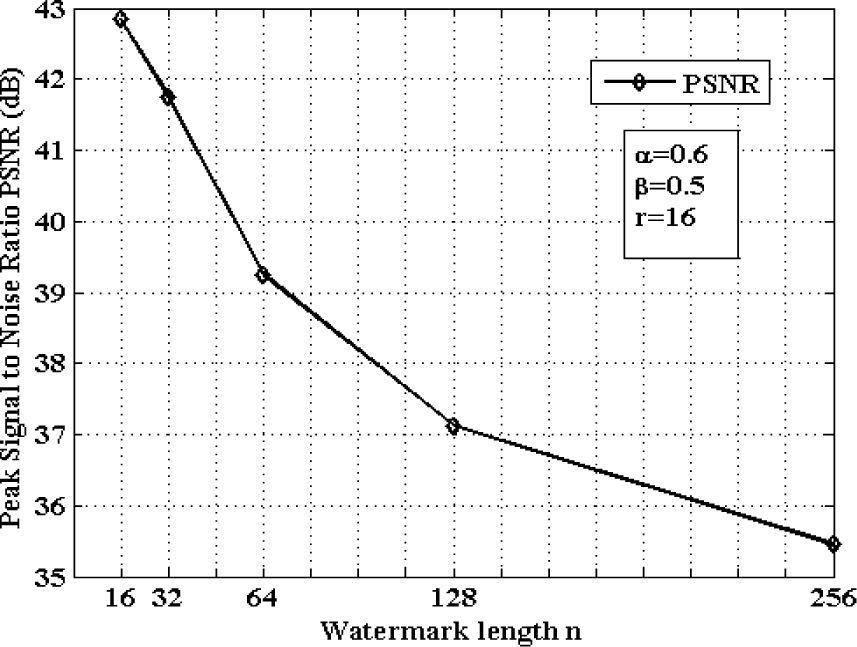
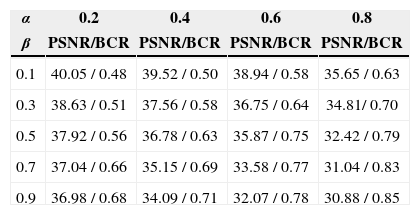
4.1

Parameters settings

Firstly, to determine the adequate parameters values: the watermark embedding parameters (α,β) and the watermark length n, several experiments were carried out. Using ten watermarked test images to analyze the effect of α and β on the watermark imperceptibility and robustness Table 1 presents the average Peak Signal to Noise Ratio (PSNR) and the average BCR of the extracted watermark respect to the original one. Here watermarked images are compressed by JPEG compression with a quality factor of 70 and rotated by 7°. In the table, N₁/N₂ is the quotient average PSNR/average BCR. From Table 1, we can conclude that the adequate values of α and β are 0.6 and 0.5, respectively, in order to obtain acceptable watermark imperceptibility and robustness. Other important factors are the optimal radio of the circular filter r and the watermark length n. The value of r=16 can be used which is the same value proposed in [11]. To obtain an adequate watermark length n, the quality of the watermarked image with several watermark lengths is evaluated. Figure 8 presents the average PSNR of the ten different watermarked images with several watermark lengths n using the parameters r = 16, α = 0.6, β = 0.5.

Table 1.

The average PSNR of the color components and the BCR extracted from a watermarked image with JPEG compression QF=70 and rotation by 7°. n = 128 and r = 16.

α	0.2	0.4	0.6	0.8
β	PSNR/BCR	PSNR/BCR	PSNR/BCR	PSNR/BCR
0.1	40.05 / 0.48	39.52 / 0.50	38.94 / 0.58	35.65 / 0.63
0.3	38.63 / 0.51	37.56 / 0.58	36.75 / 0.64	34.81/ 0.70
0.5	37.92 / 0.56	36.78 / 0.63	35.87 / 0.75	32.42 / 0.79
0.7	37.04 / 0.66	35.15 / 0.69	33.58 / 0.77	31.04 / 0.83
0.9	36.98 / 0.68	34.09 / 0.71	32.07 / 0.78	30.88 / 0.85

Figure 8.

Average PSNR with variable watermark length.

From Figure 8 an adequate value of n can be determined as 128, because a small value for n reduces the number of watermark bits that can be embedded and then the robustness against geometric attacks is severely affected. On the other hand, if a bigger value for n is selected, the robustness against geometric attacks increases, but the watermark imperceptibility can be affected. Thus using n = 128 it can be obtained a good watermark imperceptibility because the PSNR of the watermarked image is larger than 37 dB, providing at the same time enough robustness against geometric attacks as shown in Table 3.

In the detection process a threshold value T must be defined to determine if the watermark W_{g (g=1,2)} is present or not into the image. Considering a binomial distribution with success probability equal to 0.5, the false alarm probability P_fa for n bits embedded watermark data is given by (6), and then the threshold value T must be controlled in order that P_fa be smaller than a predetermined value. Thus

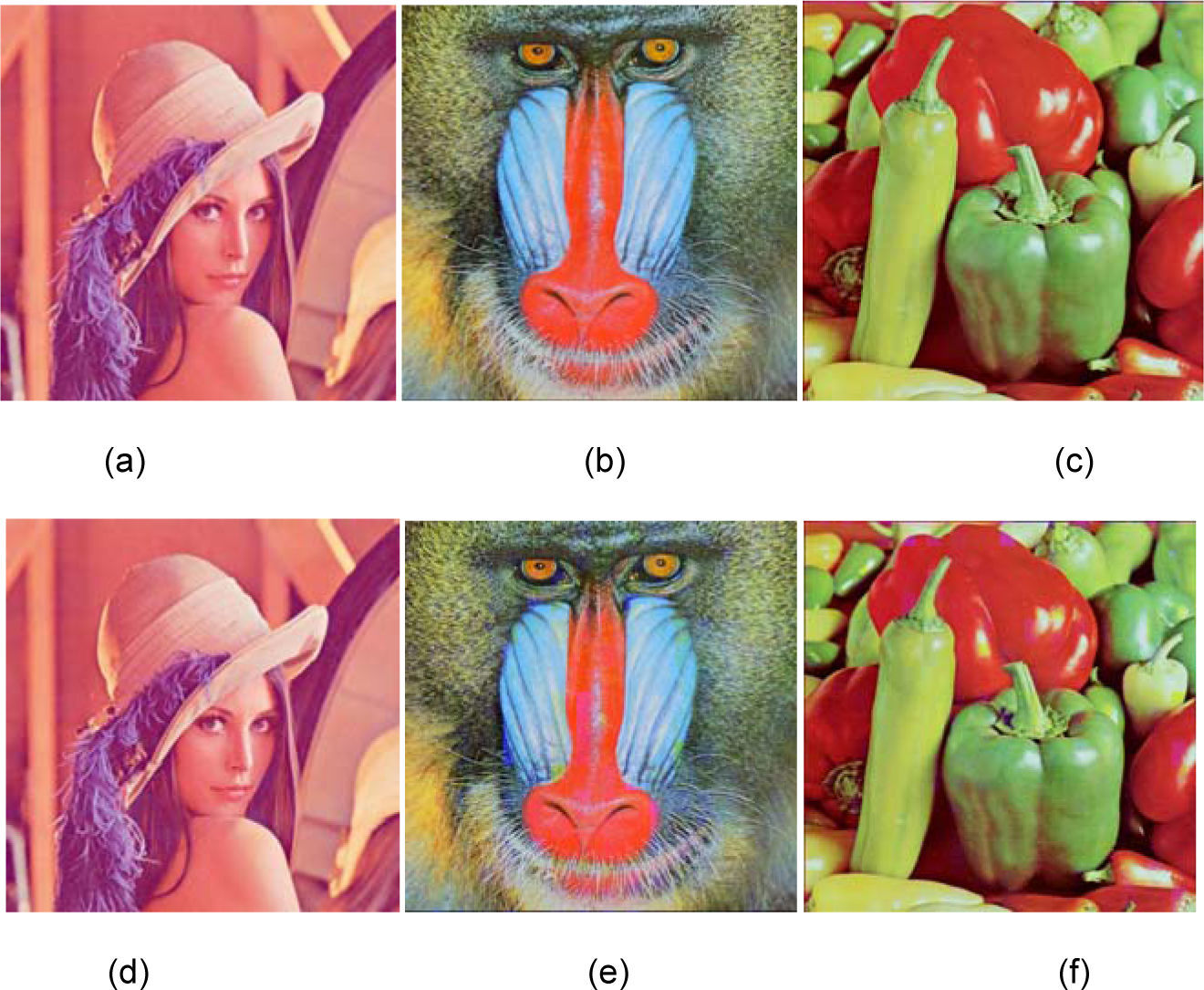
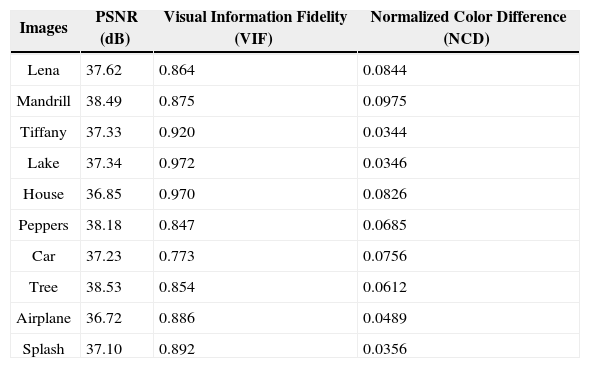
where n is the total number of watermark data bits, whose value is set to 128 and T is the number of correct extracted bits. Empirically the false alarm probability must be less than P_fa = 10⁻⁵ for a reliable detection, and then an adequate normalized threshold value T_N (=T/n) is equal to 0.7. Thus the following parameters, n = 128, r = 16, α = 0.6, β = 0.5, and T_N = 0.7 with P_fa = 10⁻⁵, are the more adequate.

4.2

Watermark imperceptibility

Unlike HOWA [11], the proposed algorithm embeds a watermark sequence twice in different histogram domains; therefore careful watermark imperceptibility evaluation is strong required. Using the parameters estimated in 4.1, the watermark imperceptibility was evaluated in terms of the PSNR, the Visual Information Fidelity (VIF) [14] and the normalized color difference (NCD) [15], [16]. The VIF value reflects perceptual distortions more precisely than the PSNR. The range of VIF is [0, 1] and the closer the value to 1 represents the better fidelity respect to the original image. On the other hand the NCD is based on the CIELAB color space and it is applied to measure the difference of color between two images. Table 2 shows the average values of PSNR, VIF and NCD of ten watermarked test images respect to the original ones and in Figure 9, some original images (a-c) together with their watermarked version (d-f) are shown. From Table 2 and Figure 9, it follows that the proposed scheme provides a fairly good fidelity of the watermarked image, as well as the fact that the difference of colors between the watermarked image and the original one is insignificant [17].

Table 2.

Watermark imperceptibility measured in terms of PSNR, VIF and NCD.

Images	PSNR (dB)	Visual Information Fidelity (VIF)	Normalized Color Difference (NCD)
Lena	37.62	0.864	0.0844
Mandrill	38.49	0.875	0.0975
Tiffany	37.33	0.920	0.0344
Lake	37.34	0.972	0.0346
House	36.85	0.970	0.0826
Peppers	38.18	0.847	0.0685
Car	37.23	0.773	0.0756
Tree	38.53	0.854	0.0612
Airplane	36.72	0.886	0.0489
Splash	37.10	0.892	0.0356

Figure 9.

Three of the original (a-c) and watermarked (d-f) test images.

4.3

Watermark robustness

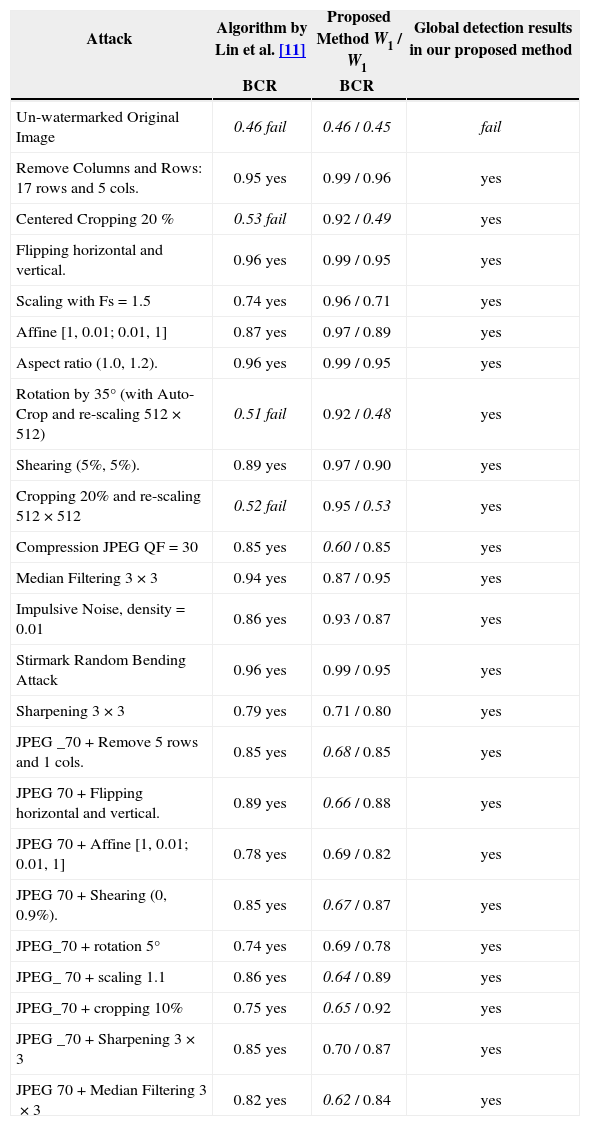
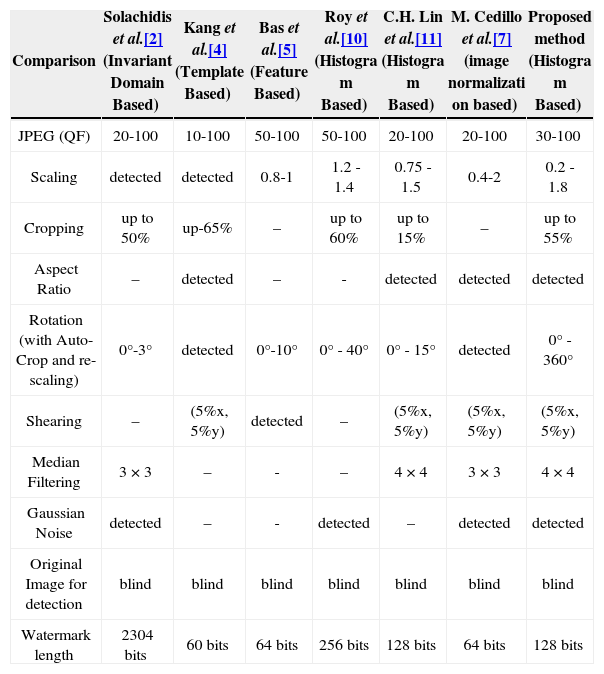
To evaluate the watermark robustness of the proposed algorithm, the StirMark Benchmark [18], combined attacks of the several geometrical distortions and common signal processing methods are carried out. Table 3 provides a performance comparison between the proposed method and HOWA [11] both with 128 bits embedded watermark data. The reason of this comparison is because HOWA provides the watermark robustness to more kinds of geometric attacks, including combined attacks with common signal processing, than other watermarking methods reported in the literature. In Table 3 the average BCRs of the extracted watermark sequence respect to the original one, using the HOWA and the proposed algorithm, are shown. In the proposed algorithm, the BCRs of two watermark sequence W₁ and W₂ are shown separately in order to visualize the robustness (vulnerability) of each watermark sequence to different attacks. The experimental results show that the proposed method provides more robustness than the HOWA against rotations greater than 10° with auto-cropping, centered cropping and cropping combined with re-scaling attacks. The better performance of the proposed method is accomplished by the complementary techniques described in Section 3.2. The first R-G 2D histogram modification is implemented principally to combat geometric distortions, such as rotation, cropping, scaling, and shearing, among others, while the second B-R_wf 2D histogram modification complements the first modification to resist against JPEG compression and other common signal processing operations. The analysis of the watermark robustness of the HOWA and the proposed algorithm are provided in the next section. A performance comparison of the proposed algorithm with previous works was also carried out. The previous works considered here are the image normalization based scheme [7], the color histogram method [10], the HOWA [11], the feature-based scheme proposed by [5], the invariant domain scheme developed by [2] and the template-based scheme [4]. This comparison includes JPEG compression, scaling, cropping, aspect ratio change, rotation, shearing, Gaussian noise contamination, and median filtering. Table 4 shows the performance comparisons together with the watermark detection methods, i.e. if the detection algorithm is blind or if the original image is required, and the watermark length associated with each scheme. These results show the better performance of the proposed method compared with the principal methods reported previously against most common geometric and signal processing attacks.

Table 3.

Average number of BCR of extracted watermark sequence respect to the original one. The watermarked images were attacked by several geometrical and signal processing distortions. Watermark length n is equal to 128 bits and normalized threshold TN = 0.7

Attack	Algorithm by Lin et al. [11]	Proposed Method W1 / W1	Global detection results in our proposed method
	BCR	BCR
Un-watermarked Original Image	0.46 fail	0.46 / 0.45	fail
Remove Columns and Rows: 17 rows and 5 cols.	0.95 yes	0.99 / 0.96	yes
Centered Cropping 20 %	0.53 fail	0.92 / 0.49	yes
Flipping horizontal and vertical.	0.96 yes	0.99 / 0.95	yes
Scaling with Fs = 1.5	0.74 yes	0.96 / 0.71	yes
Affine [1, 0.01; 0.01, 1]	0.87 yes	0.97 / 0.89	yes
Aspect ratio (1.0, 1.2).	0.96 yes	0.99 / 0.95	yes
Rotation by 35° (with Auto-Crop and re-scaling 512 × 512)	0.51 fail	0.92 / 0.48	yes
Shearing (5%, 5%).	0.89 yes	0.97 / 0.90	yes
Cropping 20% and re-scaling 512 × 512	0.52 fail	0.95 / 0.53	yes
Compression JPEG QF = 30	0.85 yes	0.60 / 0.85	yes
Median Filtering 3 × 3	0.94 yes	0.87 / 0.95	yes
Impulsive Noise, density = 0.01	0.86 yes	0.93 / 0.87	yes
Stirmark Random Bending Attack	0.96 yes	0.99 / 0.95	yes
Sharpening 3 × 3	0.79 yes	0.71 / 0.80	yes
JPEG _70 + Remove 5 rows and 1 cols.	0.85 yes	0.68 / 0.85	yes
JPEG 70 + Flipping horizontal and vertical.	0.89 yes	0.66 / 0.88	yes
JPEG 70 + Affine [1, 0.01; 0.01, 1]	0.78 yes	0.69 / 0.82	yes
JPEG 70 + Shearing (0, 0.9%).	0.85 yes	0.67 / 0.87	yes
JPEG_70 + rotation 5°	0.74 yes	0.69 / 0.78	yes
JPEG_ 70 + scaling 1.1	0.86 yes	0.64 / 0.89	yes
JPEG_70 + cropping 10%	0.75 yes	0.65 / 0.92	yes
JPEG _70 + Sharpening 3 × 3	0.85 yes	0.70 / 0.87	yes
JPEG 70 + Median Filtering 3 × 3	0.82 yes	0.62 / 0.84	yes

Table 4.

Performance comparison.

Comparison	Solachidis et al.[2] (Invariant Domain Based)	Kang et al.[4] (Template Based)	Bas et al.[5] (Feature Based)	Roy et al.[10] (Histogra m Based)	C.H. Lin et al.[11] (Histogra m Based)	M. Cedillo et al.[7] (image normalizati on based)	Proposed method (Histogra m Based)
JPEG (QF)	20-100	10-100	50-100	50-100	20-100	20-100	30-100
Scaling	detected	detected	0.8-1	1.2 - 1.4	0.75 - 1.5	0.4-2	0.2 - 1.8
Cropping	up to 50%	up-65%	–	up to 60%	up to 15%	–	up to 55%
Aspect Ratio	–	detected	–	-	detected	detected	detected
Rotation (with Auto-Crop and re-scaling)	0°-3°	detected	0°-10°	0° - 40°	0° - 15°	detected	0° - 360°
Shearing	–	(5%x, 5%y)	detected	–	(5%x, 5%y)	(5%x, 5%y)	(5%x, 5%y)
Median Filtering	3 × 3	–	-	–	4 × 4	3 × 3	4 × 4
Gaussian Noise	detected	–	-	detected	–	detected	detected
Original Image for detection	blind	blind	blind	blind	blind	blind	blind
Watermark length	2304 bits	60 bits	64 bits	256 bits	128 bits	64 bits	128 bits

4.4

Analysis of watermark robustness

In this section the embedding methods proposed by the HOWA and the proposed algorithm are analyzed from the watermark robustness point of view.

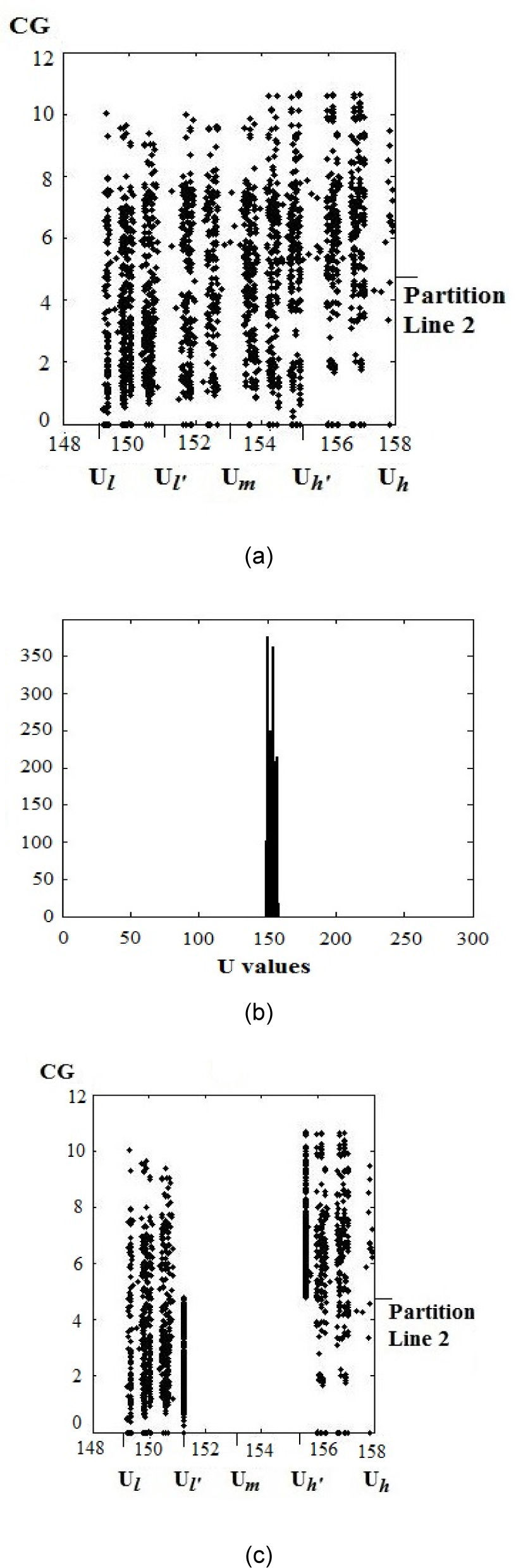
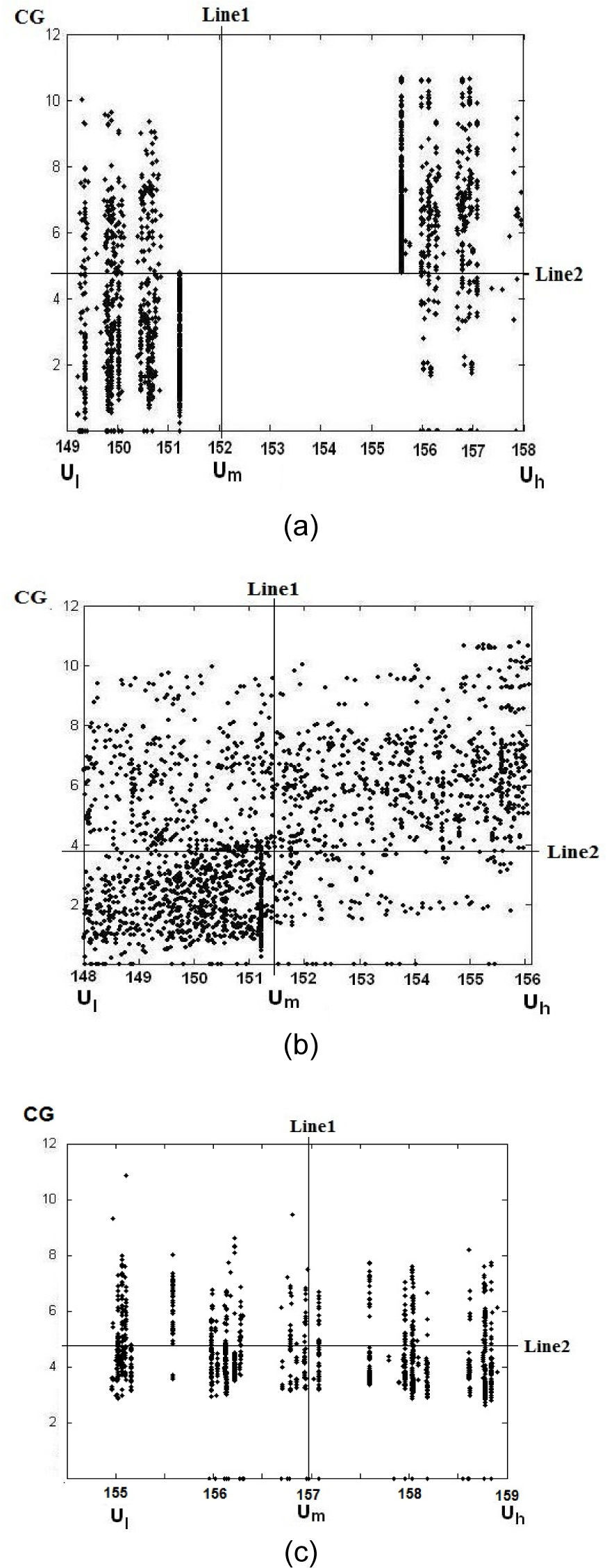
4.4.1

HOWA

In [11], the HOWA reported watermark robustness to a wide range of geometrical distortions, common signal processing, and combination attacks of geometrical distortion and common signal processing tasks. However the HOWA shows some vulnerability respect to cropping, rotation and combined attacks in which cropping and rotation are involved. The principal reason of this deficiency is the loss of synchronization of the block segmentation caused by cropping or rotations. Figure 10 (a) shows the distribution of pixels in U-CG plane of a specific block of the watermarked image without any distortion. Figure 10 (b) shows the pixel distribution of the watermarked and compressed image by JPEG compression with quality factor equal to 50, and Figure 10 (c) shows the pixel distribution of the watermarked and cropped image (10% cropping). From Figure 10 (a), the condition |SA| + |SB| < |SC| + |SD| is clearly satisfied, therefore the watermark bit ‘0’ is correctly extracted from this block. Figure 10(b) shows that after JPEG compression the distribution of the pixels are modified and also the values of U_l, U_m and U_h, as a consequence the positions of two partition lines are slightly modified due to the dynamic block segmentation used in HOWA, however the condition generated by the embedding process is satisfied (|SA| + |SB|<|SC| + |SD|) and then the watermark bit can be correctly extracted. On the other hand, in the distribution of the cropped image, the values of U_l, U_m and U_h, and the positions of two partition lines are drastically changed as shown in Figure 10 (c). It is due to the loss of some values of U components because of the cropping attack, which leads to an extraction error of the watermark bit.

Figure 10.

Pixel distributions in a specific block. (a) Distribution of the watermarked image (b) distribution of the watermarked and JPEG compressed image, (c) distribution of the watermarked and 10% cropped image.

4.4.2

Proposed Algorithm

To solve these vulnerabilities caused by synchronization loss in the dynamic block segmentation, the first histogram modification in the 2D R-G histogram is introduced in the proposed algorithm. In Table 3, the role of the watermark embedded in this domain is clearly observed. The global distribution of 2D histogram, as shown by Figure 4, can be sufficiently robust against attacks such as cropping and rotation, because these attacks only reduce the number of pixels in some color combination (ex. R-G), moreover the distribution of pixels generated by the proposed watermarking can be maintained.

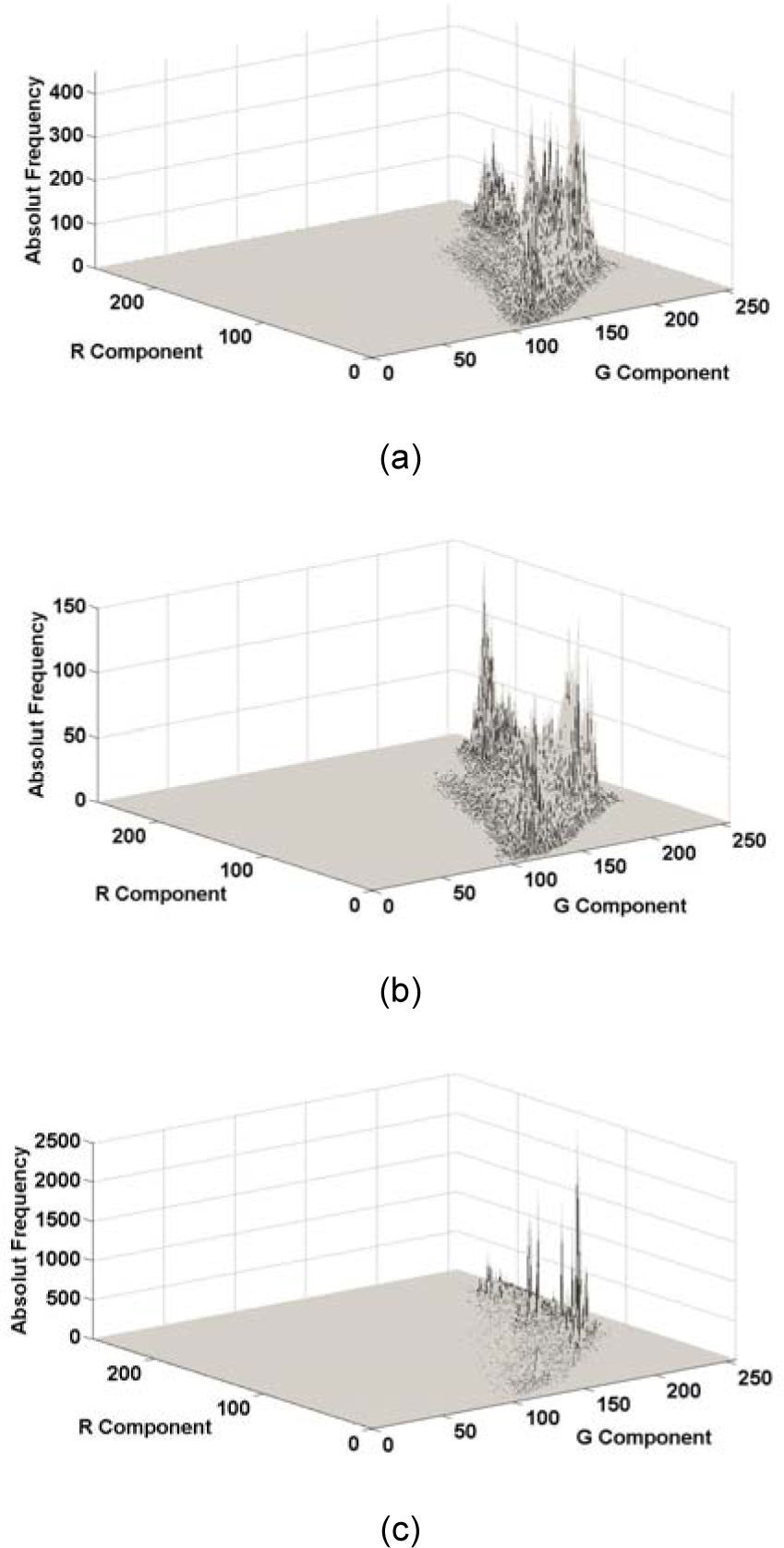
On the other hand, JPEG compression and some image processing modify the number of pixels of all color combination, generating a drastic change of the distribution. Figure 11 shows the situations mentioned above, in which z-axis shows the number of pixels of each color combination (note that the scales of these axes are not unified among (a)-(c) for a better visualization). In the watermarking method proposed by Roy et al. [10], the global distribution of the 2D histogram Cr-Cb is modified using EMD, therefore the embedded watermark is robust against cropping attack, although it can suffer from JPEG compression.

Figure 11.

R-G histogram. (a) Watermarked image without attack. (b) Centered cropping by 40%. (c) JPEG Compression by QF = 50.

Figure 12 shows 2D histogram distributions after several geometrical modifications (rotation by 75° with auto-cropping, centered cropping 40%, cropping 40% with re-scaling 512 × 512 and JPEG compression with quality factor QF = 50) to the watermarked images generated by the proposed algorithm. From this figure, it follows that the embedded watermark sequence resists to these geometric attacks (Figure 12 (a)-(d)), but it disappears after JPEG compression as shown by Figure 12(e).

Figure 12.

2D R-G histograms. (a) Watermarked image without attack. (b) Rotation of 75° with auto-crop. (c) Centered cropped image 40%. (d) Cropped by 40% and re-scaling to 512 × 512. (e) JPEG with QF = 50.

4.5

Detector capability

In the detection stage, the number of the extracted watermark bits has the binomial distribution given by

where n is the total number of watermark bits, T is the number of correct extracted bits, T is the threshold value and P_s is a success probability.

For a non-watermarked image, the extracted bits can be assumed as a Bernoulli trial with success probability equal to 0.5, therefore the false alarm probability with a threshold value T is given by (6). The watermark detection probability, when the image really contains the user's watermark sequence, is calculated by (7) using different values of the success probability P_s. The value of success probability P_s depends on attacks that the watermarked image has received, which is determined by (8).

The total number of matching bits is obtained applying a similar criterion that is used in [5], in which the matching bits are got after the watermarked image is attacked with a combined distortion (geometrical and signal processing attacks).

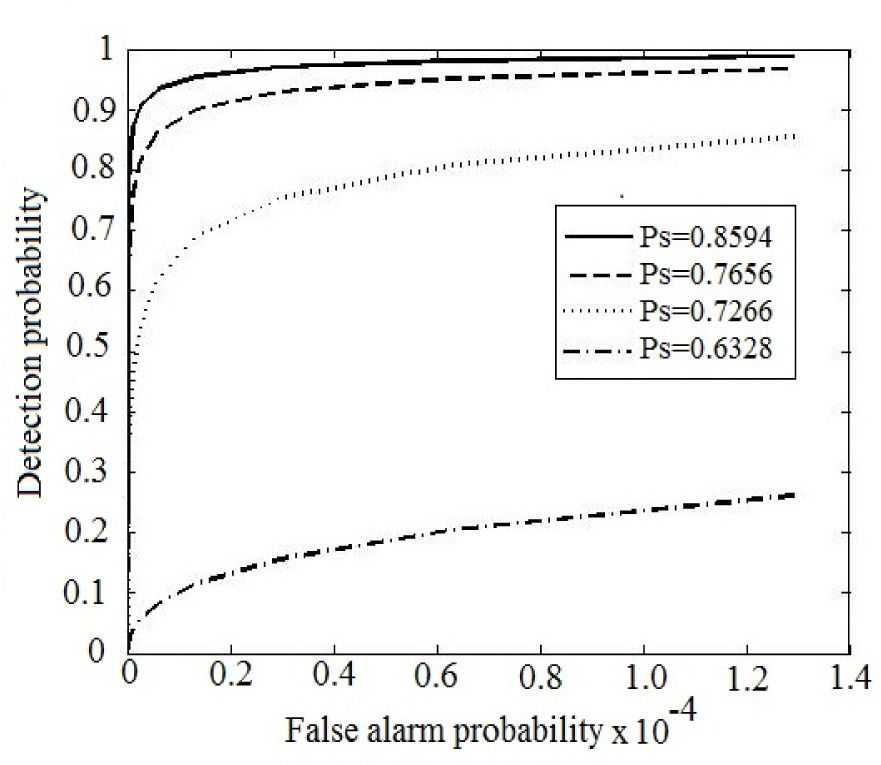
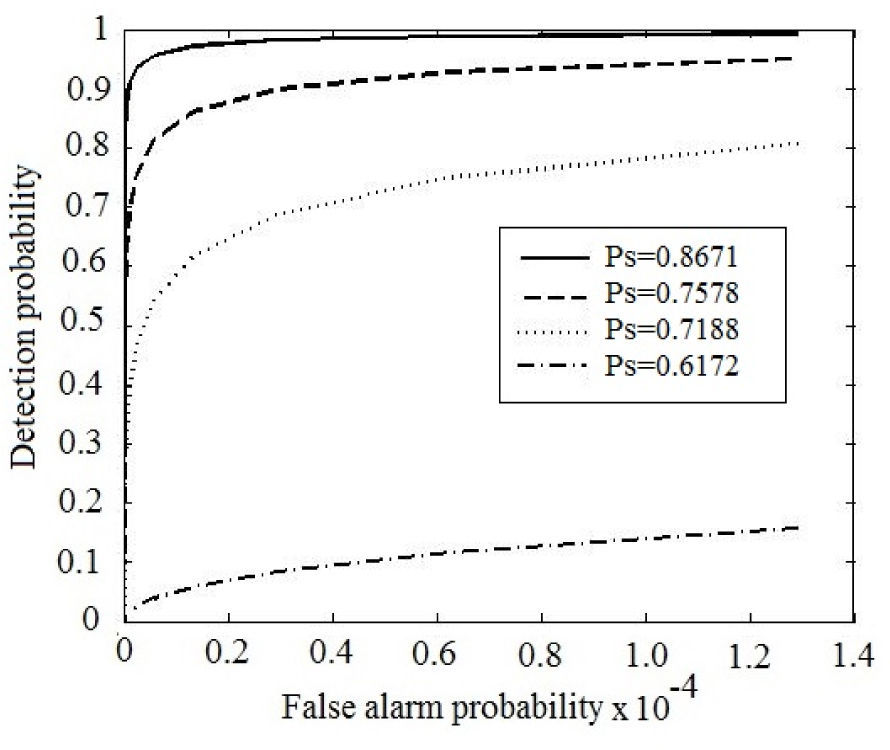
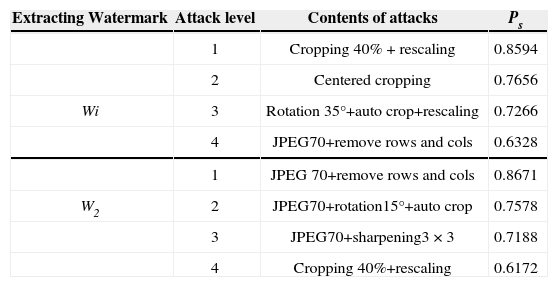
As mentioned before, due to the different embedding domains, the detection difficulties of two watermark sequences W₁ and W₂ against a specific attack are different; therefore the success probabilities P_s for two watermark sequences against several attacks are given in Table 5.

Table 5.

Success probabilities for two watermarks W₁ and W₂ under four different detection difficulties.

Extracting Watermark	Attack level	Contents of attacks	Ps
	1	Cropping 40% + rescaling	0.8594
	2	Centered cropping	0.7656
Wi	3	Rotation 35°+auto crop+rescaling	0.7266
	4	JPEG70+remove rows and cols	0.6328
	1	JPEG 70+remove rows and cols	0.8671
W2	2	JPEG70+rotation15°+auto crop	0.7578
	3	JPEG70+sharpening3 × 3	0.7188
	4	Cropping 40%+rescaling	0.6172

The receiver operating characteristics (ROC) curves for detection of W₁ and W₂ with different Ps are shown in Figures 13 and 14, respectively.

Figure 13.

Receiver Operating Characteristics Curves for W₁.

Figure 14.

Receiver Operating Characteristics Curves for W₂.

From the ROCs of the detector of the first watermark W₁ (Figure 13), the embedded watermark is sufficiently robust respect to cropping attacks with high cropping rate, however the detector capability drastically drops down when the watermarked image is compressed by JPEG compression. On the other hand, the ROCs of the detector for the second watermark W₂ indicates a fairly good detection performance when the watermarked image suffers JPEG compression attacks; however its performance drops down if the watermarked image is cropped 40. So there is a complementary behavior with W₁ and W₂.

5

Conclusions

Until now several histogram-based watermarking algorithms have been proposed, because histogram is considered as a suitable domain to embed watermark sequences, robust to several geometrical distortions. However these algorithms show watermark vulnerability against cropping attacks, or combined attacks of cropping and common signal processing methods such as JPEG compression. Considering the above limitations, in this paper a cropping resilient watermarking algorithm based on histogram modification was proposed. In the proposed algorithm, a watermark sequence is embedded modifying two 2D-histograms (R-G histogram and filtered R-B histogram). The first modification provides robustness respect to geometrical distortions, specially cropping and rotation attacks that cause synchronization loss, and the second one provides robustness respect to common signal processing, such as JPEG compression, filtering and Stirmark attacks.

The watermark imperceptibility of the proposed algorithm is evaluated in terms of three image quality assessment measures (PSNR, VIF and NCD), concluding that the visual distortion caused by the proposed watermarking algorithm is imperceptible. The watermark robustness of the proposed algorithm is evaluated using a wide range of attacks and a fairly good performance is obtained, which is compared with several watermarking algorithms reported in the literature. Also the embedding methods of the HOWA [11] and the proposed algorithm are analyzed from the watermark robustness point of view to justify the improvement of the watermark robustness obtained using the proposed embedding method.

Acknowledgements

The authors would like to thank the Council of Science and Technology (CONACYT) in Mexico, to the National Polytechnic Institute (IPN) of Mexico and to the Program of Post-Doctoral Scholarships DGAPA in the National Autonomous University of Mexico (UNAM) by the support provided during the realization of this work.