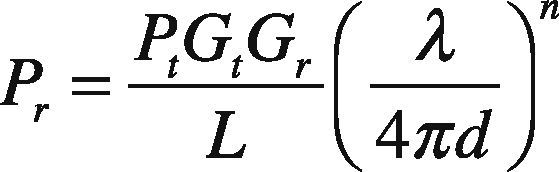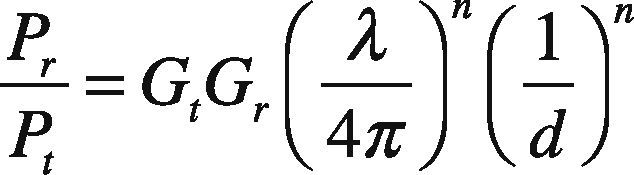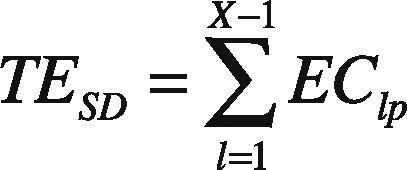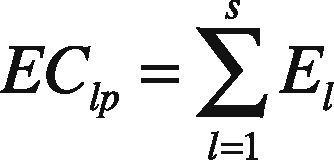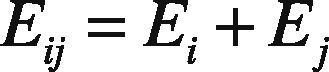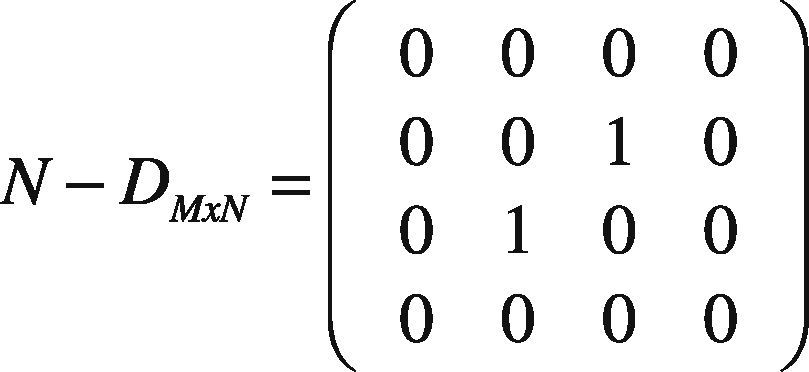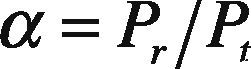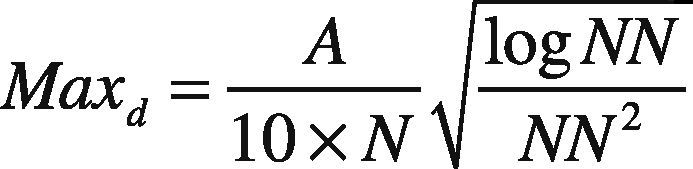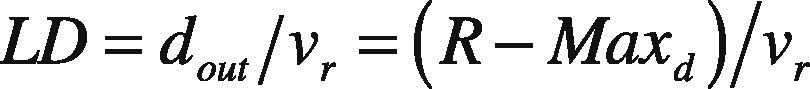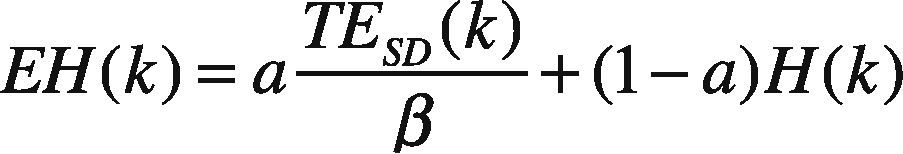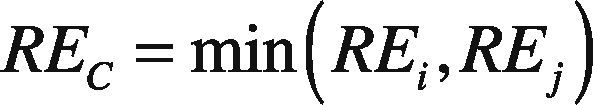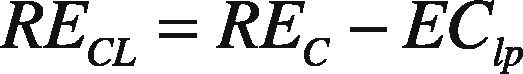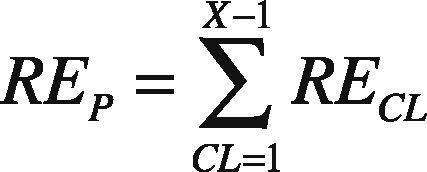The nodes in mobile ad-hoc network depend on battery for its power. Therefore, effective utilization of energy is necessary for efficient transfer of data between the persons involved in rescue without connection termination in disaster situation. An Optimal Path Selection Model (OPSM) is proposed to achieve this. First, routes are identified with the links having high power ratio and link duration. The path selection aims at reducing the number of node failures which in turn obtains energy saving. Then, the source will select a node-disjoint path based on energy and hop for data transfer and store the remaining paths in cache. Priority based path maintenance is also proposed for the selection of routes from cache based on remaining energy if the primary selection fails. Path selection and maintenance extend the network lifetime by reducing the energy usage in transmission. Simulation results revealed that OPSM achieves 64% and 50% reduction in energy consumption compared to Dynamic Source Routing (DSR) and Multipath DSR (MDSR). The number of path breakages is also 11 times and 5.5 times lesser than DSR and MDSR. Thus, it can be said that OPSM is a better choice for optimal path selection for performance enhancement by saving energy and improving lifetime.
Mobile Ad-hoc Network (MANET) is an attractive type of wireless networks without infrastructure. The battery dependent nodes pose many problems. It mainly affects the lifetime of mobile nodes. Nodes communicate in multi-hop nature. Some of the applications of MANET are mission critical data applications, such as disaster response, recovery systems, and military battlefields (Catarci et al., 2008). Many reasons are stated in the literature for the inefficient routing such as node mobility, limited battery capacity, node failure due to node sharing and energy depletion. The authors (Bahi & Salomon, 2010) introduced an energy controlled load balancing problem to improve overall lifetime of heterogeneous MANET. Node mobility causes failure of wireless links between nodes which leads to more number of route reconstructions. The number can be reduced if reliable links are used. Most commonly used link reliability metrics are link expiration time, probabilistic link reliable time, link packet error rate, and link received signal strength.
Minimum Transmission Power Consumption Routing protocol (MTPCR) (Chen & Weng, 2012) selects the path with minimum power consumption. It also implements a path maintenance mechanism for obtaining good path bandwidth. The authors concentrated on the received signal power and contentions in the MAC to determine the success ratio. Our task is to design a routing method that finds a reliable and efficient path. The reliable path is one in which the links in the path should have high power ratio and Link Duration (LD). Power ratio is the ratio of the received signal power to transmit power. This is used to determine the packet-forwarding capability. If this is high, then we can say that the path has high transmission bandwidth, i.e. high packet delivery ratio. LD can be said as an estimate of route expiry times and this measure can be used to reduce the burden on network bandwidth, when the node fails in a link. A performance study on LD given in (Huang et al., 2008) reveals that LD is independent of routing protocol but it depends on node speed and mobility. Analytical model of link duration for random waypoint mobility model is detailed in Tsao et al. (2006). The LD calculation is carried out based on the idea given in this. They analyzed how the relative speed and distance affects LD. For this computation, maximum transmission range of one hop neighbours is modeled based on number of neighbours, area, and total number of nodes. In Chen et al. (2002), they have analyzed the optimal transmission range based on physical layer which minimizes the total Energy Consumption (EC) and its impact on channel parameters. The work by Deng, Han, Chen, & Varshney (2007) explains the influence of network parameters like node density, network radius on the optimal transmission range in a two dimensional poison network.
In Huang and Fang (2009), the expected duration a node that is connected to the rest of the network is analyzed. They also focused on how to set up multiple best paths that are node-disjoint. Split Multipath Routing (SMR) (Lee & Gerla, 2000) has been designed to provide multiple paths. However, not all the paths can be used simultaneously and it can be used as a backup path. SMR concentrated on reducing the frequency of route discovery processes and thereby reducing the control overhead in the network.
In Braided Multipath Routing (BMR) (Ganesan, Govindan, Shenker, & Estrin, 2001), authors suggested that the node-disjoint multipath routing is not energy efficient, because disjoint path may contain longer hops and consumes more energy. In order to overcome the disadvantages in multipath; it is decided to choose a single optimal path based on a bi-objective function, which is dependent on EC, and hop. The process of optimizing multi-objectives is discussed by many authors (Deb, 2002, Colletter & Siarry, 2003, Tanino, Tanaka, & Inuiguchi, 2003). They found that the optimization of multi-objectives is difficult to analyze and to proceed. Therefore, a single objective function is derived from the defined two objectives. An intelligent power aware routing based on fuzzy concepts to select stable routes is dealt in Abirami et al. (2012) that have a balance between its battery efficiency and power consumption.
Communication quality also reduces due to node energy depletion, which results in link failure. Node failure may be due to node sharing. So, it is decided to extend the node battery lifetime by incorporating node-disjoint multiple paths. Multipath routing is mainly to protect route failure and these distribute packets among more than one path. It leads to a problem of fragmenting and re-assembling the packets from different paths at the destination. For this, some additional control messages are necessary to collect neighbor information and this lead to additional overhead in the network. To overcome this, one best path from multiple paths is chosen in the present design.
In this paper, Optimal Path Selection Model (OPSM) is proposed that finds an optimal node-disjoint path with less EC and number of hops. The proposal also utilizes the Power Saving Mode (PSM) of 802.11. Theoretical analysis reveals that the proposed is energy efficient with enhanced network lifetime. Network lifetime computation is taken from Bahi and Salomon (2010). Further, to reduce the overheads, priority based path maintenance is also implemented based on residual energy of the path. Simulation analysis using NS-2 proves that OPSM gives a reduction in EC and number of node failures thereby enhancing the network lifetime when compared to the existing. The rest of this paper is structured as follows. Previous works on energy aware routing protocols including multipath are reviewed in the second section. Third concentrates on the theoretical background of the proposed model. Fourth section elaborates the proposed OPSM. Result analysis is dealt in the fifth section. The last concludes the work.
2Related WorksDynamic Source Routing (DSR) (Johnson & Maltz, 1996) is an on-demand routing protocol. It comprises of two mechanisms: route discovery and maintenance. Route discovery is the process in which a source node discovers a route to a destination by broadcasting a Route Request (RREQ) after searching in its route cache for data transfer. RREQ packet consists of source and destination addresses, as well as unique route identification (ID). When a node receives a RREQ, it checks the request ID to verify whether it has already processed or not. Based on this, the node will forward the RREQ by adding its address. This process is repeated until it reaches the destination. Suppose, if the receiving node is the destination, then it simply sends a Route Reply (RREP) to the source. Among all the traced paths, DSR dynamically selects one path to transmit data with the minimum number of hops. In the route maintenance phase, if a node detects a link failure, it removes the link from its cache and sends a Route Error (RERR).
An extension of DSR protocol called Multipath Dynamic Source Routing (MDSR) is given in Nasipuri and Das (1999), where flooding of RREQ is minimized. In this, a destination replies only to a selected set of request messages after receiving all requests. The paths are link-disjoint. The alternative path selection from the received path continues until all paths are used. If there are no routes in a cache, source initiates route discovery. Although this eliminates frequent route discoveries, the alternate paths may be longer. Thus, it results in delay. In addition, a few intermediate nodes have alternate paths to destination and it can also increase the route discovery. Therefore, this scheme will end up in increased overhead. So, the proposed OPSM takes into consideration the number of hops to reduce the path length.
In Sheikhan and Hemmati (2012), a transient chaotic neural network is chosen to train the nodes in the network which are used to obtain optimal or sub-optimal high reliable disjoint paths. To improve transmission reliability, multiple paths are selected to be node-disjoint or link-disjoint. They proved that, without extra overhead and with less number of iterations, the system could find the high reliable disjoint path set in MANETs. Their intention in this is to find as many disjoint paths as possible that are most reliable. Routes are discovered by flooding. They declared that finding multiple paths in a single route discovery reduces the routing overhead. However, the main disadvantage here is computational complexity.
DPSP (Papadimitratos et al., 2002) is called Disjoint Path set Selection Protocol for multipath routing. They found highly reliable paths from a set of all paths, and argued that their obtained path set is the best in all the ways and no more link-disjoint paths can be found from the network. They claimed that it is advantageous in terms of minimum number of route discoveries and transmission delay. The main drawback of this is that it can give only link-disjoint path.
The proposed presents an optimal path selection method that includes finding and selecting a path. Its objective is to conserve the energy and prolong the network lifetime by reducing the overheads and the number of node failures.
3Theoretical Background of the Proposed OPSMThis section briefly describes about the assumptions and notations used for the design methodology, computation of power ratio, EC and formation of node-disjoint paths.
3.1Assumptions and Notations for the Path Finding ApproachThe following assumptions are considered for the proper reception of the signals:
- 1.
Receiver sensitivity is kept at –80 dBm.
- 2.
SNR threshold is set as 10dB.
- 3.
All nodes generate a random number between 0 and 1 once it receives a RREQ for checking whether the signal is properly received or not.
- 4.
Nodes in the PS mode are expected to synchronize in a distributed way (Huang & Lai, 2002).
- 5.
All nodes in the network have same fixed transmission range.
- 6.
The threshold for LD is set as 0.
Path finding approach involves two factors such as power ratio and LD. In signal transmission, the signal is affected by noise and interference in the radio channel. During the reception, the received signal power will be very much lesser than the transmitted one. For proper reception, the received power level should be higher than the receiver sensitivity and minimum Signal to Noise Ratio (SNR). Receiver sensitivity is defined as the power of the weakest signal which can be correctly received and demodulated by the receiver. SNR gives us the ratio between the signal and noise power. Therefore, the receiver will receive transmitted signal only if the receiver satisfies the above two.
The general notations used throughout this paper are tabulated in Table 1.
General notations.
| Symbol | Descriptions |
|---|---|
| Pt & Pr | Transmitted & received power in dBm |
| α | Power ratio |
| Gt & Gr | Gain of the transmitting & receiving antenna |
| λ | Wavelength in meters |
| d | Distance between transmitter and receiver in meters |
| n | Path loss coefficient (2 to 4) |
| L | Path loss component (L=1) |
| NN | Number of one hop neighbours |
| NR | Number of neighbours broadcasted the RREQ |
| N | Total nodes in network |
| Etxi | Energy spent for the transmission of data by node i; |
| Erxj | Energy spent for receiving data by the node j |
| Esleepj | Energy spent in the sleep state j |
| Etransj | Energy spent for the transition from awake to sleep for node j |
| A | Area of the network |
| R | Defined transmission range |
| dout | Distance that a node becomes out of transmission range |
| vr | Relative speed |
| LDth | Link duration threshold |
| r(0,1) | Random number between 0 and 1 |
| EH(k) | Objective function for path selection based on energy and hop |
| H(k) | Hop count |
Nodes in MANET use radio waves for their communication. Therefore, the transmitted data will travel as a wave in the space. In general, the received power attenuates with respect to the distance. Based on Friis transmission formula (Wesel, 1998), the received power in dBm of the links is computed using the Eq. (1) as follows:
In the above, Gt and Gr are the unity gains of the transmitting and receiving antennas, path loss coefficient (n) takes a value of 2 to 4. Usually value ‘2’ is for free space model, and ‘4’ for two-ray ground propagation model. The Eq. (1) is rewritten as follows:
If we assume gain of the antennas as unity, then from the Eq. (2), it is clear that the power ratio at a node is inversely proportional to the distance raised to the power of n. Therefore, the power factor is dependent on distance.
3.3Analysis of ECThe EC for the OPSM is computed as given in Eqs. (3) and (4) and it is updated in the TESD field of RREQ for all the (X – 1) links. X represents the number of nodes in the path. Eq. (4) denotes the EC of the individual link for transmitting the entire data.
Energy consumed by the individual link El between a pair of nodes i, j for transferring the entire data is EClp, and it is given as in Eq. (4):
In Eq. (4), s represents the number of packets. EC of the individual link El between a pair of nodes i and j is given in Eq. (5) as Eij:
subject to Ei=Etxi and Ej=Erxj+Esleepj+Etransj
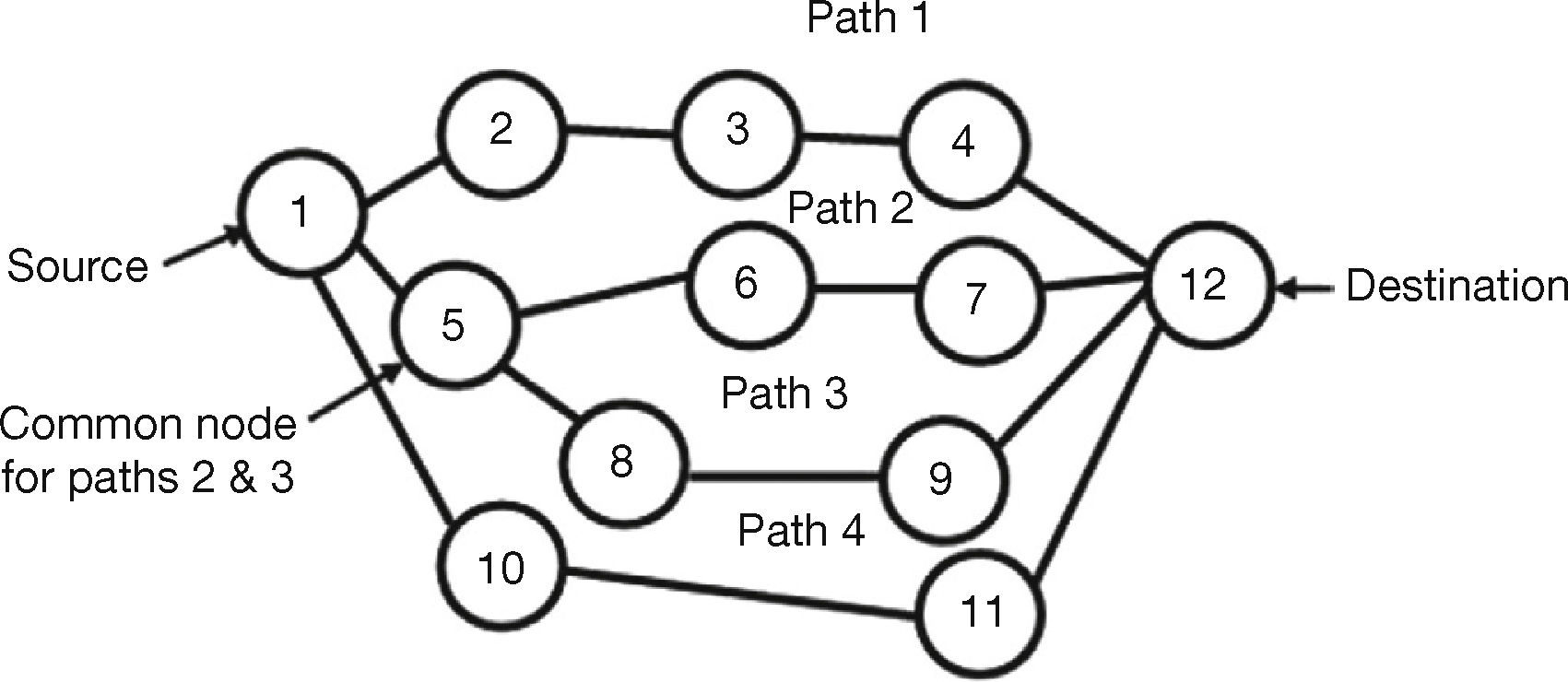
3.4Node-Disjoint Path FormationFor the proposed path selection, the multiple paths formed are node-disjoint. The link-disjoint is left unconsidered. Because, node-disjoint are more advantageous than link-disjoint, since there are no common node or link. Therefore, node failure in one path does not affect the other paths. An example of multiple paths between source and destination is shown in Figure 1. From this, it can be seen that path 1 and 4 are the node-disjoint paths. Path 2 and 3 are not node-disjoint, since node numbered 5 is shared. The received multiple paths are stored as a matrix of size M × N where M = N. Here the matrix size is 4 × 4.
The elements for the square matrix for node-disjoint (N-D) for the size M × N is formed as given by the following condition in Eq. (6):
The ith path is compared with the remaining jth paths based on the condition i ≠ j, i.e. first path is compared with the remaining paths (2, 3 and 4) for finding the elements of the first row. It can be seen that there is no common node. The first row of the matrix is made all zeros. Second path is compared with first, third and fourth paths. It is found out that there is a common node number 5 in second and third path. Therefore, the third element in second row is marked with one. Similarly, the remaining paths are checked for finding the third and fourth rows. It is noted from the output matrix that all the diagonal elements are zero. Because comparison of first row with first and second with second definitely are same and based on the above condition in Eq. (6), the diagonal elements are made zero. The matrix for Figure 1 is given in Eq. (7) as follows based on the above condition:
The row containing all zeros is node-disjoint path in the path finding process. Here the chosen paths are two out of four. The destination checks this node-disjointedness for the received RREQs and gives RREPs.
4Description of the Proposed OPSM Method4.1Path FindingThe source node broadcasts a RREQ message to discover a route to all neighbor nodes currently within the transmission range of the source. Initially, the transmit power level is assigned as 200 mW (23 dBm). As soon as the nodes receive RREQ, it generates a random number (r). This number is used to compare with the power ratio in order to determine whether the node is eligible for forwarding the RREQ. We compute the ratio of received power to the transmit power as mentioned in the Eq. (2) and it is defined as the power ratio (α) as given in Eq. (8):
In order to compute the LD, a term ‘Maxd’ is introduced, and it is nothing but the maximum distance between any two nodes. This value is modeled as a dependent factor on area, total number of nodes, and neighbours in the selected network. It is found out using the following formula:
The valuelogNN indicates that there exists one neighbour definitely. Maxd can be either zero or defined transmission range (R). Eq. (9) is valid only if the following conditions are satisfied:N≥(A)1/3; R≥A4 and NN≥3. The condition is set because in real MANET applications, for example in a disaster situation like a fire accident, the efficiency of rescuer depends on how many neighbours they have in a particular area, because too high results in congestion and too low will end up in a failure. Hence, it is modeled as above and the maximum distance between two rescuers can be as given in Eq. (9). The main aim is to route the information through only a limited number of reliable nodes for energy saving and also to maintain the connectivity. By keeping these in mind, it is modeled based on the number of neighbours, total nodes and area.
Power ratio alone does not give a reliable route. Therefore, LD is found out in order to improve the reliability. If the value is very much smaller, then it is understood that the link is going to break. Hence, it is decided to validate LD in path finding process. LD is defined as the active link time between two nodes.
From the above Eq. (10), a link is considered as broken if the value of dout becomes zero. The path finding is carried out as per the following algorithm:
Path finding approach finds multiple paths, which satisfies the condition. Then, the path selection is carried out to find the reliable paths.
4.2Path SelectionPath selection involves finding the node-disjoint paths from the received multiple paths. These are given as RREP's back to the source by the destination node. The source stores a maximum of three optimal node-disjoint paths in its cache and selects one. The optimal path in the sense is that the path with minimum energy and hop. The focus is to reduce path breakage and to increase the network lifetime. The EC is calculated based on the Eq. (3) and it is updated in the RREQ field. After receiving all the RREQ's, the destination finds multiple node-disjoint paths and gives back reply to the source to make a decision based on the updated EC and hop count for all the received Multiple Paths (MP).
A single objective model is proposed as given in Eq. (11). The source node validates the node-disjoint paths based on the following objective function for selecting the best optimal possible route. Equal weight is given to both the energy and hop in the minimum path selection. Minimization of energy without taking the hops may lead to a node-disjoint path selection with increased number of hops and vice versa. The following is the mathematical model for the OPSM design.
Subject to
where H(k)≥3; 0
Based on the above Eq. (11) optimal node-disjoint path can be found that consumes least energy with minimum number of hops. The source node after validating based on the above
starts data transfer. In Eq. (12), if the adjustable parameter a is zero, then path selection is purely depends on the hop count and vice versa. Normalization is necessary here because of the usage of two different quantities. The normalization coefficient β is introduced in order to maintain a balance between the energy and hop count. If the energy is in J, then the value of β is also in J.
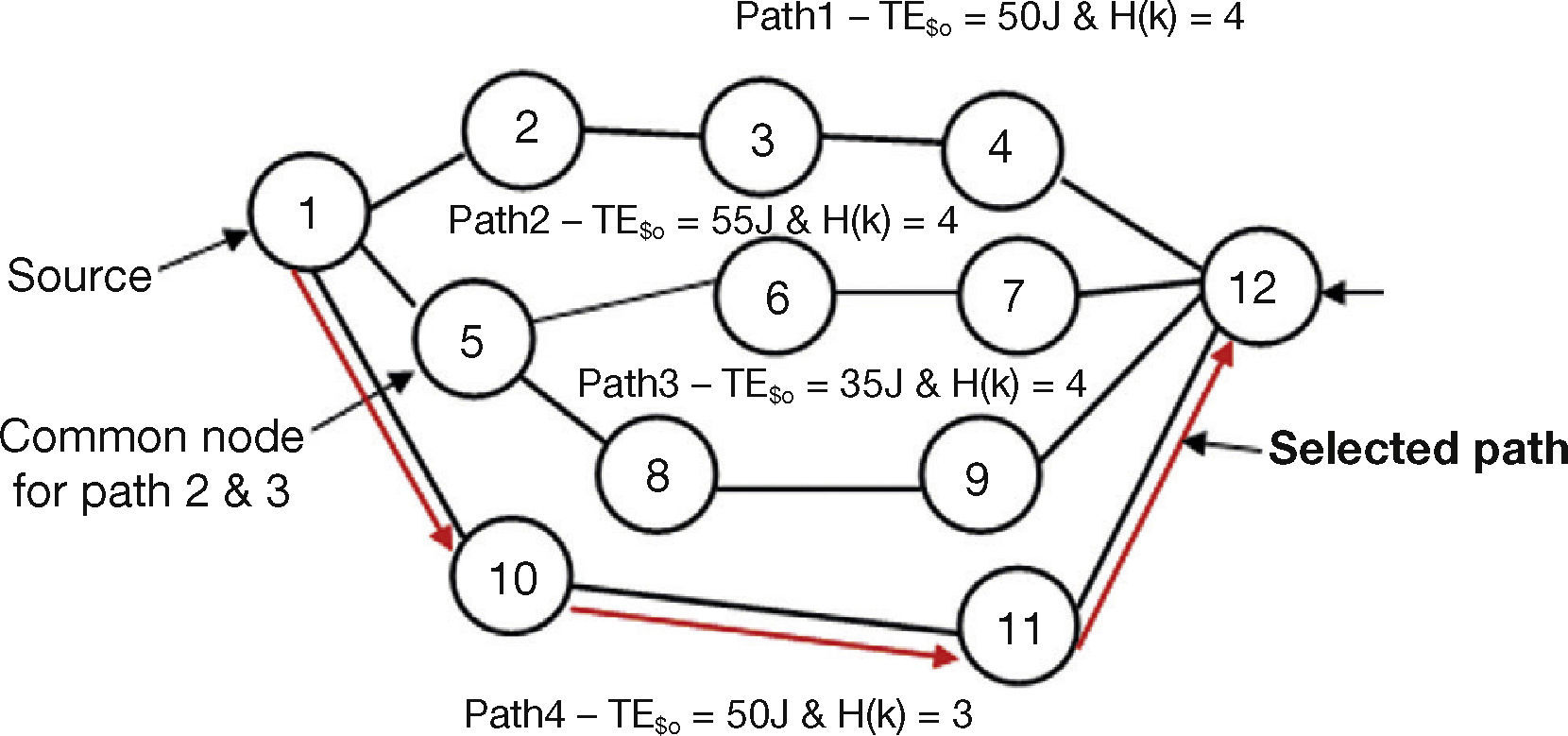
For example, the EC of a path TESD(k) is 3J and H(k) is 3, then the β value is chosen as 1.1J × 3 = 3.3J. The maximum energy consumed for a single hop in the selected path is 1.1J. Therefore, the optimal decision could be either energy or hop based or minimal of both. The path selection based on optimal node-disjoint is shown diagrammatically with an example in Figure 2.
It can be noticed from the diagram that it contains two node-disjoint paths namely path 1 and path 2. The selection at the source is subject to the objective function based on energy and hop. So, the path chosen for data transfer is path 4. And path 1 is stored as a backup path in the source cache. The proposed system invokes a path maintenance mechanism if the selected fails in order to reduce the overhead. It is done based on a simple selection process of stored routes based on remaining energy by round robin fashion.
4.3Path MaintenanceWhen forwarding a packet to a destination, if there is a route failure, path maintenance is activated to manage the data transfer. Each node along the route is responsible for detecting whether the link to the next hop is broken or not. When the retransmission and acknowledgement mechanism detects that the link is broken, then it returns a RERR packet to the source. The node will then check its route cache to find if there is any alternative route present. If there is one, the node will change the source route in the packet header based on priority and sends it using this new route. This is called as “packet salvaging.” Priority is based on residual energy whether it is high, medium, and low. REC is Current Residual Energy of the Link and it is computed as given in Eq. (13).
REi and REj are the residual energies of the nodes i and j. The individual link's residual energy is assumed to be greater than the computed value of EClp. The link's residual energy is calculated based on Eq. (14).
This REP field is updated in the RREQ. The source assigns the priority, based on this value, and selects the path from the cache. First chance is given to the path with high priority and then to medium and low. When a RERR is received or overheard, the link in error is removed from the local route cache. If all the routes in the route cache are used, then a new route discovery mechanism is activated.
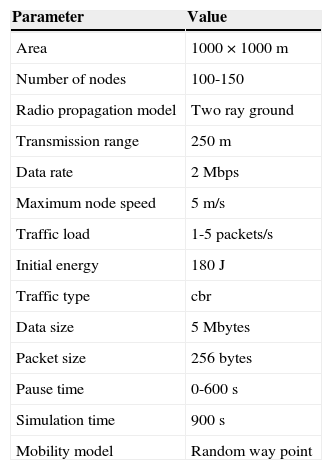
5Performance EvaluationOPSM is evaluated using C++ based NS2 simulator. The proposed is compared with the basic DSR, and MDSR. Simulation results are taken after 50 runs to obtain steady state value. The simulation setup parameters are summarized in Table 2. Mobility model chosen is Random Way Point (RWP) model (Bettstetter, Hartenstein, & Pérez-Costa, 2004) in which each node takes its new location and speed. For simulation analysis, the random motion value for each and every change is taken and the relative speed for LD computation is found out.
Default simulation parameters.
| Parameter | Value |
|---|---|
| Area | 1000 × 1000 m |
| Number of nodes | 100-150 |
| Radio propagation model | Two ray ground |
| Transmission range | 250 m |
| Data rate | 2 Mbps |
| Maximum node speed | 5 m/s |
| Traffic load | 1-5 packets/s |
| Initial energy | 180 J |
| Traffic type | cbr |
| Data size | 5 Mbytes |
| Packet size | 256 bytes |
| Pause time | 0-600 s |
| Simulation time | 900 s |
| Mobility model | Random way point |
Observations have been made for the following parameters: EC, control packets, PDR, overall EC, latency for different load conditions, number of path breakages and path lifetime.
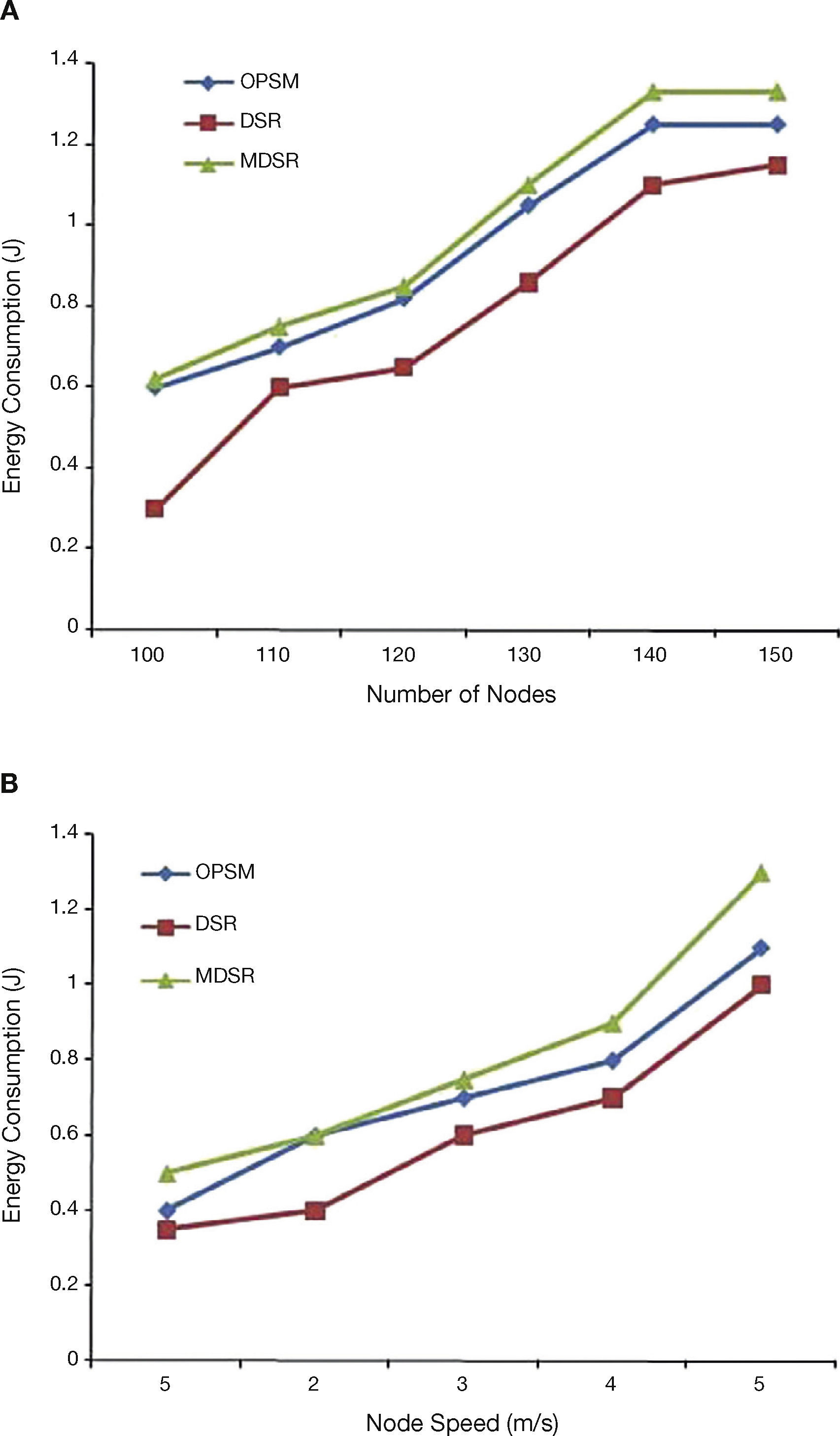
5.1Impact on ECFigure 3 shows the illustration for EC in path finding approach. EC here is dependent on the number of control packets utilized to obtain reliable path based on power ratio and LD.
Figure 3A is plotted by varying the number of nodes and keeping the node speed as 2 m/s.
Figure 3B is by varying the node speed and keeping the nodes in the network as 100. It is observed from the above that more energy is spent for finding the reliable paths in path discovery process in the proposed compared to DSR and lesser compared to MDSR. The reduction is due to the reason that our proposed system restricts the unnecessary flow of RREQ based on power ratio and LD. These computations are not available in MDSR.
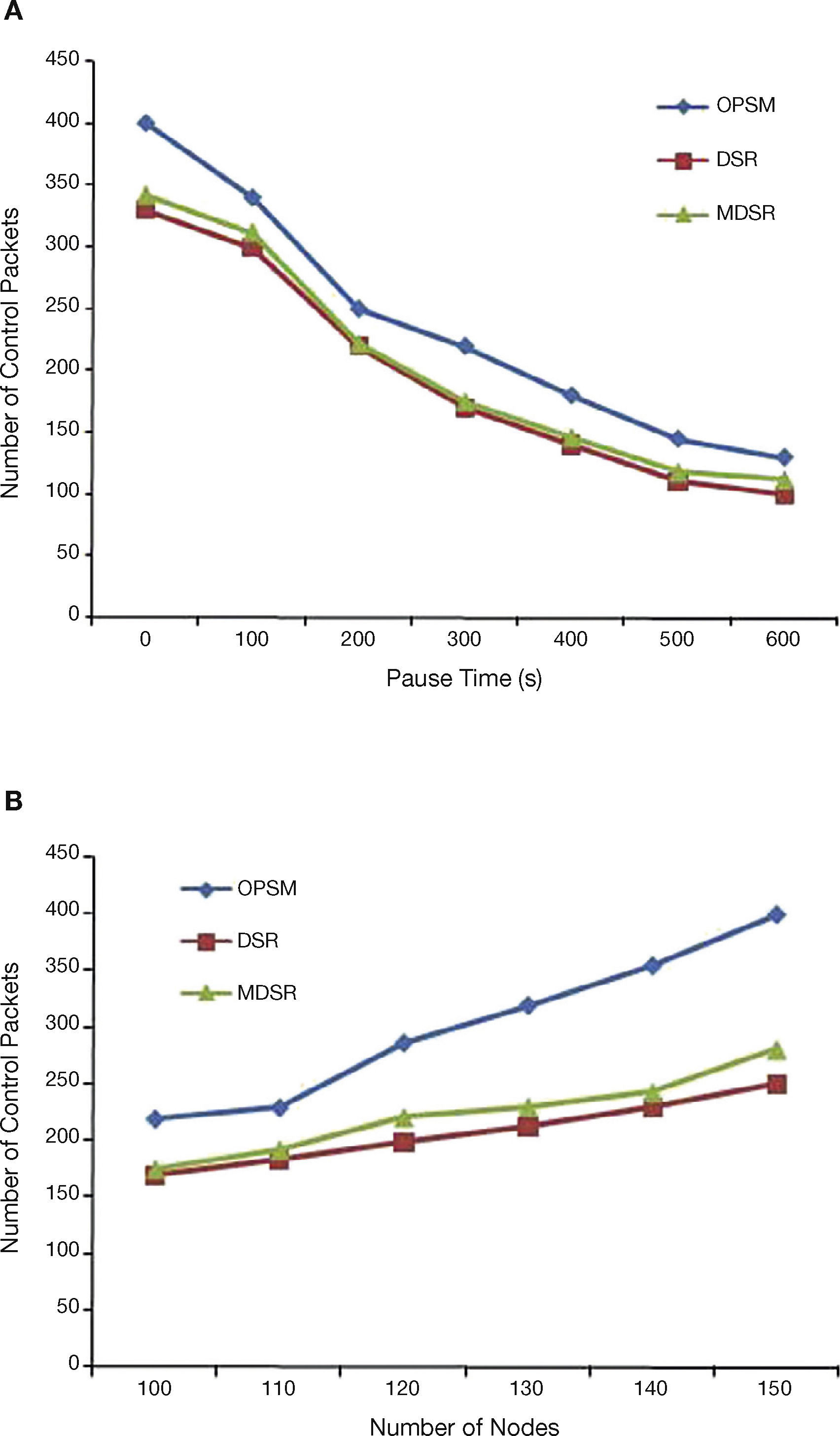
5.2Impact of Control PacketsThe overhead analysis in path discovery phase is shown above based on pause time and number of nodes in Figures 4 A and B.
OPSM costs more number of control packets compared to other two in path finding process. This increase in number of control packets compared to DSR and MDSR are due to the eligible node selection for forwarding RREQ to obtain reliable paths. It results in less EC in data transfer and high PDR with reduced number of route re-finding. In addition, the path maintenance mechanism and node-disjoint selection results in reduced number of path breakages.
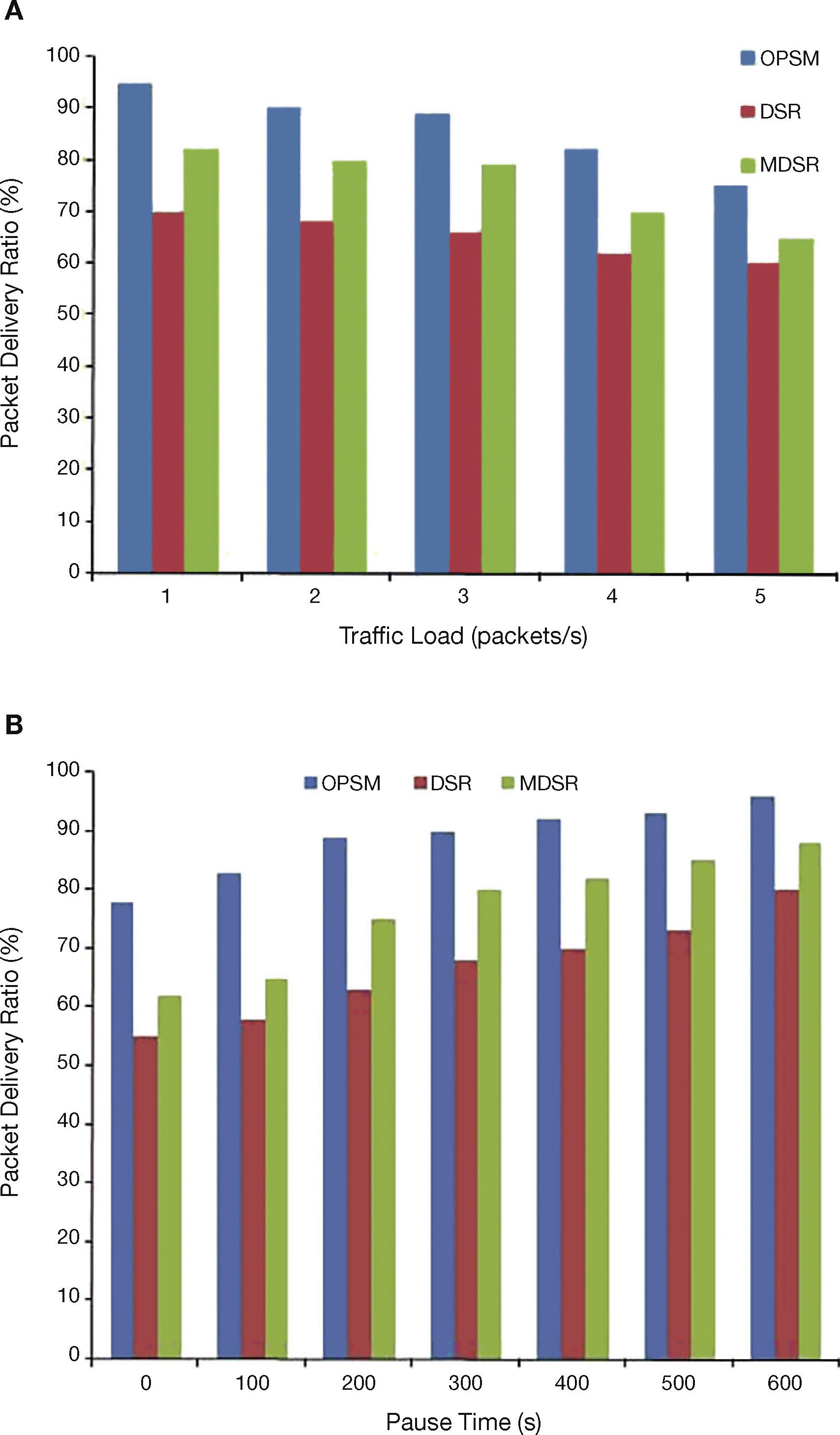
5.3Impact of Packet Delivery Ratio (PDR)PDR is illustrated in Figure 5A by varying the traffic load in the network from 1 to 5 packets/s for a total of 100 nodes in the network.
Figure 5B presents the PDR by varying the pause time from 0 to 600 s and maintaining a constant traffic load of 2 packets/s for the same number of nodes in the network.
The performance of PDR is appealing in the proposed system. This is because that OPSM selects reliable node-disjoint paths that satisfy the mathematical model for data transfer.
Therefore, the chances for path breakage due to node failure are very less. PDR of MDSR is also higher compared to DSR, because of the prediction of paths based on link disjoint. Proposed method keeps only three backup paths in addition to the reliable path discovery based on LD. So, the selected paths are very much reliable in delivering the data.
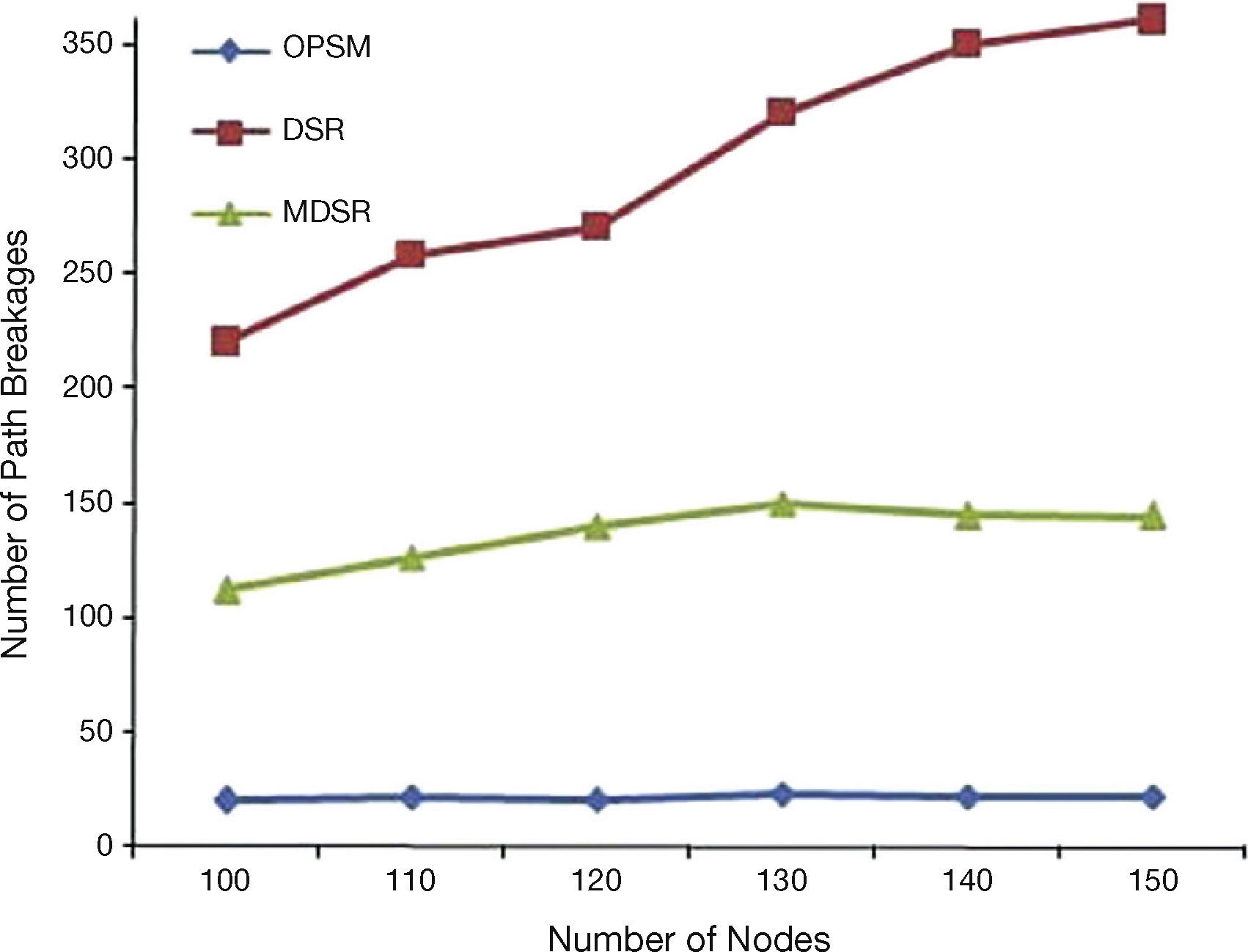
5.4Path Breakage AnalysisAnalysis of path breakage is illustrated in Figure 6. OPSM achieves an average of 22 path breakages. Reduced number of path breakages in OPSM is the result of the inclusion of LD and node-disjoint in path finding process.
LD is one of the metric in determining the mobility. This computation considers the nodes in the links having a value greater than the threshold. So, the nodes move out of the transmission range are not included in the selected path. In addition, path selection results in the selected path with minimum number of hops and energy. But MDSR does not consider these factors. Therefore, except the primary path, the hops in alternate paths are more in number if the design focus is only on disjoint paths. Therefore, route failure will increase in MDSR. Out of the three, OPSM's performance is the best.
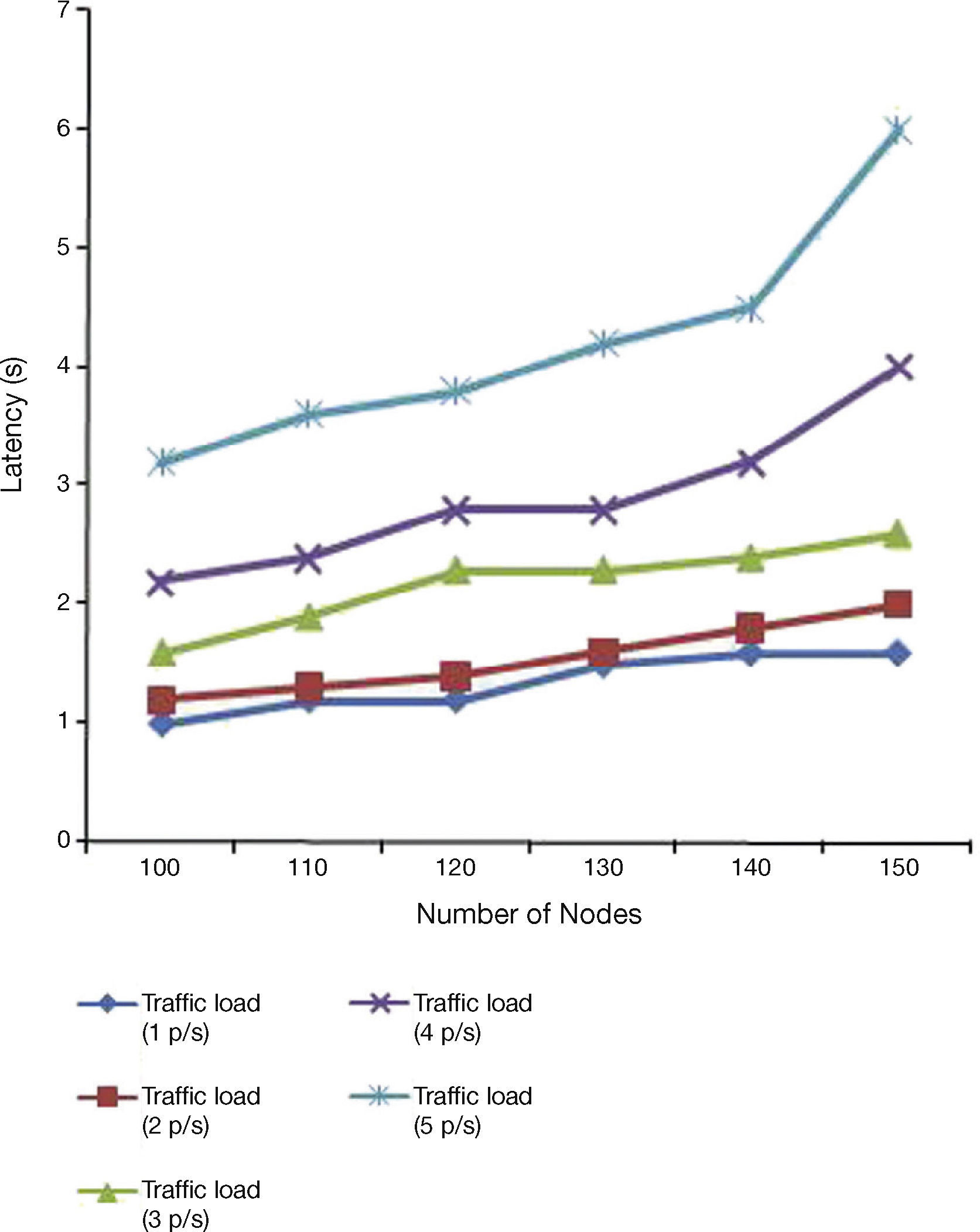
5.5Impact on LatencyIn general, delay is not avoidable in power save mode operation. The reason is that every time a node has to wait for the beacon interval for transmission. In path finding approach, delay is more, because our proposed OPSM selects the reliable node-disjoint paths based on power ratio and LD. However, the overall delay for transferring the data is tolerable.
Average latency measure for different number of nodes is shown in Figure 7 for different traffic loads (packets/s) injected into the network.
Average packet latency shows an increasing trend as the traffic load varies from 1 packet/s to 5 packets/s. This is due to the reason that, if the node density is more, there are chances that the packet has to travel more number of hops. Therefore, every time the node has to wait for its beacon interval. On the average, for a traffic load of 5 packets/s, OPSM latency is three times that of the traffic load of 1 packet/s.
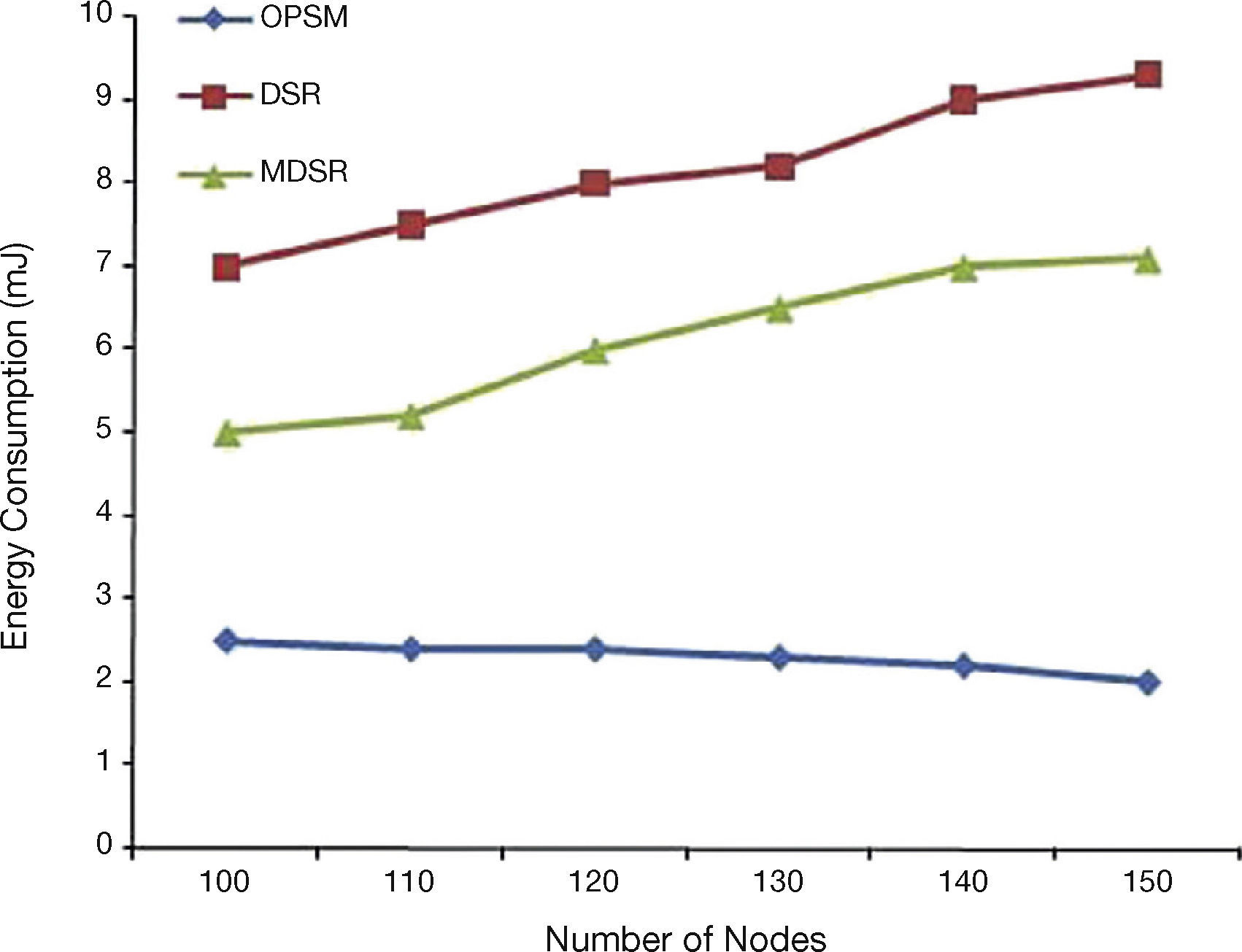
5.6Impact on Overall ECThe overall EC analysis is illustrated in Figure 8 for the pause time of 300 s. It shows the energy consumed for transmitting one byte of information. The reason behind the reduction in the energy for OPSM is flooding of RREQs is restricted using the path finding and also the presence of optimum path selection model.
From the analysis, it is seen that in OPSM, the node density increases with the decrease in EC. This is due to the reason that the transmission range maximum between the neighbors are reducing and it leads to a reduction in energy usage for transmission and reception.
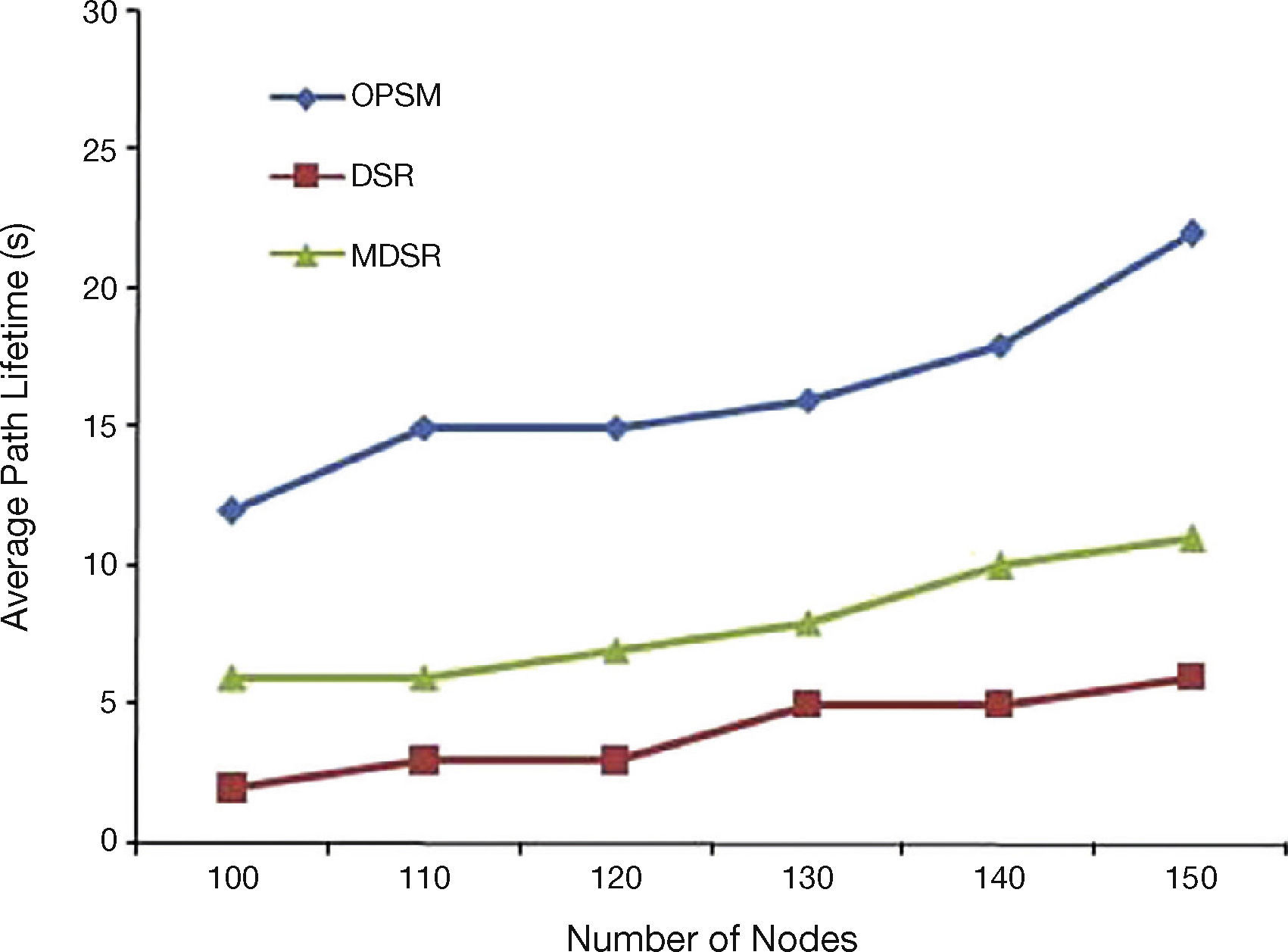
5.7Impact on Path LifetimePath lifetime in seconds is shown in Figure 9. It is measured here as the time between the starting time of the path setup and the time up to which all the nodes in the path are alive.
From the graph, it is seen clearly that as the nodes are increasing, the lifetime is also increasing. The reason behind this is the random power ratio computation and LD consideration in
path finding. MDSR shows an improved performance than the basic DSR, because it considers link disjoint approach. However, it does not consider the link duration. Therefore, the chances of node energy depletion will be there in their design. Out of all, proposed OPSM obtains a higher degree of path lifetime.
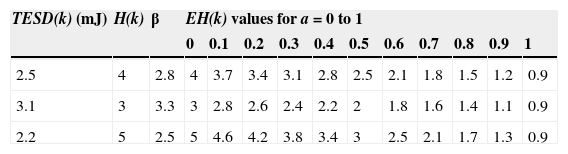
5.8Path Selection Based on Mathematical ModelTable 3 shows the results of the analytical computation of the mathematical model based on the defined objective function as given in Eq. (11). Three sets of EC and hop are taken and it is tabulated by varying parameter a from zero to one. From the values, it is understood that the value of a = 0 gives us minimum hop selection and a = 1 leads to minimum energy. Thus, the optimal path is chosen as the lowest path having the values of 3.1mJ of EC and 3 as the Hop count. Because for all the values of a except 0 and 1, the mathematical model gives us the lowest values.
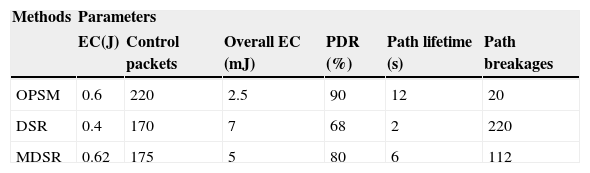
5.9Performance Analysis of OPSM With Other MethodsThe analysis shown in Table 4 is for a network of 100 nodes with a traffic load as 2 packets/s and pause time as 300 s. As far as EC in path finding approach is concerned, from Table 4, it is inferred that OPSM is similar to MDSR and it is very much higher than DSR. But OPSM achives a higher EC than all in terms of overall EC. It is seen that the number of control packets for the proposed is 27% more than that of MDSR and 29.5% more than that of DSR. In terms of overall EC, the proposed system achieves a reduction in terms of 64% and 50% than DSR and MDSR respectively. The reason behind proposed is that it involves optimal path selection and maintenance. Packet delivery ratio of OPSM reaches comparatively 32% and 12.5% higher than that of DSR and MDSR. Node depletion due to insufficient energy is almost eliminated in OPSM. It's objective is to avoid the unnecessary refinding of routes so the network can continue the data transfer with minimum interruption.
Path lifetime attains a higher percentage than all the other methods. There are two reasons for this; first, during route discovery itself, the link is validated. Second, node-disjoint path selection is done to eliminate the path with sharing of nodes. Path breakages are lesser compared to all other approaches because of the path finding based on power ratio and LD. Our system utilizes the node-disjoint paths for data transfer, and this has not been followed in any of the methods. The overall system is concerned, the proposed OPSM achieves a better performance in terms of all factors comparatively.
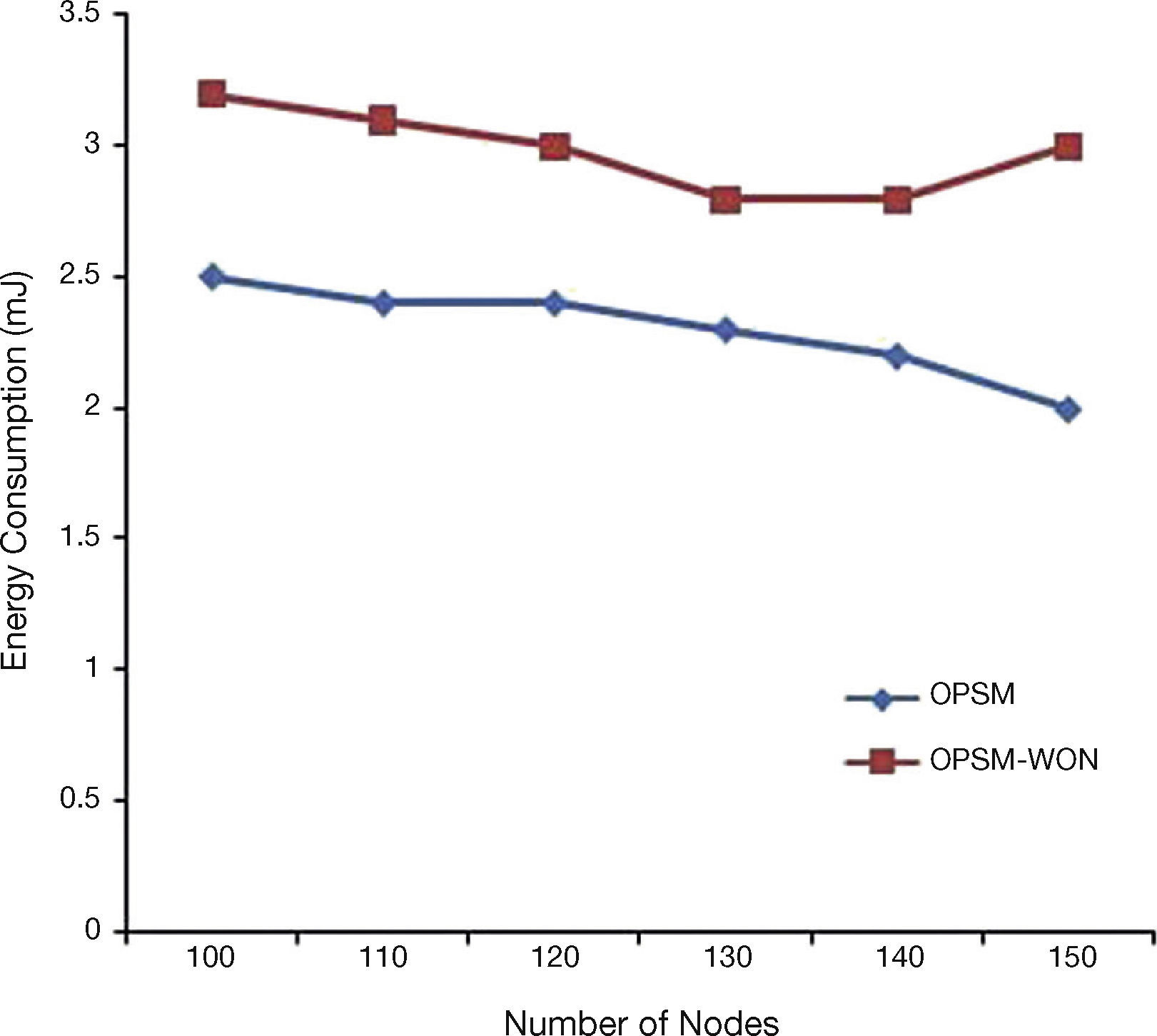
5.10Analysis of OPSM for EC With and Wihout Node-DisjointThe analysis for overall energy is done for with and without node-disjoint path selection and it is plotted in Figure 10.
It is clear from the representation that the node-disjoint path achieves energy saving compared to the system without node-disjoint. This is because node-disjoint does not make use of the nodes in common. Hence the node energy depletion due to node sharing is eliminated and the route rediscovery and number of path breakages are automatically reduced thus resulting in energy saving.
6ConclusionsA new energy efficient routing method that consists of path finding, selection and maintenance, named OPSM, has been designed to provide an energy efficient communication with enhanced lifetime. Path finding is designed first for accomplishing this task with the inclusion of power ratio and LD in finding the eligibility of node for forwarding. Selection method utilizes the mathematical model that chooses a path with less EC and number of hops for extending the network lifetime. This selection process also involves in finding a reliable node-disjoint path that satisfies the mathematical model. Node-disjoint path selection has been done to avoid the path failure due to sharing of nodes by multiple paths. The source node stores multiple node-disjoint paths in its cache. Once the selected route is found to be broken, then path maintenance is invoked. This path maintenance mechanism is mainly to reduce the refinding of new routes. Simulation results reveal that the proposed system is more energy efficient by providing better network latency and PDR. From the analysis, it is concluded that the system gives an optimum performance for the network of 100 nodes with pause time of 300 s, and traffic load of 2 packets/s. Further, it can be enhanced for higher EC by taking the transmission bandwidth into account.