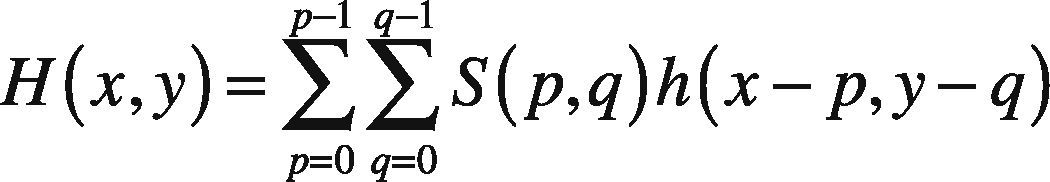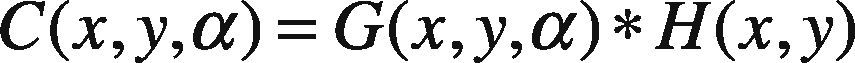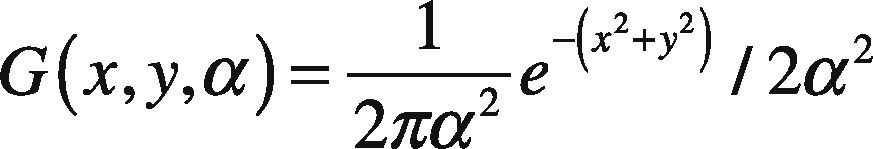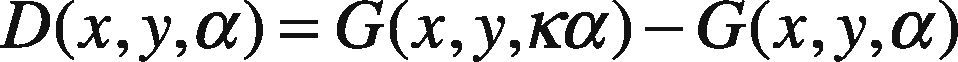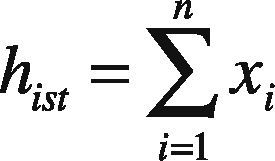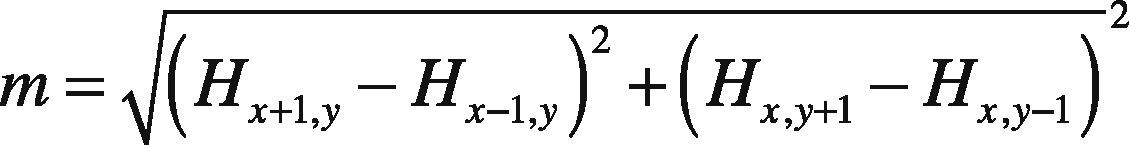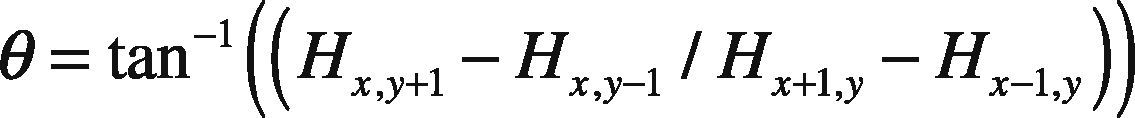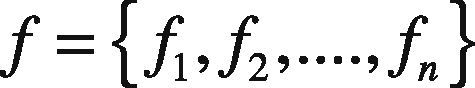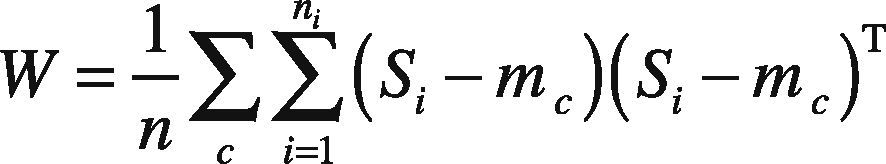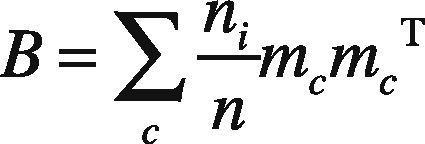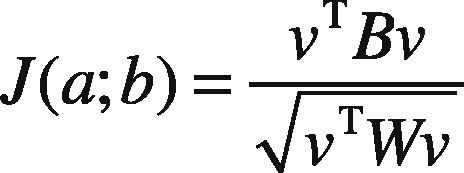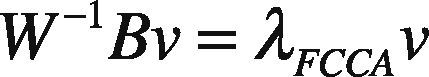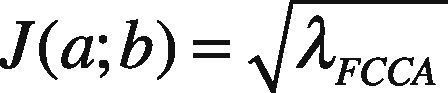Feature transformation and key-point identifi is the solution to many local feature descriptors. One among such descriptor is the Scale Invariant Feature Transform (SIFT). A small effort has been made for designing a hexagonal sampled SIFT feature descriptor with its applicability in face recognition tasks. Instead of using SIFT on square image coordinates, the proposed work makes use of hexagonal converted image pixels and processing is applied on hexagonal coordinate system. The reason of using the hexagonal image coordinates is that it gives sharp edge response and highlights low contrast regions on the face. This characteristic allows SIFT descriptor to mark distinctive facial features, which were previously discarded by original SIFT descriptor. Furthermore, Fisher Canonical Correlation Analysis based discriminate procedure is outlined to give a more precise classification results. Experiments performed on renowned datasets revealed better performances in terms of feature extraction in robust conditions.
Image retrieval (Mikolajczyk & Schmid, 2001; Sharif et al., 2012), pattern recognition and a lot of computer vision applications entail the use of local descriptors (Harris & Stephens, 1988; Lowe, 2004). Their utilizations in such applications provide invariance to noisy or corrupted pixels, illumination and even viewpoint changes (Lowe, 2004). A lot of work is conducted in discovering stable local descriptors with varying image scale. Some researchers used tree like structure while others use graph based matching strategy for obtaining consistent features. Work under this category is mostly performed by using general object categorization and classification. Others have taken into consideration planar surfaces and varying projection approaches (Lowe, 2004). When application concerning face recognition is involved, feature detection and selection becomes cumbersome (Ramírez-Valdez & Hasimoto-Beltran, 2009). The reason is its limited number of structures with sharp edge responses or high contrast regions. Mostly feature-based techniques include Gabor wavelets (Zhou & Wei, 2009), Active Appearance Models (AAM) (Weiwei & Nannan, 2009), graph based methods. While other methods for feature extraction make use of dimensionality reduction techniques such as Principal Component Analysis (PCA) (Zhao et al., 2009), Fisher Discriminate Analysis (Wang & Ruan, 2010), etc. The conversion of the high dimensional data into its subsequent low dimensional pattern eliminates some noisy pixels incorporated in the input image (Vázquez et al., 2003). Apparently, local descriptors are used for general objects but less work is seen regarding recognition of facial images.
Literature regarding the use of local descriptors in face recognition applications includes certain variations in original Scale Invariant Feature Transform (SIFT). One such work is presented in Ke and Sukthankar (2004), that uses PCA in combination with SIFT feature therefore, named PCA-SIFT. In Krizaj et al. (2010), authors of the paper have used fixed location on the face image to provide a robust solution against illumination changes. The advantage of using fixed location provides a way to save those key-points that are usually eliminated by SIFT features. So fixing the feature points restricts the elimination of distinctive information (Krizaj et al., 2010).
In Kisku et al. (2010), a graph based technique is adopted for matching the purpose. While authors in Bicego et al. (2006) have developed a local constraints on eyes and mouth region as well as a grid is applied on the local facial features whereas neighboring pixels are used for matching images. Another method using both local and global features is outlined in Luo et al. (2007). In Rattani et al. (2007), fusion-based strategy is adopted to extract effective facial information for recognition purpose. A graph based matching technique is accomplished in Kisku et al. (2007) while key-point preserving methodology is achieved in Geng and Jiang (2009). In this method, all the key-points that are reserved are usually discarded by the original SIFT features descriptor. This paper focuses in designing a framework for facial images using hexagonal approach. The methodology followed in the later text is briefed as: section 3 illustrates the experiments and results and finally discussion and conclusions are drawn in sections 4 and 5 respectively.
2Materials and MethodsScale Invariant Feature Transform (SIFT) is one of the popular feature descriptor used in general object recognition tasks. SIFT extracts a large set of local feature vectors from an image, each of which are invariant to translation, scale, geometrical distortions and illumination changes. Due to its spatially localized nature, SIFT features are less affected by noise and corrupted pixels. Based on this fact, a SIFT based feature extraction procedure is outlined in this text with its applicability in face recognition tasks. Most of the work regarding SIFT based feature descriptors in this particular field depends on square image pixels. Using SIFT on square image coordinates gives less number of features across edges and it eliminates low contrast pixels containing discriminate facial features.
Proposed technique makes use of hexagonal converted image pixels and processing is applied on hexagonal coordinate system instead of traditional square image coordinates. Hexagonal image coordinates have an inherit advantage of giving sharp edges and makes the discriminate features along edges more prominent. A detailed description of the work is outlined in the succeeding sections.
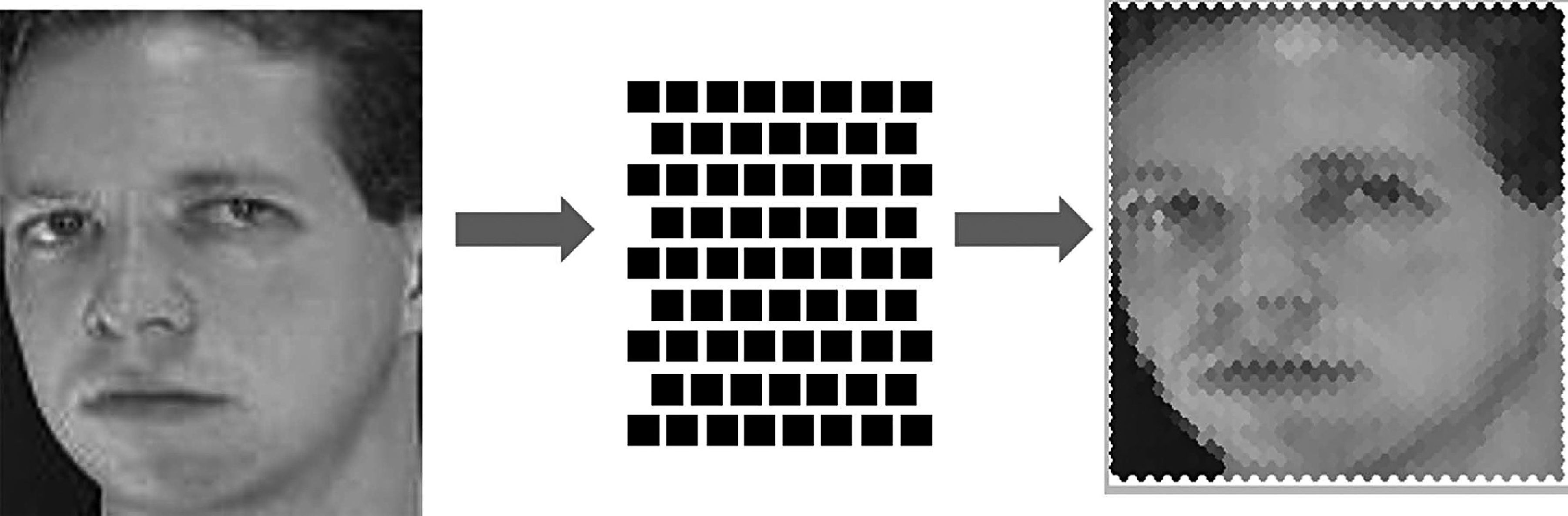
2.1Hexagonal SIFT FeaturesThe square image is converted into hexagonal shaped image pixels. First phase begins with designing original SIFT features to the corresponding hexagonal form. In order to accomplish this task, the original square pixels that form a rectangular grid is shifted by half the width of pixels. More precisely, every alternative pixel row is either left or right shifted by half of its width. Hence it forms the shape of a brick wall. This procedure will enhance the image features and makes the edges more sharp for further operations during the key-point identification phase.
The mathematical representation is shown in Eq (1) and image after re-sampling can be depicted in Figure 1.
More precisely, the conversion of square image S(p, q) with the pixels p × q and its corresponding square lattice Ls=mb1+nb2;m,n∈Z is converted into hexagonal lattice with following mathematical notations (Middleton & Sivaswamy, 2005):
From Eq (1), h symbolize kernel for interpolating the square image into subsequent hexagonal image. The symbols (p,q) and (x,y) are associated with pixels of square and converted hexagonal image respectively (Middleton & Sivaswamy, 2005).
Next phase begins by finding the key-points in the image, by filtering in different scales. This allows for the detection of invariant key-point location (Lowe, 1999). The most commonly used process in convolution is Gaussian function G(x,y,α). The convolution process involved with hexagonal image H(x,y) is illustrated in following mathematical formulations. The resultant convolved image is represented by the function C(x,y,α).
In the above expression, the Gaussian function is elaborated in Eq (3):
The symbol * in Eq (2) represents the convolution operation that results in regular blurring of the image in different scales and α is the scale factor. To highlight the highest peaks in the Gaussian scale space, the hexagonal image undergoes above process so that distinctive facial features and their respective edges can be marked. Above formulation also eliminates noisy pixels contained in an image via regular blurring. An inherit advantage of hexagonal image processing is its ability to enhance edges, which is not the fact in regular square image. Another reason of using hexagonal converted image over square image is its ability to highlight the areas with low contrast and poor edge response. These areas were originally discarded when convolution was applied on square pixels.
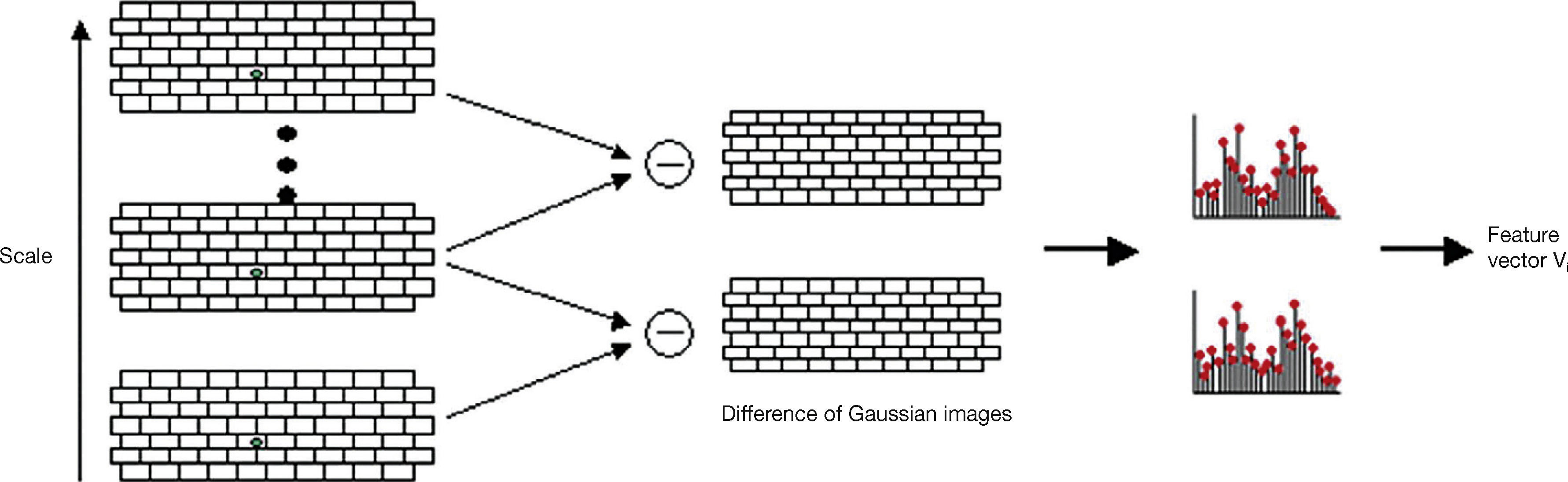
To mark the enhanced image features, subtraction on consecutive Gaussian scales is performed, therefore, named as difference of Gaussian (DOG) (Lowe, 2004) images by a factor κ. This functionality results in smooth image for further operations. Formally, it can be written as:
Once the DOG images are produced, pixels containing maximum and minimum intensities are extracted using histogram approach. Suppose xi is the candidate key-point in each of the DOG images, then histogram for that particular image is given by Eq (5):
From Eq (5) i represents the DOG image and n is the total number of scales in DOG image. So above equation basically computes the summation of the entire candidate key-points identified in the DOG images with varying intensity levels.
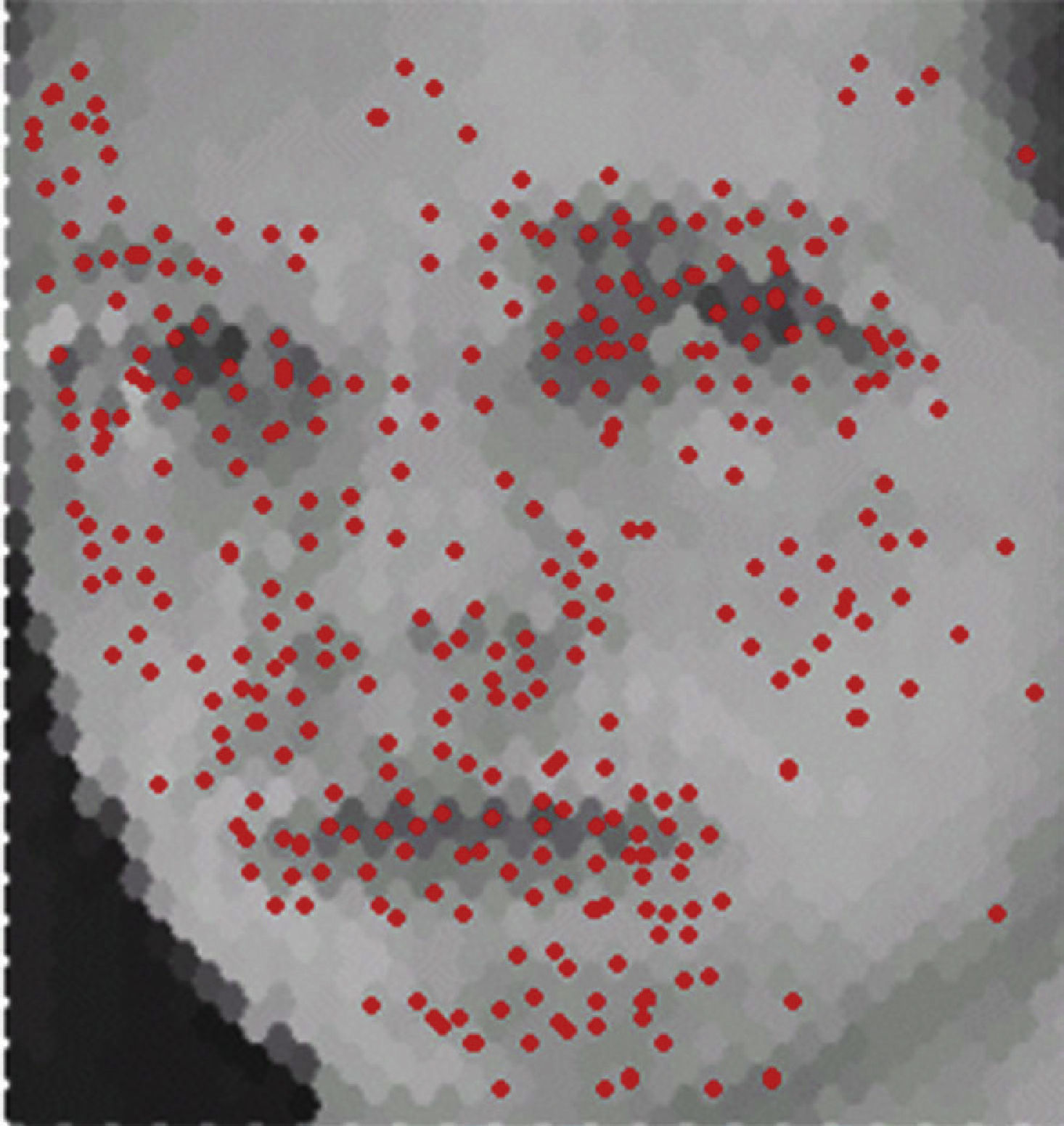
Figure 2 shows the Gaussian Scale Space with its DOG images which form the DOG images key-points with varying intensities levels for which histogram is constructed. The image regions closer to darker areas or edges are represented as higher peaks in the histogram, i.e. contour of eyes, mouth and nose region, which tend to show local maxima. While portion around cheeks, forehead show low contrast areas and hence lead to local minima. The low contrast point in this case are not eliminated in contrast to the functionality of SIFT features. Once the candidate points are identified, orientation is assigned to each key-point leading to invariant property of rotation. This functionality is also helpful for recognition of images with varying viewpoint. In this case the magnitude m and θ direction can be computed for each hexagonal image (Lowe, 2004) H(x,y):
The direction θ (Lowe et al., 2004) is given for each pixel as:
After the required phases are accomplished in determining the key-points of facial area, a fusion mechanism is adopted to give more compact representation. A sample image with candidate key-point identification on hexagonal converted image is shown in Figure 3.
The extracted key-points are of high dimensional space and require the conversion into low dimensional space. This is accomplished by using Fisher based Canonical Correlation Analysis (CCA) (Sun et al., 2011), hence named FCCA classifier which reduces the dimensional space by efficiently implementing the matching process. The employed discriminate analysis procedure augmented with CCA procedure derives the projection matrix. This maximizes the between class variance and minimizes the within class variance. Consider n training samples of y classes with Si hexagonal SIFT features arranged in a matrix S such that S∈ℜmxn.
For each training sample belonging to its relevant class, keypoint fusion approach is applied using Simple Sum rule. This allows clustering of all key-points relevant to one class in compact feature vector f. Equation (9) represents the fused feature vector of n training samples:
Matching is based on the combined feature vectors descriptors rather than individually comparing each key-point. This strategy allows less computation in terms of matching. According to the requirement of Fisher Discriminate Analysis (Wang
& Ruan, 2010), the covariance matrixes are computed for which W and B corresponds to within and between-class covariance, c represents the number of classes, ni is total number of training samples and mc is the mean of each class, i.e. mc∈ℜmxn. The requisite equations of each covariance are given by following mathematical equations.
Instead of using the Fisher's criteria for transformation matrix, apply the canonical correlation (Sun et al., 2011) among the feature points. To provide an effective and compact representation of the covariance matrixes, let ai∈ℜd denote the sample feature of class i and bj∈ℜd represents the feature point of class j. Then according to the projection of CCA as given in Eq. (12):
The set criterion is said to obtain maximum convergence by computing the Eigen-value decomposition, where λ corresponds to highest Eigen-values. The orthogonal projection of highly correlated eigenvectors can thus be obtained as:
Above formulations can further be evaluated by the set of experiments presented in subsequent section. The robustness of the presented work is checked on the basis of facial expression, slight head orientation, varying lighting conditions and presence of natural occlusion.
3Experiments and ResultsThis section details the performance of proposed face recognition technique using hexagonally sampled images. One of the most renowned datasets, namely AR (Martinez, 1998), ORL (Samaria & Harter, 1994), Yale B (Georghiades et al., 2001), and FERET (Phillips et al., 2000), are used for the experimentations. The images are cropped to a standard size and histogram is equalized to make the performance consistent in terms of recognition rates (RR).
Yale B is publicly available dataset, which Exhibits 11 frontal images of 15 subjects. Each face is cropped and histogram equalized to a standard size. Select randomly half of the images for each subject for training purpose and rest is used for testing set.
While experiments are also performed on the ORL dataset where each image varies with slight head orientation, facial expression, and accessories like glasses, etc. This dataset is composed of 40 subjects with 10 images per person. First five images are used for training the system and rest are used for the probe set. Performance is evaluated on the basis of the presence of facial expression and head orientation.
AR database contains images of 126 subjects with 26 images taken in two different sessions. The images vary in facial expressions, lighting conditions and contain natural occlusion in upper and lower part of face. In the experiments, expressions and occluded images are used. The occluded face is used for testing purpose to check the robustness of the system. Performance of presented algorithm is compared with methods in literature (Bartlett et al., 2002; Park et al., 2005; Penev & Atick, 1996) that have dealt with expressions. Performance evaluation of the presented framework is also tested on the FERET dataset containing gray scale frontal profiles. Main contribution in using this dataset is the availability of different scaled images. Using this strategy, different scale version of images is used from the dataset while some have been resized using the MATLAB functions to further check the results. The scaled images are varied in reverse direction according to the size of the original images (128 × 192). Experiment is performed on set of 100 probe and gallery images.
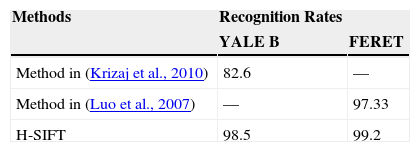
3.1Experiment #1First set of experiments is performed on the aforementioned datasets in which the lighting conditions are varied. Neutral images are used for training set while images affected with varying lighting conditions constitute the testing set. The dataset involved in this experiment is YALE B and FERET. Obtained recognition results in % are shown in Table 1.
Recognition accuracies on Yale B and FERET database.
| Methods | Recognition Rates | |
|---|---|---|
| YALE B | FERET | |
| Method in (Krizaj et al., 2010) | 82.6 | — |
| Method in (Luo et al., 2007) | — | 97.33 |
| H-SIFT | 98.5 | 99.2 |
The results demonstrate the effectiveness of the proposed method on the above datasets. The use of hexagonal features greatly enhances the feature extraction process, which is a positive aspect of the proposed technique. Traditional SIFT algorithms eliminates low contrast key-points from the facial regions hence show decrease in recognition results.
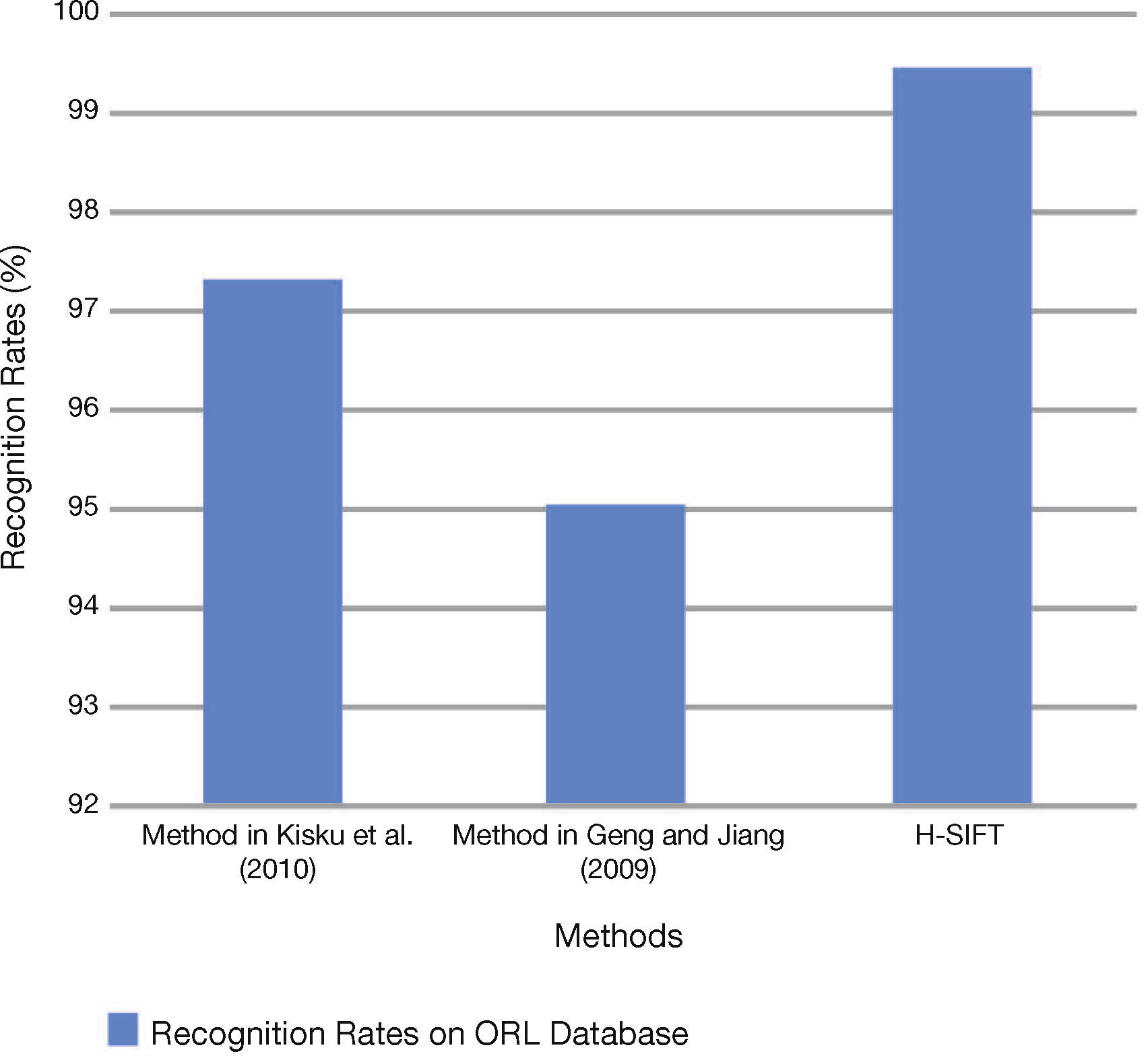
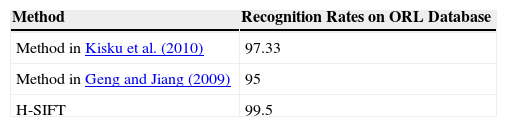
3.2Experiment #2This experiment is performed on the images in which head orientations are considered with accessories like glasses/without glasses, open and closed eyes, and varying facial expressions. These settings are tested using the ORL dataset; results after evaluation on different methods are represented in Table 2, and its visual illustration is shown in Figure 4.
Recognition rates on ORL database.
| Method | Recognition Rates on ORL Database |
|---|---|
| Method in Kisku et al. (2010) | 97.33 |
| Method in Geng and Jiang (2009) | 95 |
| H-SIFT | 99.5 |
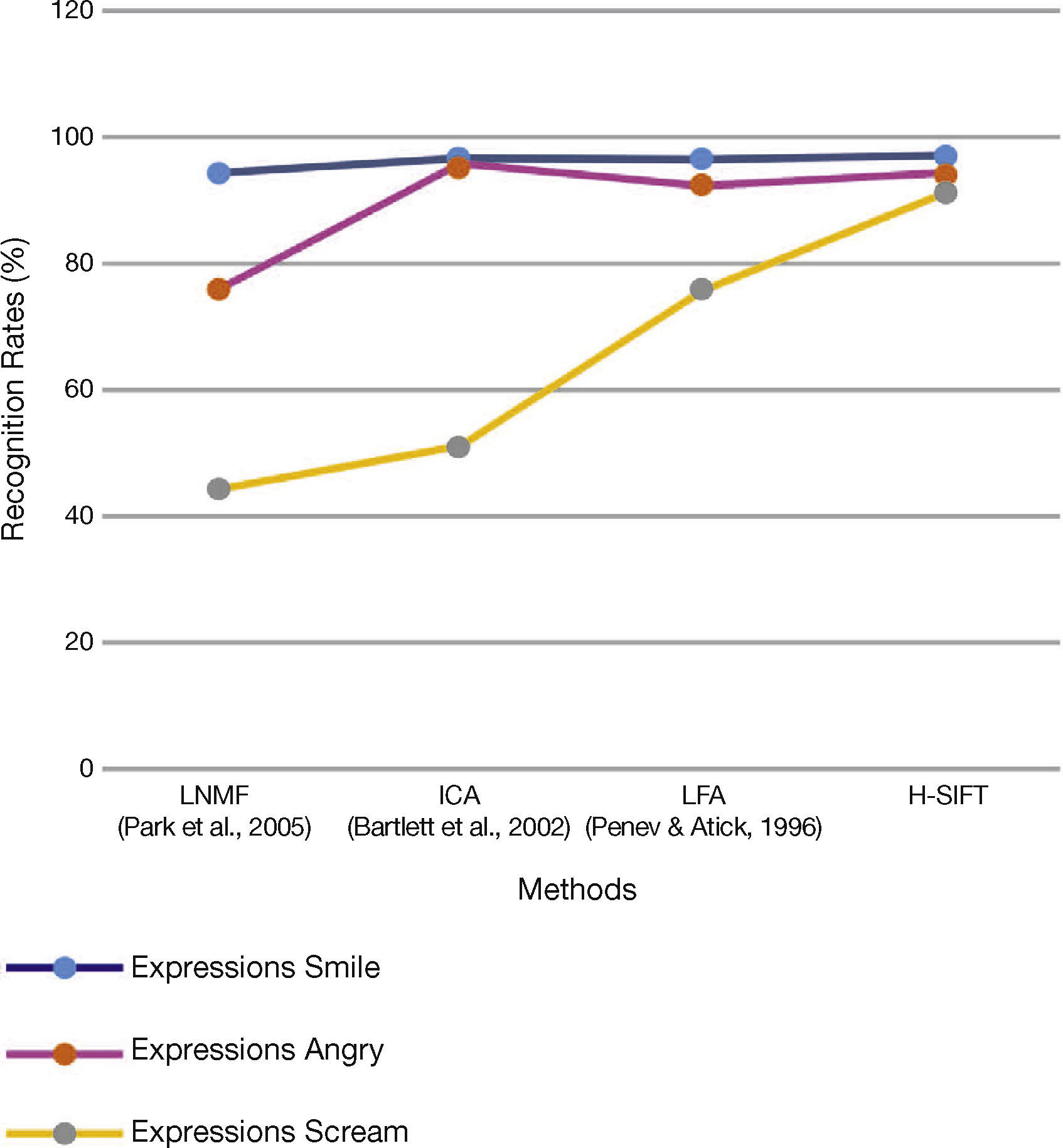
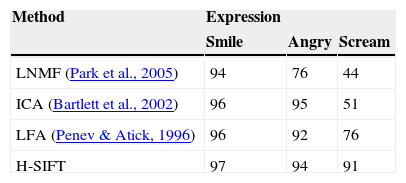
To further evaluate the recognition performance of the presented framework, the algorithm is tested on images with varying facial expressions. Three expressions are considered — i.e. smile, angry and scream. AR dataset is used to check the functionality in which the neutral face is used for training, while expression faces are for the probe set. Table 3 shows the performance accuracies with its graphical illustration in Figure 5.
Recognition rates on AR database with varying expression.
| Method | Expression | ||
|---|---|---|---|
| Smile | Angry | Scream | |
| LNMF (Park et al., 2005) | 94 | 76 | 44 |
| ICA (Bartlett et al., 2002) | 96 | 95 | 51 |
| LFA (Penev & Atick, 1996) | 96 | 92 | 76 |
| H-SIFT | 97 | 94 | 91 |
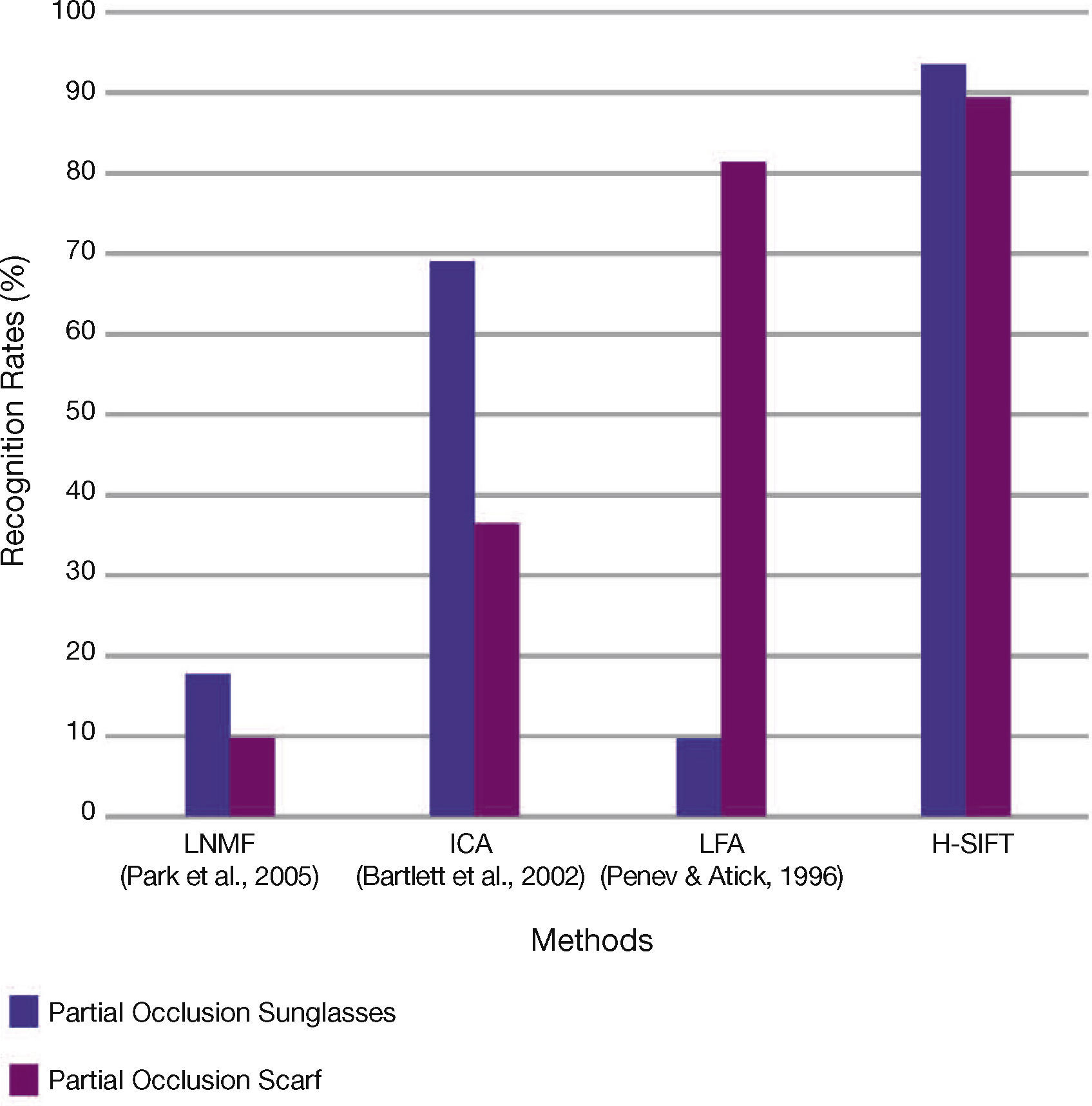
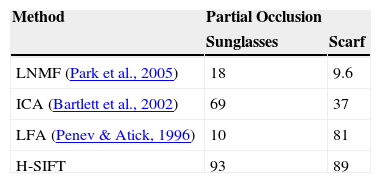
The results of partially occluded face recognition using different algorithms as in Bartlett et al. (2002), Park et al. (2005), and Penev and Atick (1996), and H-SIFT are shown in Table 4. Figure 6 shows its corresponding graphical illustration. The results shown below represent the performance of different algorithms dealing with partial occlusions, but each is suitable for its particular domain in which it has been implemented. The variation in the recognition accuracies clearly shows the algorithmic background of each method that has been used to solve the partial occlusion problem.
Recognition rates on AR database with partial occlusion.
| Method | Partial Occlusion | |
|---|---|---|
| Sunglasses | Scarf | |
| LNMF (Park et al., 2005) | 18 | 9.6 |
| ICA (Bartlett et al., 2002) | 69 | 37 |
| LFA (Penev & Atick, 1996) | 10 | 81 |
| H-SIFT | 93 | 89 |
In this experiment tests are performed on FERET database where different scales are used to check the performance of the presented work. The scaling factor α is varied from 5, 10 and 15% of the original size of image in reverse directions, i.e. the images are decreased in scale. Table 5 represents the variation in scale of FERET images; it can be seen that recognition rates lies between 90 and 95% with varying scales. The results shown in the table represent the average of test results after performing the experiment several times.
4DiscussionAfter performing a set of experiments on the renowned datasets, it can be evaluated that the feature extraction on hexagon based sampled images provides robustness in face recognition systems. This hexagonal version of image is also useful in SIFT feature descriptors due to inherit nature of enhancing the facial features. The low contrast areas on face constituting the local features are highlighted with the use of hexagonal image processing. The matching procedure using Fisher Canonical Correlation Analysis (FCCA) further boosts the recognition accuracy. Therefore, makes the system robust to aforesaid conditions. Different types of experiments were performed in Recognition Rates (%)
which varying illumination, expression and head rotation was considered. Experiments were also performed on partial occlusions and different scaled versions of images. All the evaluation procedures applied revealed outstanding performance of the presented framework.
Each method described in literature has its own pros and cons and each depends upon the feature extraction process. Main focus of this paper was to modify the original SIFT descriptor to further enhance its capabilities by using hexagonal images. Although there exist certain methods in literature that have higher recognition accuracies compared to the current work but again it depends on the type of descriptor used for feature extraction process. The ultimate concern of this paper was to check the robustness of images under various constraints.
5ConclusionsThis paper deals with a robust approach towards face recognition systems. Main focus of the presented work is to effectively locate the facial features, which were discarded by original SIFT descriptor. The use of hexagonal re-sampling enhances the capability of low contrast areas on the face images to be highlighted for effective feature extraction. Also, the modified matching procedure further increases the recognition performances of the outlined face recognition framework.