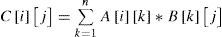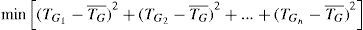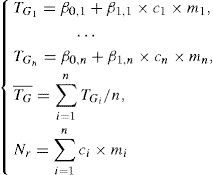Efficient Workload Balancing on Heterogeneous GPUs using MixedInteger Non-Linear Programming

Abstract

Recently, heterogeneous system architectures are becoming mainstream for achieving high performance and power efficiency. In particular, many-core graphics processing units (GPUs) now play an important role for computing in heterogeneous architectures. However, for application designers, computational workload still needs to be distributed to heterogeneous GPUs manually and remains inefficient. In this paper, we propose a mixed integer non-linear programming (MINLP) based method for efficient workload distribution on heterogeneous GPUs by considering asymmetric capabilities of GPUs for various applications. Compared to the previous methods, the experimental results show that our proposed method improves performance and balance up to 33% and 116%, respectively. Moreover, our method only requires a few overhead while achieving high performance and load balancing.

1

Introduction

Nowadays, a hybrid system consisting of general purpose processors (CPUs) and accelerators are becoming mainstream in system architecture design for achieving high performance and power efficiency. In particular, many-core graphics processing units (GPUs) now play an important role for computing in heterogeneous architectures for many fields like optimization [1], neural network [2], and bioinformatics. For example, Titan is ranked first in the list of supercomputers of Top500 [3] in Nov. 2013, and is equipped with 18,688 Nvidia Tesla K20 GPU and 18,688 AMD Opteron 6274. As for embedded systems, Nvidia Tegra [4] integrates ARM processor and a 16-core GPU into a chip for mobile devices.

In order to catch up with the progress of the above domains, the most critical task is to enhance the performance of more and more complex applications running on heterogeneous GPUs efficiently. Most work concentrate on providing programming environments such as CUDA [5], OpenCL [6], and DirectCompute [7] for application developers to transform serial programs to heterogeneous parallel programs. However, with the progressive number of heterogeneous GPUs, computational workload distribution (CWD) becomes more attractive due to the asymmetric capabilities of GPUs. There are two regards to distribute computational workload on heterogeneous GPUs: the constraints of memory capacity of GPUs and the load balancing among GPUs. First, in general, the applications running on GPUs have extremely large data size, thus the memory capacity of GPUs dominates the workload distribution of applications. Second, the workload of application should be distributed to heterogeneous GPUs based on their computing capabilities for load balancing and further minimizing the overall execution time. In this paper, we model computational workload distribution on heterogeneous GPUs as a mixed-integer non-linear programming (MINLP) problem for efficient workload balancing.

Consequently, we make the following contributions in this paper:

• •

  We model the problem of computational workload distribution on heterogeneous GPUs as MINLP for efficient load balancing and further optimize the overall performance.

• •

  Based on our formulation of MINLP, our approach can support various numbers of heterogeneous GPUs.

• •

  The overhead of our approach is quite minimum because only a few number of training samples are required.

This paper is organized as follows. In Section II, we review the related work about workload distribution and load balancing. Section III describes our proposed method for computational workload balancing. In Section IV, we present our evaluation and compare with the previous methods. Finally, we present concluding remarks and future work in Section V.

2

Related work

The approaches of CWD on heterogeneous processors can generally be classified with two types: static [8-11] and dynamic [12-15]. For static strategy, Qilin [8] proposes an adaptive mapping method on heterogeneous parallel processing platforms (HPPPs) consisting of one CPU and one GPU. The purpose of Qilin is to make load balancing on HPPPs, so it maps the partitioned workload to all processors according to their capabilities. First in the offline phase, Qilin samples execution times of a task with different problem (data) sizes, and then formulating linear regression as prediction model. Second in online phase with the new coming problem size, the optimal partition proportion of workload of task on CPU and GPU is obtained by the model. All of the tasks are sampled and recorded in the database. Qilin searches the database for the partition proportion while distributing workload on HPPPs. Luk et al. proposes an effective method for workload partition, however, the approach only deals with one CPU and one GPU. The number of heterogeneous processors is a limitation of CWD especially on HPPPs consisting of multiple CPUs and GPUs. Another work related to CWD proposes a waterfall energy consumption model [9] for power issue. The authors adopt a task mapping method, β-migration, on GPU. Tasks could be partitioned into CPU sub-task and GPU sub-task. In this method, CPU sub-task does not move parts to GPU because CPU sub-task is not suitable to GPU. While CPU sub-task and GPU sub-task do not work in a balanced way, the β proportion of GPU sub-task is migrated to CPU.

As for dynamic strategy, [12, 13] present a mechanism that distributes workload to processors uniformly in the initial state (e.g., the first iteration of a for-loop in a program), and then collects the execution times of all processors and re-distribute the workload based on their performance measured by minimum code intrusion run-time. After several steps of re-distributing workload, the system converges to a balanced state. The dynamic strategy can be regarded as a lightly runtime profiling, so the most critical issue of this strategy is how to measure the performance of each processor with minimum overhead. In comparison with static strategy, dynamic strategy cannot reach an accurate proportion of workload distribution initially for efficient load balancing. Furthermore, dynamic approach requires data migrations among processors thus causes communication overhead than static approach.

In this paper, we propose a MINLP-based approach for computational workload distribution on various numbers of heterogeneous GPUs for efficient workload balancing and optimal performance.

3

Motivation

As the trend of Platform as a Service (PaaS) in cloud computing, keeping platform balancing and fully utilized become an important issue for high performance. However, distributing workload of a data-parallel application to a computing node which consists of asymmetric-capabilities processing elements efficiently is difficult because the proportion of distributed workload to processing elements should be based on their abilities to an application. This phenomenon is very common especially in a platform consisting of heterogeneous GPUs for science computing.

We now motivate the need of efficient workload distribution on heterogeneous GPUs with a case study of matrix multiplication. For the case of matrix multiplication, it is commonly known that each element in the product matrix is obtained by the inner product of one row vector of one input matrix and one column vector of the other input matrix. The Eq. 1 formally depicts the matrix multiplication.

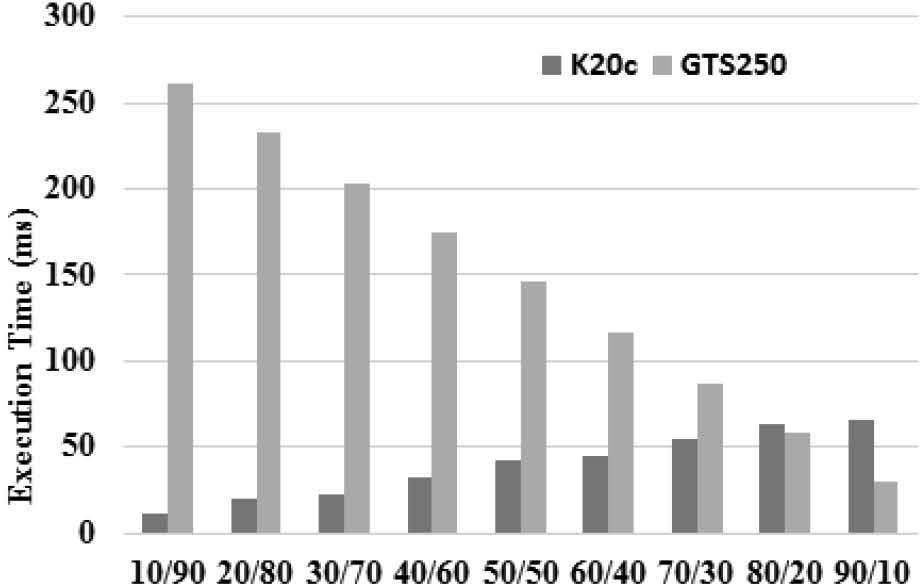
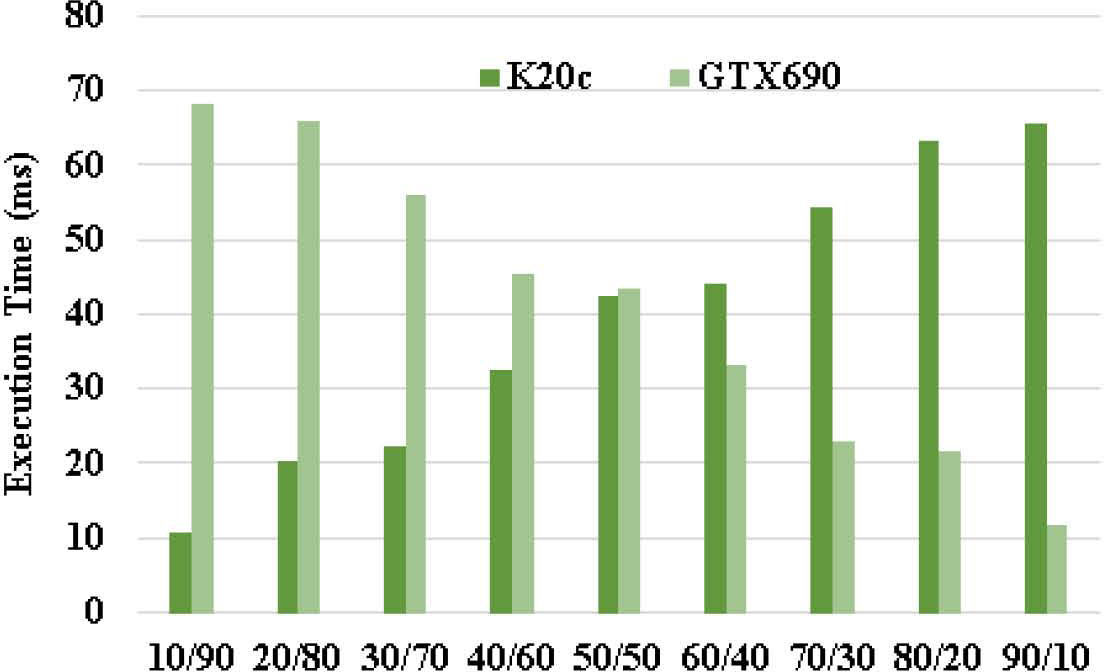
We did two motivating experiments with two heterogeneous GPUs used. In each experiment, we set the input size of matrix as 3200 and varied the distribution of workload between GPUs. As the data parallelism of matrix multiplication C = A × B, A can be divided into smaller matrices by row and B can be divided into smaller matrices by column for computing in parallel. Consider the feature of coalesced access on GPU, we only divided A by row. Finally, we combine the partial results into C. We use the CUDA CUBLAS library [16].

Figure 1(a) and 1(b) show the results of matrix multiplication experiments with different combinations of GPUs (details of the machine configuration are given in Section 6). The x-axis is the distribution of workload between the two GPUs. The notation “A/B” means A% of workload mapped to K20c and B% of workload mapped to GTS250 in Figure 1(a) or GTX690 in Figure 1(b). The y-axis is the execution time in millisecond. In Figure 1(a) and 1(b), we can see the optimal workload distributions are located between 80/20 and 50/50, respectively. This is because of the asymmetric computing capabilities of GPUs. It is very clear from these experiments, the optimal workload distribution depends on the hardware capability for an application. Assume that the proportion of workload distributed to a GPU is either increased or decreased by 10%. For two GPUs, there are nine combinations to search for optimal distribution in brute-force style. As for three GPUs, there are up to sixty three combinations. There will be a large amount of combinations if the number of GPUs is increased or the proportion of distributed workload is more subtle. Therefore, we propose an efficient method for workload distribution on heterogeneous GPUs with the considerations of number of GPUs and accuracy.

Figure 1(a).

Matrix multiplication experiments with K20c and GTS 250.

Figure 1(b).

Matrix multiplication experiments with K20c and GTX690.

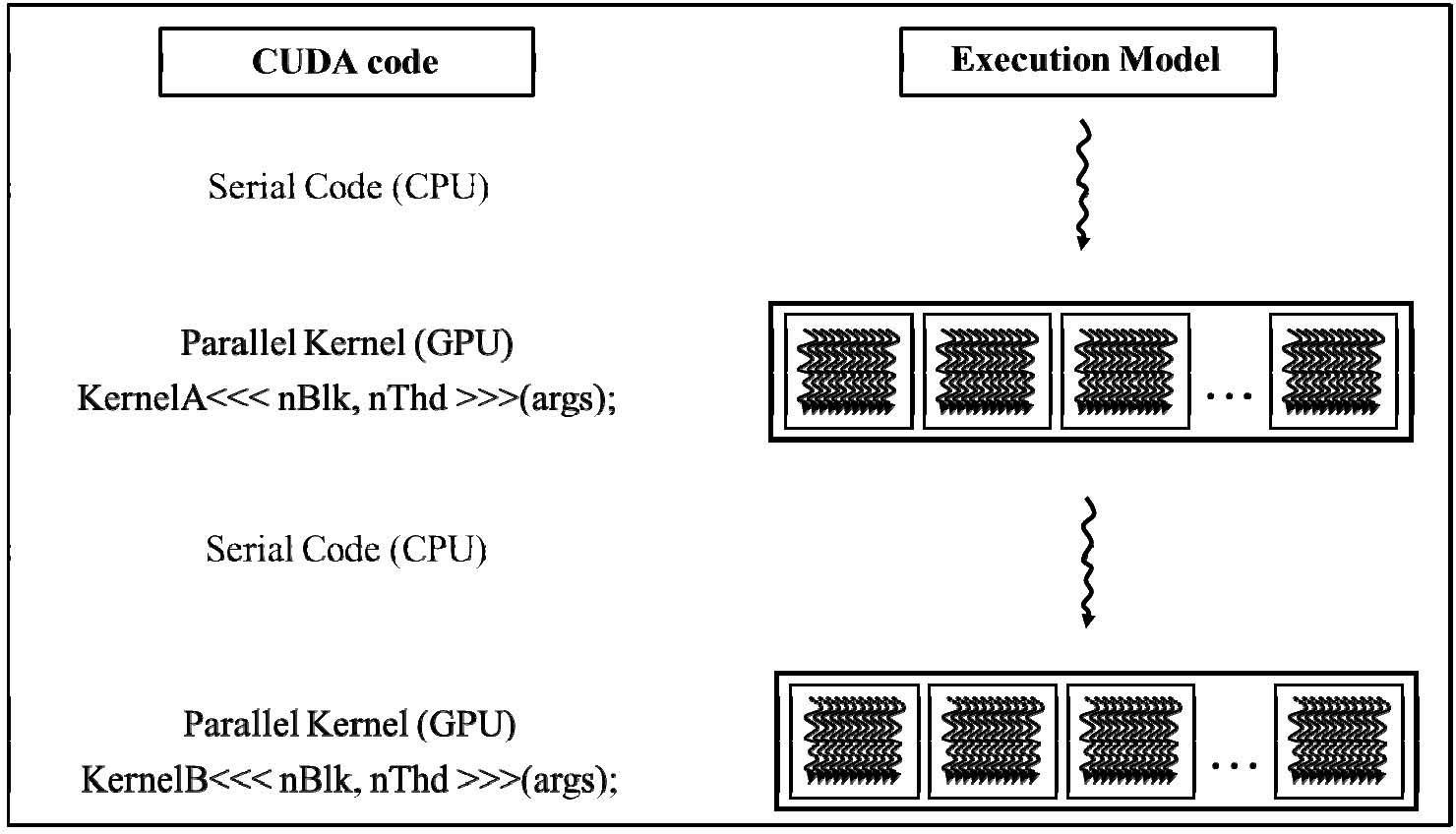
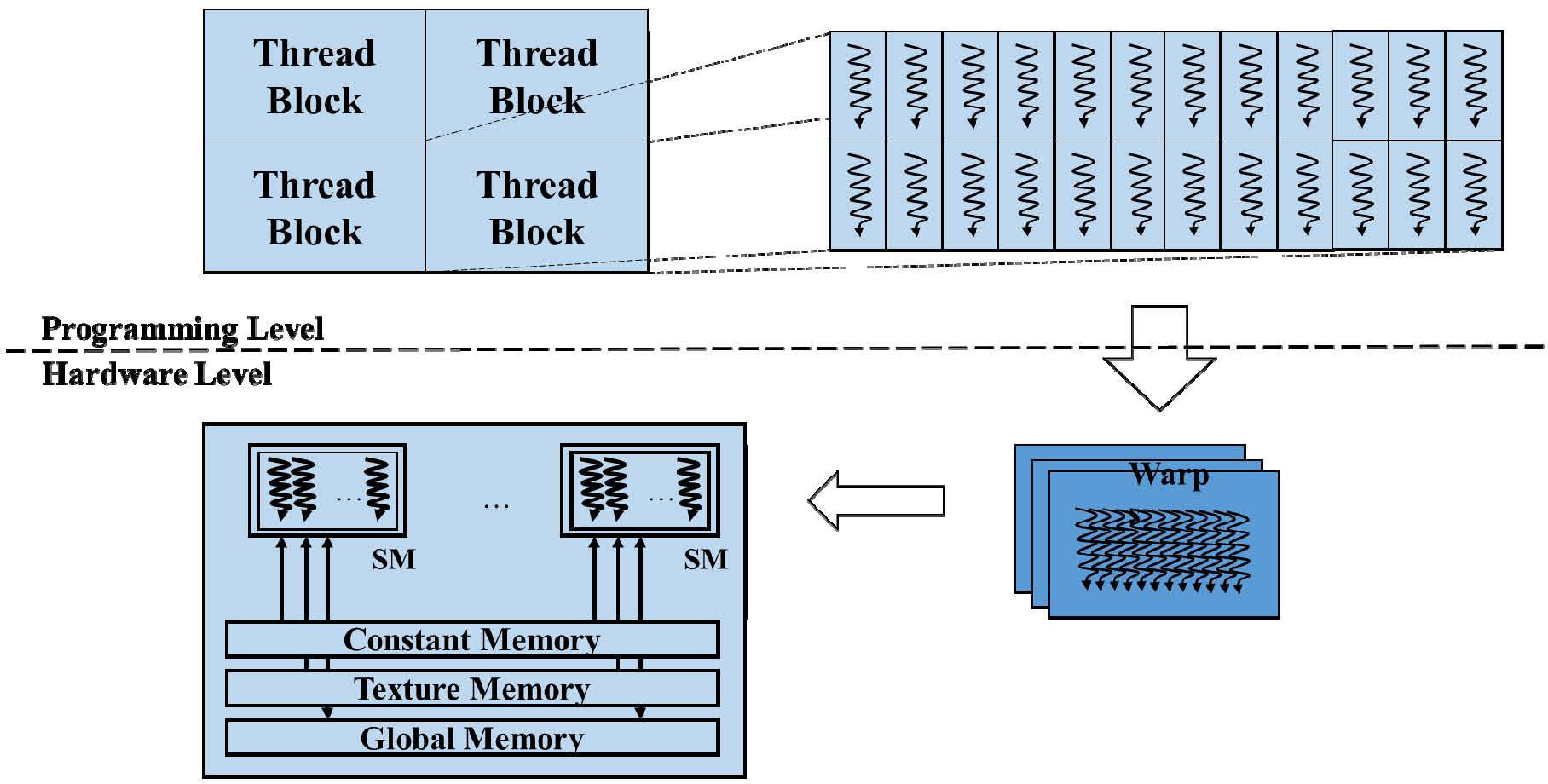
4

Compute Unified Device Architecture (CUDA)

Compute Unified Device Architecture (CUDA) is a GPU programming model developed by NVIDIA. CUDA provides a programming interface [5] to utilize the highly-parallel nature of GPUs and hide the complexity of controlling GPUs. A programmer specifies a kernel as a series of instructions and a data set, then the kernel is executed by thread blocks, each of which consists of a number of threads as shown in. Precisely, a thread block is divided into warps of 32 threads. Each warp is executed by an streaming multiprocessor (SM) within 4 cycles if the input data is cached for computing. For utilizing an SM efficiently, the threads of each warp should execute the same instructions.

Figure 3 shows CUDA programming and execution model. In the CUDA code shown in the left part, the serial code such as for file I/O is executed by CPU. As for the highly data-parallel code section such as vector addition with large data, is written as a kernel function which is executed on GPU launched by the CPU. The parameters nBlk and nThd represent the number of thread blocks and the number of threads in each thread block, respectively. The parameters nBlk and nThd are called execution configuration in CUDA programming.

Figure 3.

Programming and execution model of CUDA.

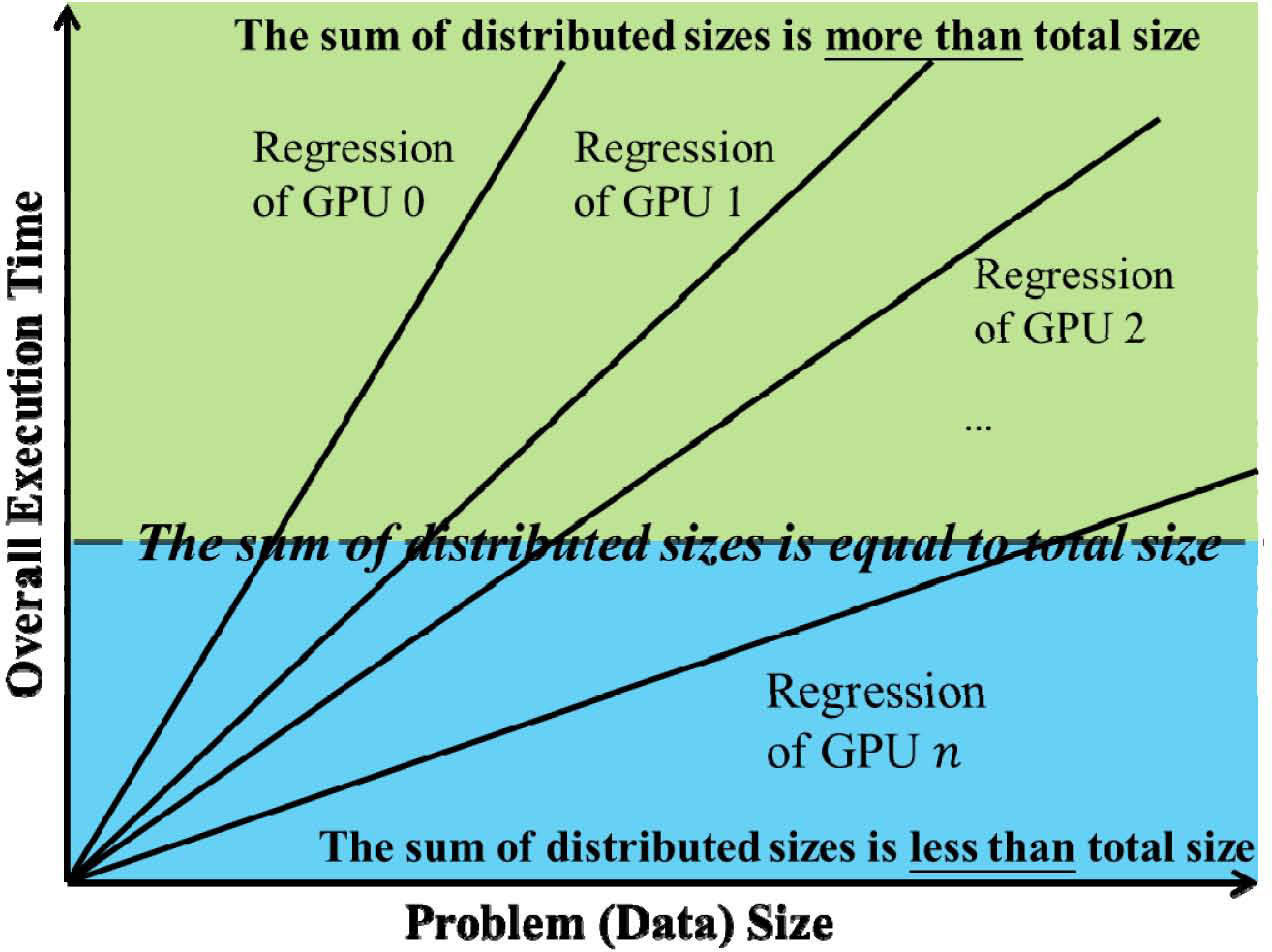
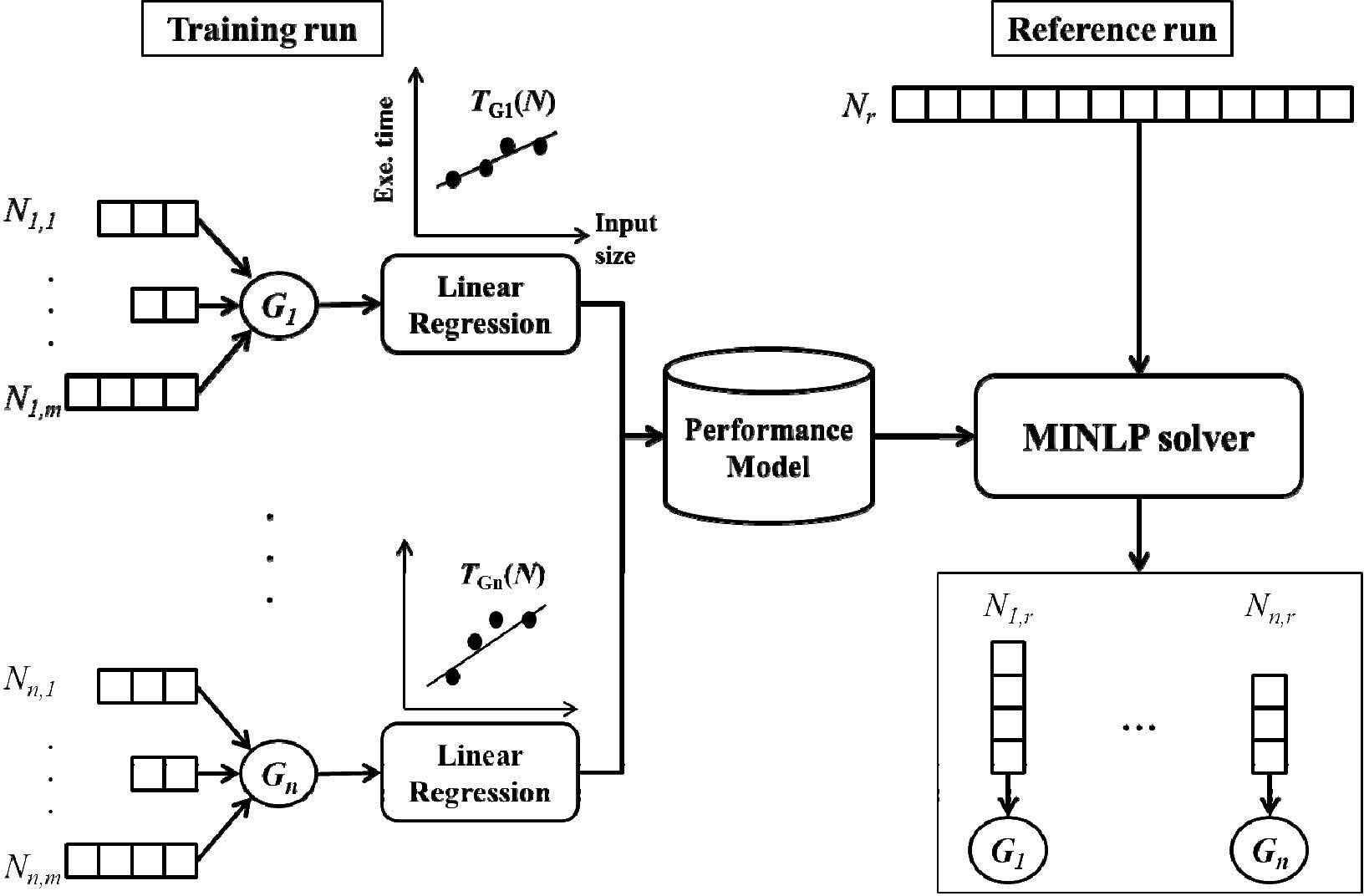
5

Methodology

Figure 4 shows the concept of our proposed approach. For a given problem (data) size of an application, the goal of workload balancing on heterogeneous GPUs is to search a set of problem sizes distributed on GPUs that makes the equal execution time on GPUs. In other words, the variance of execution times on GPUs is minimized as possible. Note that many sets of distributed sizes can make the variance minimum, however only one single set of distributed sizes accumulated to the given problem size.

Figure 4.

The concept of proposed approach for efficient workload distribution.

The flow of our approach for CWD is shown in Figure 5. Left part is the phase of training run. In the training run, task with different sizes are run on n heterogeneous GPUs (G₁, G₂,..., G_n) and then the execution times are collected to build linear regressions for GPUs. Then, the linear regressions which are TG1,TG2,…,TGn shown in Eq. 3 are stored in the database as performance model for reference run. Note that in Eq. 3, c_i is the execution confiugration of parallel program (i.e., number of threads in a thread block which is intriduced in Section 4) and is equal to the size of data which are distributed to G_i because the distributed size should be equal to the multiples of execution configuration without any other techniques (e.g., adding extra paddings to size). Furthermore, TG¯ and N_r indicate the avergae execution time on GPUs and the referenced problem size on runtime, respectively. Right part in Figure 5 is the phase of reference run. In the reference run, the reference size of task is used as the input for mixed-integer non-linear programming (MINLP) with the objective function and the constraints as shown in Eq. 2 and 3. In Eq. 2, we take load balancing into our consideration, thus we adopt the concept of standard deviation and minimize it. After solving Eq. 2 with Eq. 3 by MINLP solver, the optimal partition proportion of workload to each GPU is obtained.

Figure 5.

Flow of the proposed approach for CWD on heterogeneous GPUs.

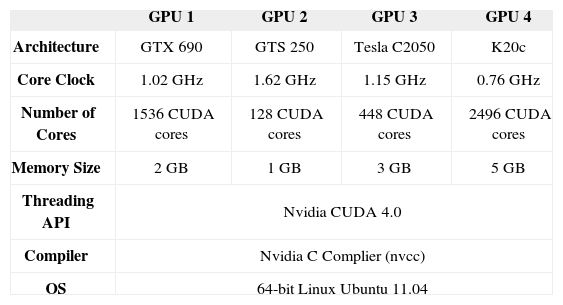
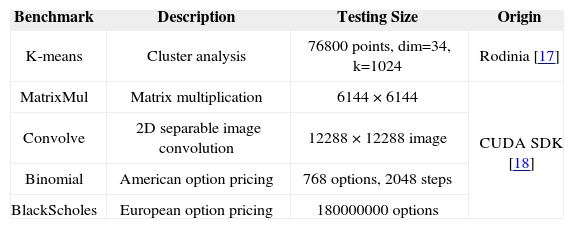
6

Evaluations

Table 1 lists the experimental setup of evaluations. We take four heterogeneous GPUs as our target platform. Table 2 lists our benchmarks which are workload divisible and guaranteed that the computational workload can be partitioned and distributed to GPUs without any synchronization for communication in thread level. For MINLP solver, we adopt Matlab R2012a with the package of solver BONMIN. In our experiments, we take overall execution time and imbalance as two metrics for evaluating approaches. The metric of imbalance is the standard deviation of execution times among GPUs. In other words, the less imbalance among GPUs, the superior distribution is obtained. We take uniform distribution (UD) and specification-based distribution (SBD) as the comparisons in the experiments. UD distributes workload to GPUs uniformly while SBD distributes workload to GPUs base on specifications (i.e., number of cores multiplies clock frequency).

Table 1.

Experimental setup.

	GPU 1	GPU 2	GPU 3	GPU 4
Architecture	GTX 690	GTS 250	Tesla C2050	K20c
Core Clock	1.02 GHz	1.62 GHz	1.15 GHz	0.76 GHz
Number of Cores	1536 CUDA cores	128 CUDA cores	448 CUDA cores	2496 CUDA cores
Memory Size	2 GB	1 GB	3 GB	5 GB
Threading API	Nvidia CUDA 4.0
Compiler	Nvidia C Complier (nvcc)
OS	64-bit Linux Ubuntu 11.04

Table 2.

Benchmark summary.

Benchmark	Description	Testing Size	Origin
K-means	Cluster analysis	76800 points, dim=34, k=1024	Rodinia [17]
MatrixMul	Matrix multiplication	6144 × 6144	CUDA SDK [18]
Convolve	2D separable image convolution	12288 × 12288 image
Binomial	American option pricing	768 options, 2048 steps
BlackScholes	European option pricing	180000000 options

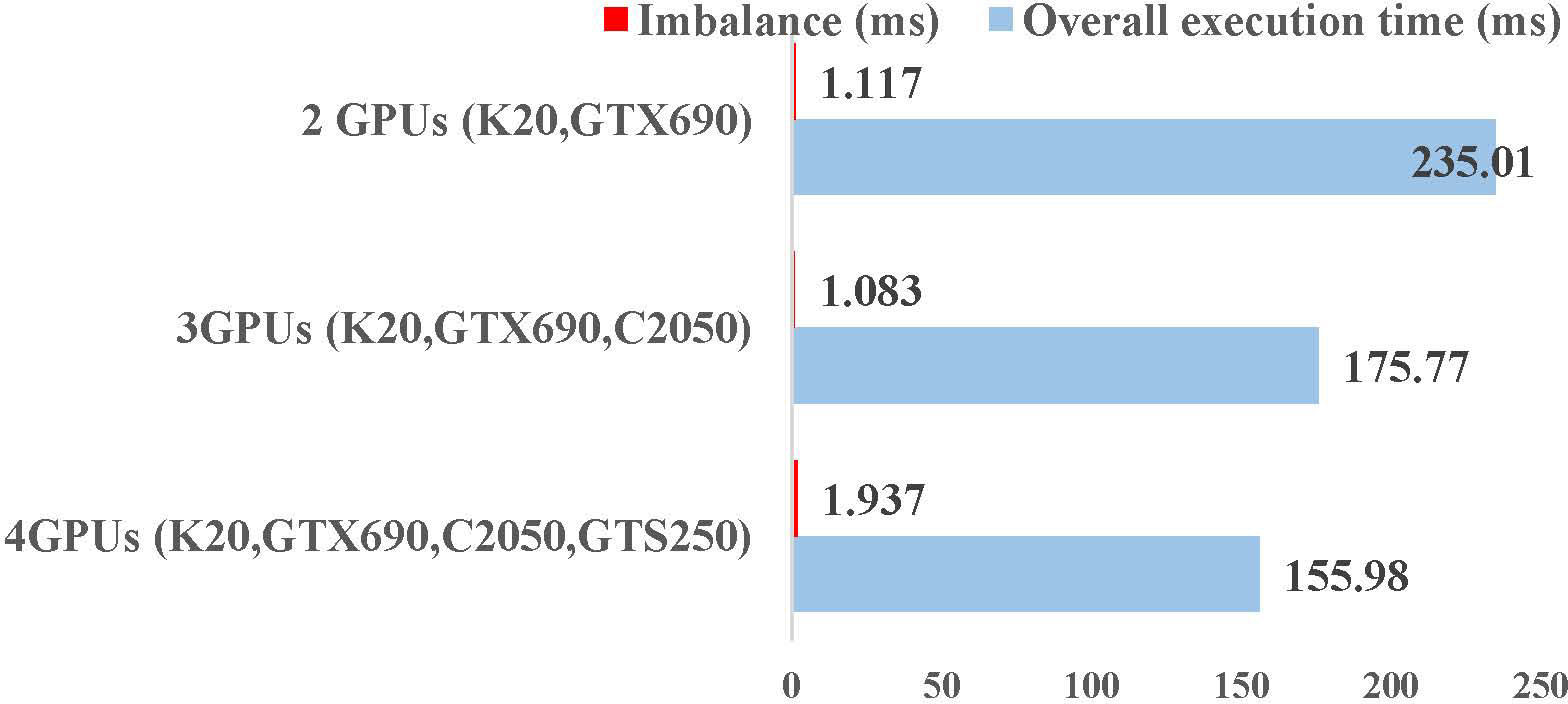
In the first experiment, we evaluate our approach for different numbers of GPUs with twelve training samples. As shown in Figure 6, the overall execution time reduces while the number of heterogeneous GPUs increases. As for imbalance, our approach can efficiently reduce the variance of execution times among GPUs by our objective function no matter the number of GPUs used. Compared to the overall execution time, our approach constrains the imbalance under 1.2%.

Figure 6.

Impact on performance and imbalance of matrix multiplication with number of GPUs.

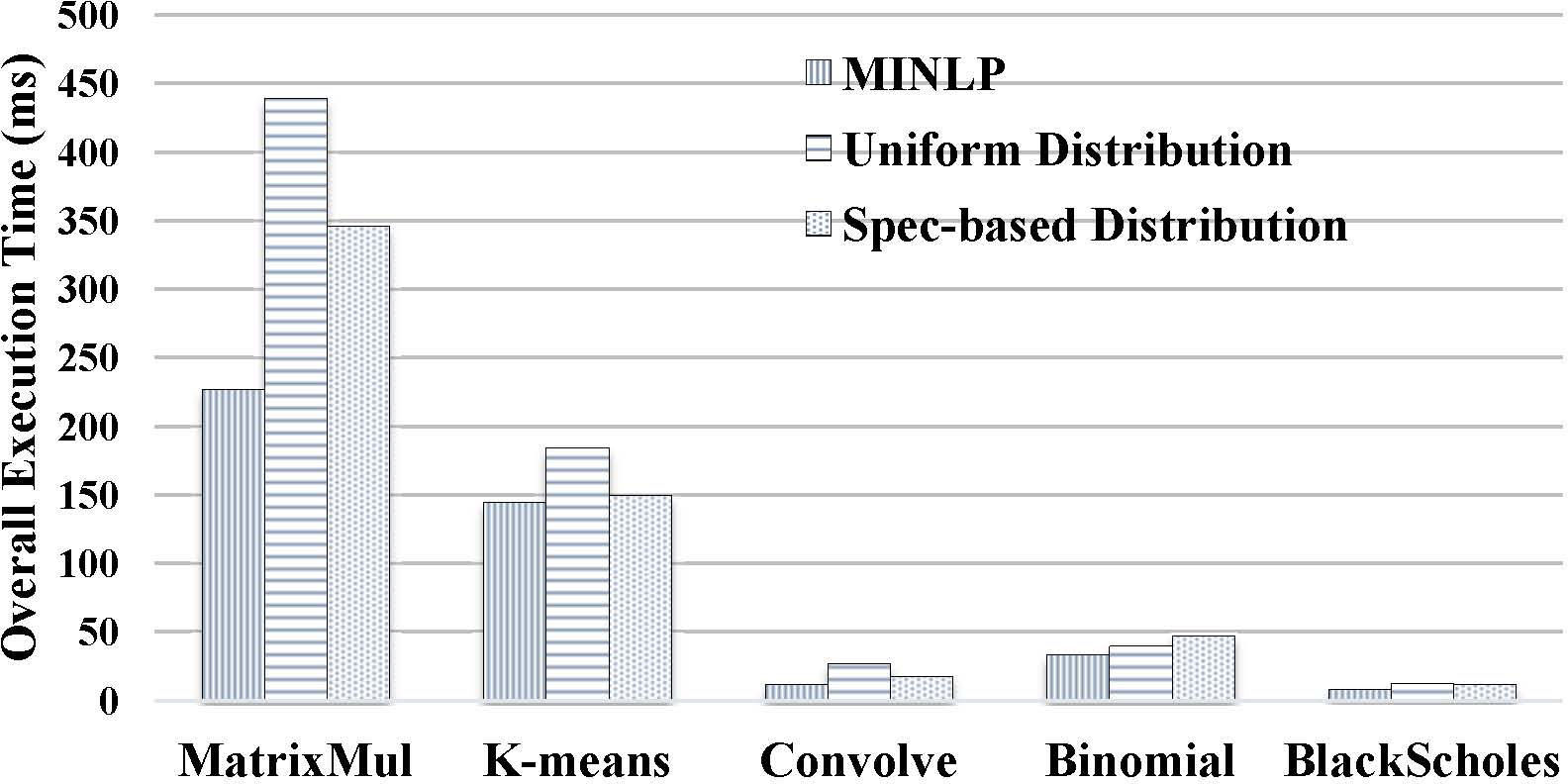
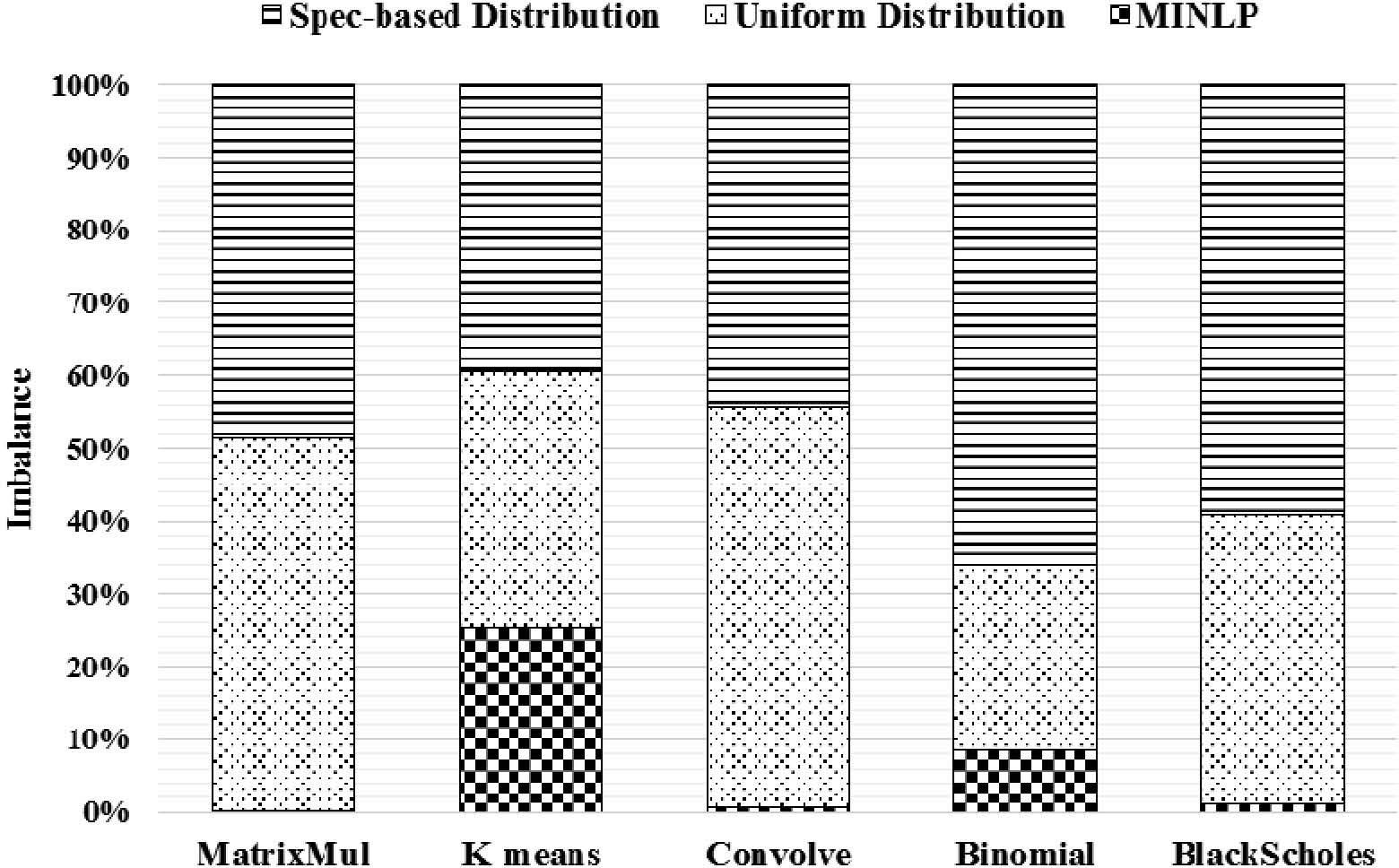
Figure 7 and 8 show the performance and imbalance comparison of MINLP-based, UD, and SBD with twelve training samples, respectively. In these two experiments, we use GTX 690, C2050, and GTS250. Note that our main objective is workload balancing among GPUs.

Figure 7.

Performance comparison.

Figure 8.

Imbalance comparison.

In Figure 7, the average performance of MINLP-based is 1.66x and 1.35x speedup to UD and SBD, respectively. And for load balancing in Figure 8, MINLP-based outperforms 2.8 and 3.2 times better than UD and SBD in average, respectively.

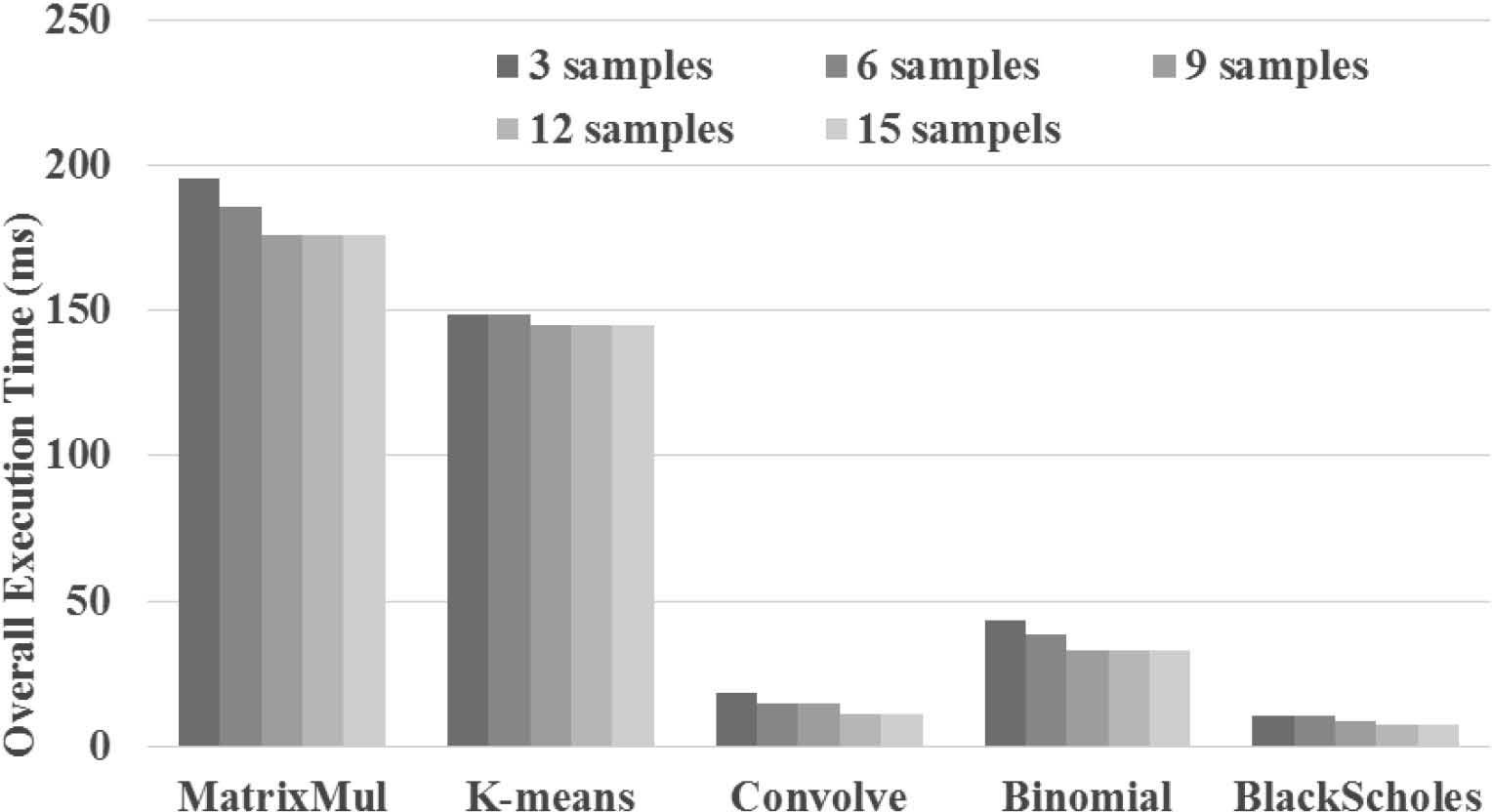
The final experiment is to evaluate our approach on performance with various numbers of training samples. As shown in Figure 9, the performance of all benchmarks improve while the number of training samples increase. In addition, the performance of most benchmarks converge when the number of training samples is more than nine. Therefore, our approach requires minimum overhead for building regressions and reach the optimal performance.

Figure 9.

Impacts on performance with different number of training samples.

7

Conclusion

We have proposed MINLP-based method for computational workload distribution on heterogeneous GPUs. The proposed method shows superiority than other methods on workload balancing. In addition, the proposed method only requires a few training samples thus remain the overhead as low as possible. For the number of heterogeneous GPUs, our method can support more than two GPUs. We will clarify the relation between performance and load balance in the future work.

Acknowledgments

We are grateful to the National Center for HighPerformance Computing for computer time and facilities.