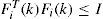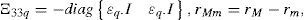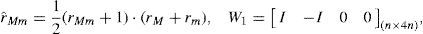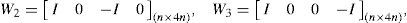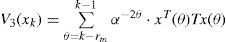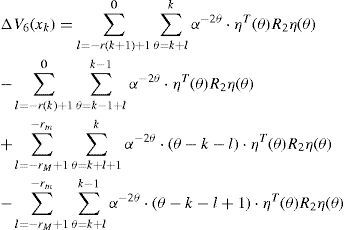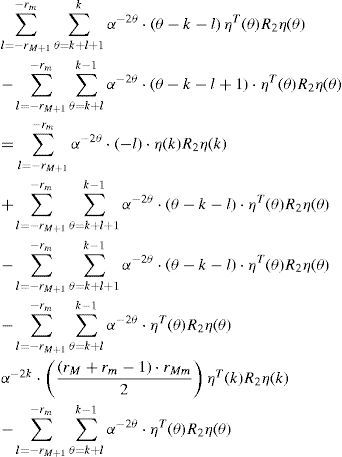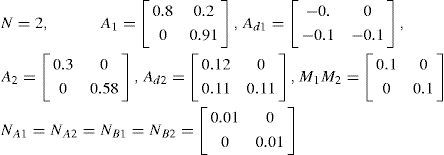Robust Exponential Stability for Uncertain Discrete-Time Switched Systems with Interval Time-Varying Delay through a Switching Signal

Abstract

This paper deals with the switching signal design to robust exponential stability for uncertain discrete-time switched systems with interval time-varying delay. The lower and upper bounds of the time-varying delay are assumed to be known. By construction of a new Lyapunov-Krasovskii functional and employing linear matrix inequality, some novel sufficient conditions are proposed to guarantee the global exponential stability for such system with parametric perturbations by using a switching signal. In addition, some nonnegative inequalities are used to provide additional degrees of freedom and reduce the conservativeness of systems. Finally, some numerical examples are given to illustrate performance of the proposed design methods.

1

Introduction

A switched system is composed of a family of subsystems and a switching signal that specifies which subsystem is activated to the system trajectories at each instant of time [1]. Some real examples for switched systems are automated highway systems, automotive engine control system, chemical process, constrained robotics, power systems and power electronics, robot manufacture, and stepper motors [2-14]. Switching among linear systems may produce many complicate system behaviors, such as multiple limit cycles and chaos [1]. It is also well known that the existence of delay in a system may cause instability or bad performance in closed control systems [15-17]. Time-delay phenomena are usually appeared in many practical systems, such as AIDS epidemic, chemical engineering systems, hydraulic systems, inferred grinding model, neural network, nuclear reactor, population dynamic model, and rolling mill. Hence stability analysis and stabilization for discrete switched systems with time delay have been researched in recent years [2-4, 7, 9-10, 12-14].

It is interesting to note that the stable property for each subsystem cannot imply that the overall system is also stable under arbitrary switching signal [4, 6, 8-9]. Another interesting fact is that the stability of a switched system can be achieved by choosing the switching signal even when each subsystem is unstable [5, 7-8]. In [7], a switching signal design technique is proposed to guarantee the asymptotic stability of discrete switched systems with interval time-varying delay. In [14], the switching signal is identified to guarantee the stability of discrete switched time-delay system. Additional nonnegative inequality terms had been used to improve the conservativeness for the obtained results in our past results [4-5]. Hence the global exponential stability problems for uncertain switched discrete systems with interval time-varying delay under some certain switching signal will be considered in this paper. Some numerical examples are provided to demonstrate the use of obtained results. From the simulation results, our proposed approach provides some less conservative results.

The notations are used throughout this paper. For a matrix A, we denote the transpose by A^T, spectral norm by A, symmetric positive (negative) definite by A>0 (A<0), maximal eigenvalue by λ_max(A), minimal eigenvalue by λ_min(A), n×m dimension by A_(nxm). A≤B means that matrix B−A is symmetric positive semi-definite. 0 and I denote the zero matrix and identity matrix with compatible dimensions. diag{…} stands for a block-diagonal matrix. For a vector x, we denote the Euclidean norm by x. Define N―=1,2,⋅⋅⋅,N,N>1, xKS=maxθ=−rM,−rM+1,⋅⋅⋅,0x(k+θ).

2

Problem statement and preliminaries

Consider the following uncertain discrete switched system with interval time-varying delay of the form

where x(k) ∈ℜⁿ is the state vector, x_k is the state at time k defined by x_k(θ):=x(k + θ), ∀θ ∈ {−r_M, −r_M +1, …,0}, switching signal law σ(k,x(k)) is a piecewise constant function depending on the state in each time. The switching signal σ(k,x(k)) takes its value in the finite set N― and will be designed. Moreover, the σ(k) = i implied that the i-th subsystem A¯i,A¯di is activated, and ϕ(k) ∈ℜⁿ is a vector-valued initial state function. The time-varying delay r(k) is a function from {0,1,2,3,⋯} to {0,1,2,3,⋯}, and satisfies the following condition:

where r_m and r_M are two given positive integers.

The matrices A¯i,A¯di are assumed to be A¯i=Ai+ΔAi(k), A¯di=Adi+ΔAdi(k), where A_i, A_di∈ℜ^n×n, i = 1,2, ⋯,N, are some given constant matrices. ∆A_i(k), A_di(k), i = 1,2,⋯,N, are some perturbed matrices and satisfy the following conditions

where M_i and N_ji, j = 1,2 i = 1,2, …,N, are some given constant matrices of system with appropriate dimensions, and F_i(k), i = 1,2, …,N, are unknown matrices representing the parameter perturbations which satisfy

In order to derive our main results, the Lemmas are introduced as follows:

Lemma 1.

[4] Let U, V, W and M be real matrices of appropriate dimensions with M satisfying M = M^T, then M+UVW+W^TV^TU^T <0 for all V^TV≤I, if and only if there exists a scalar ε>0 such that M+ε⁻¹·UU^T+ ε·W^TW=M+ε⁻¹·UU^T+ε⁻¹·(εW)^T(εW)<0

Lemma 2.

(Schur complement of [18]). For a given matrix W=W11W12W12TW22 with W11=W11T,  W22=W22T, then the following conditions are equivalent:

(1) W<0, (2) W₂₂<0, W11−W12W22−1W12T<0.

Define the some sets

where 0< α <1, P>0, and Q>0, then we obtain

From the above sets definition, then the switching law is designed as follows:

where Ω¯i is defined in (6).

The key lemma can be easily proved by the similar way in [7].

Lemma 3.

If there exist some scalars 0≤ α ≤1, 0≤ α_i ≤1, i∈N¯, and ∑i=1Nαi=1, some matrices P > 0 and Q > 0, such that ∑i=1Nαi⋅−P+UAiTP*−α2⋅P<0 Obviously, we can obtain ∪i=1N Ω¯i=ℜn and Ω¯i∩Ω¯j=φ, i ≠ j, i, j =1,2, …,N, where φ is an empty set and Ω¯i is defined in (6).

Remark 1.

Consider a discrete switched system: x(k + 1) = A_σ(k)x(k).

Now we can choose the Lyapunov function as V(x_k) = α^−2k·x^T(k)Px(k)

where matrix P>0. We can obtain ∆V(x_k) = α^−2k·[α⁻²·x^T(K+1)Px(K+1)−x^T(k)Px(k)].

Assume σk,x(k)=q∈N¯, then we have ΔV(xk)=α−2k⋅xT(k)(α−2⋅AqTPAq−P+U−U)x(k) where the matrix U>0.

If the condition in Lemma 3 is satisfied, then we can get

By Lemma 2 with (8), then we can have the following result:

To achieve the exponential stability of discrete switched system, the condition in Lemma 3 is a reasonable choice and feasible setting.

3

Main results

Theorem 1.

System (1) is globally exponentially stable with convergence rate 0 < α < 1 for any time-varying delay r(k) satisfying (2), if there exist some nxn matrices P>0, S>0, T>0, Q>0, U >0, R_i>0, i = 1,2,3,4, R_j11∈ℜ^4n×4n, R_j12∈ℜ^4n×nj = 1,2,3,4,5, and the positive numbers ε_q, q = 1,2, ⋯,N, such that the following LMI conditions are feasible:

where

Proof.

The Lyapunov-Krasovskii functionals candidate is given by

where

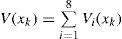
where P>0, S>0, Q>0, T>0, R_i>0, i = 1,2,3,4, and η(θ)=x(θ +1) −x(θ). Taking the difference of Lyapunov functionals V_j(x_k), j = 1,2,3,4,5,6,7,8, along the solutions of system (1) has the form

By some simple derivations, we have

By some simple derivations, we have

Then we can obtain the following result from (21)-(31)

Define

From LMIs in (9) with ∑θ=k−r(k)k−1η(θ)=x(k)−xk−r(k) and the similar equations, we have

Assume the particular case σ(k,x(k)) = q, then we can obtain the following result

Where ϵ(k)=r(k)−rmrMm

with Ξ11qi, W_j, i = 1,2, j = 1,2,3,4,5, q = 1,2, …,N, are defined in (10).

Since 0< ε(k)<1, the ϵ(k)⋅Ξ¯1q+(1−ϵ(k))⋅Ξ¯2q is a convex combination of Ξ¯1q and Ξ¯2q. Hence ϵ(k)⋅Ξ¯1q+(1−ϵ(k))⋅Ξ¯2q<0 will imply Ξ¯1q<0 and Ξ¯2q<0

Define

where

ΛqT=0000MqTPMqTR1MqTR2MqTR3MqTR4ΓqT=N1q0N2q000000, and Ξ11qi, Ξ12q, Ξ22q are defined in (10).

By the condition (11) with Lemma 3 and the switching signal in (8), we can obtain the following result

By Lemmas 1-3 with above conditions, the conditions Ξiq<0, i = 1,2, in (10) will imply Ξˆiq<0, i =1,2, in (40), the conditions Ξˆiq<0, i=1,2, in (40) will also imply Ξ¯iq<0 in (39) Therefore, the conditions Ξ¯iq<0, i = 1,2, in (39) are equivalent to ϵ(k)⋅Ξ¯1q+(1−ϵ(k))⋅Ξ¯2q<0 in (38). From the condition (41) and the matrix ϵ(k)⋅Ξ¯1q+(1−ϵ(k))⋅Ξ¯2q<0 in (28) with (9), we have

This implies

where

By some simple derivations, we have

Therefore, we conclude that the system (1) is exponentially stable with convergence rate 0<α<1. This completes this proof.

Remark 2.

By setting α = 1 in Theorem 1, the global asymptotic stability of system (1) can be achieved.

Remark 3.

In Theorem 1, some additional nonnegative inequalities in (33) - (37) are proposed. Rj>0, j = 1,2,3,4, R_i11 ∈ℜ^4n×4n, R_i12∈ℜ^4n×n, i = 1,2,3,4,5, in (9), are determined appropriately by LMI toolbox of MATLAB.

4

Illustrative examples

Example 1.

Consider the system (1) with no uncertainties and the following parameters: (Example 3.1 of [7])

In order to show the obtained results, the allowable delay upper bound and switching sets that guarantees the global exponential stability for system (1) with (42) is provided in Table 1.

Table 1.

Some obtained results for our proposed results in this paper.

The delay upper bound and switching sets of switched system (1) with (42)
[7]	α = 1, rm=1, rM =5 globally asymptotically stable (choose α1= α2=0.5)
	Ω¯1=x1x2T∈ℜ2:−12.0213x12−38.8254x1x2−31.6356x2<0,Ω¯2=ℜ2−Ω¯1.
Our results	α = 1, rm=1, rM =187 globally asymptotically stable (α1=0.1 and α2=0.9)
	Ω¯1=x1x2T∈ℜ2:2.9225x12+10.1092x1x2+7.7291x2<0,Ω¯2=ℜ2−Ω¯1.
	α = 0.85, rm=1, rM =7 globally exponentially stable (α1=0.1 and α2=0.9)
	Ω¯1=x1x2T∈ℜ2:−1.5344x12+5.7566x1x2−5.0051x2<0,Ω¯2=ℜ2−Ω¯1.

Example 2.

Consider the system (1) with the following parameters: (Example 3.1 of [10]).

In order to show the obtained results, the allowable delay upper bound that guarantees the global asymptotic stability for system (1) with (43) is provided in Table 2.

Table 2.

Some delay bounds to guarantee the global asymptotic stability (α = 1) of system

The delay upper bound and switching sets of switched system (1) with (43)
[10]	rm=1,rM=5 (under arbitrary switching signal)
[4]	r =1,rM=6 (under arbitrary switching signal)
Our result	rm=1,rM=11(α1=0.1 and α2=0.9)
	Ω¯1=x1x2T∈ℜ2:18.6759x12+0.6803x1x2+0.4395x2<0,Ω¯2=ℜ2−Ω¯1..

Example 3.

Consider the system (1) with the following parameters:

In order to show the obtained results, the allowable delay bounds that guarantee the global asymptotic stability for system (1) with (44) is provided in Table 3.

Table 3.

Some delay bounds to guarantee the global asymptotic stability (α = 1), of system.

The delay upper bound and switching sets of switched system (1) with (44)
[10]	rm=1, rM=2 (under arbitrary switching signal)
[4]	rm=1, rM=3(under arbitrary switching signal)
	rm=2, rM=3 (under arbitrary switching signal)
Our result	rm=1, rM=4 (α1 = 0.1 and α2 = 0.9)
	Ω¯1=x1x2T∈ℜ2:3.4451x12+3.4325x1x2+1.7489x2<0,Ω¯2=ℜ2−Ω¯1.
	rm=2, rM=4 (α1 =0.1 and α2 =0.9)
	Ω¯1=x1x2T∈ℜ2:1.2306x12+1.5704x1x2+0.7528x2<0,Ω¯2=ℜ2−Ω¯1.

Example 4.

Consider the system (1) with the following parameters: (Example of [9])

In order to show the obtained results, the allowable delay bounds that guarantee the global asymptotic stability for system (1) with (45) is provided in Table 4.

Table 4.

Some delay bounds to guarantee the global asymptotic stability (α = 1) of system.

The delay upper bound and switching sets of switched system (1) with (45)
[9]	rm=2, rM=6 (under arbitrary switching signal)
[4]	rm =1, rM=10 (under arbitrary switching signal)
	rm=2, rM =10(under arbitrary switching signal)
	rm=4, rM=11(under arbitrary switching signal)
	rm =8, rM=12 (under arbitrary switching signal)
Our result	rm=1, rM=11 (α1 = 0.1 and α2 = 0.9)
	Ω¯1=x1x2T∈ℜ2:−0.7576x12+18.2930x1x2+50.3305x2<0          ,Ω¯2=ℜ2−Ω¯1.
	rm=2, rM=11 (α1 = 0.1 and α2 = 0.9)
	Ω¯1=x1x2T∈ℜ2:−0.1590x12+1.4113x1x2+4.4661x2<0          ,Ω¯2=ℜ2−Ω¯1.
	rm=4, rM=13 (α1 = 0.1 and α2 = 0.9)
	Ω¯1=x1x2T∈ℜ2:−0.7476x12+9.8448x1x2+29.7229x2<0         ,Ω¯2=ℜ2−Ω¯1.
	rm=8, rM=16 (α1 = 0.1 and α2 = 0.9)
	Ω¯1=x1x2T∈ℜ2:−0.4987x12+2.8498x1x2+8.0945x2<0         ,Ω¯2=ℜ2−Ω¯1.

Note that comparing the proposed examples, we can design a new switching signal to guarantee the global exponential stability for system (1). At the same time, less conservative results are reached without tuning any parameters.

5

Conclusions

In this paper, the global exponential stability for uncertain discrete switched systems with interval time-varying delay has been considered. Some additional nonnegative inequalities and LMI approach are used to guarantee the proposed results of the system. The obtained results have shown to be less conservative via some numerical examples. In [19-20], the practical applications have been successfully designed in the different control fields.

Acknowledgments

The research reported here was supported by the National Science Council of Taiwan, R.O.C. under grant no. NSC102-2221-E-507-006.