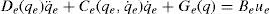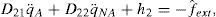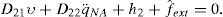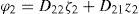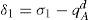Experimental Estimation of Slipping in the Supporting Point of a Biped Robot

Abstract

When developing a gait cycle on a low-friction surface, a biped robot eventually tends to slip. In general, it is common to overcome this problem by means of either slow movements or physical adaptations of the robot at the contact point with the walking surface in order to increase the frictional characteristics. In the case of slipping, several types of sensors have been used to identify the relative displacement at the contact point of the supporting leg with the walking surface for control purposes. This work is focused on the experimental implementation of a low-cost force sensor as a measurement system of the slipping phenomenon. It is shown how, supported on a suitable change of coordinates, the force measurement at the contact point is used to obtain the total displacement at the supporting point due to the low-friction conditions. This is an important issue when an accurate Cartesian task is required.

Resumen

Cuando un robot bípedo desarrolla ciclos de marcha en una superficie con baja fricción, eventualmente tiende a patinar; sin embargo es común evitar este problema mediante ejecuciones de movimientos de baja velocidad o bien, mediante adaptaciones físicas en el punto de contacto con la superficie para aumentar las caractersticas de fricción. Cuando este fenómeno se presenta, la existencia y magnitud del desplazamiento relativo en el punto de contacto puede ser identificada a partir de una gran variedad de sensores. Este trabajo se enfoca en la medición del patinado descrito anteriormente a través de un sensor de fuerza de bajo costo. Se muestra además cómo, a través de un cambio de coordenadas, la lectura de la fuerza en el punto de contacto es utilizada para conocer la magnitud del desplazamiento en el apoyo debido al patinado.

1

Introduction

In the large and increasing variety of works that deal with biped locomotion, there are some dynamic characteristics that have not been widely studied since they do not represent critical conditions on a specific task. However, there exist some cases in which those dynamics must be considered. In particular, the slipping phenomenon describes one of these situations that, in general, is avoided by providing a suitable environment. Nevertheless, if the circumstances are such that the walking surface has low-friction characteristics, then the slippage becomes substantial and this situation implies a challenge in the measurement of the resulting displacement that provides crucial information for control tasks.

There are some works in the literature that consider the slipping phenomenon as a fundamental dynamics in their analysis. In [5], the frictional characteristics are regulated by following a previously calculated walking pattern, which considers safety conditions for not falling down. In [2] and [9], it is implemented a feedback control that allows the robot to modify its posture from an undesired movement due to an undesirable skid; this control strategy has the advantage of fast convergence to stable trajectories. In [6], it is implemented an observer scheme that compares a reference force profile with a measured one in order to obtain an estimated slip force and, in this way, determine a possible slip condition for a biped robot in a low-friction surface. In order to obtain the magnitude of the displacement produced by the slip, in [7], the relative movement between two bodies is measured by means of an integrated device constituted by multiple force/torque and tactile sensors.

The knowledge of a slide due to a slipping condition is crucial in control schemes where Cartesian based evolution is very important and, in more complex situations, where the slipping effects imply an unstable condition that could lead the robot to fall down. When the friction conditions are low, it is important to know how a robot can develop a correct and stable walking trajectory in order to avoid falls; for doing this, the measurement of the slipping motion is a critical requirement.

A simple low-cost way to measure the slippage is addressed in this work by considering a particular resistive force sensor. This approach considers the incorporation of an additional degree of freedom that takes into account this type of movement at the end of the stance leg. In this way, the slipping dynamics is characterized in terms of forces acting at the contact point, involving the frictional and tangential forces that result from the evolution of the robot posture during the gait cycle. The analysis and experiments carried out in this work show how the displacement and velocity due to the slipping phenomenon can be obtained. This information could eventually be taken into account in a corrective control action in order to preserve the stability of the walking cycle in the Cartesian space.

The rest of the paper is organized as follows: In Section 2, the dynamic model of the biped robot under study is described together with the main hypotheses that are considered in the rest of the work. The conditions for the existence of the slipping phenomenon are also stated taking into account the friction force described by a simple Coulomb model and the resulting tangential force due to the articular dynamics. The system is represented in a suitable error coordinates in Section 3 and the system in closed loop with a particular feedback law is analyzed in Section 4. The physical platform and the experimental results are described in Section 5 and finally, some general conclusions are presented in Section 6.

2

Class of underactuated biped robot

The considered biped robot that is subject of analysis consists of four articular and actuated degrees of freedom. However, in order to analyze the slipping dynamics, an additional prismatic and nonactuated degree of freedom is incorporated at the contact point of the stance leg with the walking surface, characterizing an under-actuated system. Preliminary considerations assume that i) the robot evolves in the single-support phase; the double-support phase is assumed to be instantaneous and can be treated as an external perturbation; ii) the robot dynamics is defined in the sagittal plane with punctual contact with the ground; iii) there is neither rebound nor penetration in the normal direction of the walking surface.

The dynamic model is obtained by means of the Euler-Lagrange formulation [12]. It is first assumed that the robot can freely move on the plane and has the representation,

where qe=[q31,q32,q41,q42,ζ1,ζ1¯]T is the generalized coordinates vector.D_e ∈ R^6×6 and C_e ∈ R^6×6 represent the inertia and coriolis matrices, respectively, while G_e ∈ R^6×1 corresponds to the gravity force vector. B_e ∈ R^6×6 is the input matrix and u_e = [τT,0_2×1]T ∈ R^6×1 with τ ∈ R^4×1 is the input signal vector. Figure 1 describes this configuration. The right-hand side of Equation 1 acts as the control action and it is defined by considering independent actuators. Taking into account the choice of the generalized coordinates q_e, the torque influence on these coordinates is expressed by means of matrix B_e that can be obtained as [14]

Figure 1.

Description of the General Model of The Biped Robot.

where qB=[q31,q32,q41-q31,q42-q32,ζ1,ζ1¯]T.

By restricting the robot to be always in contact with the ground, that is, by considering ζ1¯=0, model (1) can be reduced to obtain the single-support dynamics as

where now, q = [q₃₁,q₃₂,q₄₁,q_42,ζ₁]^T, u = τ^T and Fext=[04×1,-fˆext(q)]T. Vector F_ext represents the external forces acting on the supporting point in the tangential direction. The involved matrices in model (2) are given as

where, in order to simplify the notation, it was defined c_(·) = cos(·) and s_(·) = sin(·) ; and

Being g the gravity constant, the parameters of the above matrices are given in Table 1.

Table 1.

Structural Parameters of The Model.

a1=L32(54M3+M4+MH)	a2=L32(12M3+M4)
g1=L3g(32M3+M4+MH)	z1 = L4a2/L3
g3=L4g(2M3+32M4+MH)	g4=-12L4M4g
g2=-L3g(12M3+M4)	k2=-12M4L3L4
k1=L4(a1L3+14L3M3)	k3=L32(14M3+M4)
k4=L42(54M4+2M3+MH)	k5=12M4L3L4
MT = MH+2M3+2M4	k6=12M4L42
b1=L3(32M3+M4+MH)	b2=-L3(12M3+M4a)
b3=L4(32M4+2M3+MH)	b4=-12M4L4

The actuated coordinates vector is defined as q_A = [q_31,q₃₂,q₃₂,q₄₂]T and the nonactuated coordinate, the translational one is denoted as q_NA = ζ₁. In addition, it is possible to consider a block decomposition for the inertia, coriolis and gravity matrices from model (2) as D(q) = [D₁₁,D₁₂;D₂₁,D₂₂], C(q,q) = [C₁₁,0_4×1;C₂₁,0] and G(q) = [G₁,G₂]T such that C₁₁ ∈ R^4×4, C₂₁ ∈ R^1×4, D₁₁ ∈ R^4×4, D21=D12T∈R1×4, D₂₂ = M_T ∈ R, G₁ ∈ R^4×1 and G₂ = 0. Correspondingly, input matrix B_R is also decomposed as B_{R =} [B,0_1×4]T, where B ∈ R^4×4. Under these conditions, model (2) can be rewritten as

where h1=C11q˙A, h2+C21q˙A. The input signal τ is defined as τ = [τ₃₁, τ₃₂, τ₄₁, τ₄₂]T.

2.1

Conditions for the existence of slipping motion

From Equation 4, it is clear that external force fˆext plays a very important role since the nonactuated coordinate is directly affected by its magnitude. In this work, fˆext is defined as the total force acting at the contact point in the horizontal direction when the robot develops a gait cycle. This force involves friction force f_F as a restrictive one and tangential force f_T which is generated at the support point as a consequence of the articular and actuated dynamics. Under these considerations, force fˆext is defined as

Forces in Equation 5 interact in such a way that when the magnitude of friction force f_F, a force that does not produce any work is larger than f_T, there is not any slipping and, therefore, the robot becomes four dimensional and completely actuated as in the case that the stance leg is attached to the ground. This is a nonslip condition and it is expressed as

Friction force f_F is described by means of a simple Coulomb component, that is,

where μ is the friction coefficient and fNe is the current normal force acting at the supporting point. Force f_T acts always in opposite direction to the friction and it is produced because of inertial and postural components of the robot during the execution of the walking cycle. Force f_T is a component of force F_S along the line that connects the center of mass CM of the robot and the supporting point, as shown in Figure 2. This figure shows the acting forces at the supporting point.

Figure 2.

Tangential Forces at the Support Point.

When the articular dynamics is such that the magnitude of f_T increases and it eventually overpasses friction force f_F, relation (6) is violated and a slippage begins. Such a situation makes the overall system underactuated. In general, this condition is more susceptible to appear at the beginning and the end of the step, depending on the dynamic requirements for the center of mass (x_CM, y_CM) at any time of the walking cycle, which causes changes on angle α and on F_S magnitude.

3

Error coordinates representation

From the general representation of the biped robot (4), it is not an easy task to determine the influence of external force fˆext over the possible slipping dynamics due to the coupling between the actuated and the nonactuated dynamics of the system. In order to overcome this problem, in what follows, a new system representation will be considered by taking into account a set of desired trajectories that are required to be tracked in a walking cycle. As a first step, a “collocated linearization” [13] together with a change of coordinates will be used in order to get a decoupled subsystem that will allow analyzing the required slipping phenomenon.

3.1

Partial linearization

In order to decouple the dynamics of the actuated (4a) and nonactuated (4b) subsystems, an input-output feedback linearization is proposed by considering

where D¯=D11-D12D22-1D21 and υ describes a new input signal. Remember that matrix D21=D12T is derived from the last row in matrix D from model (2) and depends on the articular coordinates q_A. The closed-loop system (4)-(8) produces

System (9) is the result of the “collocated linearization” [13], which refers to a feedback that linearizes the equations associated with the actuated coordinates.

In order to express system (9) in state space form, consider the set of coordinates

.

Then, system (9) can be expressed as

where the z subsystem (10a) represents the linear and completely actuated articular dynamics, whereas the ζ subsystem (10b) determines the evolution of the slipping dynamics. Notice that in Equation 10, the new input υ appears in both z and ζ subsystems, a situation that complicates the control design for the entire system. To overcome this problem, it is possible to rewrite (10) in a particular form such that the nonactuated coordinates can be decoupled with respect to input υ.

3.2

Decoupling of the control input

Subsystem (10b) can be decoupled with respect to υ by considering the global change of coordinates [8],

where γ(z1)=∫D22-1D21dz1. It can be shown, by developing the integral, that γ(z₁) describes the horizontal position x_CM(t) of the center of mass of the robot with respect to frame {A} (see Figure 1); hence, the new coordinate ϕ₁ defines the position of the center of mass with respect to the inertial frame {0}. Applying this change of coordinates, system (10) becomes

By considering a particular desired trajectory qAd, based on the error coordinates:

system (12) takes the following form:

Notice that the second equation of the ϕ subsystem (14b) describes exactly the force Newton law given that a specific force fˆext modifies the rate of movement through acceleration changes that are implicit in φ˙2.

Depending on the initial conditions, a high demand of torque signals could appear at each joint in order to get the convergence of subsystem δ given in (14a); this situation causes an increment in force f_T and eventually a slippage. When this situation occurs, subsystem (14b) evolves according to the induced effects from the articular performance and consequently of the δ subsystem behavior. Therefore, although the articular and slipping dynamics seem to be decoupled, there is a direct influence of the articular behavior on the slipping phenomenon. In general, an articular movement with specific conditions of velocity and posture could eventually produce a slippage, however, the analysis of the slipping phenomenon is naturally developed during stable walking cycles, thus it is meaningless to analyze a slippage produced from random articular movements. The following section is focused on the tracking of a reference trajectory, assuring a desired performance that could eventually imply the existence of realistic slides.

4

Closed-loop analysis and finite-time convergence

With the consideration of a feedback law already used in the biped robots literature [4], in what follows, a brief analysis of the closed-loop dynamics is presented.

4.1

Single-support phase

Notice that the δ subsystem (14a) is a double integrator that can be easily stabilized with a specific feedback ω. Because of the nature of the robot dynamics with respect to the walking cycle, it is necessary to ensure the error convergence before the step ends in order to guarantee a desired behavior. A finite-time convergence has already been implemented for biped robots, see for instance [4, 10]. In this work, the feedback law used in [4] is considered and originally defined in [1] for a double-integrator system. Regarding Equation 13(c), the auxiliary input υ is given by

where

ν=δ1+12-αsign(εδ2)|εδ2|2-α, for α ∈ (0, 1) and ε > 0. Equation 15 corresponds to a continuous feedback which renders the closed loop (14)-(13c)-(15) globally finite-time stable. As it has been proved in [1], the global stability of (13c)-(15) in closed loop with a double-integrator system, as the one of the δ subsystem (14a), can be stated by using a suitable Lyapunov function.

In general, the rate of convergence of error δ in subsystem (14a) determines the evolution of the ϕ subsystem (14b). Notice that, for the double-integrator subsystem (14a), a critical situation appears at the transient response, where the evolution of the error δ is different from zero and depends on the initial conditions; however, when δ converges to the origin, external force fˆext is only influenced by means of suitable references qAd and q˙Ad which could avoid critical postures and dangerous velocities that eventually may induce a nondesired slipping motion.

It can be inferred from Equation 5 that term fˆext never grows up indefinitely because of the bounded nature of f_F and f_T. Friction force f_F, modeled as in (7), takes its maximal value when the center of mass of the robot is located on the vertical axis, that is, when x_CM = 0 and α = 0 (see Figure 2). At this position, a maximal supporting force fNe=Fmax appears and the tangential force f_T becomes null. In any other situation, the normal force fNe is lower than F_max and the friction force is reduced; consequently, f_T tends to increase. This is the reason why the desired trajectory should be designed in order to limit the magnitude of f_T. It is then clear that the robot does not slip over the complete step given that force f_T does not always overpass the friction force magnitude. An external perturbation could also imply variations in the forces at the contact point, nevertheless, if the closed-loop system remains stable, the feedback law will indirectly compensate this disturbance. For the expressed reasons, it is possible to state from Equation 14(b) that ϕ₂ remains bounded and, consequently, ζ₂ is bounded too. As a direct consequence of this fact, the displacement of contact point ζ₁ will never grow indefinitely.

4.2

Double-support phase: impact dynamics

In general, the slipping phenomenon could not only appear at the single-support phase, but also the double-support phase could produce slip conditions because of the impact forces at the end of the step. Nonetheless, given that the double support is assumed as an instantaneous event, it is only characterized by an isolated and resetting map that allows to define the initial condition for a new step. This map is defined by a coordinate swapping such that the stance leg becomes the swing leg and vice versa and it is done once the impact has occurred, which in turns produces a natural discontinuity in the velocities. For the considered approach, the impact dynamics and the described map define the double-support phase.

The conditions for the existence of slipping at the double-support phase can also be determined in terms of the impact forces and friction characteristics as in (6). However, a non slipping condition can be assured by considering a specific behavior such that, at the end of the step, the robot hit the ground with sufficiently slow velocity. This implies that the tangential forces at the impact point are lower than the friction force.

In a general case where the robot slips, according to the instantaneous assumption, the slippage in the double-support phase could be considered as the one at the beginning of the single-support phase. This implies that the eventual slippage will correspond to an initial condition for ζ₁ and ζ₂. In this case, it can be shown that the boundedness of the closed-loop system holds even when the slipping at the impact point is produced. A critical situation arises when the velocity is such that the impact produces a high discontinuity at the joint velocities, nevertheless, based on [3], it can be shown that they are expressed as

where D is given in Equation 2, L ∈ R2x5 is a bounded matrix, and E ∈ R2x5is a Jacobian such that E=∂P2∂q, being P₂ the Cartesian position of the end point of the swing leg. Regarding the boundedness property of these matrices, the impulse generated by the discontinuity of velocities is also bounded and, consequently, the double-support phase can be considered a perturbation that eventually is absorbed by the control strategy.

5

Experimental results

Before presenting the experimental results of the work, a general description of the biped robot laboratory prototype is given.

5.1

Experimental platform

The biped robot prototype has been designed in order to be dynamically analyzed only in the sagittal plane. This is done by means of an external and restrictive frame which allows only translational free movements along vertical and horizontal axes. The biped robot is fixed to the exostructure at the hip, allowing a simple and noninvasive support. Figure 3 shows the physical platform.

Figure 3.

Physical Platform.

Based on [11], the biped robot is built with a special actuator mechanism which allows generating the high-torque requirements at the joints from a low-torque actuator; however, it has an important drawback: the high-velocity demand for the same actuator. The actuation method consists basically on a linkage mechanism, where the main input is provided by a brushed DC motor producing a translational movement through a ball-bearing screw which results in the required rotational movement for the knee and hip joints.

This mechanism is depicted in Figure 4 for the knee joints.

Figure 4.

Detail of the Linkage Mechanism.

The mechanical advantage of the transmission is determined by gain factors that are directly related with the current state of each joint. The input-output torque and velocity relations can be manipulated by changing the mechanical parameters of the mechanism.

The proposed mechanical interface limits the working space because of the admissible displacement of the nut along the screw as well as the length of the involved elements. Because of this, the resulting bounds for the joints can be described as

where q_h and q_k are the hip and knee joint angles respectively, measured with respect to the absolute vertical axis according to the generalized coordinates in Figure 1. Notice that qhmin and qhmax, that define the rotation of the femur, are defined with respect to the hip, which is assumed to be always aligned with the absolute frame {0} ; while qkmin and qkmax, the tibia rotation, are defined with respect to the femur.

As mentioned before, the contact with the walking surface is designed to be punctual and at the end of each leg a pressure mechanism has been implemented such that, at each contact point with the ground, the measurement of the contact force is obtained by means of a strategically located low-cost resistive sensor. This implementation is depicted in Figure 5. A Flexiforce sensor is used that has an approximate linear resistive response to an applied force.

Figure 5.

Pressure Mechanism at the End of Each Leg.

In order to compute the articular position, an optical encoder is installed at each joint. There is also an inclinometer at each tibia to sense an eventual fall of the robot. In addition, limit switches are used to prevent a mechanical damage as a consequence of displacements out of the ranges previously defined.

It is clear that the complexity of the mechanical prototype is not totally described by the mathematical model (2), obtained in Section 2, because it does not consider the auto-lock characteristic induced by the type of actuation, that is, the model assumes that the motor acts directly at the joint, a fact that actually does not happen. Nonetheless, it is possible to add the effect of the actuation mechanism as a gain factor ξ(q) for the control input, in this way, the actual input motor torque τ_m, is expressed as

where subscript j defines the hip joint (j = h) or the knee joint (j = k) and τ is the control signal for each joint derived from the closed-loop system.

5.2

Experimental slip estimation

To carry out the experiments, feedback law (13c)-(15) is implemented in a Matlab-Simulink platform supported on a DSP system DS1104 from DSpace. This board acts as real-time interface for the four 1000cpr optical encoders, the two Flexiforce resistive force sensors, the two axes and 9000cpr inclinometers at each tibia and the limit switches. Also, the DSP system provides the analog output torque signals for driving the DC motors. A general scheme of the experimental platform is depicted in Figure 6. For all the experiments it was considered a sampling time of 5 ms.

Figure 6.

Experimental Platform.

The slipping motion at the supporting point of the biped robot can be induced by developing one step. The slip estimation will be obtained by processing the information provided by the force sensor that measures the actual force at the contact point. This force is split in tangential and normal components, according to angle α that describes the position of the center of mass as depicted in Figure 2. Once the tangential force is known, a preliminary analysis is implemented in order to obtain the ϕ coordinates evolution and then, with the help of map (11), to obtain the real displacement ζ₁ at the base of the stance leg.

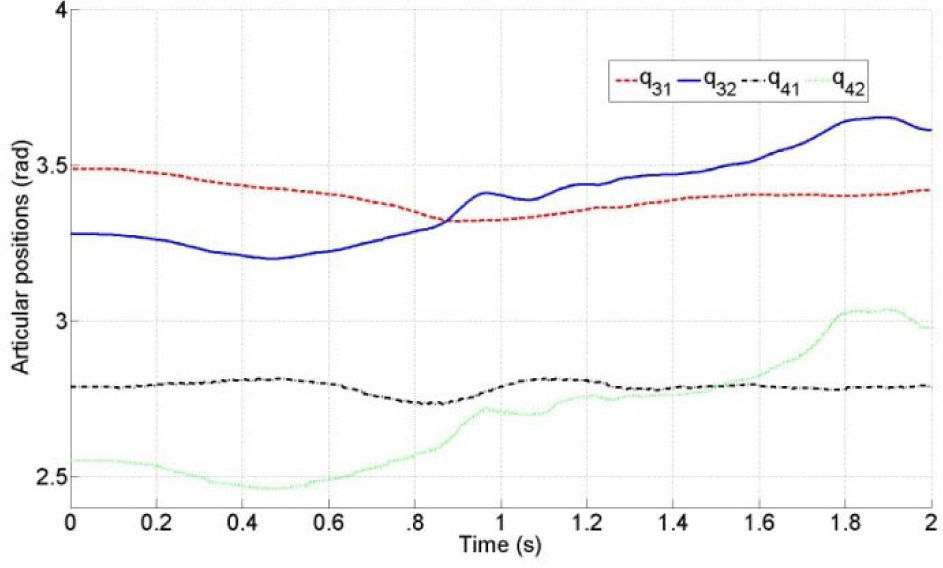
Figure 7 shows the articular performance for the experiment during one step. The reference parameters are such that the step length is set to 10 cm to be executed in two seconds. The height of the hip is defined as yHr=44cm and the maximal elevation of the free leg is y2r=2cm. These requirements are attained by means of suitable polynomial functions which, after an inverse kinematic mapping, describe the articular reference. For the experiment, the initial conditions are close enough to the reference.

Figure 7.

Position Articular Coordinates.

Tangential forces acting at the contact point, that is, friction f_F and the resulting tangential force f_T due to the articular dynamics, are depicted in Figure 8. Notice that in this particular case, it is at the end of the step where the nonslipping condition is violated, being | f_T | larger than | f_F |.

Figure 8.

Tangential Forces at the Contact Point.

Figure 9 shows displacement ζ₁ due to the slipping phenomenon. In order to satisfy (11c), the effective displacement of the contact point is affected by an offset defined by the horizontal position of the center of mass x_CM and the ϕ₁ coordinate. A representative effective displacement is indicated in Figure 9 at the end of the step, with an approximate magnitude of 4 mm in the opposite direction to the advance.

Figure 9.

Relative displacement at the support point.

Notice that the offset, that appears to be of 4.8 cm, is mainly dominated by the position of the CM at the beginning of the slippage.

The evolution of the auxiliary coordinates ϕ₁ and ϕ₂ are shown in Figures 10 and 11, respectively. Notice that these coordinates are active only in the case that the nonslipping condition is violated; before this, the value of both coordinates is irrelevant and does not mean anything. However, when slipping occurs, the ϕ₁ coordinate describes a displacement, which results from the definition of Equation 11(c), whereas both slide ζ₁ and γ evolve. The case of ϕ₂ has a similar active dynamics, but the coordinate represents a momentum according to Equation 11(d).

Figure 10.

Auxiliary Coordinate ϕ₁

Figure 11.

Auxiliary Coordinate ϕ_2.

The Cartesian components for the center of mass are depicted in Figure 12, whereas the evolution of the swing leg and the hip are shown in Figures 13 and 14, respectively. Notice that the magnitude of the X -coordinate of the CM at the beginning of the slip mainly corresponds to the offset shown in Figure 9.

Figure 12.

Position of the Center of Mass.

Figure 13.

Position of the End Point of. the Swing Leg.

Figure 14.

Cartesian Coordinates of the Hip.

6

Conclusions

This work has addressed a simple and low-cost method to measure the relative displacement of the contact point between the supporting leg of a biped robot and the walking surface. Such a displacement is due to the slipping dynamics produced as a consequence of a performance under low-friction conditions together with high-control actions required to achieve an adequate error convergence to desired articular trajectories. The implementation of this estimation strategy is based on a low-cost force sensor that supported on a suitable change of coordinates allows obtaining a good estimation of the actual displacement that takes place at the support point. The information obtained from the force sensors identifies all the forces involved not only as a consequence of the posture of the robot, but also of the inertial components which are not explicitly taken into account in a theoretical development. The magnitude of the displacement is obtained while the biped robot is driven along a walking cycle produced by a specific set of desired trajectories. As a second stage of our research, it is intended to use the estimated sliding measurement directly on the control feedback law in order to compensate the slipping phenomenon on a particular gait.