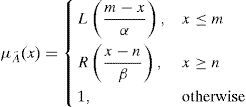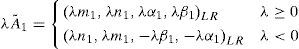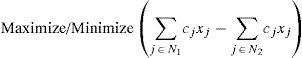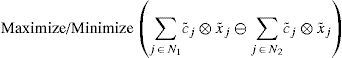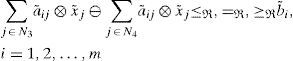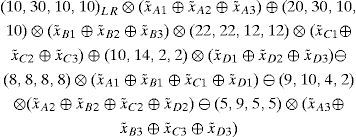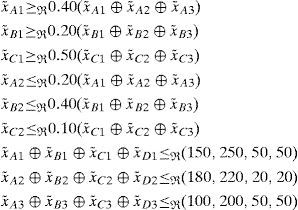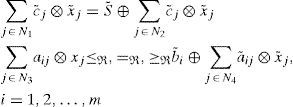General Form of Linear Programming Problems with Fuzzy Parameters

Abstract

In this paper, it is pointed out that the existing general form of such fully fuzzy linear programming problems in which all the parameters are represented by such flat fuzzy numbers for which is valid only if there is not a negative sign. However, if there is a negative sign, then the existing general form of fully fuzzy linear programming problems is not valid. Thus, a new general form is proposed.

1

Introduction

Linear programming is one of the most frequently applied operation research techniques. Although it has been investigated and expanded for more than six decades by many researchers and from various points of view, it is still useful to develop new approaches in order to fit better real-world problems within the framework of linear programming.

In conventional approach, parameters of linear programming models must be well defined and precise. However, in a real-world environment, this is not a realistic assumption. Usually, the value of many parameters of a linear programming model is estimated by experts. Clearly, it cannot be assumed that the knowledge of experts is precise enough. Bellman and Zadeh [2] proposed the concept of decision making in fuzzy environments. After that, a number of researchers have exhibited their interest to solve the fuzzy linear programming problems [1, 5–30].

In this paper, the shortcomings of existing general form of fully fuzzy linear programming problems are pointed out and a new general form of fully fuzzy linear programming problems is proposed.

This paper is organized as follows: In Section 2, some basic definitions and arithmetic operations are presented. In Section 3, the shortcomings of existing general form of fully fuzzy linear programming problems are pointed out. In Section 4, a new general form of fully fuzzy linear programming problems is proposed and the advantages of the proposed form over the existing form are discussed. Conclusions are discussed in Section 5.

2

Preliminaries

In this section, some basic definitions and arithmetic operations are presented [20].

2.1

Basic definitions

Definition 2.1: [4] A function, usually denoted by L :[0,∞) → [0,1] or R : [0,∞) → [0,1] is said to be the reference function of fuzzy number if and only if (i) L(0) = 1 (ii) L is nonincreasing in [0,∞).

Definition 2.2:[4] A fuzzy number à defined on the set of real numbers R, denoted as à = (m,n,α,β)_LR is said to be an LR flat fuzzy number if

Where, α > 0,β > 0.

Definition 2.3:[4] Let à = (m,n,α,β)_LR be an LR flat fuzzy number and λ be a real number in the interval [0,1] then the crisp set, A_λ = {x ∈ X : μ_à (x) ≥ λ} = [m − αL⁻¹ (λ),n + βR⁻¹(λ)], is said to be ^λ-cut of Ã.

Definition 2.4:[3] An LR flat fuzzy number à = (m,n,α,β)_LR is said to be non-negative LR flat fuzzy number if m − α ≥ 0 and is said to be nonpositive LR flat fuzzy number if n + β ≤ 0.

2.2

Arithmetic operations

In this section, the arithmetic operations between LR flat fuzzy numbers are presented [4].

Let Ã₁ = (m₁,n₁,α₁,β₁)_LR, Ã₂ = (m₂,n₂,α₂,β₂)_LR be two LR flat fuzzy numbers and Ã₃ = (m₃,n₃,α₃,β₃)_RL be a RL flat fuzzy number.

Then

If Ã₁, and Ã₂ both are non-negative, then Ã₁ ⊗ Ã₂ = (m₁m₂,n₁n₂,m₁α₂ + α₁m₂ − α₁α₂,n₁β₂ + β₁n₂ + β₁β₂)_LR

If Ã₁ is nonpositive and Ã₂ is non-negative, then Ã₁ ⊗ Ã₂ = (m₁n₂,n₁m₂,α₁n₂ − m₁β₂ + α₁β₂,β₁m₂ − n₁α₂ − β₁α₂)_LR

If Ã₁ is non-negative and Ã₂ is nonpositive, then Ã₁ ⊗ Ã₂ = (n₁m₂,m₁n₂,n₁α₂ − β₁m₂ + β₁α₂,m₁β₂ − α₁n₂ − α₁β₂)_LR

If Ã₁ and Ã₂ both are nonpositive, then Ã₁ ⊗ Ã₂ = (n₁n₂,m₁m₂,−n₁β₂ − β₁n₂ − β₁β₂,−m₁α₂ − α₁m₂ + α₁α₂)_LR

and scalar multiplication is defined as

3

Shortcomings of existing general form of fully fuzzy linear programming problems

In the existing methods [1, 12–17] it is assumed that the general form of fully fuzzy linear programming problems (P₂) is obtained by replacing the crisp parameters c_j, a_ij, b_i and x_j of crisp linear programming problem (P₁) by fuzzy parameters c˜j,a˜ij,b˜i and x˜j respectively.

Subject to

Where, x_j, a_ij, b_i, c_j are any real numbers and N₁ ∪ N₂ = {1,2,…,n}, N₃ ∪ N₄ = {1,2,…,n}, N₁ ∩ N₂ = φ, N₃ ∩ N₄ = φ.

Subject to

Where, x˜j, a˜ij, b˜i, c˜j are unrestricted fuzzy numbers and N₁ ∪ N₂ = {1,2,…,n}, N₃ ∪ N₄ = {1,2,…,n}, N₁ ∩ N₂ = φ, N₃ ∩ N₄ = φ.

However, if all the parameters of (P₂) are represented by LR flat fuzzy numbers then it is not genuine to use the fully fuzzy linear programming problem (P₂) to find the fuzzy optimal solution of real life problems due to the following reasons:

In previous studies, it was pointed out that only a RL flat fuzzy number Ã₂ can be subtracted from an LR flat fuzzy number Ã₁ i.e., if Ã₁ and Ã₂ both are LR flat fuzzy numbers such that L(⋅) ≠ R(⋅) then Ã₁ ⊖ Ã₂ does not exist. Hence, if all the parameters of the fully fuzzy linear programming problem (P₂) are represented by such LR flat fuzzy numbers for which L(⋅) ≠ R(⋅) then due to the existence of ∑j∈N1c˜j⊗x˜j⊖ ∑j∈N2c˜j⊗x˜j and ∑j∈N3a˜ij⊗x˜j⊖∑j∈N4a˜ij⊗x˜j, the fully fuzzy linear programming problem (P₂) is not valid.

Example 3.1 A manufacturer of biscuits is considering four types of gift packs containing three types of biscuits: orange cream (OC), chocolate cream (CC) and wafers (W). A market research conducted recently according to consumer preferences demonstrated that the assortments shown in Table 1 are to be in demand.

Table 1.

Most preferred assortments of biscuits.

Assortments	Contents	Fuzzy selling price per kg. (Rs.)
A	Not less than 40% of OC, not more than 20% of CC, any quantity of W	(10,30,10,10)LR
B	Not less than 20% of OC, not more than 40% of CC, any quantity of W	(20,30,10,10)LR
C	Not less than 50% of OC, not more than 10% of CC, any quantity of W	(22,22,12,12)LR
D	No restrictions	(10,14,2,2)LR

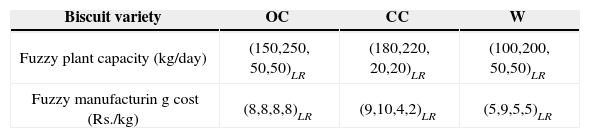
For the biscuits, the fuzzy manufacturing capacity and fuzzy costs are shown in Table 2.

Table 2.

Fuzzy manufacturing capacity and fuzzy cost for biscuits.

Biscuit variety	OC	CC	W
Fuzzy plant capacity (kg/day)	(150,250, 50,50)LR	(180,220, 20,20)LR	(100,200, 50,50)LR
Fuzzy manufacturin g cost (Rs./kg)	(8,8,8,8)LR	(9,10,4,2)LR	(5,9,5,5)LR

Formulate a model to find the production schedule which maximizes the fuzzy profit by assuming that there are no market restrictions.

3.1

Existing fuzzy linear programming formulation of the chosen problem

Using the existing general form of fully fuzzy linear programming problems (P₂), the chosen problem can be formulated into the following fully fuzzy linear programming problem

Maximize

Subject to

Where, x˜ij(i=A,B,C,D;j=1,2,3) is a non-negative LR flat fuzzy number and

• (i)

  x˜A1,x˜A2,x˜A3 denote the fuzzy quantity in kg. of OC, CC and W type of biscuits for the gift pack A.

• (ii)

  x˜B1,x˜B2,x˜B3 denote the fuzzy quantity in kg. of OC, CC and W type of biscuits for the gift pack B.

• (iii)

  x˜C1,x˜C2,x˜C3 denote the fuzzy quantity in kg. of OC, CC and W type of biscuits for the gift pack C.

• (iv)

  x˜D1,x˜D2,x˜D3 denote the fuzzy quantity in kg. of OC, CC and W type of biscuits for the gift pack D.

3.2

Drawbacks of the obtained fuzzy optimal value

To the best of our knowledge, only the existing method [1] can be used to find the fuzzy optimal value of such fully fuzzy linear programming problems in which the parameters are represented by LR flat fuzzy numbers.

In this section, to show the shortcomings of the existing general form of fully fuzzy linear programming problems (P₂), the fuzzy optimal value of fully fuzzy linear programming problem (P₃) obtained by using the existing method [1] is shown in Table 3.

Table 3.

Results of the chosen problem using existing formulation (P₃).

Method	Fuzzy optimal value	L(⋅) & R(⋅)
Existing method [1]	(P3) is not valid	L(x) = maximum{0,1 − x}R(x) = maximum{0,1 − x^2}
Existing method [1]	(P3) is not valid	L(x) = maximum{0,1 − x}R(x) = maximum{0,1 − x^4}

In the objective function of fully fuzzy linear programming formulation (P₃) of the problem, chosen in Example 3.1, subtraction of two LR flat fuzzy numbers is occurring. Hence, if L(⋅) ≠ R(⋅) then the fully fuzzy linear programming formulation (P₃) is not valid i.e., it is not possible to find the fuzzy optimal solution of the chosen problem by using the fully fuzzy linear programming formulation (P₃).

Remark 1. The shortcomings, pointed out in Section 3, will also occur in the existing general form of fuzzy linear programming problems [5–11, 18–30].

4

Proposed general form of fully fuzzy linear programming problems

In this section, to solve the shortcomings of the existing general form of fully fuzzy linear programming problems, pointed out in Section 3, a new general form of the fully fuzzy linear programming problems is proposed.

Maximize/Minimize S

Subject to

Where, x_j, a_ij, b_i, c_j and S are real numbers.

Replacing all the crisp parameters of the crisp linear programming problems (P₄) by fuzzy parameters general form of the fully fuzzy linear programming problems (P₅) can be written as

Maximize/Minimize S˜

Subject to

Where, x˜j,  a˜ij,  b˜i,  c˜j and S˜ are LR flat fuzzy numbers.

4.1

Advantages of the proposed general form of fully fuzzy linear programming problems

Because in the proposed general form (P₅) the subtraction of LR flat fuzzy numbers is not occurring, hence using the proposed general form the shortcomings of the existing general form pointed out in Section 3 are solved.

To show the advantage of the proposed general form over the existing general form, it was demonstrated that if the problem chosen in Example 3.1 is formulated by using the proposed general form, then all the shortcomings pointed out in Section 3 are solved.

Using the proposed general form of fully fuzzy linear programming problems (P₅), the problem, chosen in Example 3.1, can be formulated into fully fuzzy linear programming problem (P₆):

Maximize P˜

Subject to

Where, x˜ij(i=A,B,C,D; j=1,2,3) is a non-negative LR flat fuzzy number and P˜ is an LR flat fuzzy number.

Fuzzy optimal value of the formulated problem (P₆) by using the existing method [1] is shown in Table 4.

Table 4.

Results of the chosen problem using proposed formulation (P₆).

Method	Fuzzy optimal value	L(⋅)&R(⋅)
Existing method [1]	(14555,14555, 0,0)LR	L(x) = maximum{0,1 − x}R(x) = maximum{0,1 − x^2}
Existing method [1]	(14759,14759, 0,0)LR	L(x) = maximum{0,1 − x}R(x) = maximum{0,1 − x^4}

It is obvious from Table 4 that the proposed formulation (P₆) is valid for all values of L(⋅) and R(⋅). Therefore, by using the proposed general form of fully fuzzy linear programming problems (P₅) all the shortcomings, pointed out in Section 3, are solved.

5

Conclusions

Based on the present study it can be concluded that it is better to use the proposed general form of fully fuzzy linear programming problems as it was compared to the existing general form of fully fuzzy linear programming problems.

Acknowledgements

I, Dr. Amit Kumar, want to acknowledge the adolescent inner blessings of Mehar. I believe that Mehar is an angel for me and without Mehar's blessing it would not be possible to develop the idea proposed in this paper. Mehar is the lovely daughter of Parmpreet Kaur (Research Scholar under my supervision). The second author acknowledges the financial support given by the University Grant Commission under Maulana Azad National Fellowship Scheme.