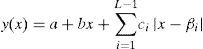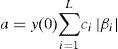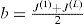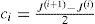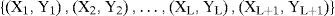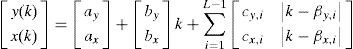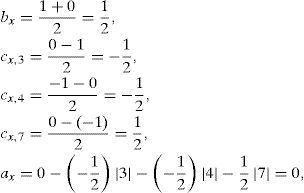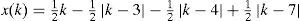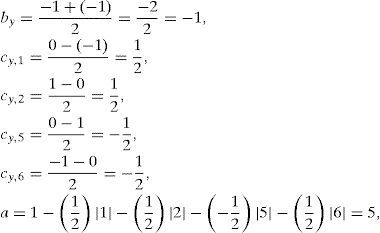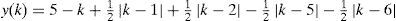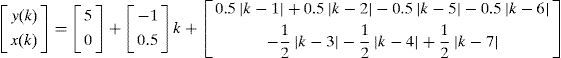This paper presents a curve-fitting technique for multivalued two-dimensional piecewise-linear paths. The proposed method is based on a decomposed formulation of the canonical piecewise linear model description of Chua and Kang. The path is treated as a parametric system of two position equations (x(k), y(k)), where k is an artificial parameter to map each variable (x and y) into an independent k-domain.
Este artículo presenta una técnica de ajuste de curva para trayectorias lineales a tramos bidimensionales multivaluadas. El método propuesto se basa en una formulación descompuesta del modelo canónico para descripción lineal a tramos de Chua y Kang. La trayectoria es tratada como un sistema paramétrico de dos ecuaciones de posición (x(k), y(k)), donde k es un parámetro artificial para mapear cada variable (x and y) en un dominio k independiente.
A two-dimensional path is a curve with a specific orientation and direction defined in the (x,y)-Cartesian plane. A piecewise linear (PWL) path is a sequence of connected line segments which define a curve [1]. Such a curve usually follows both forward and backward trajectory directions which describe regions with multivalued correspondence between the x and y axes in the Cartesian plane. In order to gain insights into the univalued and multivalued correspondence concepts, the following definitions are introduced:
Definition 1. Univalued curveA curve described by two variables x and y is defined as univalued if a value of one variable corresponds with one and only one value of the other variable. This condition enables the curve to be expressed as a function, either y(x) or x(y).
Definition 2. Multivalued curveA curve described by two variables x and y is multivalued if at least one value of either variable has correspondence with more than one value of the other variable. This condition excludes the possibility of expressing the curve in explicit function form.
If we are interested in determining a particular position associated with the PWL path, a mathematical model is needed. However, although many publications deal with the problem of finding a model description for univalued PWL curves [2–5] it is difficult to find a closed representation for multivalued curves because the imperative requirement of a function is not fulfilled, that is a correspondence that associates its variables (x and y) in terms of a one to one mathematical relation. Nevertheless, several methods have been proposed with which to fit and model multivalued PWL curves, for example: an algorithmic strategy based on the generalized linear complementary problem reported in Bart De Moor et al. [6]; a decomposed form of the state model devised by Van Bokhoven described in Brozobohaty-Kolka [7] and electronic realizations for modeling multivalued characteristics proposed by Chua-Kang in [8] and by Tadeusiewicz-Halgas in [9].
The present paper proposes a piecewise linear curve-fitting technique applied to two-dimensional paths. The technique uses the canonical PWL representation of Chua and Kang in its one-dimensional form; i.e., for a function f=R→R, which describes a PWL curve composed of L-segments, L-slopes (J(1),J(2),…,J(L)) and (L-1)-breakpoints (β1,β2,…,βL−1), as follows:
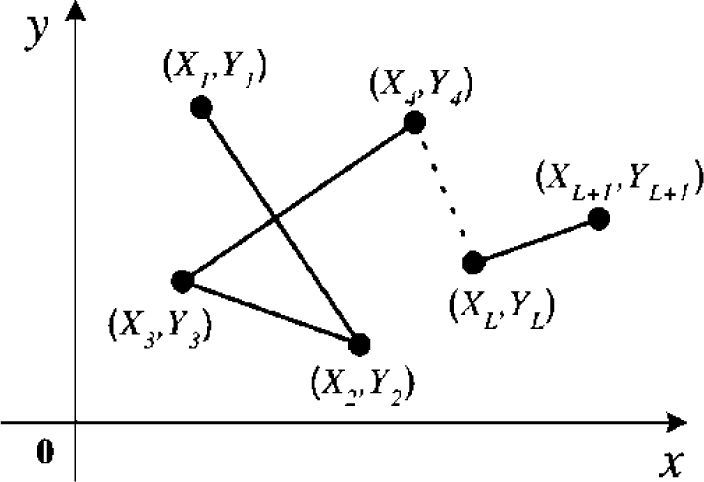
where the model parameters can be computed by:for i=1,2,…,L+1.2Two-dimensional piecewise linear pathLet the two dimensional PWL path, depicted in Figure 1, be characterized by L linear segments and (L+1) coordinates:
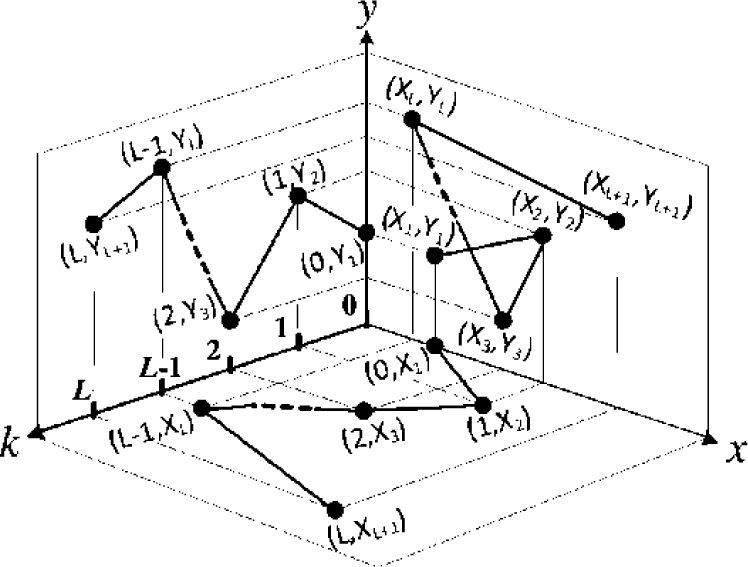
To overcome the problem of finding a mathematical representation for the path described in Figure 1, one axis k (with 0<k<L) is incorporated to form a three-dimensional kxy-system. In this system, the path of interest is referred in the xy-plane. The geometric projection of the coordinates Xi and Yi for i={1,2,…,L+1} together with their respective k-th value (for k=(i−1)) are sketched as two univalued PWL curves with the function descriptions x(k) and y(k), respectively. This procedure is depicted in Figure 2.
Note that both paths (kx and ky) are constructed by independently collecting the abscissas (Xi for i=0,1,…,L+1) and ordinates (Yi for i=0,1,…,L+1) belonging to the breakpoint coordinates presented in the xy-path. It is also worth mentioning that this collection is carried out by following the order of appearance of each breakpoint along the xy-path, with the respective Xi and Yi coupled with an iterative k value (k=0,1,…,L) in a (k,Xi) and (k,Yi) ordering pair. This means that in the kx-plane, the set of coordinate points given by {(0,X1),(0,X2),…,(0,XL+1)} is taken into account while in the ky-plane the set formed by {(0,Y1),(0,Y2),…,(0,YL+1)} is considered. It is important to note that due to the k parameter always goes from 0 to L, its inclusion always yields univalued piecewise linear paths (in the kx plane as well as in the ky plane), thus ensuring explicit piecewise linear function descriptions for x(k) and y(k). Taking Equation 1 as a reference, both functions can be associated together and expressed in parametric form as follows:
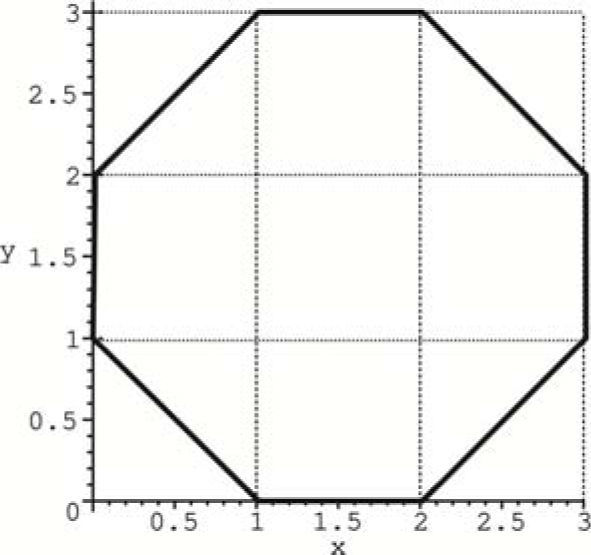
for i=1,2,…,L−1, where the parameters (ax,ay,bx,by,cx,i and cy,i) can be computed using Equations 2, 3, and 4.3ExampleIn order to illustrate the application of the proposed fitting technique, consider the octagon described by the path depicted in Figure 3. Importantly, this path is a closed curve which implies a multivalued correspondence between the position variables x and y.
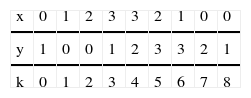
First, the breakpoint coordinates (x,y) are collected in Table 3. Note that a third row for the k parameter has been included.
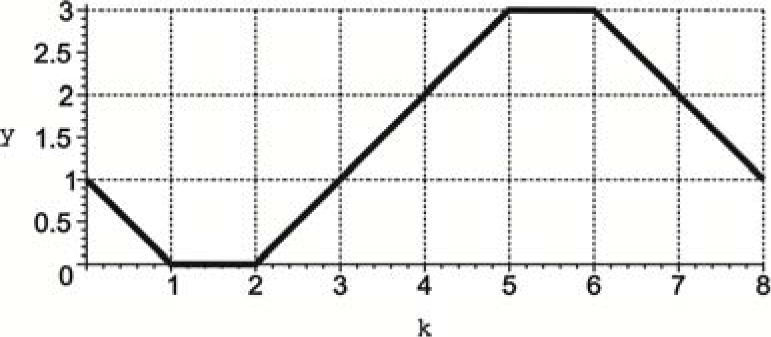
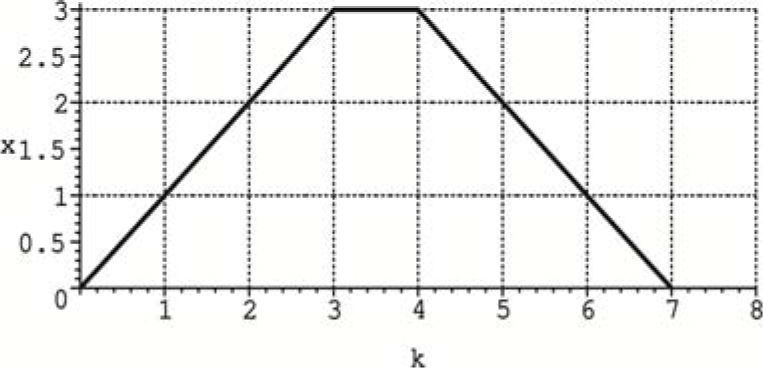
Then, the two PWL paths (in the ky-plane and the kx-plane) are sketched as shown in Figure 4 and Figure 5.
After that, the PWL parameters are computed using Equations 2, 3, and 4 as follows:for function x(k) we obtain:
After substituting the computed parameters into the canonical PWL formulation of Chua-Kang from Equation 1, the following equation is obtained:
Using the procedure described above, the PWL parameters of the function y(k) are determined as follows:
and the function y(k) is expressed asFinally, Equations 6 and 7 can be rearranged in the form of Equation 5 as follows:
4ConclusionIn this paper a curve-fitting technique for multivalued two-dimensional piecewise-linear paths was presented. A parametric formulation considering only the breakpoints of a two-dimensional PWL path was successfully applied to obtain a decomposed system of equations {x(k), y(k)}. Each constitutive equation, x(k) and y(k), was written in the form of the Chua and Kang canonical PWL model, which provides a systematic methodology for computing the model parameters. In order to demonstrate the effectiveness of the proposed curve-fitting technique, an example of a closed PWL path was presented. Following the use of the technique, a parametric and decomposed formulation capable of reproducing the graph of the previously established path was achieved. Our ongoing work focuses on exploring potential applications of the proposed curve-fitting technique such as robot path planning and nonlinear device characterization.
This research was partially supported by CB-CONACyT project 102669 of Instituto Tecnologico Superior de Xalapa, Veracruz, Mexico.