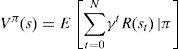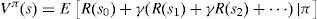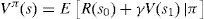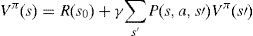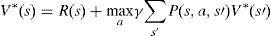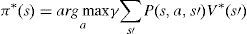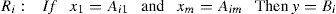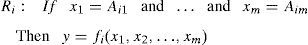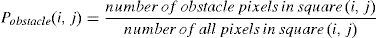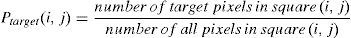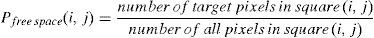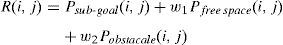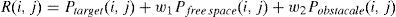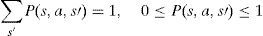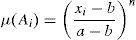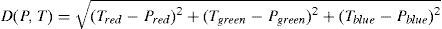Humanoid robot path planning with fuzzy Markov decision processes

Abstract

In contrast to the case of known environments, path planning in unknown environments, mostly for humanoid robots, is yet to be opened for further development. This is mainly attributed to the fact that obtaining thorough sensory information about an unknown environment is not functionally or economically applicable. This study alleviates the latter problem by resorting to a novel approach through which the decision is made according to fuzzy Markov decision processes (FMDP), with regard to the pace. The experimental results show the efficiency of the proposed method.

1

Introduction

The word “robot” originates from robota in Czech language, robota means work. So, we expect robots to work like expert labors. In the other words, we want robots to work in industry instead of human labor forces. Since humans have appropriately built their environments with their ergonomic, robots that have same physical body as human bodies are more useful than other types.

In order to design humanoid robots which are suitable for working efficiently in industrial applications, several control and navigation problems such as stability, mapping, interacting, computing, grasping and path planning must be investigated, most especially path planning which is an open problem in this research field.

There is need for users and industries to have a robot that can work in the real world. Since the real world is dynamic; it is impossible to save all environments in robot memory. This means that we must prepare the robots to work in unknown environment.

Path planning has been studied in several research fields. Although programming of a mobile robot to move from an initial position to a target position in a known environment is a well-known problem in robotics, but there are few methods in path planning in an unknown environment.

Medina-Santiago, Camas-Anzueto, Vazquez-Feijoo, Hernández-de León, and Mota-Grajales (2014) implemented neural control systems in mobile robots in obstacle avoidance using ultrasonic sensors with complex strategies.

Fuzzy logic is one of these methods that have been used in some related projects. A fuzzy-based navigator has been proposed by Zavlangas, Tzafestas, and Althoefer (2000) for the obstacle avoidance and navigation problem in omni-directional mobile robots. Their proposed navigator considered only the nearest obstacle in order to decide upon the robot's next moving step. This method utilized three parameters for path planning as follows:

• •

  the distance between the robot and the nearest obstacle,

• •

  the angle between the robot and the nearest obstacle, and

• •

  the angle between the robot direction and the straight line connecting the current position to the target point.

Although this method was in real time and truly works, these three parameters are not needed for a camera humanoid robot. In other words, this method can be utilized for any robot that has omni-directional range sensors.

Fatmi, Yahmadi, Khriji, and Masmoudi (2006) proposed a useful way of implementing the navigation task in order to deal with the problem of wheeled mobile robot navigation. In their work, issues of individual behavior design and action coordination of the behaviors were addressed utilizing fuzzy logic. The coordination technique used in this work comprises two layers, i.e., layer of primitive basic behaviors and the supervision layer. They used 14 range sensors to achieve the position of any obstacle surrounding the mobile robot. Thus, this method cannot be employed with most humanoid robots.

Medina-Santiago, Anzueto, Pérez-Patricio, and Valdez-Alemán (2013) presented a real-time programming for a prototype robot to control its movement from one moment to another one without showing response delays.

Iancu, Colhon, and Dupac (2010) presented a fuzzy reasoning method of a Takagi–Sugeno type controller which was applied in two wheels autonomous robot navigation. This mobile robot is equipped with a sensorial system. The robot's sensor area is divided into seven radial sectors labeled: large left, medium left and small left for the left areas, EZ for the straight area, and large right, medium right and small right for the right area, respectively. Each radial sector was further divided into other three regions: small, medium and large. The sensor's range could recognize up to 30 m, and the robot could identify an obstacle anywhere inside the interval [−90°, 90°]. Undoubtedly, most humanoid robots are not equipped with this large amount of sensors, hence, applying this method on humanoid robots seems to be impossible.

The simplest path planning algorithms for an unknown environment are called Bug algorithms (Lumelsky & Stepanov, 1984). Bug algorithms solve the navigation problem by storing only a minimal number of way points, without generating a full map of the environment. Traditional bug algorithms work with only tactile sensors. New bug algorithms, such as Distbug (Kamon & Rivlin, 1997), Visbug (Lumelsky & Skewis, 1990), Tangentbug (Kamon, Rimon, and Rivlin, 1998) and Sensbug (Kim, Russell, and Koo, 2003), work with only range sensors. Bug algorithms need to continuously update their position data, while as we know, it is impossible to achieve a continuous update in practice. Moreover, the bug model makes some simplifying assumptions about the robot, i.e., the robot is a point object, it has perfect localization ability and it has perfect sensors. These three assumptions are unrealistic for robots, and so bug algorithms are not usually applied for practical navigation tasks directly.

Michel, Chestnutt, Kuffner, and Kanade (2005) proposed a path planning algorithm for humanoid robots. They used an external camera that showed the top view of the robot working region, hence, they could extract information about the position of the robots and the obstacles. Their method is not applicable for most situations because it is impossible to use a camera with a global view of the robot work sites.

Furthermore, Nakhaei and Lamiraux (2008) utilized a combination of online 3D mapping and path planning. They utilized a 3D occupancy grid that is updated incrementally by stereo vision for constructing the model of the environment. A road map-based method was employed for motion planning because the dimension of the configuration space was high for humanoid robots. Indeed, it was necessary to update the road map after receiving new visual information because the environment was dynamic. This algorithm was tested on HRP2. As a conclusion, their method was not efficient because it needs exact stereo vision and a lot of time to find a path in each step.

In addition, Sabe et al. (2004) presented a method for path planning and obstacle avoidance for QRIO humanoid robot, allowing it to walk autonomously around the home environment. They utilized an A* algorithm in their method; thus, it needs a lot of time to process. Furthermore, they utilized online mapping and stereo vision. Their method seems effective, but it needs stereo vision and high computational processes. As a result, it cannot be applied in most conditions.

Other path planning project on HRP-2 humanoid robot has been carried out by Michel et al. (2006). This method uses several cameras in the robot environment in order to produce a suitable map. As mentioned before, we cannot utilize many cameras wherever we want to use humanoid robots and so this method cannot be applied either.

Moreover, in another project, Chestnutt, Kuffner, Nishiwaki, and Kagami (2003) used the Best-first search and A* algorithms for foot step path planning on a H7 humanoid robot. they demonstrated that A* is more effective than Best-first search. But both of them need stereo vision and high computational processes.

In addition, Okada, Inaba, and Inoue (2003) followed a different route for humanoid robot path planning: robot and obstacle were considered cylindrical shapes, the floor was extracted based on vision and then the robot made a decision. This method may encounter a conflicting problem when the robot confronts a big obstacle at its start point. In this situation, the robot could not be able to detect the floor which in turn leads to missing the path.

In addition, Gay, Dégallier, Pattacini, Ijspeert, and Victor (2010) used artificial potential field algorithms in a recent path planning project on iCub (a humanoid robot). At first, in their proposed algorithm, iCub calculated 3D position of each obstacle and transformed it in 2D, and then the artificial potential field was calculated. Their method needs perfect knowledge of the extracted images to find the position of the obstacles; therefore, it may not be utilized in some humanoid robots applications.

As seen from the above study, an efficient and suitable method for path planning for humanoid robots in dynamic unknown environments has not yet been proposed. Considering the identified research gap in this paper, a new procedure, combining the effects of fuzzy inference system and Markov decision processes, is proposed.

The application of Markov decision processes results in faster execution of the procedure when compared to the ones proposed in studies such as those by Sabe et al. (2004). Moreover, in the proposed method, using a fuzzy inference system leads to a smoother optimal path than the other previous past methods.

Moreover, resorting to fuzzy Markov decision processes (FMDP) obviates the necessity of having knowledge of the precise shape, position and orientation of the surrounding obstacles, as well as the need for relatively enormous volumes of memory for stocking information gathered in 2D and 3D maps. The extended experimental results demonstrate the efficiency of the proposed method.

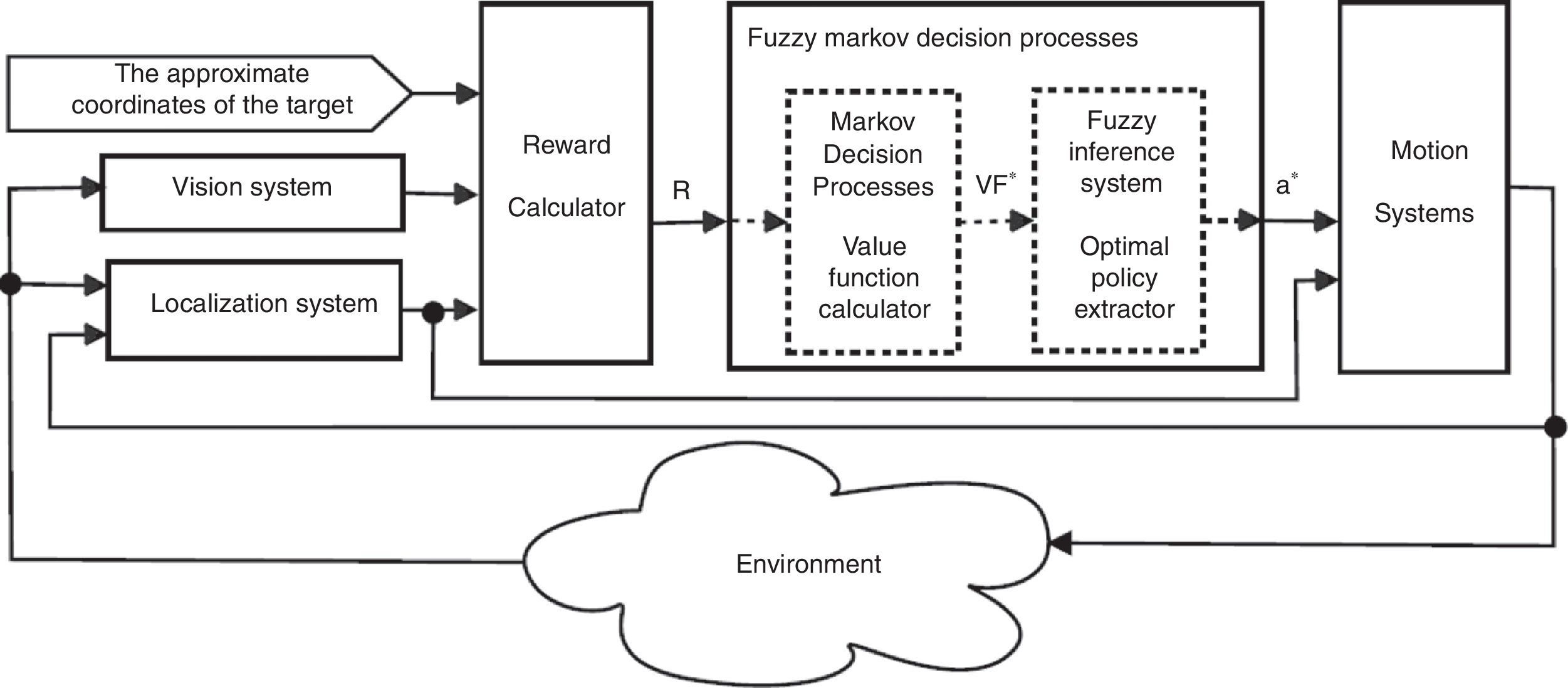
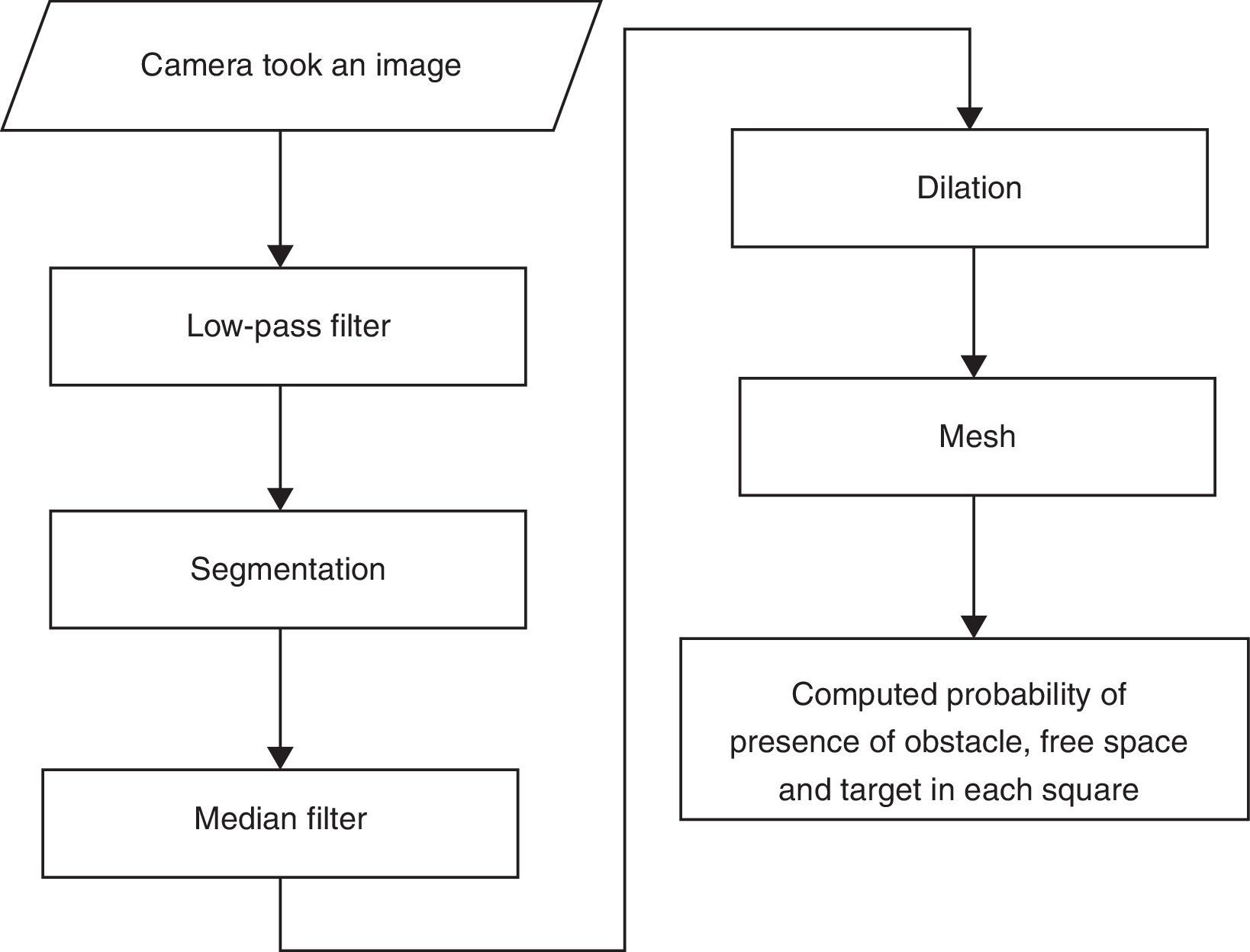
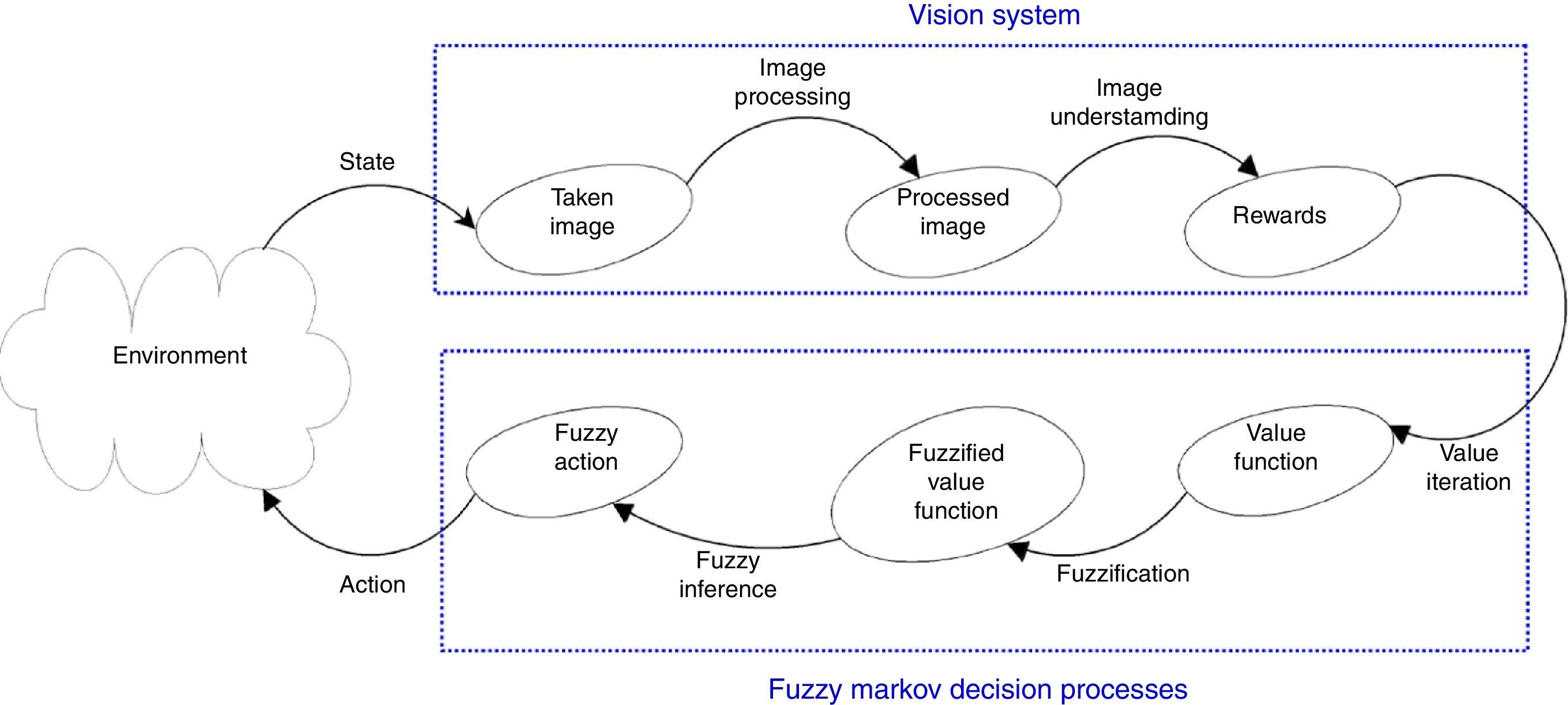
2

Functional block diagram

An Aldebaran humanoid robot – NAO H25 V4 (Fig. 1) – was selected for description and verification of our presented method. This humanoid robot has a camera, which is the only source of environmental sensory information used for the analysis in this approach. After taking an image, it passes through a low-pass filter in order to obviate the effect of the concomitant noises. Thereafter, the image is segmented and subsequently, in order to clear up the effect of the noise caused by segmentation, the image passes through a mode filter. In addition, the dilation process is applied so that the final image can be produced.

Fig. 1.

Aldebaran humanoid robotics – NAO H25 V4.

Moreover, after computing the rewards associated with each part of the image, the Markov decision processes serve as an input for the fuzzy inference system, so as to feed the robot with the information needed for deciding on the direction and its movement. The functional block diagram of FMDP is illustrated in Fig. 2.

Fig. 2.

Functional block diagram of FMDP.

The related flowchart of the vision system is presented in Fig. 3.

Fig. 3.

Flowchart of vision system.

3

Theoretical background

3.1

Markov decision processes

Markov decision processes (MDP) can be considered as an extension of Markov chains with some differences such as allowing choice and giving motivation. MDP, is a mathematical decision making tool which may be applicable in situations where series are partly random and partly under the control of a decision maker.

Specifically, a Markov decision process may be defined as a discrete time stochastic control process. At each time step, the process is in state s, and the decision maker may choose any admissible action a which is achievable in the state s. The process proceeds at the next time step by randomly selecting and moving into a new state s′, and giving the decision maker a corresponding reward R(s,a,s′). The probability that the process departs toward its new state s′ may be affected by the chosen action. Specifically, it is given by the state transition function P(s,a,s′). Thus, the next state s′ may depend on the current state s and the decision maker's action a. But given s and a, it is conditionally independent of all previous chosen states and actions; in other words, the state transitions of an MDP could possess the Markov property (Puterman, 2014).

3.1.1

Policy

Finding a “policy” for the decision maker is the main problem in MDPs. “Policy” can be interpreted as a function π that specifies the action π(s) which the decision maker will choose when is in state s.

The goal is to select a policy π which could maximize some cumulative function of the random rewards, typically the expected discounted sum over a potentially infinite horizon.

3.1.2

Value function

Value function V^π(s) is the expected value of total reward if the system starts from state s and acts according to policy π. So each policy has its value function. It can be formulated as follows:

Eq. (1) could be rewritten as follows:

The Bellman equations can be gained by the simplification of Eq. (4) as follows:

3.1.3

Optimal policy and optimal value function

In the optimal case, we will have:

If there are n states, then there are n Bellman equations, one for each state. In addition, there are n unknown values. Therefore, by simultaneously solving these equations, the optimal policy and optimal value function can be achieved.

3.1.4

Value iteration algorithm

As we can see, the Bellman equations (6) are nonlinear, hence they are difficult to solve. In this case, we utilize an algorithm to extract the optimal policy or optimal value function without directly solving the Bellman equations as shown in Algorithm 1.

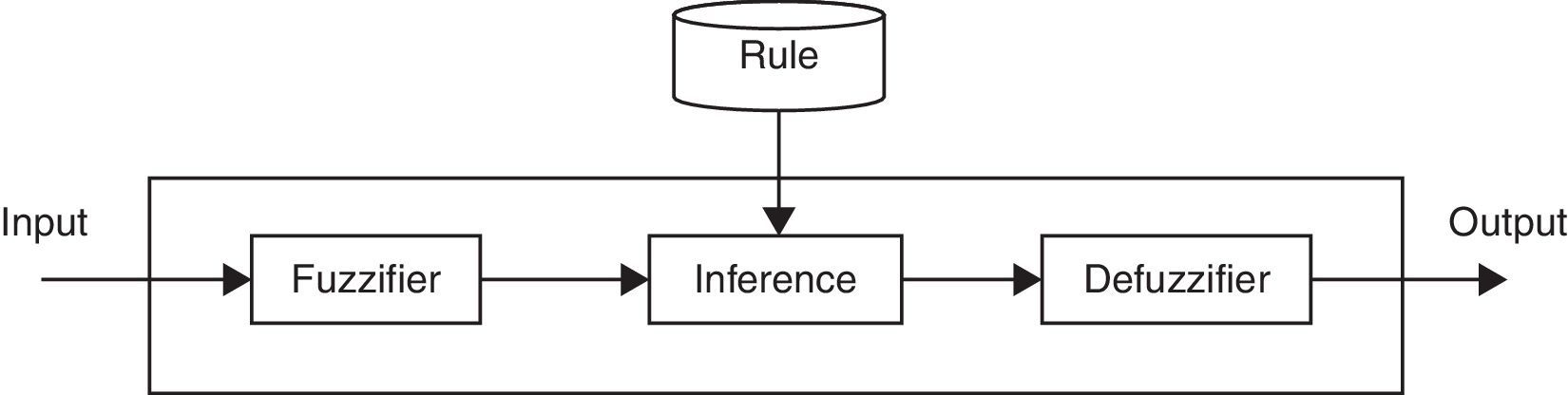
3.2

Fuzzy logic

Zadeh (1965) explained fuzzy set theory and fuzzy logic. In contrast to traditional logic that employs fixed and exact values, fuzzy logic uses approximate values. In other words, traditional logic has two-valued logic, false or true (0 or 1) but fuzzy logic has infinite-valued, interval between completely false and completely true (interval [0,1]). It is similar to linguistic variables that use multi-valued. Therefore, we can utilize linguistic inference in fuzzy logic. Fuzzy rules use fuzzy sets and every linguistic term has a membership function that defines the degree of membership of a specific variable for the fuzzy set. Membership functions are usually shown with μ(x). A fuzzy inference system is a system that has a fuzzy inference unit as illustrated in Fig. 4.

Fig. 4.

Fuzzy inference system (Stieler, Yan, Lohr, Wenz, & Yin, 2009).

In the real world, a specified system gains its needed data via its sensors. As we know, the gathered data throw sensors are crisp and therefore for fuzzy inference systems, a fuzzifier unit (preprocessing unit) should be improvised to change acquired data into fuzzy data. Also, actuators need crisp data; because the inference unit gives fuzzy data, fuzzy inference systems have a defuzzifier unit (post processing unit). There are few types of fuzzy inference systems, Mamdani and Takagi–Sugeno are more widely known than other types (Kaur and Kaur, 2012). Mamdani rules are interpreted as follows:

And for Takagi–Sugeno rules we have:

These rules could be defined by experts. But there is no standard method for explaining database in fuzzy Inference systems. Also, there is no standard method for defining the membership function to minimize error or maximize the output accuracy.

4

Vision system

4.1

Preprocessing (low-pass filter)

Most humanoid robots have at least one camera to see their environment. Robots need some process to percept their environment through raw data gained by their sensors. Cameras give a 3D matrix and each array of the camera has a value between 0 and 255 and as we know, most of these data are not necessary. Also, these data are mixed with noise. Image noise is a random variation of brightness or color information in images and is usually an aspect of electronic noise. Therefore, these data must first pass through a low-pass filter (s).

There are many low-pass filters for image noise canceling. Most robotics projects employ the Gaussian filter that produces a smooth blur image. The median filter is another filter widely used for image noise canceling; however, all smoothing techniques are effective at removing noise, but they adversely affect edges. In other words, at the same time, as noise is reduced, smooth edges will be created. For small to moderate levels of Gaussian noise, the median filter is significantly a better choice than Gaussian blur at removing noise whilst retaining the edges for a given fixed window size (Arias-Castro & Donoho, 2009). Therefore, in this method, the robot utilized a median filter for noise canceling as described in Algorithm 2.

4.2

Image segmentation

In the path planning process, robots need to understand the location of obstacles and free spaces, but they do not need to understand the color of each pixel. In this way, the robot must segment images. The main purpose of the segmentation process may be to simplify and change the representation of an image into something that is more significant and easier to analyze (Shapiro & Stockman, 2001, Chap. 12). In this case, obstacles were revealed by red pixels, free space was revealed by green pixels, and undefined pixels reveal other colors that are closer to it.

There are various image segmentation algorithms such as thresholding, clustering, histogram-based, edge detection, region-growing and graph partitioning method. The selection of an image segmentation algorithm is related to where the robot works. For example, in our case study, we examined the proposed methodology in our Robotic Lab, thus the simplest image segmentation algorithm works very well.

4.3

Improvement segmentation (mode filter)

Segmentation may produce some noises; therefore, after segmentation, the produced images must pass through the mode filter with the Algorithm 3 defined.

These processes made a simple data of any image (Fig. 5).

Fig. 5.

Original images in comparison with the segmented and filtered image and the final ones.

4.4

Image dilations

Dilation means expanding obstacles to obtain configuration space (Choset et al., 2005). In other words, dilation increases the effects of an obstacle by developing the volume of the obstacle.

4.5

Mesh

In the situations in which the angle of the robot head is constant and the ground is flat, each pixel shows the same distance. We used this property to approximate the distances from elements of obstacles. Since the robot has a specific physical size and predefined interval foot step, the exact position of each pixel is not that important. Therefore, we should mesh the images. Now every square of the image shows information on the presence of the obstacle in relative position.

Because the camera is located in the head of the humanoid robot and it takes a specified angle with the ground, the image picture by the robot is a perspective view. Fig. 6 illustrates the effect of the perspective view on a checkerboard. It reveals that the meshes are not square. While it is expected that the result of the robot vision must be at some distance from the obstacles, but for computed distance from the robots's image, the mesh must be non-homogeneous. In other words, the number of pixels in each box at the bottom of the image must be greater than the number of pixels in each box at the top of the image; in addition, the number of pixels in each box at the middle of the image must be greater than the number of pixels in each box on the sides of the image.

Fig. 6.

Example of effect of camera angle; top and perspective view.

4.6

Probability calculation

The Markov decision process works on discrete states. Therefore, Markov decision processes need to understand the presence of the obstacle in each state. The best way to show the existence of obstacles in a state is by determining the probability of the existence. In this way, the robot divides the number of obstacle pixels in each square by the number of all pixels in the square. Furthermore, Markov decision processes need to understand the presence of the obstacle in each state, which could be calculated in a similar way. The following relations fully interpret this concept:

5

Reward calculation

Reward calculation is related to observation of the target. If the robot can see the target, it can use only the information extracted from the image; however, if the robot cannot see the target (because of long distance), in addition to these information, it needs extra information on the coordination of the target and itself to create a sub-goal.

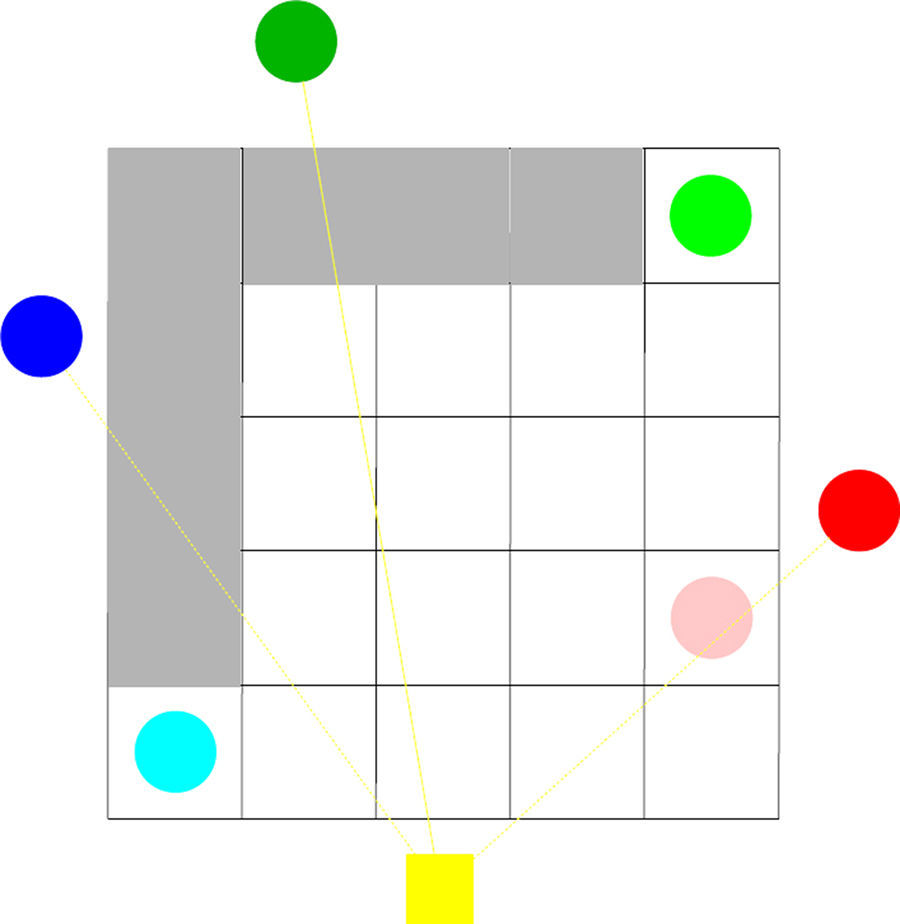
5.1

Sub-goal

A sub-goal is defined as a virtual goal in vision space such that achieving it could guide the robot toward the original target. Fig. 7 illustrates how the sub-goal state could be calculated. As we can see, if the dark green circle is considered to be the target, then the state in light green is defined as the sub-goal; in a similar way, if the blue circle is considered to be the target, then the state in cyan is known as the sub-goal state.

Fig. 7.

Example of determining sub-goal state. Dark green: target 1; blue: target 2; red: target 3; light green: sub-goal 1; cyan: sub-goal 2; pink: sub-goal 3. (For interpretation of reference to color in this figure legend, the reader is referred to the web version of this article.)

5.2

Reward when the robot cannot see the obstacle

In this condition, the free space has −w1 point, the obstacle has −w2 point, and the sub-goal has +1 point; therefore, the reward function could be calculated as follows:

5.3

Reward when the robot can see the obstacle

In this condition, the target has +1, the free space has −w1 point, and the obstacle has −w2 point; thus, the reward function could be calculated as follows:

6

Designed Fuzzy Markov Decision Process

A Fuzzy Markov Decision Process (FMDP) represents the uncertain knowledge about the environment in the form of offer-response patterns such as triangular and Gaussian membership functions.

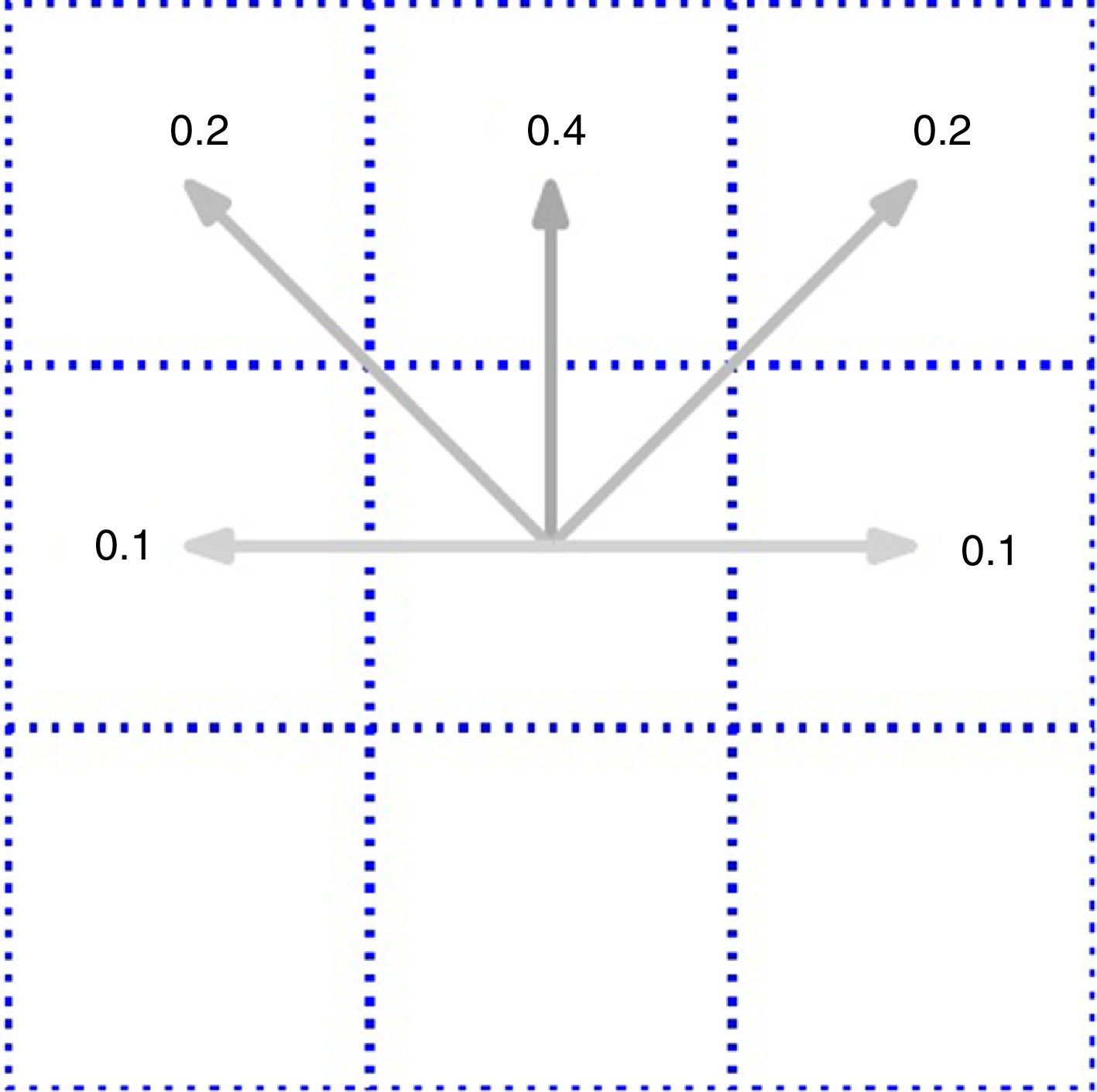
In the Fuzzy Markov Decision Process (FMDP) designed, the robot begins from its start state, it must choose a suitable action at each time step. In this problem, it is supposed that the actions which lead the robot to go out of its state do not work, in other words, we could say that the adjacent has a similar reward. The solution that is called policy (π(s)) is infrequence from the value function. The designed policy is illustrated in Fig. 8, which is a fuzzy mapping from state to action. Indeed, an optimal policy is a policy that maximizes the expected value of accumulated rewards throughout time.

Fig. 8.

Data flow.

6.1

Value function

Unfortunately, in the real world, humanoid robot's actions are unreliable for some recognized reasons such as noise of input data, ineffectiveness control systems, un-modeled system dynamic and environment changes throughout time; therefore, the probability of going from state s to state s′ by choosing action a with P(s, a, s′) will be:

As a result, the robot must decide to act for increasing the probability of success throughout time. An example of probability in the robot action when the robot wants to go to the next state decided is illustrated in Fig. 9.

Fig. 9.

Example of probability in action when robot wants to go to next state decide.

At first, it is supposed that the optimal policy is equal to the traditional optimal policy; hence, the value function will be achieved by solving Eqs. (6) and (7). As mentioned before, this nonlinear equation can be solved with a value iteration (Section 3.1.4).

In the next step, forgetting the gained optimal policy, the value function will be determined based on decision making. In other words, we utilize the value function as an input for the fuzzy inference system.

6.2

Fuzzification

As we know, the extremum of the value function is related to the reward function, while the reward function is related to the environment and user definition, therefore the value function can take any interval. But as we know, the fuzzy input must be a vector where the array is a real number between 0 and 1. Thus, the fuzzification is important for continuation.

The first route to fuzzification is linear transformation. This way is not logical because the difference between the value on the left side and right side of robot is not significant to guide the robot in the true path. In other words, linear transformer fuzzification for this approach is over fuzzified.

Although other prevalent fuzzification such as triangular and Gaussian methods could result in a significant increase in the number of rules applied in the fuzzy inference part, it is not advisable to use them. The fuzzification proposed in this study is a drastic transformation. If the maximum and minimum of the value function is shown by a and b, respectively, the proposed fuzzification can be written as:

where a and b are the maximum and minimum of the value function among inputs, respectively, and x_i is the value function of the ith input.

6.3

Fuzzy inference

As illustrated in Fig. 2, the traditional Markov decision process considers only the adjacent states to choose the optimal policy. According to the traditional approach, the robot must choose one of the candidate states and continue there. Although this policy is known as optimal policy, but it is true only when discrete states are considered. Because in traditional Markov decision process the robot can choose action from finite existence actions, it seems logical to consider only neighbor states.

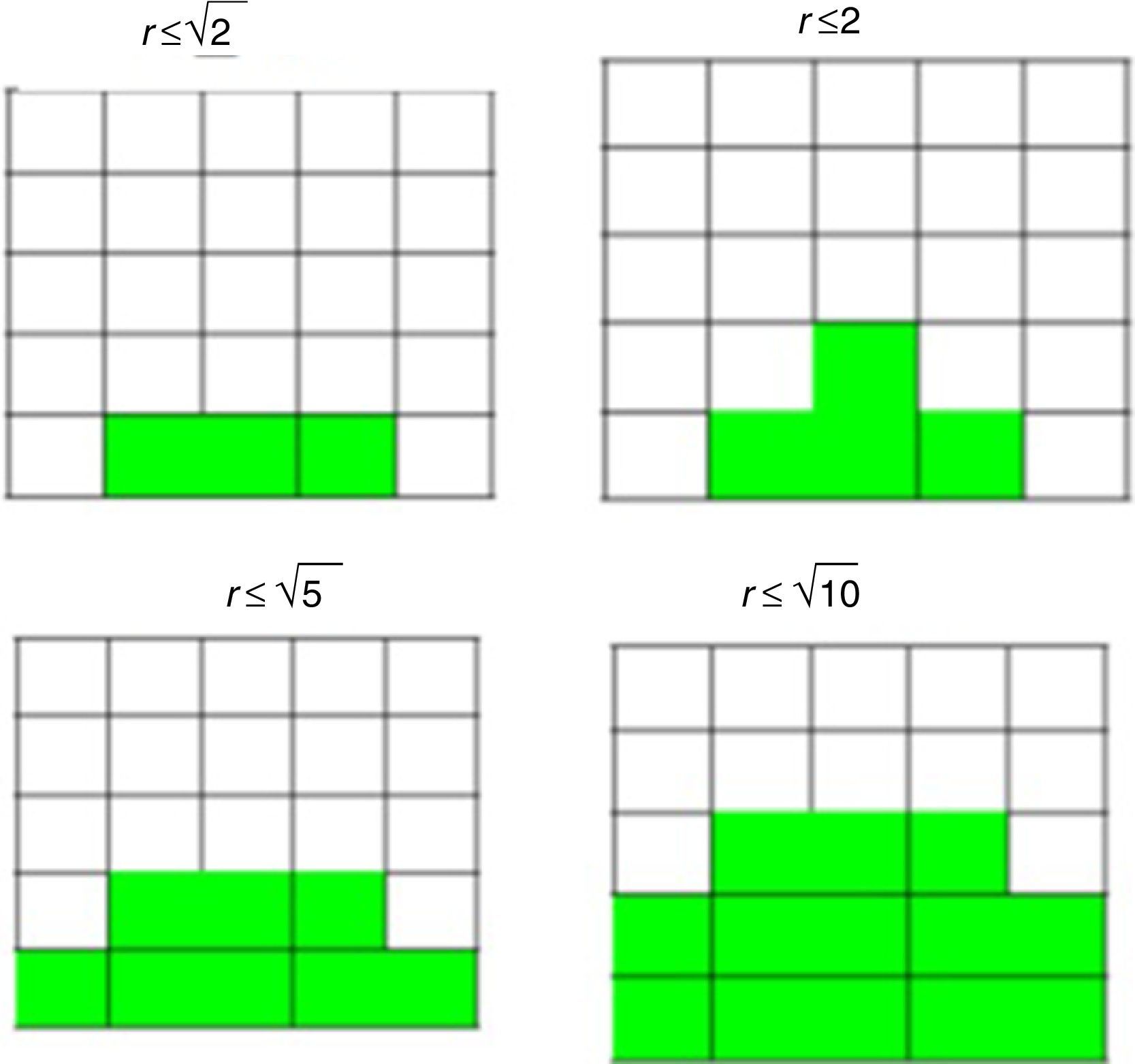
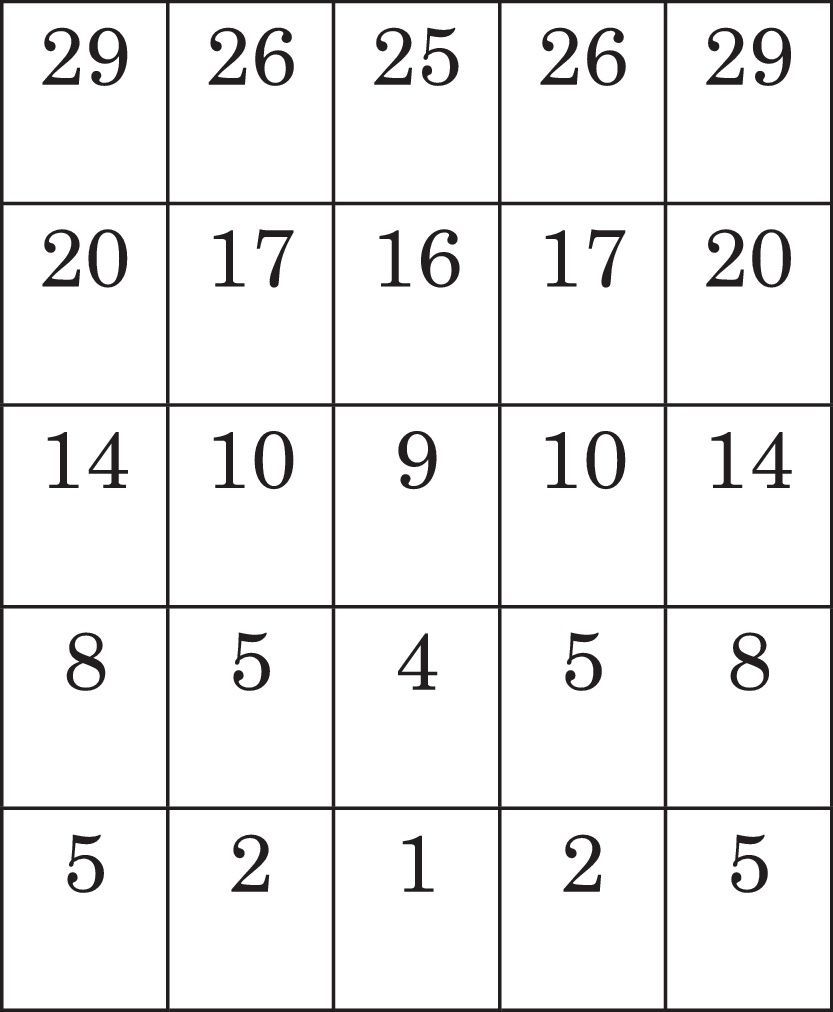
Nevertheless, in the FMDP, the robot is able to choose infinite actions because it is assumed to be continuous. Nevertheless, the traditional process is yet applicable by considering only adjacent states; in this case, it is not logical to only look at next states; in other words, it is wise for the robot to consider nearer states, as illustrated in Fig. 10. The square distance of each state from the robot's state is presented in Table 1.

Fig. 10.

Traditional Markov decision.

Table 1.

Square distance.

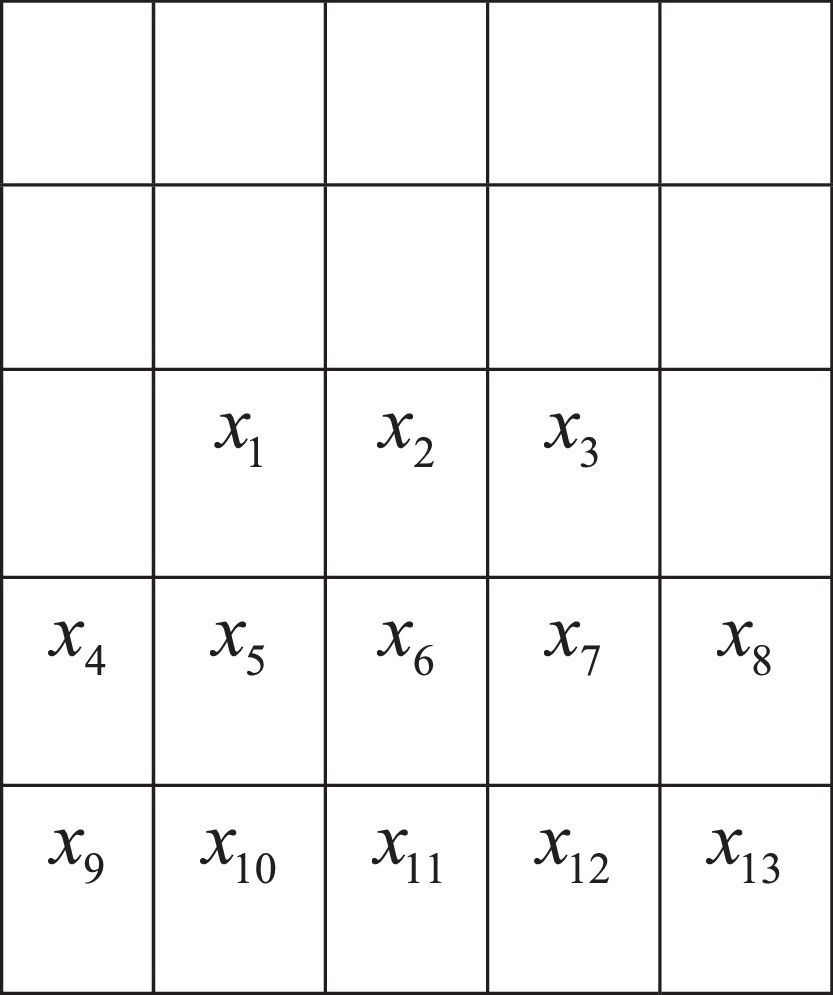
As a result, there are many choices for the selection of the number of inputs. The explanation for this problem will continue with r=10 that results in 13 inputs (Table 2).

Table 2.

Fuzzy input.

If the robot direction is considered by angle φ which is defined as the clockwise angle from the front side of the robot, the fuzzy rule for Fig. 10 (r≤10) can be easily written as:

If A₁, then φˆ is a very small positive.

If A₂, then φˆ is zero.

If A₃, then φˆ is a very small negative.

If A₄, then φˆ is a medium positive

If A₅, then φˆ is a small positive

If A₆, then φˆ is zero

If A₇, then φˆ is a small negative

If A₈, then φˆ is a medium negative

If A₉, then φˆ is a big positive

If A₁₀, then φˆ is a medium positive

If A₁₁, then φˆ is zero

If A₁₂, then φˆ is a medium negative

If A₁₃, then φˆ is a big negative

There are some ways to defuzzify the φˆ in order to gain φ. Among these ways, weighted average is logical.

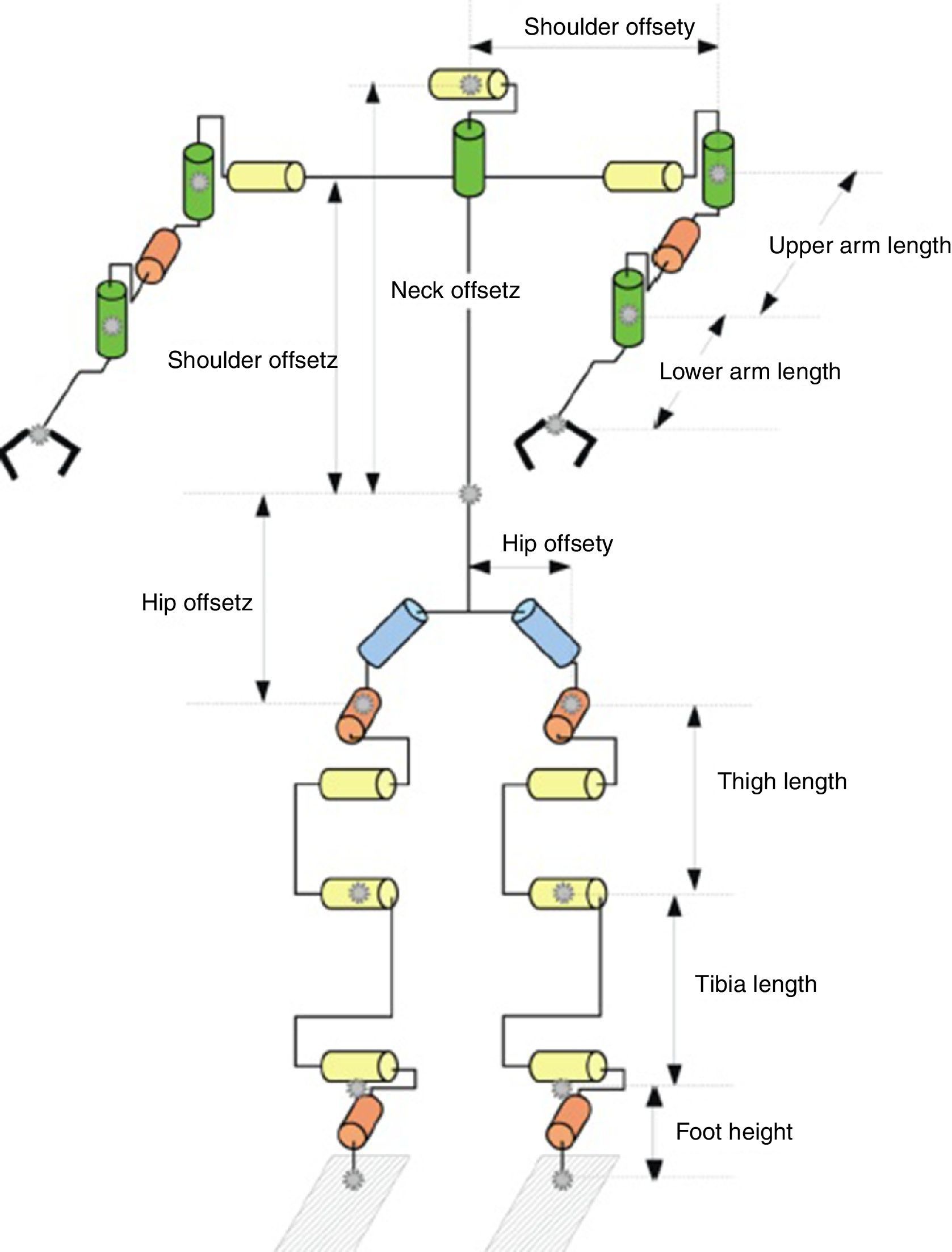
7

Experiments

We applied our presented method on a NAO H25 V4 that is produced by the French company Aldebaran Robotics (Fig. 1). The NAO has 25 degree of freedom. There are five DOF in each leg; two in the ankle, two in the hip and one at its knee. An additional degree of freedom exists at the pelvis for yaw; nevertheless, it is shared between both legs, that is to say, both legs are rotated outward or inward, together, using this joint. Moreover, NAO has 6 DOFs in each hand and 2 DOFs on its head (Fig. 11). The NAO has two cameras, an inertial measuring unit, sonar sensors in its chest, and force-sensitive resistors under its feet. NAO was designed to perform smooth walking gaits, even when changing speed and direction. The walking speed must be similar to the walking speed of a 2-year-old child of the same size, which is about 0.6 km/h (Gouaillier et al., 2009).

Fig. 11.

Detailed kinematics of NAO. Wrist joint not represented (Gouaillier et al., 2009).

The software architecture was developed using Aldebaran's NaoQi as a framework and an extended code in C⁺⁺. NaoQi gives access to all the features of the robot, like sending commands to the actuators, retrieving information from the robot memory, and managing Wi-Fi connections. In this way, we use Kubuntu 12.0.4 and Open CV 2.3.1 writing program in C⁺⁺ in Qt creators. In the study experiment, the robot took a 160 × 120 pixel image. Results revealed that the robot was able to achieve its goal without colliding with any obstacle. Fig. 12 illustrates how the robot truly works. This figure illustrates the fact that the robot can work in noisy environments (Fig. 5).

Fig. 12.

RGB color space.

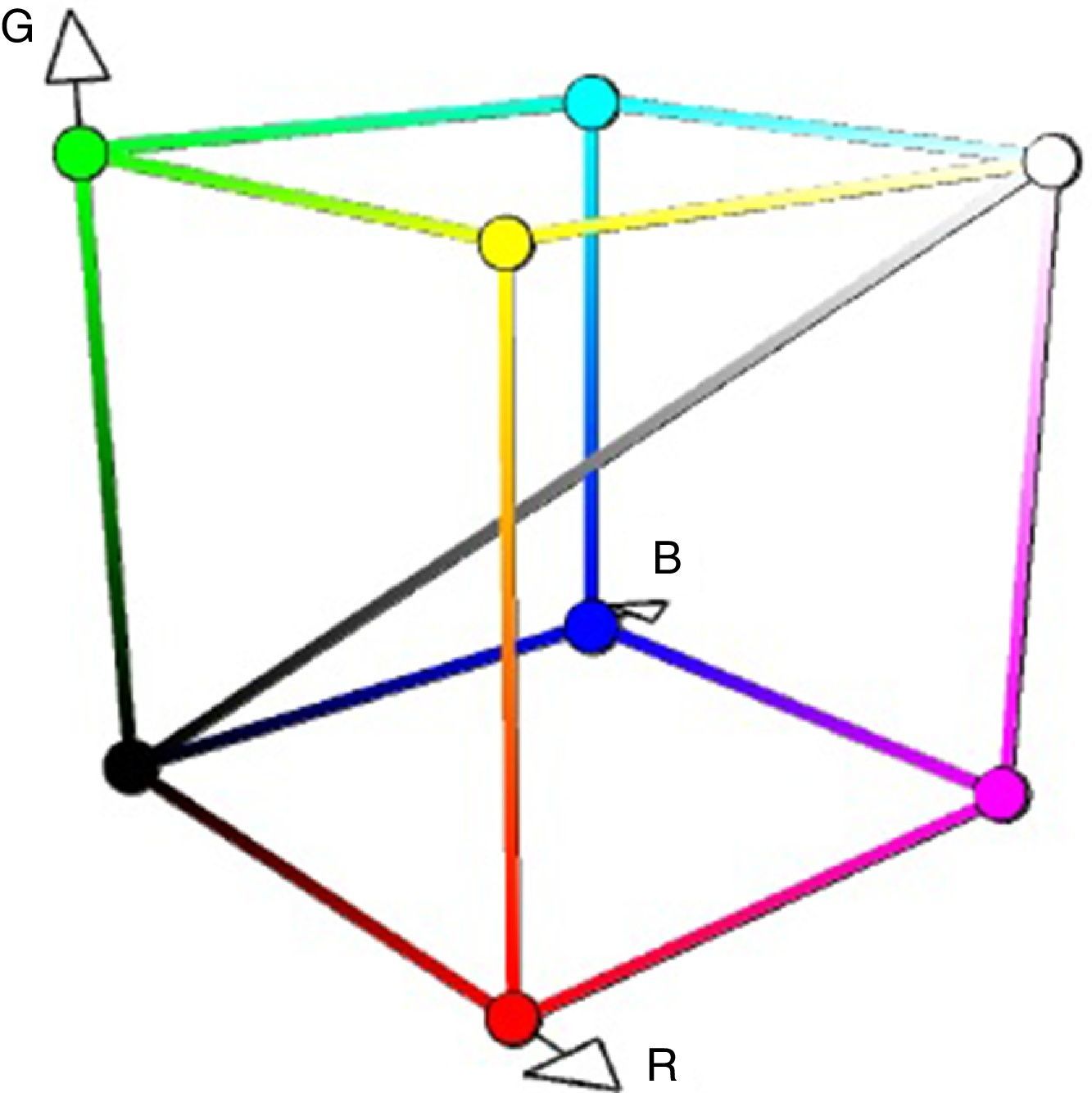
7.1

Euclidean distance-based image segmentation

Path planning was tested in laboratory conditions; therefore, a simple image segmentation algorithm could work without any problem. The simplest image segmentation algorithm is Euclidean distance. Assuming that all pixels are in RGB color space (Fig. 12), then each pixel will have three Cartesian coordinates. Distance between each color can be calculated by Eq. (15).

In this algorithm, the distances between the color of each pixel and the color of the target have been calculated. Then the color of the target pertaining to the shorter distance could be treated as the new color of the pixels.

Many experiments have been carried out in order to prove the effectiveness and correctness of our presented algorithm. Fig. 13 illustrates a path planning scenario as an example.

Fig. 13.

NAO robot path planning scenario.

8

Conclusions

In this study, a new successful and effective algorithm has been proposed for the real-time optimal path planning of autonomous humanoid robots in unknown complex environments. This method uses only vision data to obtain necessary knowledge on its surrounding. It was developed by mixing Markov decision processes and fuzzy inference systems. This method improves the traditional Markov decision processes. The reward function has been calculated without exact estimation of the distance and shape of the obstacles. We also use value iteration to solve the Bellman equation in real time. Unlike other exiting algorithms, our method can work with noisy data. The whole locomotion, vision, path planning and motion planning is thus fully autonomous. These features demonstrate that the robot can work in a real situation. Moreover, this method requires only one camera and does not need range computing. The method discussed ensures collision avoidance and convergence to the optimal goal. This method has been developed and successfully tested on an experimental humanoids robot (NAO H25 V4).

Conflict of interest

The authors have no conflicts of interest to declare.