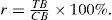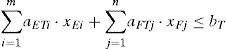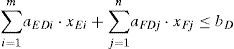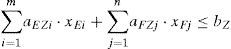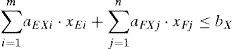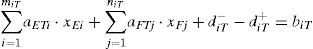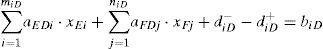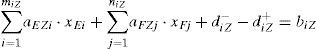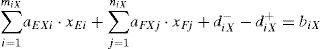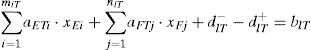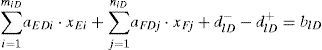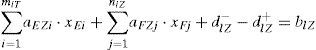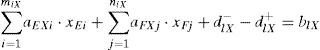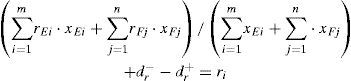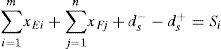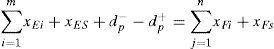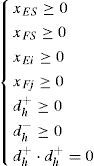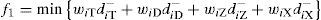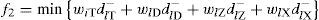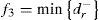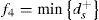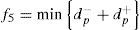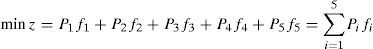The scheduling method of shiplock has a strong influence on the improvement of shiplock capacity. On the condition that the number of the ships waiting for the lock was relatively stable, the paper constructed an optimization model for joint scheduling of double line shiplock based on the nonlinear goal programming. The hard constraints included that the number of ships arranged in the shiplocks couldn’t exceed the number of the ships waiting for the lock. The soft constraints included arranging the ships with the priority and time limit as far as possible, and maximizing the utility of the lock chambers. Then the objective function was constructed. Considering the characteristics of the nonlinear goal programming mode, the Hooke - Jeeves algorithm was used to solve the model. In the end, a double line shiplock of Jiangsu province was taken to verify the scientificity and feasibility of the model.
Shiplocks are the major influence factors which will restrict the navigation capacity of waterway [1]. With the rapid development of social economy, as infrastructure of logistics network, the inland waterway is valued more by people. But the shiplocks still affect the efficiency of inland waterway transport. The optimization of shiplocks’ scheduling is very important to improve the throughput of shiplocks and the utilization of lock chamber. According to the number of ships sailing parallel on the channel the shiplocks can be divided into singel line, double line, three line etc. As the number of double line and three line locks increases gradually, the study of how to realize joint scheduling of double line locks and giving full play to the advantages of the combination is of great significance.
There’re many researches on the shiplock scheduling made by domestic and overseas scholars. Kim et al. [2] proposed the general Packing aggregating model for the arrangement of ships and analyzed the two main advantages of this method. Wang et al. [3] investigated a ship lock scheduling problem and proposed a data-driven approach, which is a typical optimizing and decision-making problem. Siswanto et al. [4] presented a ship inventory routing and scheduling problem with undedicated compartments, and their objective of the problem is to find a minimum cost solution while satisfying a number of technical and physical constraints within a given planning horizon. Andersson et al. [5] introduced and solved a planning problem faced by shipping companies operating in a special segment of tramp shipping called project shipping. Guo [6] set up a dynamic model on the traffic capacity of the three gorges ship lock based on the structural and dynamic method to obtain the potential capacity, which describes the dynamic relationship between the cargo-boat tonnage, operating time, ship number, efficiency of using area with traffic capacity. Xu et al. [7] analyzed the concepts and features of symmetric shiplock, designed a dispatching model of secondary symmetric ship lock with high feasibility and applicability, constructed an open symmetric shiplock’s dispatching model contains information model, queue model, ship combination in lock chamber model and joint scheduling model. Li et al. [8] established a mathematical scheduling model considering the two goals of the utilization rate of lock chamber and the first come first serve and made the Xiangjiang as an experiment. Shang et al. [9] analyzed influential factors of multiple-lane lock’s joint scheduling for Changzhou hydro-junction project and then built a computer simulation model based on the lockage operating procedures, which included anchorage, channel & approach channel, parallel four-lane ship lock, ship’s joint scheduling, etc. Zhao [10] proposed a new model of lock service satisfaction degree which is constructed by the method of structural equation modeling based on the analysis of the lock service theory and the satisfaction theory. Wang [11] made a simulation research on the scheduling of shiplock from the perspective of quality of service. Liu [12] studied on how to reduce two-dimensional packing problem to one-dimension, the mathematical model is constructed and then algorithm for the problem based on greedy algorithm. With the technology development, the scheduling simulation is also studied [13-15].
The above-mentioned studies mainly carried out for single ship lock, rarely researched on specific model of double line lock operation. In fact, with the increasing demand for shipping, double line and three line shiplock have become a very common phenomenon. Double line shiplock scheduling problem is not a simple combination of single lock scheduling. It includes not only the design of single lock queue rules, the reasonable arrangements of lock chamber, but also how to realize the two lock joint scheduling to take advantage of the combination and realize the maximization of the lock throughput.
Basing on the situation that the number of ships waiting in line lock at a certain time is relatively stable, the paper aims at using the nonlinear goal programming model to study the double lock joint optimization scheduling model,. It also uses a global scheduling strategy based on the analysis of the double line shiplock [16].
2Description of the problem2.1Design for the ships in the waiting queuesThe ships are divided into four types according to the width in order to facilitate to realize the optimization of scheduling. And the ships that arrive at the dispatching station queue according to the four types. The four types are: extremely large-sized (T, W>7m), large-sized (D, 6mm), medium-sized (Z, 5mm), small-sized (X, W ≤ 5m), where “W” represents the width of the ships.
2.2Rules design for the queuing shipsIn combination with the practical operation scheduling of shiplock, the paper consider mainly four modes.
Mode1: The first service for the first arrival way. The principle of “first service for the first arrival” is applied to the common ships in the waiting queues.
Mode2: The single service way. The principle of “single service” is applied to the ships (such as the ships with hazardous articles on it) which accord with the condition to pass the ship lock separately. It should be noted that the number of ships which can meet this way is small, and usually corresponding ship lock can be directly prearranged according to the size of the ship. Therefore, in the later discussion of the model, related symbols are in the situation that ships which meet this way have been arranged in addition to the number of locks.
Mode3: The priority service way. The principle of “priority service” is applied to the ships (such as the ships which transport national emergency supplies) which accord with the preferential condition to pass the ship lock.
Mode4: The time limit service way. Define the “waiting time limit” according to the different ships, and once the waiting time of some ships exceeds the limit, these ships should be arranged to pass the ship lock as soon as possible.
The ships that do not meet Mode 2 to Mode 4 should be orderly arranged to pass the corresponding ship lock according to mode one.
3Methodology3.1Related conditions and variable hypothesis- (1)
To make general significance, we assume that ships meet the requirements of draft. The paper sets that two shiplocks are available in different sizes, lengths and widths of the lock are not the same.
The first shiplock E, specification lE×qE, the second shiplock F, specification lF×qF. If two shiplocks are of the same specification, it can be seen as an exception of the above-mentioned situation, the model of this paper can be used as well.
- (2)
In the queue line, after ships of the Mode 2 has been scheduled, four types of ships are recorded respectively as {bT, bD, bZ, bX}. Ships of the Mode 3 are recorded as {bPT, bPD, bPZ, bPX}. Ships of the Mode 4 are recorded as {bLT, bLD, bLZ, bLX }.
- (3)
For two shiplocks, we set up the shiplock feasible schemes of two ship locks under the premise of the insurance of safe distance according to the specification of shiplocks and the type of queuing ships. Each feasible scheme provides the number of combinations of different types of ships. Suppose that the number of feasible schemes of shiplock E is m, among them the ith feasible scheme, the numbers of especially large ships, large ships, medium-sized ships and small ships it accommodates are respectively (aETi, aEDi, aEZi, aEXi), the ith feasible scheme Ei=(aETi, aEDi, aEZi, aEXi), i=1,2,…,m. Similarly, suppose that the number of feasible schemes of shiplock F is n, the jth feasible scheme Fj=(aETj, aEDj, aEZj, aEXj), j=1,2,…n.
- (4)
Calculate the utilization rate of the chamber of Ei and Fj separately according to the total size of the ship, rEi and rFj. The calculation formula is:
In Eq. (1), r stands for chamber utilization, TB stands for the sum of all ships’ area, CB stands for a total effective area of locks. TB can be calculated in the case of ships had not yet been fully implemented standardized, using the sampling method according to the actual size of ship registered.
- (5)
The optimization model needs to determine the frequency of two locks using different options respectively, in order to ensure the arrangement of ships waiting and the maximized utilization of lock chamber. Suppose that the frequency of shiplock E adopting feasible scheme Ei is xEi, the frequency of shiplock F adopting feasible scheme Fj is xFj.
- (1)
The tough constraints
The actual arrangement number of the extremely large-sized ships in the two large chamber does not exceed the number of the extremely large-sized ships in the waiting queues, it means:
Similarly, for large, medium and small ships respectively, we can get:
- (2)
Soft constraint
- 1)
For the ships which meet the Mode 3, we should complete the arrangements as far as possible before the priority lockage of ordinal number of the two shiplocks. For the extremely large-sized ships that meets the he Mode 3, we can get:
Where miT and niT stand for the ordinal number of the allowing priority arrangements of shiplocks’ lockage which meet the Mode 3 for shiplock E and F, they can be determined in accordance with the rule one. diT+ and diT− stand for the positive and negative deviation value between the actual arrangement number of the extremely large-sized ships and the number of ships that need to be arranged before ordinal number of the allowing priority arrangements of shiplocks’ lockage.
Similarly, as for the large, medium and small ships which meet the type three, we can get:
The symbol meaning of miD, niD, miZ, niZ, miX, nix, diD+, diD−, diZ+, diZ−, diX+ and diX− are the same with the Eq. (6).
- 2)
For the ships which meet the Mode 4, we should complete the arrangements as far as possible before ordinal number of the allowing priority arrangements of shiplocks’ lockage. As to the extremely large-sized ships that meet Mode 4, we can get:
Where mlt and nlt are the ordinal number of E and F shiplocks’ priority lockage that meets the Mode 4, which can be calculated according to the each lockage time and the limit of the allowed lockage time. diT+ and diT− stand for the positive and negative deviation value of the extremely large-sized ships between the actual arrangement number of the extremely large-sized ships and the number of ships that need to be arranged before ordinal number of the allowing priority arrangements of shiplocks’ lockage.
Similarly, as for the large, medium and small ships which meet the type four respectively:
The meanings of mlD, nlD, mlZ, nlZ, mlX, nlx, dlD+, dlD−, dlZ+, dlZ−, dlX+ and dlX− are the same with Eq. (10).
- 3)
The average utilization rate of the two lock chamber should be as large as possible, so we can get:
Where ri stands for the ideal utilization rate of the lock chamber and we can analyze and calculate it based on previous actual lock data. dr− and dr+ are positive and negative deviation between the actual value and the ideal value of two locks’ utilization rate of the average lock chamber.
- 4)
The frequency of total arrangement of the two shiplocks’ lockage should be as little as possible, so we can get:
Si is the ideal total lockage of the two shiplocks and it can be set according to the actual data of the shiplock’s operation, ds− and ds+ are positive and negative deviation between the actual value and the ideal value of two shiplocks’ total arrangement of the lockage.
- 5)
Considering the point of the technology and safety of the combined operation, the number of the two shiplock’s lockage should be basically the same. Then:
xEs and xFs are single lockages of the two shiplocks’ arrangement. dp− and dp+ is positive and negative deviation between the two shiplocks’ total arrangement of the lockage.
- 1)
- (3)
The constraints of the decision variables
Considering the actual situation of shiplocks’ scheduling and goal programming, the decision variables have the following constraints:
Where i=1,2,…,m; j=1,2,…,n; h=iT, iD, iZ, iX, IT, ID, IZ, IX, s, r, p.
- (4)
The objective function
- 1)
In level 1, to meet the ships with the prior service, then:
Where WiT, WD, WiZ, WiX stand for the weights of four different types of ships in the service prior arrangements. Propose that wT > wD > wiZ > wiX.
- 2)
In level 2 to meet the ships with the time-limited service, then:
Where WIT, WID, WIZ, WIX are the weights of four different types of ships in the service time-limited arrangements. Propose that WIT > WID > WIZ > WIX.
- 3)
In level 3, in order to make the average utilization rate of the lock chamber maximum, then:
The utilization rate is higher, the greater the benefits [17].
- 4)
In level 4, the frequency of the total arrangements of the two shiplocks’ lockage should be as little as possible, then:
- 5)
In level 5, the number of the two shiplock’s lockage should be basically the same, then:
- 1)
On the basis of Eq. (17) - (21), the objective function is:
Pi is the prior weight of the five sub-goals, there is P1>>P2>>P3>>P4>>P5.
In summary, this paper constructs the optimal joint operation model of the double line shiplock and the objective function is the Eq. (23) and constraints are the Eq. (2)- (17). The model can be written as Eq. (24). In Eq. (24), XEs, XFs, XB, XFj, dh+, dh− ≥ 0, dh+⋅dh− =0, here i = 1, 2,…, m; j = 1, 2,…, n; h =iT, iD, iZ, iX, IT, ID, IZ, IX, s, r, p. From Eq. (24), it can be seen that the model is a nonlinear goal programming model.
4AlgorithmAs the construction of joint optimization scheduling model is a nonlinear goal programming model, it impossible to use simplex method to solve the problem. According to the features of this model, we are ready to adopt the Hooke-Jeeves algorithm [18] to solve the model.
Hooke - Jeeves algorithm was originally a method to solve unconstrained problem and its calculation includes two kinds of motion: detection motion and imitation motion. The detection motion moves along the axis direction to find out the decreasing direction of the objective function. The imitation of
movement moves along the decreasing direction of the objective function in order to further reduce the value of the objective function. The effectiveness of this model is based on goal programming problems in each priority class that has multiple solutions for constraint conditions, but the number of solutions decreases as the priority decreases. Combining the detection motion and imitation motion, Hooke - Jeeves algorithm is used to solve the joint optimization scheduling model.The steps that the paper constructed are as follows:
- Step1:
Fix the initial point X=(X1, X2, XN)T, the movement step δ=(δ1, δ2, δN)T and the calculation precision ε.
- Step2:
Set x(0)=x, start from x(0) to detect motion by using Hooke- Jeeves algorithm.
- Step3:
Whether the detective movement is successful? If it is successful, turn to Step5, otherwise, turn to Step4.
- Step4:
Determine whether δi≤ε for all i=1,…,N is right. If it is successful, the calculation is over. Otherwise, setting <δi= δi/10, turn to Step2 and continue the calculation.
- Step5:
Use the Hooke-Jeeves algorithm to imitate the movement.
- Step6:
Judge whether the imitative movement is successful. If it is successful, this process is completed. If not, set X=X¯ (X¯ is a new base point), turn to Step2 and continue the calculation. Otherwise, keep the value of X, turn to Step2and continue the calculation.
Detection motion and imitation motion in the calculation of Hooke-Jeeves algorithm can refer to reference [19].
We take the lockage case of a ship in a double lock of Jiangsu, PR China as an example to verify that the model is scientific and feasible. The size of the first shiplock E of the double lock is 23×90m, the size of the second shiplock F is 18×70m. We take randomly one day’s ship data. There’re totally 264 ships which pass the shiplock. The shiplock E and F run 27 times everyday separately. The average utilization rate of lock chamber of E and F is 48.62% and 47.19%.
According to registration information, the combination of 264 ships is: 42 extremely large-sized ships, 75 large-sized ships, 94 medium-sized ships and 53 small-sized ships. We use Lindo software to get 79 and 62 feasible scheme of ship lock E and F respectively by counting 264 ships’ size and combine the scale of the double line shiplock.
By counting 264 ships’ service ways, we find that there are no ships that meet the single service way. There are 6 extremely large-sized ships, 9 large-sized ships, 5 medium-sized ships and 4 small-sized ships that meet the priority service way. There are 10 extremely large-sized ships, 14 large-sized ships, 8 medium-sized ships and 9 small-sized ships that meet the time limit service way. The number of the priority order of the lockage of shiplock E and F is 5 and 5, the number of allowing time limit service is 7and 7.
According to past data, the utilization rate of the double chamber is less than 50%, so we assume that the ideal utilization was 50%. Considering the actual situation in lock management, the ideal number of two shiplocks is 25 respectively. The total ideal number is 50.
In addition, according to the actual situation of ships scheduling and ships lockage requirements, we set WiT=WIT=5, WiD=WID=4, WiZ=WIZ=2, WiX=WIX=1.
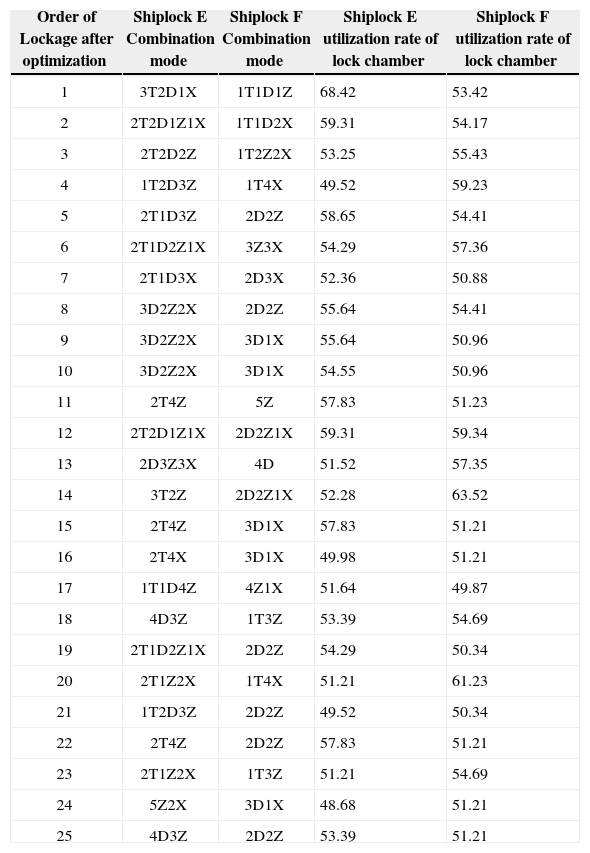
According to the relevant data, the corresponding optimization model can be built and Hooke-Jeeves algorithm can be used to detect and imitate. The initial feasible point x = (xExF, d+, d-) = 0, step length δ=1, calculation accuracy ε=0.0001, 0 and 1 are the corresponding column vector. And XE= (XE1, XE2, …, XE79), XF= (XF1, XF2, …, XF62), d+= (diT+, diD+, diZ+, diX+, dIT+, dID+, dIZ+, dIX+, dr+, ds+, dp+), d−=(diT−, diD−, diZ−, diX−, dIT−, dID−, dIZ−, dIX−, dr−, ds−, dp−). After a number of detection and imitation motion, the final lockage arrangement of the double line shiplock is shown in Table 1.
Lockage arrangement of a double line shiplock.
| Order of Lockage after optimization | Shiplock E Combination mode | Shiplock F Combination mode | Shiplock E utilization rate of lock chamber | Shiplock F utilization rate of lock chamber |
|---|---|---|---|---|
| 1 | 3T2D1X | 1T1D1Z | 68.42 | 53.42 |
| 2 | 2T2D1Z1X | 1T1D2X | 59.31 | 54.17 |
| 3 | 2T2D2Z | 1T2Z2X | 53.25 | 55.43 |
| 4 | 1T2D3Z | 1T4X | 49.52 | 59.23 |
| 5 | 2T1D3Z | 2D2Z | 58.65 | 54.41 |
| 6 | 2T1D2Z1X | 3Z3X | 54.29 | 57.36 |
| 7 | 2T1D3X | 2D3X | 52.36 | 50.88 |
| 8 | 3D2Z2X | 2D2Z | 55.64 | 54.41 |
| 9 | 3D2Z2X | 3D1X | 55.64 | 50.96 |
| 10 | 3D2Z2X | 3D1X | 54.55 | 50.96 |
| 11 | 2T4Z | 5Z | 57.83 | 51.23 |
| 12 | 2T2D1Z1X | 2D2Z1X | 59.31 | 59.34 |
| 13 | 2D3Z3X | 4D | 51.52 | 57.35 |
| 14 | 3T2Z | 2D2Z1X | 52.28 | 63.52 |
| 15 | 2T4Z | 3D1X | 57.83 | 51.21 |
| 16 | 2T4X | 3D1X | 49.98 | 51.21 |
| 17 | 1T1D4Z | 4Z1X | 51.64 | 49.87 |
| 18 | 4D3Z | 1T3Z | 53.39 | 54.69 |
| 19 | 2T1D2Z1X | 2D2Z | 54.29 | 50.34 |
| 20 | 2T1Z2X | 1T4X | 51.21 | 61.23 |
| 21 | 1T2D3Z | 2D2Z | 49.52 | 50.34 |
| 22 | 2T4Z | 2D2Z | 57.83 | 51.21 |
| 23 | 2T1Z2X | 1T3Z | 51.21 | 54.69 |
| 24 | 5Z2X | 3D1X | 48.68 | 51.21 |
| 25 | 4D3Z | 2D2Z | 53.39 | 51.21 |
In Table 1, ship combination “3T2D1X” stands for the scheme of arrangement of three extremely large-sized ships, two large-sized ships and one small-sized ship, other combinations have similar meanings. It should be noted that the same combination of the ships do not mean the same chamber utilization because of some difference between ship sizes. For example, in the combination mode “3D2Z2X” of shiplock E, utilization rate of lock chamber is 55.64% and 54.55% respectively.
From Table 1, we can see that after using joint nonlinear optimization model, two lockages of lock E and F are reduced respectively, and the average utilization rates of lock chamber of E and F are raised to 54.46% and 53.99% which exceed the setting ideal utilization rate of lock chamber. The optimization is useful to reduce operating costs of lock scheduling. Actually, if we take the shipping tonnage of each ship into consideration, the optimization will have greater economic benefits. It indicates that the joint optimization model is scientific and feasible.
6ConclusionsShiplock scheduling directly affects the shipping capacitity of the waterway. When the size of shiplock is of certain, the optimization of shiplock scheduling is of particularly importance to improve channel efficiency and economic efficiency. The previous researches were more about single-line shiplock. But with the development of social economy, double line shiplock is more and more popular and its scheduling is more complicated.
- (1)
In our paper, the ships are divided into four types according to the width: extremely large-sized, large-sized, medium-sized and small-sized, and service rules includes four modes: the first service for the first arrival way, the single service way, the priority service way and the time limit service way. It is the same as the practical operation scheduling of shiplock, which lays a good theoretical premise for the application of the scheduling model of double line shiplock.
- (2)
The paper uses the actual arrangement number of the ships to construct the hard constraints, and uses the average utilization rate of the two lock chamber et al to construct the soft constraints, then establishes the optimization model of the joint scheduling of double line shiplock, which is a nonlinear programming model.
According to the feature of the model, we demonstrate the Hooke-Jeeves algorithm to solve the model.
- (3)
A double line shiplock of Jiangsu province is taken to verify the scientificity and feasibility of the model. it should be pointed out that the data of the double line shiplock is randomly selected. The results show that the analytical techniques are appropriate for the theory and research questions and they are applied appropriately.
It is noted that Because of the limitation of objective conditions, such as data accuracy, emergencies, a feasibility study is needed before applying the model.
This research was supported by the Fundamental Research Funds for the Central Universities (No. 2012B13914)