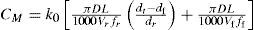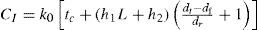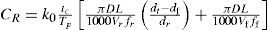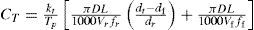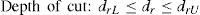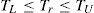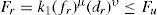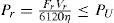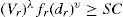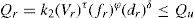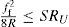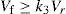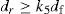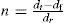Optimization of Turning Operations by Using a Hybrid Genetic Algorithm with Sequential Quadratic Programming

Abstract

The determination of optimal cutting parameters is one of the most important elements in any process planning of metal parts. In this paper, a new hybrid genetic algorithm by using sequential quadratic programming is used for the optimization of cutting conditions. It is used for the resolution of a multipass turning optimization case by minimizing the production cost under a set of machining constraints. The genetic algorithm (GA) is the main optimizer of this algorithm whereas SQP Is used to fine tune the results obtained from the GA. Furthermore, the convergence characteristics and robustness of the proposed method have been explored through comparisons with results reported in literature. The obtained results indicate that the proposed hybrid genetic algorithm by using a sequential quadratic programming is effective compared to other techniques carried out by different researchers.

1

Introduction

The selection of optimal cutting parameters, like the number of passes, depth of cut for each pass, feed rate and cutting speed, is a very important issue for every machining process [1].

Several cutting constraints must be considered in machining operations. Turning operation can be performed in a single pass or in multiple passes. Multipass turning is preferable over single-pass turning in the mechanical industry for economic reasons [2].

The optimization problem of machining parameters in multipass turning becomes very complicated when plenty of practical constraints have to be considered [3].

Conventional optimization techniques such as graphical methods [4], linear programming [5], dynamic programming [6, 7], and geometric programming [8, 9] have been used to solve optimization problems of machining parameters in multipass turning. However, these optimization methods may be useless for some problems. Numerous constraints and multiple passes make machining optimization problems complicated and consequently these methods are inclined to converge to local optimal results. Thus, meta-heuristic algorithms have been developed to solve machining economics problems because of their power in global searching. There have been some works regarding optimization of cutting parameters [2, 3, 10, 11, 12, 13, and 14] for different situations. In these works, authors have tried to bring out the utility and advantages of ant colony system, genetic algorithm, simulated annealing, swarm intelligence, evolutionary approach and scatter search approach. It is proposed to use the hybrid genetic algorithm by using sequential quadratic programming for the machining optimization problems.

The present paper is focused on the application of a new optimization technique, the hybrid genetic algorithm by using sequential quadratic programming, to determine the optimal machining parameters that minimize the production unit cost in multipass turning processes.

2

Cutting process model

2.1

Decision variables

In the construction of the optimization problem, six decision variables are considered: cutting speeds for rough and finish machining (V_rV_f), feed rates for rough and finish machining (f_r,f_f) and depth of cut for each pass for rough and finish machining (d_r,d_f).

2.2

Objective function

Based on the minimum unit production cost, UC, criterion, the objective function for a multipass turning operation is given as follows [10],

With:

2.3

Constraints

Some constraints that affect the selection of optimal cutting conditions will be considered. The constraints for rough and finish machining are as outlined below:

2.3.1

Rough machining

Parameter bounds

Due to the limitations on the machine and cutting tool and due to the safety of machining, the cutting parameters are limited with the bottom and top limit.

Tool-life constraint

The constraint on the tool life is

Cutting force constraint

The maximum amount of cutting forces Fu should not exceed a certain value as higher forces produce shakes and vibration. This constraint is given as

Power constraint

The nominal power of the machine P_U limits the cutting process:

With efficiency η = 0.85

Stable cutting region constraint

This constraint is given as

The constraint on the stable cutting region has been suggested by Philipson and Ravindran [15] in order to take into account the prevention of chatter vibration, adhesion and formation of a built-up edge. Equation (12) adopted in this research for determination of the stable cutting region was proposed by Narang and Fischer (1993) for multipass turning operations.

The values of λ and SC are based on the values used by Philipson and Ravindran [15] while the value for v is assumed to be that proposed by Narang and Fischer [16].

Chip–tool interface temperature constraint

This constraint is given as

2.3.2

Finish machining

All the constraints other than the surface finish constraint are similar for rough and finish machining. [17].

Surface finish constraint

In the finishing operations, the obtained surface roughness must be smaller than the specified value SR_U, given by technological criteria so that the following equation is satisfied:

Constraints for roughing and finishing parameters relations

2.3.3

The number of rough cuts

The possible number of rough cuts is restricted by

Where n_L ≤ n ≤ n_U

The optimization problem in multipass turnings is divided into m = (n_U − n_{L +} 1) subproblems. In each subproblem, the number of rough cuts n is fixed; hence, the search for the solution of the optimization problem is to find the solutions of msubproblems, the minimum of these results will be the solution of the global optimization problem.

3

Genetic algorithm (GA) and Sequential quadratic programming (SQP)

Due to the good coverage of the genetic algorithm and sequential quadratic programming techniques in the literature [18, 19, 20], only the hybrid GASQP method will be briefly mentioned here.

4

Hybrid GA-SQP

SQP requires a smaller number of objective and constraint function calls than the GA. It can also find accurate optimum results as it is a deterministic algorithm. However, because SQP uses gradient information in its search algorithm, it tends to be trapped in the local optimum and suffers from noise in objective or constraint functions whereas the GA searches more globally and has more chance to find a global optimum. The GA should be used to perform the initial global search. The results are used to guide the local search.

In order to benefit the global search ability of a GA and the accurate local search of a SQP, they are used as a complement of each other. To do so, the GA stopping criteria are set so that the GA would stop prematurely, for example, with a low generation, a low population or a high tolerance. It is assumed that the GA should find its optimal results near the true global optimum. The GA results are therefore used as an initial point for the SQP algorithm. The SQP proceeds the local search and find its local optimum, which is the global optimum searched.

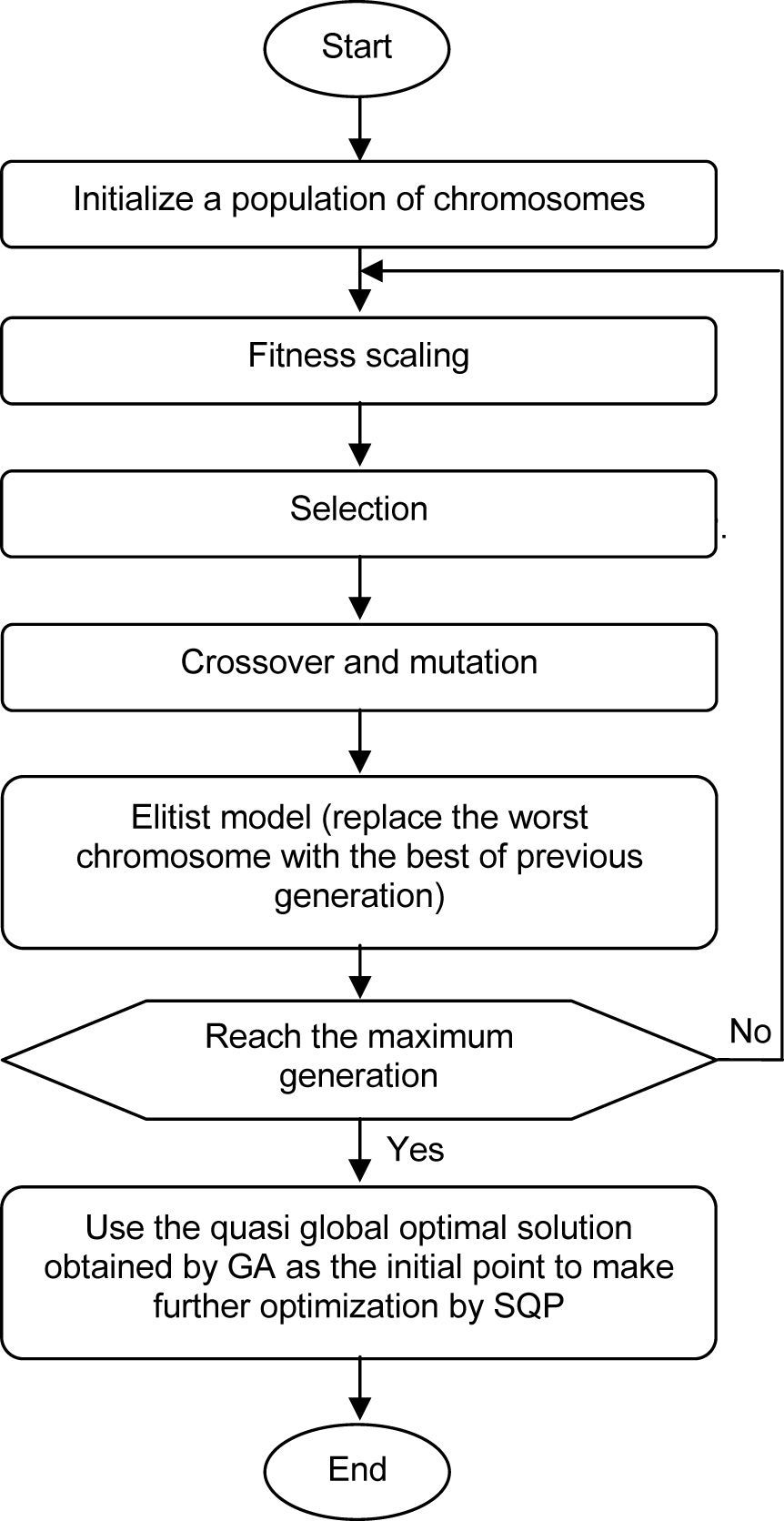
Figure 1 shows the flowchart of the hybrid GA. At the beginning, the genetic algorithm searches the global optimum in the whole solution region to obtain a quasi-optimal solution, and then, the global optimal solution can be obtained by sequential quadratic programming. The method is named GA+SQP.

Figure 1.

Flowchart of the hybrid GA-SQP.

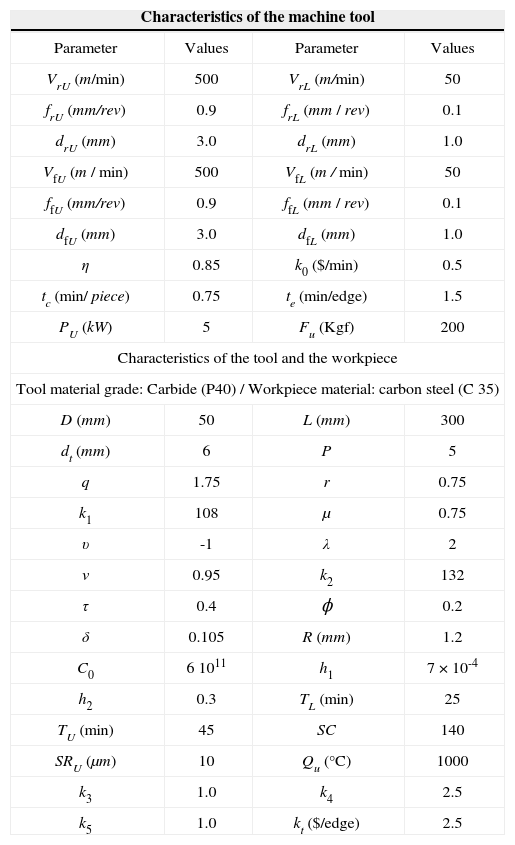
5

Example of Application

Now, an example of application is considered to validate the used hybrid GA-SQP method for the optimization of a multipass turning operation. The parameters used for the numerical application are mentioned in Table 1.

Table 1.

Machining data from reference [10].

Characteristics of the machine tool
Parameter	Values	Parameter	Values
VrU (m/min)	500	VrL (m/min)	50
frU (mm/rev)	0.9	frL (mm / rev)	0.1
drU (mm)	3.0	drL (mm)	1.0
VfU (m / min)	500	VfL (m / min)	50
ffU (mm/rev)	0.9	ffL (mm / rev)	0.1
dfU (mm)	3.0	dfL (mm)	1.0
η	0.85	k0 ($/min)	0.5
tc (min/ piece)	0.75	te (min/edge)	1.5
PU (kW)	5	Fu (Kgf)	200
Characteristics of the tool and the workpiece
Tool material grade: Carbide (P40) / Workpiece material: carbon steel (C 35)
D (mm)	50	L (mm)	300
dt (mm)	6	P	5
q	1.75	r	0.75
k1	108	μ	0.75
υ	-1	λ	2
ν	0.95	k2	132
τ	0.4	ϕ	0.2
δ	0.105	R (mm)	1.2
C0	6 10^11	h1	7 × 10^-4
h2	0.3	TL (min)	25
TU (min)	45	SC	140
SRU (μm)	10	Qu (°C)	1000
k3	1.0	k4	2.5
k5	1.0	kt ($/edge)	2.5

5.1

Results and Discussion

The genetic algorithm was run with the following parameters (Table 2):

Table 2.

Parameters used in the genetic algorithm.

Parameter	Value or type
Population size	20
Scaling function	Rank (The scaling function converts raw fitness scores returned by the fitness function to values in a range that is suitable for the selection function)
Selection function	Roulette
Reproduction	Elite count: 2
Crossover fraction	0.8
Mutation	It randomly generates directions that are adaptive with respect to the last successful or unsuccessful generation. A step length is chosen along each direction
Crossover	Scattered (it creates a random binary vector. It then selects the genes where the vector is a 1 from the first parent, and the genes where the vector is a 0 from the second parent, and it combines the genes to form the child)
Migration fraction	0.2
Migration interval	20
Number maximal of iterations	100

Several GA generations are performed in order to identify the most promising areas and then the SQP optimization algorithm is applied using, as an initial guess, the best individual found by the GA. It should be noted that in this approach the GA is used to specify a good initial guess for the SQP algorithm.

The results found by the hybrid GA-SQP are mentioned in Table 3.

Table 3.

The optimized turning parameters.

n	Rough machining			Finish machining			UC ($)
	Vr (m / min)	fr (mm / rev)	dr (mm)	Vf(m / min)	ff (mm / rev)	df (mm)
1	94.4640	0.8660	3.0000	162.2890	0.2580	3.0000	1.9308
2	182.9710	0.4520	2.4996	217.3229	0.1794	1.0009	2.5840
3	145.6160	0.9000	1.6670	191.3630	0.2580	1.0000	2.6450
4	157.2560	0.9000	1.2430	171.6070	0.2580	1.0260	3.1230
5	166.5110	0.9000	1.0000	191.3630	0.2580	1.0000	3.4585

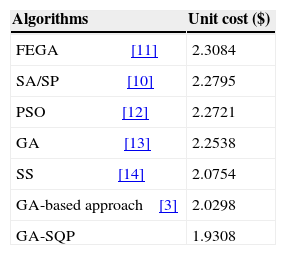
We find that the lowest value is 1.9308 $ under which the minimum number of rough cuts (1)n = is taken. The performance of the hybrid GA-SQP in comparison with other methods is shown in Table 4

Table 4.

Results of optimization using different algorithms.

Algorithms	Unit cost ($)
FEGA [11]	2.3084
SA/SP [10]	2.2795
PSO [12]	2.2721
GA [13]	2.2538
SS [14]	2.0754
GA-based approach [3]	2.0298
GA-SQP	1.9308

The proposed hybrid approach is applied and evaluated with the same model and data provided in the references [3, 10, 11, 12, 13 and 14], but the authors of these references have used other methods.

According to Table 4 we conclude that the hybrid GA-SQP yields much better results that the other methods. Thus the hybrid GA-SQP can solve the optimization of the multipass turning operation problem efficiently to achieve better results in reducing the unit production cost.

6

Conclusion

This work presents a hybrid GA-SQP optimization for solving the multipass turning operations problem. To decrease the complexity of the problem, the whole problem was divided into several subproblems according to the number of possible rough cuts.

The results obtained by comparing the hybrid GASQP with those taken from recent literature prove its efficiency.

The hybrid GA-SQP can achieve much better results than other approaches proposed previously, and the production unit cost was significantly reduced. In addition, the present method is a generalized solution method so that it can be easily employed to consider the optimization models of turning regarding various objectives and constraints.

In the machining models, no specific workpiece and tool was identified. Therefore, the solution approach can be used with any workpiece for turning optimization problems.

This study definitely indicates some directions for future work. For example: the application of the hybrid GA-SQP in complex machining systems and automated process planning systems.