Parallelizing fully homomorphic encryption for a cloud environment

Abstract

Cloud computing is a boon for both business and private use, but data security concerns slow its adoption. Fully homomorphic encryption (FHE) offers the means by which the cloud computing can be performed on encrypted data, obviating the data security concerns. FHE is not without its cost, as FHE operations take orders of magnitude more processing time and memory than the same operations on unencrypted data. Cloud computing can be leveraged to reduce the time taken by bringing to bear parallel processing. This paper presents an implementation of a processing dispatcher which takes an iterative set of operations on FHE encrypted data and splits them between a number of processing engines. A private cloud was implemented to support the processing engines. The processing time was measured with 1, 2, 4, and 8 processing engines. The time taken to perform the calculations with the four levels of parallelization, as well as the amount of time used in data transfers are presented. In addition, the time the computation servers spent in each of addition, subtraction, multiplication, and division are laid out. An analysis of the time gained by parallel processing is presented. The experimental results shows that the proposed parallel processing of Gentry's encryption improves the performance better than the computations on a single node. This research provides the following contributions. A private cloud was built to support parallel processing of homomorphic encryption in the cloud. A client-server model was created to evaluate cloud computing of the Gentry's encryption algorithm. A distributed algorithm was developed to support parallel processing of the Gentry's algorithm for evaluation on the cloud. An experiment was setup for the evaluation of the Gentry's algorithm, and the results of the evaluation show that the distributed algorithm can be used to speed up the processing of the Gentry's algorithm with cloud computing.

1

Introduction

In conventional computing, data centers with computing resources are usually established for data processing. Running a data center is costly in order to meet an organization's maximum needs of data processing. In addition, the computing resources are often largely idle where the computing resources are underutilized.

Cloud computing provides advantages over the conventional computing with data centers. An organization can obtain the computing resources from cloud computing provided by a provider. Instead of purchasing the computing resources, organizations can purchase computing services from cloud computing providers where it is much cheaper then purchasing the computing resources. Cloud providers are responsible for efficiently providing the on-demand computing resources to the organizations as clients to the cloud providers. The organizations do not need to maintain the computing resources and the services are charged on the time use of computing resources.

Cloud computing is not without the issues. Organizations have concerns in moving their data to a cloud due to the data privacy. Possible threats to the data privacy could be from cloud providers’ employees, clients, and network hackers. To protect data in a public computing environment such as cloud, encryption seems to be an effective way of enforcing data security in a cloud. However, most of existing encryption schemes require data to be decrypted for computations where data becomes vulnerable during computation of decrypted data. If computations can be performed on encrypted data without decryption, then the security of data would not be a concern. Homomorphic encryption makes it possible to process encrypted data without decryption whereby the encrypted results can only be decrypted by the client who requests the service.

Homomorphic encryption is an encryption scheme which allows for computations on encrypted data and obtains an encrypted result which decrypted produces the same result of computations on the original data. In this paper, we will survey several efficient, partially homomorphic schemes, and a number of fully homomorphic, but less efficient schemes. The Gentry's algorithm for fully encryption algorithm will be examined in detail for the performance issue (Naone, 2015). We then present a parallel processing method which can be applied to improve the performance of the Gentry's fully homomorphic encryption algorithm by taking advantage of ample computing power of a cloud. Finally, the paper is summarized.

2

Homomorphic encryption schemes

Homomorphic encryption schemes allow computations on encrypted data and then decrypting the result produces the same result as performing the same computations on the unencrypted data.

Rivest, Shamir and Adelman (RSA) published the first cryptosystem which was based on the work from Diffie and Hellman (Diffie & Hellman, 1976; Rivest et al., 1978a). RSA is multiplicatively, but not additively homomorphic (Rivest et al., 1978b). If the product of two encrypted data is computed, then the decrypted result of the product will be the product of the two original data. ElGamal encryption scheme is also based on the Diffie and Hellman key exchange (Diffie & Hellman, 1976; ElGamal, 1985). Like RSA, ElGamal is multiplicatively, but not additively homomorphic.

Paillier encryption scheme allows for homomorphic addition of two encrypted data by computing their product and the decrypted result of the product will give the sum of their respective original data (Paillier, 1999). The Paillier encryption scheme is not fully homomorphic because it is not possible to compute the product of two ciphertexts.

Partially homomorphic encryption schemes including RSA, ElGamal, and Paillier allow only either addition or multiplication computation on the data, which are not practical for most of applications (Lauter et al., 2011). A fully homomorphic encryption scheme which supports arbitrary computations on data has far more practical use than partially homomorphic encryption.

3

Gentry scheme and cloud computing

In 2009, Gentry presented a fully homomorphic encryption scheme (Gentry, 2009). Gentry's scheme starts with a somewhat homomorphic encryption using ideal lattices that can only perform a limited number of homomorphic operations on encrypted data. Gentry then modifies the scheme to a fully homomorphic encryption scheme by adding bootstrapping procedure to it (Gentry, 2009). Gentry's scheme was shown to take seconds to perform addition, subtraction, and comparison operations on two 8-bit integers. The multiplication of two 8-bit integers took minutes and the division of two 8-bit integers took hours. The long computational time makes the Gentry's scheme impractical for many applications. Because fully homomorphic encryption is a young endeavor, there will almost certainly be improvements made to Gentry's algorithm, reducing the time taken for instructions. For example, Fujitsu (Fujitsu, 2013) develops a homomorphic encryption scheme which performs data encryption at a batch level. Compared to the Gentry's algorithm, Fujitsu claims that their batch encryption method can perform encryption faster.

The cloud computing has been widely used for parallel processing of mass data (Kamara & Raykova, 2013; Amazon Web Services, 2015; Cloudera, 2015; Dean & Ghemawat, 2008). The algorithm used in this work's evaluation is based on the implementation presented in a 2011 paper by Gentry and Halevi (Gentry & Halevi, 2011). The Gentry's fully homomorphic algorithm seems to be a perfect fit for the cloud because the tasks of performing mathematical operations can be analyzed, split, and distributed to the nodes in the cloud.

Existing cloud computing offerings are mostly proprietary or software that is not amenable to experimentation or instrumentation. In this research, a private cloud based on OpenStack was created for experimental instrumentation and study (Hayward & Chiang, 2013a, 2013b). The cloud environment consists of two computation servers providing the virtualized infrastructure for execution. The primary cloud server is running on a Dell Inspiron N5510. The processor is an Intel Core i5-2410M CPU which provides 2 cores running at 2.30 GHz. The computer has 6 GB of RAM. The secondary cloud server is a Lenovo T410. It has an Intel M560 CPU which provides 2 cores at 2.67 GHz. The secondary server has 4 GB of RAM.

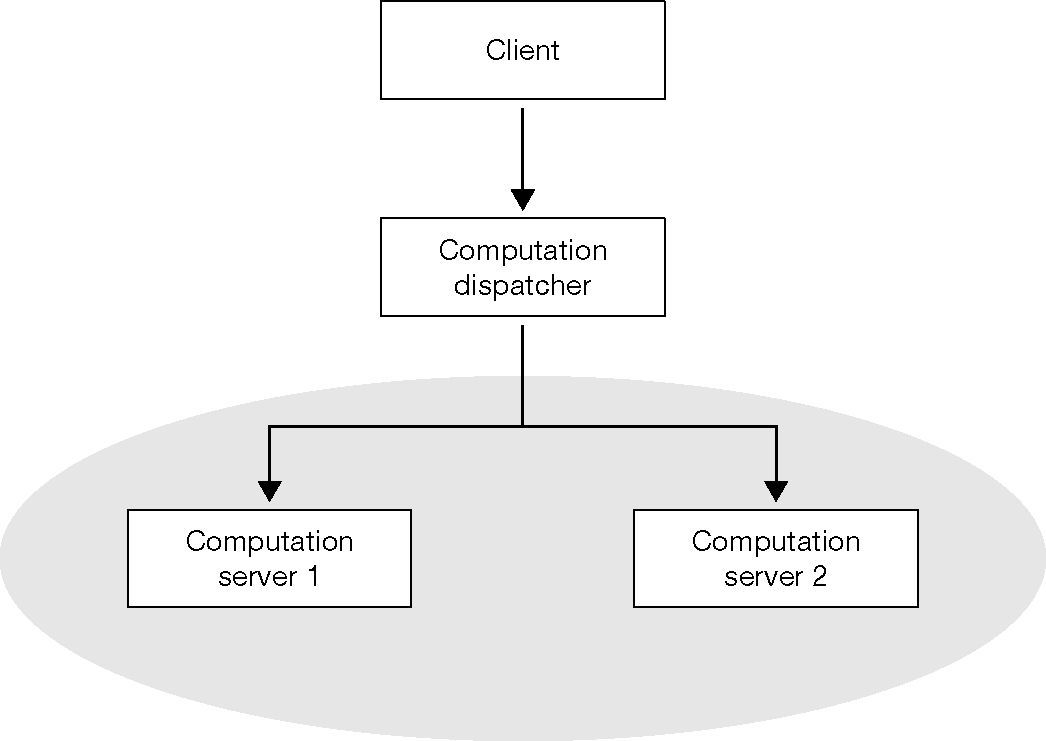
A client-server model shown in Figure 1 was built to support the parallel processing of the Gentry's algorithm in the cloud.

Fig. 1.

Client-server model.

The user inputs a set of data in the form of integers and a set of computations to perform on the data for the calculation. The input data from the user are forwarded to a computation dispatcher. The input integers are labeled and referenced as i₀, i₁, i₂, ..., and i_N. The computation string must be a list of calculations, and will be performed in the order specified. Each calculation must further be in the form of an algebraic equation, with the input integers being combined with only the addition, subtraction, multiplication, and division operators. Parentheses are available for changing the order of operations. The results of any calculation can be assigned to any number of input, output, or temporary variables. The output variables are referenced as o₀, o₁, ..., and o_N, and the temporary variables are referenced as t₀, t₁, ..., and t_N. Only the output variables are returned to the user.

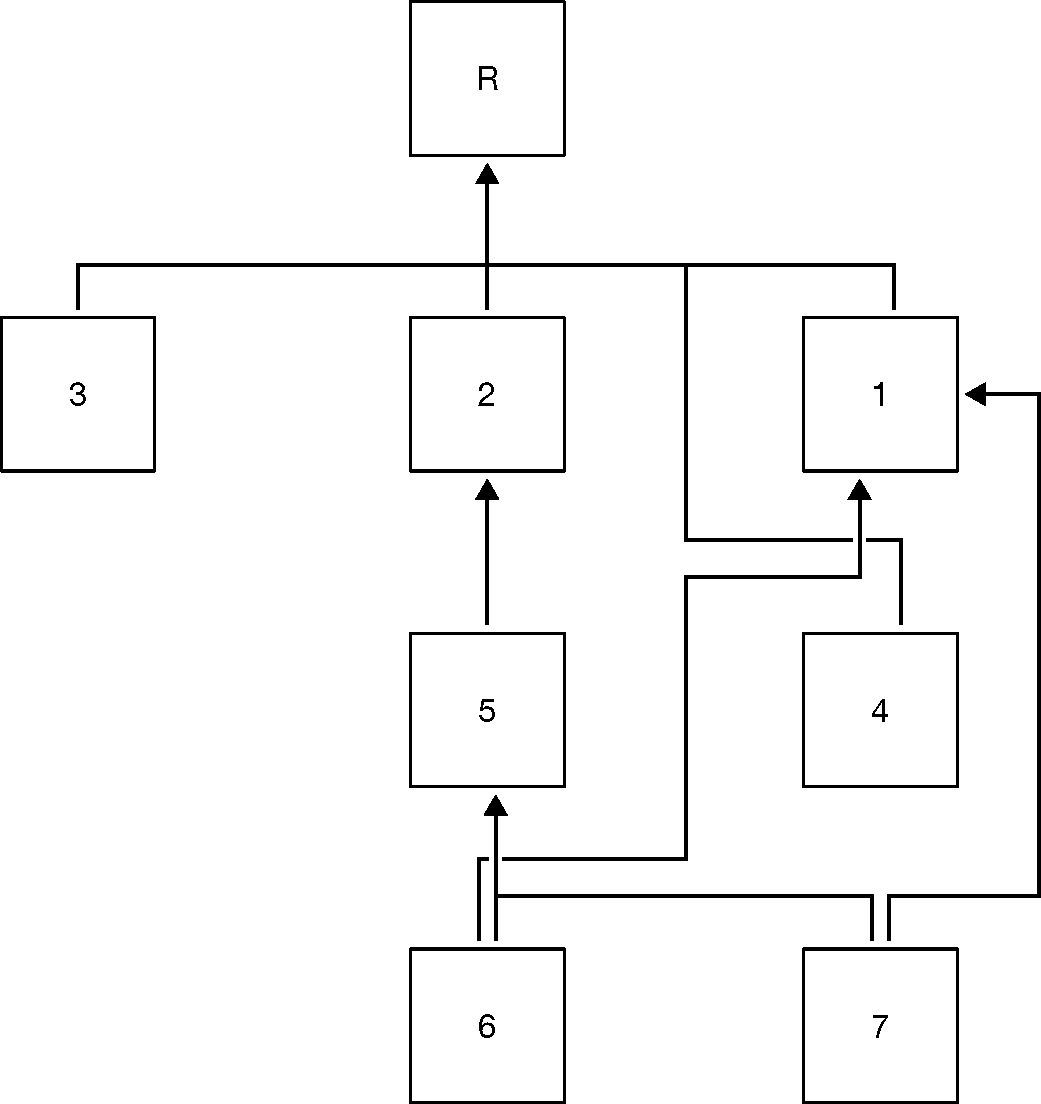
As the computation dispatcher takes the input data and computations from the user, it converts the input data into a set of encrypted bits for use by the computation server. It also converts the input computation into a list of bit-wise calculations to perform on the input data. This list is then parsed into a directed graph, such that each node in the graph represents a calculation, and the edge represents the child that depends on the output of the parent. If a node has no such requirement, then it has an edge to the root node. For example, if a computation was given as Table 1, then Figure 2 shows the graph that would be computed. The dispatcher finds a chain of nodes starting from the root node, stopping when there is a requirement from a different chain. It then transmits the un-branched chain to the first computation server. The dispatcher marks that chain as sent, and then repeats until there are no more chains to dispatch. When the dispatcher receives a response, it removes the calculated node from the graph and updates all edges which point to the removed node to instead point to the node's parent. It then repeats the process of finding chains over again. If there are no more nodes in the graph, then the dispatcher converts the encrypted bits back into their respective output integers, and returns the array of those integers.

Table 1.

Example instruction input.

Number	Instruction
1	a = b * c
2	c = d * e
3	d = b * e
4	f = a + b
5	b = c + c
6	d = a * b
7	e = a + b

Fig. 2.

Example data dependency graph.

The computation server receives a public key, an ordered array of encrypted bits, and a circuit to evaluate on from the computation dispatcher. It then performs the requested calculations in order, placing the results in any of the input, output, or temporary arrays. When the calculations are complete, it then returns the output array. The calculations must be in the form of a comma delimited list. The first item in the list must be the instruction, and every other element in the list denotes an element of one of the input, output or temporary arrays. The supported instructions include add and multiply, which are binary operations assigning the first data element to be the binary addition or multiplication of the second and third data elements. A binary half-adder is supported, with the first and second data element being the sum and carry bit of the addition of the third and fourth data element. Similarly, a binary full-adder is also supported, with the same bit assignments as the half-adder, but with an additional carry-in bit added as well.

4

Algorithm

The details of the distributed algorithm for the execution of the Gentry's encryption algorithm in parallel are described in this section. When the computation dispatcher receives a request from the user, it creates a data dependency graph, as detailed in section 4.1. The computation dispatcher then finds a sub-circuit for execution as outlined in section 4.2 and dispatching that sub-circuit, waiting on an execution node to free if necessary. When any computation server completes, the computation dispatcher updates the local data store, as well as removing the completed instructions from the data dependency graph, updating the references to the completed instructions to point to the root node. When the root node has no children, then the computation is complete and the dispatcher returns to the user the requested data.

4.1

Creating data dependency graph

The algorithm in Figure 3 describes how to create the data dependency graph from the input circuit E, begin by letting P and C be arrays that will have an empty array for each element e ∈ E. These two arrays will indicate the parent and child pointers in the graph. Further, let D be an associative array that will contain the owner of data. D will begin as empty, which will be treated as 0, which will denote the root node. Once initialization is done, the main loop iterates through the elements of E as e and index, where index is offset 1, not 0. Take the inputs of e and look up from D, which owns the input elements. Let this node be d. Denote d as a parent of the current node, and the current node as a child of d. For each output, denote owner as the node which holds the output. Every dependent of owner will be marked as a parent of index, and index will be marked as a child of each dependent. Each output of the current operation will be updated to be owned by the current operations in D.

Fig. 3.

Creating data dependency graph.

4.2

Finding sub-circuit

To find a sub-circuit for execution, the computation dispatcher finds any child of the root node (i.e. any member of C[0]) which is a child only of the root node, and is not currently pending execution. Let this q be c, and let the set E contain only that one element. The computation dispatcher marks this node as pending execution. It then takes all of the children of c and adds them to an ordered array of nodes, candidates, to evaluate for execution.

The computation dispatcher then removes the top of the candidates array as c. If all of c's parents are in E, and c is not already pending execution, then mark c as pending execution, add it to E, and add all of its children to candidates. The dispatcher repeats this process of candidate evaluation until there are no more nodes in candidates []. Figure 4 presents this process.

Fig. 4.

Finding sub-circuit.

4.3

Blind addition and multiplication

When addition or multiplication computation performed on the encrypted data, the maximum output size of the computation needs be determined. To determine the output size required for an addition of n bit-arrays₁, a₂, …, and a_n>, having bit-sizes₁, s₂, …, and s_n>, the computation server would need to find the smallest power of two greater than the sum of the maximum size of each a_i. To put it another way, the server would need to compute

To determine the output size required for a multiplication of n bit-arrays₁, a₂, …, and a_n>, having bit-sizes₁, s₂, …, and s_n>, the computation server would need to find the smallest power of 2 greater than the product of the maximum size of each a_i. To put it another way, the server would need to compute

5

Evaluation of the algorithm

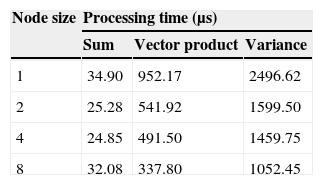
Three computations are performed on the cloud system for testing. All three computations are using the same set of data which contain 20 random 8-bit integers. The first experiment is to compute the sum of these 20 integers. The second is to compute the vector product of the integers. The third one is to compute the variance of the integers.

In each evaluation, the time taken to compute the dependency graph and each sub-circuit was recorded by the computation dispatcher. The time to execute each sub-circuit was recorded by the individual computation servers and returned to the dispatcher for accumulation. The dispatcher also recorded the overall time to complete the computation. While the algorithm is capable of evaluating more fine-grained operations, integer addition and multiplication were chosen as primitives to simplify the evaluation.

5.1

Setup

To generate the 20 8-bit integers, the random integer generator from random.org was used (RANDOM.ORG, 2015). The number of integers generated was 20, and the range used was 0 to 255. The integers generated were 16; 195; 35; 129; 103; 198; 212; 105; 252; 58; 51; 184; 219; 39; 244; 179; 154; 129; 217; 171. The three evaluation circuits were hand generated, with the sum circuit used independently as well as being used as part of the variance circuit.

For the trials with 1, 2, and 4 nodes operations occurred only on the primary computer. When processing with 8 nodes, the additional 4 nodes were provided by a secondary computer. The network connection between them was a wireless network.

The data and keys were transferred to the compute nodes with each sub-circuit. This was done to model a real-world scenario where the keys for a given computation would be dynamic, and would need to be retrieved before each execution.

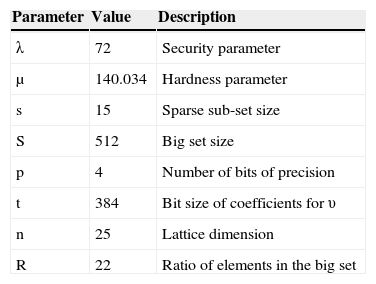
The keys were generated via the keyGen method provided by the Gentry-Halevi code with n = 2⁵. Table 2 shows the computed parameters, including s, the number of σ vectors, S, the size of the bit vectors, p, the bits of precision, and logR, the big set size ration. The public key generated was 2.5 MB, and the private key was 2.6 MB. They were saved for later use in the evaluation.

Table 2.

Key generation parameters.

Parameter	Value	Description
λ	72	Security parameter
μ	140.034	Hardness parameter
s	15	Sparse sub-set size
S	512	Big set size
p	4	Number of bits of precision
t	384	Bit size of coefficients for υ
n	25	Lattice dimension
R	22	Ratio of elements in the big set

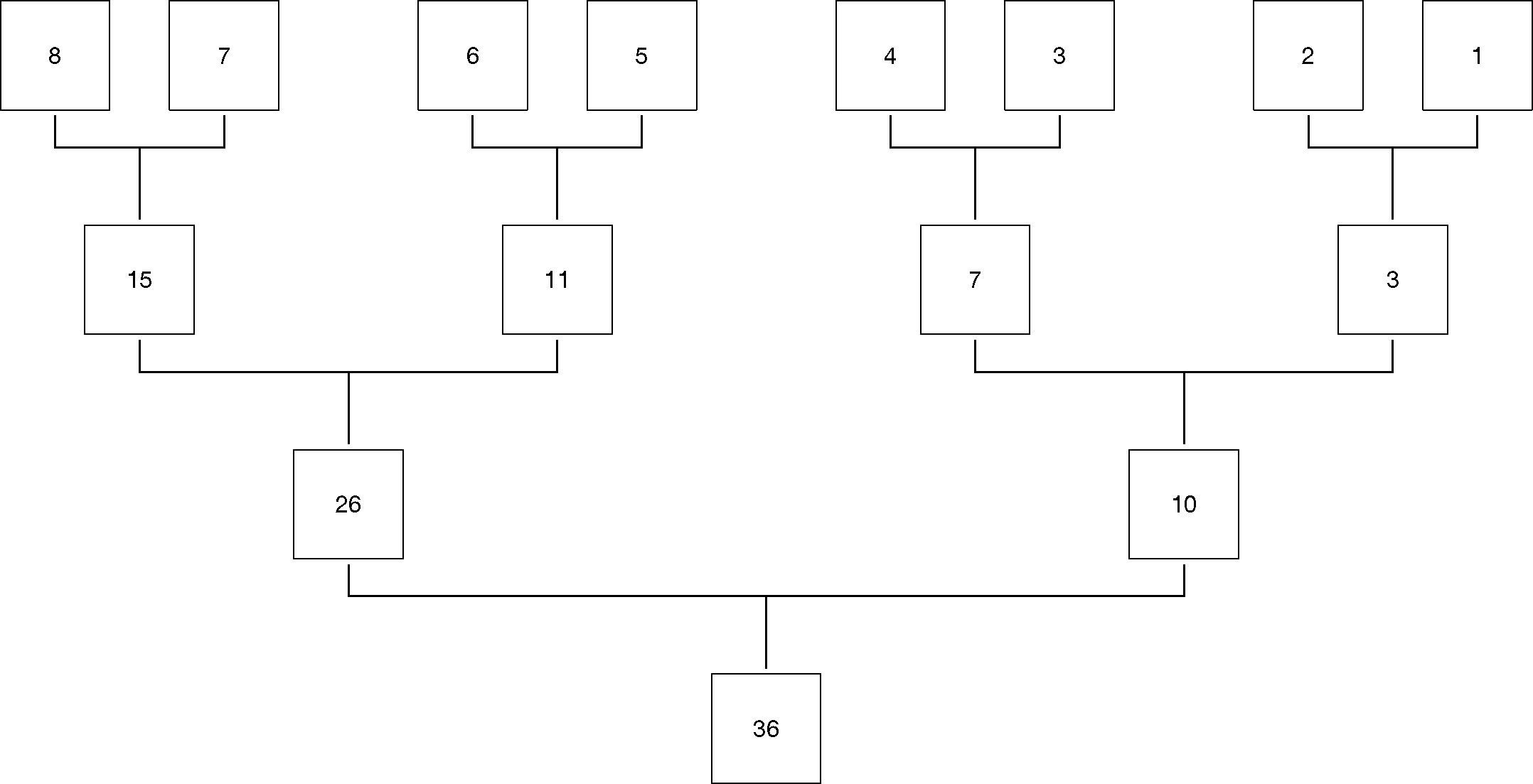
5.2

Tests performed

The sum of the integers was taken by splitting the 20 integers into 10 pairs and finding the sum of each pair. The resulting 10 integers were then split into 5 pairs, and summed, and so on. This pairing for addition was chosen to maximize the parallel processing of the computation. See Figure 5 for a visual representation of the process.

Fig. 5.

Sum procedure.

The vector product was found by first taking the pair-wise product of the integers, producing 10 integers. These integers were then summed.

The numerator of the variance of the integers was taken as the square of the sum of the integers plus the sum of the squares of the integers. The circuit generated to compute the sum of the integers was taken as the base circuit. The sum was squared into a new output, and each integer was then squared, giving a total of 21 integers. These integers were then summed.

5.3

Tests results

The time to perform the three evaluations on 1, 2, 4, and 8 compute nodes is shown together in Table 3. The computations gain the performance as we increase the nodes in the system. Most computations are not completely parallelizable and require some amount of communication between machines. Network communication time can remove the benefits of the parallel algorithm on a cloud system when the computation is short. In the sum problem, the communications overhead seems monopolize the processing time. The algorithm doesn’t take into account the network speed, nor does it make predictions about operation speed. Also, the algorithm does not prefer to dispatch long or slow operations before quick ones, instead dispatching them in the order they are discovered.

Table 3.

Nodes vs. time in microseconds.

Node size	Processing time (μs)
	Sum	Vector product	Variance
1	34.90	952.17	2496.62
2	25.28	541.92	1599.50
4	24.85	491.50	1459.75
8	32.08	337.80	1052.45

The time taken to compute the sum of the integers is presented in Table 3. The speedup of the sum algorithm when increasing from 1 computation node to 2 computation nodes was 1.3806. The speedup when increasing from 1 node to 4 nodes was similar at 1.4044. This lack of speedup can be attributed to the hardware used in the evaluation, as it provides two processor cores. Each core is hyper-threaded, so that each one appears to be two processors to the underlying operating system, but the operations performed meant that only one process can operate at a time. The speedup from 2 to 4 nodes was 1.0172, despite the lack of additional processor resources. The time to execution increased from 4 to 8 nodes, which is most likely due to the time taken to transfer data from the dispatcher to the remote computation servers. The speedup from 1 to 8 nodes was 1.0881.

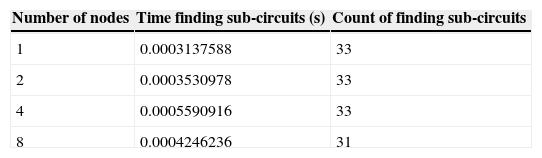
Table 4 shows for each trial the time the dispatcher spent finding sub-circuits, and the number of times the method was called to find sub-circuits. Although there were fewer calls to the find sub-circuits method in the 4 and 8 node trials, the finding of sub-circuits took longer, though not by a significant factor. A probable explanation for the increase in time is that the dispatcher was running on the same hardware as the computation servers, even though they were on different virtual computers. This explanation is supported by the lack of increase from 4 to 8 nodes, as the additional 4 compute nodes were on separate hardware. There were 2 fewer calls to the find sub-circuit method in the 8 node trial, which is common with the variance trials.

Table 4.

Finding sum sub-circuits time and count.

Number of nodes	Time finding sub-circuits (s)	Count of finding sub-circuits
1	0.0003137588	33
2	0.0003530978	33
4	0.0005590916	33
8	0.0004246236	31

The time spent evaluating sub-circuits is presented in Table 5. Similar to the time to find sub-circuits, there was an increase from 2 to 4 nodes, but a decrease from 4 to 8 nodes. The jump in level is once again most likely due to the limit in processor availability across threads, leading to execution waiting for processor resources.

Table 5.

Evaluating sum sub-circuits time and count.

Number of nodes	Time evaluating sub-circuits (s)	Count of evaluating sub-circuits
1	33.89	16
2	37.00	16
4	50.20	16
8	49.24	15

The time taken to compute the vector product of the integers is presented in Table 3. The speedup from 1 to 2 compute nodes when computing the vector product of the 20 integers was 1.757. The speedup from 1 to 4 compute nodes was 1.9373, and the increase from 2 to 4 compute nodes did not include an increase in processor availability. In spite of the lack of additional processors, there was still a 1.1026 speedup between the 2 and 4 compute server trials. When increasing from 1 to 8 compute nodes, there was a 2.8187 speedup.

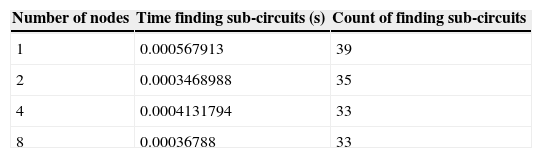
The time spent finding the vector product sub-circuits is presented in Table 6. The time spent finding sub-circuits was less in the 2, 4, and 8 node trials than the 1 node trial, with the 2 and 8 node trials being less than the 1 and 4 node trials. The difference in time remains negligible. As with the finding of the variance and sum sub-circuits, the least number of calls to the find sub-circuits method was in the 8 node trial.

Table 6.

Finding vector product sub-circuits time and count.

Number of nodes	Time finding sub-circuits (s)	Count of finding sub-circuits
1	0.000567913	39
2	0.0003468988	35
4	0.0004131794	33
8	0.00036788	33

The time spent evaluating the vector product circuits is presented in Table 7. There was a jump from the 1 and 2 node level to the 4 and 8 node level and the least number of circuits evaluated was in the 8 node configuration.

Table 7.

Evaluating vector product sub-circuits time and count.

Number of nodes	Time evaluating sub-circuits (s)	Count of evaluating sub-circuits
1	950.87	19
2	1032.99	17
4	1730.39	16
8	1813.90	16

The time taken to compute the numerator of the variance of the integers is presented in Table 3. The speedup from 1 to 2 compute nodes when computing the variance of the 20 integers was 1.5609. The speedup from 1 to 4 compute nodes was 1.7103, but the increase from 2 to 4 compute nodes did not also include an increase in processor availability. In spite of the lack of additional processors, there was still a 1.0957 speedup between the 2 and 4 compute server trials. When increasing from 1 to 8 compute nodes, there was a 2.3722 speedup.

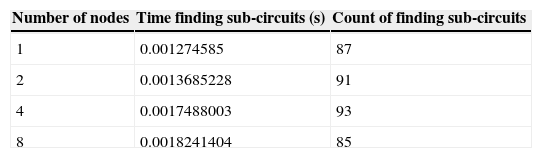
The overall time spent finding the variance sub-circuits is presented in Table 8. There was once again an increase from the time to find sub-circuits with 1 and 2 nodes to 4 and 8 notes, though the difference in time is negligible. As with the finding of the sum sub-circuits, the least number of calls to the find sub-circuits method was in the 8 node trial.

Table 8.

Finding variance sub-circuits time and count.

Number of nodes	Time finding sub-circuits (s)	Count of finding sub-circuits
1	0.001274585	87
2	0.0013685228	91
4	0.0017488003	93
8	0.0018241404	85

The time spent by the computation servers evaluating the variance circuit is presented in Table 9. There was a jump from the 1 and 2 node level to the 4 and 8 node level. The least number of sub-circuits evaluated was in the 8 node configuration.

Table 9.

Evaluating variance sub-circuits time and count.

Number of nodes	Time evaluating sub-circuits (s)	Count of evaluating sub-circuits
1	2494.11	43
2	2684.95	45
4	4340.87	46
8	4643.11	42

5.4

Discussion

The sum trial showed good speedups while all computation servers were on the same computer as the dispatcher, but dropped off when computation servers were on a separate computer. This drop off is most likely due to network transfer time coupled with the small amount of time taken to perform the sum operations.

The algorithm showed a good speedup in the more complex and time consuming vector product and variance circuits, with a speedup of 2.3722 and 2.8187 when distributed over 8 nodes and two computers.

Despite the lackluster performance of the sum trial, the speedup of the vector product and variance circuits suggests that the algorithm is useful for decreasing the time to evaluate homomorphic circuits.

The time to compute sub-circuits was on the order of 0.0003 s in the sum trials, 0.0004 s in the vector product trials, and 0.0018 s in the variance trials. This time is very low when compared with the time spent performing the actual computations.

6

Conclusions

The computing power and resources of cloud computing are more provided than a single machine where the computations on data are performed by clusters of machines. Cloud computing has been widely used to process massive data. However, for cloud computing, organizations have a concern of data privacy for their data. In this paper, we described the problem of data privacy in cloud computing. Fully homomorphic encryption is a solution to resolve the data privacy in the cloud where the encrypted data are processed and the encrypted results are returned. However, fully homomorphic encryption runs slow and the faster fully homomorphic encryption schemes are needed.

Gentry's encryption scheme is fully homomorphic with slow performance. Several methods have been proposed to speed up the performance of fully homomorphic encryption schemes. Parallel processing is one effective way of doing this (Vukmirović et al., 2012; Ortega-Cisneros et al., 2014). Our parallel processing for Gentry's encryption was presented in this paper and tested in a private cloud computing environment. The experimental results show that the proposed parallel processing of Gentry's encryption improves the performance better than the computations on a single node.