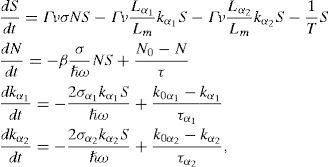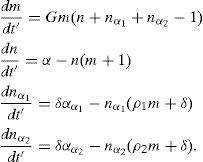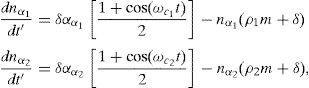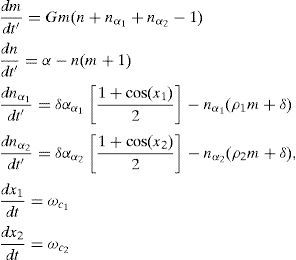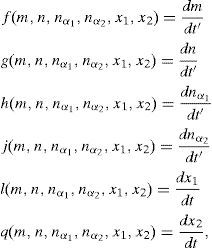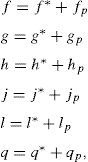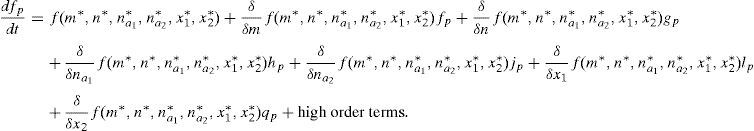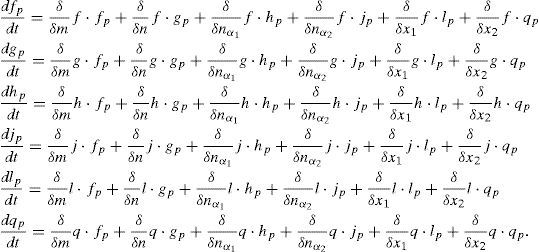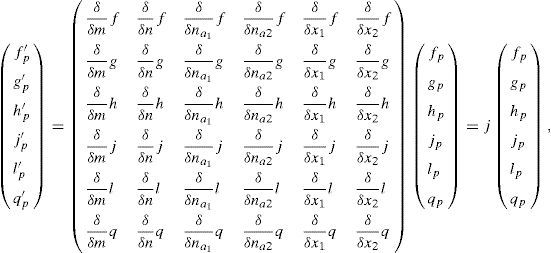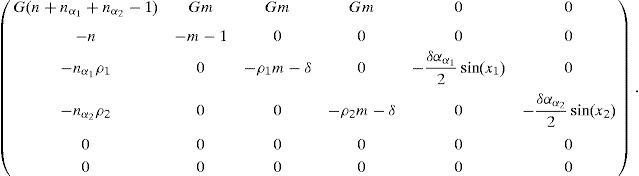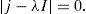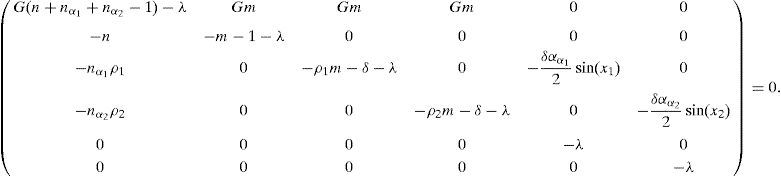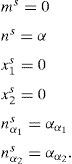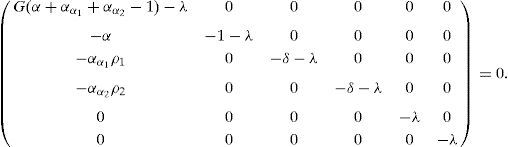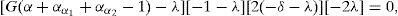Stability analysis of a laser with two modulated saturable absorbers

Abstract

The stability analysis of a model for a laser system with two modulated saturable absorbers, each one modulated at a different frequency, is performed. The model is based on four equations describing the temporal evolution of the photon flux, the population inversion in the active media, and the saturation coefficients of each saturable absorber. The system dynamics is discussed in order to find stable system control regions.

1

Introduction

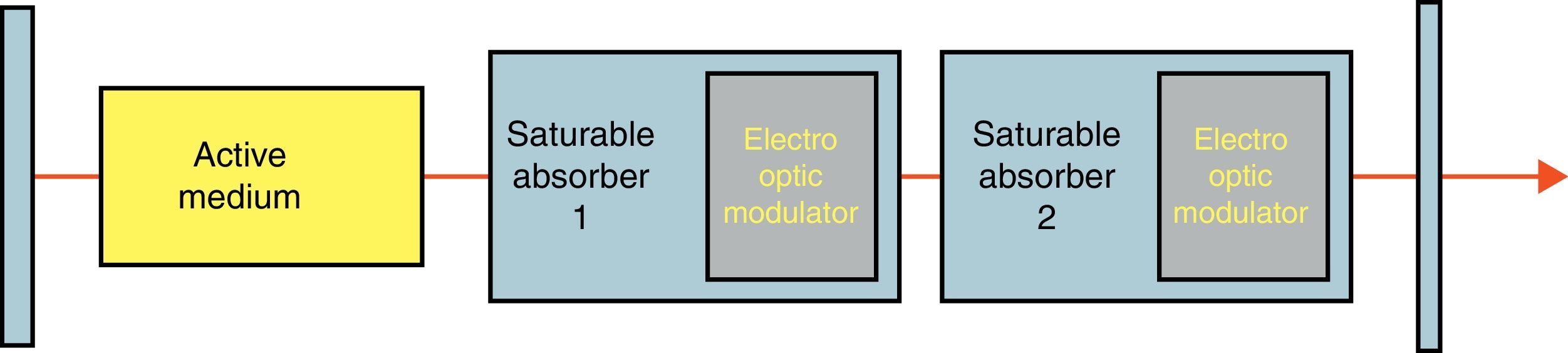
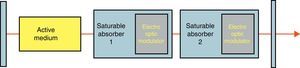
The dynamics of a laser system with two saturable absorbers (see Fig. 1) can be described by a model based on the Statz–DeMars equations, which originally were developed to describe oscillations in a Maser (Statz & DeMars, 1960). This model has undergone many modifications to be adopted for laser systems (Tarassov, 1985; Tang & Statz, 1963; Thompson & Malacara, 2001). For a complete phenomenological description of a laser with two saturable absorbers, only four equations are needed: the photon-flux equation, an equation for the population inversion density in the active medium and two saturable population inversion equations that give the saturation coefficient for each saturable absorber (Wilson & Aboites, 2013). Therefore, the Statz–DeMars equations for a three level laser system with two saturable absorbers without modulation are written as follows:

where S is the emitted photon density, N is the population inversion of the active medium, kα1 and kα2 are the resonant absorptions of the saturable absorbers 1 and 2 respectively, σα1 and σα2 are the saturable absorbers cross-sections, and Nα1 and Nα2 are the population inversions of the saturable absorbers (kα1=−σα1Nα1 and kα2=−σα2Nα2). Γ, ν, σ and T stand, respectively, for cavity filling coefficient, optical frequency, active medium cross-section and photon lifetime in the cavity; β is the coefficient which accounts for the difference in population inversion coursed by lasing; Lm, Lα1 and Lα2 are, respectively, the active medium and the saturable absorbers lengths; k0α1 and k0α2 are the linear resonant saturable absorbers absorption coefficients without lasing; N0 is the population inversion in the active medium without radiation; τ, τα1 and τα2 stand for relaxation time in the active medium and in the saturable absorbers, respectively; finally, ℏω is the photon energy (Aboites & Ramírez, 1989).

Fig. 1.

Three-level laser system with two saturable absorbers with electro-optic modulators.

Assuming that the two saturable absorbers have equal relaxation times (τα1=τα2=τα), and defining the next adimensional parameters and variables: t′=t/τ, G=τ/t, δ=τ/τα, ρ1=2σα1/βσ, ρ2=2σα2/βσ, α=ΓνσTN and αα1=−ΓνTk0α1Lα1/Lm=−ΓνTσα1nα1/Lm, αα2=−ΓνTk0α2Lα2/Lm=−ΓνTσα2nα2/Lm; n(t′)=ΓνσTN(t′), nα1(t′)=−ΓνTkα1(t′)Lα1/Lm, nα1(t′)=−ΓνTkα2(t′)Lα2/Lm and n(t′)=βBτS(t′)/ν=βστS(t′)/ℏω, the above system can be rewritten as:

All the parameters used to define the saturable absorbers are fixed, except for αα1 and αα2, which include a measure of the active center absorbent density; for this reason, αα1 and αα2 are used as the saturable absorber identifying parameters. Adding an external linear sinusoidal modulation (e.g. using an Electro Optic Modulator (EOM)) directly into the saturable absorbers through their main parameter (i.e. αα1 and αα2), the last two above equations may be transformed into

where ωc1 and ωc2 stand for the external modulation frequencies applied to the EOM. These four differential equations compose the working system. It must be noted that in absence of a modulation frequency applied to the EOM, ωc1 and ωc2, the system returns to Eq. (2), i.e. rate equations for a laser with two passive saturable absorbers (Wilson, Aboites, Pisarchik, Pinto, & Barmenkov, 2011).

2

Linear Stability Analysis

Linear Stability Analysis is used to understand the system dynamics (Tabor, 1989; Braun, 1992). The analysis is based on the linear disturbance equations; these equations are derived from the original equations (Pinto Robledo et al., 2012). As it is well known, the method consists in linearizing the describing equations, obtaining the initial state condition (i.e. when the derivatives are zero), expanding the system about the initial state condition, constructing the Jacobian matrix, and finding the eigenvectors and eigenvalues with a determinant equal to zero. This gives, as a result, the fixed points of the equation system, which must be analyzed in order to know what type of points there are (i.e. fixed, source, saddle, etc.) (Wilson, Aboites, Pisarchik, Ruiz-Oliveras, & Taki, 2011; Wilson, Aboites, Pisarchik, Pinto, & Taki, 2011). The equations of interest are Eqs. (2) and (3); these equations are non-autonomous due to the explicit time-dependence found in the cosine of the third and fourth expressions. To be able to perform the Linear Stability Analysis, those dependences must be eliminated; to do that, variable changes must be applied, yielding, the next equation system:

Naming Eq. (4) as:

and assuming that (m*,n*,nα1*,nα2*,x1*,x2*) is the steady state, that is, f(m*,n*,nα1*,nα2*,x1*,x2*)=0, g(m*,n*,nα1*,nα2*,x1*,x2*)=0, h(m*,n*,nα1*,nα2*,x1*,x2*)=0, j(m*,n*,nα1*,nα2*,x1*,x2*)=0, l(m*,n*,nα1*,nα2*,x1*,x2*)=0, and q(m*,n*,nα1*,nα2*,x1*,x2*)=0, then in order to find whether the steady state is stable or unstable, a small perturbation (represented by the subscript p) must be added to it,

With (fp,gp,hp,jp,lp,qp)≪1

Now, the main question for practical purposes is whether will the perturbations grow (steady state unstable) or decay (steady state stable). To be able to observe whether the perturbations grow or decay, the perturbation derivatives must be found (Wilson, Aboites, Pisarchik, et al., 2011).

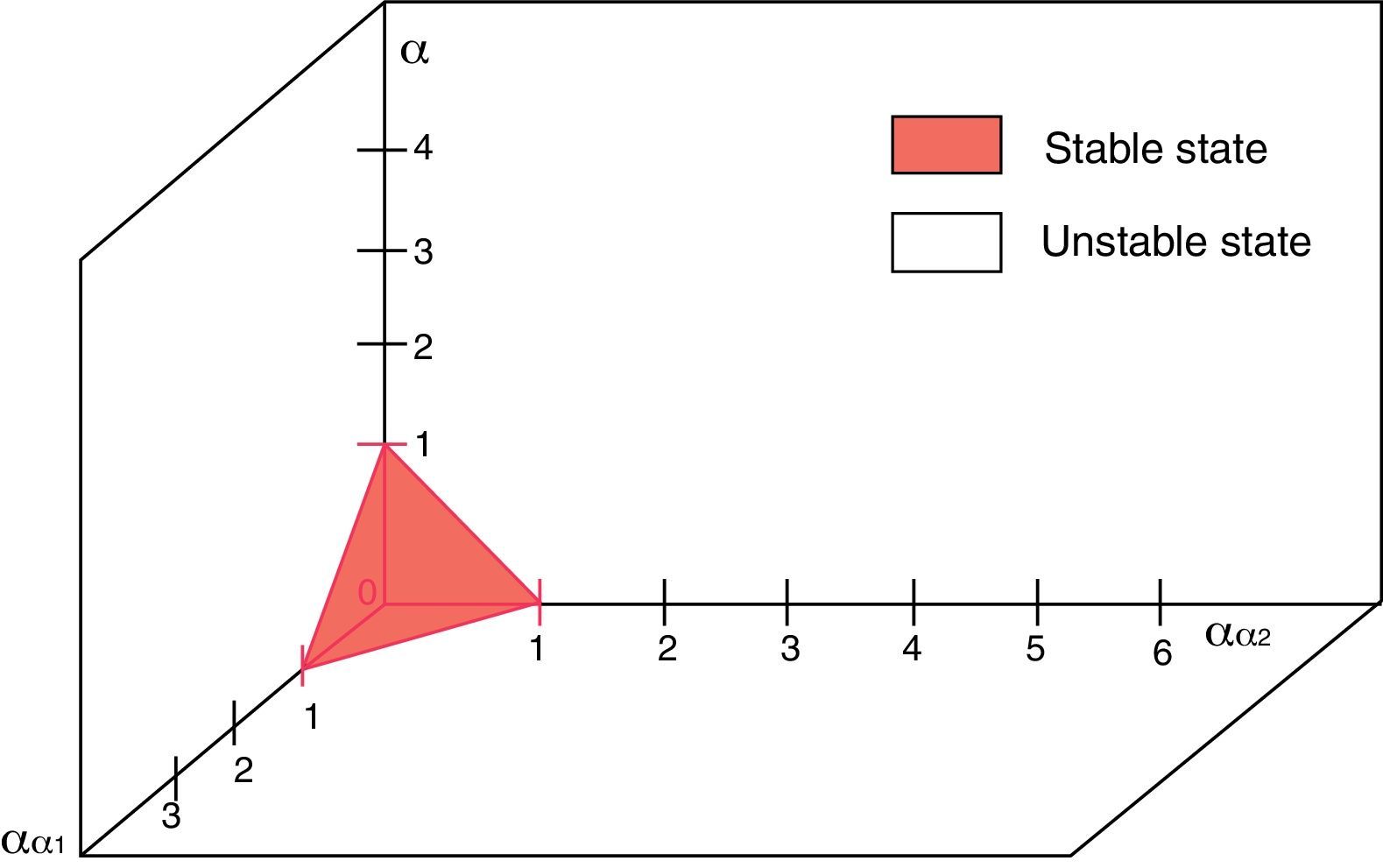
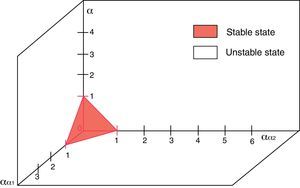
Following the Taylor series expansion shown in Eq. (7) the derivatives for each perturbation are:

The system presented in Eq. (8) can be rewritten in the matrix form:

where j denotes the Jacobian matrix of the original system at the steady state. Substituting the values in the Jacobian function, the next matrix is obtained:

The next step is to find the eigenvectors and eigenvalues of the system (j−λI)∂p=0; so, the determinant would be:

The matrix for the former equation is:

The solutions for the perturbed steady-state of the original system are:

Substituting the former solutions in Eq. (12), the matrix transforms into:

Matrix (14) has the following characteristic equation:

where λ1=G(α+αα1+αα2−1), λ2=−1, λ3=−δ, λ4=−δ, λ5=0 and λ6=0 are eigenvalues which are all real; λ2, λ3 and λ4 are always negative (i.e. the perturbation will decay), and λ5 and λ6 are critically stable. Therefore, the stability condition is defined only by the sign of λ1, i.e. the fixed point is a source when (αα1+αα2+α)>1, as shown in Figure 2.

Fig. 2.

Stability condition given by the relation between αα1, αα2 and α.

3

Conclusions

The stability analysis of the model for a laser system with two modulated saturable absorbers is performed. The model is based on four equations describing the temporal evolution of the photon flux, the population inversion in the active media, and the saturation coefficients of the two saturable absorbers. The stability condition of the systems is found to depend only on the sign of the first eigenvalue of the system λ. As it is graphically shown, the stability conditions are given by the relation between α, αα1 and αα2.

Conflict of interest

The authors have no conflicts of interest to declare.