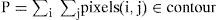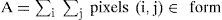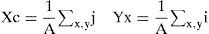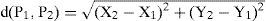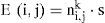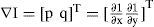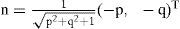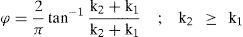Using Object’s Contour, Form and Depth to Embed Recognition Capability into Industrial Robots

Abstract

Robot vision systems can differentiate parts by pattern matching irrespective of part orientation and location. Some manufacturers offer 3D guidance systems using robust vision and laser systems so that a 3D programmed point can be repeated even if the part is moved varying its location, rotation and orientation within the working space. Despite these developments, current industrial robots are still unable to recognize objects in a robust manner; that is, to distinguish an object among equally shaped objects taking into account not only the object’s contour but also its form and depth information, which is precisely the major contribution of this research. Our hypothesis establishes that it is possible to integrate a robust invariant object recognition capability into industrial robots by using image features from the object’s contour (boundary object information), its form (i.e., type of curvature or topographical surface information) and depth information (from stereo disparity maps). These features can be concatenated in order to form an invariant vector descriptor which is the input to an artificial neural network (ANN) for learning and recognition purposes. In this paper we present the recognition results under different working conditions using a KUKA KR16 industrial robot, which validated our approach.

Resumen

Los sistemas de visión para robots pueden diferenciar partes mediante el apareamiento de patrones sin considerar su orientación o localización. Algunos fabricantes ofrecen sistemas de guiado 3D utilizando sistemas robustos de visión y laser, de tal forma que un punto programado puede ser repetido aún si la parte se ha movido cambiando su orientación, localización o rotación dentro del espacio de trabajo. A pesar de estos desarrollos, los robots industriales actuales son todavía incapaces de reconocer objetos de manera robusta; esto es, distinguir un objeto de entre varios objetos similares tomando información no solo de su contorno, sino también su forma y profundidad, lo que se constituye la contribución principal de esta investigación. Nuestra hipótesis establece que es posible integrar la capacidad de reconocimiento invariante de objetos en robots industriales mediante el uso de características de contorno del objeto (información de la frontera del objeto), su forma (i.e., tipo de curvatura o información topográfica de la superficie) e información de profundidad (mediante mapas estéreo de disparidad). Estas características pueden ser concatenadas para formar un vector descriptivo que sea presentado a la entrada de una red neuronal artificial (RNA) para propósitos de aprendizaje y reconocimiento. En este artículo presentamos los resultados de reconocimiento para diferentes condiciones de trabajo empleando un robot industrial KUKA KR16, lo que valida nuestro enfoque.

1

Introduction

Industrial robots are not equipped with a built-in object recognition capability in its standard version, but as an option. Robot vision systems can differentiate parts by pattern matching irrespective of part orientation and location and even some manufacturers offer 3D guidance using robust vision and laser systems so that a 3D programmed point can be repeated even if the part is moved varying its rotation and orientation within the working space. Despite these developments, current industrial robots are still unable to recognise objects in a robust manner; that is, to distinguish among equally shaped objects under different lighting conditions unless an alternative method is used. When the objects within the workspace have different shapes and the area is well illuminated, the recognition task is relatively simple; however, the task becomes complicated when objects are identical or similar in shape but with slightly different form. The form of a piece can be thought of a three-dimensional feature that includes the shape and also its depth. In this work, we present an original approach to solve the problem of recognizing a specific object using three main algorithms: BOF (boundary object function), SFS (shape from shading) and to estimate the object’s height, the use of stereo vision algorithms. The information is concatenated into an input vector with an artificial neural network (ANN) which determines the object’s type and depth information in order to provide the information to the manipulator for selection and grasping purposes.

In this article, after presenting related and original work in Section 2, the contour vector description (BOF), the SFS vector and the stereo disparity map (Depth) are explained in Sections 3, 4 and 5, respectively. A description of the learning algorithm using the FuzzyARTMAP ANN is given in Section 6, whereas the employed testbed is described in Section 7, followed by Section 8 that describes the results considering the recognition rates of the algorithm and some grasping tasks using an industrial manipulator. Finally, conclusions and future work are described in Section 9.

2

Related work

Some authors have contributed with techniques for invariant pattern classification using classical methods such as invariant moments [1]; artificial intelligence techniques, as used by CemYüceer & Kemal Oflazer [2], which describe a hybrid pattern classification system based on a pattern preprocessor and an ANN invariant to rotation, scaling and translation. Stavros J. & Paulo Lisboa developed a method to reduce and control the number of weights of a third-order network using moment classifiers [3] and Shingchern D. You & G. Ford, 1994) proposed a network for invariant object recognition of objects in binary images using four subnetworks [4]. Montenegro used the Hough transform to invariantly recognize rectangular objects (chocolates) including simple defects [5]. This was achieved by using the polar properties of the Hough transform, which uses the Euclidian distance to classify the descriptive vector. This method showed to be robust with geometric figures, however for complex objects it would require more information coming from other techniques such as histogram information or information coming from images with different illumination sources and levels. Gonzalez et al. used a Fourier descriptor, which obtains image features through silhouettes from 3D objects [6]. Their method is based on the extraction of silhouettes from 3D images obtained by laser scanning, which increases recognition times.

Another interesting method for 2D invariant object representation is the use of the compactness measure of a shape, sometimes called the shape factor, which is a numerical quantity representing the degree to which a shape is compact. Relevant work in this area within the theory of shape numbers was proposed by Bribiesca and Guzman [7].

Worthington studied topographical information from image intensity data in grey scale using the shape from shading (SFS) algorithm [8]. This information is used for object recognition. It is considered that the shape index information can be used for object recognition based on the surface curvature. Two attributes were used, one was based on low-level information using a curvature histogram, and the other was based on the structural arrangement of the shape index maximal patches and its attributes in the associated region.

Lowe defines a descriptor vector named SIFT (Scale Invariant Feature Transform), which is an algorithm that detects distinctive image points and calculates its descriptor based on the orientation histograms of the encountered key points [9]. The extracted points are invariants to scale, rotation as well as source and illumination level changes. These points are located within a maximum and minimum of a Gaussian difference applied to the space scale. This algorithm is very efficient, but the processing time is relatively high and furthermore the working pieces have to have a rich texture.

M. Peña et al. [10] introduced a method that finds the centroid, orientation, edges of parts, among other characteristics for the object recognition system. This method consists primarily in determining the distance from the centroid to the object perimeter, making a sweep angle that generates a descriptive vector called Boundary Object Function (BOF), which is classified by an ANN. However, its scope was limited only to 2D invariant object recognition. The above mentioned methods are summarised in Table 1.

Table 1.

Some techniques for invariant object recognition.

Technique	Authors	Year
Moment invariants	Hu	1962
Compactness measure of a shape	Bribiesca and Guzman	1980
Moment classifiers and ANN	Perantonis and Lisboa	1992
Preprocessing using translational, scale and rotational blocks	CemYüceer and KemaOflazer	1993
Four subnetworks (Radon and rapid transform)	You and Ford	1994
Shape from shading (topographical information)	Worthington and Hancock	2001
Fourier descriptor	Gonzalez, et al.	2004
Scale Invariant Feature Transform	Lowe	2004
Boundary Object Function (BOF)	Pena et al.	2005
Hough Transform	Montenegro	2006

2.1

Original work and main contribution

Classic algorithms such as moment invariants are popular descriptors for image regions and boundary segments; however, computation of moments of a 2D image involves a significant amount of multiplications and additions in a direct method. In many real-time industrial applications, the speed of computation is very important, the 2D moment computation is intensive and involves parallel processing, which can become the bottleneck of the system when moments are used as major features. In addition to this limitation, observing only the piece’s contour is not enough to recognize an object since objects with the same contour can still be confused.

In order to cope with this limitation, in this paper a novel method that includes a parameter about the piece contour (BOF), the shape of the object’s curvature as its form (SFS) and the depth information from the stereo disparity map (Depth) is presented as main contribution.

The BOF algorithm determines the distance from the centroid to the object’s perimeter and the SFS calculates the curvature of the way that light is reflected on parts, whereas the depth information is useful to differentiate similar objects with different height. These features (contour, form and depth) are concatenated in order to form an invariant vector descriptor which is the input to an artificial neural network (ANN).

3

Object’s contour

As mentioned earlier, the Boundary Object Function (BOF) method considers only the object’s contour to recognise different objects. It is very important to obtain as accurately as possible, metric properties such as area, perimeter, centroid point, and distance from the centroid to the points of the contour of the object. In this section, a description of the BOF method is presented.

3.1

Metric properties

The metric properties for the algorithm are based on the Euclidean distance between two points in the image plane. The first step is to find the object in the image performing a pixel-level scan from top to bottom (first criterion) and left to right (second criterion). For instance, if an object in the image plane is higher than the others, this object will be considered first. In the event that all objects are from the same height, then the second criterion applies and the selected object will be the one located more to the left.

3.1.1

Perimeter

The definition of perimeter is the set of points that make up the shape of the object, in discrete form and is the sum of all pixels that lie on the contour, which can be expressed as:

where contour is formed by pixels from the object’s border.

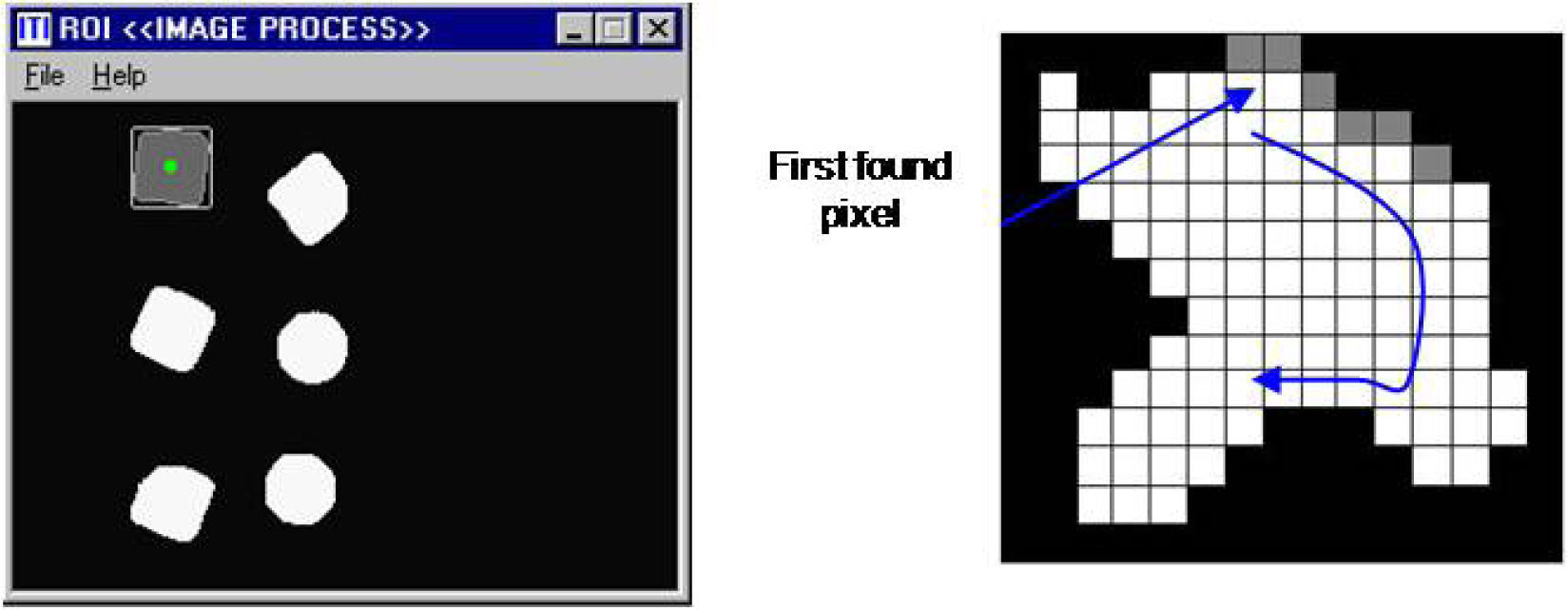
Equation (1) shows how to calculate the perimeter; the problem lies in finding which pixels in the image belong to the perimeter. For searching purposes, the system calculates the perimeter obtaining the number of points around a piece grouping X and Y points coordinates corresponding to the perimeter of the measured piece in clockwise direction. The perimeter calculation for every piece in the region of interest (ROI) is performed after the binarization. Search is always accomplished, as mentioned earlier, from top to bottom and left to right. Once a white pixel is found, all the perimeter is calculated with a search function as it is shown in Figure 1.

Figure 1.

Perimeter calculation of a workpiece.

The next definitions are useful to understand the algorithm:

• •

  A nearer pixel to the boundary is any pixel surrounded mostly by black pixels in 8-connectivity.

• •

  A farther pixel to the boundary is any pixel that is not surrounded by black pixels in 8-connectivity.

• •

  The highest and lowest coordinates are the ones that create a rectangle (boundary box).

The search algorithm executes the following procedures once it has found a white pixel:

• 1

  Searches for the nearer pixel to the boundary that has not been already located.

• 2

  Assigns the label of actual pixel to the nearer pixel to the boundary recently found.

• 3

  Paints the last pixel as a visited pixel.

• 4

  If the new coordinates are higher than the last higher coordinates, the new values are assigned to the higher coordinates.

• 5

  If the new coordinates are lower than the last lower coordinates, the new values are assigned to the lower coordinates.

• 6

  Steps 1 to 5 are repeated until the procedure returns to the initial point, or no other nearer pixel to the boundary is found.

This technique will surround any irregular shape very fast and will not process useless pixels of the image.

3.1.1

Area

The area of an object is defined as the space between a region, in other words, the sum of all pixels that form the object, which can be defined by Equation (2):

where form is defined as all pixels (i,j) = 1 inside the ROI, in a binarized image.

3.1.2

Centroid

The center of mass of an arbitrary shape is a pair of coordinates (X_c, Y_c) in which all its mass is considered concentrated and on which all the resultant forces are acting on. In other words it is the point where a single support can balance the object. Mathematically, in the discrete domain, the centroid is defined as:

where A is obtained from Equation (2).

3.2

Generation of the descriptive vector

The generation of the descriptive vector called The Boundary Object Function (BOF) is based on the Euclidean distance between the object’s centroid and the contour [10]. If we assume that P₁(X₁, Y₁) are the centroid coordinates (Xc, Yc) and P₂(X₂, Y₂) is a point on the perimeter, then this distance is determined by the following equation:

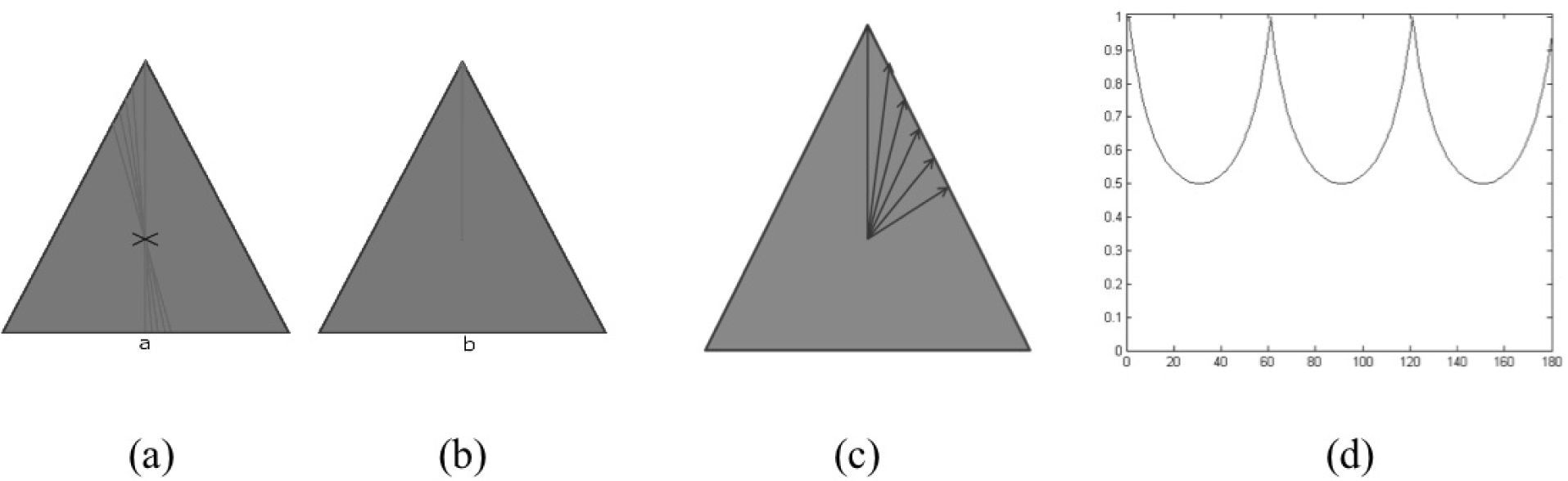
The descriptive vector (BOF) in 2D contains the distance calculated in eq. (4) for the whole object’s contour. The vector is composed by 180 elements where each element represents the distance data collected every two degrees. The vector is normalized by dividing all the vector elements by the element with maximum value. Figure 2 shows an example where the object is a triangle. In general, the starting point for the vector generation is crucial, so the following rules apply: the first step is to find the longest line passing through the center of the piece, as shown in Figure 2(a), there are several lines. The longest line is taken and divided by two, taking the center of the object as reference. Thus, the longest middle part of the line is taken as shown in Figure 2(b) and this is taken as starting point for the BOF vector descriptor generation as shown in Figure 2(c). The object’s pattern representation is depicted in Figure 2(d).

Figure 2.

Example for the generation of the BOF vector.

4

Object’s form

The use of shading is taught in art class as an important cue to convey 3D shape in a 2D image. Smooth objects, such as an apple, often present a highlight at points where a reception from the light source makes equal angles with reflection toward the viewer. At the same time, smooth object get increasingly darker as the surface normal becomes perpendicular to rays of illumination. Planarsurfaces tend to have a homogeneous appearance in the image with intensity proportional to the angle between the normal to the plane and the rays of illumination. In other words, the Shape From Shading algorithm (SFS) is the process of obtaining three-dimensional surface shape from the reflection of light in a greyscale image. It consists primarily of obtaining the orientation of the surface due to local variations in brightness that is reflected by the object, and the intensities of the greyscale image are taken as a topographic surface.

In the 70’s, Horn formulated the problem of Shape From Shading finding the solution of the equation of brightness or reflectance trying to find a single solution [11]. Today, the issue of Shape from Shading is known as an ill-posed problem, as mentioned by Brooks, causing ambiguity between what has a concave and convex surface, which is due to changes in lighting parameters [12]. To solve the problem, it is important to study how the image is formed, as mentioned by Zhang [13]. A simple model of the formation of an image is the Lambertian model, where the grey value in the pixels of the image depends on the direction of light and surface normal. So, if we assume a Lambertian reflection, we know that the direction of light and brightness can be described as a function of the object surface and the direction of light, and then the problem becomes a little simpler.

The algorithm consists in finding the gradient of the surface to determine the normals. The gradient is perpendicular to the normals and appears in the reflectance cone whose center is given by the direction of light. A smoothing operation is performed so that the normal direction of the local regions is not very uneven. When this is performed, some normals still lie outside of the normal cone reflectance, so that it is necessary to rotate and place them within the cone. This is an iterative process to finally obtain the kind of local surface curvature.

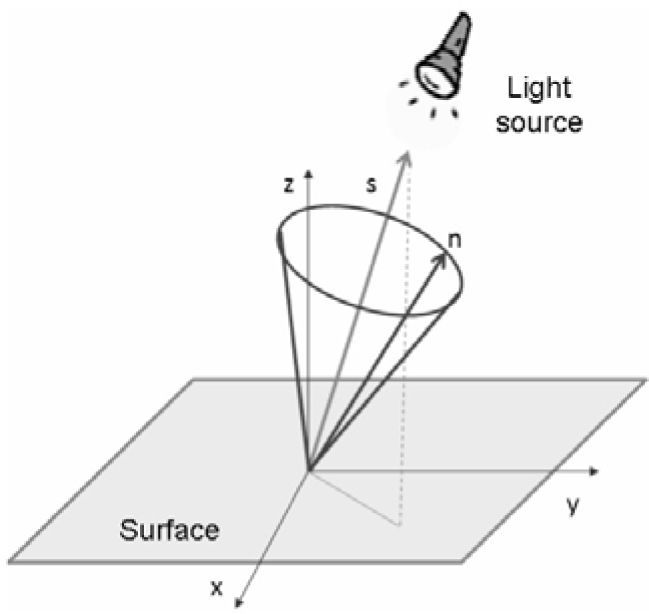
The procedure is as follows, first the light reflectance E in (i, j), is calculated using the expression:

where: S is the unit vector for the light direction, and the term ni,jk is the normal estimation in the K^th iteration. The reflectance equation of the image is defined by a cone of possible normal directions to the surface as shown in Figure 3 where the reflectance cone has an angle of cos^-1(E(i,j)).

Figure 3.

Possible normal directions to the surface over the reflectance cone.

If the normals satisfy the recovered reflectance equation of the image, then these normals must fall on their respective reflectance cones.

4.1

Image’s gradient

The first step is to calculate the surface normals which are calculated using the gradient of the image (I), as shown in Equation (6).

(6) Where [p q] are used to obtain the gradient and are known as Sobel operators.

4.2

Normals

Since the normals are perpendicular to the tangents, the tangents can be found by the cross product, which is parallel to (-p, -q, 1)^T. Then we can write for the normal expression:

Assuming that the z component of the normal to the surface is positive.

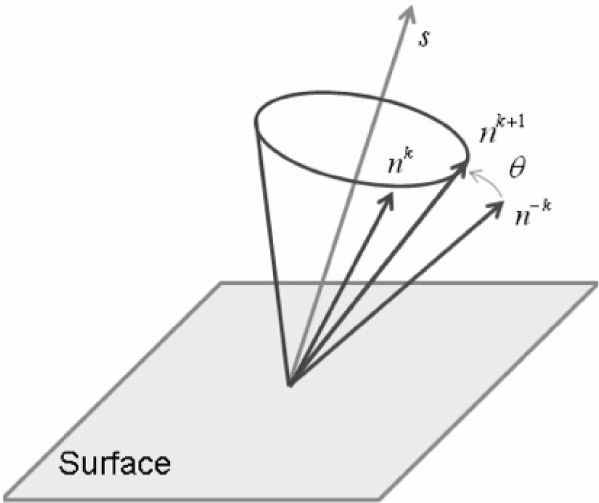
4.3

Smoothness and rotation

Smoothing, in few words can be described as avoiding abrupt changes between normal and adjacent. The Sigmoidal Smoothness Constraint makes the restriction of smoothness or regularization, forcing the error of brightness to satisfy the matrix rotation θ, deterring sudden changes in direction of the normal through the surface.

With the normal smoothed, then the next step is to rotate these normals so that they lie in the reflectance cone as shown in Figure 4.

Figure 4.

Normals rotation within the reflectance cone.

Where ni,jk are the smoothed normals, ni,j-k are the normals after the smoothness and before the rotation, and ni,jk+1 are the normals after a rotation of θ degrees. The smoothness and rotation of the normals involve several iterations represented by the letter k.

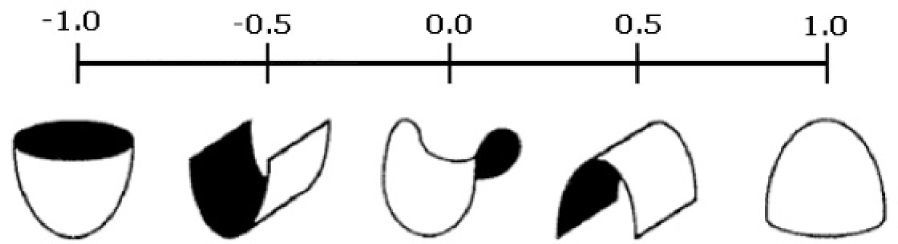
4.4

Shape index

Koenderink separated the shape index in different regions depending on the type of curvature, which is obtained through the eigenvalues of the Hessian matrix, which is represented by K₁ and K₂ as given by-the-following-Equation-[14].

The result of the shape index φ has values between [-1, 1] which can be classified, according to Koenderink, depending on its local topography, as shown in Table 2.

Table 2.

Classification of the Shape Index.

Cup	Rut	Saddle rut	Saddle Point	Plane	Saddle Ridge	Ridge	Dome
-1,-58	-58,-38	-38,-18	-18,-18	---	18,38	38,58	58,1

Figure 5 shows the image from the surface local form depending on the value of the Shape Index, and Figure 6 shows an example of the SFS vector.

Figure 5.

Representation of local forms in the Shape Index classification.

Figure 6.

Example of SFS Vector descriptor.

5

Histogram of disparity map (depth)

With binocular vision, the robot vision system is able to interact in a three-dimensional world coping with volume and distance within the environment. Due to the separation between both cameras, two images are obtained with small differences between them; such differences are called disparity and form a so-called disparity map. The epipolar geometry describes the geometric relationships of images formed in two or more cameras focused on a point or pole.

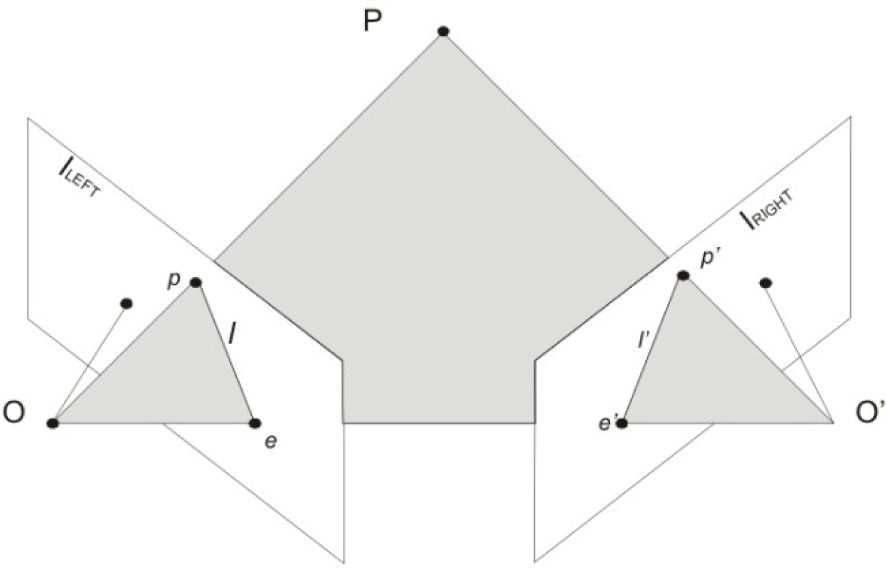
The most important elements for this geometric system as illustrated in Figure 7 are: the epipolar plane, consisting of the pole (P) and two optical centers (O and O’) from two chambers. The epipoles (e and e’) are the virtual images of the optical centers (O and O’). The baseline, which joins the two optical centers and epipolar lines (l and l’), formed by the intersection of the epipolar plane with both images (ILEFT and IRIGHT), connects the epipoles with the image of the observed points (p, p’).

Figure 7.

Elements of epipolar geometry.

The epipolar line is crucial in stereoscopic vision, because one of the most difficult parts of the stereoscopic analysis is the one related to establishing the correspondence between two images, mating stereo, deciding which point in the right image corresponds to which on the left. The epipolar constraint allows you to narrow the search for stereoscopic, correspondence of two-dimensional (whole image) to a search in a dimension on the epipolar line.

One way to further simplify the calculations associated with stereoscopic algorithms is the use of rectified images; that is, to replace the images by their equivalent projections on a common plane parallel to the baseline. It projects the image, choosing a suitable system of coordinates, the rectified epipolar lines are parallel to the baseline and they are converted to single-line exploration and p’, located on the same line of exploration the left image and right image, with coordinates (u, v) and (u’, v’), the disparity is given as the difference d = u’- u. If B is the distance between the optical centers, also known as baseline, it can be shown that the depth of P is z = −B / d.

5.1

Stereoscopic matching algorithms

The stereoscopic matching algorithm reproduces the human stereopsis process so that a machine, for instance a robot, can perceive the depth of each point in the observed scene and thus is able to manipulate objects, avoid or recreate three-dimensional models. For a pair of stereoscopic images, the main goal of these algorithms is to find for each pixel in an image its corresponding pixel in the other image (mating), in order to obtain a disparity map that contains the position difference for each pixel between two images which is proportional to the depth map. To determine the actual depth of the scene, it is necessary to take into account the geometry of the stereoscopic system to obtain a metric map. As mating a single pixel is almost impossible, each pixel is represented by a small region that contains it, a so-called window correlation, thereby realizing the correlation between the windows of one image and the other, using the colour of pixels within. Once the disparity map is obtained, then the histogram of this map is the region of interest.

6

Learning and recognition

It is the aim of this research to investigate ANN methods to embed intelligence into industrial robots for object recognition and learning in order to use these skills for grasping purposes. The selection of the ANN for this purpose was based on previous results where the convergence time for some ANN architectures was evaluated during recognition tasks of simple geometrical parts. The assessed networks were Backpropagation, Perceptron and Fuzzy ARTMAP using the BOF vector. Results showed that the FuzzyARTMAP network outperformed the other networks with lower training/testing times (0.838ms/0.0722ms) compared with Perceptron (5.78ms/0.159 ms) and Backpropagation (367.577ms/0.217 ms) [15].

The FuzzyARTMAP network is a supervised network based on the Adaptive Resonance Theory (ART) and whose implementation using the BOF was previously described in [10]. In this paper, we continue working in improving our method including not only the BOF vector, but also information about the surface from the object (SFS) and depth information from stereo vision that resulted in an improved performance as it is described later in the paper.

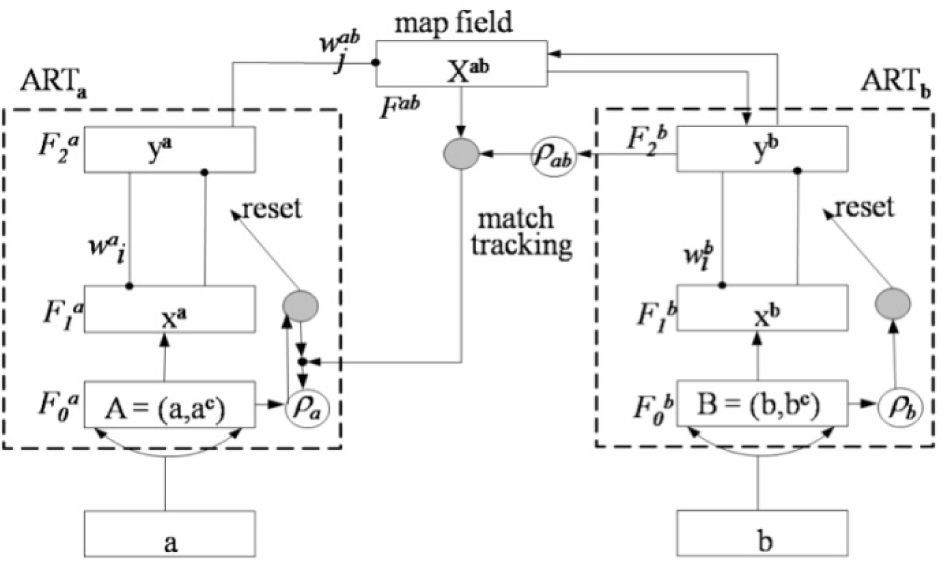
In the Fuzzy ARTMAP (FAM) network there are two modules ART_a and ART_b and an inter-ART “map field” module that controls the learning of an associative map from ART_a recognition categories to ART_b categories [16]. This is illustrated in Figure 8.

Figure 8.

FuzzyARTMAP architecture.

The map field module also controls the match tracking of ART_a vigilance parameter. A mismatch between map field and ART_a category activated by input I_a and ART_b category activated by input I_b increases ART_a vigilance by the minimum amount needed for the system to search for, and if necessary, learn a new ART_a category whose prediction matches the ART_b category. The search initiated by the inter-ART reset can shift attention to a novel cluster of features that can be incorporated through learning into a new ART_a recognition category, which can then be linked to a new ART prediction via associative learning at the map field.

A vigilance parameter measures the difference allowed between the input data and stored patterns. Therefore, this parameter affects the selectivity or granularity of the network prediction. For learning, the FuzzyARTMAP has 4 important factors: vigilance in the input module (ρ_a), vigilance in the output module (ρ_b), vigilance in the map field (ρ_ab) and learning rate (β).

For the specific case of the work presented in this article, the input information is concatenated and presented as a sole input vector A, while vector B receives the correspondence associated to the respective component, during the training process.

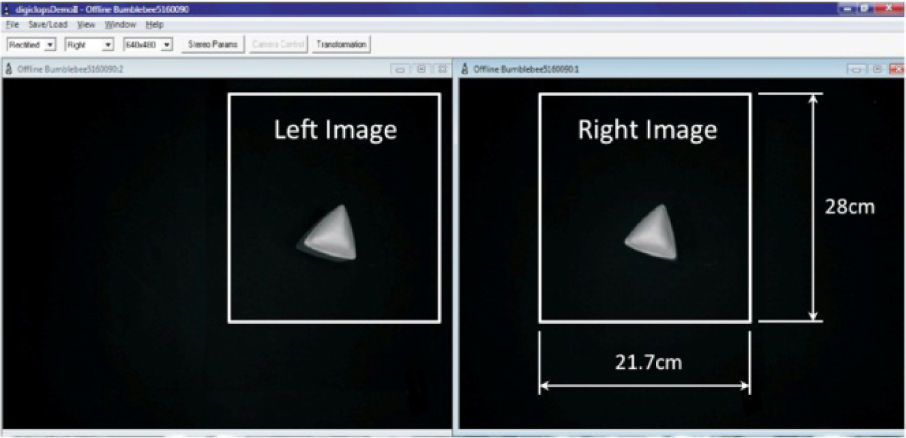
7

Robotics testbed

The robotic testbed is shown in Figure 9. It was integrated basically by a KUKA KR16 industrial robot, a Bumblebee stereo camera with 3.8mm focal length, 12cm baseline and 640 x 480 pixel resolution. The lighting consisted of 4 reflectors with a dimmer control to set the appropriate light intensity and a PC as a cell controller. The cell controller hosts the vision and position control algorithms. The communication between the cell controller and the KUKA robot is established via the serial port and is primarily intended to move the robot arm to the desired position for grasping; that is, closer to the centroid of the workpiece.

Figure 9.

Robotic testbed.

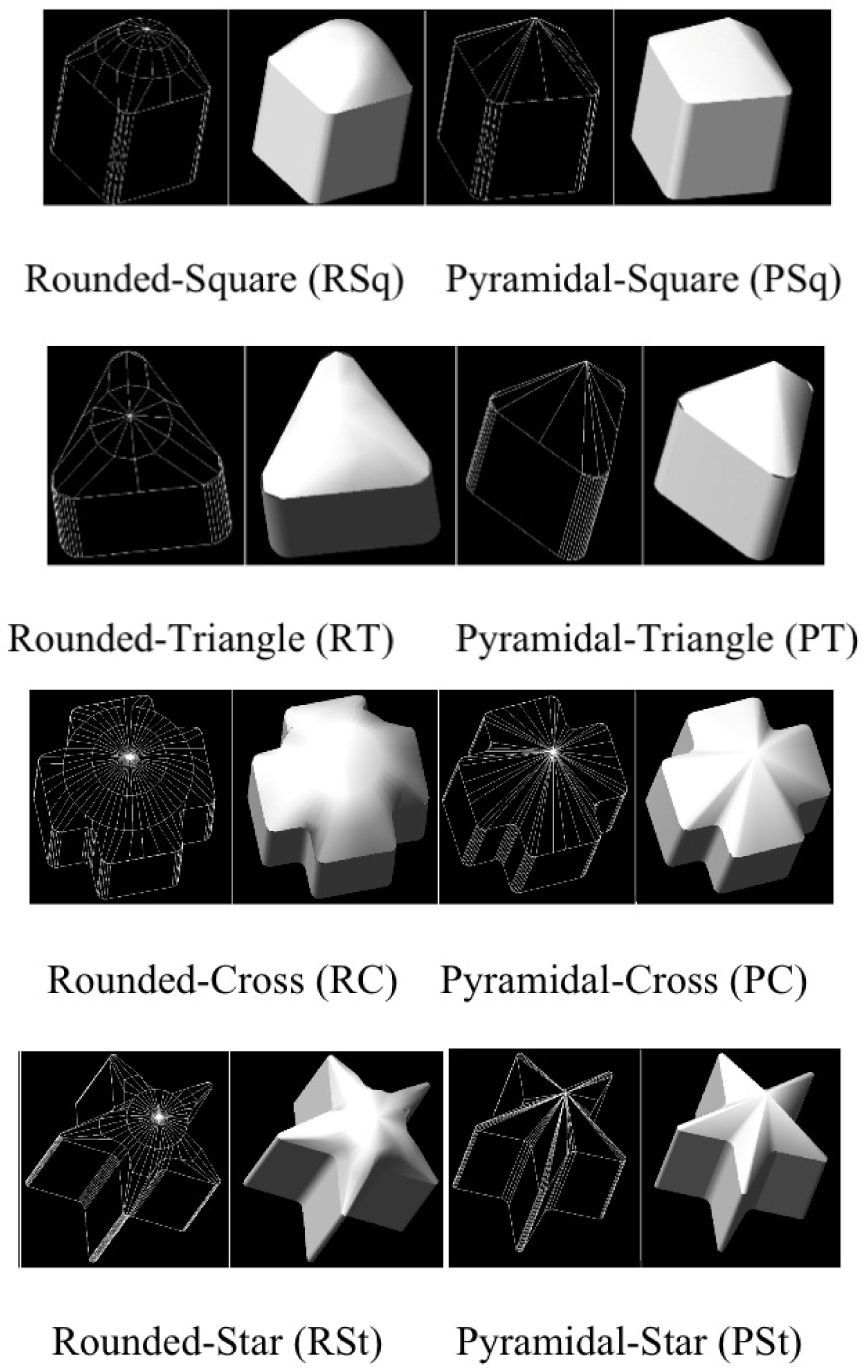
The experimental results were obtained using two sets of four 3D working pieces of different cross-section: square, triangle, cross and star. One set had its top surface rounded, so that these were referred to as being of rounded type. The other set had a flat top surface and referred to as pyramidal type. The working pieces are shown in Figure 10.

Figure 10.

Working pieces.

8

Experimental results

The total working space was defined by the field of view from both cameras as shown in Figure 11.

Figure 11.

Total working space.

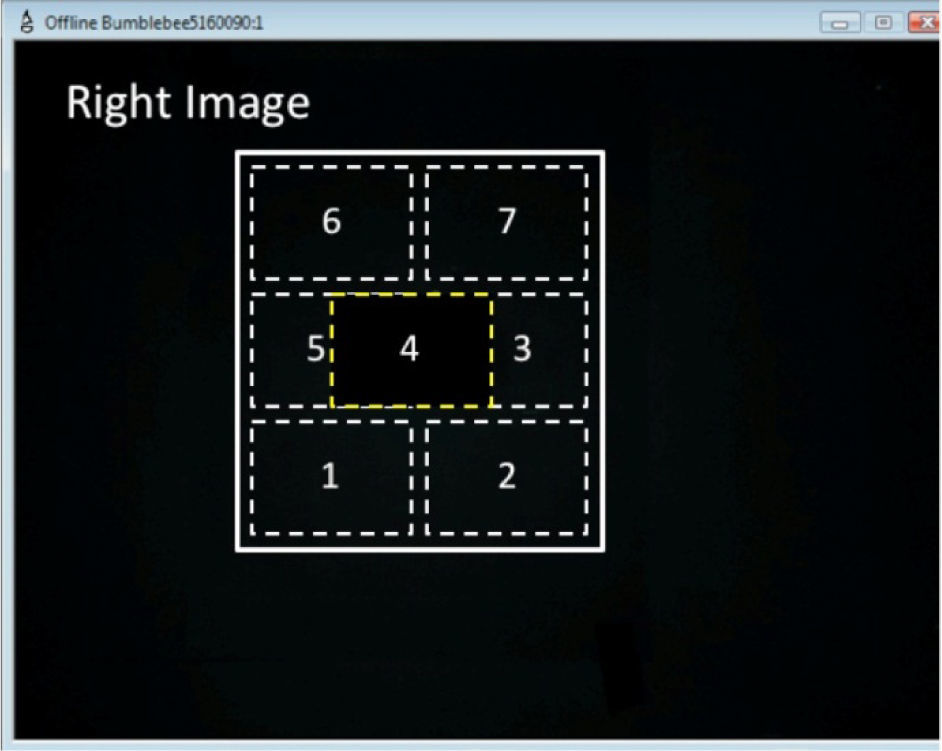
It was decided using the field of view from the right camera as working space for the whole set of experiments reported in this paper. This working space was further divided in six regions where the working pieces were located during training/testing stages as indicated in Figure 12.

Figure 12.

Effective working space.

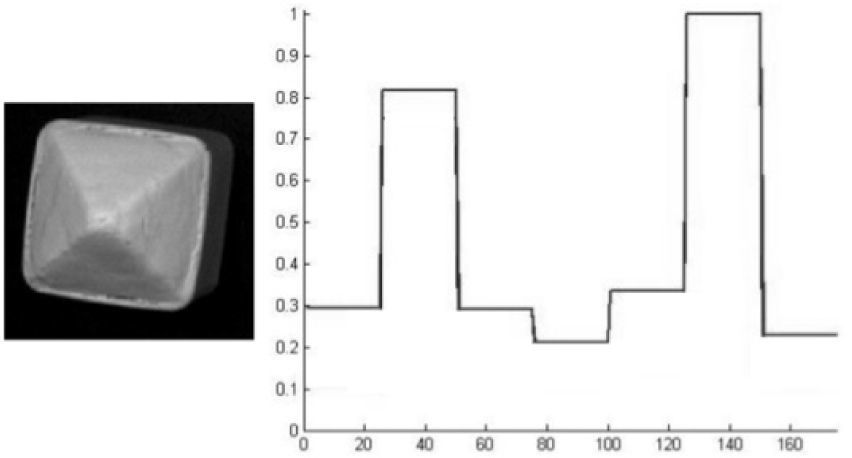
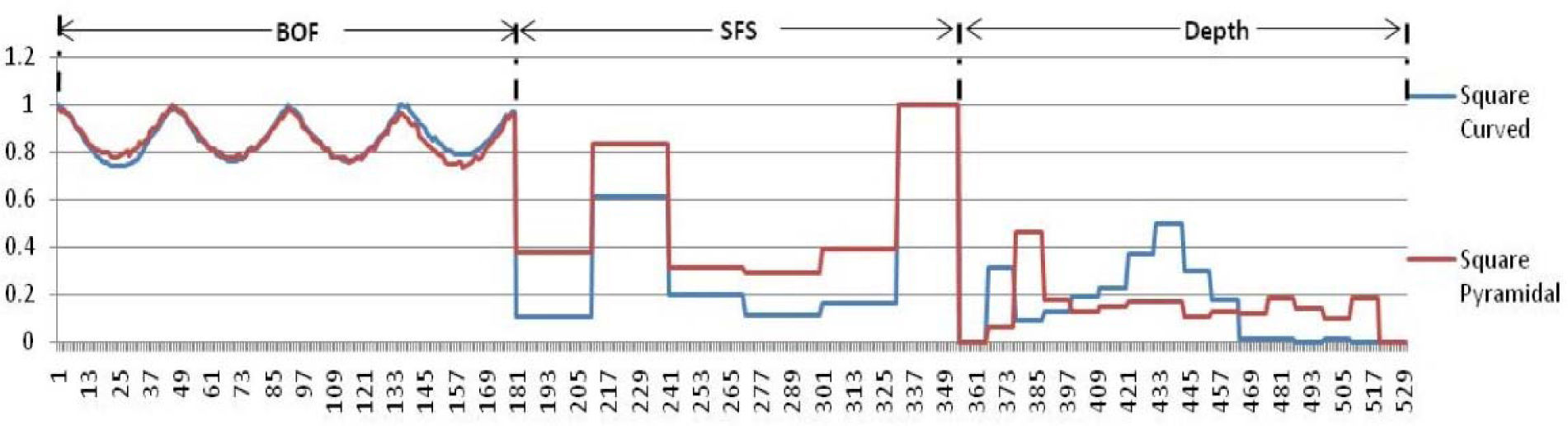
The object recognition experiments using the FuzzyARTMAP (FAM) neural network were carried out using the above working pieces. The network parameters were set for fast learning (β = 1), choice parameter α = 0.1, vigilance parameter (ρ_ab = 0.95) and three epochs. Four types of experiments were carried out. The first experiment considered only data from the contour of the piece (BOF), the second experiment took into account the reflectance of the light on the surface (SFS), the third experiment was performed using only depth information (Depth), and the fourth experiment used the concatenated vector from all three previous descriptors (BOF+SFS+Depth). An example of how an object was coded using the three descriptors is shown in Figure 13. Two graphs are presented; the first graph corresponds to the descriptive vector from the rounded square object and the other corresponds to the pyramidal square object. The BOF descriptive vector is formed by the 180 first elements (observe that both patterns are very similar since the object’s cross-sectional contour is the same). Following, there are 175 elements corresponding to the SFS values (every value corresponds to one of the seven shape index values repeated 25 times). The following 176 values corresponded to the depth information obtained from the disparity histogram that contained 16 values repeated 11 times each.

Figure 13.

Input vector example.

8.1

Recognition rates

Several experiments were defined to test the invariant object recognition capability of the system. For these experiments, the FuzzyARTMAP network was trained with 3 patterns for each working piece located in random areas within the workspace. The assessment during the testing phase was carried out during three different days and three different time intervals (9:00h, 13:00h and 18:00h). The objects were located in different orientations and locations within the defined working space using different size scale (by approaching the camera to the object) and using different slope value. These settings are summarized in Table 3.

Table 3.

Experimental settings.

Days	Time intervals	Locations	Scale levels (10%, 20%, 30%, 40%)	Slope degree (10º,15º, 20º, 25º)
3	3	6	4	4

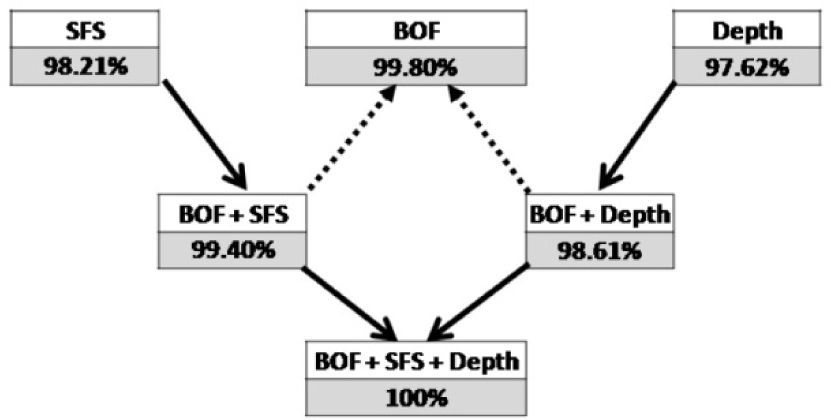
The overall recognition results under the above conditions are illustrated in Figure 14. The values from the first row correspond to the recognition rate using only the BOF, SFS, and depth vector. A high recognition rate was observed using each individual vector. Using only the BOF vector, the system was able to recognize 99.8%. Using the SFS vector, the system recognised 98.21% of pieces, and using depth information, 97.62%.

Figure 14.

Overall recognition results.

A second test was carried out by concatenating the BOF+SFS and the BOF+Depth. In both cases the recognition rate increased when compared with the use of the SFS or depth vector alone. However, the recognition rate was lower compared with the obtained results using the BOF vector only. This can be appreciated in the second row (also indicated by the dotted line).

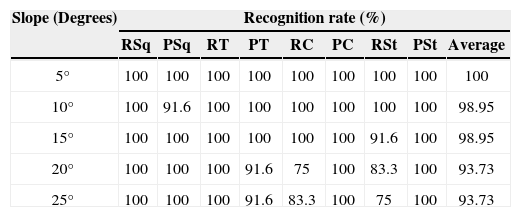
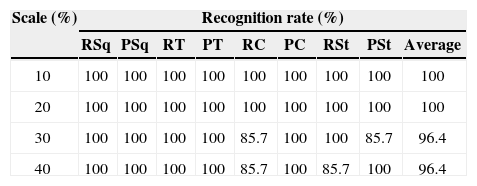
Finally, when testing the complete concatenated vector (BOF+SFS+Depth), the recognition rate increased to 100%. With the trained network, the robustness of the recognition system was tested at different scale factor and also using different inclination for the workspace. The obtained results are shown in Tables 4 and 5. From these results it can be stated that the network was able to recognize the whole set of workpieces up to an inclination of 5º. Increasing this value up to 15º, the system failed in few cases and above 15º the recognition rate decreased mainly because of an observed distortion in the BOF vector.

Table 4.

Recognition rate for the workpieces at different slope.

Slope (Degrees)	Recognition rate (%)
	RSq	PSq	RT	PT	RC	PC	RSt	PSt	Average
5°	100	100	100	100	100	100	100	100	100
10°	100	91.6	100	100	100	100	100	100	98.95
15°	100	100	100	100	100	100	91.6	100	98.95
20°	100	100	100	91.6	75	100	83.3	100	93.73
25°	100	100	100	91.6	83.3	100	75	100	93.73

Table 5.

Recognition rate for the workpieces at different scale.

Scale (%)	Recognition rate (%)
	RSq	PSq	RT	PT	RC	PC	RSt	PSt	Average
10	100	100	100	100	100	100	100	100	100
20	100	100	100	100	100	100	100	100	100
30	100	100	100	100	85.7	100	100	85.7	96.4
40	100	100	100	100	85.7	100	85.7	100	96.4

When varying the scale by approaching the camera, the system recognized the whole set of workpieces up to a 20% magnification.

8.2

Embedding the recognition capability

A further test was conducted involving the KUKA KR16 manipulator for grasping tasks with the aim of grasping the correct part between two similar shaped objects (Rounded-square and Pyramidal– Square). The 2D coordinates from the centroid was provided from the controller cell computer to the robot controller which ultimately moved the robot using incremental arm motions. The object center was taken from the optical center of the right camera. The Z-direction was obtained from the depth information provided by the stereo vision camera, which provided the object’s highest point. An additional offset in Z-axis was added to this value in order to secure a correct grasping by the robot. The experiment resulted satisfactory with the robot being able to correctly grasp the indicated workpiece: rounded or pyramidal.

9

Conclusions and future work

The research presented in this article provides an alternative methodology to integrate a robust invariant object recognition capability into industrial robots using image features from the object’s contour (boundary object information), its form (i.e., type of curvature or topographical surface information) and depth information from a stereo camera. The features can be concatenated in order to form an invariant vector descriptor which is the input to an artificial neural network (ANN) for learning and recognition purposes.

Experimental results were obtained using two sets of four 3D working pieces of different cross-section: square, triangle, cross and star. One set had its surface curvature rounded and the other had a flat surface curvature so that these objects were referred to as being of the pyramidal type.

Using the BOF information and training the neural network with this vector resulted in the whole set of pieces being recognized irrespective from its location an orientation within the viewable area. When information was concatenated (BOF + SFS and BOF + Depth), the robustness of the vision system lowered since the recognition rate in both cases was lower than using the BOF vector alone (99.4% and 98.61% respectively). However, when using the complete concatenated vector (BOF+SFS+Depth), this resulted in 100% recognition rate. The recognition was also invariant to a scaling up to 20% and also invariant to a slope change up to 50 for the whole set of working pieces. With higher inclination or scaling the recognition rate decreased.

Initial results from the object recognition system embedded in an industrial robot during grasping tasks envisaged future work in this direction. A limitation that we foresee is the setting of the camera fixed on top. A camera configuration, such as the hand-in-eye configuration and an automated light positioning system would improve the recognition tasks. It was recognized that both aspects can be improved and possibly with these settings the overall recognition rate can also be further improved.

Acknowledgements

The authors wish to thank the financial support provided by Consejo Nacional de Ciencia y Tecnología (CONACyT) through project research grant No. 61373.