Network topologies attract much theoretical attention in recent studies. Researchers adopt network topology models and assert that specific type of network topology improves product and process innovation. This study attempts to explore how network topology relates to product and process innovation in configurational terms. While this paper exploits interrelatedness between network topology configurations, and product and process innovation, it refers the firms outside contingencies obviously. Focusing on product and process innovation, outside contingencies rather than inside ones also make this paper natural to examine and contribute towards configurational theory.
Las topologías de red atraen mucha atención teorética en estudios recientes. Los investigadores adoptan nuevos modelos de topologías de red y afirman que el tipo específico de topología de red mejora la innovación del proceso y del producto. El estudio intenta explorar cómo la topología de red está relacionada con la innovación del proceso y del producto en términos de configuración. Aunque este ensayo explota la interrelación entre las configuraciones de la topología de red y la innovación del proceso y del producto, obviamente se refiere a las contingencias exteriores de las firmas. Centrándose en la innovación del proceso y del producto, en las contingencias exteriores en lugar de las interiores, también hace que sea natural para este ensayo examinar y contribuir a la teoría configuracional.
The social network is a theoretical construct useful in the social sciences to study relationships between individuals, groups, organizations, or even entire societies (social units, see differentiation). A social network is a social structure made up of individuals (or organizations) called nodes, which are tied (connected) by one or more specific types of interdependency, such as friendship, kinship, common interest, financial exchange, dislike, sexual relationships, or relationships of beliefs, knowledge or prestige. Most of the studies on network theory depend on network outputs; thus they are output-oriented studies. Why is network anatomy so important to characterize? Because structure always effects function. The topology of network affects the spread of activities. Recent theoretical research on macro networks focus on the properties of network topology (Fleming, King, & Juda, 2007; Watts & Strogatz, 1998; Watts, 1999; Watts, 2002; Yan & Assimakopoulos, 2009). Physicists and mathematicians expose three basic network topology models, small-world, random networks and scale-free networks (Barabasi & Albert, 1999; Newman, 2004; Watts & Strogatz, 1998), and they generate considerable interest from natural and social scientists alike. Many empirical research use these models and explore neuronal networks (Watts, 1999), biological networks (Koch & Laurent, 1999), scientific collaboration networks (Newman, 2004), e-mail networks (Ebel, Mielsch, & Bornholdt, 2002), telecommunications networks (Schintler, Gorman, Reggiani, Patuelli, & Nijkamp, 2003), airline transport networks (Guimerà, Mossa, Turtschi, & Amaral, 2005) and online communities (Adamic, Buyukokten, & Adar, 2003; Ravid & Rafaeli, 2004). For example in some kinds of networks information, innovation, and technology or vice versa can spread though society. This type of very famous network is known as “small-world networks” popularly known as “six-degrees of separation”.
The idea of a small-world network is that the world appears small considering the short distance of a path of friends that connects a person to almost anyone else. Small-world networks tend to contain cliques, and near-cliques, meaning sub-networks which have connections between almost any two nodes within them. This follows from the defining property of a high clustering coefficient. The clustering coefficient is a measure of an “all-my-friends-know-each-other” property. This is sometimes described as the friends of my friends are my friends. More precisely, the clustering coefficient of a node is the ratio of existing links connecting a node's neighbors to each other to the maximum possible number of such links. Secondly, most pairs of nodes will be connected by at least one short path. This follows from the defining property that the mean-shortest path length be small. As underlying the structure of network can be complex and several other network properties often associate with small-world networks, it is still difficult to summarize the whole small-world network succinctly.
Because the definition of networks is flexible, developing a language for talking about typical structure features of small-world networks will be an important step in understanding them. Structure of the small-world network is only starting point of this phenomenon, so researchers should detail who is linked to whom.
A random network is a network whose connections between the actors happen at random. In random network, arranged links between individuals are random, so that each pair has an equal probability to become connected (Fleming et al., 2007; M’Chirgui, 2004). Random networks require two assumptions; first, the size of the network is unchanged as time elapses. That means the network does not grow over time. Second, the probability of connection between any two nodes is equal for all nodes. That is, a connection happens at random with no preference whatsoever for any network member. As a result, in a random network, the number of connections each node has follows a Poisson distribution (Newman, 2003).
In the study of graphs and networks, the degree of a node in a network is the number of connections it has to other nodes and the degree distribution is the probability distribution of these degrees over the whole network. In statistics, a power law is a functional relationship between two quantities, where a relative change in one quantity results in a proportional relative change in the other quantity, independent of the initial size of those quantities: one quantity varies as a power of another. A scale-free network is a network whose degree distribution follows a power law, at least asymptotically. The key assumptions of random networks simply do not fasten on real-world networks (Yan & Assimakopoulos, 2009). Jeong (2003) explains that the random network topology is a rather over simplistic model.
Although physicists and mathematicians are first developers of these topological models, these models gain increasing attention in social science (Granovetter, 2003) and management research (Schilling & Phelps, 2007). Yan and Assimakopoulos (2009) criticize that several commentators prove that a variety of networks are both small-world and scale-free networks, for example, the movie co-star networks (Watts & Strogatz, 1998), co-authorship networks (Newman, 2004), Internet discussion groups (Adamic et al., 2003; Ravid & Rafaeli, 2004) and airway transport networks (Guimerà et al., 2005).
Researchers differentiate configurational theory from contingency theory by its “holistic” view of organizations, which are conceived as “composed of tightly interdependent and mutually supportive elements such that the importance of each element can best be understood by making reference to the whole configuration” (Miller & Friesen, 1984).
Configuration theory aims to answer how should actors structure or form their organization to be effective. Meyer, Tsui, and Hinings (1993) study on the configurational approach in its various forms continues to be influential. Since the 1990s, researchers design their study of radical organizational change in different sectors such as health (Denis, Langley, & Cazale, 1996; Meyer, Brooks, & Goes, 1990), architecture (Pinnington & Morris, 2002), municipal government (Greenwood & Hinings, 1993), and the cement industry (Keck & Tushman, 1993) with respect to configurational theory. Some of the researchers extend its use to the study of radical change at the industry level (Meyer et al., 1990). The theory has three core assumptions. First, there is a relation between organizational performance and formal organizational arrangements that managers use to coordinate activities and exercise control over employee effort. That is why sometimes people perceive organizational arrangements as organizational design or organizational form. Second, there is no “one best way” of organizing. Structural-contingency theory also asserts this assumption. But configuration theory put much more attention on types and size of these contingencies and its nature. Mintzberg argues (1979) that “How many configurations do we need to describe all organizational structures?... With our nine parameters, that number would grow rather large.... But there is order in the world... a sense of union or harmony that grows out of the natural clustering of elements, whether they are stars, ants or the characteristics of organizations. (Mintzberg, 1979:300)”
Third, the appropriateness of organizational design is not only partly dependent upon contingencies, such as an organization's size, its technology, and the rate and predictability of environmental change (the same assumption as in structural contingency theory), but is also dependent upon social (institutional) processes of approval. An organization's performance is thus a function of the degree of “fit” with respect to its strategy, organizational design, functional contingencies, and institutional processes. This study examines the interaction of process and product innovation and network topologies with respect to assumptions of configurational theory. Within this paper researchers examine that innovation process in organizational design is not only partly dependent upon companies inside contingencies but also dependent upon the outside contingencies such as network topologies.
This study intends to explain whether product and process innovation require different network topologies. In network studies researchers should evaluate their actions not in isolation but with the expectation that the world react what they do. What are the underlying mechanisms that lead to such success or radical change? In order to understand the nature of the mechanisms of innovation efficiency that lead to a certain network, is it useful to look at the topology of the finally emerging network? Do the researchers create links totally random (networks), do they create following precise rules (regular networks), or is there a combination of randomness and certain rules present (complex networks as small worlds or scale-free networks)? In addition, networks are not only different in their structure, but they also behave differently depending on different topologies.
The main aims of this paper are: (a) to survey the recent literature on configurational theory and the analysis of network topology, (b) to provide insight into the implications of network topology on the creation of technological interweavement, (c) to explore the topology of network that affects technological process of innovation and its economic relevance and (d) to inquire overall network topology for product innovation or/and for process “innovation”.
Configurational theoryOrganizational configurations rely on clusters of organizational strategies, structures, and processes. Because of its multidimensional nature, configuration theory examines organizations as systemic and holistic view. The theory assumes that there is an ideal set of organizational contents for each set of strategic contents. These configurations are ideal because they represent complex unified concepts of multiple, interdependent, and mutually reinforcing organizational components. So that organizational and strategic coherence enables company to achieve superior performance (Fiss, 2007; Sarason & Tegarden, 2003; Vorhies & Morgan, 2003).
Ketchen, Thomas, and Snow (1993) indicate in their study that two major approaches exist in the strategic management literature defining organizational configuration: (1) inductive-driven configuration theory is based on the concept of strategic groups. This approach focuses on industry-specific configurations. (2) Deductive-driven configuration theory is based on theory-based predictions. Authors also conclude in their study that deductive-driven configurations show better performance than the inductive-driven configurations and the deductive approach allows prediction of the performance differences among configurations.
Among deductive-driven approaches there are two competing schools of thought linking environmental conditions and organizational configurations: (1) strategic choice and (2) organizational ecology. The strategic choice perspective suggests that managerial decisions about how an organization will respond to environmental conditions are important determinants of organizational outcomes. This perspective considers organizations as not only adaptive but also influent through their actions. Empirical researches show that according to the strategic choice perspective there are limited number of organizational configurations that are valid (Ketchen et al., 1993). Miles and Snow's (1978) theory of strategy, structure, and process identifies three ideal forms of organization: prospector, analyzer, and defender (Vorhies & Morgan, 2003) which differ primarily in terms of product-market strategy choices. Prospector strategic types proactively seek and exploit new market opportunities and often response to changing market trends. Prospectors are the creators of change in their markets. They aggressively compete on innovation by developing new offerings and pioneering new markets to gain first-mover advantages. Defender strategic types focus on maintaining safety of their position in existing product-markets. Defenders often compete through operations or quality-based investments that offer efficiency-related advantages in current products and markets. They rarely pioneer the development of new markets or products. Analyzer strategic types have characteristics of both defenders and prospectors. Analyzers balance a focus on safety of their position in existing core markets with incremental moves into new product markets. They follow the changes much more rapidly than do defenders and compete by balancing investments in creating differentiation-based advantages with operating efficiency (Delery & Doty, 1996; Doty, Glick, & Huber, 1993; Vorhies & Morgan, 2003).
Miller (1996) indicates particular dangers of strategies that are too simple or monolithic in his study. Strategies may provide too narrowly focused and too simple to match the complexity of its environment. The author also indicates that excessive configuration can lead companies to deliver resources to a particular activity or function; an intolerant culture can lead to ignorance or expel dissenters; a narrow set of hiring and promotion criteria and a highly specialized and rigid set of programs and routines can lead organization to lose its flexibility.
Resource-based view considers configuration of factors and relationships within organizational system as a way of creation of resources that provide valuable, rare, and inimitable and organized characteristics to utilize for company strategy (Black & Boal, 1994).
On the contrary of strategic choice, organizational ecology perspective suggests environment as the primary determinant of company performance. According to ecology perspective organizational environments consist of multiple niches—industries, for example—each of which provides both resources and restrictions to a population of organizations (Ketchen et al., 1993).
Implementation of configurationsConfiguration theory refers a multidimensional aspect and focusses on coherence of strategies, structures, and processes with company's dominant problems, operational environment, and strategic goals (Sarason & Tegarden, 2003). Because of multidimensional feature of configuration the task characteristic of functional organization needs to comply with the nature of the functional activities and the performing ways. In the literature there are three identified task characteristics: task complexity indicates extent of variability in activities and the degree that is easily operable; capabilities indicate the abilities of company enabling to perform common work routines; and work group interdependence indicates that the degree of workflows within the company and cooperation is necessary between teams in operating functional activities efficiently. The literature indicates that each strategic type requires different functional activities and functional organizations with different configurations of structural and task characteristics and it leads to competitive advantage of company (Vorhies & Morgan, 2003).
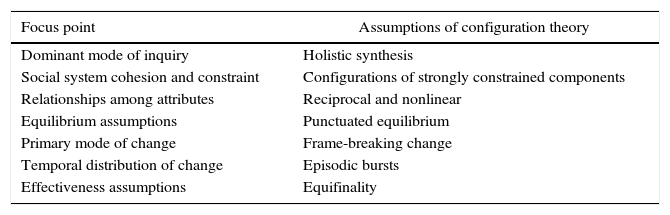
A high degree of configuration extends beyond aspects of competitive strategy and includes synergy, clarity of direction and coordination, difficulty of imitation, distinctive competence, commitment to valuable resources, speed, economy (Miller, 1996). This complexity and ambiguity lead to complex causality and nonlinear relationships in the context of organizational system. As a result relationships between variables expose asymmetric characteristics, and synergetic effects take place of traditional bivariate interaction effects. Furthermore, because of different initial conditions, a variety of different paths can take organization to same final state called equifinality. According to configuration theory different sets of context of strategies, structures, and processes arranged by organizations lead to different features and different outcomes. On the other hand it also means there are frequently multiple paths to achieve a given goal. Namely equifinality assumes that two or more organizational configurations can equally be effective in achieving high performance even with the same contingencies. Furthermore internally consistent concept leads to achieve goals even under different conditions. In other words organizations need internal consistency between environment, size, technology, and organization and performance targets (Fiss, 2007; Gresov & Drazin, 1997; Miller, 1996). Table 1 illustrates assumptions of configuration theory in terms of focus point.
Assumptions of configuration theory.
| Focus point | Assumptions of configuration theory |
|---|---|
| Dominant mode of inquiry | Holistic synthesis |
| Social system cohesion and constraint | Configurations of strongly constrained components |
| Relationships among attributes | Reciprocal and nonlinear |
| Equilibrium assumptions | Punctuated equilibrium |
| Primary mode of change | Frame-breaking change |
| Temporal distribution of change | Episodic bursts |
| Effectiveness assumptions | Equifinality |
Configuration theory considers organizations as social entity. It also explains organizational parts holistically, and tries to determine how effective and efficient order emerges from interaction of those parts as a whole. Nonlinearity represents variables may be convenient in one configuration, but may not be in another. Organizations have to alter between disequilibrium and equilibrium with discontinuous change in temporary stability periods. Configuration theory considers change as episodic. Changes have to emerge as time-dependent. According to configuration theory there are many ways to succeed in each type of setting. These settings accommodate effectiveness in terms of equifinality (Meyer et al., 1993).
Social networksNetworks are any collection of objects in which some pairs of these objects are connected by links. So many different types of relationships or connections can be defined for links. Organizational network theories are comprised of studies on the characteristics of relational edges of organizations (Burt, 1980; Freeman, 1977; Granovetter, 1973), social embeddedness, (Granovetter, 1985; Coleman, 1988), social capital (Adler & Kwon, 2002; Bourdieu & Wacquant, 1992; Burt, 1997; Coleman, 1988; Fukuyama, 1995). In addition to these, researchers obtain some basic perspectives by analyzing the relations of nodes in organizational networks using some organizational theories and behavioral concepts such as power (Brass, 1984), leadership (Brass & Krackhardt, 1999), work performance (Mehra, Kilduff, & Brass, 2001), acquisition of knowledge (Tsai, 2001), maximization of profit (Burt, 1992).
Network topologyTopological features such as degree distribution, clustering, and shortest path are three major concepts or pattern of connections which define each kind of these network models, whether they share the same number of nodes (n) and the same number of links n k/2 (k number of ties). Short average path length, L, indicates that the distance between any two nodes on the network is short. It takes only a few numbers of steps between two nodes. The clustering coefficient, C, provides measure of how well locally interconnected are the neighbors of any node. The maximum value of the clustering coefficient C is 1, corresponding to a fully connected network. Random networks have connected nodes at random with a fixed probability p, and the clustering coefficient decreases with the network size n as C=k/n. On the contrary, it remains constant for regular lattices. While the path length is a measure of the global structure of a network, the clustering coefficient is in contrast a measure of local network structure. The frequency distributions of node density (degrees) often follow power laws. A power law distribution is a statistical distribution in which one variable is proportional to a power of the other. When researchers plot on a log/log scale, distributed individual points are about a straight line. This means that there are a small number of nodes (the “hubs”) that have many neighbors and a large number of nodes that have only a few neighbors.
Two properties of many real world networks are that the distance between any pairs of nodes is relatively small while at the same time the level of transitivity or clustering is relatively high.
Erdös-Rényi random networks (ER random networks) have a low average path length, meaning that a path between a pair of nodes that involves only a few edges. In many real world networks, the small-world networks show this property. This notion is popular with the terms like the “six degrees of separation” between any two people, meaning they are typically connected by a chain of six or fewer edges in a social network graph where people are nodes and acquaintances linked by an edge in the graph.
A weakness of these topology models is, however, that they only model the existence or absence of a connection between any two nodes and assume the mutuality of ties, ignoring the ‘strength’ or ‘frequency’ of the connection between the actors. In other words, researchers determine all linkages as equally important. Many real-life networks, however, show diversity in the ‘strength’ or ‘significance’ of linkages. For example, in advice-seeking networks among Chinese software engineers, some pairs of engineers have more frequent discussions about technical problems than others (Assimakopoulos & Yan, 2006).
Small-world networkWatts and Strogatz (1998) assert a certain category of small-world networks that are a class of random graphs. They argue that two independent structural features, the clustering coefficient and average node-to-node distance (average shortest path length), are fundamental tools in describing graphs. Purely random graphs, built according to the Erdős-Rényi (ER) model, exhibit a small average shortest path length (varying typically as the logarithm of the number of nodes) along with a small clustering coefficient. Watts and Strogatz (1998) measure that in fact many real-world networks not only have a small average shortest path length, but also a clustering coefficient significantly higher than expectation of random chance.
Guare (1990) is the first researcher of the concept of “six degrees of separation”, the beginning idea of “small-world phenomenon”. He explains a play of this title and indicates there are only “six degrees of separation” between us and everyone else on this planet; interestingly, the name comes from an experiment Stanley Milgram did in the mid-sixties (Milgram, 1967). This experiment is a social psychological one and has at first glance nothing to do with mathematical definitions. In one description of the experiment (accounts of the exact details vary), Milgram asks people to send a letter to “a stockbroker” friend of his living in Boston, but he does not give them the address. To forward the letter, he asks them to send it only to someone they know personally and whom they think might be socially “closer” to the “stockbroker”. Most of the letters arrive, and surprisingly, take on average only six steps. The phrase “six degrees of separation” comes out of this experiment. The relevance to small world networks is that it makes the structure of ties—the social network—between people visible. Watts and Strogatz (1998) come with the concept of “small-world networks” to characterize networks in which nodes are linked to each other by only a few nodes in between (Watts, 1999; Watts & Strogatz, 1998). They (1998) integrate the ideas of clustering and path length by considering the extremes of regular and random graphs. Regular graphs, where each node connects to its k nearest neighbors, exhibit high clustering and long path length. For example, for k=4, your immediate neighbors directly connect both to you and one another. Distant neighbors, however, connect through a large number of indirect ties.
A small-world network is a type of mathematical graph in which most nodes are not neighbors of one another, but most nodes can be reached from every other by a small number of nodes. Travers and Milgram (1969) conduct several experiments about the small-world and other researchers examine the average path length for social networks of people in the United States. The research is groundbreaking in that it suggests that human society is a small-world-type network characterized by short path-lengths.
Specifically, a small-world network is a network where the typical distance L between two randomly chosen nodes (the number of steps required) grows proportionally to the logarithm of the number of nodes N in the network, that is (Watts & Strogatz, 1998): In the context of a social network, this results in the small world phenomenon of strangers linking by a mutual acquaintance. Many empirical graphs are well-modeled by small-world networks. Social networks such as the connectivity of the Facebook and Wikipedia are all exhibit small-world network characteristics.
Small-world networks tend to contain cliques, and near-cliques, meaning sub-networks which have connections between almost any two nodes within them. This follows from the defining property of a high clustering coefficient. The clustering coefficient is a measure of an “all-my-friends-know-each-other” property. This is sometimes described as the friends of my friends are my friends. More precisely, the clustering coefficient of a node is the ratio of existing links connecting a node's neighbors to each other to the maximum possible number of such links.
Secondly, most pairs of nodes will be connected by at least one short path. This follows from the defining property that the mean-shortest path length be small. When researchers are talking about social networks, nodes indicate people (or groups of people) and edges indicate kinds of social interaction. Sequence of nodes with the property that each consecutive pair in the sequence is connected by is important. Briefly, the sequence of edges that link the nodes constitutes the path in the “small-world phenomenon,” and social networks tend to have very short paths between essentially arbitrary pairs of people. A network is characterized as the extent to which the nodes connect to a certain node and to each other. A network compares the number of existing links in a neighborhood of a node with the number of all of the possible links in that neighborhood.
Several other properties may be evocation of small-world networks. Typically there is an over-abundance of hubs—nodes in the network with a high number of connections (known as high degree nodes). These hubs serve as the common connections mediating the short path lengths between other edges. By analogy, the small-world network of airline flights has a small mean-path length (i.e., between any two cities you are likely to have to take three or fewer flights) because many flights route through hub cities.
Random networksThe degree distribution is a fundamental tool for explaining properties of networks. If researchers have a complex real world network and calculate its degree-distribution, they explore to what extent the degree distribution captures certain aspects of the network. If they generate an ensemble of networks with the given degree distribution, they compare the properties of the ensemble with the original network. So they determine the ensembles properties and properties that depend on network structure other than the degree distribution.
When Watts and Strogatz (1998) fulfill the ideas of clustering and path length they examine the random graph that has random nodes, exhibiting low clustering and short path length. In a purely random graph someone is as likely to connect to its immediate neighbors as to distant neighbors. Hence, local neighbors can isolate and distant neighbors connect through only a few indirect ties. They assume that intermediate small-world regimes are between these two extremes. Fleming et al. (2007) determine that these are regular graphs with a small number of random connections actually. In these graphs, high clustering (relative to a random graph) and low path length (relative to a regular graph) coexist simultaneously.
Assimakopoulos and Yan (2006) explain the random networks which also show small-world network properties, i.e., a small average path length with respect to the size of the network. They exemplify a large community with millions of members and everybody has 20 connections randomly. A person can reach 20 members directly, and reach 20n (n power of 20) members through n intermediaries. When n is equal to 5, 20n is equal to 3,200,000. They claim that in such a community with more than three million members, on average, everybody can reach others by a chain of five ‘friends of friends’.
Without any restrictions, a random network model is very high-dimensional model. On the other side, one can make tractable random network models through various simplifications. The simplest random network model is the Erdös-Rényi random network (ER random network), where all edges are independent. Real world networks tend to have much broader degree distributions than in ER random networks, where all nodes have similar degrees. Thus, random network models that add minimal structure beyond a degree distribution can allow one to explore the consequences having a large spread of degrees, including hubs that have a much larger degree than most nodes.
Assimakopoulos and Yan (2006) explain the random networks that do not demonstrate clustering effects. All the connections happen randomly as a result the probability of a connection between a person's two friends to be friends is equal to those who are complete strangers. That is why the clustering coefficient in random networks is very low compared to small-world networks. For this reason, they determine the clustering coefficient as the key indicator which distinguishes random from small-world networks. To sum up a small-world network may have an average path length equivalent to a random network's, but it ought to demonstrate a much higher clustering coefficient than the random network.
Scale-free networksMany social networks do not satisfy the key assumptions of random networks. For example, membership does grow over time and linkages obviously do not form at random, but show preferential attachment in an Internet community. Individual members show their preference over some types of members who dominate specific attributes. As a result, they play active roles in the community (Yan & Assimakopoulos, 2009).
A common feature of real world networks is the presence of hubs, or a few nodes that are highly connected to other nodes in the network. The presence of hubs will give the degree distribution a long tail, indicating the presence of nodes with a much higher degree than most other nodes. Barabasi and Albert (1999) assert a new topology model and they discuss the issues above with random networks. They argue that Scale-free networks are a type of network with respect to the presence of large hubs. A scale-free network is one with a power-law degree distribution. The Barabási-Albert (BA) model is an algorithm for generating random scale-free networks using a preferential attachment mechanism. The vast majority of nodes have only few linkages and a small number of nodes play a significant role by connecting an extremely large number of nodes. Yan and Assimakopoulos (2009) assert this uneven distribution of networks that they often develop over time by adding new nodes and new linkages and the new nodes are more likely to connect to the nodes that already have developed a large number of linkages. These types of network are ‘scale-free network’. Scale-free networks are in natural and human-made systems, including the Internet, the World Wide Web, citation networks, and some social networks. Biological networks (Koch & Laurent, 1999), the World Wide Web (Broder et al., 2000), cellular, protein and metabolic networks (Jeong, Tombor, Albert, Oltvai, & Barabasi, 2000), e-mail networks (Ebel et al., 2002), and telecommunication networks (Schintler et al., 2003) are scale-free networks.
Discussion and conclusionsOrganizational researchers have adopted the formal models of network topology and assert that some kinds of network topology improve innovation. Researchers argue these arguments with respect to the influences of clustering, path length, and their interaction.
Davis, Yoo, and Baker (2003) show that while the individual actors who make up a system can change in terms of capabilities, political interests, technology, or strategy, the underlying organizational structure of a network topology such as small world continues to replicate, suggesting that a small-world network offers a high level of flexibility for organizing a diversity of actors.
Uzzi and Spiro (2005) focus on clustering and argue that it improves creativity in musical productions “because clustering promotes collaboration, resource pooling, and risk sharing.” These beneficial effects result from the increased trust that occurs within closed and embedded social contexts (Granovetter, 1985; Uzzi & Spiro, 2005). Uzzi and Spiro (2005) add that the effect of clustering is non-monotonic because extreme clustering promotes recirculation of redundant information.
Schilling and Phelps (2007) explain similar arguments for clustering coefficient. They explore that once information crosses between clusters it flows more easily within clusters. All the reviewed works on small worlds and innovation (Cowan & Jonard, 2004; Schilling & Phelps, 2007; Uzzi & Spiro, 2005; Verspagen & Duysters, 2004) argued that decreased path length should improve innovation because of easier and improved information transfer.
Newman (2004) explains co-authorship networks in biology, physics and mathematics using the medline, Physics E-Prints archive, and mathematical reviews databases respectively. He develops a work on the bibliometric properties of published paper archives and databases in accordance with the organizational and institutional properties of collaboration (De Solla Price, 1963), and analyses these networks using the standard tools of small worlds. He explains that all these networks have small world properties.
Fleming et al. (2007) agree with the path length argument and expect that decreased path length improves innovative productivity. Inventors profit from exposure to new information, although at some extreme they may face cognitive overload and be better off if they limited or filtered their exposure. Short path lengths expose inventors to new information because they connect them with different sources and nonlocal perspectives. Do short path lengths in a network indicate that distant information?
Cowan and Jonard (2004) develop an agent based model that demonstrates the benefit of decreased path length for the diffusion of innovations. Without this exposure to new information and perspectives from others, inventors will become insular and less creative.
Faster diffusion of innovations and the juxtaposition of diverse knowledge flows should increase the subsequent innovative productivity of regions whose largest components exhibit short average path length.
This study reviews the recent literature on configurational theory and asserts that the appropriateness of organizational design is not only partly dependent upon companies inside contingencies but also dependent upon the outside contingencies such as social and institutional ones. This study explains interrelatedness between network topology configurations, and product and process innovation. Thus it exposes the firms outside contingencies obviously. Focusing on these products and process innovation outside contingencies rather than inside contingencies also makes this study natural to understand and contributes towards configurational theory.