Buenas prácticas en metodología científica en salud
Más datosEn esta píldora le explicaremos qué opciones ofrece el diseño de un estudio clínico para controlar o ajustar por terceras variables. Le recomendamos además el vídeo docente en la página https://tinyurl.com/ybonn7hn1.
Confusión de efectosEn la píldora anterior2 explicamos que una característica (C) se considera una variable confusora en el contexto médico si cumple 2 criterios: está relacionada con la Evolución (E) del problema de salud de interés y su distribución es distinta en los grupos en estudio (T) tal y como se representa en la figura 1.
Como consecuencia, si el análisis de la relación entre T y E ignora la característica C; la estimación directa del tamaño del efecto TE, por ejemplo, el riesgo relativo, lleva combinado o «confundido» el efecto CE. Es lo que observamos en el estudio de Charig et al.3, sobre el efecto de 2 tratamientos de cálculos renales.
En cambio, si la característica C se distribuye de forma igual en los grupos de estudio, según el esquema de la figura 2, no se trata de una variable confusora, independientemente de que esté relacionada con E o no.
Solución del diseño para no confundir¿Cómo garantizar entonces que una característica que está relacionada con E, no llegue a ser una variable confusora de la relación entre T y E? Usar un diseño balanceado o, lo que es lo mismo: recoger los datos de tal manera que la distribución de la característica C sea la misma en los distintos grupos de intervención T. De esta manera, el efecto que pueda tener la característica sobre la enfermedad será el mismo en cada grupo de intervención T y, por ende, el posible efecto de la intervención T no puede ser confundido con el efecto de la condición C.
Veamos un ejemplo numérico. En el estudio de Charig et al., el tamaño del cálculo renal fue una variable confusora, ya que el éxito de una intervención depende del mismo y, además, la proporción de los pacientes con cálculos renales pequeños fue muy superior en el grupo de la nefrolitotomía percutánea. De ahí que en el total de la muestra observáramos mejores resultados en caso de este tratamiento, a pesar de que las probabilidades de éxito fueron mayores con la cirugía abierta tanto en los pacientes con cálculos pequeños como en los pacientes con cálculos grandes. La confusión de los efectos se habría podido evitar si se hubiera diseñado el estudio con la misma proporción de los pacientes con cálculos renales pequeños (y con grandes) en ambos grupos de intervención.
En el ejemplo a continuación (tabla 1) tenemos los mismos números que en el estudio original para el caso de los cálculos pequeños. En cambio, para los cálculos grandes los forzamos a simular un diseño balanceado y mantener la misma razón entre ambas intervenciones (uno con cirugía abiera por cada 2,89 con nefrolitotomía) que en los cálculos pequeños; aunque dejamos igual las probabilidades de éxito del estudio original.
Reconstrucción artificial sin relación TC, pero idénticas relaciones del tamaño C con la intervención CT. La estimación del posible efecto del tratamiento T sobre la evolución (E) no estará distorsionada por la variable C debido a que ella se distribuye de forma igual (ausencia de relación ET) en ambos grupos de tratamiento
| Cálculos pequeños (< 2 cm) | Cálculos grandes (≥ 2 cm) | |||||
|---|---|---|---|---|---|---|
| Éxito | Complicación | Total | Éxito | Complicación | Total | |
| Cirugía abierta | 81 | 6 | 87 | 42 | 16 | 58 |
| Nefrolitotomía | 234 | 36 | 270 | 123 | 57 | 180 |
Así, los riesgos de complicación siguen como en el estudio original: para nefrolitotomía 36/270 = 0,133 (13,3%) en cálculos pequeños; y 57/180 = 0,317 (31,7%) en cálculos grandes. Y lo mismo para la cirugía abierta, 6/87 = 0,069 (6,9%) y 16/58 = 0,276 (27,6%), respectivamente. Por ende, los riesgos relativos asociados a la nefrolitotomía percutánea serían iguales a 0,133/0,069 = 1,94 y 0,317/0,276 = 1,15, respectivamente.
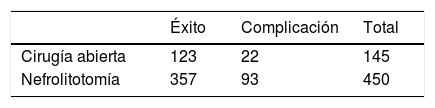
Ahora, si sumamos ambas tablas obtenemos la tabla 2. El riesgo relativo sería 93/450 / (22/145) = 1,36 (valor entre 1,15 y 1,94) lo que igualmente indicaría un riesgo de complicación mayor con nefrolitotomía.
Es decir, con un diseño balanceado se habrían podido evitar los resultados aparentemente contradictorios del estudio original.
ResumenEl diseño balanceado es una opción útil y eficiente para evitar la confusión de efectos en un estudio clínico. En nuestro ejemplo, si la intervención y el tamaño del cálculo renal son independientes, las estimaciones de sus efectos van cada una por su lado y no se «confunden». Llegamos a la misma conclusión —mayor riego de complicación con nefrolitotomía percutanea— al ajustar el análisis que cuando no lo hacemos.
La mejor manera para proveer al estudio de este balanceo es con un diseño experimental: asignar la intervención al azar. Por supuesto, siempre que sea posible por cuestiones logísticas y éticas —más viable en los tratamientos, de pretendidos efectos positivos; que en las exposiciones, de supuestos efectos negativos —. La asignación al azar logra que «cualquier» característica tenga la misma distribución poblacional en los distintos grupos de estudio y se evita que sea una variable confusora. Nótese que «cualquier» incluye a las variables desconocidas y también a las medidas con error. Aunque el azar garantiza la misma distribución a nivel poblacional, en una muestra podrían existir variaciones --que las leyes de probabilidad permiten anticipar-.
FinanciaciónPID2019-104830RB-I00 DOI (AEI): 10.13039 / 501,100,011,033: STATISTICAL METHODOLOGIES FOR CLINICAL AND OMICS DATA AND THEIR APPLICATIONS IN HEALTH SCIENCES (SAMANTHA) del Ministerio de Ciencia e Innovación.
Responsabilidades éticasNo implica pacientes y no requiere permiso ético.