Sesgo de selección

Cuentan que las sacerdotisas griegas enseñaban a sus visitantes los magníficos presentes de marineros que, tras rezar a los dioses, se habían salvado de terribles tormentas. Y decían: «¿Qué mayor evidencia quieren del poderío de los dioses?», a lo que cierto visitante escéptico respondió: «Bueno, me queda por saber cuántos marineros rezaron y no se salvaron». Es un caso típico del sesgo de selección. Tan frecuente que pequeñas variantes del mismo reciben diversos nombres: del superviviente, de respuesta, de Berkson¹, del collider, etc. Aquí los agrupamos todos en «sesgo de selección».

En esta píldora se lo explicamos y, mediante 2 ejemplos, qué consecuencias puede tener.

Una definición del sesgo de selección

Rothman (2012)² lo define de la siguiente manera:

«Sesgo de selección es un error sistemático que resulta del procedimiento empleado para seleccionar los sujetos y de los factores que influyen en la participación de un estudio».

Como consecuencia de este sesgo³, «(…) la asociación entre exposición y respuesta entre los sujetos seleccionados para el análisis difiere de la asociación entre todos aquellos elegibles».

Un primer ejemplo

Imaginémonos que en una ciudad de 10.000 personas se quiere estudiar el impacto de la calidad del aire sobre la salud de las personas y que fuera posible agrupar tanto la calidad del aire (buena/mala) en un barrio, como la salud (buena/mala) de sus habitantes en solamente 2 categorías. Sea la situación real (y desconocida) en la población la que muestra la tabla 1.

Tabla 1.

Ejemplo de relación entre una exposición (calidad del aire buena o mala) y la evolución (salud buena o mala). Datos inventados que representan la situación real, en toda la población

	Mala salud	Buena salud	Total
Calidad del aire mala	400	1.600	2.000
Calidad del aire buena	400	7.600	8.000

Si calculamos el riesgo relativo o cociente de probabilidades, vemos que vale (400/2.000)/(400/8.000), que significa que es 4 veces más probable que una persona que vive en un barrio con mala calidad del aire tenga problemas de salud que una persona que goza de buena calidad del aire.

Si invitáramos a un 10% de voluntarios, podría pasar que las personas con problemas de salud o de los barrios con mala calidad del aire tuvieran un gran interés en participar en tal estudio; supongamos que un 90% de las personas invitadas participaría. En cambio, una persona que goza de buena salud o que vive en un barrio con buena calidad del aire probablemente estaría menos dispuesta a participar en el estudio; supongamos que solamente la mitad de estas personas participaría, un 45%. La tabla de la encuesta resultante podría ser la que muestra la tabla 2.

Tabla 2.

Hipotética observación de la tabla 1 con sesgo de selección. Asume que solo un 45% de los casos con salud y calidad del aire buenas responden, mientras que lo hacen un 90% de las restantes combinaciones

	Mala salud	Buena salud	Total
Calidad del aire mala	400 · 0,1 · 0,9 = 36	1.600 · 0,1 · 0,9 = 144	180
Calidad del aire buena	400 · 0,1 · 0,9 = 36	7.600 · 0,1 · 0,45 = 342	378

Podemos ver que según los nuevos datos del estudio el cociente de probabilidades asociado a la mala calidad del aire es (36/180)/(36/378) aproximadamente 2, muy inferior a 4. En este ejemplo, el sesgo de selección causaría una infraestimación del valor real.

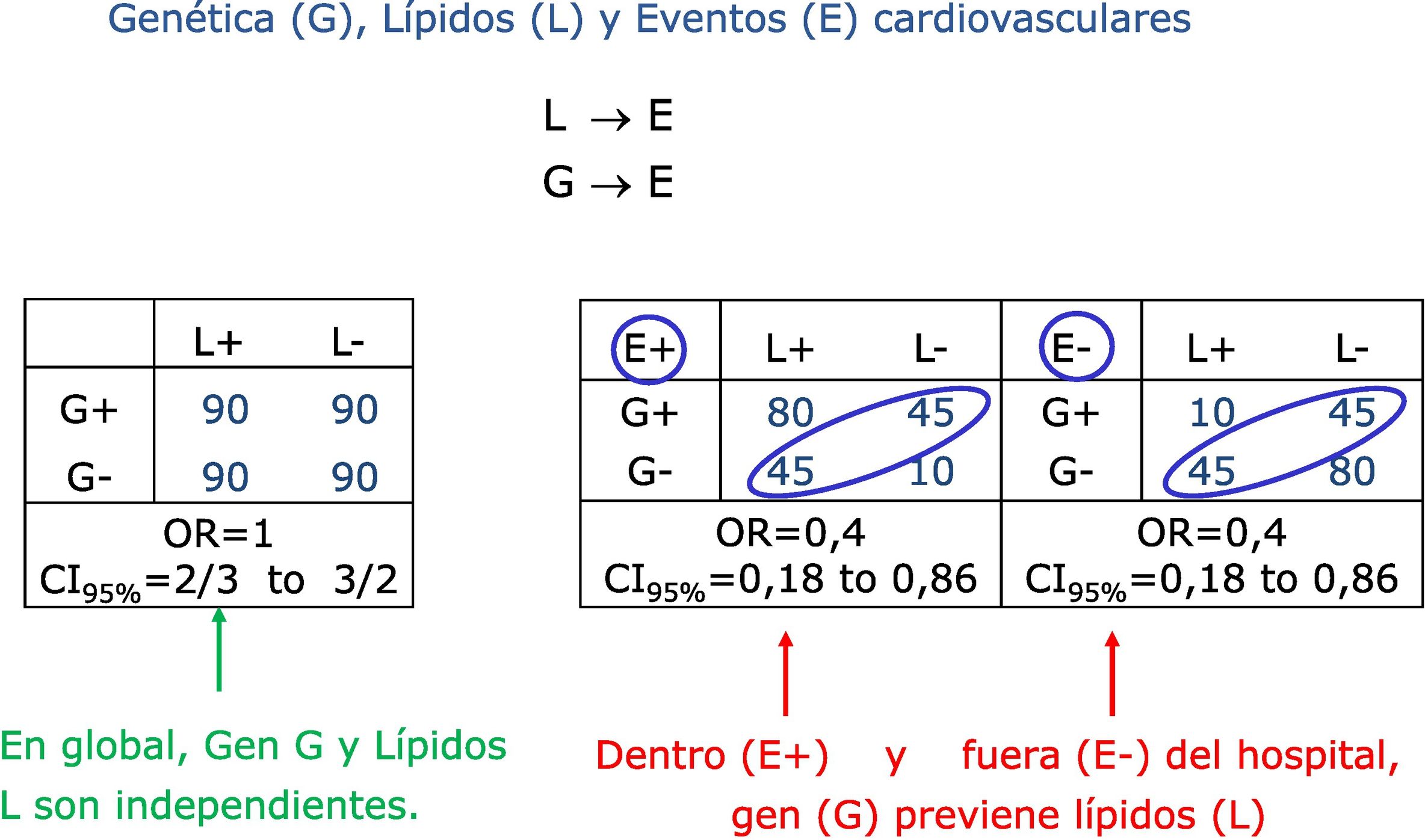
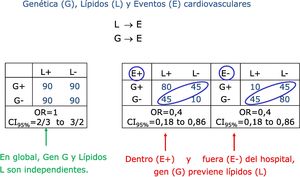
Un ejemplo clínico

Veamos ahora un posible ejemplo clínico⁴. Para habituarnos a otro estadístico, en lugar del cociente de probabilidades, trabajaremos ahora con el odds ratio (OR) o cociente de odds o cociente de apuestas. Supongamos que tanto los lípidos altos L como cierto gen G provocan eventos cardiovasculares E. Supongamos también que G y L no tienen relación, como muestra la tabla izquierda de la Figura 1. Ahora bien, los casos que presenten eventos, E +, irán al hospital (ver subtabla central), donde vemos una odds aproximada de 2 a 1 en la primera fila y de 4 a 1 en la segunda, resultando en un OR de 0,4, marcando una relación negativa. En el hospital, con pacientes que han sufrido un evento, existe relación negativa entre gen y lípidos, que podríamos sobre-interpretar como que el gen previene de los lípidos altos. Y lo mismo en aquellos que no van al hospital porque no presentan eventos (E-; ver subtabla derecha de la Figura 1). Pero esta relación no es real: en el conjunto de la población (tabla izquierda de la Figura 1), no existe ninguna relación entre gen y lípidos. Haber sobreseleccionado por una variable posterior que depende de las 2 previas hace aparecer una relación ficticia. El resultado es el sesgo de selección.

Figura 1.

Tanto gen G como lípidos altos L provocan eventos cardiovasculares E. A la izquierda, en toda la población, no hay relación entre gen y nivel de lípidos, variables previas a los eventos E. A la derecha, relación negativa entre G y L, variables previas, si sobre-seleccionamos según una variable posterior, presentar o no un evento cardiovascular -y terminar, o no, en un centro sanitario.

En resumen, el sesgo de selección revela, en un subgrupo de pacientes, una relación entre 2 variables que NO existe en el conjunto de toda la población. Aparece cuando se selecciona a los casos por otra variable posterior relacionada con ambas variables³. Por ejemplo, siempre es peligroso excluir casos de un ensayo clínico porque han dejado de seguir lo indicado: ¿Y si su decisión de interrumpir el tratamiento está relacionada con su respuesta al mismo?

Es importante añadir que el sesgo de selección puede causar tanto una sobre- como una infraestimación de la medida de interés. Este error de estimación no se puede observar, más bien se ha de sospechar por cómo se han seleccionado los sujetos de un estudio.

Financiación

PID2019-104830RB-I00 DOI (AEI): 10.13039 / 501100011033: STATISTICAL METHODOLOGIES FOR CLINICAL AND OMICS DATA AND THEIR APPLICATIONS IN HEALTH SCIENCES (SAMANTHA) del Ministerio de Ciencia e Innovación.

Responsabilidades éticas

No implica pacientes y no requiere permiso ético.